EricGrig
Я хотел бы начать предисловие со слов благодарности двум замечательным программистам из Одессы: Андрею Киперу (Lohica) и Тимуру Гиоргадзе (Luxoft), за независимую проверку полученных мною результатов, на начальном этапе исследования.
Предисловие к статье оказалось таким же длинным, как и сама статья. Семейный формат изложения на Хабре позволяет более свободно излагать свои мысли, но, судя по размеру, я достаточно свободно этим воспользовался. Хотелось написать кратко, а «получилась как всегда».
P.S. Я подумал, что членам Хабра-Сообщества будет интересно узнать, с какими трудностями я столкнулся при попытке опубликовать результаты исследования. Когда статья была подготовлена, я переформатировал ее в .tex формат согласно требованиям Journal of Artificial Intelligence Research (JAIR) и отправил туда. Там раньше были публикации на похожую тему. Особо можно выделить статью C. Gent, I.-P. Jefferson and P. Nightingale (2017) (Complexity of n-queens completion), в которой авторы доказали, что рассматриваемая проблема относится к множеству NP-Complete и рассказали о сложностях, с которыми столкнулись, в попытке решения этой задачи. В выводах авторы пишут: «For anybody who understands the rules of chess, n-Queens Completion may be one of the most natural NP-Complete problems of all» (Для всех кто понимает правила шахмат, задача n-Queens Completion может стать одним из самых естественных NP-Complete задач).
Через 10 дней мне пришел отказ из JAIR, с формулировкой: «статья не соответствует формату журнала», т.е. даже не взяли статью на рассмотрение. Такого ответа я не ожидал. Я полагал, что если журнал публикует статьи, в которых авторы делают вывод о большой сложности решения данной задачи и не приводят какого либо конкретного решения, то статья, в которой приводится эффективный алгоритм решения – будет, безусловно принята к рассмотрению. Однако, у редакции было свое мнение по этому поводу. (Полагаю, что там работают грамотные специалисты, и, скорее всего у них вызвало сомнение «наглое» названия статьи и все то, что там излагается. Подумали, «здесь, скорее всего какая-то ошибка и мягко послали меня подальше, ссылаясь на формат").
Мне предстояло выбрать другое рецензируемое периодическое научное издание по соответствующей тематике. Вот тут я столкнулся с суровой действительностью. Дело в том, что примерно 80% всех журналов являются платными: либо я должен платить журналу приличную сумму, чтобы статья была свободно доступна всем читателям, либо нужно им отдать статью как подарок «в бантике», и они будут взимать плату с каждого, кто захочет ознакомиться с данным исследованием. И первый и второй варианты для меня принципиально неприемлемы. Этот способ рэкета издателей я хорошо почувствовал на себя, когда пытался ознакомиться с некоторыми публикациями.
Очередным журналом, где исповедуется принцип свободного доступа к информации был «SMAI Journal of Computational Mathematics». Здесь тоже отказали с той же формулировкой, правда намного быстрее – через два дня.
Дальше был выбран журнал: «Discrete Mathematics & Theoretical Computer Science». Здесь требования простые, вначале необходимо опубликовать статью в arXiv.org, и лишь после этого зарегистрировать статью для рассмотрения. Ладно, будем соблюдать правила – подал статью в arXiv.org. Написали мне, что опубликуют статью через 8 часов. Однако этого не произошло ни через 8 часов, не через 8 дней. Статья был на «удержании» у менторов, и только через 9 дней ее опубликовали. Никаких претензий по форме и сути статьи не было. Думаю, как и в случае с JAIR, у менторов были сомнения в возможности «такое сделать и об этом написать». Спустя некоторое время, после исправления технических ошибок, статья была обновлена и в окончательном виде вышла в ночь на новый год.
Я вынужден подробно остановиться на этом, чтобы показать, что на этапе публикации результатов исследования могут быть проблемы, которые не поддаются логическому объяснению.
Далее следует статья, перевод которой на английский, был опубликован в (arXiv.org).
Среди различных вариантов формулировки n-Queens problem, рассматриваемая задача the n-Queens Completion занимает особое положение ввиду своей сложности. В своей работе (Gent at all (2017)) показали, что the n-Queens Completion problem относится к множеству NP-Complete (showed that n-Queens Completion is both NP-Complete and # P-Complete). Предполагается, что решение данной проблемы, возможно, откроет нам путь к решению некоторых других задач из множества NP-Complete.
Задача формулируется следующим образом. Имеется композиция из k ферзей, которые непротиворечиво распределены на шахматной доске размера n x n. Требуется доказать, что данная композиция может быть комплектована до полного решения, и привести хотя бы одно решение, либо доказать, что такого решения не существует. Здесь, под непротиворечивостью, мы понимаем такую композицию из k ферзей, для которой выполняются три условия задачи: в каждой строке, каждом столбце, а также на левой и правой диагоналях, проходящих через ячейку, где расположен ферзь, не расположено более одного ферзя. Задача в таком виде была впервые сформулирована Nauk (1850).
1.1 Определения
Здесь и далее, размер стороны шахматной доски мы будем обозначать символом n. Решение мы будем называть полным, если все n ферзей непротиворечиво расставлены на шахматной доске. Все остальные варианты решения, когда количество k правильно расставленных ферзей меньше n – мы будем называть композицией. Назовем композицию из k ферзей положительной, если она может быть комплектована до полного решения. Соответственно, композицию, которую невозможно комплектовать до полного решения – назовем отрицательной. В качестве аналога «шахматной доски» размера n x n, мы будем рассматривать также «матрицу решения» размера n x n. В качестве примера, все алгоритмы, разработанные для решения поставленной задачи, будут представлены на языке Matlab.
Исследование проводилось на основе компьютерного моделирования ( computational simulation). Чтобы проверить ту или иную гипотезу, мы проводили вычислительные эксперименты в широком диапазоне значений n= (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10000, 30000, 50000, 80000, 105, 3*105, 5*105, 106, 3*106, 5*106, 107, 3*107, 5*107, 8*107, 108) и, в зависимости от значения n, генерировали достаточно большие выборки для анализа. Назовем такой список «базовым списком значений n» для проведения вычислительных экспериментов. Все расчеты проводились на обычном компьютере. На момент сборки (начало 2013 года) это была достаточно удачная конфигурация: CPU – Intel Core i7-3820, 3.60 GH, RAM-32.0 GB, GPU- NVIDIA Ge Forse GTX 550 Ti, Disk device- ATA Intel SSD, SCSI, OS- 64-bit Operating system Windows 7 Professional. Назовем такой комплект просто — desktop-13.
Работа алгоритма начинается со считывания файла, который содержит одномерный массив данных о распределении произвольной композиции из k ферзей. Предполагается, что данные подготовлены следующим способом. Пусть имеется обнуленный массив Q( i )=0, i=(1,…,n), где индексы ячеек этого массива соответствуют индексам строк матрицы решения. Если в некоторой произвольной строке i матрицы решения располагается ферзь в позиции j, то выполняется присваивание Q( i )=j. Таким образом, размер композиции k, будет равен количеству ненулевых ячеек массива Q. (Например, Q=( 0, 0, 5, 0, 4, 0, 0, 3, 0, 0) означает, что рассматривается композиция из k=3 ферзей на матрице n=10, где ферзи расположены в 3-ей, 5-ой и 8-ой строках, соответственно в позициях: 5, 4, 3).
Для исследований нам нужен алгоритм, который позволил бы за короткое время определить правильность решения n-Queens problem. Контроль расположения ферзей в каждой строке и каждом столбце выполняется просто. Вопрос состоит в учете диагональных ограничений. Мы могли бы построить эффективный алгоритм такого учета, если бы нам удалось сопоставить каждой ячейке матрицы решения определенную ячейку некого контрольного вектора, который однозначно характеризовал бы влияние диагональных ограничений на рассматриваемую ячейку. Тогда, на основе того, свободна или занята ячейка контрольного вектора, можно судить о том, свободна или закрыта соответствующая ячейка матрицы решения. Такая идея впервые была использована в работе Sosic & Gu (1990) для учета и накопления числа конфликтных ситуаций между различными позициями ферзей. Подобная идея используется нами в представленном ниже алгоритме, но только для учета того, свободна или занята ячейка матрицы решения. На рисунке 1, в качестве примера приведена шахматная доска 8 х 8 над которой сверху расположена последовательность из 24 ячеек.
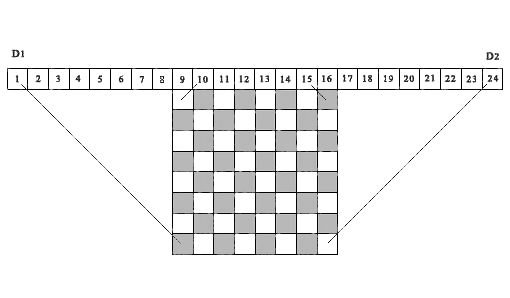
Рис. 1. Демонстрационный пример соответствия диагональных проекций ячеек матрицы, соответствующим ячейкам контрольных массивов D1 и D2, (n=8)
Рассмотрим первые 15 ячеек, как элементы контрольного вектора D1. Проекции всех левых диагоналей из любой ячейки матрицы решения попадают в одну из ячеек контрольного вектора D1. В самом деле, все такие проекции расположены внутри двух параллельных отрезков прямых, одна из которых соединяет ячейку матрицы (8,1) с первой ячейкой вектора D1, а вторая – ячейку матрицы (1,8) с 15-ой ячейкой контрольного вектора D1. Приведем аналогичное определение для правых диагональных проекций. Для этого, переместим вправо начало отсчета из ячейки 1 в ячейку 9, и рассмотрим последовательность из 16 ячеек, как элементы контрольного вектора D2 (на рисунке, это ячейки c 9-го по 24-ый).Проекции всех правых диагоналей из любой ячейки матрицы решения попадут в одну из ячеек этого контрольного вектора, начиная со 2-ой ячейки по 16-ую (на рисунке, с 10-ой по 24-ю). Здесь, все такие проекции, расположены между двумя отрезками параллельных прямых — отрезком, соединяющим ячейку (8,8) матрицы решения с ячейкой 16 вектора D2 (на рисунке ячейка 24), и отрезком, соединяющий ячейку (1,1) матрицы решения с ячейкой 2 контрольного вектора D2 (на рисунке ячейка 10). Проекции всех ячеек матрицы решения, лежащие на одной и той же левой диагонали, попадают в одну и ту же ячейку левого контрольного вектора D1, соответственно, проекции всех ячеек матрицы решения, лежащие на одной и той же правой диагонали, попадают в одну и ту же ячейку правого контрольного вектора D2. Таким образом, эти два контрольных вектора D1 и D2, позволяет вести полный контроль всех диагональных запретов для любой ячейки матрицы решения.
Важно отметить, что идею использования диагональных проекций на ячейки контрольных векторов для определения того, свободна или занята ячейка матрицы решения с координатами ( i ,j ), позже была реализована также в работе Richards (1997). В ней приводится один из быстрых рекурсивных алгоритмов поиска всех решений, основанный на операциях с битовой маской. Важное отличие состоит в том, что указанный алгоритм предназначен для последовательного поиска всех решений, начиная с первой строки матрицы решения – вниз, или с последней строки матрицы — вверх. Предложенный нами алгоритм основан на том условии, что выбор номера каждой строки для расположения ферзя должен быть произвольным. Для рассматриваемого алгоритма это имеет принципиальное значение. Отметим, что представленный выше рисунок 1, построен нами по аналогии с тем, что опубликован в данной работе.
Программа для проверки того, является ли правильным данное решение n-Queens problem, или является ли верным данная композиция из k ферзей, выглядит следующим образом.
1. Для контроля диагональных запретов, создадим два массива D1(1:n2) и D2(1:n2), где n2= 2*n, и массив B(1:n) для контроля занятости столбцов матрицы решения. Обнулим эти три массива.
2. Введем в рассмотрение счетчик числа правильно установленных ферзей ( totPos = 0). Последовательно, в цикле, начиная с первой строки, рассмотрим все предоставленные позиции ферзей. Если Q( i ) > 0, то на основе индекса строки i и индекса позиции ферзя в этой строке j = Q( i ) сформируем соответствующие индексы для контрольных массивов D1( r ) и D2( t ):
r = n + j – i
t = j + i
3. Если будут выполнены все условия ( D1( r ) = 0, D2( t ) = 0, B( j ) = 0 ), то это будет означать, что ячейка ( i, j ) свободна и не попадает в проекционную зону диагональных ограничений, сформированных ранее установленными ферзями. Расположение ферзя в такой позиции является правильным. Если, хотя бы одно из этих условий не выполняется, то выбор такой позиции будет ошибочным, соответственно и решение будет ошибочным.
4. Если решение правильное, то инкрементируем счетчик числа правильно установленных ферзей ( totPos=totPos+1), и закроем соответствующие ячейки контрольных массивов: (D1( r )=1, D2( t ) = 1, B( j )=1). Таким образом, мы закроем все ячейки столбца (j) и те ячейки матрицы решения, которые расположены вдоль левой и правой диагоналей, пересекающихся в ячейке ( i, j ).
5. Повторим процедуру проверки для всех оставшихся позиций.
Возможно, это один из самых быстрых алгоритмов оценки правильности решения n-Queens problem. Время проверки одного миллиона позиций для матрицы решения 106 x 106 на desktop-13 составляет 0.175 секунды, что примерно соответствует времени нажатия клавиши «Enter». Очевидно, что данный алгоритм по времени счета является линейным относительно n.
Общее. n-Queens Completion problem является классической не детерминированной задачей. Основная сложность ее решения связана с вопросом выбора индекса строки и индекса позиции в этой строке, в условиях, когда пространство состояния имеет огромные размеры. Когда ведется поиск всех возможных решений, то такой проблемы не возникает. Мы должны рассмотреть все допустимые ветви поиска в пространстве состояния и то, в какой последовательности они рассматриваются, не имеет значения. Однако, когда произвольную композицию из k ферзей необходимо комплектовать до полного решения, то в этом случае нужен алгоритм выбора индексов строк и столбцов, который адекватно воспринимает существующую композицию и быстрее других приводит к получению решения. В данном проекте, вопрос с выбором мы решали исходя из следующего общего положения – если мы не можем сформулировать условия, которые дают предпочтение какой-либо строке, или какой-либо позиции в этой строке по сравнению с другими, то используется алгоритм случайного отбора на основе равномерно распределенных случайных чисел. Подобный метод случайного отбора для решения задач, в которых пространство состояния имеет огромные размеры, является вполне естественным. Один из выпусков серии Proceedings of a DIMACS Workshop (1999) был полностью посвящен использованию метода случайного отбора при разработке алгоритмов решения сложных задач. Правильная реализация алгоритма случайного отбора может быть достаточно продуктивным решением, хотя, это является необходимым, но не достаточным условием завершения решения. Публикация Sosic and Gu (1990) является одним из первых исследований, где использовался алгоритм случайного отбора для решения n-Queens Problem. В основе рассмотренного ими алгоритма лежит достаточно простая и лаконичная идея. Пусть имеется последовательность чисел от 1 до n, которые случайно переставлены местами. Такой набор чисел имеет важное свойство. Состоит оно в том, что каким бы образом не были распределены эти числа на различных строках матрицы решения в качестве позиций ферзя (по одному числу на строку), всегда будут выполнены первые два правила в постановке задачи: в каждой строке и каждом столбце будет расположено не более одного ферзя. Однако, только часть, полученных таким образом позиций будут свободны от диагональных ограничений. Другая часть будет находиться в состоянии «конфликта» с ранее установленными ферзями. Для выхода из этой ситуации, авторы использовали метод сравнения и перестановки местами конфликтующих позиций для получения полного решения. В предложенном нами алгоритме невозможны конфликтные ситуации, так как на каждом шаге решения задачи, ферзь устанавливается в ячейку рассматриваемой строки только в том случае, если ячейка свободна.
4.1 Выбор модели для организации процедуры Back Tracking (BT)
В процессе поиска решения задачи, может наступить ситуация, когда последовательная цепочка решения приводит в тупик. Это «генетическое» свойство не детерминированных задач. В таком случае, нужно сделать возврат назад, на один из предыдущих шагов, восстановить состояние задачи в соответствии с этим уровнем и начинать снова поиск решения с этой позиции. Вопрос состоит в том, на какой из предыдущих уровней следует возвращаться и сколько таких уровней должно быть (под уровнем, мы понимаем некоторый шаг решения задачи с заданным количеством правильно установленных ферзей). Очевидно, что выбор уровня решения для возврата назад, является такой же актуальной задачей, как и выбор индекса строки или индекса позиции в этой строке. Поэтому, независимо от подхода к решению данной задачи, необходимо предварительно определить количество базовых уровней для возврата назад, а также механизм и условия возврата на один из этих уровней. В предложенном нами алгоритме, мы делим матрицу решения на три базовых уровня. Это точки возврата. Если, в результате решения, возникает тупиковая ситуация, то, в зависимости от параметров задачи, мы возвращаемся назад на один из этих трех базовых уровней. Первый базовый уровень (baseLevel1) соответствует состоянию, когда проверка данных рассматриваемой композиции завершена. Это начало работы программы. Значения следующих двух базовых уровней (baseLevel2 и baseLevel3) зависят от размера матрицы n. Эмпирическая зависимость этих базовых значений от размера матрицы решения была установлена на основе большого числа вычислительных экспериментов. Для более точного представления этой зависимости, мы разделили весь рассматриваемый интервал от 7 до 108 на две части. Пусть u=log(n), тогда, если n < 30 000, то
baseLevel2 = n — round(12.749568*u3 — 46.535838*u2 + 120.011829*u — 89.600272)
baseLevel3 = n — round(9.717958*u3 – 46.144187*u2 +101.296409*u – 50.669273)
иначе
baseLevel2 = n — round(-0.886344*u3 + 56.136743*u2 + 146.486415*u + 227.967782)
baseLevel3 = n — round(14.959815*u3 – 253.661725*u2 +1584.713376*u – 3060.691342)
4.2 Блочная структура
Алгоритм построен в виде последовательности из пяти блоков-событий, где каждое событие связано с выполнением определенной части решения задачи. Алгоритмы обработки в каждом блоке различаются друг от друга. Только три блока из этих пяти служат для формирования последовательной цепочки решения, а оставшиеся два блока являются подготовительными. Выбор номера блока, с которого начинаются расчеты, зависит от значения n и от результатов сравнения размера композиции k со значениями baseLeve2 и baseLevel3. Исключением является интервал значений n=(7,…,99), который можно назвать «турбулентной зоной» ввиду особенностей поведения алгоритма на этом участке. Для значений n=(7,…,49), независимо от размера композиции, после ввода и контроля данных, расчеты начинаются с 4-го блока. Для значений n=(50,…,99), в зависимости от размера композиции, расчеты начинаются либо со второго блока, либо с четвертого. Как было сказано выше, на каждом шаге решения задачи рассматриваются только те позиции в строке, которые не попадают в зону ограничений, созданных ранее установленными ферзями. Именно такие позиции называются свободными.
Опишем кратко, какие расчеты выполняются в каждом из этих пяти блоков программы.
4.3 Начало алгоритма
Производится ввод данных и проверка правильности композиции. На каждом шаге проверки производится изменение ячеек контрольных массивов. Проводится учет количества правильно установленных ферзей. Если в композиции нет ошибок, то решение продолжается, иначе выводится сообщение об ошибке. После завершения проверки, создаются копии основных массивов для их повторного использования на данном уровне. После этого управление передается в Блок-1.
4.4 Блок-1
Начало формирования ветви поиска. Рассматривается k ферзей, расположенных на шахматной доске в качестве стартовой позиции. Требуется продолжить комплектацию этой композиции и расположить ферзи на шахматной доске до тех пор, пока их общее количество не окажется равным baseLevel2. Алгоритм, который используется здесь, называется randSet & randSet. Связано это с тем, что здесь постоянно сравниваются два случайных списка индексов, в поисках пар, свободных от соответствующих диагональных ограничений. Для этого выполняются следующие действия:
a) формируются два списка: список индексов свободных строк и список индексов свободных столбцов;
b) производится случайная перестановка чисел в каждом из этих списков;
c) в цикле, каждая последовательная пара значений ( i, j ), где индекс ( i ) выбирается из списка индексов свободных строк, а индекс ( j ) — из списка индексов свободных столбцов, рассматривается как потенциальная позиция ферзя и проверяется, попадает ли данная позиция в проекционную зону диагональных исключений.
Если правило диагональных исключений не нарушается, то позиция считается верной, и в данную позицию располагается ферзь. После этого, производится инкрементация счетчика числа правильно установленных ферзей, и изменяются соответствующие ячейки контрольных массивов. Если позиция ( i, j ) попадает в зону диагональных ограничений, сформированных ранее установленными ферзями, то ничего не меняется и совершается переход к рассмотрению следующей пары значений.
Когда завершается цикл сравнения всех пар списка, то, на основе оставшихся индексов, которые оказались в зоне диагональных исключений, снова формируется список индексов оставшихся свободных строк и свободных столбцов, и данная процедура повторно выполняется до тех пор, пока общее число правильно расставленных ферзей (totPos) не окажется равным или превысит граничное значение baseLevel2. Как только выполняется это условие, управление передается в Блок-2. Если окажется, что в результате поиска решения, возникла такая ситуация, что из всего списка индексов оставшихся свободных строк и свободных столбцов, ни одна из пар не подходит для расположения ферзя, то в этом случае, восстанавливаются исходные значения контрольных массивов на основе ранее сформированных копий, и управление передается на начало Блока-1 для повторного счета.
4.5 Блок-2
Данный блок служит в качестве подготовительного этапа для перехода в Блок-3. На данном уровне количество оставшихся свободных строк (freeRows) значительно меньше n. Это позволяет перенести события из исходной матрицы размера n x n на матрицу меньшего размера L(1: freeRows, 1: freeRows). При этом, на основе информации об оставшихся свободных строках и свободных столбцах в исходной матрице решения, записываются нули в соответствующие ячейки массива L, показывающие, что данные ячейки свободны. При таком «проекционном» переходе сохраняется соответствие индексов строк и столбцов новой матрицы, с соответствующими индексами исходной матрицы. Важно отметить, что хотя, в процессе решения данной задачи, все события разворачиваются на исходной матрице размера n x n, и такая матрица является главной ареной действий, реально такая матрица не создается, а рассматриваются только контрольные массивы учета индексов строк A(1: n) и столбцов B(1: n) этой матрицы.
Наряду с массивом L, в данном блоке формируются также два рабочих массива rAr(1: freeRows) и tAr(1: freeRows), для сохранения соответствующих индексов контрольных массивов D1 и D2. Это связано с тем, что когда мы устанавливаем очередной ферзь в ячейку ( i, j ) исходной матрицы размера n x n, то после этого должны исключить ячейки массива L, попадающие в проекционную зону диагональных исключений исходного «большого» массива. Так как контроль диагональных ограничений производится только в пределах исходной матрицы размера n x n, то наличие рабочих массивов rAr и tAr позволяет сохранить соответствие и транслировать запрещенные ячейки в пределы массива L. Это значительно упрощает учет исключенных позиций.
После завершения подготовительной работы в данном блоке, создаются копии основных массивов для повторного использования на данном уровне, и управление передается в Блок-3.
4.6 Блок-3
В данном блоке продолжается формирование ветви поиска решения на основе данных, подготовленных в предыдущем блоке. Количество строк, в которых правильно установлены ферзи, равно или превышает значение baseLevel-2. Требуется продолжить комплектацию, пока количество установленных ферзей не окажется равным baseLevel-3. Здесь используется алгоритм поиска решения rand & rand, т.е. для формирования позиции ферзя, вместо списка свободных индексов, используются только два индекса, случайное значение индекса свободной строки и случайное значение индекса свободной позиции в этой строке. Данная процедура циклически повторяется до тех пор, пока общее число расставленных ферзей не окажется равным значению baseLevel-3. Как только выполняется данное условие, управление передается в Блок-4. Если в результате расчетов ветвь поиска окажется тупиковой, то данный участок формирования ветви поиска закрывается и производится возврат на начало Блока-3, откуда расчеты повторяются снова. Для этого восстанавливаются исходные значения всех контрольных массивов.
4.7 Блок-4
В данном блоке производится подготовка данных для передачи управления в Блок-5. К данному шагу, после выполнения процедуры в Блоке-3, количество свободных строк (nRow) стало еще меньше. Поэтому, здесь так же выгодно перевести события из массива большего размера в массив меньшего размера. Такой подход дает нам возможность гораздо быстрее определить необходимые характеристики для оставшихся строк, которые нам нужны на данном этапе. Особое значение имеет тот факт, что на основе такого массива, можно прогнозировать перспективность ветви поиска на много шагов вперед, не проводя расчеты до конца. Условие достаточно простое. Если окажется, что среди оставшихся свободных строк имеется строка, в которой нет свободной позиции, то рассматриваемая ветвь поиска закрывается и управление передается в один из блоков нижнего уровня. Подготовительные действия, выполняемые здесь, во многом аналогичны тому, что делалось в Блоке-2. На основе исходных индексов свободных строк и свободных столбцов формируется новый 2-мерный массив, нулевые значения которого соответствуют свободным позициям в исходной матрице решения. Кроме того, в данном блоке создается специальный массив E(1: nRow, 1: nRow), на основе которого можно определить, количество свободных позиций в оставшихся свободных строках, которые будут закрыты, если выбрать позицию ( i, j ) для установки ферзя в исходной матрице. Перед тем, как передать управление в Блок-5, выполняются следующие действия:
a) определяется сумма свободных позиций во всех оставшихся строках,
b) массив суммы свободных позиций, для рассматриваемых строк, сортируется в порядке возрастания,
c) если во всех оставшихся свободных строках имеются свободные позиции (т.е. минимальное значение в этом ранжированном списке отлично от 0), то управление передается в Блок-5.
Если окажется, что в какой либо из оставшихся строк нет свободной позиции, то восстанавливаются необходимые массивы на основе сохраненных копий, и, в зависимости от параметров задачи, управление передается на один из базовых уровней.
d) формируются резервные копии всех контрольных массивов для данного 4-го уровня.
4.8 Блок-5
Данный этап является завершающим, и здесь, формирование ветви поиска выполняется более «взвешенно» и «рационально». Это «последняя миля», осталось лишь небольшое число свободных строк. Но одновременно, это самый трудный участок. Все ошибки, которые потенциально могли быть допущены на предыдущих этапах формирования ветви поиска решения, в совокупности проявляются здесь – в виде отсутствия свободной позиции в строке.
Алгоритм данного блока выполняется на основе двух вложенных циклов, внутри которых выполняется третий цикл. Особенность третьего цикла состоит в том, что он может выполняться повторно, без изменения параметров двух внешних циклов. Это происходит в том случае, если сформированная ветвь поиска оказывается тупиковым. Число таких повторений не превышает граничное значение repeatBound, оптимальное значение которого было установлено на основе вычислительных экспериментов.
Индекс внешнего цикла связан с последовательным выбором индексов строк, оставшихся свободными после расчетов на третьем базовом уровне. Выполняется это на основе ранее ранжированного списка строк по сумме свободных позиций в строке. Выбор начинается со строки, с минимальным числом свободных позиций и далее, в последующих шагах – в порядке возрастания. Внутри данного цикла формируется второй цикл, индекс которого перебирает индексы всех свободных позиций в рассматриваемой строке. Назначение первого цикла состоит только в том, чтобы на данном уровне выбрать индекс одной из свободных строк. Соответственно, назначение второго цикла состоит только в том, чтобы в пределах рассматриваемой строки выбрать одну свободную позицию. Эти действия происходят только на третьем базовом уровне. После такого выбора, производится инкрементация числа установленных ферзей, и изменяются соответствующие ячейки всех контрольных массивов. Далее, управление передается внутрь вложенного (третьего) цикла, зоной активности которого являются уже все оставшиеся свободные строки. Внутри данного цикла, выбор индекса строки и выбор свободной позиции в этой строке, выполняются на основе следующих правил:
a)Выбор свободной строки. Рассматриваются все оставшиеся свободные строки, и в каждой строке определяется число свободных позиций. Выбирается та строка, у которой число свободных позиций минимально. Это позволяет минимизировать риски, связанные с возможностью исключения последних свободных позиций, в некоторых из оставшихся строк, у которых состояние по числу свободных позиций минимально и является критичным (правило минимального риска). Кстати, именно с учетом этого правила, индекс первого цикла в данном пятом блоке, начинается с последовательного отбора строк с минимальным значением числа свободных позиций в строке. Если на каком то шаге окажется, что две строки имеют одинаковое минимальное число свободных позиций, то случайно выбирается индекс одной из двух позиций, перечисленных первыми в ранжированном списке. Если число строк, имеющих одинаковое минимальное число свободных позиций, больше двух, то случайно выбирается индекс одной из трех позиций, перечисленных первыми в ранжированном списке.
b)Выбор свободной позиции в строке. Из списка всех свободных позиций в рассматриваемой строки, выбирается та, которая наносит минимальный ущерб свободным позициям во всех оставшихся строках. Это выполняется на основе ранее сформированного массива E. Под «минимальным ущербом», мы подразумеваем выбор такой позиции в данной строке, которая исключает наименьшее количество свободных позиций во всех оставшихся строках (правило минимального ущерба). Если окажется, что две или более свободных позиций в строке, имеют одинаковые минимальные значения по критерию ущерба, то случайно выбирается индекс одной из двух позиций, перечисленных первыми в списке. Выбор позиции, которая исключает минимальное число свободных позиций в оставшихся строках, минимизирует «ущерб», связанный с расположением ферзя в данной позиции. Использование обоих этих правил, позволяет более рационально использовать ресурсы на каждом шаге формирования ветви поиска. Это в значительной степени уменьшает риски и повышает вероятность комплектации произвольной композиции до полного решения, если рассматриваемая композиция имеет решение. Если на каком-то шаге решения окажется, что в одной из оставшихся для рассмотрения строк, отсутствуют свободные позиции, то данная ветвь поиска закрывается. В этом случае, на основе резервных копий восстанавливаются все контрольные массивы, и если счетчик числа повторений не превышает граничное значение repeatBound, то без изменения индексов первого и второго внешних циклов, вновь повторяется работа третьего вложенного цикла. Это связано с тем, что в тех случаях, когда совпадали минимальные значения соответствующих критериев, мы производили случайный отбор. Повторное формирование ветви поиска на одних и тех же условиях базового уровня, позволяет более эффективно использовать «стартовые ресурсы», предоставленные на данном уровне. Число повторных запусков третьего вложенного цикла ограничено, и при превышении граничного значения, работа этого цикла прерывается. После этого, восстанавливаются значения контрольных массивов, и управление передается в цикл третьего базового уровня для перехода на следующее значение индекса. Данная процедура циклически повторяется до тех пор, пока не будет получено полное решение, либо не окажется, что мы использовали все свободные строки и все свободные позиции в этих строках на данном базовом уровне. В этом случае, в зависимости от общего количества повторных вычислений на различных базовых уровнях, и с учетом размера матрицы решения и размера композиции, происходит возврат на один из нижних уровней для повторного выполнения расчетов, либо выносится суждение о том, что рассматриваемая композиция не может быть комплектована до полного решения. В программе, с целью ограничения общего времени счета, принято, что процедура Back Tracking, независимо от того, на какой из предыдущих уровней совершается возврат, может быть выполнена не более totSimBound раз. Это граничное значение выбрано на основе вычислительных экспериментов для различных значений n.
Эффективность алгоритма randSet & randSet. Для анализа возможностей данного алгоритма был проведен вычислительный эксперимент, который состоял в том, чтобы на основе модели randSet & randSet расположить ферзи в матрице решения до тех пор, пока существует такая возможность. Как только ветвь поиска доходила до тупика, или было получено полное решение, фиксировался размер композиции, время решения, и испытание повторялось снова. Вычислительные эксперименты проводились для всего базового списка значений n. Количество повторных испытаний для значений n= (30, 40,… ,90, 100, 200, 300, 500, 800, 1000) было равно одному миллиону, для остальных значений, количество испытаний, с ростом n, постепенно уменьшалось от 100000 до 100. Анализ результатов вычислительных экспериментов позволяет делать следующие выводы:
a) В результате работы только первого цикла процедуры randSet & randSet в среднем оказываются правильно расставленными около 60% всех ферзей. Для n=100, число правильно расставленных ферзей составляет 60.05%. С увеличением значения n, эта величина постепенно уменьшается, и, для n=107 составляет 59.97%.
b) Гистограмма распределения значений длины полученных композиций, имеет одинаковый вид, независимо от размера матрицы решения n. Причем все они имеют характерную особенность – левая часть распределения (до модального значения) отличается от правой части. На рисунке 2, в качестве примера, представлена соответствующая гистограмма для

Рис. 2. Гистограмма распределения решений различной длины для модели randSet & randSet (n=100, размер выборки= 106).
n=100. Создается впечатление, будто гистограмма собрана из распределения частот двух разных событий, так как частоты наступления событий в левой и правой частях распределения – различается. Для описания данного распределения, скорее всего, подойдет использование двух функций плотности нормального распределения, одна из которых охватывает интервал до модального значения, другая – интервал после модального значения.
c) Среднее значение количества ферзей (qMean), которые можно установить в матрице решения на основе данного алгоритма, увеличивается с ростом значения n. Как видно из рисунка 3, где представлен график зависимости отношения qMean/n от размера матрицы n, с увеличением размера матрицы это отношение увеличивается. Например,

Рис. 3. Зависимость отношения qMean/n от значения n для различных размеров матрицы решения. Модель – randSet & randSet, qMean – среднее значение длины решения.
если для матрицы размера 100х100 алгоритм выбора позиций randSet & randSet позволяет «без остановки» расставить ферзи в среднем на 89 строках, то уже для матрицы 1000х1000, количество таких строк увеличивается в среднем до 967.
d) На основе алгоритма randSet & randSet можно получить полное решение, однако «продуктивность» такого подхода является крайне низкой. Как видно из рисунка 4, для
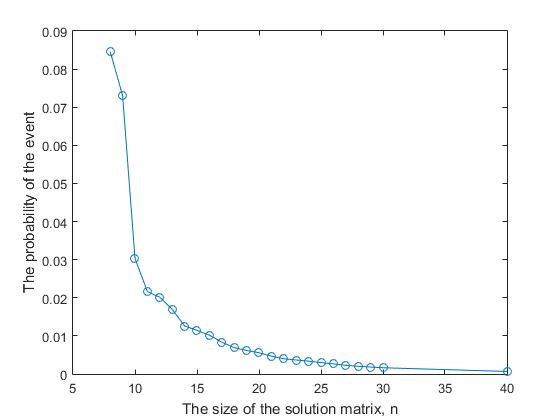
Рис. 4. Уменьшение вероятности получения полного решения в модели randSet & randSet с увеличением значения n.
значения n=7 вероятность получения полного решения составляет 0.057. Далее, с увеличением значения n вероятность получения полного решения быстро уменьшается, асимптотически приближаясь к нулю. Начиная со значения n = 48, вероятность получения полного решения имеет порядок 10-6. После порогового значения n=70, для последующих значений n не было получено ни одного полного решения (при числе испытаний равном одному миллиону).
e) Модель randSet & randSet формирует ветви поиска с очень высокой скоростью. Для n=1000 среднее время получения композиции составляет 0.0015 секунд. При этом средняя длина композиций составляет 967. Соответственно, для n=106 среднее время составляет 2.6754 секунды при средней длине композиций 999793.
f) За исключением небольшого интервала n<=70, когда модель randSet & randSet в очень редких случаях может привести к получению полного решения, во всех остальных случаях ветвь решения завершается формированием отрицательной композиции, которая не может быть комплектована до полного решения. Таким образом, алгоритм randSet & randSet имеет важное преимущество – высокую скорость формирования ветви поиска, и существенный недостаток, состоящий в том, что если размер композиции превышает некоторое пороговое значение, то данный алгоритм приводит к формированию композиций, которые не могут быть комплектованы до полного решения. Чтобы преодолеть этот недостаток, мы останавливаем формирование ветви поиска, при достижении порогового значения baseLevel-2.
Эффективность алгоритма rand & rand. Чтобы определить возможности алгоритма rand & rand, было проведено достаточно подробное компьютерное моделирование для базового списка значений n. Как и в случае модели randSet & randSet, число повторных испытаний в большинстве случаев было равно одному миллиону. Для остальных значений, количество испытаний постепенно уменьшалось от 100000 до 100.
В основе обоих алгоритмов лежит принцип случайного отбора. Поэтому следовало ожидать, что выводы, полученные здесь, в основном будут идентичны выводам, сформулированным для модели randSet & randSet. Однако, между ними имеется принципиальное различие, и состоит оно в следующем:
a) модель rand & rand работает не так «жёстко» как модель randSet & randSet. Если говорить о некотором «индексе рационального использования предоставленных возможностей», то модель rand & rand на каждом шаге использует ресурсы более рационально. Это приводит к тому, что, например, при n=30, вероятность получения полного решения 0.00170 в данной модели в 15 раз больше, чем аналогичная величина 0.00011 для модели randSet & randSet. Кроме того, здесь, вплоть до порогового значения n=370 сохраняется вероятность получения хотя бы одного полного решения при проведении одного миллиона испытаний. После этого порогового значения, для последующих значений n при числе испытаний равном одному миллиону, на основе модели rand & rand не было получено ни одного полного решения.
b) данный алгоритм работает намного медленнее, чем алгоритм randSet & randSet. Если для n=1000 провести генерацию композиции размером 967, то среднее время получения одной композиции составит 0.0497 секунд, что в 33 больше соответствующего значения 0.0015 для модели randSet & randSet.
Причина различий двух близких по сути методов случайного отбора связана с тем, что в модели randSet & randSet, с целью ускорения расчетов, на каждом шаге не проводится случайный отбор из оставшегося списка. Вместо этого производится последовательный отбор пары индексов из двух списков, элементы которого были случайно переставлены. Такой отбор является случайным не в полной мере, однако хорошо вписывается в логику задачи и позволяет быстро считать.
Чтобы визуально продемонстрировать работу алгоритма rand & rand, был проведен следующий эксперимент:
a) Для шахматной доски размером 100х100, после каждого шага расположения ферзя в какой-либо строке, определялось количество свободных позиций в каждой из оставшихся свободных строк. Таким образом, после каждого шага решения задачи мы получали список свободных строк и соответствующий список числа свободных позиций в этих строках. Это дало возможность построить график, где по оси абсцисс отложены индексы столбцов рассматриваемой матрицы, а по оси ординат – количество оставшихся свободных позиций. Для сравнения, расчеты проводились также и для модели последовательного отбора позиций. Под последовательным отбором подразумевается следующее. Рассматривается первая строка, в которой отбирается первая по списку свободная позиция. Потом, рассматривается вторая строка, в которой также отбирается первая свободная позиция в списке и т.д. На рисунках 5 и 6
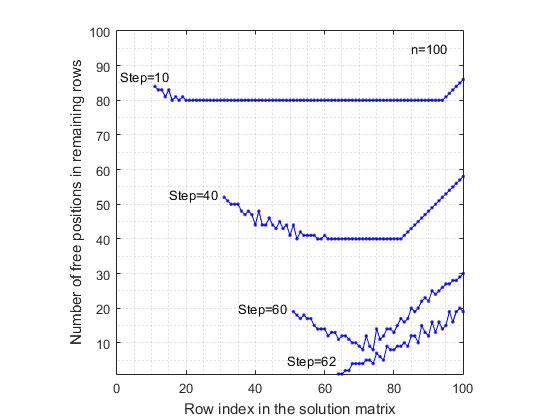
Рис. 5. Уменьшение количества свободных позиций в оставшихся свободных строках после расстановки ферзей. Последовательно-регулярный отбор позиций.
представлены результаты, которые соответствуют рассматриваемым моделям. Для наглядности, на графике представлены результаты только после шагов (10, 40, 60). Для модели последовательно отбора позиций последним приводится график после 62-го шага, так как ветвь поиска обрывается из-за отсутствия свободной позиции в 63-й строке. С другой стороны, в модели rand & rand, последним представлен график после 70-го шага расстановки ферзя, хотя здесь, среднее количество правильно расставленных ферзей достигает 89, что на 26 шагов больше чем в последовательной модели. «Странный» вид графиков в модели rand & rand связан с тем, что индекс строки отбирается случайным образом среди оставшихся свободных строк, и поэтому они случайно разбросаны по всей матрице решения. Из сравнения этих двух рисунков видно, что в последовательной модели выбора позиций, размах изменчивости числа свободных позиций выше, чем в модели rand & rand. Это связано с тем, что при регулярном отборе, диагональные ограничения неоднородно исключают свободные позиции в оставшихся строках, что приводит к тому, что в некоторых строках скорость сокращения количества свободных позиций оказывается выше, чем в остальных строках.

Рис. 6. Уменьшение количества свободных позиций в оставшихся свободных строках после расстановки ферзей. Модель отбора позиций – rand & rand.
В противоположность этому, при случайном отборе индекса свободной строки и индекса свободного столбца, позиции ферзя равномерно распределяются по «площади» матрицы решения, что уменьшает «среднюю» скорость сокращения числа свободных позиций в оставшихся строках. Таким образом, учитывая возможности алгоритма rand & rand, мы используем его в программе для продолжения формирования ветви поиска решения, пока не будет достигнуто значение базового уровня baseLevel-3.
Следует отметить, что если бы даже алгоритмы выбора (randSet & randSet, rand & rand) не были бы столь эффективными, нам бы все равно пришлось использовать какой либо иной метод случайного отбора при разработке алгоритма. Это обусловлено самой постановкой задачи n-Queens Completion problem. Если представить, что существует некий оптимальный алгоритм, который решает поставленную задачу, то на входе такой алгоритм всегда будет получать некий случайный набор индексов строк и столбцов. Каждый раз это будет новый случайный набор индексов строк и столбцов из огромного множества возможностей. Чтобы можно было «принять на вход» алгоритма такое многообразие случайных композиций сам алгоритм должен быть построен на основе случайного отбора. Соответствие должно быть как ключ к замку. Если мы построим алгоритм на этом принципе, то любая непротиворечивая композиция из k ферзей будет рассматриваться как начальная (стартовая) позиция в цикле поиска решений. И далее, цель будет состоять лишь только в том, чтобы продолжить формирование ветви поиска решения, пока не будет найдено решение для данной композиции, либо будет доказано, что такого решения не существует.
На начальном этапе поиска решения, когда количество свободных позиций в строках не критично, то выбор индекса свободной строки, или индекса позиции в этой строке, не является фатальным. Однако, на последней стадии, когда количество свободных позиций в некоторых строках равно 1 или 2, то в этом случае следует выбрать другой алгоритм отбора. На этом уровне, алгоритмы случайного отбора randSet & randSet и rand & rand, уже не будут работать.
Причину, почему алгоритмы случайного отбора не будут работать, можно объяснить на следующем простом примере. Пусть на некотором шаге решения задачи, для произвольного значения n, в оставшихся строках i1, i2, …, ik число свободных позиций (указано в скобках) равно: i1( 1 ), i2( 2 ), i3( 4 ), i4( 5 ), i5( 3 ), i6( 4 ) и т.д. Если выбрать случайным образом любую строку, но не строку i1, в которой осталась только одна свободная позиция, то это может привести к рисковой ситуации, когда диагональные запреты, связанные с расположением ферзя в отобранной строке, могут привести к закрытию единственной свободной позиции в строке i1, что приведет решение в тупик. Из всех строк i1, i2, …, ik наиболее уязвимым и чувствительным к выбору индекса строки является строка i1. В таких ситуациях, в первую очередь следует отобрать ту строку, состояние которой является наиболее критичным и создает риск для решения задачи. Поэтому, на последнем этапе решения задачи, на каждом шаге необходимо выбрать позицию строки на основе простого алгоритма минимального риска.
Рассмотрим для наглядности, в качестве примера, для матрицы размером 100 x 100, последний этап формирования некоторого реального решения, после 88-го шага. До завершения задачи осталось 12 свободных строк, для каждого из которых было найдено число свободных позиций (строки ранжированы в порядке возрастания числа свободных позиций): Шаг-89 — 25(1), 12(2), 22(2), 82(2), 88(2), 7(3), 64(3), 3(4), 76(4), 91(4), 4(5), 96(5) — указывается индекс свободной строки, а в скобках – число свободных позиций в этой строке. Согласно правилу минимального риска, на 89-ом шаге решения задачи, выбирается строка 25 и та одна свободная позиция, которая в ней имеется. В результате пересчета, у нас остается 11 свободных строк: Шаг-90 – 7(2), 12(2), 22(2), 82(2), 88(2), 3(3), 64(3), 76(3), 4(4), 91(4), 96(4). Как видим, число свободных позиций в первых пяти строках одинаково и равно 2. Поэтому случайно отбирается индекс одной из первых трех строк. В данном случае была отобрана 12-ая строка и та позиция из двух, оставшихся в этой строке, которая приводит к минимальному ущербу. Таким образом, на 91-ом шаге формирования решения у нас осталось 10 свободных строк: Шаг-91 – 22(1), 3(2), 7(2), 82(2), 88(2), 64(3), 76(3), 91(3), 4(4), 96(4). На данном шаге отбирается строка 22 и та одна свободная позиция, которая в ней имеется. Продолжая аналогичным образом, была сформирована следующая последовательность решений (Таблица 1). Индексы отобранных строк выделены жирным шрифтом.
В данном конкретном примере, в 11 случаях из 12, была ситуация, когда в списке оставшихся свободных строк была, как минимум, одна строка, в которой осталась только одна свободная позиция. Если бы мы не использовали правило минимального риска, то не смогли бы дойти до конца. Так как одно «неверное движение» в выборе индекса свободной строки, с большой вероятностью привело бы к уничтожению единственной свободной позиции, которая имелась в одной из оставшихся свободных строк. Именно это является причиной того, что при использовании только алгоритма randSet x randSet или rand x rand для получения полного решения, на последних этапах, решение уходит в тупик.
Следует отметить, что алгоритм минимального риска имеет простой житейский смысл, и часто используется при принятии решений. Например, врач в первую очередь оперирует того больного, состояние которого наиболее критично для жизни, аналогично, фермер, во время сильной засухи, пытаясь спасти урожай, в первую очередь поливают те участки, которые находятся в наиболее критическом состоянии, …
Для оценки эффективности работы алгоритма при различных значениях n, был поставлен достаточно длительный (по совокупному времени) вычислительный эксперимент. Вначале был разработан достаточно быстрый алгоритм формирования массивов решений nQueens Problem для произвольного значения n. Потом, на основе этой программы были сформированы большие выборки решений для базового списка значений n. Размеры полученных выборок решений nQueens Problem для различных значений n, соответственно были равны: (10)--1000, (20, 30, …, 90, 100, 200, 300, 500, 800, 1000, 3000, 5000,10000)--10000, (30000, 50000, 80000)--5000, (105, 3*105)--3000, (5*105, 8*105, 106)--1000, (3*106)--300, (5*106)--200, (10*106)--100, (30*106)--50, (50*106)--30, (80*106, 100*106)--20. Здесь, в скобках указывается список значений n, а через двойное тире — размер выборки полученных решений. После этого, на основе каждой выборки решений формировались случайные композиции произвольного размера. Например, для каждого из 10000 решений для n=1000, было сформировано по 100 случайных композиций произвольного размера. В результате была получена выборка из одного миллиона композиций. Так как любая композиция произвольного размера, сформированная на основе существующего решения, может быть комплектована до полного решения хотя бы один раз, то задача состояла в том, чтобы на основе алгоритма решения n-Queens Completion Problem, комплектовать каждую композицию из сформированной выборки до полного решения. Так как в рассматриваемом алгоритме на каждом шаге проверяется правильность расстановки ферзя на шахматной доске, то здесь, в принципе, не могут быть False Positive решения (т.е. неверные решения, которые мы ошибочно считаем правильными). Однако, могут быть False Negative решения — в том случае, если какая либо композиция, сформированная на основе существующего решения, не будет комплектована программой до полного решения (хотя, мы знаем, что все композиции имеют решение). Проводя вычислительный эксперимент в таком широком диапазоне значений n, мы перед собой ставили следующие цели:
a) определить временную сложность работы алгоритма,
b) определить вероятность появления False Negative решений при различных значениях n,
c) определить частоту, с которой используется процедура Back Tracking при различных значениях n.
Результаты такого вычислительного эксперимента представлены в таблице 2.
Общий вывод, который можно сделать на основе полученных результатов, состоит в следующем:
a) Алгоритм работает достаточно быстро. Например, среднее время комплектации произвольной композиции для шахматной доски размером 1000 x 1000, полученное на основе одного миллиона вычислительных экспериментов, составляет 0.062157 секунды. Это означает, что если композиция имеет решение, то оно будет найдено сразу, после нажатия клавиши «Enter». Среднее время комплектации произвольной композиции, для всех значений n, в интервале от 7 до 30000, не превышает одной секунды.
b) В каждой выборке, имеется приблизительно до 10% композиций, для комплектации которых требуется намного больше времени. Такие композиции формируют длинный правый хвост в гистограмме распределения. Если исключить эти 10% композиций и провести расчеты для оставшихся 90% решений, то время счета (t90mean), окажется намного меньше. Например, для шахматной доски 1000 x 1000, среднее время счета будет равно 0.027727 секунды, что в 2.24 раза меньше среднего значения времени, полученной на основе всей выборки.
c) Для значений n≤800, в выборке композиций встречались такие, которые не удалось комплектовать до полного решения. Это False Negative решения. В пределах заданного в программе лимита, допускающего выполнение процедуры Back Tracking до 1000 раз, алгоритму не удалось комплектовать эти композиции. Они ошибочно были классифицированы как отрицательные композиции, т.е. такие, которые не имеют решение. Количество таких False Negative решений незначительно, и их доля в выборке меньше 0.0001. Далее, при увеличении значения n, доля False Negative решений уменьшается. Для всех значений n>800, в данной серии вычислительных экспериментов, не было ни одного случая False Negative решения. Однако очевидно, что если многократно увеличить размер выборки, то не исключается возможность появления False Negative решения, хотя вероятность такого события будет очень маленьким числом.
Временная сложность алгоритма. На рисунке 7 представлен график изменения среднего времени комплектации случайных композиций для различных значений n.
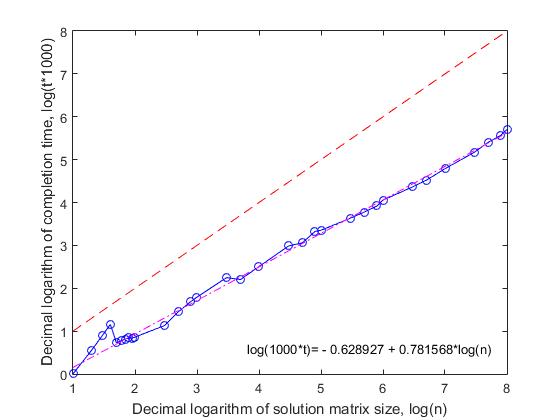
Рис. 7. Зависимость среднего времени комплектации (t) случайных композиций от размера (n ) матрицы решения.
По оси абсцисс отложен десятичный логарифм значения n, по оси ординат – логарифм, увеличенной в 1000 раз, среднего времени счета. Для наглядности, на рисунке также пунктиром указана линия диагонали данного квадранта. Видно, что время комплектации растет линейно, с увеличением значения n. На всем интервале значений n от 50 до 108 экспериментальные значения времени счета формируют прямую линию, которая с достаточно высокой корреляцией (R=0.9998) описывается уравнением линейной регрессии
log(1000*t) = — 0.628927 + 0.781568*log(n)
Небольшое отклонение от общей тенденции характерно только для значений n=(10, … 49), что связано с тем, что для решения задачи в этом диапазоне используется только пятый блок вычислений, алгоритм которого существенно отличается от работы алгоритмов первого и третьего блоков. В полученной зависимости линейный коэффициент (0.781568) меньше единицы, что приводит к тому, что с ростом значения n, линия регрессии и диагональ квадранта расходятся. Для того, чтобы наглядно объяснить причину такого расхождения вместо исходного времени, рассмотрим среднее время, которое необходимо для расположения одного ферзя на одной строке, т.е. разделим среднее время счета на значение n. Назовем такой показатель приведенным временем. Очевидно, что, если приведенное время не будет меняться с ростом значения n, то такое решение будет линейным ( O(n) ). Как видно из рисунка 8, где представлен график зависимости логарифма приведенного времени
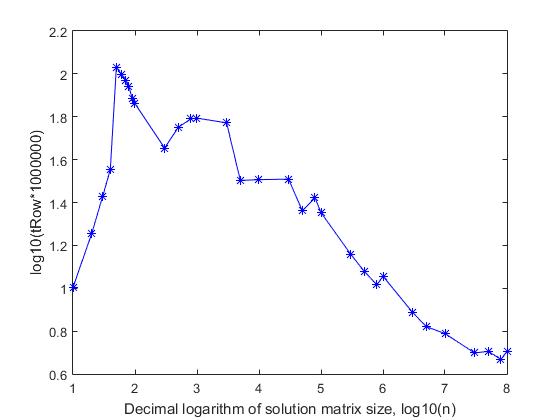
Рис. 8 Зависимость среднего времени (trow), которое необходимо для расположения ферзя на одной произвольной строке, от размера (n) матрицы решения.
(tRow), увеличенного в 106 раз, от логарифма размера матрицы решения, в интервале значений n от 50 до 108, приведенное время уменьшается с ростом значения n. Если приведенное время для n=50 составляет 10.7146*10-6 секунд, то соответствующее время для n= 108 уменьшается в 21 раз и составляет 0.5084*10-6 секунд. Такое поведение алгоритма, на первый взгляд кажется ошибочным, так как нет объективных причин, почему при малых значениях n алгоритм будет считать медленнее, чем при больших значениях. Однако, здесь ошибки нет, и это является объективным свойством данного алгоритма. Связано это с тем, что данный алгоритм является композицией из трех алгоритмов, которые работают с разной скоростью. Причем, количество строк, обрабатываемых каждым из этих алгоритмов, изменяется с ростом значения n. Именно по этой причине растет время счета на начальном интервале значений n=(10, 20, 30, 40), так как все расчеты на этом маленьком участке проводятся только на основе пятого блока процедур, который работает очень эффективно, но не так быстро, как первый блок процедур. Таким образом, учитывая, что время счета, необходимое для расположения ферзя на одной строке, уменьшается с увеличением размера шахматной доски, временную сложность данного алгоритма можно назвать убывающей – линейной.
Число случаев использования процедуры Back Tracking (BT). Во всех случаях вычислительного эксперимента, мы отслеживали число случаев использования процедуры BT при решении каждой задачи. Производилось накопительное суммирование всех случаев использования BT, не зависимо от того, на какой базовый уровень происходил возврат, в процессе поиска решения. Это дало нам возможность определить для каждой выборки, долю тех решений, в которых процедура BT ни разу не использовалась. На рисунке 9 представлен

Рис. 9. Доля решений в выборке, в которых процедура Back Tracking ни разу не использовалась
график, который показывает как изменяется доля случаев решения без применения процедуры BT (Zero Back Tracking ) с увеличением значения n. Видно, что в интервале значений n= ( 7,…,100000 ), число решений, в которых ни разу не используется процедура BT, превышает 35%. Причем, в интервале значений n= ( 320,…,22500 ), число таких случаев превышает 50%. Наиболее эффективные результаты были получены для шахматной доски размером 5000 x 5000, где, в выборке из 10000 композиций, в 61.92% случаях выполнялось «детерминированное» решение не детерминированной задачи, т.к. процедура BT в 61.92% случаях ни разу не использовалась. В оставшихся решениях, в 21.87% случаях процедура BT использовалась 1 раз, в 9.07% случаях — 2 раза, и в 3.77% случаях — 3 раза. В совокупности это составляет 96.63% случаев. Тот факт, что после значения n=5000, число случаев решения задачи комплектации без применения процедуры BT постепенно уменьшается, связан с выбранной моделью подбора граничных значений baseLevel2 и baseLevel3. Можно изменить данные параметры и добиться увеличения числа решений без применения процедуры BT. Однако, это приведет к увеличению времени счета, так как увеличится доля участия пятого блока в работе алгоритма.
Гистограмма распределения времени комплектации. На рисунке 10, для значения n=1000 представлена гистограмма распределения времени комплектации для одного миллиона решений. Не совсем обычный вид гистограммы распределения (который, скорее напоминает ночной силуэт высотных зданий) не связан с ошибкой в подборе длины или количества интервалов. Это естественное свойство работы данного алгоритма. Чтобы понять,

Рис. 10. Гистограмма времени комплектации композиций произвольных размеров. (n=1000; размер выборки = 1000000)
почему гистограмма имеет такую форму, рассмотрим распределение времени комплектации для композиций, которые имеют одинаковый размер. Для этого, в качестве примера, из исходной выборки отберем все композиции, размер которых равен 800. Таких композиций оказалось 998 в выборке из одного миллиона. На рисунке 11 представлена гистограмма распределения времени счета для этой выборки. Из рисунка видно, что распределение состоит из шести отдельных гистограмм, с убывающими размерами.

Рис. 11. Гистограмма времени комплектации композиций одинакового размера (k=800). (n=1000; размер выборки = 998)
Причиной того, почему время комплектации 998 композиций, в каждой из которых случайно распределены 800 ферзей, «кластеризуется» в 6 групп, является использование процедуры Back Tracking. Первая гистограмма на рисунке, с максимальным размером выборки, это те решения комплектации, где ни разу не использовалась процедура BT. Это группа самых быстрых решений. Вторая гистограмма, которая значительно меньше по размеру, чем первая, это те решения, в которых процедура BT использовалась только один раз. Поэтому время решения в данной группе чуть больше, чем в первой. Соответственно, в третьей группе процедура BT использовалась два раза, в четвертой – три раза и т.д., т.е. решения, в которых процедура BT использовалась многократно, выполнялись за более длительное время. Такие решения формируют длинный правый хвост искомого распределения.
False Negative решения. Если разделить все возможные композиции для произвольного значения n, на положительные и отрицательные, то среди положительных композиций найдутся такие, которые данный алгоритм может классифицировать как отрицательные. Это связано с тем, что в пределах установленных ограничений по параметрам поиска, алгоритму не удается найти верный путь для комплектации подобных композиций. Как показывают результаты экспериментов (Таблица 2), число таких случаев не превышает 0.0001 от размера выборки и величина этой ошибки уменьшается с ростом значения n. Кроме того, для всех значений n >800 не было ни одного случая False Negative решения. Даже увеличение размера выборки до одного миллиона для значения n=1000, не привело к появлению False Negative решений. Полученный результат позволяет нам формулировать следующее правило решения поставленной задачи: «Любая случайная композиция из k ферзей, которая непротиворечиво распределена на произвольной шахматной доске размером n x n, может быть комплектована до полного решения, либо будет принято решение, что данная композиция является отрицательной, и не может быть комплектована. Вероятность ошибки принятия такого решения не превышает значение 0.0001. С увеличением размера шахматной доски, вероятность принятия ошибочных решений уменьшается. Временная сложность работы алгоритма является линейной».
1. Представлен алгоритм, который, позволяет за линейное время решить задачу о комплектации до полного решения случайной композиции из k ферзей, непротиворечиво распределенных на шахматной доске произвольного размера n x n. При этом, для любой композиции из k ферзей (1≤ k < n) предоставляется решение, если оно есть, либо принимается решение, что данная композиция не может быть комплектована. Вероятность ошибки принятия такого решения не превышает 0.0001, и эта величина уменьшается с увеличением размера шахматной доски.
2. Работа данного алгоритма основана на использовании двух важных правил:
a) На завершающем этапе решения задачи, из всех оставшихся свободных строк, отбирается та, у которой число свободных позиций минимально (правило минимального риска). Это позволяет минимизировать риски, связанные с возможностью исключения последних свободных позиций, в некоторых из оставшихся строк.
b) Из всех свободных позиций в рассматриваемой строке, отбирается та позиция, которая наносит минимальный ущерб свободным позициям в оставшихся свободных строках (правило минимального ущерба). Под «минимальным ущербом», подразумевается выбор такой позиции в строке, которая исключает наименьшее количество свободных позиций во всех оставшихся свободных строках.
3. Установлено, что в результате работы данного алгоритма, среднее время, которое необходимо для расположения ферзя на одной строке, уменьшается с ростом значения n. Среднее время, необходимое для расположения ферзя на одной строке в случае, когда n равняется 108 в 21 раз меньше соответствующего времени для случая n=50.
4. Установлено, что в интервале значений n= ( 7,…,100000) число решений, в которых ни разу не используется процедура Back tracking, превышает 35%. Причем, в интервале значений n= ( 320,…,22500), число таких случаев превышает 50%, что говорит о высокой эффективности данного алгоритма.
5. Предложена модель организации процедуры Back Tracking, на основе разделения последовательности шагов решения на базовые уровни. Под уровнем подразумевается некоторый шаг решения с заданным количеством правильно расставленных ферзей. Приводятся регрессионные формулы для расчета значений второго и третьего базовых уровней в зависимости от n.
6. Приводятся результаты сравнительного анализа двух методов случайного отбора, которые получили название randSet & randSet и rand & rand. Установлено, что алгоритм randSet & randSet работает быстро, но грубо. Поэтому его применение ограничивается при достижении второго базового уровня. После этого используется алгоритм rand & rand, который выполняется не столь быстро, но более эффективно расставляет ферзи на шахматной доске.
7. Приводится эффективный алгоритм проверки правильности решения n-Queens Problem. Данная программа предназначена также для проверки правильности случайной композиции произвольного размера. Программа работает достаточно быстро. Например, время, необходимое для проверки решения, состоящего из 5 миллионов позиций, составляет 0.85 секунды.
1. Как было указано в начале статьи, исследования проводились в диапазоне значений n, от 7 до 100 миллионов. Однако, программа тестировалась в более широком диапазоне значений n, вплоть до одного миллиарда. Правда, в последнем случае пришлось слегка адаптировать программу, учитывая большие размеры массивов. Поэтому, если позволяет размер оперативной памяти, то можно проводить расчеты для больших значений n.
2. Значения показателей базового уровня, а также граничные значения числа повторений на различных уровнях, были оптимизированы для решения задачи в пределах всего диапазона исследований. Их можно изменить в пределах меньшего диапазона и добиться уменьшения времени счета. Важно, чтобы при этом не увеличить долю False Negative решений.
3. В этой статье я использовал время нажатия клавиши Enter как некую меру времени, для оценки того, насколько быстро работает алгоритм. Если результат появляется сразу после нажатия клавиши, то на уровне восприятия пользователя кажется, что программа работает «очень» быстро. Независимо от того, насколько быстро работает алгоритм, результат появится на экране не раньше, чем будет завершено нажатие клавиши. Поэтому мне показалось, что такая условная мера времени может служить пороговым уровнем для не строго сравнения скорости различных алгоритмов.
4. Философское … В ходе исследования было рассмотрено большое количество публикаций, связанных с решением не детерминированных задач. В большинстве случаев это были задачи, в которых необходимо было сделать выбор в большом пространстве состояний в условиях заданных ограничений. Сравнивая их, было интересно узнать, насколько далеко можно продвинуться в решении таких задач с использованием стандартного математического подхода. У меня сложилось впечатление, что только на основе определений, формулировке лемм и доказательстве теорем невозможно решить такие проблемы. Мне кажется, что для решения таких задачах необходимо использовать методы алгоритмической математики, используя компьютерное моделирование. Чтобы продемонстрировать обоснованность этого вывода, в качестве простого примера я подготовил для шахматной доски, размер которого составляет 109 х 109 две композиции одинакового размера, состоящие из 999 999 482 ферзей. Они подготовлены так, как описано в начале статьи, и представлены в виде двух файлов в формате .mat. Их можно загрузить по данной ссылке (Два тестовых файла). Файлы достаточно «тяжелые», размер каждого из них составляет около 3.97 Gb. В 999 997 976 строках (в 99.9998 % случаях) позиции ферзей в обеих композициях совпадают, и лишь в произвольных 1506 строках позиции ферзей различаются.
Чтобы комплектовать данные композиции до полного решения, нужно правильно расставить ферзи в оставшихся 518 свободных строках. Число возможных способов расстановки 518 ферзей в оставшихся свободных строках (с учетом только числа способов выбора свободной позиции в отобранной строке), составляет примерно 101466. Различие этих двух композиций состоит только в том, что одна из них является положительной и может быть комплектована до полного решения, а другая композиция является отрицательной – ее невозможно комплектовать до полного решения. Вопрос: «Можно ли на основе строгого математического подхода (т.е. без проведения алгоритмических вычислительных операций), определить, какая из этих двух композиций является положительной?» Если это невозможно решить, то можно считать, что высказанное суждение доказано методом от противного.
Хочу отметить, что каким бы не был подход к строго математическому решению данной задачи, здесь нужно определить статус 518*109 ячеек в оставшихся свободных строках. Для этого необходимо рассмотреть каждую позицию ранее установленных ферзей, а их почти один миллиард, чтобы установить ограничения, которые накладывает каждый установленный ферзь на свободные позиции в оставшихся 518 строках. Я не нашел «точку опоры», которая позволила бы выполнить эту работу лишь на основе строго математического подхода, без алгоритмических вычислений.
Я привел здесь минимальный пример, состоящий только из двух композиций. При необходимости, количество таких композиций можно увеличить.
Следует отметить, что на основе предложенного линейного алгоритма, слегка адаптированного для работы с композициями большого размера, задач о том, какая из двух тестовых композиций может быть комплектована до полного решения, выполняется на desktop-13, примерно за 4.5 минуты (без учета времени загрузки входных данных).
Заслуживает уважение действие профессоров, которые рекомендуют способным студентам сложные задачи для разработки и исследования. Это требует значительных усилий, но преодолев трудности, исследователь иначе смотрит на другие сложные задачи. Я подумал, что было бы полезно расширить варианты постановки n-Queens Problem для таких целей. Если посмотреть на одну и ту же задачу с разных позиций, то можно увидеть разные вещи. Ниже сформулированы некоторые из них.
1. Рассмотрим задачу расстановки n ферзей на прямоугольной «шахматной» доске размером n x m. Обозначим k = m — n. Пусть получено некоторое решение, и в каждой из n строк было расположено по одному ферзю. Исключим те позиции, где расположены ферзи из дальнейшего рассмотрения. Теперь в каждой строке осталась m-1 свободная позиция. В пределах оставшихся свободных позиций, снова найдем одно решение. Как и прежде, исключим из дальнейшего рассмотрения позиции, где расположены ферзи второго решения. Теперь в каждой строке осталось m-2 свободных позиций. Очевидно, что первое и второе решение по своим позициям ни в одной строке не пересекаются – они ортогональны. Требуется определить максимальное количество взаимно ортогональных решений для различных значений k. Если будет найдено n взаимно ортогональных решений для значения k=0, то тем самым будет построен королевский латинский квадрат (Queens Latin Square).
Замечание. В работе Grigoryan E. (2018) было показано, что для любого решения n-Queens Problem существует комплементарное решение, которое с ним не пересекается. Это означает, что для произвольного значения n, множество всех решений n-Queens Problem делится на два равных по размеру подмножества. Любое решение из второго подмножества является комплементарным решением соответствующего решения из первого подмножества. Правило достаточно простое, если Q1( i ) некоторое решение из первого множества, то соответствующее комплементарное решение Q2( i ) из второго подмножества определяется по формуле Q2( i ) = n+1 – Q1( i ), где i=(1,…,n). Именно это правило объясняет тот факт, что число всех решений n-Queens Problem, для произвольного значения n, всегда является четным числом. (Это правило позволяет сократить в два раза время расчета всех полных решений для произвольного размера n шахматной доски. Если обозначить через 2*k общее число всех решений, то значение k равно индексу в последовательном списке всех решений, когда Q( k ) + Q( k+1 ) = n+1 ).
2. В исходной постановке задачи n-Qeens Problem, после расположения ферзя в позицию ( i, j ), выполняются следующие действия:
a) исключаются все ячейки строки i и столбца j
b) исключаются все ячейки, которые расположены на линии левой и правой диагоналей, проходящих через ячейку ( i, j ).
Изменим условие b) в постановке задачи. Вместо исключения ячеек, воспользуемся переключением ячеек. Если ячейка, расположенная на линии левой или правой диагоналей свободна, то мы ее закроем, если ячейка закрыта – то мы ее откроем. Это облегчает возможность поиска решения. Однако, вместо квадратной матрицы n x n, будем рассматривать прямоугольную матрицу размером n x ( n – k ). Требуется, для заданного значения n, найти максимальное значение k, при котором можно получить не менее трех ортогональных решений. Как будет меняться значение k, с увеличением значения n?
3. Изменим некоторые условия в исходной постановке задачи n-Queens Problem. При расположении ферзя в позицию ( i, j ) на шахматной доске размером n x n:
a) исключим все ячейки в строке i,
b) если индекс j четное число, то:
b1) исключим ячейки в четных строках столбца j,
b2) исключим ячейки в четных строках, пересекающихся с левой и правой диагоналями, проходящими через ячейку ( i, j ),
с) Если индекс j нечетное число, то пункты b1) и b2) выполняются для ячеек, расположенных на нечетных строках.
3.1 Известно (Sloane-2016), что список значений всех решений nQueens Problem, для n=(8, 9, 10, 11, 12, 13, 14, 15, 16), соответственно составляет (92, 352, 724, 2680, 14200, 73712, 365596, 2279184, 14772512). Как изменится количество всех решений, если в постановке задачи стандартное условие диагональных исключений изменить на пункт b) или на пункт c)?
3.2 Известно Grigoryan (2018), что если определить частоту участия различных ячеек матрицы решения в формировании списка всех решений, то можно обнаружить, что между всеми ячейками существуют гармоничные отношения в виде вертикальной и горизонтальной симметрии соответствующих частот. Это означает, что если принять, что k<n/2, то частота ячеек k-ой строки будет идентична частотам ячеек строки n-k+1. Аналогично, частота ячеек k-го столбца будет идентична частотам ячеек столбца n-k+1. Вопрос: «Как изменятся эти гармоничные отношения в условиях поставленной задачи?»
4. Все клетки шахматной доски по своему цвету разделяются на два класса. Принято считать, что один цвет белый, другой – черный. Рассмотрим две шахматные доски и расположим одну из них на другую так, чтобы края полностью совпали. В результате получим «сэндвич» из двух шахматных досок, у которых расположение белых и черных клеток совпадают. Задача состоит в том, чтобы найти решения одновременно на двух досках, соблюдая следующие условия:
a) Если на одной из досок ферзь располагается на черной ячейке с индексами ( i, j ), то:
— на обеих досках исключаются все черные ячейки, которые встречаются на строке i и на столбце j,
— на обеих досках исключаются все черные ячейки, которые расположены вдоль левой и правой диагоналей, проходящих через ячейку ( i, j ).
b) Если на одной из досок ферзь располагается на белой ячейке с индексами ( i, j ), то выполняются все действия пункта a) только для белых ячеек.
5. Представим, что в матрице решения размером n x n, строки могут скользить друг относительно друга вправо или влево, с шагом в k клеток. Причем, если предыдущая строка была смещена, например, влево, то следующая строка должна быть смещена вправо, т.е. каждая следующая строка смещается в направлении противоположной смещению предыдущей строки. В результате такого построения получим прямоугольную матрицу размером n x (n+k), где в каждой строке будут исключены из рассмотрения k ячеек от начала строки или от конца. Задача состоит в том, чтобы для произвольного значения n, найти максимальное значение k, при котором существует хотя бы одно решение n-Queens Problem.
Рассмотреть вариант задачи, при котором смещение одной строки по отношению другой, является случайным числом в пределах от k1 до k2.
6. Одномерная формулировка nQueens Problem. Пусть, на полуоси отложены n отрезков произвольной длины, пронумерованных от 1 до n. Разделим каждый отрезок на n ячеек произвольного размера, и в пределах каждого отрезка, пронумеруем ячейки от 1 до n. Назовем такие ячейки открытыми. Требуется закрыть по одной ячейке на каждом отрезке, учитывая следующие ограничения:
а) Мы можем выбрать открытую ячейку с номером j из i-го сегмента, если:
D1 ( r ) = 0;
D2 ( t ) = 0;
где r = n + j – i, t = j + i, D1 и D2 — одномерные контрольные массивы, состоящие из 2n ячеек, которые были ранее обнулены.
б) После такого выбора будут закрыты сегмент i и ячейки с номером j во всех оставшихся свободных сегментах. Также необходимо закрыть соответствующие ячейки в контрольных массивах:
D1 ( r ) = 1;
D2 ( t ) = 1;
В такой постановке задача полностью идентична исходной. Представляет интерес постановка этой задачи с другими условиями ограничения. Например, если вместо формул:
r = n + j – i, t = j + i, ,
будут рассматриваться другие соотношения, которые функционально связывают индексы r и t с индексами (i, j) матрицы решений.
7. Формулировка задачи на основе урны с шарами (идентична предыдущей формулировке). Пусть имеется n урн, пронумерованных от 1 до n, и в каждой урне находится n шаров, также пронумерованных от 1 до n. Требуется из каждой урны отобрать по одному шару, учитывая следующие ограничения:
а) Мы можем выбрать шар с номером j из i-ой урны, если:
D1 (r ) = 0,
D2 ( t ) = 0,
где r = n + j – i, t = j + i, D1 и D2 — одномерные контрольные массивы, состоящие из 2n ячеек, которые были ранее обнулены.
б) После такого выбора будут закрыты урна i и шары с номером j во всех оставшихся свободных урнах. Также необходимо закрыть соответствующие ячейки в контрольных массивах:
D1 ( r ) = 1,
D2 ( t ) = 1.
В такой постановке задача полностью идентична исходной. Как и в предыдущем случае, представляет интерес постановка этой задачи с другими условиями, которые функционально связывают индексы r и t с индексами (i, j) матрицы решений.
8. Игра. Рассмотрим шахматную доску размером n x n. Вернем ферзям цвет, пусть одни ферзи имеют белый цвет, другие – черный. Так же вернем чередующийся белый и черный цвет клеткам шахматной доски, исходя из того, что клетка с индексом (1, n) должна быть белого цвета. Все клетки в начале игры считаются свободными. Первый ход делают белые ферзи. Игрок располагает ферзь в произвольную свободную клетку с индексами ( i, j ). Пусть это будет клетка белого цвета. В результате такого выбора закрываются:
a) все белые клетки строки i,
b) все белые клетки столбца j,
c) все белые клетки, которые лежат на левой и правой диагоналях, проходящих через клетку ( i, j ).
Если клетка ( i, j ) окажется черного цвета, то выполняются все пункты (a,b,c), и соответственно, закрываются все клетки черного цвета. Далее, ход выполняют черные, располагая ферзь в любую из оставшихся свободных клеток. После этого, аналогичным образом, закрываются клетки, как описано выше. Время на обдумывание очередного хода является фиксированной, и выбирается по согласованию сторон. Если в течение указанного времени, один из игроков не выполняет свой ход, то игра передается другому. Игра завершается, если оба игрока, один за другим, не выполнят свой ход за указанное время. Выигрывает тот, кто сможет расположить на доске больше ферзей.
9. О стабильности случайного отбора. Рассмотрим модель randSet & randSet. В результате сравнения n случайных пар индексов строки и столбца, на первом этапе цикла, удается установить ферзи в среднем на k*n строках. Значение k можно считать постоянной величиной, равной 0.6. Ее значение меняется от величины 0.605701 при n=10, и до 0.599777, при n=106, причем, с ростом значения n, дисперсия этой величины уменьшается. С чем связано такое «постоянство»? Почему, при случайном отборе индекса строки и индекса позиции ферзя в этой строке, на основе двух списков чисел, полученных на основе случайной перестановки чисел от 1 до n, удается непротиворечиво расположить ферзи (в среднем) на 60% строках?
10. Пусть размер шахматной доски равен n x n. На основе процедуры randSet & randSet расположим ферзи на шахматной доске до тех пор, пока ветвь поиска не достигнет тупика. Обозначим длину, полученной таким образом композиции, через k. Если, для заданного значения n повторить эту процедуру многократно, и построить гистограмму распределения значений k, то окажется, что изменение частот наступления событий до значения моды распределения, отличается от изменения частот наступления событий после этого значения. Если на основе модального значения разделить гистограмму на две части, то левая часть не будет совпадать с правой частью. Эта закономерность характерна для любого значения n. Почему после перехода длины композиции через модальное значение, частота наступления событий принимает другую форму? Под событием мы понимаем получение композиции заданного размера, до достижения состояния тупика.
1. Nauck,F.(1850). Briefwechsel mit allen fur alle. Illustrierte Zeitung, 15, 182.
2. Gent,I.P., Jefferson,C. & Nightingale,P.(2017). Complexity of n-Queens completion,
Journal of Artificial Intelligence Research., 59, 815-848.
3. Sosic, R., & Gu, J. (1990). A polynomial time algorithm for the n-queens problem. SIGART Bulletin, 1 (3), 7–11.
4. Richards, M. (1997). Backtracking algorithms in MCPL using bit patterns and recursion.
Tech. rep., Computer Laboratory, University of Cambridge.
5. Randomization Methods in Algorithm Design, Proceedings of a DIMACS Workshop, Princeton, New Jersey, USA, December 12-14, 1997. DIMACS Series in Discrete Mathematics and Theoretical Computer Science 43, DIMACS/AMS 1999, ISBN 978-0-8218-0916-7
6. Grigoryan E. (2018). Investigation of the Regularities in the Formation of Solutions n-Queens Problem. Modeling of Artificial Intelligence, 5(1), 3-21
7. Sloane N.-J. A. (2016). The on-line encyclopedia of integer sequences.
Предисловие
Я хотел бы начать предисловие со слов благодарности двум замечательным программистам из Одессы: Андрею Киперу (Lohica) и Тимуру Гиоргадзе (Luxoft), за независимую проверку полученных мною результатов, на начальном этапе исследования.
- Статья «Linear algorithm for solution n-Queens Completion Problem» была опубликована в (arXiv.org) в начале первого дня 2020 года. Изначально статья была написана на русском, поэтому здесь представлено базовое изложение, а там — перевод.
- Данная задача, и некоторые другие из множества NP-Complete (задача выполнимости булевых формул (3-SAT), задача о поиске максимальной клики, или клики заданного размера …) в разное время, входили в сферу моих интересов. Я искал алгоритмическое решение на основе различных вычислительных экспериментов, но конкретного успеха не было. Это было похоже на то, как человек пытается научиться подтянутся на турнике на одной руке. Результата нет, но каждый раз появляется надежда, что скоро все получится. Последний раз я решил, что следует подольше остановиться на задаче n-Queens Completion (как одной из представителей семейства) и попытаться что-то сделать. Здесь уместно вспомнить замечательный Одесский анекдот: «В переполненном автобусе, который вечером по ухабистой дороге возвращается в пригород, раздается голос женщины – Мужчина, если уж полностью на меня легли, так сделайте хоть что-нибудь».
- Исследование длилось достаточно долго – почти полтора года. С одной стороны, это связано с тем, что в процессе исследования, рассматривались и другие задачи, с другой – по ходу решения были сложные вопросы, без ответа на которые не удалось бы идти вперед. Перечислю некоторые из них:
- В матрице решения n строк, в какой последовательности следует выбирать индекс строки, если число возможностей для такого выбора составляет n!
- когда сделан выбор строки, какую из оставшихся свободных позиций в этой строке следует выбрать, ведь число возможностей такого отбора настолько большое, что его можно считать «близким родственником» бесконечности (например, число возможных способов выбора свободной позиции во всех строках для шахматной доски размера 100 х 100 составляет примерно 10124)
- Совместно, эти два показателя формируют пространство состояния (пространство выбора). Казалось бы, огромные возможности, можно выбирать какую хочешь. Но за каждым конкретным выбором на каждом шаге, скрывается другая проблема – ограничение возможностей выбора во всех последующих шагах. Причем, это особо чувствительно на последних этапах решения задачи. Можно сказать, что матрица решения «злопамятна». Все «неосознанные ошибки», которые вы допускаете, совершая выбор на предыдущих этапах, «накапливаются», и под конец решения это проявляется в том, что в тех строках, где вы должны расположить ферзь, не остается свободных позиций и ветвь поиска заходит в тупик. Здесь как у Жванецкого: «одно неверное движение, и вы беременны».
- Когда ветвь поиска решения заходит в тупик, у нас есть возможность возврата назад, на какую-то из предыдущих позиций (Back Tracking), чтобы с этой позиции снова начать формирование ветви поиска решения. Это естественное «свойство» не детерминированных задач. Вопрос состоит в том, на какой из предыдущих уровней следует возвращаться. Это такая же открытая проблема, как и вопрос выбора индекса строки, или выбора свободной позиции в этой строке.
- Наконец, следует отметить проблему, связанную со скоростью работы алгоритма. Было бы грустно, если бы не было цели создавать быстро работающие алгоритмы. В процессе моделирования не удалось разработать один алгоритм, который быстро и эффективно работал бы на всех участках решения задачи. Пришлось разработать три алгоритма. Они передают результаты один-другому, как эстафетную палочку. Один из них работает очень быстро, но грубо, другой – наоборот, работает медленно, но эффективно. Каждый из них работает в «зоне своей ответственности».
- Изначально, цель исследования состояла только в том, чтобы найти хоть какое-то решение. Пришлось много с чем разобраться, прежде чем был разработан первый вариант решения. На это потребовалось больше четырех месяцев. Можно было на этом остановиться, цель достигнута – ну и ладно. Но мне показалось, что не все возможности алгоритмического решения данной проблемы исчерпаны. Естественно, появилось желание усовершенствовать разработанный алгоритм таким образом, чтобы по временной сложности алгоритм был линейным-O(n). Когда такое линейное решение было найдено, появилось «еще одно желание» — уменьшить число случаев применения процедуры Back Tracking (BT ) при формировании ветви поиска решения. Это было «наглое» желание перевести задачу из не детерминированной, в условно детерминированную (насколько это возможно). На это потребовалось много времени, но цель была достигнута, например, в интервале значений размера шахматной доски n = (320, ..., 22500), число случаев, когда процедура BT ни разу не используется – превышает 50%. Получается, что в 50% случаев запуска программы, алгоритм «целенаправленно» формирует решение, ни разу не «спотыкаясь». (Помня сказку про золотую рыбку, я на этих двух желаниях и остановился…)
- Сравнивая публикации, с которыми мне удалось познакомиться в процессе исследования, я пришел к выводу, что данную задачу, и другие задачи подобного рода не удастся решить на основе строгого математического подхода, т. е. только на основе определений, формулировке лемм и доказательстве теорем. Об этом в статье есть «философское замечание». Я уверен, что многие задачи из множества NP-Complete удастся решить только на основе алгоритмической математики с применение компьютерного моделирования. Такой вывод не означает ограничение математики, наоборот – это означает расширение возможностей математики, через развитие методов алгоритмической математики. Для каждого семейства задач нужно использовать свой адекватный математический подход. (Зачем поручать аспиранту решать задачу из семейства NP-Complete без применения методов алгоритмической математики и компьютерного моделирования, если известно, что из такой затеи ничего толком не выйдет).
- Любой алгоритм (программа) имеет простое свойство – или работает, или нет! Я хочу обратиться к тем членам нашего Хабро-Сообщества, у которых в зоне доступности есть компьютер с установленным Матлабом. Хочу попросить Вас протестировать работу рассматриваемого алгоритма решения n-Queens Completion Problem. Для этого потребуется всего 5-10 минут. Чтобы протестировать алгоритм, нужно выполнить несколько простых шагов:
- Генерировать случайную композицию из k ферзей и проверить правильность этой композиции.
- На основе предложенного алгоритма решения комплектовать данную композицию до полного решения. Либо программа должна принять решение, что данная композиция не имеет решения.
- Проверить правильность решения, полученного в результате комплектации.
Вам не придется писать какой либо код для такого тестирования. Кроме основной программы, я подготовил еще две программы на языке Матлаб:
1. Generarion_k_Queens_Composition – генерация случайной композиции размера k для произвольной шахматной доски размера n x n
2.Completion_k_Queens_Composition.m – комплектация произвольной композиции до полного решения, либо принятие решение, что данная композиция не имеет решения (основная программа).
3.Validation_n_Queens_Solution.m – проверка правильности решения n-Queens Problem, либо правильности композиции из k ферзей.
Они работают очень быстро. Например, для шахматной доски, размер которой составляет 1000 х 1000 клеток, общее время, которое в среднем необходимо для генерации произвольной композиции (0.0015 с.), комплектации данной композиции (0.0622 с.), и проверки правильности полученного решения (0.0003 с.) не превышает 0.1 секунды. (исключая время, которое необходимо для загрузки данных, или сохранения полученных результатов)
Напишите мне (ericgrig@gmail.com), если у Вас есть возможность оказать помощь другу, я сразу вышлю Вам эти три программы. Я буду благодарен всем коллегам, которые смогут объективно провести тестирование алгоритма, и выскажут свое мнение в рамках обсуждения. - Я подготовил исходный текст программы, с подробными комментариями, который, надеюсь, в ближайшее время будет опубликован на Хабре. Думаю, что те, кто интересуется решением сложных задач из семейства NP-Complete, найдут для себя что-нибудь интересное.
- Я хотел бы снова обратиться к членам ХабраСообщества, но уже по другому поводу. Здесь, в Марселе (Франция), идет процесс формирования команды France Fold Group, целью которой является исследование и разработка алгоритмов для предсказания физико-химических свойств высокомолекулярных соединений. Думаю, не стоит говорить, что это достаточно сложная задача, с многолетней историей, и, что над этой проблемой работают серьезные команды в разных странах, в том числе и команда Хасабиса из Deep Mind ( можно посмотреть статью на Хабре (habr.com_Folding). Цель – создать сильную команду, которая не боится решать сложные задачи. Форма организации совместной работы – распределенная. Каждый член команды живет в своем городе и работает над проектом в свободное от основной работы время. Нужны программисты-исследователи (физики, химики, математики, биологи), и просто «безбашные»-программисты-(в квадрате). Напишите мне, если сочтете это интересным, выше приведен мой e-mail. Более подробно я смогу рассказать в ответном письме.
Предисловие к статье оказалось таким же длинным, как и сама статья. Семейный формат изложения на Хабре позволяет более свободно излагать свои мысли, но, судя по размеру, я достаточно свободно этим воспользовался. Хотелось написать кратко, а «получилась как всегда».
P.S. Я подумал, что членам Хабра-Сообщества будет интересно узнать, с какими трудностями я столкнулся при попытке опубликовать результаты исследования. Когда статья была подготовлена, я переформатировал ее в .tex формат согласно требованиям Journal of Artificial Intelligence Research (JAIR) и отправил туда. Там раньше были публикации на похожую тему. Особо можно выделить статью C. Gent, I.-P. Jefferson and P. Nightingale (2017) (Complexity of n-queens completion), в которой авторы доказали, что рассматриваемая проблема относится к множеству NP-Complete и рассказали о сложностях, с которыми столкнулись, в попытке решения этой задачи. В выводах авторы пишут: «For anybody who understands the rules of chess, n-Queens Completion may be one of the most natural NP-Complete problems of all» (Для всех кто понимает правила шахмат, задача n-Queens Completion может стать одним из самых естественных NP-Complete задач).
Через 10 дней мне пришел отказ из JAIR, с формулировкой: «статья не соответствует формату журнала», т.е. даже не взяли статью на рассмотрение. Такого ответа я не ожидал. Я полагал, что если журнал публикует статьи, в которых авторы делают вывод о большой сложности решения данной задачи и не приводят какого либо конкретного решения, то статья, в которой приводится эффективный алгоритм решения – будет, безусловно принята к рассмотрению. Однако, у редакции было свое мнение по этому поводу. (Полагаю, что там работают грамотные специалисты, и, скорее всего у них вызвало сомнение «наглое» названия статьи и все то, что там излагается. Подумали, «здесь, скорее всего какая-то ошибка и мягко послали меня подальше, ссылаясь на формат").
Мне предстояло выбрать другое рецензируемое периодическое научное издание по соответствующей тематике. Вот тут я столкнулся с суровой действительностью. Дело в том, что примерно 80% всех журналов являются платными: либо я должен платить журналу приличную сумму, чтобы статья была свободно доступна всем читателям, либо нужно им отдать статью как подарок «в бантике», и они будут взимать плату с каждого, кто захочет ознакомиться с данным исследованием. И первый и второй варианты для меня принципиально неприемлемы. Этот способ рэкета издателей я хорошо почувствовал на себя, когда пытался ознакомиться с некоторыми публикациями.
Очередным журналом, где исповедуется принцип свободного доступа к информации был «SMAI Journal of Computational Mathematics». Здесь тоже отказали с той же формулировкой, правда намного быстрее – через два дня.
Дальше был выбран журнал: «Discrete Mathematics & Theoretical Computer Science». Здесь требования простые, вначале необходимо опубликовать статью в arXiv.org, и лишь после этого зарегистрировать статью для рассмотрения. Ладно, будем соблюдать правила – подал статью в arXiv.org. Написали мне, что опубликуют статью через 8 часов. Однако этого не произошло ни через 8 часов, не через 8 дней. Статья был на «удержании» у менторов, и только через 9 дней ее опубликовали. Никаких претензий по форме и сути статьи не было. Думаю, как и в случае с JAIR, у менторов были сомнения в возможности «такое сделать и об этом написать». Спустя некоторое время, после исправления технических ошибок, статья была обновлена и в окончательном виде вышла в ночь на новый год.
Я вынужден подробно остановиться на этом, чтобы показать, что на этапе публикации результатов исследования могут быть проблемы, которые не поддаются логическому объяснению.
Далее следует статья, перевод которой на английский, был опубликован в (arXiv.org).
1. Введение
Среди различных вариантов формулировки n-Queens problem, рассматриваемая задача the n-Queens Completion занимает особое положение ввиду своей сложности. В своей работе (Gent at all (2017)) показали, что the n-Queens Completion problem относится к множеству NP-Complete (showed that n-Queens Completion is both NP-Complete and # P-Complete). Предполагается, что решение данной проблемы, возможно, откроет нам путь к решению некоторых других задач из множества NP-Complete.
Задача формулируется следующим образом. Имеется композиция из k ферзей, которые непротиворечиво распределены на шахматной доске размера n x n. Требуется доказать, что данная композиция может быть комплектована до полного решения, и привести хотя бы одно решение, либо доказать, что такого решения не существует. Здесь, под непротиворечивостью, мы понимаем такую композицию из k ферзей, для которой выполняются три условия задачи: в каждой строке, каждом столбце, а также на левой и правой диагоналях, проходящих через ячейку, где расположен ферзь, не расположено более одного ферзя. Задача в таком виде была впервые сформулирована Nauk (1850).
1.1 Определения
Здесь и далее, размер стороны шахматной доски мы будем обозначать символом n. Решение мы будем называть полным, если все n ферзей непротиворечиво расставлены на шахматной доске. Все остальные варианты решения, когда количество k правильно расставленных ферзей меньше n – мы будем называть композицией. Назовем композицию из k ферзей положительной, если она может быть комплектована до полного решения. Соответственно, композицию, которую невозможно комплектовать до полного решения – назовем отрицательной. В качестве аналога «шахматной доски» размера n x n, мы будем рассматривать также «матрицу решения» размера n x n. В качестве примера, все алгоритмы, разработанные для решения поставленной задачи, будут представлены на языке Matlab.
Исследование проводилось на основе компьютерного моделирования ( computational simulation). Чтобы проверить ту или иную гипотезу, мы проводили вычислительные эксперименты в широком диапазоне значений n= (10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 500, 800, 1000, 3000, 5000, 10000, 30000, 50000, 80000, 105, 3*105, 5*105, 106, 3*106, 5*106, 107, 3*107, 5*107, 8*107, 108) и, в зависимости от значения n, генерировали достаточно большие выборки для анализа. Назовем такой список «базовым списком значений n» для проведения вычислительных экспериментов. Все расчеты проводились на обычном компьютере. На момент сборки (начало 2013 года) это была достаточно удачная конфигурация: CPU – Intel Core i7-3820, 3.60 GH, RAM-32.0 GB, GPU- NVIDIA Ge Forse GTX 550 Ti, Disk device- ATA Intel SSD, SCSI, OS- 64-bit Operating system Windows 7 Professional. Назовем такой комплект просто — desktop-13.
2. Подготовка данных
Работа алгоритма начинается со считывания файла, который содержит одномерный массив данных о распределении произвольной композиции из k ферзей. Предполагается, что данные подготовлены следующим способом. Пусть имеется обнуленный массив Q( i )=0, i=(1,…,n), где индексы ячеек этого массива соответствуют индексам строк матрицы решения. Если в некоторой произвольной строке i матрицы решения располагается ферзь в позиции j, то выполняется присваивание Q( i )=j. Таким образом, размер композиции k, будет равен количеству ненулевых ячеек массива Q. (Например, Q=( 0, 0, 5, 0, 4, 0, 0, 3, 0, 0) означает, что рассматривается композиция из k=3 ферзей на матрице n=10, где ферзи расположены в 3-ей, 5-ой и 8-ой строках, соответственно в позициях: 5, 4, 3).
3. Алгоритм проверки правильности решения n-Queens problem
Для исследований нам нужен алгоритм, который позволил бы за короткое время определить правильность решения n-Queens problem. Контроль расположения ферзей в каждой строке и каждом столбце выполняется просто. Вопрос состоит в учете диагональных ограничений. Мы могли бы построить эффективный алгоритм такого учета, если бы нам удалось сопоставить каждой ячейке матрицы решения определенную ячейку некого контрольного вектора, который однозначно характеризовал бы влияние диагональных ограничений на рассматриваемую ячейку. Тогда, на основе того, свободна или занята ячейка контрольного вектора, можно судить о том, свободна или закрыта соответствующая ячейка матрицы решения. Такая идея впервые была использована в работе Sosic & Gu (1990) для учета и накопления числа конфликтных ситуаций между различными позициями ферзей. Подобная идея используется нами в представленном ниже алгоритме, но только для учета того, свободна или занята ячейка матрицы решения. На рисунке 1, в качестве примера приведена шахматная доска 8 х 8 над которой сверху расположена последовательность из 24 ячеек.
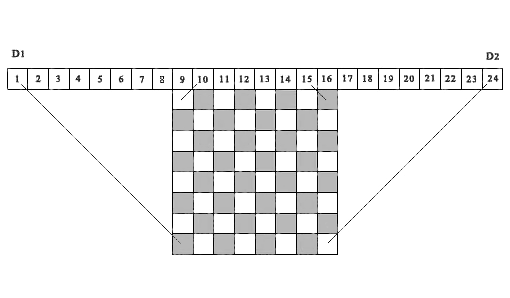
Рис. 1. Демонстрационный пример соответствия диагональных проекций ячеек матрицы, соответствующим ячейкам контрольных массивов D1 и D2, (n=8)
Рассмотрим первые 15 ячеек, как элементы контрольного вектора D1. Проекции всех левых диагоналей из любой ячейки матрицы решения попадают в одну из ячеек контрольного вектора D1. В самом деле, все такие проекции расположены внутри двух параллельных отрезков прямых, одна из которых соединяет ячейку матрицы (8,1) с первой ячейкой вектора D1, а вторая – ячейку матрицы (1,8) с 15-ой ячейкой контрольного вектора D1. Приведем аналогичное определение для правых диагональных проекций. Для этого, переместим вправо начало отсчета из ячейки 1 в ячейку 9, и рассмотрим последовательность из 16 ячеек, как элементы контрольного вектора D2 (на рисунке, это ячейки c 9-го по 24-ый).Проекции всех правых диагоналей из любой ячейки матрицы решения попадут в одну из ячеек этого контрольного вектора, начиная со 2-ой ячейки по 16-ую (на рисунке, с 10-ой по 24-ю). Здесь, все такие проекции, расположены между двумя отрезками параллельных прямых — отрезком, соединяющим ячейку (8,8) матрицы решения с ячейкой 16 вектора D2 (на рисунке ячейка 24), и отрезком, соединяющий ячейку (1,1) матрицы решения с ячейкой 2 контрольного вектора D2 (на рисунке ячейка 10). Проекции всех ячеек матрицы решения, лежащие на одной и той же левой диагонали, попадают в одну и ту же ячейку левого контрольного вектора D1, соответственно, проекции всех ячеек матрицы решения, лежащие на одной и той же правой диагонали, попадают в одну и ту же ячейку правого контрольного вектора D2. Таким образом, эти два контрольных вектора D1 и D2, позволяет вести полный контроль всех диагональных запретов для любой ячейки матрицы решения.
Важно отметить, что идею использования диагональных проекций на ячейки контрольных векторов для определения того, свободна или занята ячейка матрицы решения с координатами ( i ,j ), позже была реализована также в работе Richards (1997). В ней приводится один из быстрых рекурсивных алгоритмов поиска всех решений, основанный на операциях с битовой маской. Важное отличие состоит в том, что указанный алгоритм предназначен для последовательного поиска всех решений, начиная с первой строки матрицы решения – вниз, или с последней строки матрицы — вверх. Предложенный нами алгоритм основан на том условии, что выбор номера каждой строки для расположения ферзя должен быть произвольным. Для рассматриваемого алгоритма это имеет принципиальное значение. Отметим, что представленный выше рисунок 1, построен нами по аналогии с тем, что опубликован в данной работе.
Программа для проверки того, является ли правильным данное решение n-Queens problem, или является ли верным данная композиция из k ферзей, выглядит следующим образом.
1. Для контроля диагональных запретов, создадим два массива D1(1:n2) и D2(1:n2), где n2= 2*n, и массив B(1:n) для контроля занятости столбцов матрицы решения. Обнулим эти три массива.
2. Введем в рассмотрение счетчик числа правильно установленных ферзей ( totPos = 0). Последовательно, в цикле, начиная с первой строки, рассмотрим все предоставленные позиции ферзей. Если Q( i ) > 0, то на основе индекса строки i и индекса позиции ферзя в этой строке j = Q( i ) сформируем соответствующие индексы для контрольных массивов D1( r ) и D2( t ):
r = n + j – i
t = j + i
3. Если будут выполнены все условия ( D1( r ) = 0, D2( t ) = 0, B( j ) = 0 ), то это будет означать, что ячейка ( i, j ) свободна и не попадает в проекционную зону диагональных ограничений, сформированных ранее установленными ферзями. Расположение ферзя в такой позиции является правильным. Если, хотя бы одно из этих условий не выполняется, то выбор такой позиции будет ошибочным, соответственно и решение будет ошибочным.
4. Если решение правильное, то инкрементируем счетчик числа правильно установленных ферзей ( totPos=totPos+1), и закроем соответствующие ячейки контрольных массивов: (D1( r )=1, D2( t ) = 1, B( j )=1). Таким образом, мы закроем все ячейки столбца (j) и те ячейки матрицы решения, которые расположены вдоль левой и правой диагоналей, пересекающихся в ячейке ( i, j ).
5. Повторим процедуру проверки для всех оставшихся позиций.
Возможно, это один из самых быстрых алгоритмов оценки правильности решения n-Queens problem. Время проверки одного миллиона позиций для матрицы решения 106 x 106 на desktop-13 составляет 0.175 секунды, что примерно соответствует времени нажатия клавиши «Enter». Очевидно, что данный алгоритм по времени счета является линейным относительно n.
4. Описание алгоритма решения задачи
Общее. n-Queens Completion problem является классической не детерминированной задачей. Основная сложность ее решения связана с вопросом выбора индекса строки и индекса позиции в этой строке, в условиях, когда пространство состояния имеет огромные размеры. Когда ведется поиск всех возможных решений, то такой проблемы не возникает. Мы должны рассмотреть все допустимые ветви поиска в пространстве состояния и то, в какой последовательности они рассматриваются, не имеет значения. Однако, когда произвольную композицию из k ферзей необходимо комплектовать до полного решения, то в этом случае нужен алгоритм выбора индексов строк и столбцов, который адекватно воспринимает существующую композицию и быстрее других приводит к получению решения. В данном проекте, вопрос с выбором мы решали исходя из следующего общего положения – если мы не можем сформулировать условия, которые дают предпочтение какой-либо строке, или какой-либо позиции в этой строке по сравнению с другими, то используется алгоритм случайного отбора на основе равномерно распределенных случайных чисел. Подобный метод случайного отбора для решения задач, в которых пространство состояния имеет огромные размеры, является вполне естественным. Один из выпусков серии Proceedings of a DIMACS Workshop (1999) был полностью посвящен использованию метода случайного отбора при разработке алгоритмов решения сложных задач. Правильная реализация алгоритма случайного отбора может быть достаточно продуктивным решением, хотя, это является необходимым, но не достаточным условием завершения решения. Публикация Sosic and Gu (1990) является одним из первых исследований, где использовался алгоритм случайного отбора для решения n-Queens Problem. В основе рассмотренного ими алгоритма лежит достаточно простая и лаконичная идея. Пусть имеется последовательность чисел от 1 до n, которые случайно переставлены местами. Такой набор чисел имеет важное свойство. Состоит оно в том, что каким бы образом не были распределены эти числа на различных строках матрицы решения в качестве позиций ферзя (по одному числу на строку), всегда будут выполнены первые два правила в постановке задачи: в каждой строке и каждом столбце будет расположено не более одного ферзя. Однако, только часть, полученных таким образом позиций будут свободны от диагональных ограничений. Другая часть будет находиться в состоянии «конфликта» с ранее установленными ферзями. Для выхода из этой ситуации, авторы использовали метод сравнения и перестановки местами конфликтующих позиций для получения полного решения. В предложенном нами алгоритме невозможны конфликтные ситуации, так как на каждом шаге решения задачи, ферзь устанавливается в ячейку рассматриваемой строки только в том случае, если ячейка свободна.
4.1 Выбор модели для организации процедуры Back Tracking (BT)
В процессе поиска решения задачи, может наступить ситуация, когда последовательная цепочка решения приводит в тупик. Это «генетическое» свойство не детерминированных задач. В таком случае, нужно сделать возврат назад, на один из предыдущих шагов, восстановить состояние задачи в соответствии с этим уровнем и начинать снова поиск решения с этой позиции. Вопрос состоит в том, на какой из предыдущих уровней следует возвращаться и сколько таких уровней должно быть (под уровнем, мы понимаем некоторый шаг решения задачи с заданным количеством правильно установленных ферзей). Очевидно, что выбор уровня решения для возврата назад, является такой же актуальной задачей, как и выбор индекса строки или индекса позиции в этой строке. Поэтому, независимо от подхода к решению данной задачи, необходимо предварительно определить количество базовых уровней для возврата назад, а также механизм и условия возврата на один из этих уровней. В предложенном нами алгоритме, мы делим матрицу решения на три базовых уровня. Это точки возврата. Если, в результате решения, возникает тупиковая ситуация, то, в зависимости от параметров задачи, мы возвращаемся назад на один из этих трех базовых уровней. Первый базовый уровень (baseLevel1) соответствует состоянию, когда проверка данных рассматриваемой композиции завершена. Это начало работы программы. Значения следующих двух базовых уровней (baseLevel2 и baseLevel3) зависят от размера матрицы n. Эмпирическая зависимость этих базовых значений от размера матрицы решения была установлена на основе большого числа вычислительных экспериментов. Для более точного представления этой зависимости, мы разделили весь рассматриваемый интервал от 7 до 108 на две части. Пусть u=log(n), тогда, если n < 30 000, то
baseLevel2 = n — round(12.749568*u3 — 46.535838*u2 + 120.011829*u — 89.600272)
baseLevel3 = n — round(9.717958*u3 – 46.144187*u2 +101.296409*u – 50.669273)
иначе
baseLevel2 = n — round(-0.886344*u3 + 56.136743*u2 + 146.486415*u + 227.967782)
baseLevel3 = n — round(14.959815*u3 – 253.661725*u2 +1584.713376*u – 3060.691342)
4.2 Блочная структура
Алгоритм построен в виде последовательности из пяти блоков-событий, где каждое событие связано с выполнением определенной части решения задачи. Алгоритмы обработки в каждом блоке различаются друг от друга. Только три блока из этих пяти служат для формирования последовательной цепочки решения, а оставшиеся два блока являются подготовительными. Выбор номера блока, с которого начинаются расчеты, зависит от значения n и от результатов сравнения размера композиции k со значениями baseLeve2 и baseLevel3. Исключением является интервал значений n=(7,…,99), который можно назвать «турбулентной зоной» ввиду особенностей поведения алгоритма на этом участке. Для значений n=(7,…,49), независимо от размера композиции, после ввода и контроля данных, расчеты начинаются с 4-го блока. Для значений n=(50,…,99), в зависимости от размера композиции, расчеты начинаются либо со второго блока, либо с четвертого. Как было сказано выше, на каждом шаге решения задачи рассматриваются только те позиции в строке, которые не попадают в зону ограничений, созданных ранее установленными ферзями. Именно такие позиции называются свободными.
Опишем кратко, какие расчеты выполняются в каждом из этих пяти блоков программы.
4.3 Начало алгоритма
Производится ввод данных и проверка правильности композиции. На каждом шаге проверки производится изменение ячеек контрольных массивов. Проводится учет количества правильно установленных ферзей. Если в композиции нет ошибок, то решение продолжается, иначе выводится сообщение об ошибке. После завершения проверки, создаются копии основных массивов для их повторного использования на данном уровне. После этого управление передается в Блок-1.
4.4 Блок-1
Начало формирования ветви поиска. Рассматривается k ферзей, расположенных на шахматной доске в качестве стартовой позиции. Требуется продолжить комплектацию этой композиции и расположить ферзи на шахматной доске до тех пор, пока их общее количество не окажется равным baseLevel2. Алгоритм, который используется здесь, называется randSet & randSet. Связано это с тем, что здесь постоянно сравниваются два случайных списка индексов, в поисках пар, свободных от соответствующих диагональных ограничений. Для этого выполняются следующие действия:
a) формируются два списка: список индексов свободных строк и список индексов свободных столбцов;
b) производится случайная перестановка чисел в каждом из этих списков;
c) в цикле, каждая последовательная пара значений ( i, j ), где индекс ( i ) выбирается из списка индексов свободных строк, а индекс ( j ) — из списка индексов свободных столбцов, рассматривается как потенциальная позиция ферзя и проверяется, попадает ли данная позиция в проекционную зону диагональных исключений.
Если правило диагональных исключений не нарушается, то позиция считается верной, и в данную позицию располагается ферзь. После этого, производится инкрементация счетчика числа правильно установленных ферзей, и изменяются соответствующие ячейки контрольных массивов. Если позиция ( i, j ) попадает в зону диагональных ограничений, сформированных ранее установленными ферзями, то ничего не меняется и совершается переход к рассмотрению следующей пары значений.
Когда завершается цикл сравнения всех пар списка, то, на основе оставшихся индексов, которые оказались в зоне диагональных исключений, снова формируется список индексов оставшихся свободных строк и свободных столбцов, и данная процедура повторно выполняется до тех пор, пока общее число правильно расставленных ферзей (totPos) не окажется равным или превысит граничное значение baseLevel2. Как только выполняется это условие, управление передается в Блок-2. Если окажется, что в результате поиска решения, возникла такая ситуация, что из всего списка индексов оставшихся свободных строк и свободных столбцов, ни одна из пар не подходит для расположения ферзя, то в этом случае, восстанавливаются исходные значения контрольных массивов на основе ранее сформированных копий, и управление передается на начало Блока-1 для повторного счета.
4.5 Блок-2
Данный блок служит в качестве подготовительного этапа для перехода в Блок-3. На данном уровне количество оставшихся свободных строк (freeRows) значительно меньше n. Это позволяет перенести события из исходной матрицы размера n x n на матрицу меньшего размера L(1: freeRows, 1: freeRows). При этом, на основе информации об оставшихся свободных строках и свободных столбцах в исходной матрице решения, записываются нули в соответствующие ячейки массива L, показывающие, что данные ячейки свободны. При таком «проекционном» переходе сохраняется соответствие индексов строк и столбцов новой матрицы, с соответствующими индексами исходной матрицы. Важно отметить, что хотя, в процессе решения данной задачи, все события разворачиваются на исходной матрице размера n x n, и такая матрица является главной ареной действий, реально такая матрица не создается, а рассматриваются только контрольные массивы учета индексов строк A(1: n) и столбцов B(1: n) этой матрицы.
Наряду с массивом L, в данном блоке формируются также два рабочих массива rAr(1: freeRows) и tAr(1: freeRows), для сохранения соответствующих индексов контрольных массивов D1 и D2. Это связано с тем, что когда мы устанавливаем очередной ферзь в ячейку ( i, j ) исходной матрицы размера n x n, то после этого должны исключить ячейки массива L, попадающие в проекционную зону диагональных исключений исходного «большого» массива. Так как контроль диагональных ограничений производится только в пределах исходной матрицы размера n x n, то наличие рабочих массивов rAr и tAr позволяет сохранить соответствие и транслировать запрещенные ячейки в пределы массива L. Это значительно упрощает учет исключенных позиций.
После завершения подготовительной работы в данном блоке, создаются копии основных массивов для повторного использования на данном уровне, и управление передается в Блок-3.
4.6 Блок-3
В данном блоке продолжается формирование ветви поиска решения на основе данных, подготовленных в предыдущем блоке. Количество строк, в которых правильно установлены ферзи, равно или превышает значение baseLevel-2. Требуется продолжить комплектацию, пока количество установленных ферзей не окажется равным baseLevel-3. Здесь используется алгоритм поиска решения rand & rand, т.е. для формирования позиции ферзя, вместо списка свободных индексов, используются только два индекса, случайное значение индекса свободной строки и случайное значение индекса свободной позиции в этой строке. Данная процедура циклически повторяется до тех пор, пока общее число расставленных ферзей не окажется равным значению baseLevel-3. Как только выполняется данное условие, управление передается в Блок-4. Если в результате расчетов ветвь поиска окажется тупиковой, то данный участок формирования ветви поиска закрывается и производится возврат на начало Блока-3, откуда расчеты повторяются снова. Для этого восстанавливаются исходные значения всех контрольных массивов.
4.7 Блок-4
В данном блоке производится подготовка данных для передачи управления в Блок-5. К данному шагу, после выполнения процедуры в Блоке-3, количество свободных строк (nRow) стало еще меньше. Поэтому, здесь так же выгодно перевести события из массива большего размера в массив меньшего размера. Такой подход дает нам возможность гораздо быстрее определить необходимые характеристики для оставшихся строк, которые нам нужны на данном этапе. Особое значение имеет тот факт, что на основе такого массива, можно прогнозировать перспективность ветви поиска на много шагов вперед, не проводя расчеты до конца. Условие достаточно простое. Если окажется, что среди оставшихся свободных строк имеется строка, в которой нет свободной позиции, то рассматриваемая ветвь поиска закрывается и управление передается в один из блоков нижнего уровня. Подготовительные действия, выполняемые здесь, во многом аналогичны тому, что делалось в Блоке-2. На основе исходных индексов свободных строк и свободных столбцов формируется новый 2-мерный массив, нулевые значения которого соответствуют свободным позициям в исходной матрице решения. Кроме того, в данном блоке создается специальный массив E(1: nRow, 1: nRow), на основе которого можно определить, количество свободных позиций в оставшихся свободных строках, которые будут закрыты, если выбрать позицию ( i, j ) для установки ферзя в исходной матрице. Перед тем, как передать управление в Блок-5, выполняются следующие действия:
a) определяется сумма свободных позиций во всех оставшихся строках,
b) массив суммы свободных позиций, для рассматриваемых строк, сортируется в порядке возрастания,
c) если во всех оставшихся свободных строках имеются свободные позиции (т.е. минимальное значение в этом ранжированном списке отлично от 0), то управление передается в Блок-5.
Если окажется, что в какой либо из оставшихся строк нет свободной позиции, то восстанавливаются необходимые массивы на основе сохраненных копий, и, в зависимости от параметров задачи, управление передается на один из базовых уровней.
d) формируются резервные копии всех контрольных массивов для данного 4-го уровня.
4.8 Блок-5
Данный этап является завершающим, и здесь, формирование ветви поиска выполняется более «взвешенно» и «рационально». Это «последняя миля», осталось лишь небольшое число свободных строк. Но одновременно, это самый трудный участок. Все ошибки, которые потенциально могли быть допущены на предыдущих этапах формирования ветви поиска решения, в совокупности проявляются здесь – в виде отсутствия свободной позиции в строке.
Алгоритм данного блока выполняется на основе двух вложенных циклов, внутри которых выполняется третий цикл. Особенность третьего цикла состоит в том, что он может выполняться повторно, без изменения параметров двух внешних циклов. Это происходит в том случае, если сформированная ветвь поиска оказывается тупиковым. Число таких повторений не превышает граничное значение repeatBound, оптимальное значение которого было установлено на основе вычислительных экспериментов.
Индекс внешнего цикла связан с последовательным выбором индексов строк, оставшихся свободными после расчетов на третьем базовом уровне. Выполняется это на основе ранее ранжированного списка строк по сумме свободных позиций в строке. Выбор начинается со строки, с минимальным числом свободных позиций и далее, в последующих шагах – в порядке возрастания. Внутри данного цикла формируется второй цикл, индекс которого перебирает индексы всех свободных позиций в рассматриваемой строке. Назначение первого цикла состоит только в том, чтобы на данном уровне выбрать индекс одной из свободных строк. Соответственно, назначение второго цикла состоит только в том, чтобы в пределах рассматриваемой строки выбрать одну свободную позицию. Эти действия происходят только на третьем базовом уровне. После такого выбора, производится инкрементация числа установленных ферзей, и изменяются соответствующие ячейки всех контрольных массивов. Далее, управление передается внутрь вложенного (третьего) цикла, зоной активности которого являются уже все оставшиеся свободные строки. Внутри данного цикла, выбор индекса строки и выбор свободной позиции в этой строке, выполняются на основе следующих правил:
a)Выбор свободной строки. Рассматриваются все оставшиеся свободные строки, и в каждой строке определяется число свободных позиций. Выбирается та строка, у которой число свободных позиций минимально. Это позволяет минимизировать риски, связанные с возможностью исключения последних свободных позиций, в некоторых из оставшихся строк, у которых состояние по числу свободных позиций минимально и является критичным (правило минимального риска). Кстати, именно с учетом этого правила, индекс первого цикла в данном пятом блоке, начинается с последовательного отбора строк с минимальным значением числа свободных позиций в строке. Если на каком то шаге окажется, что две строки имеют одинаковое минимальное число свободных позиций, то случайно выбирается индекс одной из двух позиций, перечисленных первыми в ранжированном списке. Если число строк, имеющих одинаковое минимальное число свободных позиций, больше двух, то случайно выбирается индекс одной из трех позиций, перечисленных первыми в ранжированном списке.
b)Выбор свободной позиции в строке. Из списка всех свободных позиций в рассматриваемой строки, выбирается та, которая наносит минимальный ущерб свободным позициям во всех оставшихся строках. Это выполняется на основе ранее сформированного массива E. Под «минимальным ущербом», мы подразумеваем выбор такой позиции в данной строке, которая исключает наименьшее количество свободных позиций во всех оставшихся строках (правило минимального ущерба). Если окажется, что две или более свободных позиций в строке, имеют одинаковые минимальные значения по критерию ущерба, то случайно выбирается индекс одной из двух позиций, перечисленных первыми в списке. Выбор позиции, которая исключает минимальное число свободных позиций в оставшихся строках, минимизирует «ущерб», связанный с расположением ферзя в данной позиции. Использование обоих этих правил, позволяет более рационально использовать ресурсы на каждом шаге формирования ветви поиска. Это в значительной степени уменьшает риски и повышает вероятность комплектации произвольной композиции до полного решения, если рассматриваемая композиция имеет решение. Если на каком-то шаге решения окажется, что в одной из оставшихся для рассмотрения строк, отсутствуют свободные позиции, то данная ветвь поиска закрывается. В этом случае, на основе резервных копий восстанавливаются все контрольные массивы, и если счетчик числа повторений не превышает граничное значение repeatBound, то без изменения индексов первого и второго внешних циклов, вновь повторяется работа третьего вложенного цикла. Это связано с тем, что в тех случаях, когда совпадали минимальные значения соответствующих критериев, мы производили случайный отбор. Повторное формирование ветви поиска на одних и тех же условиях базового уровня, позволяет более эффективно использовать «стартовые ресурсы», предоставленные на данном уровне. Число повторных запусков третьего вложенного цикла ограничено, и при превышении граничного значения, работа этого цикла прерывается. После этого, восстанавливаются значения контрольных массивов, и управление передается в цикл третьего базового уровня для перехода на следующее значение индекса. Данная процедура циклически повторяется до тех пор, пока не будет получено полное решение, либо не окажется, что мы использовали все свободные строки и все свободные позиции в этих строках на данном базовом уровне. В этом случае, в зависимости от общего количества повторных вычислений на различных базовых уровнях, и с учетом размера матрицы решения и размера композиции, происходит возврат на один из нижних уровней для повторного выполнения расчетов, либо выносится суждение о том, что рассматриваемая композиция не может быть комплектована до полного решения. В программе, с целью ограничения общего времени счета, принято, что процедура Back Tracking, независимо от того, на какой из предыдущих уровней совершается возврат, может быть выполнена не более totSimBound раз. Это граничное значение выбрано на основе вычислительных экспериментов для различных значений n.
5. Анализ эффективности алгоритмов отбора
Эффективность алгоритма randSet & randSet. Для анализа возможностей данного алгоритма был проведен вычислительный эксперимент, который состоял в том, чтобы на основе модели randSet & randSet расположить ферзи в матрице решения до тех пор, пока существует такая возможность. Как только ветвь поиска доходила до тупика, или было получено полное решение, фиксировался размер композиции, время решения, и испытание повторялось снова. Вычислительные эксперименты проводились для всего базового списка значений n. Количество повторных испытаний для значений n= (30, 40,… ,90, 100, 200, 300, 500, 800, 1000) было равно одному миллиону, для остальных значений, количество испытаний, с ростом n, постепенно уменьшалось от 100000 до 100. Анализ результатов вычислительных экспериментов позволяет делать следующие выводы:
a) В результате работы только первого цикла процедуры randSet & randSet в среднем оказываются правильно расставленными около 60% всех ферзей. Для n=100, число правильно расставленных ферзей составляет 60.05%. С увеличением значения n, эта величина постепенно уменьшается, и, для n=107 составляет 59.97%.
b) Гистограмма распределения значений длины полученных композиций, имеет одинаковый вид, независимо от размера матрицы решения n. Причем все они имеют характерную особенность – левая часть распределения (до модального значения) отличается от правой части. На рисунке 2, в качестве примера, представлена соответствующая гистограмма для

Рис. 2. Гистограмма распределения решений различной длины для модели randSet & randSet (n=100, размер выборки= 106).
n=100. Создается впечатление, будто гистограмма собрана из распределения частот двух разных событий, так как частоты наступления событий в левой и правой частях распределения – различается. Для описания данного распределения, скорее всего, подойдет использование двух функций плотности нормального распределения, одна из которых охватывает интервал до модального значения, другая – интервал после модального значения.
c) Среднее значение количества ферзей (qMean), которые можно установить в матрице решения на основе данного алгоритма, увеличивается с ростом значения n. Как видно из рисунка 3, где представлен график зависимости отношения qMean/n от размера матрицы n, с увеличением размера матрицы это отношение увеличивается. Например,

Рис. 3. Зависимость отношения qMean/n от значения n для различных размеров матрицы решения. Модель – randSet & randSet, qMean – среднее значение длины решения.
если для матрицы размера 100х100 алгоритм выбора позиций randSet & randSet позволяет «без остановки» расставить ферзи в среднем на 89 строках, то уже для матрицы 1000х1000, количество таких строк увеличивается в среднем до 967.
d) На основе алгоритма randSet & randSet можно получить полное решение, однако «продуктивность» такого подхода является крайне низкой. Как видно из рисунка 4, для

Рис. 4. Уменьшение вероятности получения полного решения в модели randSet & randSet с увеличением значения n.
значения n=7 вероятность получения полного решения составляет 0.057. Далее, с увеличением значения n вероятность получения полного решения быстро уменьшается, асимптотически приближаясь к нулю. Начиная со значения n = 48, вероятность получения полного решения имеет порядок 10-6. После порогового значения n=70, для последующих значений n не было получено ни одного полного решения (при числе испытаний равном одному миллиону).
e) Модель randSet & randSet формирует ветви поиска с очень высокой скоростью. Для n=1000 среднее время получения композиции составляет 0.0015 секунд. При этом средняя длина композиций составляет 967. Соответственно, для n=106 среднее время составляет 2.6754 секунды при средней длине композиций 999793.
f) За исключением небольшого интервала n<=70, когда модель randSet & randSet в очень редких случаях может привести к получению полного решения, во всех остальных случаях ветвь решения завершается формированием отрицательной композиции, которая не может быть комплектована до полного решения. Таким образом, алгоритм randSet & randSet имеет важное преимущество – высокую скорость формирования ветви поиска, и существенный недостаток, состоящий в том, что если размер композиции превышает некоторое пороговое значение, то данный алгоритм приводит к формированию композиций, которые не могут быть комплектованы до полного решения. Чтобы преодолеть этот недостаток, мы останавливаем формирование ветви поиска, при достижении порогового значения baseLevel-2.
Эффективность алгоритма rand & rand. Чтобы определить возможности алгоритма rand & rand, было проведено достаточно подробное компьютерное моделирование для базового списка значений n. Как и в случае модели randSet & randSet, число повторных испытаний в большинстве случаев было равно одному миллиону. Для остальных значений, количество испытаний постепенно уменьшалось от 100000 до 100.
В основе обоих алгоритмов лежит принцип случайного отбора. Поэтому следовало ожидать, что выводы, полученные здесь, в основном будут идентичны выводам, сформулированным для модели randSet & randSet. Однако, между ними имеется принципиальное различие, и состоит оно в следующем:
a) модель rand & rand работает не так «жёстко» как модель randSet & randSet. Если говорить о некотором «индексе рационального использования предоставленных возможностей», то модель rand & rand на каждом шаге использует ресурсы более рационально. Это приводит к тому, что, например, при n=30, вероятность получения полного решения 0.00170 в данной модели в 15 раз больше, чем аналогичная величина 0.00011 для модели randSet & randSet. Кроме того, здесь, вплоть до порогового значения n=370 сохраняется вероятность получения хотя бы одного полного решения при проведении одного миллиона испытаний. После этого порогового значения, для последующих значений n при числе испытаний равном одному миллиону, на основе модели rand & rand не было получено ни одного полного решения.
b) данный алгоритм работает намного медленнее, чем алгоритм randSet & randSet. Если для n=1000 провести генерацию композиции размером 967, то среднее время получения одной композиции составит 0.0497 секунд, что в 33 больше соответствующего значения 0.0015 для модели randSet & randSet.
Причина различий двух близких по сути методов случайного отбора связана с тем, что в модели randSet & randSet, с целью ускорения расчетов, на каждом шаге не проводится случайный отбор из оставшегося списка. Вместо этого производится последовательный отбор пары индексов из двух списков, элементы которого были случайно переставлены. Такой отбор является случайным не в полной мере, однако хорошо вписывается в логику задачи и позволяет быстро считать.
Чтобы визуально продемонстрировать работу алгоритма rand & rand, был проведен следующий эксперимент:
a) Для шахматной доски размером 100х100, после каждого шага расположения ферзя в какой-либо строке, определялось количество свободных позиций в каждой из оставшихся свободных строк. Таким образом, после каждого шага решения задачи мы получали список свободных строк и соответствующий список числа свободных позиций в этих строках. Это дало возможность построить график, где по оси абсцисс отложены индексы столбцов рассматриваемой матрицы, а по оси ординат – количество оставшихся свободных позиций. Для сравнения, расчеты проводились также и для модели последовательного отбора позиций. Под последовательным отбором подразумевается следующее. Рассматривается первая строка, в которой отбирается первая по списку свободная позиция. Потом, рассматривается вторая строка, в которой также отбирается первая свободная позиция в списке и т.д. На рисунках 5 и 6
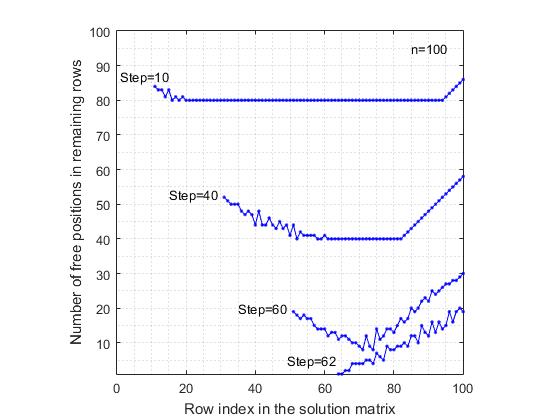
Рис. 5. Уменьшение количества свободных позиций в оставшихся свободных строках после расстановки ферзей. Последовательно-регулярный отбор позиций.
представлены результаты, которые соответствуют рассматриваемым моделям. Для наглядности, на графике представлены результаты только после шагов (10, 40, 60). Для модели последовательно отбора позиций последним приводится график после 62-го шага, так как ветвь поиска обрывается из-за отсутствия свободной позиции в 63-й строке. С другой стороны, в модели rand & rand, последним представлен график после 70-го шага расстановки ферзя, хотя здесь, среднее количество правильно расставленных ферзей достигает 89, что на 26 шагов больше чем в последовательной модели. «Странный» вид графиков в модели rand & rand связан с тем, что индекс строки отбирается случайным образом среди оставшихся свободных строк, и поэтому они случайно разбросаны по всей матрице решения. Из сравнения этих двух рисунков видно, что в последовательной модели выбора позиций, размах изменчивости числа свободных позиций выше, чем в модели rand & rand. Это связано с тем, что при регулярном отборе, диагональные ограничения неоднородно исключают свободные позиции в оставшихся строках, что приводит к тому, что в некоторых строках скорость сокращения количества свободных позиций оказывается выше, чем в остальных строках.

Рис. 6. Уменьшение количества свободных позиций в оставшихся свободных строках после расстановки ферзей. Модель отбора позиций – rand & rand.
В противоположность этому, при случайном отборе индекса свободной строки и индекса свободного столбца, позиции ферзя равномерно распределяются по «площади» матрицы решения, что уменьшает «среднюю» скорость сокращения числа свободных позиций в оставшихся строках. Таким образом, учитывая возможности алгоритма rand & rand, мы используем его в программе для продолжения формирования ветви поиска решения, пока не будет достигнуто значение базового уровня baseLevel-3.
Следует отметить, что если бы даже алгоритмы выбора (randSet & randSet, rand & rand) не были бы столь эффективными, нам бы все равно пришлось использовать какой либо иной метод случайного отбора при разработке алгоритма. Это обусловлено самой постановкой задачи n-Queens Completion problem. Если представить, что существует некий оптимальный алгоритм, который решает поставленную задачу, то на входе такой алгоритм всегда будет получать некий случайный набор индексов строк и столбцов. Каждый раз это будет новый случайный набор индексов строк и столбцов из огромного множества возможностей. Чтобы можно было «принять на вход» алгоритма такое многообразие случайных композиций сам алгоритм должен быть построен на основе случайного отбора. Соответствие должно быть как ключ к замку. Если мы построим алгоритм на этом принципе, то любая непротиворечивая композиция из k ферзей будет рассматриваться как начальная (стартовая) позиция в цикле поиска решений. И далее, цель будет состоять лишь только в том, чтобы продолжить формирование ветви поиска решения, пока не будет найдено решение для данной композиции, либо будет доказано, что такого решения не существует.
6. Пример использования правила минимального риска (n=100)
На начальном этапе поиска решения, когда количество свободных позиций в строках не критично, то выбор индекса свободной строки, или индекса позиции в этой строке, не является фатальным. Однако, на последней стадии, когда количество свободных позиций в некоторых строках равно 1 или 2, то в этом случае следует выбрать другой алгоритм отбора. На этом уровне, алгоритмы случайного отбора randSet & randSet и rand & rand, уже не будут работать.
Причину, почему алгоритмы случайного отбора не будут работать, можно объяснить на следующем простом примере. Пусть на некотором шаге решения задачи, для произвольного значения n, в оставшихся строках i1, i2, …, ik число свободных позиций (указано в скобках) равно: i1( 1 ), i2( 2 ), i3( 4 ), i4( 5 ), i5( 3 ), i6( 4 ) и т.д. Если выбрать случайным образом любую строку, но не строку i1, в которой осталась только одна свободная позиция, то это может привести к рисковой ситуации, когда диагональные запреты, связанные с расположением ферзя в отобранной строке, могут привести к закрытию единственной свободной позиции в строке i1, что приведет решение в тупик. Из всех строк i1, i2, …, ik наиболее уязвимым и чувствительным к выбору индекса строки является строка i1. В таких ситуациях, в первую очередь следует отобрать ту строку, состояние которой является наиболее критичным и создает риск для решения задачи. Поэтому, на последнем этапе решения задачи, на каждом шаге необходимо выбрать позицию строки на основе простого алгоритма минимального риска.
Рассмотрим для наглядности, в качестве примера, для матрицы размером 100 x 100, последний этап формирования некоторого реального решения, после 88-го шага. До завершения задачи осталось 12 свободных строк, для каждого из которых было найдено число свободных позиций (строки ранжированы в порядке возрастания числа свободных позиций): Шаг-89 — 25(1), 12(2), 22(2), 82(2), 88(2), 7(3), 64(3), 3(4), 76(4), 91(4), 4(5), 96(5) — указывается индекс свободной строки, а в скобках – число свободных позиций в этой строке. Согласно правилу минимального риска, на 89-ом шаге решения задачи, выбирается строка 25 и та одна свободная позиция, которая в ней имеется. В результате пересчета, у нас остается 11 свободных строк: Шаг-90 – 7(2), 12(2), 22(2), 82(2), 88(2), 3(3), 64(3), 76(3), 4(4), 91(4), 96(4). Как видим, число свободных позиций в первых пяти строках одинаково и равно 2. Поэтому случайно отбирается индекс одной из первых трех строк. В данном случае была отобрана 12-ая строка и та позиция из двух, оставшихся в этой строке, которая приводит к минимальному ущербу. Таким образом, на 91-ом шаге формирования решения у нас осталось 10 свободных строк: Шаг-91 – 22(1), 3(2), 7(2), 82(2), 88(2), 64(3), 76(3), 91(3), 4(4), 96(4). На данном шаге отбирается строка 22 и та одна свободная позиция, которая в ней имеется. Продолжая аналогичным образом, была сформирована следующая последовательность решений (Таблица 1). Индексы отобранных строк выделены жирным шрифтом.
| Step | row | row | row | row | row | row | row | row | row | row | row |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 89 | 25(1) | 12(2) | 22(2) | 82(2) | 7(3) | 64(3) | 3(4) | 76(4) | 91(4) | 4(5) | 96(5) |
| 90 | 7(2) | 12(2) | 22(2) | 82(2) | 3(3) | 64(3) | 76(3) | 4(4) | 91(4) | 96(4) | |
| 91 | 22(1) | 3(2) | 7(2) | 82(2) | 64(3) | 76(3) | 91(3) | 4(4) | 96(4) | ||
| 92 | 88(1) | 3(2) | 7(2) | 82(2) | 91(2) | 64(3) | 76(3) | 4(4) | 96(4) | ||
| 93 | 3(1) | 7(2) | 76(2) | 82(2) | 91(2) | 4(3) | 64(3) | 96(4) | |||
| 94 | 76(1) | 4(2) | 7(2) | 82(2) | 91(2) | 64(3) | 96(4) | ||||
| 95 | 91(1) | 7(2) | 82(2) | 64(3) | 96(3) | ||||||
| 96 | 4(1) | 82(1) | 7(2) | 64(3) | 96(3) | ||||||
| 97 | 7(1) | 82(1) | 64(2) | 96(3) | |||||||
| 98 | 82(1) | 64(2) | 96(2) | ||||||||
| 99 | 64(1) | 96(1) | |||||||||
| 100 | 64(1) |
В данном конкретном примере, в 11 случаях из 12, была ситуация, когда в списке оставшихся свободных строк была, как минимум, одна строка, в которой осталась только одна свободная позиция. Если бы мы не использовали правило минимального риска, то не смогли бы дойти до конца. Так как одно «неверное движение» в выборе индекса свободной строки, с большой вероятностью привело бы к уничтожению единственной свободной позиции, которая имелась в одной из оставшихся свободных строк. Именно это является причиной того, что при использовании только алгоритма randSet x randSet или rand x rand для получения полного решения, на последних этапах, решение уходит в тупик.
Следует отметить, что алгоритм минимального риска имеет простой житейский смысл, и часто используется при принятии решений. Например, врач в первую очередь оперирует того больного, состояние которого наиболее критично для жизни, аналогично, фермер, во время сильной засухи, пытаясь спасти урожай, в первую очередь поливают те участки, которые находятся в наиболее критическом состоянии, …
7. Анализ эффективности работы алгоритма
Для оценки эффективности работы алгоритма при различных значениях n, был поставлен достаточно длительный (по совокупному времени) вычислительный эксперимент. Вначале был разработан достаточно быстрый алгоритм формирования массивов решений nQueens Problem для произвольного значения n. Потом, на основе этой программы были сформированы большие выборки решений для базового списка значений n. Размеры полученных выборок решений nQueens Problem для различных значений n, соответственно были равны: (10)--1000, (20, 30, …, 90, 100, 200, 300, 500, 800, 1000, 3000, 5000,10000)--10000, (30000, 50000, 80000)--5000, (105, 3*105)--3000, (5*105, 8*105, 106)--1000, (3*106)--300, (5*106)--200, (10*106)--100, (30*106)--50, (50*106)--30, (80*106, 100*106)--20. Здесь, в скобках указывается список значений n, а через двойное тире — размер выборки полученных решений. После этого, на основе каждой выборки решений формировались случайные композиции произвольного размера. Например, для каждого из 10000 решений для n=1000, было сформировано по 100 случайных композиций произвольного размера. В результате была получена выборка из одного миллиона композиций. Так как любая композиция произвольного размера, сформированная на основе существующего решения, может быть комплектована до полного решения хотя бы один раз, то задача состояла в том, чтобы на основе алгоритма решения n-Queens Completion Problem, комплектовать каждую композицию из сформированной выборки до полного решения. Так как в рассматриваемом алгоритме на каждом шаге проверяется правильность расстановки ферзя на шахматной доске, то здесь, в принципе, не могут быть False Positive решения (т.е. неверные решения, которые мы ошибочно считаем правильными). Однако, могут быть False Negative решения — в том случае, если какая либо композиция, сформированная на основе существующего решения, не будет комплектована программой до полного решения (хотя, мы знаем, что все композиции имеют решение). Проводя вычислительный эксперимент в таком широком диапазоне значений n, мы перед собой ставили следующие цели:
a) определить временную сложность работы алгоритма,
b) определить вероятность появления False Negative решений при различных значениях n,
c) определить частоту, с которой используется процедура Back Tracking при различных значениях n.
Результаты такого вычислительного эксперимента представлены в таблице 2.
| n | m | tmean | t90mean | tmin | tmax | FalseNeg | trow |
|---|---|---|---|---|---|---|---|
| 10 | 5000 | 0.001010 | 0.000532 | 0.000168 | 0.080673 | 2 | 1.0102 |
| 20 | 105 | 0.003589 | 0.001809 | 0.000197 | 0.363096 | 5 | 1.7945 |
| 30 | 105 | 0.008025 | 0.003793 | 0.000244 | 0.495716 | 10 | 2.6752 |
| 40 | 105 | 0.014323 | 0.009127 | 0.000252 | 0.965817 | 7 | 3.5807 |
| 50 | 105 | 0.005357 | 0.003589 | 0.000313 | 0.441711 | 9 | 10.7146 |
| 60 | 105 | 0.005991 | 0.004103 | 0.000340 | 0.013738 | 10 | 9.9852 |
| 70 | 105 | 0.006533 | 0.004566 | 0.000368 | 0.583897 | 8 | 9.3328 |
| 80 | 105 | 0.006975 | 0.004987 | 0.000394 | 0.635676 | 7 | 8.7187 |
| 90 | 105 | 0.006912 | 0.004763 | 0.000393 | 1.012710 | 4 | 7.6840 |
| 100 | 105 | 0.007264 | 0.005107 | 0.000419 | 0.692387 | 4 | 7.2641 |
| 300 | 105 | 0.013518 | 0.009496 | 0.000986 | 3.349766 | 3 | 4.5060 |
| 500 | 105 | 0.028194 | 0.014554 | 0.001541 | 4.558749 | 2 | 5.6388 |
| 800 | 105 | 0.049385 | 0.022735 | 0.002367 | 6.192782 | 1 | 6.1731 |
| 1000 | 106 | 0.062157 | 0.027727 | 0.002943 | 8.015123 | 0 | 6.2156 |
| 3000 | 105 | 0.177290 | 0.088507 | 0.008537 | 16.713140 | 0 | 5.9097 |
| 5000 | 105 | 0.159239 | 0.136047 | 0.014224 | 42.181080 | 0 | 3.1849 |
| 104 | 105 | 0.321003 | 0.270927 | 0.028594 | 79.321174 | 0 | 3.2100 |
| 3*104 | 104 | 0.968795 | 0.651618 | 0.084936 | 139.28827 | 0 | 3.2293 |
| 5*104 | 5000 | 1.147196 | 0.864045 | 0.143005 | 154.38225 | 0 | 2.2944 |
| 8*104 | 4000 | 2.112079 | 1.215612 | 0.229532 | 204.27321 | 0 | 2.6401 |
| 105 | 2000 | 2.253118 | 1.433197 | 0.290566 | 224.34623 | 0 | 2.2531 |
| 3*105 | 2000 | 4.330649 | 3.181905 | 0.990932 | 340.29584 | 0 | 1.4435 |
| 5*105 | 2000 | 5.985339 | 4.532205 | 1.488209 | 382.20016 | 0 | 1.1971 |
| 8*105 | 2000 | 8.297512 | 6.554302 | 2.902425 | 75.87513 | 0 | 1.0372 |
| 106 | 1000 | 11.376632 | 7.932194 | 2.954968 | 510.6265 | 0 | 1.1377 |
| 3*106 | 400 | 23.138609 | 18.521503 | 10.433580 | 122.7597 | 0 | 0.7713 |
| 5*106 | 300 | 33.103386 | 28.057816 | 14.937556 | 155.0890 | 0 | 0.6621 |
| 10*106 | 200 | 61.444001 | 52.269241 | 31.624475 | 228.3087 | 0 | 0.6144 |
| 30*106 | 50 | 149.71717 | 136.66441 | 84.556686 | 352.0534 | 0 | 0.4991 |
| 50*106 | 40 | 253.86220 | 228.93732 | 105.37934 | 558.4629 | 0 | 0.5077 |
| 80*106 | 30 | 372.29294 | 341.56397 | 250.80182 | 728.4806 | 0 | 0.4654 |
| 100*106 | 20 | 508.43573 | 474.04890 | 354.80864 | 831.3753 | 0 | 0.5084 |
Общий вывод, который можно сделать на основе полученных результатов, состоит в следующем:
a) Алгоритм работает достаточно быстро. Например, среднее время комплектации произвольной композиции для шахматной доски размером 1000 x 1000, полученное на основе одного миллиона вычислительных экспериментов, составляет 0.062157 секунды. Это означает, что если композиция имеет решение, то оно будет найдено сразу, после нажатия клавиши «Enter». Среднее время комплектации произвольной композиции, для всех значений n, в интервале от 7 до 30000, не превышает одной секунды.
b) В каждой выборке, имеется приблизительно до 10% композиций, для комплектации которых требуется намного больше времени. Такие композиции формируют длинный правый хвост в гистограмме распределения. Если исключить эти 10% композиций и провести расчеты для оставшихся 90% решений, то время счета (t90mean), окажется намного меньше. Например, для шахматной доски 1000 x 1000, среднее время счета будет равно 0.027727 секунды, что в 2.24 раза меньше среднего значения времени, полученной на основе всей выборки.
c) Для значений n≤800, в выборке композиций встречались такие, которые не удалось комплектовать до полного решения. Это False Negative решения. В пределах заданного в программе лимита, допускающего выполнение процедуры Back Tracking до 1000 раз, алгоритму не удалось комплектовать эти композиции. Они ошибочно были классифицированы как отрицательные композиции, т.е. такие, которые не имеют решение. Количество таких False Negative решений незначительно, и их доля в выборке меньше 0.0001. Далее, при увеличении значения n, доля False Negative решений уменьшается. Для всех значений n>800, в данной серии вычислительных экспериментов, не было ни одного случая False Negative решения. Однако очевидно, что если многократно увеличить размер выборки, то не исключается возможность появления False Negative решения, хотя вероятность такого события будет очень маленьким числом.
Временная сложность алгоритма. На рисунке 7 представлен график изменения среднего времени комплектации случайных композиций для различных значений n.

Рис. 7. Зависимость среднего времени комплектации (t) случайных композиций от размера (n ) матрицы решения.
По оси абсцисс отложен десятичный логарифм значения n, по оси ординат – логарифм, увеличенной в 1000 раз, среднего времени счета. Для наглядности, на рисунке также пунктиром указана линия диагонали данного квадранта. Видно, что время комплектации растет линейно, с увеличением значения n. На всем интервале значений n от 50 до 108 экспериментальные значения времени счета формируют прямую линию, которая с достаточно высокой корреляцией (R=0.9998) описывается уравнением линейной регрессии
log(1000*t) = — 0.628927 + 0.781568*log(n)
Небольшое отклонение от общей тенденции характерно только для значений n=(10, … 49), что связано с тем, что для решения задачи в этом диапазоне используется только пятый блок вычислений, алгоритм которого существенно отличается от работы алгоритмов первого и третьего блоков. В полученной зависимости линейный коэффициент (0.781568) меньше единицы, что приводит к тому, что с ростом значения n, линия регрессии и диагональ квадранта расходятся. Для того, чтобы наглядно объяснить причину такого расхождения вместо исходного времени, рассмотрим среднее время, которое необходимо для расположения одного ферзя на одной строке, т.е. разделим среднее время счета на значение n. Назовем такой показатель приведенным временем. Очевидно, что, если приведенное время не будет меняться с ростом значения n, то такое решение будет линейным ( O(n) ). Как видно из рисунка 8, где представлен график зависимости логарифма приведенного времени

Рис. 8 Зависимость среднего времени (trow), которое необходимо для расположения ферзя на одной произвольной строке, от размера (n) матрицы решения.
(tRow), увеличенного в 106 раз, от логарифма размера матрицы решения, в интервале значений n от 50 до 108, приведенное время уменьшается с ростом значения n. Если приведенное время для n=50 составляет 10.7146*10-6 секунд, то соответствующее время для n= 108 уменьшается в 21 раз и составляет 0.5084*10-6 секунд. Такое поведение алгоритма, на первый взгляд кажется ошибочным, так как нет объективных причин, почему при малых значениях n алгоритм будет считать медленнее, чем при больших значениях. Однако, здесь ошибки нет, и это является объективным свойством данного алгоритма. Связано это с тем, что данный алгоритм является композицией из трех алгоритмов, которые работают с разной скоростью. Причем, количество строк, обрабатываемых каждым из этих алгоритмов, изменяется с ростом значения n. Именно по этой причине растет время счета на начальном интервале значений n=(10, 20, 30, 40), так как все расчеты на этом маленьком участке проводятся только на основе пятого блока процедур, который работает очень эффективно, но не так быстро, как первый блок процедур. Таким образом, учитывая, что время счета, необходимое для расположения ферзя на одной строке, уменьшается с увеличением размера шахматной доски, временную сложность данного алгоритма можно назвать убывающей – линейной.
Число случаев использования процедуры Back Tracking (BT). Во всех случаях вычислительного эксперимента, мы отслеживали число случаев использования процедуры BT при решении каждой задачи. Производилось накопительное суммирование всех случаев использования BT, не зависимо от того, на какой базовый уровень происходил возврат, в процессе поиска решения. Это дало нам возможность определить для каждой выборки, долю тех решений, в которых процедура BT ни разу не использовалась. На рисунке 9 представлен

Рис. 9. Доля решений в выборке, в которых процедура Back Tracking ни разу не использовалась
график, который показывает как изменяется доля случаев решения без применения процедуры BT (Zero Back Tracking ) с увеличением значения n. Видно, что в интервале значений n= ( 7,…,100000 ), число решений, в которых ни разу не используется процедура BT, превышает 35%. Причем, в интервале значений n= ( 320,…,22500 ), число таких случаев превышает 50%. Наиболее эффективные результаты были получены для шахматной доски размером 5000 x 5000, где, в выборке из 10000 композиций, в 61.92% случаях выполнялось «детерминированное» решение не детерминированной задачи, т.к. процедура BT в 61.92% случаях ни разу не использовалась. В оставшихся решениях, в 21.87% случаях процедура BT использовалась 1 раз, в 9.07% случаях — 2 раза, и в 3.77% случаях — 3 раза. В совокупности это составляет 96.63% случаев. Тот факт, что после значения n=5000, число случаев решения задачи комплектации без применения процедуры BT постепенно уменьшается, связан с выбранной моделью подбора граничных значений baseLevel2 и baseLevel3. Можно изменить данные параметры и добиться увеличения числа решений без применения процедуры BT. Однако, это приведет к увеличению времени счета, так как увеличится доля участия пятого блока в работе алгоритма.
Гистограмма распределения времени комплектации. На рисунке 10, для значения n=1000 представлена гистограмма распределения времени комплектации для одного миллиона решений. Не совсем обычный вид гистограммы распределения (который, скорее напоминает ночной силуэт высотных зданий) не связан с ошибкой в подборе длины или количества интервалов. Это естественное свойство работы данного алгоритма. Чтобы понять,

Рис. 10. Гистограмма времени комплектации композиций произвольных размеров. (n=1000; размер выборки = 1000000)
почему гистограмма имеет такую форму, рассмотрим распределение времени комплектации для композиций, которые имеют одинаковый размер. Для этого, в качестве примера, из исходной выборки отберем все композиции, размер которых равен 800. Таких композиций оказалось 998 в выборке из одного миллиона. На рисунке 11 представлена гистограмма распределения времени счета для этой выборки. Из рисунка видно, что распределение состоит из шести отдельных гистограмм, с убывающими размерами.

Рис. 11. Гистограмма времени комплектации композиций одинакового размера (k=800). (n=1000; размер выборки = 998)
Причиной того, почему время комплектации 998 композиций, в каждой из которых случайно распределены 800 ферзей, «кластеризуется» в 6 групп, является использование процедуры Back Tracking. Первая гистограмма на рисунке, с максимальным размером выборки, это те решения комплектации, где ни разу не использовалась процедура BT. Это группа самых быстрых решений. Вторая гистограмма, которая значительно меньше по размеру, чем первая, это те решения, в которых процедура BT использовалась только один раз. Поэтому время решения в данной группе чуть больше, чем в первой. Соответственно, в третьей группе процедура BT использовалась два раза, в четвертой – три раза и т.д., т.е. решения, в которых процедура BT использовалась многократно, выполнялись за более длительное время. Такие решения формируют длинный правый хвост искомого распределения.
False Negative решения. Если разделить все возможные композиции для произвольного значения n, на положительные и отрицательные, то среди положительных композиций найдутся такие, которые данный алгоритм может классифицировать как отрицательные. Это связано с тем, что в пределах установленных ограничений по параметрам поиска, алгоритму не удается найти верный путь для комплектации подобных композиций. Как показывают результаты экспериментов (Таблица 2), число таких случаев не превышает 0.0001 от размера выборки и величина этой ошибки уменьшается с ростом значения n. Кроме того, для всех значений n >800 не было ни одного случая False Negative решения. Даже увеличение размера выборки до одного миллиона для значения n=1000, не привело к появлению False Negative решений. Полученный результат позволяет нам формулировать следующее правило решения поставленной задачи: «Любая случайная композиция из k ферзей, которая непротиворечиво распределена на произвольной шахматной доске размером n x n, может быть комплектована до полного решения, либо будет принято решение, что данная композиция является отрицательной, и не может быть комплектована. Вероятность ошибки принятия такого решения не превышает значение 0.0001. С увеличением размера шахматной доски, вероятность принятия ошибочных решений уменьшается. Временная сложность работы алгоритма является линейной».
8. Выводы
1. Представлен алгоритм, который, позволяет за линейное время решить задачу о комплектации до полного решения случайной композиции из k ферзей, непротиворечиво распределенных на шахматной доске произвольного размера n x n. При этом, для любой композиции из k ферзей (1≤ k < n) предоставляется решение, если оно есть, либо принимается решение, что данная композиция не может быть комплектована. Вероятность ошибки принятия такого решения не превышает 0.0001, и эта величина уменьшается с увеличением размера шахматной доски.
2. Работа данного алгоритма основана на использовании двух важных правил:
a) На завершающем этапе решения задачи, из всех оставшихся свободных строк, отбирается та, у которой число свободных позиций минимально (правило минимального риска). Это позволяет минимизировать риски, связанные с возможностью исключения последних свободных позиций, в некоторых из оставшихся строк.
b) Из всех свободных позиций в рассматриваемой строке, отбирается та позиция, которая наносит минимальный ущерб свободным позициям в оставшихся свободных строках (правило минимального ущерба). Под «минимальным ущербом», подразумевается выбор такой позиции в строке, которая исключает наименьшее количество свободных позиций во всех оставшихся свободных строках.
3. Установлено, что в результате работы данного алгоритма, среднее время, которое необходимо для расположения ферзя на одной строке, уменьшается с ростом значения n. Среднее время, необходимое для расположения ферзя на одной строке в случае, когда n равняется 108 в 21 раз меньше соответствующего времени для случая n=50.
4. Установлено, что в интервале значений n= ( 7,…,100000) число решений, в которых ни разу не используется процедура Back tracking, превышает 35%. Причем, в интервале значений n= ( 320,…,22500), число таких случаев превышает 50%, что говорит о высокой эффективности данного алгоритма.
5. Предложена модель организации процедуры Back Tracking, на основе разделения последовательности шагов решения на базовые уровни. Под уровнем подразумевается некоторый шаг решения с заданным количеством правильно расставленных ферзей. Приводятся регрессионные формулы для расчета значений второго и третьего базовых уровней в зависимости от n.
6. Приводятся результаты сравнительного анализа двух методов случайного отбора, которые получили название randSet & randSet и rand & rand. Установлено, что алгоритм randSet & randSet работает быстро, но грубо. Поэтому его применение ограничивается при достижении второго базового уровня. После этого используется алгоритм rand & rand, который выполняется не столь быстро, но более эффективно расставляет ферзи на шахматной доске.
7. Приводится эффективный алгоритм проверки правильности решения n-Queens Problem. Данная программа предназначена также для проверки правильности случайной композиции произвольного размера. Программа работает достаточно быстро. Например, время, необходимое для проверки решения, состоящего из 5 миллионов позиций, составляет 0.85 секунды.
9. Замечания
1. Как было указано в начале статьи, исследования проводились в диапазоне значений n, от 7 до 100 миллионов. Однако, программа тестировалась в более широком диапазоне значений n, вплоть до одного миллиарда. Правда, в последнем случае пришлось слегка адаптировать программу, учитывая большие размеры массивов. Поэтому, если позволяет размер оперативной памяти, то можно проводить расчеты для больших значений n.
2. Значения показателей базового уровня, а также граничные значения числа повторений на различных уровнях, были оптимизированы для решения задачи в пределах всего диапазона исследований. Их можно изменить в пределах меньшего диапазона и добиться уменьшения времени счета. Важно, чтобы при этом не увеличить долю False Negative решений.
3. В этой статье я использовал время нажатия клавиши Enter как некую меру времени, для оценки того, насколько быстро работает алгоритм. Если результат появляется сразу после нажатия клавиши, то на уровне восприятия пользователя кажется, что программа работает «очень» быстро. Независимо от того, насколько быстро работает алгоритм, результат появится на экране не раньше, чем будет завершено нажатие клавиши. Поэтому мне показалось, что такая условная мера времени может служить пороговым уровнем для не строго сравнения скорости различных алгоритмов.
4. Философское … В ходе исследования было рассмотрено большое количество публикаций, связанных с решением не детерминированных задач. В большинстве случаев это были задачи, в которых необходимо было сделать выбор в большом пространстве состояний в условиях заданных ограничений. Сравнивая их, было интересно узнать, насколько далеко можно продвинуться в решении таких задач с использованием стандартного математического подхода. У меня сложилось впечатление, что только на основе определений, формулировке лемм и доказательстве теорем невозможно решить такие проблемы. Мне кажется, что для решения таких задачах необходимо использовать методы алгоритмической математики, используя компьютерное моделирование. Чтобы продемонстрировать обоснованность этого вывода, в качестве простого примера я подготовил для шахматной доски, размер которого составляет 109 х 109 две композиции одинакового размера, состоящие из 999 999 482 ферзей. Они подготовлены так, как описано в начале статьи, и представлены в виде двух файлов в формате .mat. Их можно загрузить по данной ссылке (Два тестовых файла). Файлы достаточно «тяжелые», размер каждого из них составляет около 3.97 Gb. В 999 997 976 строках (в 99.9998 % случаях) позиции ферзей в обеих композициях совпадают, и лишь в произвольных 1506 строках позиции ферзей различаются.
Чтобы комплектовать данные композиции до полного решения, нужно правильно расставить ферзи в оставшихся 518 свободных строках. Число возможных способов расстановки 518 ферзей в оставшихся свободных строках (с учетом только числа способов выбора свободной позиции в отобранной строке), составляет примерно 101466. Различие этих двух композиций состоит только в том, что одна из них является положительной и может быть комплектована до полного решения, а другая композиция является отрицательной – ее невозможно комплектовать до полного решения. Вопрос: «Можно ли на основе строгого математического подхода (т.е. без проведения алгоритмических вычислительных операций), определить, какая из этих двух композиций является положительной?» Если это невозможно решить, то можно считать, что высказанное суждение доказано методом от противного.
Хочу отметить, что каким бы не был подход к строго математическому решению данной задачи, здесь нужно определить статус 518*109 ячеек в оставшихся свободных строках. Для этого необходимо рассмотреть каждую позицию ранее установленных ферзей, а их почти один миллиард, чтобы установить ограничения, которые накладывает каждый установленный ферзь на свободные позиции в оставшихся 518 строках. Я не нашел «точку опоры», которая позволила бы выполнить эту работу лишь на основе строго математического подхода, без алгоритмических вычислений.
Я привел здесь минимальный пример, состоящий только из двух композиций. При необходимости, количество таких композиций можно увеличить.
Следует отметить, что на основе предложенного линейного алгоритма, слегка адаптированного для работы с композициями большого размера, задач о том, какая из двух тестовых композиций может быть комплектована до полного решения, выполняется на desktop-13, примерно за 4.5 минуты (без учета времени загрузки входных данных).
10. Дополнение
Заслуживает уважение действие профессоров, которые рекомендуют способным студентам сложные задачи для разработки и исследования. Это требует значительных усилий, но преодолев трудности, исследователь иначе смотрит на другие сложные задачи. Я подумал, что было бы полезно расширить варианты постановки n-Queens Problem для таких целей. Если посмотреть на одну и ту же задачу с разных позиций, то можно увидеть разные вещи. Ниже сформулированы некоторые из них.
1. Рассмотрим задачу расстановки n ферзей на прямоугольной «шахматной» доске размером n x m. Обозначим k = m — n. Пусть получено некоторое решение, и в каждой из n строк было расположено по одному ферзю. Исключим те позиции, где расположены ферзи из дальнейшего рассмотрения. Теперь в каждой строке осталась m-1 свободная позиция. В пределах оставшихся свободных позиций, снова найдем одно решение. Как и прежде, исключим из дальнейшего рассмотрения позиции, где расположены ферзи второго решения. Теперь в каждой строке осталось m-2 свободных позиций. Очевидно, что первое и второе решение по своим позициям ни в одной строке не пересекаются – они ортогональны. Требуется определить максимальное количество взаимно ортогональных решений для различных значений k. Если будет найдено n взаимно ортогональных решений для значения k=0, то тем самым будет построен королевский латинский квадрат (Queens Latin Square).
Замечание. В работе Grigoryan E. (2018) было показано, что для любого решения n-Queens Problem существует комплементарное решение, которое с ним не пересекается. Это означает, что для произвольного значения n, множество всех решений n-Queens Problem делится на два равных по размеру подмножества. Любое решение из второго подмножества является комплементарным решением соответствующего решения из первого подмножества. Правило достаточно простое, если Q1( i ) некоторое решение из первого множества, то соответствующее комплементарное решение Q2( i ) из второго подмножества определяется по формуле Q2( i ) = n+1 – Q1( i ), где i=(1,…,n). Именно это правило объясняет тот факт, что число всех решений n-Queens Problem, для произвольного значения n, всегда является четным числом. (Это правило позволяет сократить в два раза время расчета всех полных решений для произвольного размера n шахматной доски. Если обозначить через 2*k общее число всех решений, то значение k равно индексу в последовательном списке всех решений, когда Q( k ) + Q( k+1 ) = n+1 ).
2. В исходной постановке задачи n-Qeens Problem, после расположения ферзя в позицию ( i, j ), выполняются следующие действия:
a) исключаются все ячейки строки i и столбца j
b) исключаются все ячейки, которые расположены на линии левой и правой диагоналей, проходящих через ячейку ( i, j ).
Изменим условие b) в постановке задачи. Вместо исключения ячеек, воспользуемся переключением ячеек. Если ячейка, расположенная на линии левой или правой диагоналей свободна, то мы ее закроем, если ячейка закрыта – то мы ее откроем. Это облегчает возможность поиска решения. Однако, вместо квадратной матрицы n x n, будем рассматривать прямоугольную матрицу размером n x ( n – k ). Требуется, для заданного значения n, найти максимальное значение k, при котором можно получить не менее трех ортогональных решений. Как будет меняться значение k, с увеличением значения n?
3. Изменим некоторые условия в исходной постановке задачи n-Queens Problem. При расположении ферзя в позицию ( i, j ) на шахматной доске размером n x n:
a) исключим все ячейки в строке i,
b) если индекс j четное число, то:
b1) исключим ячейки в четных строках столбца j,
b2) исключим ячейки в четных строках, пересекающихся с левой и правой диагоналями, проходящими через ячейку ( i, j ),
с) Если индекс j нечетное число, то пункты b1) и b2) выполняются для ячеек, расположенных на нечетных строках.
3.1 Известно (Sloane-2016), что список значений всех решений nQueens Problem, для n=(8, 9, 10, 11, 12, 13, 14, 15, 16), соответственно составляет (92, 352, 724, 2680, 14200, 73712, 365596, 2279184, 14772512). Как изменится количество всех решений, если в постановке задачи стандартное условие диагональных исключений изменить на пункт b) или на пункт c)?
3.2 Известно Grigoryan (2018), что если определить частоту участия различных ячеек матрицы решения в формировании списка всех решений, то можно обнаружить, что между всеми ячейками существуют гармоничные отношения в виде вертикальной и горизонтальной симметрии соответствующих частот. Это означает, что если принять, что k<n/2, то частота ячеек k-ой строки будет идентична частотам ячеек строки n-k+1. Аналогично, частота ячеек k-го столбца будет идентична частотам ячеек столбца n-k+1. Вопрос: «Как изменятся эти гармоничные отношения в условиях поставленной задачи?»
4. Все клетки шахматной доски по своему цвету разделяются на два класса. Принято считать, что один цвет белый, другой – черный. Рассмотрим две шахматные доски и расположим одну из них на другую так, чтобы края полностью совпали. В результате получим «сэндвич» из двух шахматных досок, у которых расположение белых и черных клеток совпадают. Задача состоит в том, чтобы найти решения одновременно на двух досках, соблюдая следующие условия:
a) Если на одной из досок ферзь располагается на черной ячейке с индексами ( i, j ), то:
— на обеих досках исключаются все черные ячейки, которые встречаются на строке i и на столбце j,
— на обеих досках исключаются все черные ячейки, которые расположены вдоль левой и правой диагоналей, проходящих через ячейку ( i, j ).
b) Если на одной из досок ферзь располагается на белой ячейке с индексами ( i, j ), то выполняются все действия пункта a) только для белых ячеек.
5. Представим, что в матрице решения размером n x n, строки могут скользить друг относительно друга вправо или влево, с шагом в k клеток. Причем, если предыдущая строка была смещена, например, влево, то следующая строка должна быть смещена вправо, т.е. каждая следующая строка смещается в направлении противоположной смещению предыдущей строки. В результате такого построения получим прямоугольную матрицу размером n x (n+k), где в каждой строке будут исключены из рассмотрения k ячеек от начала строки или от конца. Задача состоит в том, чтобы для произвольного значения n, найти максимальное значение k, при котором существует хотя бы одно решение n-Queens Problem.
Рассмотреть вариант задачи, при котором смещение одной строки по отношению другой, является случайным числом в пределах от k1 до k2.
6. Одномерная формулировка nQueens Problem. Пусть, на полуоси отложены n отрезков произвольной длины, пронумерованных от 1 до n. Разделим каждый отрезок на n ячеек произвольного размера, и в пределах каждого отрезка, пронумеруем ячейки от 1 до n. Назовем такие ячейки открытыми. Требуется закрыть по одной ячейке на каждом отрезке, учитывая следующие ограничения:
а) Мы можем выбрать открытую ячейку с номером j из i-го сегмента, если:
D1 ( r ) = 0;
D2 ( t ) = 0;
где r = n + j – i, t = j + i, D1 и D2 — одномерные контрольные массивы, состоящие из 2n ячеек, которые были ранее обнулены.
б) После такого выбора будут закрыты сегмент i и ячейки с номером j во всех оставшихся свободных сегментах. Также необходимо закрыть соответствующие ячейки в контрольных массивах:
D1 ( r ) = 1;
D2 ( t ) = 1;
В такой постановке задача полностью идентична исходной. Представляет интерес постановка этой задачи с другими условиями ограничения. Например, если вместо формул:
r = n + j – i, t = j + i, ,
будут рассматриваться другие соотношения, которые функционально связывают индексы r и t с индексами (i, j) матрицы решений.
7. Формулировка задачи на основе урны с шарами (идентична предыдущей формулировке). Пусть имеется n урн, пронумерованных от 1 до n, и в каждой урне находится n шаров, также пронумерованных от 1 до n. Требуется из каждой урны отобрать по одному шару, учитывая следующие ограничения:
а) Мы можем выбрать шар с номером j из i-ой урны, если:
D1 (r ) = 0,
D2 ( t ) = 0,
где r = n + j – i, t = j + i, D1 и D2 — одномерные контрольные массивы, состоящие из 2n ячеек, которые были ранее обнулены.
б) После такого выбора будут закрыты урна i и шары с номером j во всех оставшихся свободных урнах. Также необходимо закрыть соответствующие ячейки в контрольных массивах:
D1 ( r ) = 1,
D2 ( t ) = 1.
В такой постановке задача полностью идентична исходной. Как и в предыдущем случае, представляет интерес постановка этой задачи с другими условиями, которые функционально связывают индексы r и t с индексами (i, j) матрицы решений.
8. Игра. Рассмотрим шахматную доску размером n x n. Вернем ферзям цвет, пусть одни ферзи имеют белый цвет, другие – черный. Так же вернем чередующийся белый и черный цвет клеткам шахматной доски, исходя из того, что клетка с индексом (1, n) должна быть белого цвета. Все клетки в начале игры считаются свободными. Первый ход делают белые ферзи. Игрок располагает ферзь в произвольную свободную клетку с индексами ( i, j ). Пусть это будет клетка белого цвета. В результате такого выбора закрываются:
a) все белые клетки строки i,
b) все белые клетки столбца j,
c) все белые клетки, которые лежат на левой и правой диагоналях, проходящих через клетку ( i, j ).
Если клетка ( i, j ) окажется черного цвета, то выполняются все пункты (a,b,c), и соответственно, закрываются все клетки черного цвета. Далее, ход выполняют черные, располагая ферзь в любую из оставшихся свободных клеток. После этого, аналогичным образом, закрываются клетки, как описано выше. Время на обдумывание очередного хода является фиксированной, и выбирается по согласованию сторон. Если в течение указанного времени, один из игроков не выполняет свой ход, то игра передается другому. Игра завершается, если оба игрока, один за другим, не выполнят свой ход за указанное время. Выигрывает тот, кто сможет расположить на доске больше ферзей.
9. О стабильности случайного отбора. Рассмотрим модель randSet & randSet. В результате сравнения n случайных пар индексов строки и столбца, на первом этапе цикла, удается установить ферзи в среднем на k*n строках. Значение k можно считать постоянной величиной, равной 0.6. Ее значение меняется от величины 0.605701 при n=10, и до 0.599777, при n=106, причем, с ростом значения n, дисперсия этой величины уменьшается. С чем связано такое «постоянство»? Почему, при случайном отборе индекса строки и индекса позиции ферзя в этой строке, на основе двух списков чисел, полученных на основе случайной перестановки чисел от 1 до n, удается непротиворечиво расположить ферзи (в среднем) на 60% строках?
10. Пусть размер шахматной доски равен n x n. На основе процедуры randSet & randSet расположим ферзи на шахматной доске до тех пор, пока ветвь поиска не достигнет тупика. Обозначим длину, полученной таким образом композиции, через k. Если, для заданного значения n повторить эту процедуру многократно, и построить гистограмму распределения значений k, то окажется, что изменение частот наступления событий до значения моды распределения, отличается от изменения частот наступления событий после этого значения. Если на основе модального значения разделить гистограмму на две части, то левая часть не будет совпадать с правой частью. Эта закономерность характерна для любого значения n. Почему после перехода длины композиции через модальное значение, частота наступления событий принимает другую форму? Под событием мы понимаем получение композиции заданного размера, до достижения состояния тупика.
Литература
1. Nauck,F.(1850). Briefwechsel mit allen fur alle. Illustrierte Zeitung, 15, 182.
2. Gent,I.P., Jefferson,C. & Nightingale,P.(2017). Complexity of n-Queens completion,
Journal of Artificial Intelligence Research., 59, 815-848.
3. Sosic, R., & Gu, J. (1990). A polynomial time algorithm for the n-queens problem. SIGART Bulletin, 1 (3), 7–11.
4. Richards, M. (1997). Backtracking algorithms in MCPL using bit patterns and recursion.
Tech. rep., Computer Laboratory, University of Cambridge.
5. Randomization Methods in Algorithm Design, Proceedings of a DIMACS Workshop, Princeton, New Jersey, USA, December 12-14, 1997. DIMACS Series in Discrete Mathematics and Theoretical Computer Science 43, DIMACS/AMS 1999, ISBN 978-0-8218-0916-7
6. Grigoryan E. (2018). Investigation of the Regularities in the Formation of Solutions n-Queens Problem. Modeling of Artificial Intelligence, 5(1), 3-21
7. Sloane N.-J. A. (2016). The on-line encyclopedia of integer sequences.