Жизнь Джона Конвея
Полагаем, всем программистам хорошо известен клеточный автомат жизнь (или эволюция), придуманный английским математиком Джоном Конвеем в 1970 году. Возможно, некоторые даже корпели над самописной программой, моделирующей клеточный автомат Конвея.
Вкратце напомним, суть модели Конвея.
1. Модель представляет собой поле конечное или бесконечное (то есть замкнутое) поле, состоящее из клеток.
2. Каждая клетка может быть либо заполненной (то есть живой), либо пустой (то есть мёртвой).
3. Состояние поля изменяется пошагово, каждое последующее состояние рассчитывается из предыдущего по правилам.
3.1. В мёртвой клетке, рядом с которой находится ровно три живые, зарождается жизнь.
3.2. Если рядом с живой клеткой находится две или три живые клетки, то она продолжает жить.
3.3. Если рядом с живой клеткой находится меньше двух или больше трёх живых клеток, то она умирает (то есть либо от одиночества, либо от перенаселённости).
Несмотря на простоту правил, модель впечатляет своим сходством с развитием популяций примитивных организмов. Наверное, каждого посещала мысль, что, немного видоизменив правила, можно добиться ещё большего сходства модели с поведением живых организмов.
Новая жизнь
Новая модель также будет представлять собой бесконечное (замкнутое) поле, состоящее из клеток. В каждой клетке может располагаться только один простейший организм, который условно назовём растением. Изначально поле может содержать в каждой клетке некоторое количество ресурса, необходимое для питания растений.
Наделим растение такими параметрами: a) начальная масса (в единицах), b) питание ресурсом (в единицах), c) продолжительность жизни (в тактах), d) репродуктивный возраст (в тактах), e) количество семян для размножения.
Состояние поля также будет меняться пошагово по определённым правилам.
1. С каждым шагом масса растения увеличивается на величину питания b. Соответственно, масса ресурса в клетке, где произрастает растение, уменьшается на эту же величину. Если в клетке больше нет ресурса для питания, растение погибает от голода.
2. Возраст растения увеличивается с каждым тактом на единицу.
3. Достигнув репродуктивного возраста d, или зрелости, растение разбрасывает в соседние клетки (так называемая окрестность Мура) семена количеством e, каждое из которых имеет начальную массу a. При этом масса родительского растения уменьшается на общую массу семян. Семян может меньше, поскольку масса родительского растения не может быть меньше начальной массы a. Если семя попадает в клетку, которая уже занята, то оно превращается в ресурс.
4. Достигнув максимального возраста c, или продолжительности жизни, растение умирает от старости. Масса почившего растения увеличивает массу ресурса в клетке.
Из этих правил сразу следуют следующие выводы.
Вывод 1. Общая масса ресурсов и растений в любой момент системы постоянна.
Вывод 2. Если в клетке ресурса меньше, чем требуется растению для достижения зрелости (то есть значения bd), то растение умрёт, не дав потомства.
Эксперимент 1.1. Благоприятная среда
Поместим в поле одно растение вида Lime, у которого определим значения параметров: a) начальная масса — 1 единица, b) питание ресурсом — 1 единица, c) продолжительность жизни — 10 тактов, d) репродуктивный возраст — 5 тактов, e) количество семян для размножения — 3 штуки.
Из этих значений заключаем, что клетка поля должна содержать хотя бы 5 единиц ресурса для роста и размножения растения. Равномерно заполним поле таким образом, чтобы в каждой клетке содержалось 7 единиц ресурса Yellow (рис. 1), и запустим процесс моделирования. Вид Lime быстро расплодится и заполнит всё поле обитания (рис. 2).


Вывод 3. При благоприятных условиях вид быстро охватывает всю доступную среду обитания.
Вывод 4. При благоприятных условиях жизнь может продолжаться практически бесконечно.
Эксперимент 1.2. Неблагоприятная среда
Поместим тот же самый вид растения Lime (эксперимент 1) на другое поле, где количество ресурсов ограничено, и, соответственно, ограничен ареал обитания (рис. 3). Запустив процесс моделирования, можно наблюдать, как вид, несмотря на ограничение, медленно увеличивает ареал обитания (рис. 4).


Ареал увеличивается, однако в каждой отдельной клетке количество ресурса уменьшается. Наконец, в клетках перестаёт хватать ресурса для достижения зрелости, и вид вымирает (рис. 5).

Вывод 5. Вид стремится увеличить ареал обитания.
Вывод 6. В процессе жизнедеятельности ресурсы распределяются по всему полю практически равномерно.
Вид не сумел выжить в неблагоприятной среде, поскольку оказался неприспособленным. Если в данном эксперименте у вида Lime изменить значения некоторых параметров, то можно добиться выживаемости. Например, можно уменьшить репродуктивный возраст у растения до 3 тактов.
Однако подбирать значения вручную не так увлекательно. Но не будем забегать вперёд и продолжим.
Эксперимент 1.3. Конкуренция
В следующем эксперименте в благоприятную среду (поле, равномерно заполненное ресурсом Yellow) поместим два вида растений — Lime и Teal (рис. 6). Значения параметров у обоих видов одинаковые (эксперимент 1), они отличаются лишь цветом, чтобы их можно было отличать визуально.
Запустив процесс моделирования, можно наблюдать, как растения заполняют всё поле (рис. 7). Конечно, эти два вида не могут явно биться друг с другом, однако они сосуществуют на одном поле, конкурируя между собой. Порой больше размножается один вид, порой — другой вид, хотя ни у одного из них нет преимущества перед другим.
Не исключено, что это противостояние не вечно, и один из видов, расплодившись, выживет другой. Но жизнь в благоприятной среде в любом случае будет продолжаться.

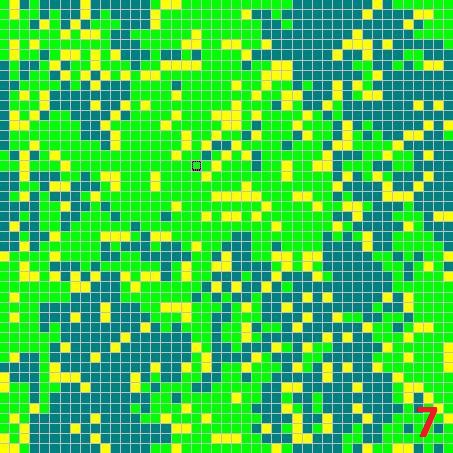
Вывод 7. Если виды одинаково приспособлены к среде, то нельзя сказать с определённостью, какой из них выживет, а какой вымрет.
Эксперимент 1.4. Симбиоз
Равномерно распределим по полю два ресурса: Yellow и Olive. Поместим в благоприятную среду те же два вида растений Lime и Teal (рис. 8). Все значения параметров у них идентичны и такие же, как в первом эксперименте, но с небольшим исключением. Вид Lime питается ресурсом Yellow, а после смерти превращается в ресурс Olive. Вид Teal питается ресурсом Olive, а после смерти превращается в ресурс Yellow. Очевидна взаимосвязь двух видов растений: они могут выжить только вместе.

Запустив процесс моделирования, можно увидеть, как сначала виды расходятся кругами от первоначальной клетки (рис. 9), каждый выедая в клетках свой питательный ресурс. Затем ожидаемо виды меняются местами обитания (рис. 10). В отличие от предыдущего эксперимента, чрезмерным размножением один вид создаёт лучшие условия не для себя, а для своего визави.
Вывод 8. При взаимозависимости двух видов вымирание одного вида тотчас же повлечёт вымирание другого.


Усложним эксперимент. Заполним поле тремя ресурсами Yellow, Olive, Purple и поместим в получившуюся среду три взаимозависимых вида растений — Lime, Teal и Green (рис. 11). Все значения параметров у них идентичны и такие же, как в первом эксперименте, но с небольшим исключением.
Вид Lime питается ресурсом Yellow, а после смерти превращается в ресурс Olive. Вид Teal питается ресурсом Olive, а после смерти превращается в ресурс Purple. Вид Green питается ресурсом Purple, а после смерти превращается в ресурс Yellow.

Запустив процесс моделирования, со временем можно наблюдать любопытные волнообразные (рис. 12) или спиралевидные (рис. 13) структуры, состоящие из разных видов. Вымирание одного вида тотчас же повлечёт вымирание и двух оставшихся видов.


Заключение
Несмотря на внешнюю простоту, клеточные автоматы представляют довольно широкие возможности для моделирования самых различных систем, и в небольшой статье мы постарались представить несколько интересных примеров моделирования простейших псевдобиологических систем.
Возможно, выводы, сделанные в статье, довольно очевидны, но в данном случае все они подкреплены результатами моделирования.
Источники
https://ru.wikipedia.org/wiki/Игра_«Жизнь»
https://ru.wikipedia.org/wiki/Клеточный_автомат