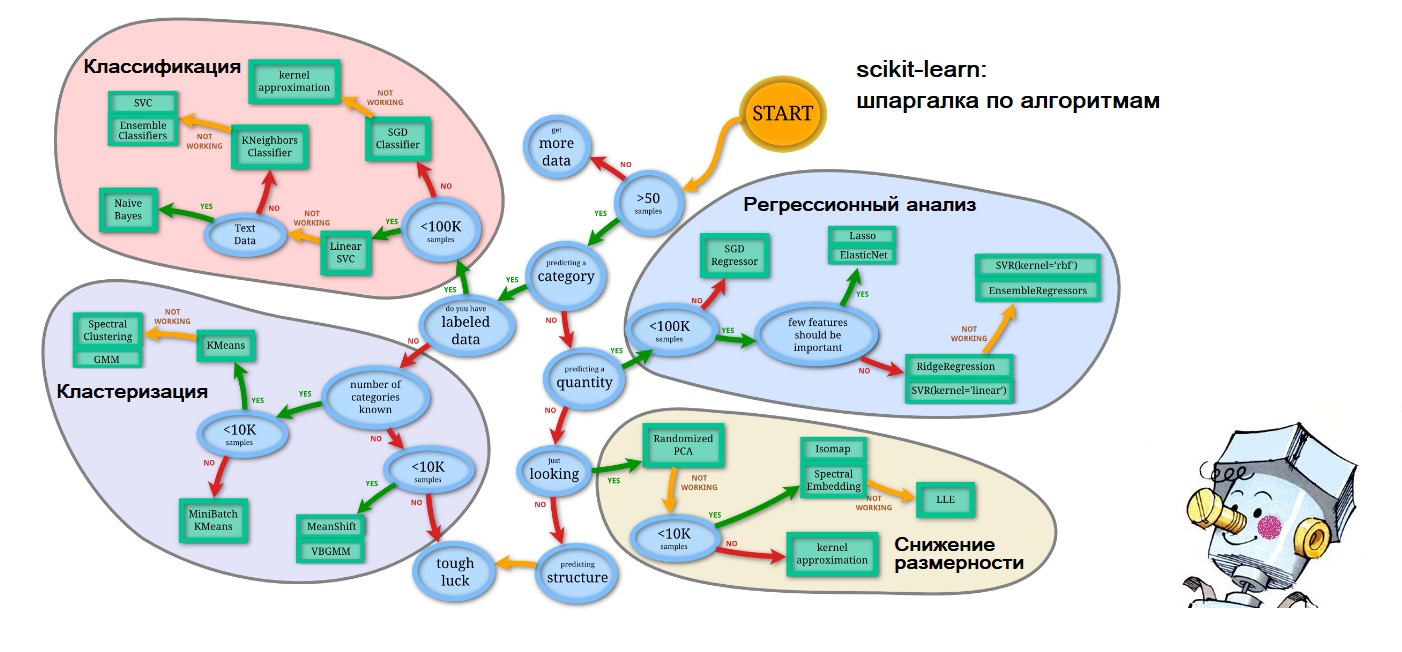
Глобальная паутина изо дня в день пополняется статьями о популярных, наиболее употребляемых алгоритмах машинного обучения для решения различных задач. Причём основа этих статей, немного изменённая по форме в том или ином месте, кочует от одного исследователя данных к другому. При этом все эти работы объединяет один общепринятый, непреложный постулат: применение того или иного алгоритма машинного обучения зависит от размера и природы имеющихся в распоряжении данных и поставленной задачи.
Вдобавок к этому особо настоявшиеся исследователи данных, делясь своим опытом, подчёркивают: «Выбор метода оценки должен частично зависеть от ваших данных и от того, в чём, по вашему мнению, модель должна быть хороша» («Data Science: инсайдерская информация для новичков. Включая язык R», авторы Кэти О’Нил, Рэйчел Шатт).
Другими словами, за плечами статистика/исследователя данных должен быть не только опыт в предметной области, но и широкий багаж разношёрстных знаний: «Исследователь данных – тот, кто обладает познаниями в следующих сферах: математика, статистика, вычислительная техника, машинное обучение, визуализация, средства обмена данными…» (из той же книги). Только основательно загрузив в голову познания из вышеупомянутых областей можно подступать к машинному обучению и находить решения обозначенных проблем.
Как по мне, подобное начало вполне годится для какой-нибудь очередной полуторакилограммовой книги по Data Science, либо научной статьи-страшилки с последующими «ниочёмными» двухэтажными формулами, символами и закорючками, оказывающими гнетущее, тягчайшее воздействие на новичков в области машинного обучения и просто случайно заинтересовавшихся данным направлением неискушённых читателей, не обременённых «необходимыми знаниями». К тому же круглое число 10 из тех же статей про 10 наиболее популярных алгоритмов машинного обучения (к примеру) только усиливают накладываемый эффект.
На habr’е также отличились: «Ответ на вопрос: “Какой алгоритм машинного обучения использовать?”- всегда звучит так: “Смотря по обстоятельствам”. Выбор алгоритма зависит от объёма, качества и природы данных. Он зависит от того, как вы распорядитесь результатом. Он зависит от того, как из алгоритма были созданы инструкции для реализующего его компьютера, а ещё от того, сколько у вас времени. Даже самые опытные специалисты по анализу данных не скажут вам, какой алгоритм лучше, пока сами не попробуют».
Бесспорно, все эти знания, а также упорство и интерес необходимы и пригодятся в достижении хороших результатов не только на пути постижения машинного обучения, но и во многих других направлениях. К тому же они облегчат понимание того, что алгоритмов машинного обучения (далее – алгоритмов) далеко не один десяток; но это уже потом, при самостоятельном изучении.
Моя цель – познакомить читателя с наиболее используемыми алгоритмами с практической и доступной точки зрения. (Подстелить интерес в повествовании должен тот факт, что я отнюдь не программист и – уж тем более – не математик (свят-свят-свят!). Инженерное образование плюс опыт в «предметной отрасти» размером 10 лет (прямо какое-то магическое число) – вот, как говорится, и все мои вещи, весь мой багаж, с которым я пошёл в лоб на машинное обучение. Благодаря накопившемуся опыту в «нефтянке», идеи применения искусственных нейронных сетей и алгоритмов машинного обучения нашлись сразу (читай – имелись необходимые наборы данных). Оставалось лишь разобраться с малым – научиться крутить-вертеть данными, чтобы корректно подать их на вход «программы» и какой, собственно, алгоритм выбрать. И далее по замкнутому кругу. Отмечу, что путь мой был тернистым и весёлым — «пули свистели над головой» (из м/ф «Приключения Фунтика»), — но всё же мне удавалось делать заметки, и если обозначится интерес, то в будущем опубликую и другие сообщения.)
Итак, предлагаю подступиться к «машинлёрнингу» с другой стороны: почему бы не скормить имеющийся у вас набор данных (в примерах будут подгружены наборы данных, хорошо поддающийся обучению) множеству алгоритмов сразу, а по результатам решить, каким из них уделить более пристальное внимание с последующим тщательным изучением и подбором оптимальных параметров, усиливающих результат. Более того, главная ценность метода, о котором речь впереди, в том, что его результаты позволят ответить на вопрос, чего стоит ваш набор данных: «начинайте с решения задачи и убедитесь в том, что вам есть что оптимизировать» (тоже от какого-то настоявшегося статистика пошло, «респект» ему, совет дельный!).
How it is made?
Известно, что основная масса задач, решаемых при помощи алгоритмов, относится к проблемам классификации (classification) и регрессионного анализа (predictive analysis). Под классификацией понимается устойчивое разграничение единиц наблюдения (экземпляров) набора данных к определённой категории (классу) по результатам обучения. Регрессионный анализ представляет собой набор статистических методов и процессов для оценки взаимосвязи между переменными [Статистика: Учеб.пособие/Под ред. проф. М.Р. Ефимовой. – М.: ИНФРА-М, 2002]. Цель регрессионного анализа состоит в том, чтобы оценить значение непрерывной выходной переменной по значениям входных переменных [ссылка].
Оставим за скобками тот факт, что регрессионный анализ имеет в своём распоряжении два разных метода – predictive modeling и forecasting. Отметим только, что если имеется временной ряд (time-series data), то с помощью регрессионной модели на основе явного тренда при соблюдении стационарности (постоянства) можно выполнить прогнозирование (forecasting). Если условия формирования уровней временного ряда изменяются, то есть стационарности (non-stationary process) не наблюдается, то дело за predictive modeling. Особо нацеленным на полное овладение ML предлагаю прочесть вот эту статью на английском языке: ссылка. Если по этому поводу возникнет дискуссия, то с удовольствием приму в ней участие.
Поскольку в примерах данной статьи временные ряды использоваться не будут, то под термином прогнозирование понимается predictive analysis.
Для решения проблем классификации и прогнозирования подходит целый диапазон алгоритмов, часть из которых мы рассмотрим далее. Для удобства последующий текст будет разделён на две части: в первой рассмотрим наиболее распространённые алгоритмы классификации, вторую посвятим алгоритмам регрессионного анализа. Для каждой части будет представлен «игрушечный» набор данных, подгруженный из библиотеки scikit-learn (v0.21.3): digits dataset (classification) и boston house-price dataset (regression), а также приведены ссылки на каждый рассматриваемый алгоритм библиотеки scikit-learn для самостоятельного ознакомления и, возможно, изучения.
Все примеры кода выполнены в консоли IDE Spyder 3.3.3 на Python 3.7.3.
Проблема классификации
Сначала импортируем необходимые модули и функции, которые мы будем использовать для решения проблемы классификации данных:
# Импортирование необходимых модулей и атрибутов
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import LinearSVC
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import Normalizer
from matplotlib import pyplotЗагружаем набор данных ‘digits’ напрямую из модуля ‘sklearn.datasets’ :
# Загрузка набора данных
dataset = load_digits()IDE Spyder предоставляет удобный инструмент «Менеджер переменных», который пригодится на всех порах изучения машинного обучения (во всяком случае, для меня), как и другие «фишки»:
Запускаем код. В консоли «менеджер переменных» кликаем на переменную dataset. Выводится следующий словарь:
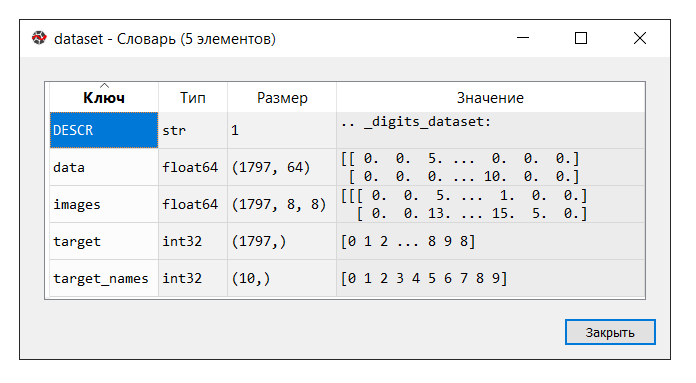
Описание набора данных следующее:
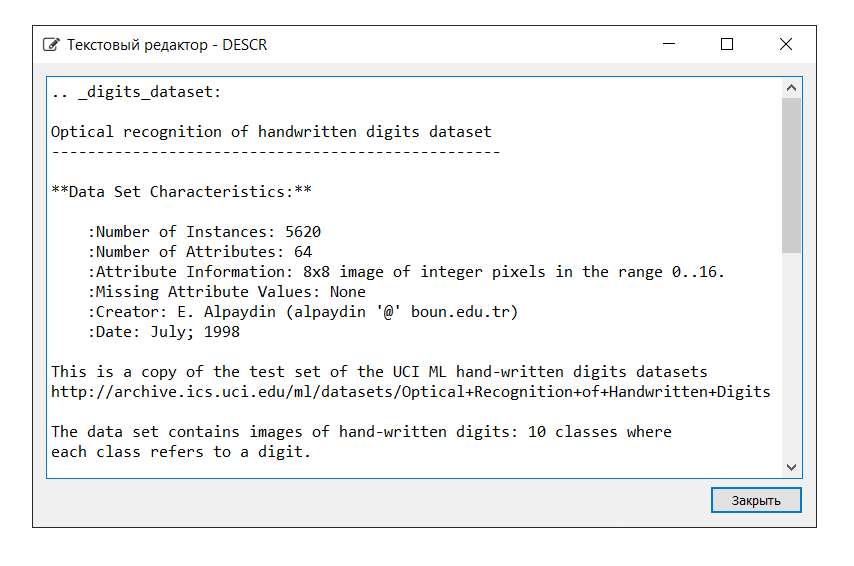
В данном примере ключ ‘images’ нам не понадобится, поэтому переменной Х присваиваем ‘data’, представляющий собой многомерный массив NumPy с набором признаков, размерностью 1797 строк на 64 столбца, а переменной Y – ‘target’, многомерный массив NumPy с маркером на каждую строку.
# Загрузка набора данных
# dataset = load_digits()
X = dataset.data
Y = dataset.targetДалее разделяем набор данных на тренировочную и тестовую части, настраиваем параметры оценивания алгоритмов (используется кросс-валидация[один, два]), определяя метрику ‘accuracy’ в параметре ‘scoring’ [ссылка]. Accuracy – это доля верно классифицированных объектов относительно общего количества объектов. Чем ближе результат к 1, тем лучше [ссылка]. При этом в одной из книг встречалось, что отличными считаются результаты от 0.95 (или 95%) и выше.
# Разделение набора данных на тренировочные и тестовые части
test_size = 0.2
seed = 7
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=test_size, random_state=seed)
# Настройка параметров оценивания алгоритма
num_folds = 10
n_estimators = 100
scoring = 'accuracy'Переменные X_train и Y_train пустим на тренировочные нужды, X_test и Y_test – на выработку прогнозных значений. При этом переменная Y_test не участвует в расчёте прогноза: с помощью метода ‘score’, одинакового для каждого из представленных далее алгоритмов, мы подсчитаем правильные ответы с помощью метрики ‘accuracy’. Это позволит нам судить о том, как справляется алгоритм с поставленной задачей. Не спорю, с нашей стороны это так по-человечески подло не подсказывать машине правильные ответы, но как иначе проверить её performance?
Ниже представлен список алгоритмов, которым-то мы и скормим набор данных. По результатам выполнения расчётов будем делать вывод, какой алгоритм (какие из алгоритмов) показывает наибольшую эффективность. Данный метод вполне может носить название «блиц-проверка алгоритмов машинного обучения» (далее – блиц-проверка).
Для удобства вывода информации рядом с каждым алгоритмом будет проставлена аббревиатура. Необходимо отметить, что настройки каждого алгоритма принимаются по умолчанию (default), за исключением некоторых моментов, дабы предоставить равные условия.
Линейные алгоритмы:
— Логистическая регрессия* / Logistic Regression (‘LR’)
* Слово «регрессия» может сбить с толку. Но не забываем, что «Логистическая регрессия» — это алгоритм классификации
— Линейный дискриминантный анализ / Linear Discriminant Analysis (‘LDA’)
Нелинейные алгоритмы:
— Метод k-ближайших соседей (классификация) / K-Neighbors Classifier (‘KNN’)
— Деревья принятия решений / Decision Tree Classifier (‘CART’)
— Наивный классификатор Байеса / Naive Bayes Classifier (‘NB’)
— Линейный метод опорных векторов (классификация) / Linear Support Vector Classification (‘LSVC’)
— Метод опорных векторов (классификация) / C-Support Vector Classification (‘SVC’)
Алгоритм искусственной нейронной сети:
— Многослойный персептрон / Multilayer Perceptrons (‘MLP’)
Ансамблевые алгоритмы:
— Bagging (классификация) / Bagging Classifier (‘BG’) (Bagging = Bootstrap aggregating)
— Случайный лес (классификация) / Random Forest Classifier (‘RF’)
— Экстра-деревья (классификация) / Extra Trees Classifier (‘ET’)
— AdaBoost (классификация) / AdaBoost Classifier (‘AB’) (AdaBoost = Adaptive Boosting)
— Градиентный boosting (классификация) / Gradient Boosting Classifier (‘GB’)
Таким образом, список ‘models’ содержит следующие модели:
models = []
models.append(('LR', LogisticRegression()))
models.append(('LDA', LinearDiscriminantAnalysis()))
models.append(('KNN', KNeighborsClassifier()))
models.append(('CART', DecisionTreeClassifier()))
models.append(('NB', GaussianNB()))
models.append(('LSVC', LinearSVC()))
models.append(('SVC', SVC()))
models.append(('MLP', MLPClassifier()))
models.append(('BG', BaggingClassifier(n_estimators=n_estimators)))
models.append(('RF', RandomForestClassifier(n_estimators=n_estimators)))
models.append(('ET', ExtraTreesClassifier(n_estimators=n_estimators)))
models.append(('AB', AdaBoostClassifier(n_estimators=n_estimators, algorithm='SAMME')))
models.append(('GB', GradientBoostingClassifier(n_estimators=n_estimators)))Как уже было сказано, оценивание эффективности каждого алгоритма выполняется с помощью кросс-валидации. В итоге выводится сообщение (msg – сокр. от message), содержащее следующие сведения: имя модели в виде аббревиатуры, средняя оценка 10-кратной перекрёстной проверки на тренировочных данных (метрика ‘accuracy’), в скобках представлено среднее квадратичное отклонение (standard deviation), а также значение метрики ‘accuracy’ на тестовых данных.
# Оценивание эффективности выполнения каждого алгоритма
scores = []
names = []
results = []
predictions = []
msg_row = []
for name, model in models:
kfold = KFold(n_splits=num_folds, random_state=seed)
cv_results = cross_val_score(model, X_train, Y_train, cv=kfold, scoring=scoring)
names.append(name)
results.append(cv_results)
m_fit = model.fit(X_train, Y_train)
m_predict = model.predict(X_test)
predictions.append(m_predict)
m_score = model.score(X_test, Y_test)
scores.append(m_score)
msg = "%s: train = %.3f (%.3f) / test = %.3f" % (name, cv_results.mean(), cv_results.std(), m_score)
msg_row.append(msg)
print(msg)После запуска кода получаем следующие результаты:
LR: train = 0.957 (0.014) / test = 0.948
LDA: train = 0.951 (0.014) / test = 0.946
KNN: train = 0.985 (0.013) / test = 0.981
CART: train = 0.843 (0.033) / test = 0.830
NB: train = 0.819 (0.048) / test = 0.806
LSVC: train = 0.942 (0.017) / test = 0.928
SVC: train = 0.343 (0.079) / test = 0.342
MLP: train = 0.972 (0.012) / test = 0.961
BG: train = 0.952 (0.021) / test = 0.941
RF: train = 0.968 (0.017) / test = 0.965
ET: train = 0.980 (0.010) / test = 0.975
AB: train = 0.827 (0.049) / test = 0.823
GB: train = 0.964 (0.013) / test = 0.968Диаграмма размаха («ящик с усами») (box-and-whiskers diagram or plot, box plot):
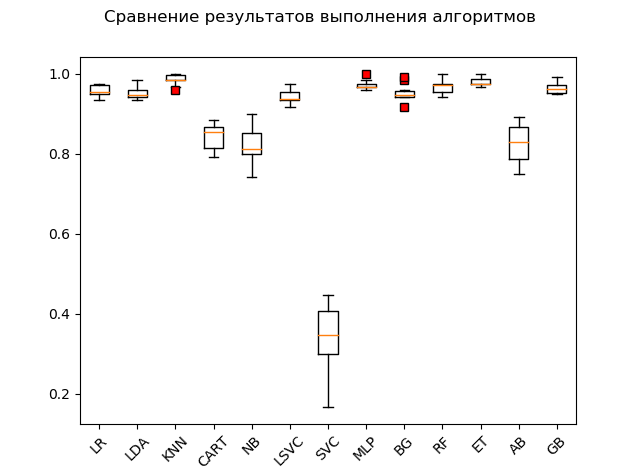
В результате выполнения блиц-проверки на «сырых» данных видно, что наибольшую эффективность на тестовых данных показали алгоритмы ‘KNN’ (k-ближайшие соседи), ‘ET’ (экстра-деревья), ‘GB’ (градиентный «бустинг»), ‘RF’ (случайный лес) и ‘MLP’ (многослойный персептрон):
KNN: train = 0.985 (0.013) / test = 0.981
ET: train = 0.980 (0.010) / test = 0.975
GB: train = 0.964 (0.013) / test = 0.968
RF: train = 0.968 (0.017) / test = 0.965
MLP: train = 0.972 (0.012) / test = 0.961
LR: train = 0.957 (0.014) / test = 0.948
LDA: train = 0.951 (0.014) / test = 0.946
BG: train = 0.952 (0.021) / test = 0.941
LSVC: train = 0.942 (0.017) / test = 0.928
CART: train = 0.843 (0.033) / test = 0.830
AB: train = 0.827 (0.049) / test = 0.823
NB: train = 0.819 (0.048) / test = 0.806
SVC: train = 0.343 (0.079) / test = 0.342При этом многие алгоритмы очень привередливы к тем данным, которые им подают. Поэтому одним из обязательных шагов является так называемая предварительная подготовка данных (data pre-processing [ссылка])
Однако бывает, что алгоритм показывает лучшие результаты без предварительной обработки. Отсюда следующая рекомендация: включить в блиц-проверку несколько преобразований исходного набора данных и по выполнении расчётов сравнить результаты, чтобы выловить суть проблемы в целом.
Наиболее часто используемыми методами предварительной подготовки данных являются:
– стандартизация;
– масштабирование (по умолчанию диапазон [0, 1]);
– нормализация
Данные операции с последующей оценкой можно автоматизировать и поставить на конвейер с помощью инструмента Pipeline.
Фрагмент кода со стандартизацией исходных данных имеет следующий вид:
# Блиц-проверка алгоритмов на стандартизованных исходных данных
# Стандартизация исходных данных (функция StandardScaler)
pipelines = []
pipelines.append(('SS_LR', Pipeline([('Scaler', StandardScaler()), ('LR', LogisticRegression())])))
pipelines.append(('SS_LDA', Pipeline([('Scaler', StandardScaler()), ('LDA', LinearDiscriminantAnalysis())])))
pipelines.append(('SS_KNN', Pipeline([('Scaler', StandardScaler()), ('KNN', KNeighborsClassifier())])))
pipelines.append(('SS_CART', Pipeline([('Scaler', StandardScaler()), ('CART', DecisionTreeClassifier())])))
pipelines.append(('SS_NB', Pipeline([('Scaler', StandardScaler()), ('NB', GaussianNB())])))
pipelines.append(('SS_LSVC', Pipeline([('Scaler', StandardScaler()), ('LSVC', LinearSVC())])))
pipelines.append(('SS_SVC', Pipeline([('Scaler', StandardScaler()), ('SVC', SVC())])))
pipelines.append(('SS_MLP', Pipeline([('Scaler', StandardScaler()), ('MLP', MLPClassifier())])))
pipelines.append(('SS_BG', Pipeline([('Scaler', StandardScaler()), ('BG', BaggingClassifier(n_estimators=n_estimators))])))
pipelines.append(('SS_RF', Pipeline([('Scaler', StandardScaler()), ('RF', RandomForestClassifier(n_estimators=n_estimators))])))
pipelines.append(('SS_ET', Pipeline([('Scaler', StandardScaler()), ('ET', ExtraTreesClassifier(n_estimators=n_estimators))])))
pipelines.append(('SS_AB', Pipeline([('Scaler', StandardScaler()), ('AB', AdaBoostClassifier(n_estimators=n_estimators, algorithm='SAMME'))])))
pipelines.append(('SS_GB', Pipeline([('Scaler', StandardScaler()), ('GB', GradientBoostingClassifier(n_estimators=n_estimators))])))
# Оценивание эффективности выполнения каждого алгоритма
scores_SS = []
names_SS = []
results_SS = []
predictions_SS = []
msg_SS = []
for name, model in pipelines:
kfold = KFold(n_splits=num_folds, random_state=seed)
cv_results = cross_val_score(model, X_train, Y_train, cv=kfold)
names_SS.append(name)
results_SS.append(cv_results)
m_fit = model.fit(X_train, Y_train)
m_predict = model.predict(X_test)
predictions_SS.append(m_predict)
m_score = model.score(X_test, Y_test)
scores_SS.append(m_score)
msg = "%s: train = %.3f (%.3f) / test = %.3f" % (name, cv_results.mean(), cv_results.std(), m_score)
msg_SS.append(msg)
print(msg)
# ящик с усами (StandardScaler)
fig = pyplot.figure()
fig.suptitle('Сравнение результатов выполнения алгоритмов на стандарт. данных')
ax = fig.add_subplot(111)
red_square = dict(markerfacecolor='r', marker='s')
pyplot.boxplot(results_SS, flierprops=red_square)
ax.set_xticklabels(names_SS, rotation=45)
pyplot.show()Обратите внимание на добавку ‘_SS’ (сокращение от StandardScaler) к именам списков. Это сделано для того, чтобы не сваливать в кучу результаты, а также для их удобного просмотра с помощью «менеджера переменных» после выполненных преобразований.
Запуск фрагмента кода выдаёт следующие результаты:
SS_LR: train = 0.958 (0.015) / test = 0.949
SS_LDA: train = 0.951 (0.014) / test = 0.946
SS_KNN: train = 0.968 (0.023) / test = 0.970
SS_CART: train = 0.853 (0.036) / test = 0.835
SS_NB: train = 0.756 (0.046) / test = 0.751
SS_LSVC: train = 0.945 (0.018) / test = 0.941
SS_SVC: train = 0.976 (0.015) / test = 0.990
SS_MLP: train = 0.976 (0.012) / test = 0.973
SS_BG: train = 0.947 (0.018) / test = 0.948
SS_RF: train = 0.973 (0.016) / test = 0.970
SS_ET: train = 0.980 (0.012) / test = 0.975
SS_AB: train = 0.827 (0.049) / test = 0.823
SS_GB: train = 0.964 (0.013) / test = 0.968Ящик с усами (StandardScaler):
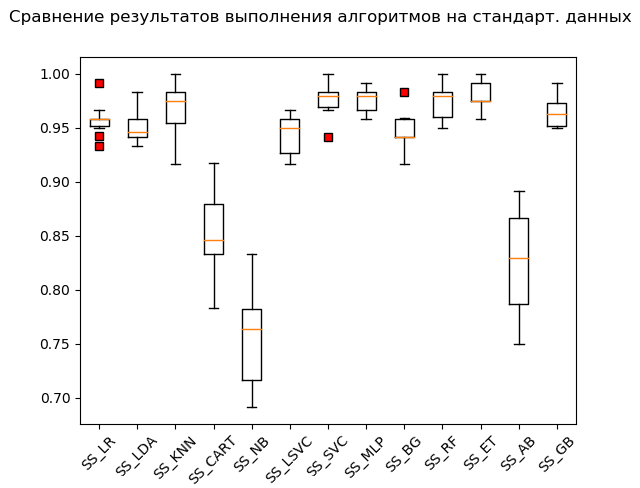
По итогам расчёта на стандартизованных данных в лидеры выбились следующие алгоритмы:
SS_SVC: train = 0.976 (0.015) / test = 0.990
SS_ET: train = 0.980 (0.012) / test = 0.975
SS_MLP: train = 0.976 (0.012) / test = 0.973
SS_KNN: train = 0.968 (0.023) / test = 0.970
SS_RF: train = 0.973 (0.016) / test = 0.970
SS_GB: train = 0.964 (0.013) / test = 0.968
SS_LR: train = 0.958 (0.015) / test = 0.949
SS_BG: train = 0.947 (0.018) / test = 0.948
SS_LDA: train = 0.951 (0.014) / test = 0.946
SS_LSVC: train = 0.945 (0.018) / test = 0.941
SS_CART: train = 0.853 (0.036) / test = 0.835
SS_AB: train = 0.827 (0.049) / test = 0.823
SS_NB: train = 0.756 (0.046) / test = 0.751Как говорится, из грязи в князи: метод опорных векторов (‘SVC’), накормленный стандартизованными данными, уделал остальные, показав отличный результат. При «ручной» проверке, сравнивая значения переменных Y_test и predictions_SS[6], алгоритм не пережевал только несколько значений.
Далее выполняется аналогичный код для функций MinMaxScaler (масштабирование) и Normalizer (нормализация). Приводить полностью код в статье не стану. Вы можете скачать его из моего репозитория на GitHub’е: ссылка.
Только не забудьте ненадолго зависнуть и посмеяться про себя над ‘for educational purpose only’! :)
В итоге, после прохода по всему коду, получаем следующие результаты:
LR: train = 0.957 (0.014) / test = 0.948
LDA: train = 0.951 (0.014) / test = 0.946
KNN: train = 0.985 (0.013) / test = 0.981
CART: train = 0.843 (0.033) / test = 0.830
NB: train = 0.819 (0.048) / test = 0.806
LSVC: train = 0.942 (0.017) / test = 0.928
SVC: train = 0.343 (0.079) / test = 0.342
MLP: train = 0.972 (0.012) / test = 0.961
BG: train = 0.952 (0.021) / test = 0.941
RF: train = 0.968 (0.017) / test = 0.965
ET: train = 0.980 (0.010) / test = 0.975
AB: train = 0.827 (0.049) / test = 0.823
GB: train = 0.964 (0.013) / test = 0.968
SS_LR: train = 0.958 (0.015) / test = 0.949
SS_LDA: train = 0.951 (0.014) / test = 0.946
SS_KNN: train = 0.968 (0.023) / test = 0.970
SS_CART: train = 0.853 (0.036) / test = 0.835
SS_NB: train = 0.756 (0.046) / test = 0.751
SS_LSVC: train = 0.945 (0.018) / test = 0.941
SS_SVC: train = 0.976 (0.015) / test = 0.990
SS_MLP: train = 0.976 (0.012) / test = 0.973
SS_BG: train = 0.947 (0.018) / test = 0.948
SS_RF: train = 0.973 (0.016) / test = 0.970
SS_ET: train = 0.980 (0.012) / test = 0.975
SS_AB: train = 0.827 (0.049) / test = 0.823
SS_GB: train = 0.964 (0.013) / test = 0.968
MMS_LR: train = 0.961 (0.013) / test = 0.953
MMS_LDA: train = 0.951 (0.014) / test = 0.946
MMS_KNN: train = 0.985 (0.013) / test = 0.981
MMS_CART: train = 0.850 (0.027) / test = 0.840
MMS_NB: train = 0.796 (0.045) / test = 0.786
MMS_LSVC: train = 0.964 (0.012) / test = 0.958
MMS_SVC: train = 0.963 (0.016) / test = 0.956
MMS_MLP: train = 0.972 (0.011) / test = 0.963
MMS_BG: train = 0.948 (0.024) / test = 0.946
MMS_RF: train = 0.973 (0.014) / test = 0.968
MMS_ET: train = 0.983 (0.010) / test = 0.981
MMS_AB: train = 0.827 (0.049) / test = 0.823
MMS_GB: train = 0.963 (0.013) / test = 0.968
N_LR: train = 0.938 (0.020) / test = 0.919
N_LDA: train = 0.952 (0.013) / test = 0.949
N_KNN: train = 0.981 (0.012) / test = 0.985
N_CART: train = 0.834 (0.028) / test = 0.825
N_NB: train = 0.825 (0.043) / test = 0.805
N_LSVC: train = 0.960 (0.014) / test = 0.953
N_SVC: train = 0.551 (0.053) / test = 0.586
N_MLP: train = 0.963 (0.018) / test = 0.946
N_BG: train = 0.949 (0.016) / test = 0.938
N_RF: train = 0.973 (0.015) / test = 0.970
N_ET: train = 0.982 (0.012) / test = 0.980
N_AB: train = 0.825 (0.040) / test = 0.820
N_GB: train = 0.953 (0.022) / test = 0.956‘Top 5’ результатов:
SS_SVC: train = 0.976 (0.015) / test = 0.990
N_KNN: train = 0.981 (0.012) / test = 0.985
KNN: train = 0.985 (0.013) / test = 0.981
MMS_KNN: train = 0.985 (0.013) / test = 0.981
MMS_ET: train = 0.983 (0.010) / test = 0.981Таким образом, по результатам блиц-проверки алгоритмов машинного обучения для решения проблемы классификации набора данных ‘digits’ наиболее подходящими алгоритмами машинного обучения являются: метод k-ближайших соседей (‘KNN’), метод опорных векторов (‘SVC’) и экстра-деревья (‘ET’). Данным алгоритмам стоит уделить более пристальное внимание для дальнейшего развития результатов, направленных на увеличение эффективности расчётов. Всё, как говорится, решаемо.
И на этой приподнятой ноте гладко переходим ко 2-й части.
Проблема прогнозирования
Двигаемся по накатанной:
# Импортирование необходимых модулей и атрибутов
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import LarsCV
from sklearn.linear_model import BayesianRidge
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.ensemble import AdaBoostRegressor
from sklearn.ensemble import BaggingRegressor
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import Normalizer
from matplotlib import pyplot
# Загрузка набора данных
dataset = load_boston()Запускаем код и разбираемся со словарём. Описание и ключи следующие:


Переменной Х присваиваем ключ ‘data’, представляющий собой многомерный массив NumPy с набором признаков, размерностью 506 строк на 13 столбцов, а переменной Y – ‘target’, многомерный массив NumPy с маркером на каждую строку.
# Загрузка набора данных
#dataset = load_boston()
X = dataset.data
Y = dataset.targetРазделяем набор данных на тренировочную и тестовую части, настраиваем параметры оценивания алгоритмов. В параметре ‘scoring’ устанавливаем одну из традиционных для регрессионного анализа метрику ‘r2’:
# Загрузка набора данных
dataset = load_boston()
X = dataset.data
Y = dataset.target
# Разделение набора данных на тренировочные и тестовые части
test_size = 0.2
seed = 7
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=test_size, random_state=seed)
# Настройка параметров оценивания алгоритма
num_folds = 10
n_iter = 1000
n_estimators = 100
scoring = 'r2'R2 – коэффициент детерминации – это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью (ссылка).
«Коэффициент детерминации для модели с константой принимает значения от 0 до 1. Чем ближе значение коэффициента к 1, тем сильнее зависимость. При оценке регрессионных моделей это интерпретируется как соответствие модели данным. Для приемлемых моделей предполагается, что коэффициент детерминации должен быть хотя бы не меньше 50% (в этом случае коэффициент множественной корреляции превышает по модулю 70%). Модели с коэффициентом детерминации выше 80% можно признать достаточно хорошими (коэффициент корреляции превышает 90%). Равенство коэффициента детерминации единице означает, что объясняемая переменная в точности описывается рассматриваемой моделью» (там же).
Для решения проблемы прогнозирования задействуем следующие алгоритмы:
Линейные алгоритмы:
— Линейная регрессия / Linear Regression (‘LR’)
— Гребневая регрессия (ридж-регрессия) / Ridge Regression (‘R’)
— Лассо-регрессия (от англ. LASSO — Least Absolute Shrinkage and Selection Operator) / Lasso Regression (‘L’)
— Метод регрессии «Эластичная сеть» / Elastic Net Regression (‘ELN’)
— Метод наименьших углов / Least Angle Regression (LARS) (‘LARS’)
— Байесовская гребневая регрессия / Bayesian ridge regression (‘BR’)
Нелинейные алгоритмы:
— Метод k-ближайших соседей (регрессия) / k-nearest neighbors regressor (‘KNR’)
— Деревья регрессии / Decision Tree Regressor (‘DTR’)
— Линейный метод опорных векторов (регрессия) / Linear Support Vector Machine – Regression / (‘LSVR’)
— Метод опорных векторов (регрессия) / Epsilon-Support Vector Regression (‘SVR’)
Ансамблевые алгоритмы:
— AdaBoost (регрессия) / AdaBoost Regressor (‘ABR’) (AdaBoost = Adaptive Boosting)
— Bagging (регрессия) / Bagging Regressor (‘BR’) (Bagging = Bootstrap aggregating)
— Экстра-деревья (регрессия) / Extra Trees Regressor (‘ETR’)
— Градиентный boosting (регрессия) / Gradient Boosting Regressor (‘GBR’)
— Случайный лес (регрессия) / Random Forest Classifier (‘RFR’)
Таким образом, список ‘models’ содержит следующие модели:
models = []
models.append(('LR', LinearRegression()))
models.append(('R', Ridge()))
models.append(('L', Lasso()))
models.append(('ELN', ElasticNet()))
models.append(('LARS', Lars()))
models.append(('BR', BayesianRidge(n_iter=n_iter)))
models.append(('KNR', KNeighborsRegressor()))
models.append(('DTR', DecisionTreeRegressor()))
models.append(('LSVR', LinearSVR()))
models.append(('SVR', SVR()))
models.append(('ABR', AdaBoostRegressor(n_estimators=n_estimators)))
models.append(('BR', BaggingRegressor(n_estimators=n_estimators)))
models.append(('ETR', ExtraTreesRegressor(n_estimators=n_estimators)))
models.append(('GBR', GradientBoostingRegressor(n_estimators=n_estimators)))
models.append(('RFR', RandomForestRegressor(n_estimators=n_estimators)))Как и в случае с классификацией, оценивание эффективности каждого алгоритма выполняется с помощью кросс-валидации. Выводимое сообщение содержит следующие сведения: имя модели в виде аббревиатуры, средняя оценка 10-кратной перекрёстной проверки на тренировочных данных (метрика ‘r2’), в скобках представлено среднее квадратичное отклонение (standard deviation), а также коэффициент детерминации r2 на тестовых данных.
# Оценивание эффективности выполнения каждого алгоритма
scores = []
names = []
results = []
predictions = []
msg_row = []
for name, model in models:
kfold = KFold(n_splits=num_folds, random_state=seed)
cv_results = cross_val_score(model, X_train, Y_train, cv=kfold, scoring=scoring)
names.append(name)
results.append(cv_results)
m_fit = model.fit(X_train, Y_train)
m_predict = model.predict(X_test)
predictions.append(m_predict)
m_score = model.score(X_test, Y_test)
scores.append(m_score)
msg = "%s: train = %.3f (%.3f) / test = %.3f" % (name, cv_results.mean(), cv_results.std(), m_score)
msg_row.append(msg)
print(msg)
# Диаграмма размаха («ящик с усами»)
fig = pyplot.figure()
fig.suptitle('Сравнение результатов выполнения алгоритмов')
ax = fig.add_subplot(111)
red_square = dict(markerfacecolor='r', marker='s')
pyplot.boxplot(results, flierprops=red_square)
ax.set_xticklabels(names, rotation=45)
pyplot.show()После запуска кода получаем следующие результаты:
LR: train = 0.746 (0.068) / test = 0.579
R: train = 0.744 (0.067) / test = 0.570
L: train = 0.689 (0.070) / test = 0.641
ELN: train = 0.677 (0.074) / test = 0.662
LARS: train = 0.744 (0.069) / test = 0.579
BR: train = 0.739 (0.069) / test = 0.571
KNR: train = 0.434 (0.288) / test = 0.538
DTR: train = 0.671 (0.145) / test = 0.637
LSVR: train = 0.550 (0.144) / test = 0.459
SVR: train = -0.012 (0.048) / test = -0.003
ABR: train = 0.810 (0.078) / test = 0.763
BR: train = 0.854 (0.064) / test = 0.805
ETR: train = 0.889 (0.047) / test = 0.836
GBR: train = 0.878 (0.042) / test = 0.863
RFR: train = 0.852 (0.068) / test = 0.819Диаграмма размаха:
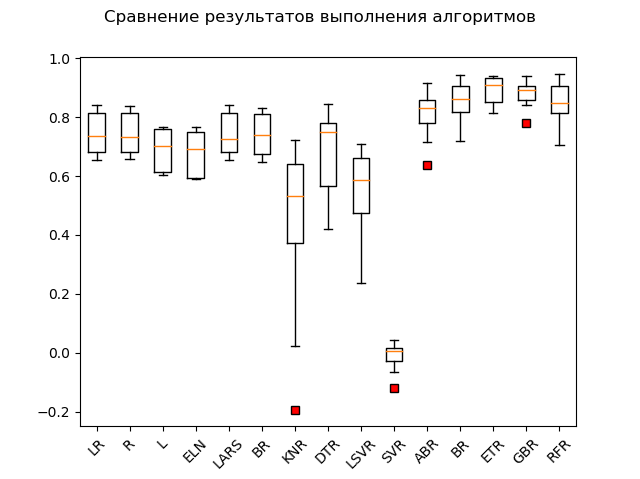
Явные лидеры – ансамблевые методы ‘GBR’ (градиентный «бустинг»), ‘ETR’ (экстра-деревья), ‘RFR’ (случайный лес) и ‘BR’ («бэггинг»):
GBR: train = 0.878 (0.042) / test = 0.863
ETR: train = 0.889 (0.047) / test = 0.836
RFR: train = 0.852 (0.068) / test = 0.819
BR: train = 0.854 (0.064) / test = 0.805
ABR: train = 0.810 (0.078) / test = 0.763
ELN: train = 0.677 (0.074) / test = 0.662
L: train = 0.689 (0.070) / test = 0.641
DTR: train = 0.671 (0.145) / test = 0.637
LR: train = 0.746 (0.068) / test = 0.579
LARS: train = 0.744 (0.069) / test = 0.579
BR: train = 0.739 (0.069) / test = 0.571
R: train = 0.744 (0.067) / test = 0.570
KNR: train = 0.434 (0.288) / test = 0.538
LSVR: train = 0.550 (0.144) / test = 0.459
SVR: train = -0.012 (0.048) / test = -0.003Один «адабуст», «лошара» эдакая, отстаёт.
Возможно, тройку лидеров причешут стандартизация и нормализация. Давайте выясним, выполнив оставшуюся часть кода.
Результаты следующие:
SS_LR: train = 0.746 (0.068) / test = 0.579
SS_R: train = 0.746 (0.068) / test = 0.578
SS_L: train = 0.678 (0.054) / test = 0.510
SS_ELN: train = 0.665 (0.060) / test = 0.513
SS_LARS: train = 0.744 (0.069) / test = 0.579
SS_BR: train = 0.746 (0.066) / test = 0.576
SS_KNR: train = 0.763 (0.098) / test = 0.739
SS_DTR: train = 0.610 (0.242) / test = 0.629
SS_LSVR: train = 0.727 (0.091) / test = 0.482
SS_SVR: train = 0.653 (0.126) / test = 0.610
SS_ABR: train = 0.811 (0.076) / test = 0.819
SS_BR: train = 0.853 (0.074) / test = 0.813
SS_ETR: train = 0.887 (0.048) / test = 0.846
SS_GBR: train = 0.878 (0.038) / test = 0.860
SS_RFR: train = 0.851 (0.071) / test = 0.818
N_LR: train = 0.751 (0.099) / test = 0.576
N_R: train = 0.287 (0.126) / test = 0.271
N_L: train = -0.030 (0.032) / test = -0.000
N_ELN: train = -0.007 (0.030) / test = 0.023
N_LARS: train = 0.751 (0.099) / test = 0.576
N_BR: train = 0.744 (0.100) / test = 0.589
N_KNR: train = 0.485 (0.192) / test = 0.504
N_DTR: train = 0.729 (0.080) / test = 0.765
N_LSVR: train = 0.182 (0.108) / test = 0.136
N_SVR: train = 0.086 (0.076) / test = 0.084
N_ABR: train = 0.795 (0.053) / test = 0.752
N_BR: train = 0.854 (0.054) / test = 0.827
N_ETR: train = 0.877 (0.048) / test = 0.850
N_GBR: train = 0.852 (0.063) / test = 0.872
N_RFR: train = 0.852 (0.051) / test = 0.801Как видно, ансамблевые методы по-прежнему впереди всех.
‘Top 5’ вмещает следующие результаты:
N_GBR: train = 0.852 (0.063) / test = 0.872
GBR: train = 0.878 (0.042) / test = 0.863
SS_GBR: train = 0.878 (0.038) / test = 0.860
N_ETR: train = 0.877 (0.048) / test = 0.850
SS_ETR: train = 0.887 (0.048) / test = 0.846Выведем диаграмму сравнения результатов:
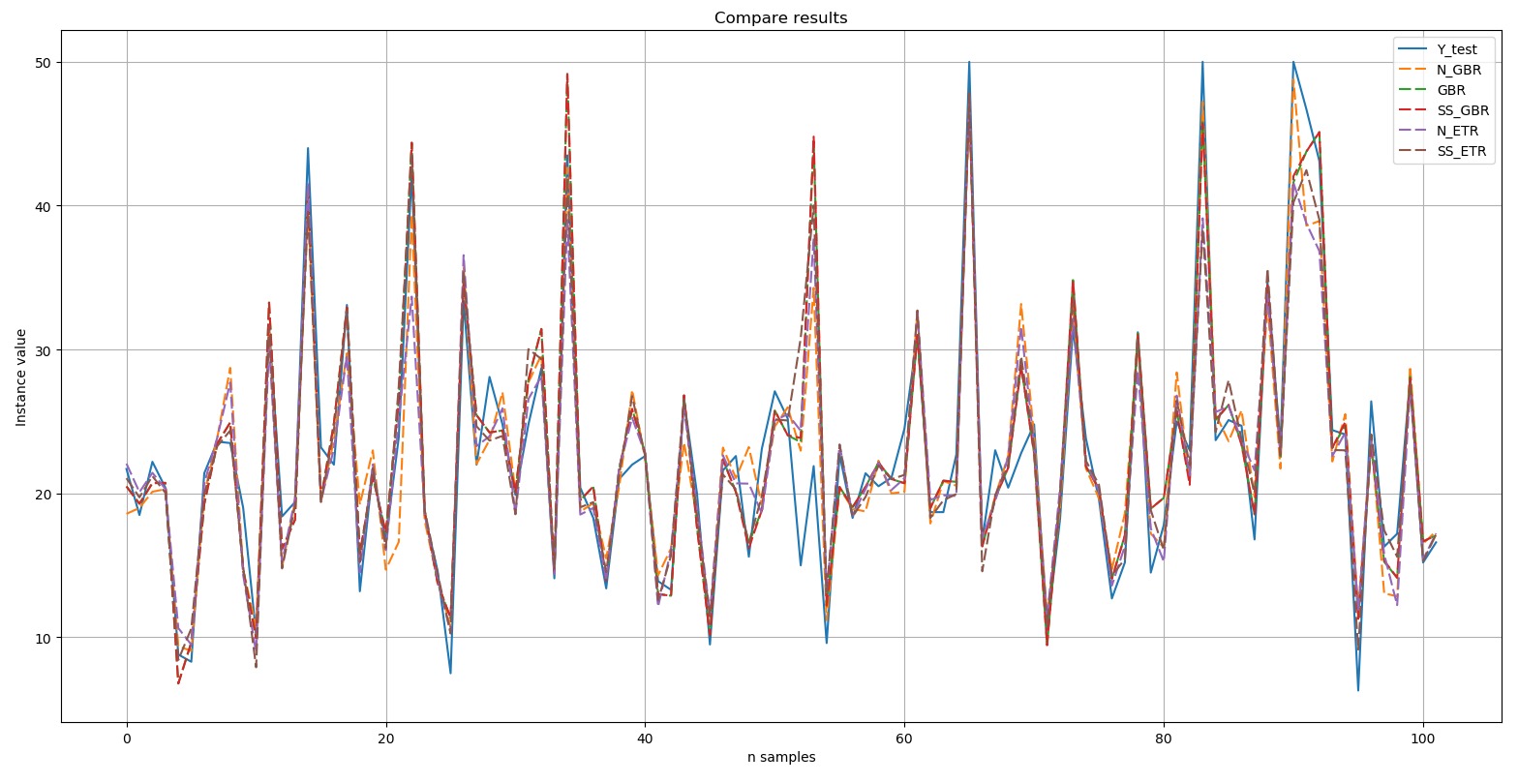
Y-test – это эталон. Пять отборных результатов, представленные на диаграмме, выделены пунктирной линией (dashed). Видно, что все пики были воспроизведены либо с точным повторением, либо в той или иной степени.
Небольшая выдержка ручного сравнения эталонных значений и прогнозных значений алгоритма, входящего в Top 5:
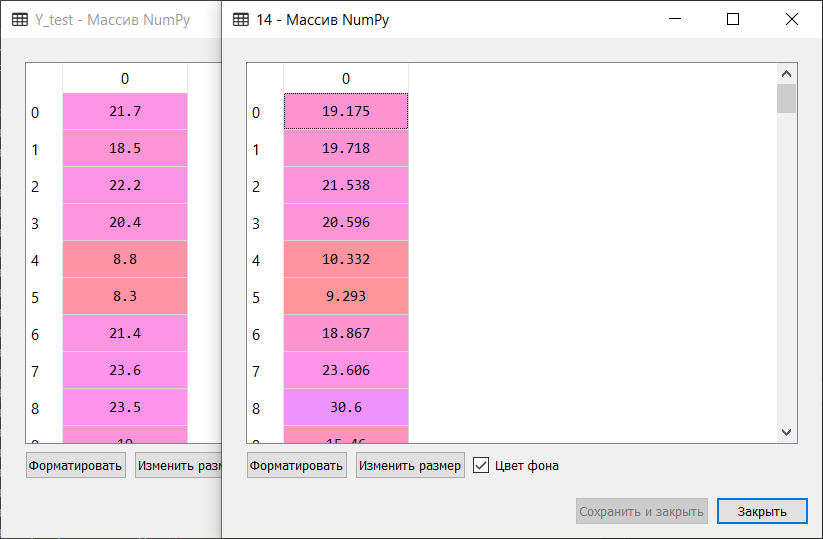
Таким образом, по результатам блиц-проверки алгоритмов машинного обучения для решения проблемы прогнозирования набора данных ‘boston house-price’ наиболее подходящими алгоритмами являются градиентный «бустинг» (‘GBR’) и экстра-деревья (‘ETR’). Данным алгоритмам стоит уделить более пристальное внимание для дальнейшего развития результатов и усиления эффективности прогнозов.
Послесловие
Блиц-проверка алгоритмов машинного обучения позволяет в первом приближении выявить наиболее эффективные алгоритмы для решения проблем классификации и регрессионного анализа (прогнозирования). Мы убедились в этом, обработав набор данных ‘digits’, блестяще рассортировав экземпляры на 10 классов, а также набор данных ‘boston house-price’, «изюмительно» разобравшись с нахождением зависимостей и выполнив «колеблющийся» прогноз зависимой переменной.
Вам же предлагается опробовать этот метод на ваших собственных наборах данных либо на тех, которые вы можете нарыть на различных репозиториях, включая GitHub. К примеру: ссылка.
Раздобудьте подходящий по цели набор данных — и натравите на него стайку алгоритмов в упряжке блиц-проверки. А там и выяснится, чья возьмёт: один в поле не воин. :)
И в заключение. Я буду благодарен за ваши комментарии, вопросы и пожелания, так как основу этой статьи составляет информация, которой я делюсь с новыми коллегами по каждому новому проекту в области машинного обучения. У каждого из них своя специализация, про машинное обучение и искусственные нейронные сети многие из них только «где-то слышали», поэтому для меня важно рассказать о сложном, многогранном и, наконец, неподступном (это я про ИНС и машинное обучение в целом):), простым и понятным языком; показать, что не боги горшки обжигают; и что если есть интерес, то можно не один десяток алгоритмов «запрячь». :)
P.S. К концу статьи уже сам стал предсказывать, поэтому на подступающие вопросы о том, где я взял схему-шпаргалку на первом рисунке выдаю: всё на том же сайте scikit-learn.org ('Choosing the right estimator'): ссылка. А олицетворение искусственного интеллекта в виде зарумянившегося Самоделкина – так это по волнам памяти моего счастливого детства.