Comments 14
Барицентрические координаты инвариантны к аффинным преобразованиям
Интересно, есть ли система координат инвариантная к проективное преобразованиям?
Не думали еще об этом? Или в задаче задаче распознавания лиц этого не требуется?
Не знаю, такой системы координат. По крайней мере, среди линейных. А жаль, очень удобно было во многих задачах. И в распознавании лиц тоже.
Любое преобразование трактуется двояко — как преобразование пространства или же как преобразование системы координат. Инвариант же — это свойство изучаемой формы, сохраняющееся после применении некоторых групп преобразований.
В случае проективного (дробно-линейного) преобразования (а барицентрические координаты являются частным случаем треугольных или однородных, — что одно и тоже) простейшим инвариантом является ангармоническое отношение четырех точек
1. Нет никакого смысла в разделении координат на барицентрические и аффинные. Есть просто разные базисы. Как правило, барицентрическими называют координаты, если базис состоит из одних точек пространства. А если точка всего одна (начало координат), а остальные элементы базиса являются векторами, то типа это привычный аффинный базис. Но могут быть и промежуточные варианты.
Важно лишь, пожалуй, что для определения координат точек пространства в базисе должна быть как минимум одна точка.
2. Из ненужного обособления барицентрических координат следуют их выдуманные недостатки. Нет никаких проблем в определении расстояния между точками. В любых координатах расстояние — это норма вектора. Вектор — это разность точек. Если метрика для базиса задана (скалярные произведения между всеми его элементами), то известны все расстояния в данном базисе.
Ну и т.д.
Пожалуй, ещё надо отметить важное свойство барицентрического базиса — в нем можно оперировать нормой точек, а не только векторов. Это следствие как раз наличия «лишней» координаты.
В целом довольно поверхностная статья, но зато доступна).
Если бы всё было так же просто — то в разных базисах было бы одинаковое число координат.
Для определения координат точки на плоскости достаточно двух любых координат. Так как 3-я всегда может быть определена из условия равенства суммы веса всех координат единице. В векторных координатах данное условие выполняется ввиду наличия начала координат. Это точка и ее вес равен 1. Вес самих векторов нулевой.
Опять же само это условие вытекает из-того, что мы заранее предполагаем, что речь идет именно о координатах точки (для вектора вес координат должен быть равен 0). Если же нужно различать точки и векторы (аффинное пространство), то понадобится еще одна координата. Опять же это требование справедливо для любого базиса.
1) вроде бы писал, что переход в барицентрические координаты, это смена базиса
2) про возможносиь измерения расстояний, если известны произведения радиусов-вектрров точек, — тоже
Но в целом, спасибо за отзыв :)
Барицентрические координаты ещё очень удобны для представления в двухмерном рисунке любых трёхэлементных векторов, суммирующихся в единицу. Например (соус):
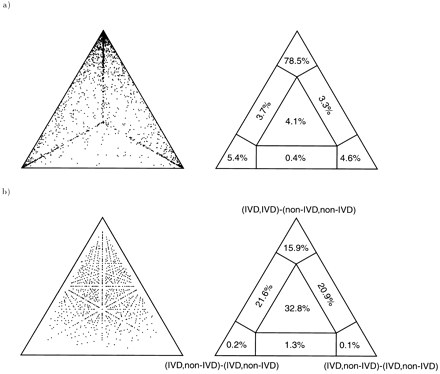
Углы треугольника соответствуют трём взаимоисключающим гипотезам, каждая точка некоторому подмножеству данных, а её координаты — правдоподобия данных под соответствующими гипотезами. Справа посчитано, сколько точек в какой сегмент ложится. Из рисунка сразу видно, как распределяется поддержка между тремя гипотезами.
О барицентрических координатах на пальцах