При обсуждении предыдущей статьи про модельно-ориентированное проектирование возник резонный вопрос: если мы используем данные эксперимента, а можно ли поступить еще проще, засунуть данные в System Identification и получить модель объекта, не заморачиваясь с физикой вообще? Не изучая всякие многоэтажные формулы Навье-Стокса, Бернулли и прочих Штангель циркулей с Рабиновичами? Испытали объект – получили результат.

Мы же представляли модель ракеты ФАУ2 в виде одной передаточной функции, можно посмотреть здесь… И, вроде, все работало. Зачем же нам нужно сначала изучать математический анализ и дифференциальные исчисления, когда есть волшебная кнопка, получающая модель из испытаний?
Действительно такой подход может применяться, но для этого нужно два условия:
В любых других случаях – «хотели как лучше, получилось как всегда» (с).
Например, в этой статье про моделирование электропривода показано, что «при некотором пороговом значении точности измерительных приборов модель привода становится неидентифицируемой, что приводит к потере управляемости и невозможности диагностирования»
В этой же статье мы разберём магию и волшебство создания моделей в виде передаточных функций из ТАУ, а потом осуществим сеанс разоблачения данной магии.
Разберем простой пример. У нас есть модель механического демпфера. Это поршень на пружине, он движется внутри цилиндра, может перемещается вверх-вниз. Его положение – это интересующая нас функция Y(t), сверху на него воздействует возмущающая сила (U(t)), на стенках поршня действует сила вязкого трения. (См. рис. 1)
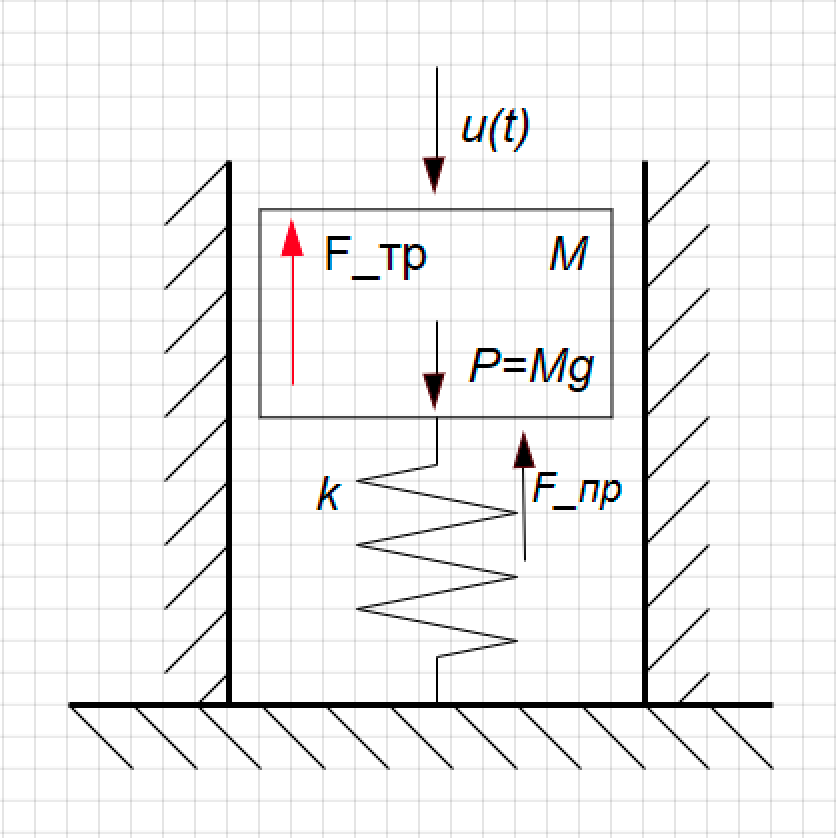
Рисунок 1. Расчетная схема амортизатора.
Выведем передаточную функцию для этого звена.
Те джедаи, кто уже знаком с магией передаточных функций, могут пропустить данную часть и перейти сразу к разоблачению магии, а для юных падаванов раскроем всю технологию получения уравнений динамики.
Согласно 2-му закону Ньютона ускорение тела пропорционально сумме сил, действующих на тело:
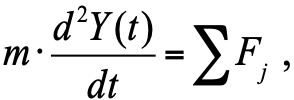 , (1)
, (1)
где m – масса тела; Fj — силы, воздействующие на тело (поршень демпфера).
Подставляя в уравнение (1) все силы согласно рис. 1, имеем:
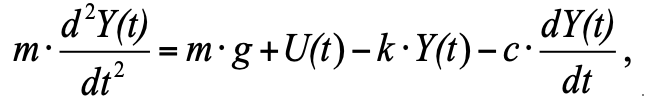 (2)
(2)
где:
Y(t) – положение поршня;
P = m∙g – сила тяжести;
F_пр = k∙Y(t) – сила сопротивления пружины;
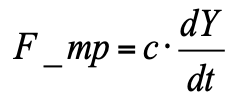 – сила вязкого трения (пропорциональная скорости движения поршня).
– сила вязкого трения (пропорциональная скорости движения поршня).
Размерности сил и коэффициентов, входящих в уравнение (2):

Считаем, что в нулевой момент времени поршень находится в равновесии. Тогда начальное положение поршня — y0 в равновесии, где скорость и ускорения равны 0, можно посчитать из уравнения 2.

Данное уравнение позволяет посчитать, в каком положении будет поршень при различных нагрузках. Эта статическая характеристика: приложили силу — получили перемещение. Ее вид для нашей системы предельно прост (См. рис. 2):
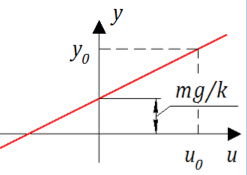
Рисунок 2. Статическая характеристика демпфера.
Казалось бы, вот оно счастье – простая линия, когда приложил силу, получил перемещение. Но не тут-то было! Нас интересует не конечное положение поршня, а процесс перехода из одного состояния в другое.
Для анализа переходного процесса и создана теория автоматического управления ТАУ. По типовой «технологии создания моделей» согласно этой теории предлагается рассматривать систему не в абсолютных значениях, а в отклонениях от равновесного состояния. Такая постановка упрощает решение и построение. И в самом деле, если заменить абсолютные значения на отклонения, то получим:

F_пр = k∙(y0+y(t)) = k∙y0 + k∙y(t) – сила сопротивления пружины;
 — сила трения.
— сила трения.
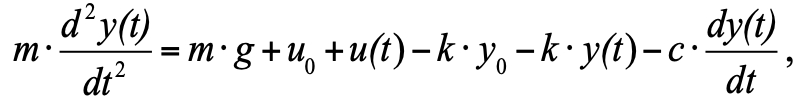 но поскольку мы приняли, что в начальный момент у нас состояние равновесия, а сумма трех сил в состоянии равновесия равна нулю, их можно убрать из уравнения, и в итоге получим:
но поскольку мы приняли, что в начальный момент у нас состояние равновесия, а сумма трех сил в состоянии равновесия равна нулю, их можно убрать из уравнения, и в итоге получим:
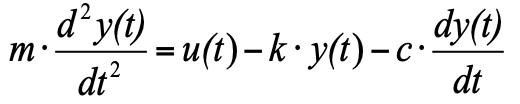 (4)
(4)
Для того, что бы перевести уравнение к виду по канону ТАУ, нужно все уравнение разделить на k, чтобы коэффициент у значение выходной переменной был равен 1, и перенести в правую часть множители с выходными значения у(t), а в левую – с входными воздействиями u(t):
 (5)
(5)
Это уравнение можно уже записать в операторной форме:
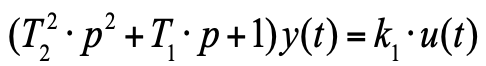 (6)
(6)
где:

р = d/dt – оператор дифференцирования. Обратите внимание, что размерности коэффициентов имеют размерность и смысл постоянных времени:

A передаточная функция для такого уравнения [6] имеет вид:
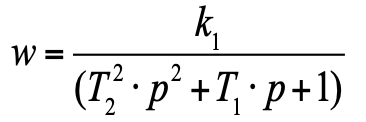
Сейчас на ваших глазах мы получили из уравнений физики передаточную функцию в виде блока, и, более того, полученный блок представляет собой стандартное колебательное звено из ТАУ.
Лично для меня, магией здесь является волшебное появление из статических характеристик, частей системы, массы поршня, упругости пружины, трения на стенках) объекта волшебным образом появилась временная характеристика переходных процессов в системе
Как научил меня Максим Андреев, при создании динамических моделей «Конец — всему голова!» (смотри здесь второй принцип моделирования — «начинай с конца»):
А в конце функции у нас – перемещение.
Поэтому Представим уравнение 2 в форме Коши, для перемещения.
Форма Коши, это когда слева – производные интересующих нас функций, справа – выражения для их вычисления. Поскольку производная в уравнении у нас второй степени, то введя новую переменную Y1 – скорость изменения положения (скрость перемещения), мы получим систему из двух уравнений в форме Коши:
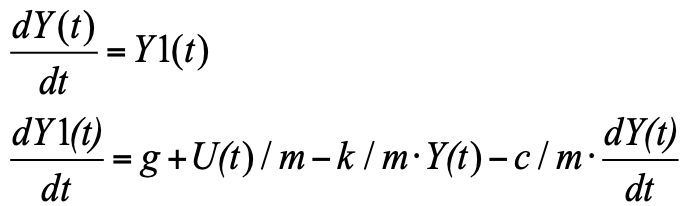
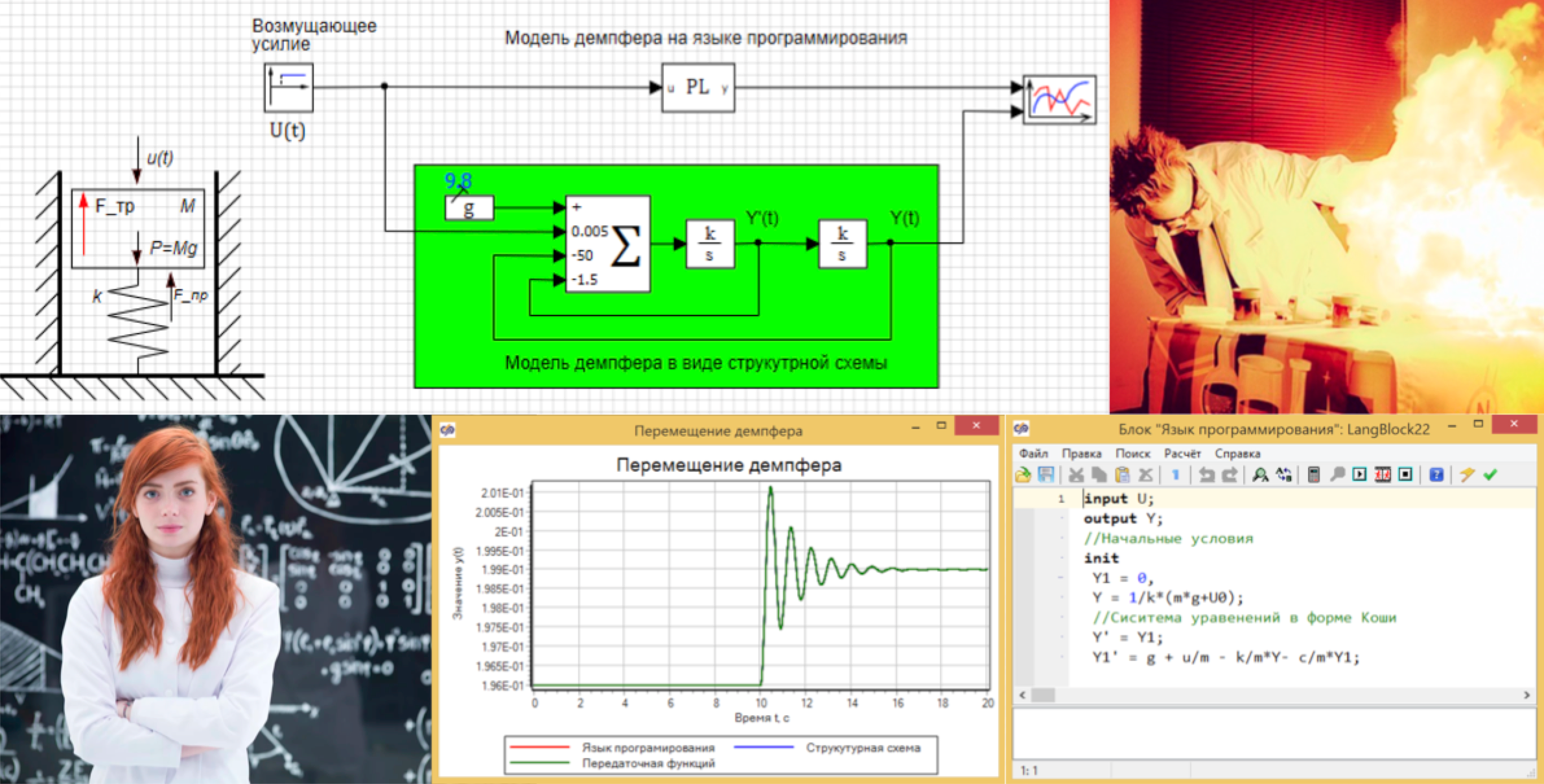
Данное уравнение можно просто записать в блок «Язык программирования» и получить модель (см. рис.3):

Рисунок 3. Модель демпфера на языке программирования.
В качестве входа используем значение силы U, выходом из блока является перемещение Y, начальное положение задается по формуле 3. Все переменные задаем как глобальные сигналы для проекта:
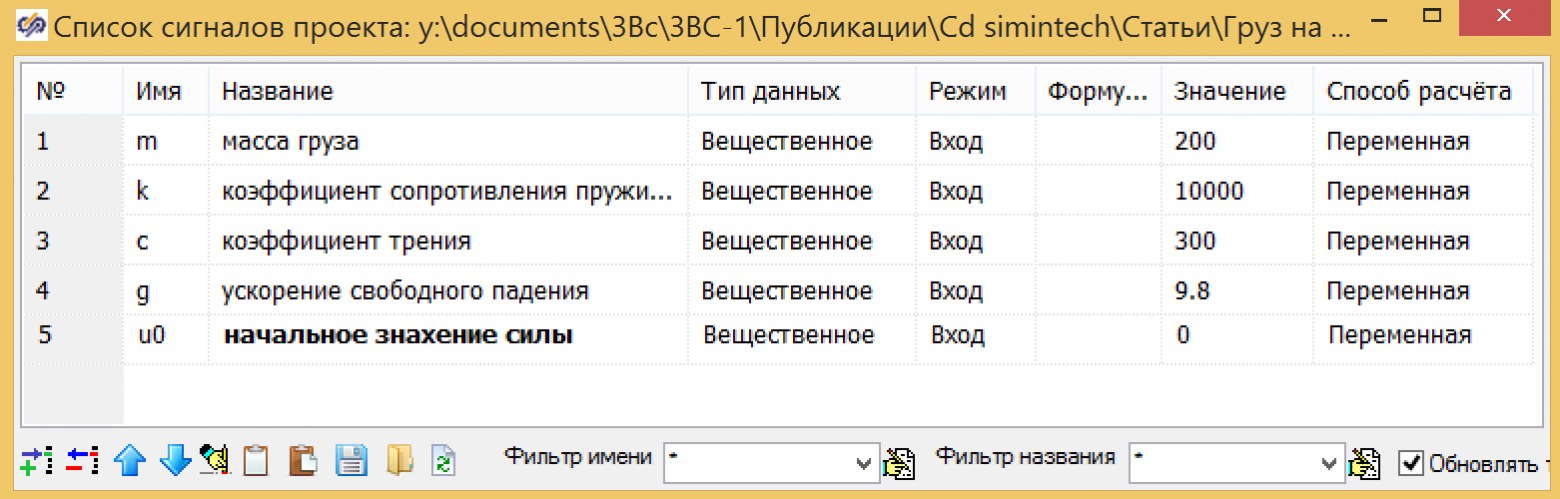
Рисунок 4. Глобальные переменные проекта.
Модель демпфера можно создать и в виде структуры, на рисунке 5, где представлена параллельная модель демпфера, созданная из стандартных блоков, в которой начальное условие находится в интеграторе у выхода (см. рис. 6), а коэффициенты внесены в сумматор (см. рис. 7)

Рисунок 5. Демпфер на языке программирования и в виде структурной схемы.

Рисунок 6. Свойство интегратора с начальными условиями.
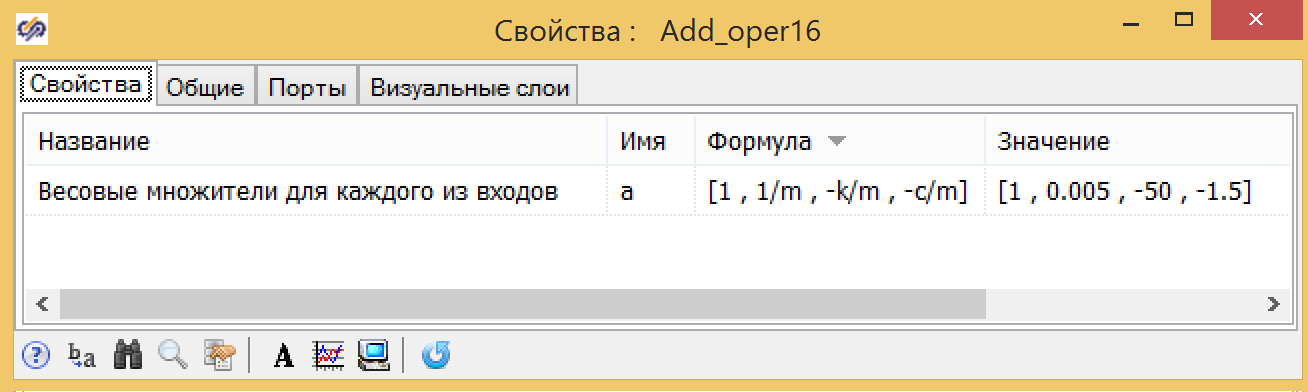
Рисунок 7. Свойства сумматора с коэффициентами.
Зададим возмущающее воздействие на 10 секунде, изменяя воздействующую силу с 0 до 30, скачком, и убедимся, что две модели показывают одинаковый результат (см. рис. 8).
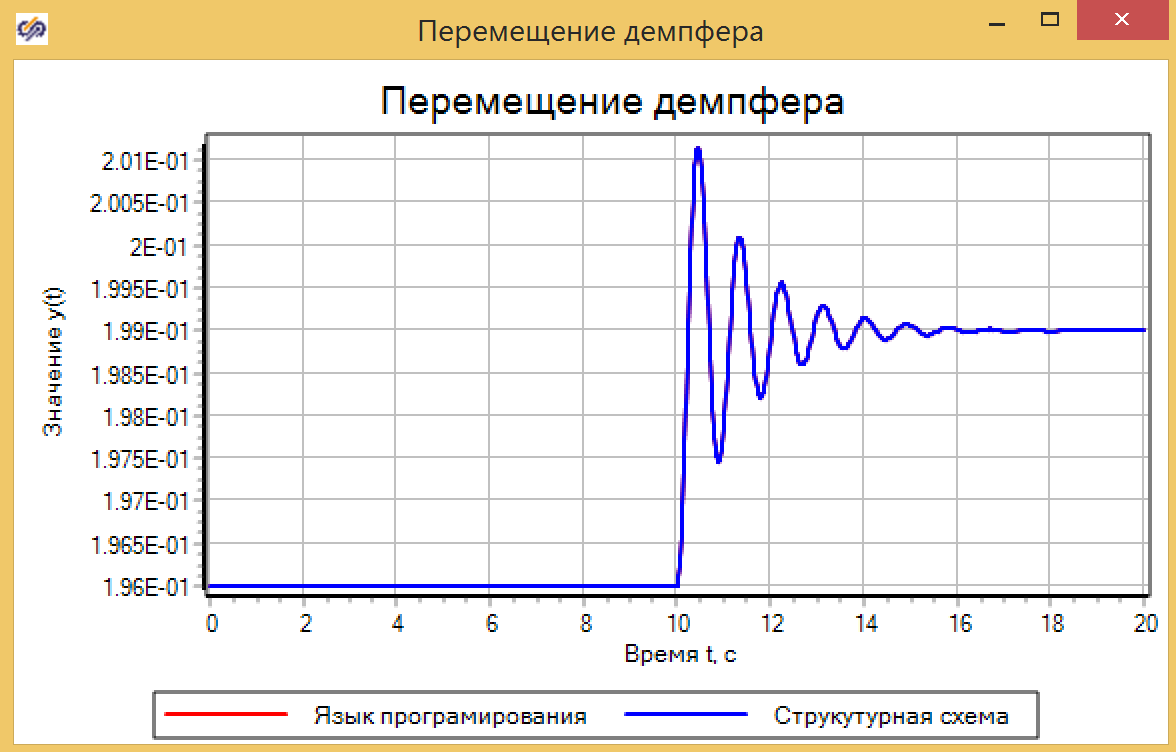
Рисунок 8. Перемещение демпфера.
Проверим модель в виде передаточной функции в общем виде и в виде колебательного звена, которым данная система и является. Для этого соберем схему, как показано на рисунке 9.

Рисунок 9. Две модели демпфера в виде передаточных функций.
Нужно учесть, что схему мы составляли в отклонениях, поэтому для получения абсолютного значения необходимо добавить константу – начальное положение поршня.
Для передаточной функции (формула 7) мы используем те же самые глобальные константы и выражения, полученные ранее для k1, T1, T2 (см. рис. 10).
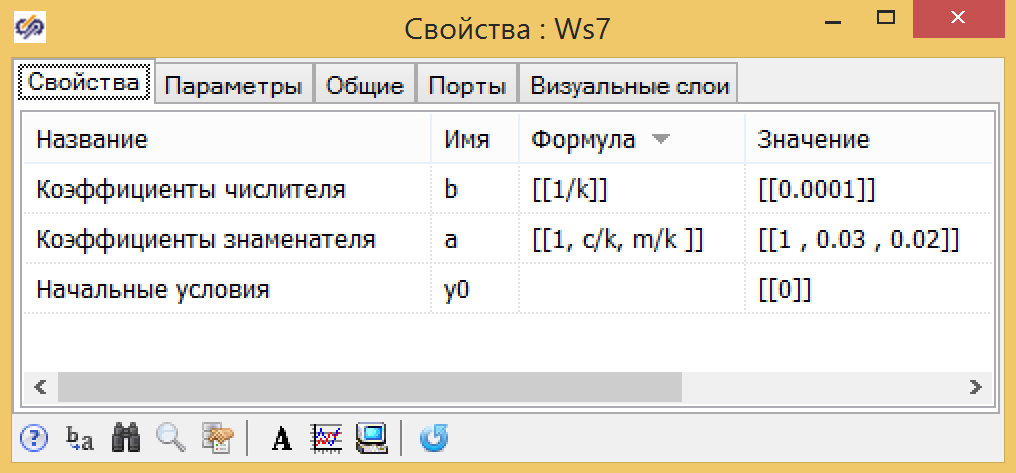
Рисунок 10. Параметры передаточной функции общего вида.
Для параметров колебательного звена формулы немного сложнее, но все также могут быть выражены через глобальные параметры: массу поршня — m, коэффициент сопротивления пружины — k, коэффициент трения — с (см. рис. 11).

Рисунок 11. Параметры колебательного звена.
Графики переходного процесса показывают (см. рис. 12), что магия ТАУ действительно работает. Передаточная функция дает точно такие же результаты как модель, составленная на основе уравнений физики.

Рисунок 12. Перемещение демпфера в моделях ТАУ.
Представим, что у нас нет модели, и мы используем блок идентификации по данным, полученным из эксперимента. Есть целая технология анализа данных и получения передаточных функций, но в рамках статьи и в качестве примера мы подключим блок построения передаточных функций к модели в виде языка программирования, как показано на рисунке 13. Считаем, что у нас модель – «черный ящик», и мы не знаем, что там внутри.

Рисунок 13. Схема подключения псевдо-идентификатора.
В результате анализа нашего блока на языке программирования мы получили передаточную функцию, которая практически не отличается от исходной, выведенной из уравнений (см. рис 14.). Сравните с рисунком 10. Вот она волшебная кнопка!

Рисунок 14. Результаты идентификации передаточной функции.
Значения числителя и знаменателя можно напрямую скопировать из блока идентификации, вставить в блок передаточной функции и убедиться, что графики совпадают. Магия ТАУ работает.
Так почему нельзя всегда использовать System Identification для процесса модельно-ориентированного проектирования, когда все так волшебно?
Чтобы понять недостаток моделей, полученных путем идентификации «черного ящика» System Identification, попробуйте ответить на простой вопрос: какое будет отклонение демпфера при увеличении массы поршня на 30%?
Тут-то и выясняется, что не все йогурты одинаково полезны.
В случае, если у вас есть честные уравнения, вы просто меняете массу груза в глобальных переменных проекта и получаете новый переходный процесс, и новую передаточную функцию.

В случае, когда у вас вместо честных уравнений физики уже готовая передаточная функция, построенная по результатам эксперимента, вам нужно снова бежать и делать эксперимент, чтобы понять, как повлияет изменение массы на поведение модели. Как говорится, дурная голова ногам покоя не дает.

Файл с моделью демпфера для эксперементов можно взять здесь...
Мы же представляли модель ракеты ФАУ2 в виде одной передаточной функции, можно посмотреть здесь… И, вроде, все работало. Зачем же нам нужно сначала изучать математический анализ и дифференциальные исчисления, когда есть волшебная кнопка, получающая модель из испытаний?
Действительно такой подход может применяться, но для этого нужно два условия:
- Объект уже должен быть (не подходит для проектируемых объектов).
- Данные измерений должны быть полными и достоверными.
В любых других случаях – «хотели как лучше, получилось как всегда» (с).
Например, в этой статье про моделирование электропривода показано, что «при некотором пороговом значении точности измерительных приборов модель привода становится неидентифицируемой, что приводит к потере управляемости и невозможности диагностирования»
В этой же статье мы разберём магию и волшебство создания моделей в виде передаточных функций из ТАУ, а потом осуществим сеанс разоблачения данной магии.
Итак, сначала магия
Разберем простой пример. У нас есть модель механического демпфера. Это поршень на пружине, он движется внутри цилиндра, может перемещается вверх-вниз. Его положение – это интересующая нас функция Y(t), сверху на него воздействует возмущающая сила (U(t)), на стенках поршня действует сила вязкого трения. (См. рис. 1)
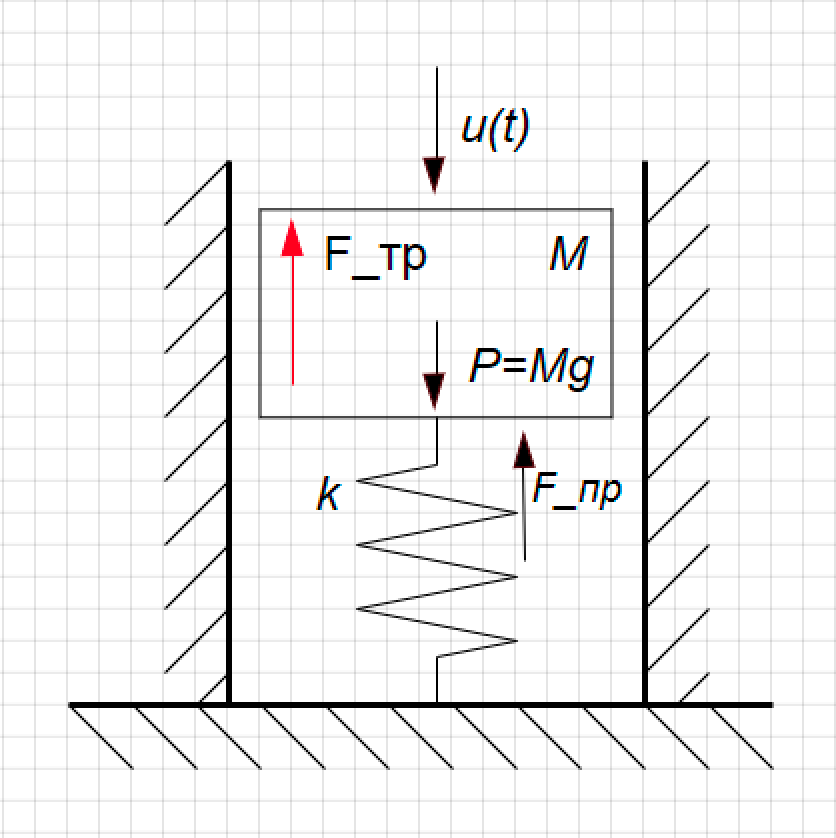
Рисунок 1. Расчетная схема амортизатора.
Выведем передаточную функцию для этого звена.
Те джедаи, кто уже знаком с магией передаточных функций, могут пропустить данную часть и перейти сразу к разоблачению магии, а для юных падаванов раскроем всю технологию получения уравнений динамики.
Согласно 2-му закону Ньютона ускорение тела пропорционально сумме сил, действующих на тело:
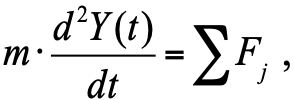 , (1)
, (1)где m – масса тела; Fj — силы, воздействующие на тело (поршень демпфера).
Подставляя в уравнение (1) все силы согласно рис. 1, имеем:
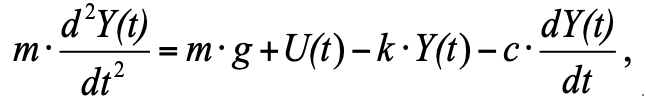 (2)
(2) где:
Y(t) – положение поршня;
P = m∙g – сила тяжести;
F_пр = k∙Y(t) – сила сопротивления пружины;
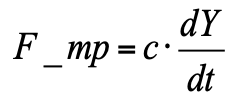 – сила вязкого трения (пропорциональная скорости движения поршня).
– сила вязкого трения (пропорциональная скорости движения поршня).Размерности сил и коэффициентов, входящих в уравнение (2):
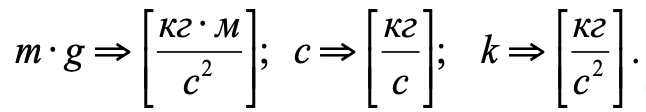
Считаем, что в нулевой момент времени поршень находится в равновесии. Тогда начальное положение поршня — y0 в равновесии, где скорость и ускорения равны 0, можно посчитать из уравнения 2.
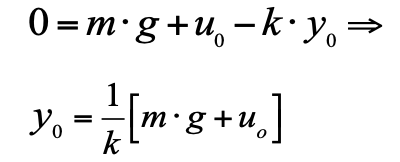
Данное уравнение позволяет посчитать, в каком положении будет поршень при различных нагрузках. Эта статическая характеристика: приложили силу — получили перемещение. Ее вид для нашей системы предельно прост (См. рис. 2):
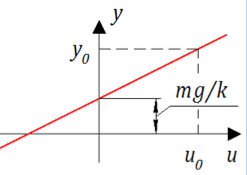
Рисунок 2. Статическая характеристика демпфера.
Казалось бы, вот оно счастье – простая линия, когда приложил силу, получил перемещение. Но не тут-то было! Нас интересует не конечное положение поршня, а процесс перехода из одного состояния в другое.
Для анализа переходного процесса и создана теория автоматического управления ТАУ. По типовой «технологии создания моделей» согласно этой теории предлагается рассматривать систему не в абсолютных значениях, а в отклонениях от равновесного состояния. Такая постановка упрощает решение и построение. И в самом деле, если заменить абсолютные значения на отклонения, то получим:
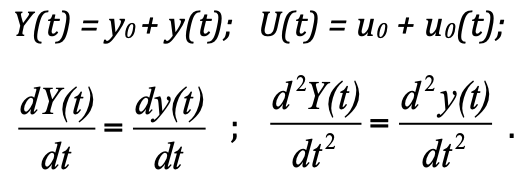
F_пр = k∙(y0+y(t)) = k∙y0 + k∙y(t) – сила сопротивления пружины;
 — сила трения.
— сила трения.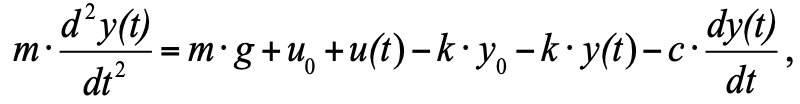 но поскольку мы приняли, что в начальный момент у нас состояние равновесия, а сумма трех сил в состоянии равновесия равна нулю, их можно убрать из уравнения, и в итоге получим:
но поскольку мы приняли, что в начальный момент у нас состояние равновесия, а сумма трех сил в состоянии равновесия равна нулю, их можно убрать из уравнения, и в итоге получим: 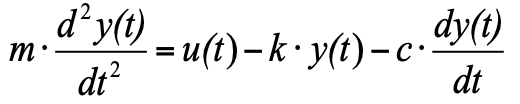 (4)
(4)Для того, что бы перевести уравнение к виду по канону ТАУ, нужно все уравнение разделить на k, чтобы коэффициент у значение выходной переменной был равен 1, и перенести в правую часть множители с выходными значения у(t), а в левую – с входными воздействиями u(t):
 (5)
(5)Это уравнение можно уже записать в операторной форме:
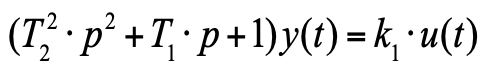 (6)
(6)где:

р = d/dt – оператор дифференцирования. Обратите внимание, что размерности коэффициентов имеют размерность и смысл постоянных времени:
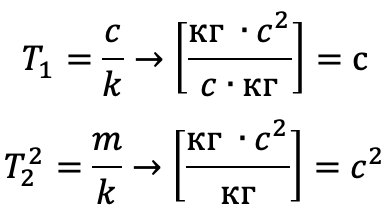
A передаточная функция для такого уравнения [6] имеет вид:

Сейчас на ваших глазах мы получили из уравнений физики передаточную функцию в виде блока, и, более того, полученный блок представляет собой стандартное колебательное звено из ТАУ.
Лично для меня, магией здесь является волшебное появление из статических характеристик, частей системы, массы поршня, упругости пружины, трения на стенках) объекта волшебным образом появилась временная характеристика переходных процессов в системе
Проверим формулы моделью
Как научил меня Максим Андреев, при создании динамических моделей «Конец — всему голова!» (смотри здесь второй принцип моделирования — «начинай с конца»):
А в конце функции у нас – перемещение.
Поэтому Представим уравнение 2 в форме Коши, для перемещения.
Форма Коши, это когда слева – производные интересующих нас функций, справа – выражения для их вычисления. Поскольку производная в уравнении у нас второй степени, то введя новую переменную Y1 – скорость изменения положения (скрость перемещения), мы получим систему из двух уравнений в форме Коши:
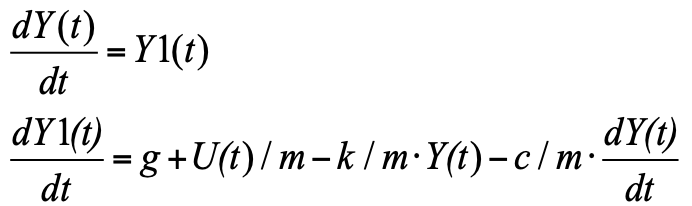
Данное уравнение можно просто записать в блок «Язык программирования» и получить модель (см. рис.3):

Рисунок 3. Модель демпфера на языке программирования.
В качестве входа используем значение силы U, выходом из блока является перемещение Y, начальное положение задается по формуле 3. Все переменные задаем как глобальные сигналы для проекта:
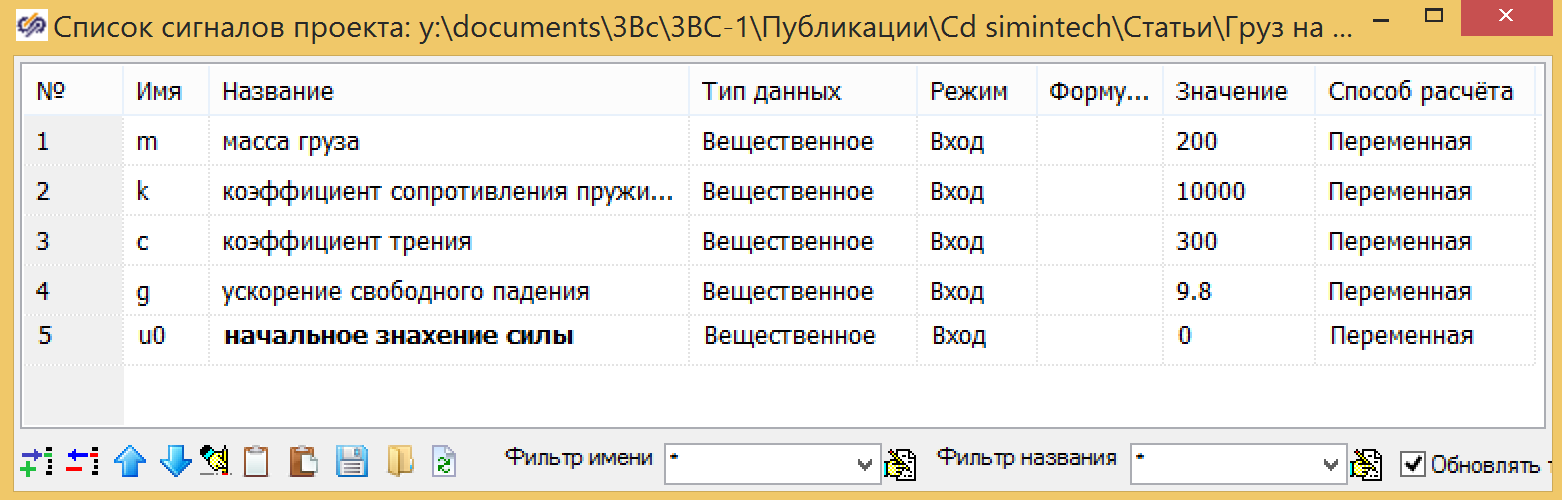
Рисунок 4. Глобальные переменные проекта.
Модель демпфера можно создать и в виде структуры, на рисунке 5, где представлена параллельная модель демпфера, созданная из стандартных блоков, в которой начальное условие находится в интеграторе у выхода (см. рис. 6), а коэффициенты внесены в сумматор (см. рис. 7)
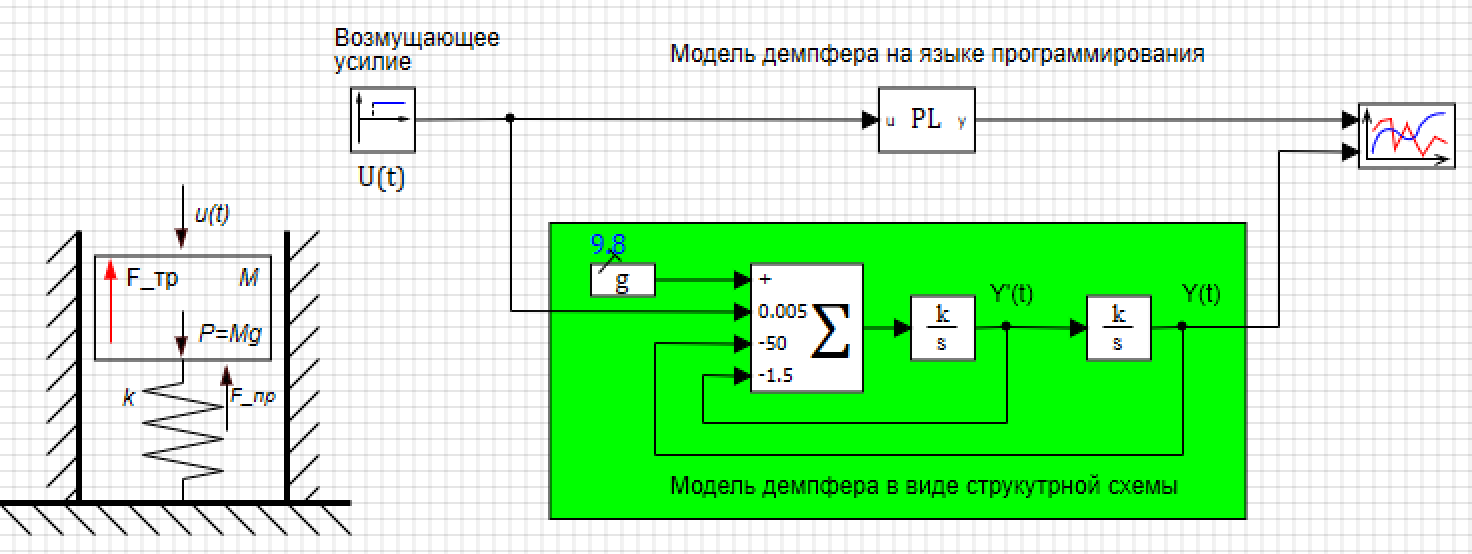
Рисунок 5. Демпфер на языке программирования и в виде структурной схемы.
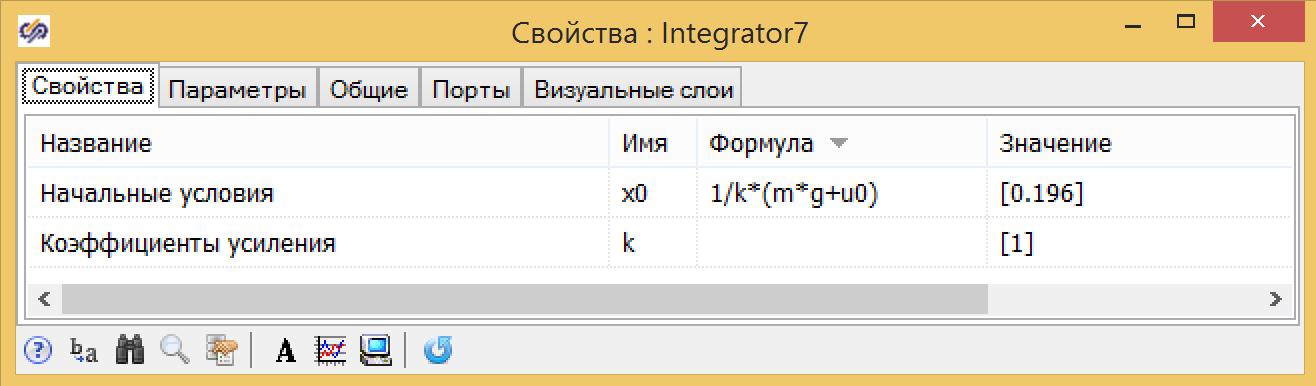
Рисунок 6. Свойство интегратора с начальными условиями.
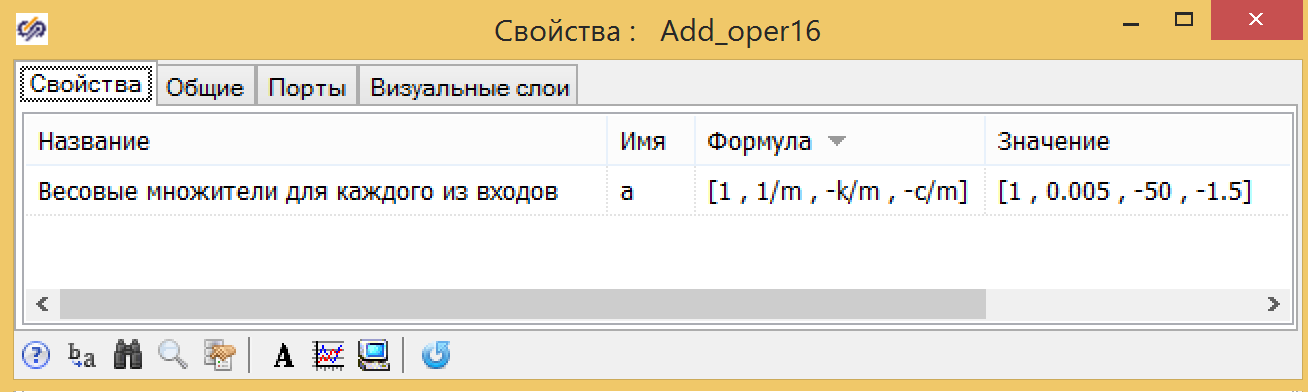
Рисунок 7. Свойства сумматора с коэффициентами.
Зададим возмущающее воздействие на 10 секунде, изменяя воздействующую силу с 0 до 30, скачком, и убедимся, что две модели показывают одинаковый результат (см. рис. 8).
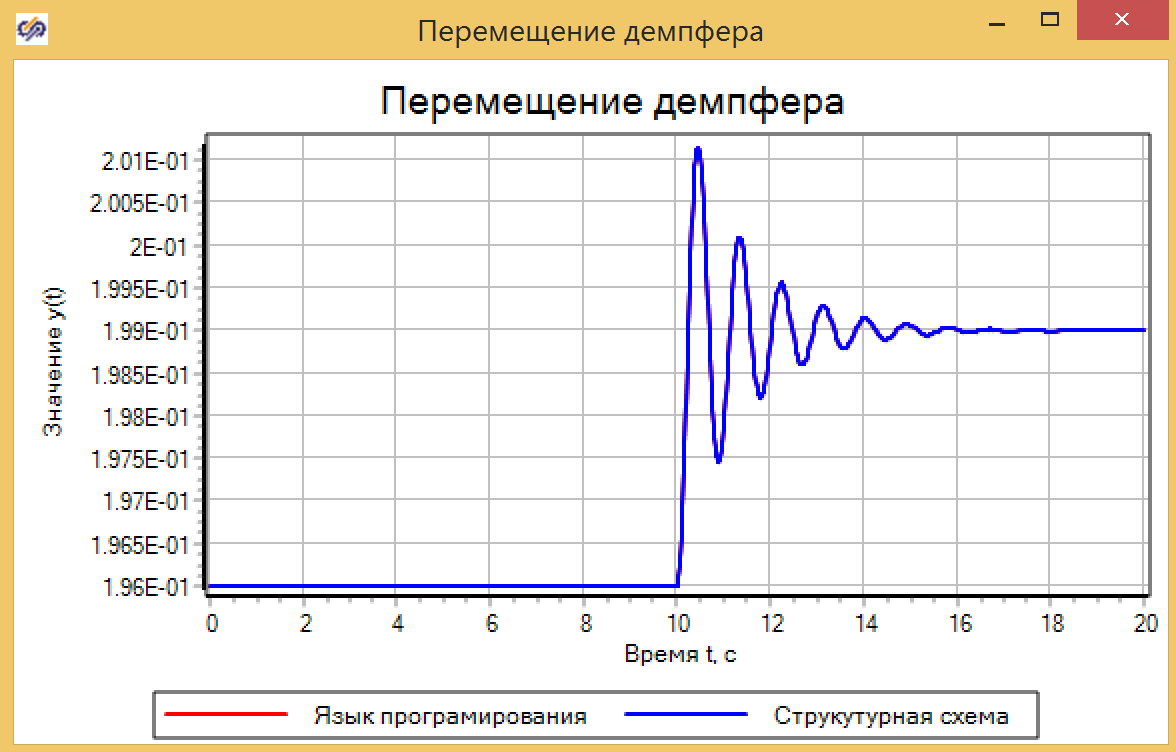
Рисунок 8. Перемещение демпфера.
Проверим модель в виде передаточной функции в общем виде и в виде колебательного звена, которым данная система и является. Для этого соберем схему, как показано на рисунке 9.

Рисунок 9. Две модели демпфера в виде передаточных функций.
Нужно учесть, что схему мы составляли в отклонениях, поэтому для получения абсолютного значения необходимо добавить константу – начальное положение поршня.
Для передаточной функции (формула 7) мы используем те же самые глобальные константы и выражения, полученные ранее для k1, T1, T2 (см. рис. 10).
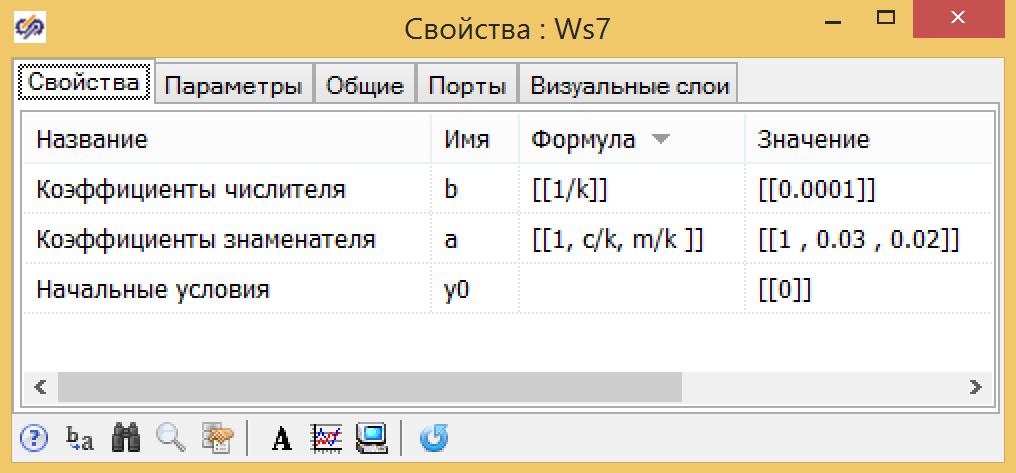
Рисунок 10. Параметры передаточной функции общего вида.
Для параметров колебательного звена формулы немного сложнее, но все также могут быть выражены через глобальные параметры: массу поршня — m, коэффициент сопротивления пружины — k, коэффициент трения — с (см. рис. 11).
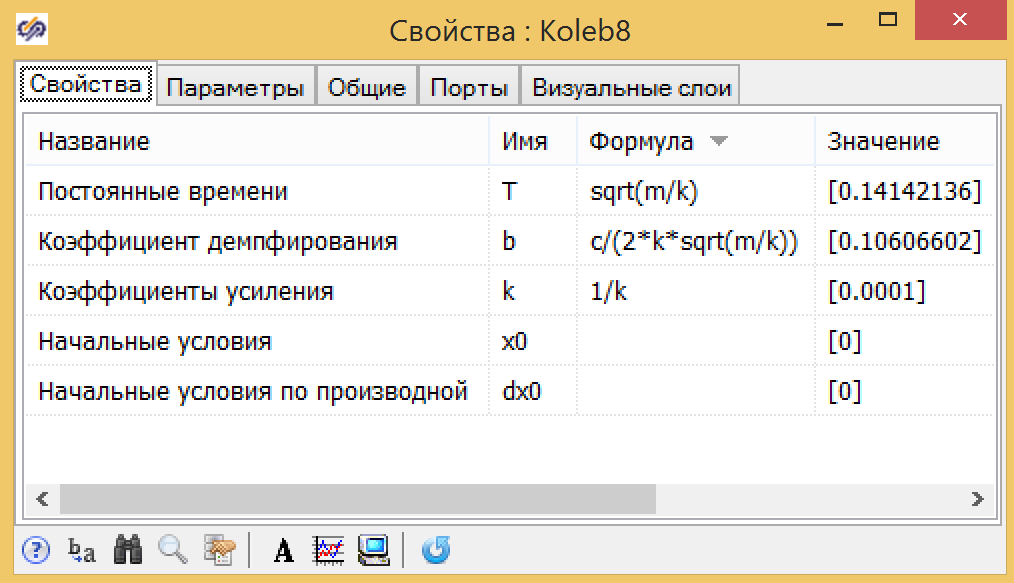
Рисунок 11. Параметры колебательного звена.
Графики переходного процесса показывают (см. рис. 12), что магия ТАУ действительно работает. Передаточная функция дает точно такие же результаты как модель, составленная на основе уравнений физики.
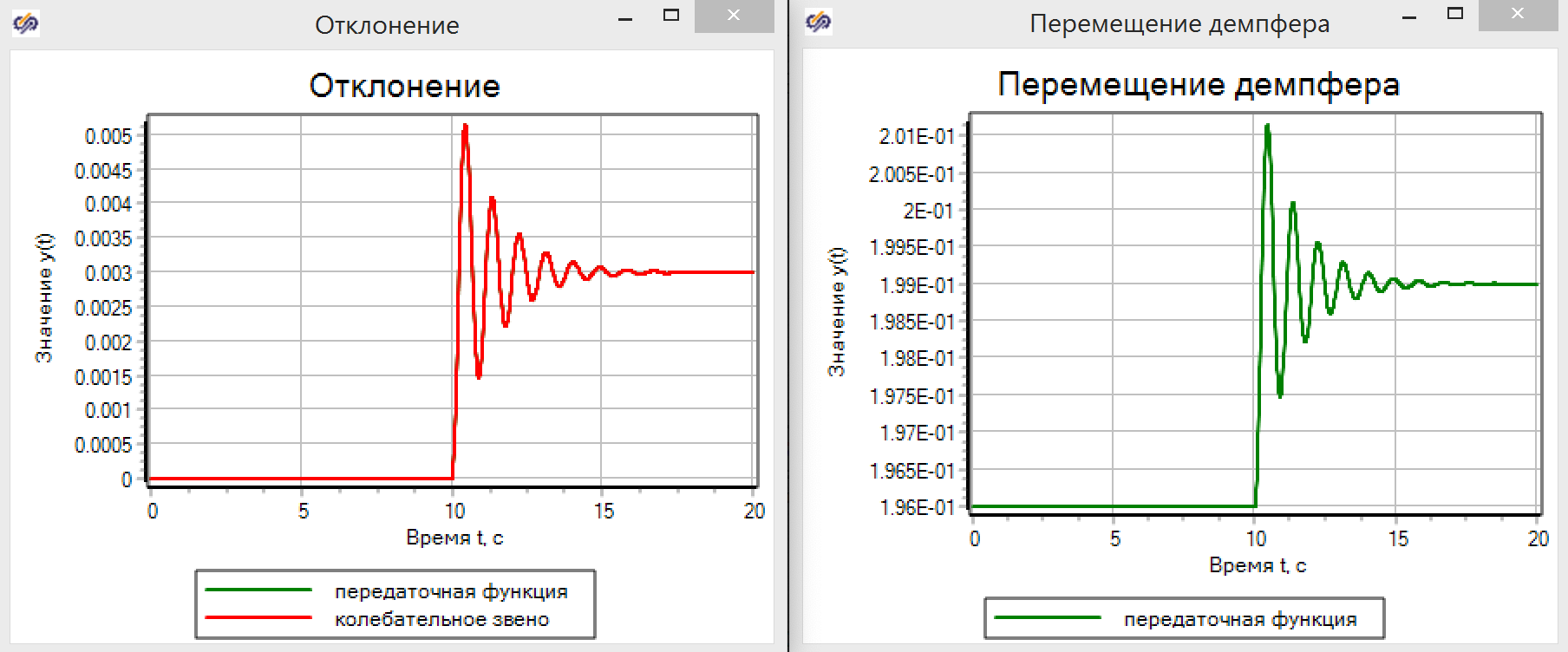
Рисунок 12. Перемещение демпфера в моделях ТАУ.
Представим, что у нас нет модели, и мы используем блок идентификации по данным, полученным из эксперимента. Есть целая технология анализа данных и получения передаточных функций, но в рамках статьи и в качестве примера мы подключим блок построения передаточных функций к модели в виде языка программирования, как показано на рисунке 13. Считаем, что у нас модель – «черный ящик», и мы не знаем, что там внутри.

Рисунок 13. Схема подключения псевдо-идентификатора.
В результате анализа нашего блока на языке программирования мы получили передаточную функцию, которая практически не отличается от исходной, выведенной из уравнений (см. рис 14.). Сравните с рисунком 10. Вот она волшебная кнопка!
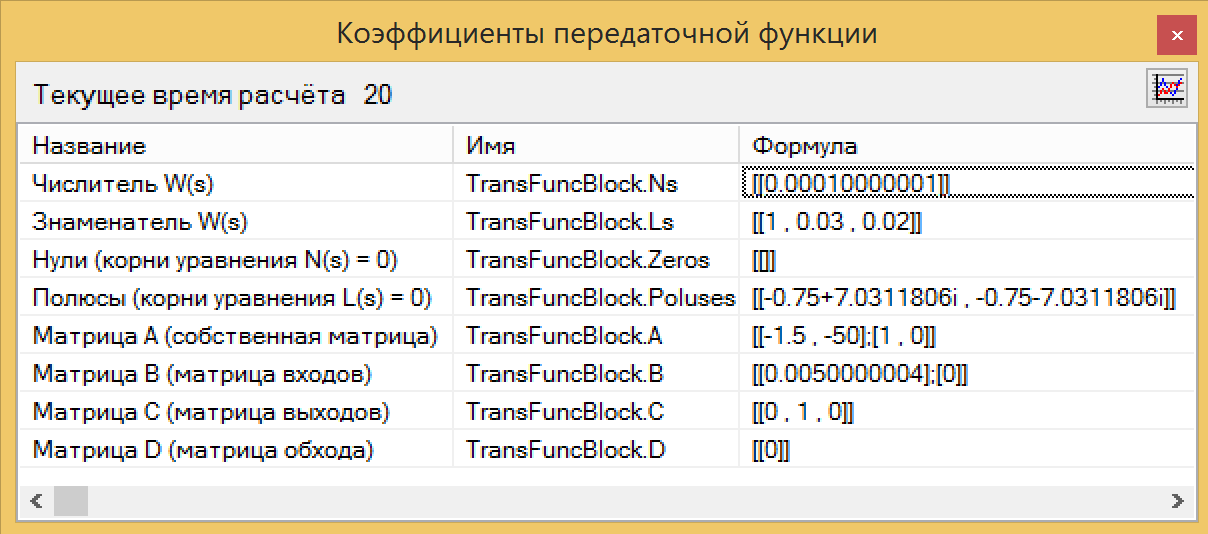
Рисунок 14. Результаты идентификации передаточной функции.
Значения числителя и знаменателя можно напрямую скопировать из блока идентификации, вставить в блок передаточной функции и убедиться, что графики совпадают. Магия ТАУ работает.
Сеанс разоблачения магии
Так почему нельзя всегда использовать System Identification для процесса модельно-ориентированного проектирования, когда все так волшебно?
Чтобы понять недостаток моделей, полученных путем идентификации «черного ящика» System Identification, попробуйте ответить на простой вопрос: какое будет отклонение демпфера при увеличении массы поршня на 30%?
Тут-то и выясняется, что не все йогурты одинаково полезны.
В случае, если у вас есть честные уравнения, вы просто меняете массу груза в глобальных переменных проекта и получаете новый переходный процесс, и новую передаточную функцию.

В случае, когда у вас вместо честных уравнений физики уже готовая передаточная функция, построенная по результатам эксперимента, вам нужно снова бежать и делать эксперимент, чтобы понять, как повлияет изменение массы на поведение модели. Как говорится, дурная голова ногам покоя не дает.

Выводы:
- Сесть и подумать над уравнениями физики – всегда полезнее и дешевле, чем экспериментировать.
- Модель, выведенная из физических уравнений процессов, гораздо вкуснее и полезнее передаточных функций.
- Эксперимент должен уточнять неизвестные коэффициенты или трудно измеряемые параметры.
- Учите физику и будет вам счастье!
Файл с моделью демпфера для эксперементов можно взять здесь...