В задачах управления бывают случаи, когда закон движения управляемого объекта известен и необходимо разработать регулятор с определенными характеристиками. Порой задача осложняется тем, что уравнения, описывающие управляемый объект, оказываются нелинейными, что осложняет построение регулятора. В связи с этим были разработаны несколько методов, позволяющих учесть нелинейные особенности строения объекта управления, одним из которых и является метод обратной задачи динамики.
Метод обратной задачи динамики естественным образом возникает при попытке «преобразовать» одну динамическую систему в другую, когда разработчик располагает двумя уравнениями, одно из которых описывает уже имеющуюся управляемую систему, а другое выражает закон движения той самой управляемой системы, превращая её в нечто полезное. Закон может выглядеть различно, но главное чтобы он был физически реализуемым. Это может быть закон синусоидального изменения напряжения на выходе генератора или системы автоподстройки частоты, закон скорости вращения турбины или перемещения коретки принтера, или даже это могут быть координаты X, Y грифеля карандаша, которым подписывает открытки манипулятор.
Однако «навязать» свой закон управления, укладывающийся в рамки физической реализуемости и управляемости объекта можно различным образом и это зачастую не самая сложная часть разработки. А вот то, что рассматриваемый метод позволяет довольно легко учесть нелинейности и многомерность объекта на мой взгляд повышает его привлекательность. Кстати здесь можно заметить связь с методом компенсации нелинейности обратной связью [1].
Известно, что в некоторых случаях правильно сформированные нелинейные регуляторы даже при управления линейной системой дают лучшие характеристики управления, в сравнении с линейными регуляторами [2]. В качестве примера можно привести регулятор, уменьшающий коэффициент демпфирования системы при росте ошибки отработки команды и увеличивающий его по мере снижения ошибки, что приводит к улучшению качества переходного процесса.
Вообще говоря, тема управления, связанного с необходимостью учета нелинейностей давно притягивает внимание ученых и инженеров, так как большинство реальных объектов все же описывается нелинейными уравнениями. Вот некоторые примеры нелинейностей, часто встречающихся в технике:
Общая постановка задачи такова. Пусть имеется объект управления, который можно описать в виде дифференциального уравнения n-го порядка
в котором присутствует возмущение (это может быть шум измерительного прибора, внешнее случайное воздействие, вибрация и тому подобное) и управляющий сигнал
(это может быть шум измерительного прибора, внешнее случайное воздействие, вибрация и тому подобное) и управляющий сигнал  (в технике управление чаще всего осуществляется с помощью напряжения). В данном случае для простоты восприятия рассматривается одномерный по управлению объект, в который входит одно возмущение. В общем случае эти величины векторные. Подразумевается, что фазовые переменные
(в технике управление чаще всего осуществляется с помощью напряжения). В данном случае для простоты восприятия рассматривается одномерный по управлению объект, в который входит одно возмущение. В общем случае эти величины векторные. Подразумевается, что фазовые переменные  , которые описывают состояние объекта управления, возмущения
, которые описывают состояние объекта управления, возмущения  и управление
и управление  зависят от времени, но этот факт для простоты восприятия не отображен. Выражение (1) может содержать нелинейности, а также быть нестационарным, т.е. параметры которого явно изменяются во времени. Примером нестационарного уравнения может быть количество ядер урана в реакторе, которое постоянно уменьшается в результате реакции распада, что приводит к непрерывному изменению оптимального закон управления стержнями-замедлителями.
зависят от времени, но этот факт для простоты восприятия не отображен. Выражение (1) может содержать нелинейности, а также быть нестационарным, т.е. параметры которого явно изменяются во времени. Примером нестационарного уравнения может быть количество ядер урана в реакторе, которое постоянно уменьшается в результате реакции распада, что приводит к непрерывному изменению оптимального закон управления стержнями-замедлителями.
Регулятор строится так, чтоб отработать заранее известный закон управления, который можно описать дифференциальным уравнением порядка, не ниже порядка уравнения (1), описывающего объект управления:
где – управляющий сигнал и его производные в количестве, позволяющем полностью описать требуемый закон управления. Так, для системы стабилизации измерять производные от управления не требуется. Для системы слежения за линейно-изменяющимся входным сигналом достаточно измерять первую производную. Чтобы отслеживать квадратично-изменяющийся сигнал, придется добавить вторую производную, и так далее. Следует заметить, что этот сигнал подается на вход регулятора, в отличии от сигнала
– управляющий сигнал и его производные в количестве, позволяющем полностью описать требуемый закон управления. Так, для системы стабилизации измерять производные от управления не требуется. Для системы слежения за линейно-изменяющимся входным сигналом достаточно измерять первую производную. Чтобы отслеживать квадратично-изменяющийся сигнал, придется добавить вторую производную, и так далее. Следует заметить, что этот сигнал подается на вход регулятора, в отличии от сигнала  , поступающего на вход объекта управления от регулятора. Это уравнение также может быть нелинейным, а также нестационарным.
, поступающего на вход объекта управления от регулятора. Это уравнение также может быть нелинейным, а также нестационарным.
Для определения требуемого управляющего сигнала выразим из (2) старшую производную
выразим из (2) старшую производную
и подставим полученное выражение вместо в уравнение (1), выражая при этом управление:
в уравнение (1), выражая при этом управление:
Из выражения (3) становится ясно, что для создания требуемого сигнала управления необходимо измерять помимо внешних возмущений (если их влияние существенно) как саму управляемую величину , так и все ее производные до порядка
, так и все ее производные до порядка  включительно, что может вызвать некоторые трудности. Во-первых, старшие производные могут быть недоступны для измерения непосредственно, как скажем производная от ускорения, в результате чего придется прибегнуть к операции дифференцирования, программно или схемотехнически. А, как известно, этого стараются избегать по причине увеличения шума. Во-вторых, измерения неизбежно содержат шумы, а это вынуждает прибегать к фильтрации. Любой фильтр является динамическим или, иначе говоря, инерционным элементом, что означает присутствие с уравнении производной. Следовательно, порядок всей системы управления в общем случае увеличится на число, равное сумме порядков уравнений, описывающих все измерители-фильтры. То есть если мы управляем объектом второго порядка и для измерений выходной величины и ее производной используем фильтры второго порядка в каждом канале измерения (то есть всего два фильтра второго порядка), то порядок системы управления возрастет на четыре. Конечно, если постоянные времени фильтров достаточно малы, то влиянием сглаживающих элементов можно пренебречь. Но они в любом случае внесут так называемые малые динамические параметры в систему и их совокупный вклад может повлиять на устойчивость системы управления в целом [2]. Также следует понимать, что этот метод позволяет задавать управление только в переходном процессе и не связан с оптимизацией по какому-либо критерию качества управления.
включительно, что может вызвать некоторые трудности. Во-первых, старшие производные могут быть недоступны для измерения непосредственно, как скажем производная от ускорения, в результате чего придется прибегнуть к операции дифференцирования, программно или схемотехнически. А, как известно, этого стараются избегать по причине увеличения шума. Во-вторых, измерения неизбежно содержат шумы, а это вынуждает прибегать к фильтрации. Любой фильтр является динамическим или, иначе говоря, инерционным элементом, что означает присутствие с уравнении производной. Следовательно, порядок всей системы управления в общем случае увеличится на число, равное сумме порядков уравнений, описывающих все измерители-фильтры. То есть если мы управляем объектом второго порядка и для измерений выходной величины и ее производной используем фильтры второго порядка в каждом канале измерения (то есть всего два фильтра второго порядка), то порядок системы управления возрастет на четыре. Конечно, если постоянные времени фильтров достаточно малы, то влиянием сглаживающих элементов можно пренебречь. Но они в любом случае внесут так называемые малые динамические параметры в систему и их совокупный вклад может повлиять на устойчивость системы управления в целом [2]. Также следует понимать, что этот метод позволяет задавать управление только в переходном процессе и не связан с оптимизацией по какому-либо критерию качества управления.
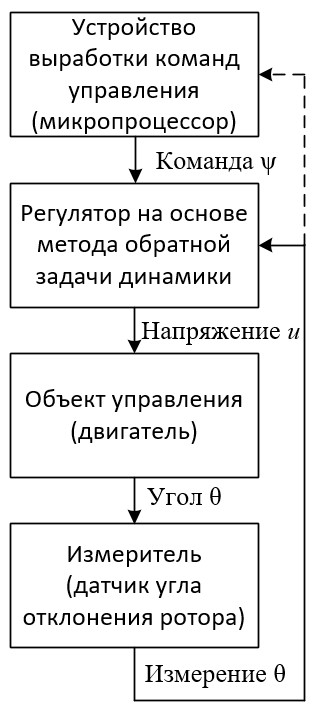
Связь регулятора и объекта управления может быть описана следующей схемой:
Рассмотрим пример синтеза регулятора для управления автоколебательной системой. Это выдуманный пример, хорошо поясняющий суть метода. Предположим, что требуется управлять системой, уравнение которой выглядит следующим образом:
Закон управления должен быть такой:
где – наш задающий сигнал управления (уставка). То есть фактически мы хотим «превратить» наш генератор с нелинейностью в линейное колебательное звено. Следует отметить, что в той же [2] эта система является системой стабилизации, так как выход
– наш задающий сигнал управления (уставка). То есть фактически мы хотим «превратить» наш генератор с нелинейностью в линейное колебательное звено. Следует отметить, что в той же [2] эта система является системой стабилизации, так как выход  стремится повторить входной сигнал
стремится повторить входной сигнал  , то есть стабилизирует выход системы на заданном постоянном уровне
, то есть стабилизирует выход системы на заданном постоянном уровне  , что можно отобразить как
, что можно отобразить как
Важно, чтобы входной задающий сигнал был постоянной или медленно меняющейся (настолько медленно, чтобы ошибка отставания
был постоянной или медленно меняющейся (настолько медленно, чтобы ошибка отставания  от
от  вписывалась в наши требования по точности) величиной или кусочно-постоянной функцией, так как вся система обладает астатизмом 0-го порядка (то есть является статической) и при любом постоянно изменяющемся задающем сигнале
вписывалась в наши требования по точности) величиной или кусочно-постоянной функцией, так как вся система обладает астатизмом 0-го порядка (то есть является статической) и при любом постоянно изменяющемся задающем сигнале  на выходе системы непременно появится динамическая ошибка, что будет выглядеть как добавление к выходной величине некоторого постоянного значения, монотонно зависящего от скорости изменения управляющего воздействия. Эта особенность в дальнейшем будет устранена.
на выходе системы непременно появится динамическая ошибка, что будет выглядеть как добавление к выходной величине некоторого постоянного значения, монотонно зависящего от скорости изменения управляющего воздействия. Эта особенность в дальнейшем будет устранена.
Итак, выражаем из уравнения (5) старшую производную:
и подставляем ее в (4), выражая :
:
Это и есть управляющий сигнал, который будет формироваться регулятором из требуемого управляющего сигнала . Из (6) также следует необходимость измерения выходной величины
. Из (6) также следует необходимость измерения выходной величины  и ее первой производной.
и ее первой производной.
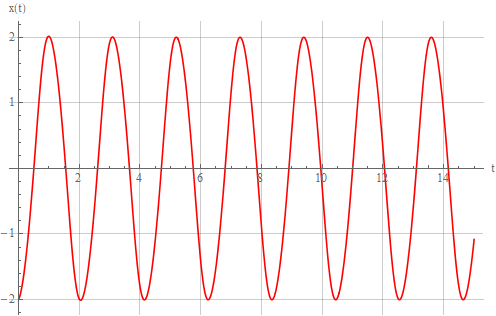
Автоколебания осциллятора Ван дер Поля с параметрами выглядят следующим образом:
выглядят следующим образом:
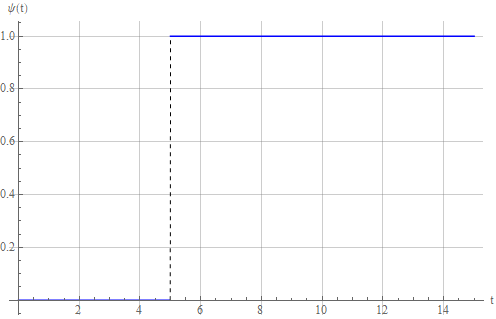
Пусть у нас имеется задающий сигнал типа «ступенька»:
и мы хотим, чтобы система его повторила.
Подадим его на вход осциллятора и посмотрим отклик:

Под действием входного единичного сигнала к колебаниям осциллятора добавилось лишь небольшое постоянное смещение.
Предположим теперь, что нам необходимо получить такую реакцию осциллятора на задающий сигнал, которая соответствовала бы реакции колебательного звена (5), с постоянной времени и коэффициентом демпфирования
и коэффициентом демпфирования  . Отклик
. Отклик  такого колебательного звена на единичную ступеньку представлен ниже:
такого колебательного звена на единичную ступеньку представлен ниже:
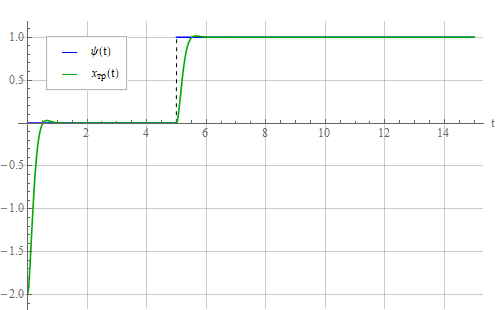
Теперь подадим на осциллятор сигнал управления , описываемый выражением (6):
, описываемый выражением (6):
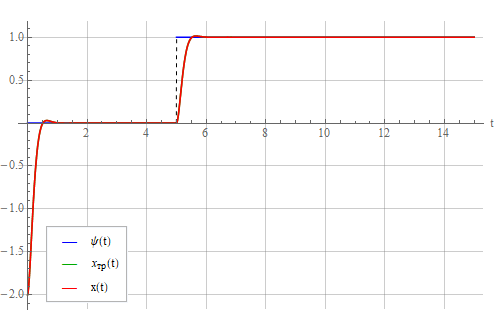
Видно что осциллятор ведет себя в соответствии с требуемым законом. Посмотрим на сигнал управления :
:
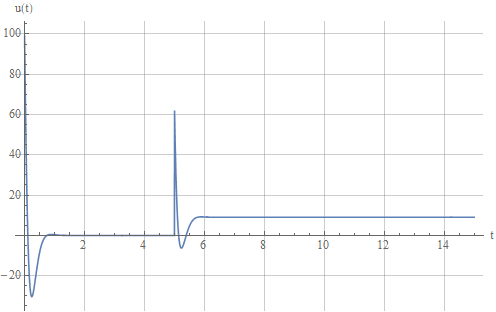
На рисунке наблюдается значительный выброс в момент переходного процесса. В реальной системе скорее всего или система войдет в насыщение (разрушение), или, дабы это предотвратить, нам придется ограничивать входной сигнал. Учтем это, ограничив амплитуду управляющего воздействия на уровне
на уровне  15. Сигнал управления теперь выглядит так:
15. Сигнал управления теперь выглядит так:
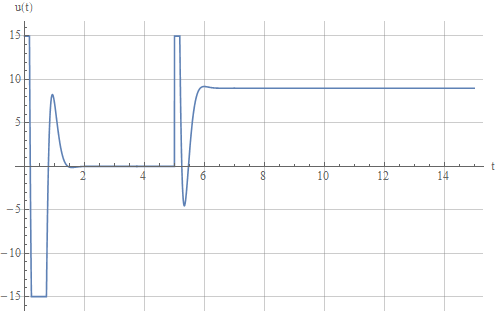
а выход осциллятора так:
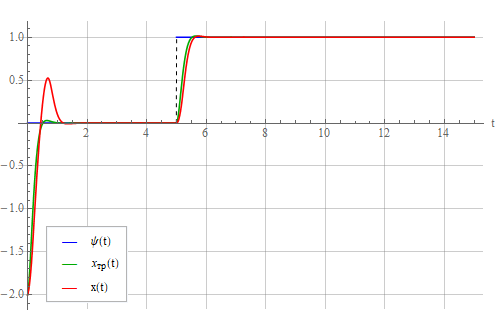
Следствие ограничения сигнала — большая ошибка переходного процесса, которая в зависимости от желаемых свойств системы может быть довольно значительной. С увеличением требуемой постоянной времени выбросы переходного процесса уменьшаются. Нужно быть внимательным, чтобы максимальный управляющий сигнал в установившемся режиме (который на данном графике начинается приблизительно с шестой секунды) не ограничивался, иначе будет бесконечный переходной процесс и система не отработает задание. Коэффициент передачи регулятора, то есть отношение управляющего сигнала на выходе регулятора к задающему воздействию
на выходе регулятора к задающему воздействию  определяется параметрами управляемой системы, а именно множителем
определяется параметрами управляемой системы, а именно множителем  .
.
Теперь подадим на вход осциллятора вот такой линейно-меняющийся сигнал:
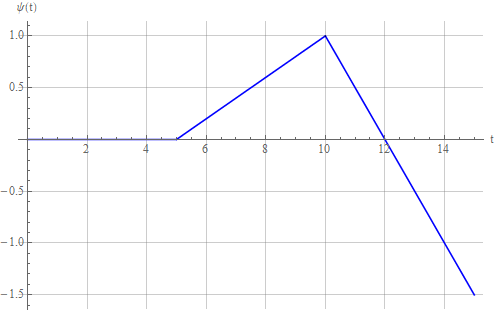
Реакция колебательного звена:
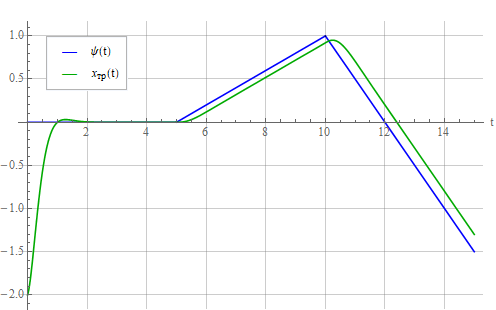
и осциллятора:
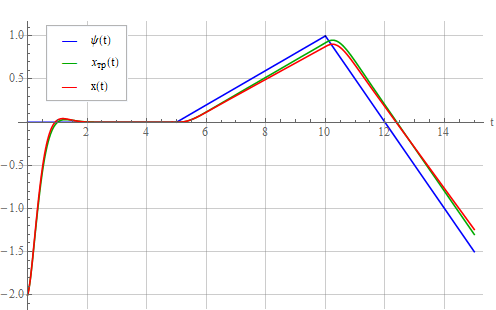
Видно, что появилось постоянное запаздывание — динамическая ошибка, потому что система спроектирована отслеживать только постоянный задающий сигнал . Для возможности отслеживания в том числе и линейно-изменяющегося сигнала необходимо оценивать скорость его изменения и учитывать ее в регуляторе. Для этого составим требуемый закон управления так:
. Для возможности отслеживания в том числе и линейно-изменяющегося сигнала необходимо оценивать скорость его изменения и учитывать ее в регуляторе. Для этого составим требуемый закон управления так:
где – ошибка отслеживания задающего сигнала осциллятором.
– ошибка отслеживания задающего сигнала осциллятором.
Также выразим из (7) старшую производную, подставим в уравнение объекта управления (4) и получим управляющий сигнал:
В новой структуре регулятора, соответствующего выражению (8) появилась скорость изменения задающего воздействия . Смотрим выход системы при подаче на вход линейно-изменяющегося задающего воздействия:
. Смотрим выход системы при подаче на вход линейно-изменяющегося задающего воздействия:
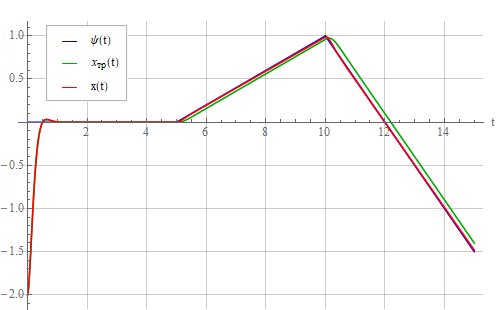
Осциллятор отслеживает задающий сигнал .
.
Но это совсем синтетический пример. В реальности будет система, структура которой возможно идентифицирована недостаточно точно — это раз. Параметры системы мы определим также с определенной погрешностью — это два. В управление входят фазовые переменные , которые придется измерять с каким-то шумом — это три. Да и параметры системы со временем могут уплывать, то есть стационарная система на достаточно длительном промежутке времени может проявить нестационарность. Хотя правильнее сказать так – на достаточно коротком интервале времени нестационарная система может казаться стационарной. В данном примере будем считать, что система идентифицирована с достаточной точностью и ее изменение во времени весьма незначительно. Тогда перепишем для ясности выражение регулятора (6) так:
, которые придется измерять с каким-то шумом — это три. Да и параметры системы со временем могут уплывать, то есть стационарная система на достаточно длительном промежутке времени может проявить нестационарность. Хотя правильнее сказать так – на достаточно коротком интервале времени нестационарная система может казаться стационарной. В данном примере будем считать, что система идентифицирована с достаточной точностью и ее изменение во времени весьма незначительно. Тогда перепишем для ясности выражение регулятора (6) так:
где – измеренные управляемая величина и ее производная;
– измеренные управляемая величина и ее производная;  – идентифицированные собственная частота и коэффициент нелинейного затухания соответственно.
– идентифицированные собственная частота и коэффициент нелинейного затухания соответственно.
Добавим 10%-ую погрешность идентификации параметров осциллятора, положив . Посмотрим на результат:
. Посмотрим на результат:
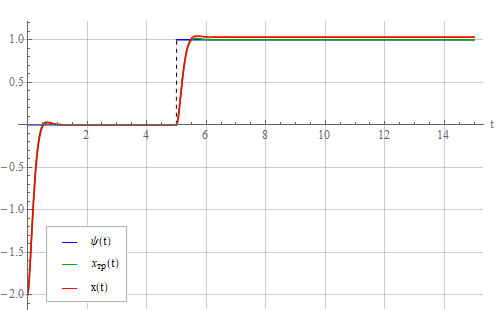
Из рисунка видно, что появилась статическая ошибка, которая растет с ростом погрешности идентификации и в установившемся режиме не зависит от ошибки
и в установившемся режиме не зависит от ошибки  . Но последняя влияет на отклонение переходного процесса осциллятора от такового для идеального колебательного звена. Можно попробовать поступить также, как и при проектировании ПИД-регуляторов (Хабр и не Хабр) – добавить в сигнал управления интеграл от ошибки (не забывая об интегральном насыщении раз, два). Но этот вопрос пока что опустим и рассмотрим выражение (9), где видно, что чем меньше собственная частота
. Но последняя влияет на отклонение переходного процесса осциллятора от такового для идеального колебательного звена. Можно попробовать поступить также, как и при проектировании ПИД-регуляторов (Хабр и не Хабр) – добавить в сигнал управления интеграл от ошибки (не забывая об интегральном насыщении раз, два). Но этот вопрос пока что опустим и рассмотрим выражение (9), где видно, что чем меньше собственная частота  по сравнению с требуемой постоянной времени
по сравнению с требуемой постоянной времени  , тем меньше влияние погрешности идентификации той самой
, тем меньше влияние погрешности идентификации той самой  . Уменьшим
. Уменьшим  с 0.125 до 0.05. Статическая ошибка также уменьшилась:
с 0.125 до 0.05. Статическая ошибка также уменьшилась:
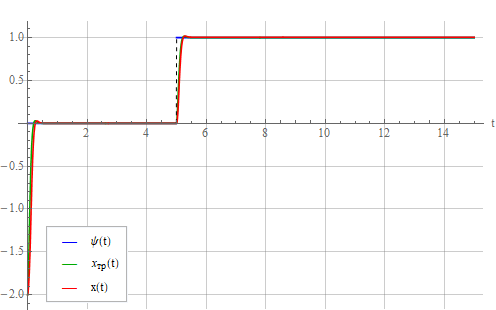
Теперь попробуем компенсировать статическую ошибку добавлением в регулятор интеграла от ошибки (как в ПИ-регуляторе). Выражение (9) превратится в
(как в ПИ-регуляторе). Выражение (9) превратится в
где – коэффициент интегральной составляющей;
– коэффициент интегральной составляющей;  – текущее время.
– текущее время.
Интеграл здесь записан формально как поясняющий общую идею, нежели математическое описание конкретного алгоритма, так как в реальном регуляторе необходимо предпринимать меры по ограничению накопленной ошибки, иначе могут возникнуть проблемы с переходным процессом. Взглянем на реакцию системы под действием получившегося регулятора, соответствующего выражению (10):
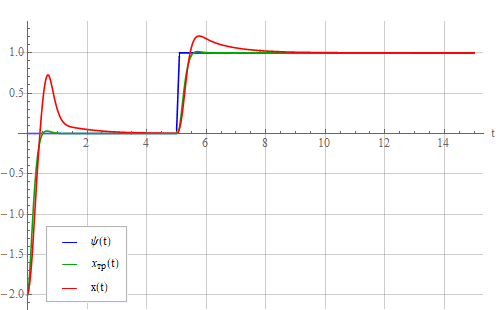
Из рисунка видно, что статическая ошибка со временем снижается, однако переходной процесс затянут. По аналогии с ПИД-регулятором можно попытаться добавить пропорциональную и дифференцирующую компоненты. Результат стал таким (коэффициенты особо тщательно не подбирались):
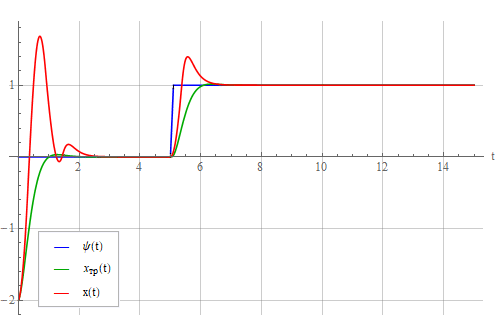
Естественно добавление интегральной и дифференциальной компонент не является уже частью метода обратной задачи динамики, а реализует собой некоторый метод оптимизации переходного процесса.
Проанализируем влияние шумов измерений переменных . Снова подадим на вход системы ступеньку и посмотрим на выход в отсутствии каких-либо шумов (есть все та же 10%-ая ошибка идентификации):
. Снова подадим на вход системы ступеньку и посмотрим на выход в отсутствии каких-либо шумов (есть все та же 10%-ая ошибка идентификации):
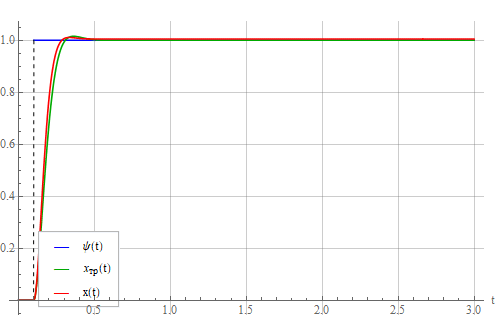
Теперь добавим к измерениям белые гауссовские шумы с нулевыми математическими ожиданиями и одинаковыми дисперсиями
белые гауссовские шумы с нулевыми математическими ожиданиями и одинаковыми дисперсиями  , пропущенные через апериодические звенья с постоянными времени
, пропущенные через апериодические звенья с постоянными времени  , которые имитируют измерительный датчик+ФНЧ. Одна из получившихся реализаций шума:
, которые имитируют измерительный датчик+ФНЧ. Одна из получившихся реализаций шума:
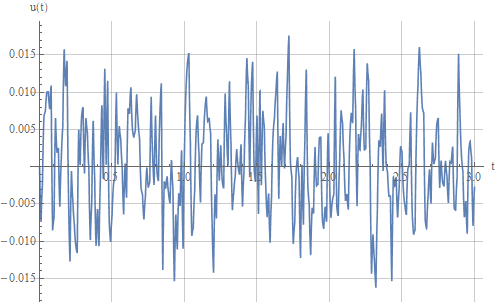
Теперь выход системы тоже стал шуметь:
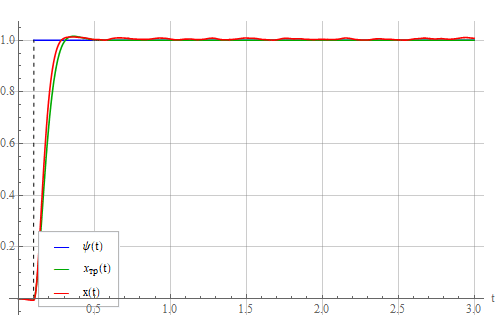
в результате зашумленного управляющего сигнала:
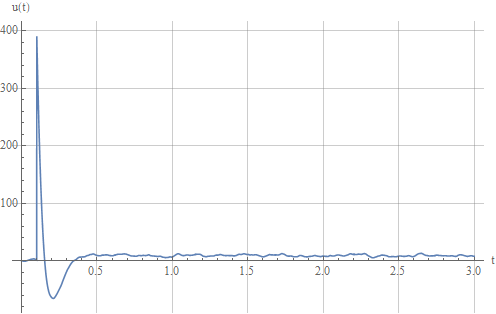
Взглянем на ошибку отработки задания:
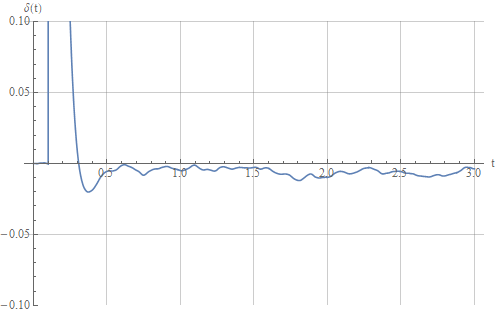
Попробуем увеличить постоянные времени датчиков и снова посмотреть на выход системы:
и снова посмотреть на выход системы:
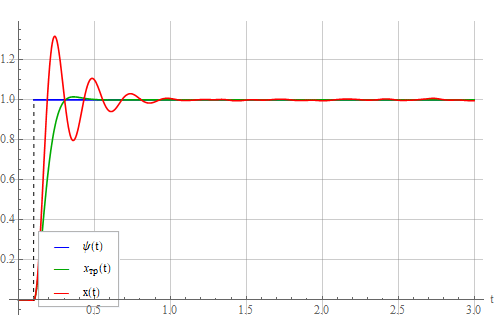
Появились значительные переколебания – результат действия тех самых неучтенных малых динамических параметров [2], описывающих датчики (их инерционность). Эти динамические параметры затрудняют фильтрацию шумов, вынуждая описывать датчики с «большими» постоянными времени, что, вообще говоря, не всегда может дать положительный результат.
Это более реальный случай применения метода обратной задачи динамики. Рассмотрим организацию управления коллекторным двигателем постоянного тока с возбуждением от постоянных магнитов (аля китайские моторчики от игрушек). В принципе тема управления такими двигателями хорошо освещена и особых сложностей не вызывает. Метод обратной задачи динамики будет использоваться по большому счету для компенсации нелинейности в уравнении динамики двигателя. Будем считать, что сам двигатель удалось описать линейными дифференциальными уравнениями, но имеется существенное влияние нелинейного вязкое трение вала, пропорционального квадрату скорости его вращения. Уравнение электромеханической системы выглядит так:
где – угловая скорость вращения вала;
– угловая скорость вращения вала;  – момент инерции всей вращающейся системы (якоря с присоединенной нагрузкой);
– момент инерции всей вращающейся системы (якоря с присоединенной нагрузкой);  – машинная постоянная, определенная для конкретной конструкции двигателя величина, связывающая магнитный поток и скорость вращения вала;
– машинная постоянная, определенная для конкретной конструкции двигателя величина, связывающая магнитный поток и скорость вращения вала;  – магнитный поток, который грубо можно считать постоянным для конкретной конструкции двигателя в диапазоне рабочих токов (но в случае больших токов нелинейно зависящим от тока обмотки);
– магнитный поток, который грубо можно считать постоянным для конкретной конструкции двигателя в диапазоне рабочих токов (но в случае больших токов нелинейно зависящим от тока обмотки);  – ток через обмотку якоря;
– ток через обмотку якоря;  – коэффициент линейного вязкого трения;
– коэффициент линейного вязкого трения;  – коэффициент нелинейного вязкого трения;
– коэффициент нелинейного вязкого трения;  – момент нагрузки;
– момент нагрузки;  – индуктивность обмотки якоря;
– индуктивность обмотки якоря;  – напряжение, приложенное к обмотке;
– напряжение, приложенное к обмотке;  – коэффициент противо-ЭДС, постоянный для конкретной конструкции двигателя;
– коэффициент противо-ЭДС, постоянный для конкретной конструкции двигателя;  – сопротивление обмотки якоря. В принципе достаточно было бы обойтись только лишь нелинейным вязким трением, но решено было нелинейную зависимость трения от скорости вращения вала представить двучленом для большей общности.
– сопротивление обмотки якоря. В принципе достаточно было бы обойтись только лишь нелинейным вязким трением, но решено было нелинейную зависимость трения от скорости вращения вала представить двучленом для большей общности.
Попытаемся сделать такой регулятор по методу обратной задачи динамики, чтобы динамика ошибки отработки задания по скорости двигателем соответствовала таковой для колебательного звена, описываемого выражением
где – угловая скорость вращения вала двигателя;
– угловая скорость вращения вала двигателя;  – уставка по скорости.
– уставка по скорости.
Уравнение (12) можно было бы составить, используя в качестве динамической переменной ошибку отработки команды :
:
но тогда в уравнении появились бы члены с производными от уставки, что видно из выражения
Это в свою очередь увеличило бы и флуктуационную составляющую ошибки. А так как мы желаем, чтобы система отрабатывала лишь постоянную скачком изменяющуюся уставку (то есть считая ее скорость, ускорение и все последующие производные нулевыми), то отслеживать нам необходимо максимум ошибку по положению, без учета ее производных, или, если так проще будет понять, с занулёнными производными от ошибки, что и привело бы к выражению (12).
Чтобы получить выражение, окончательно описывающее регулятор, необходимо свести систему двух уравнений первого порядка (11) к одному уравнению второго порядка. Для этого продифференцируем первое уравнение (11) по времени (считая момент нагрузки неизменным):
и подставим в него выраженное из второго уравнения системы (11) , что даст в итоге уравнение второго порядка
, что даст в итоге уравнение второго порядка
Подставляя в выражение (13) , полученное из (12) можем найти требуемое управление
, полученное из (12) можем найти требуемое управление  для реализации желаемого закона движения (12):
для реализации желаемого закона движения (12):
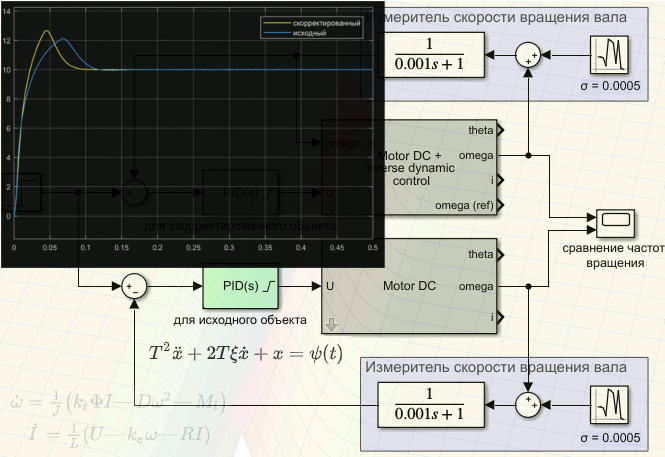
Подадим на входы двух двигателей, один из которых дополнен регулятором, реализованным по принципу обратной задачи динамики, ступеньку с единичной амплитудой в соответствии со следующей схемой:
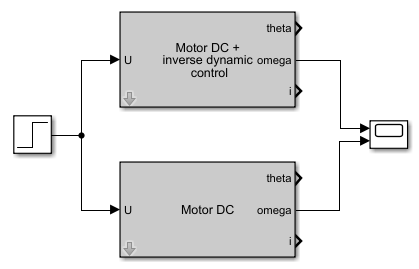
и посмотрим зависимости частот вращения валов двигателей от времени:
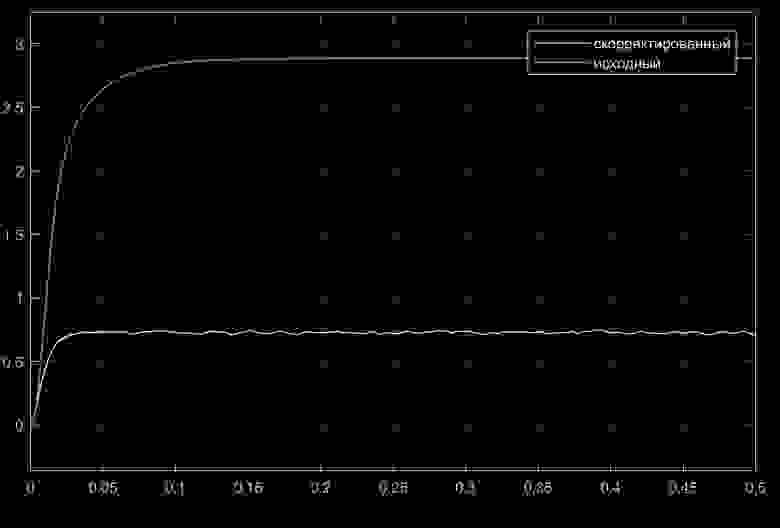
Реакция на ступеньку с амплитудой в 10 вольт:
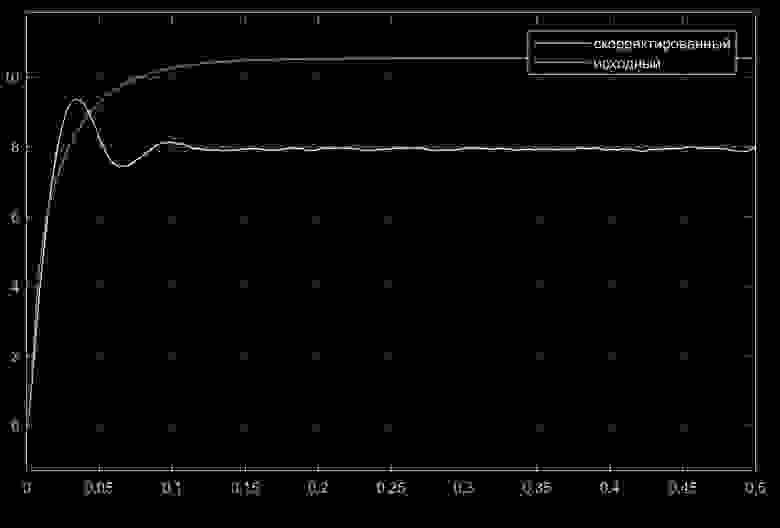
Из рисунков видна нелинейная зависимость показателя колебательности исходной системы от амплитуды входного сигнала.
Теперь сравним два двигателя с ПИД-регуляторами, структурная схема которых приведена на следующем рисунке:
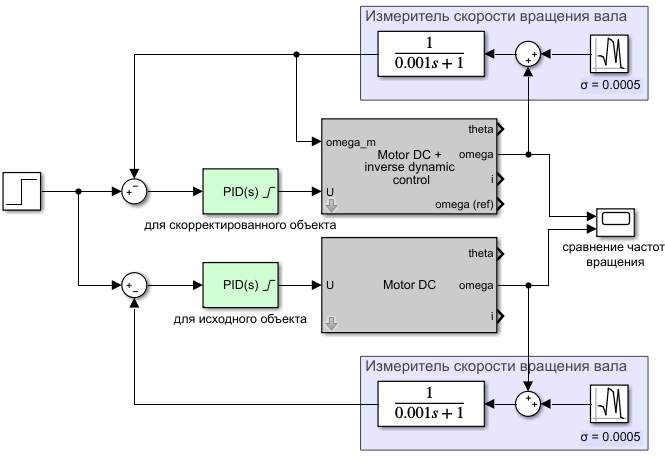
Частоты вращения валов двигателей:
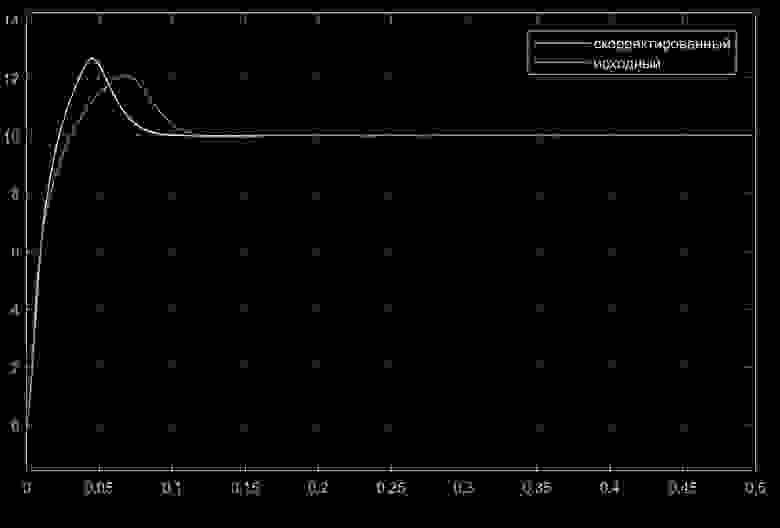
и более крупно:
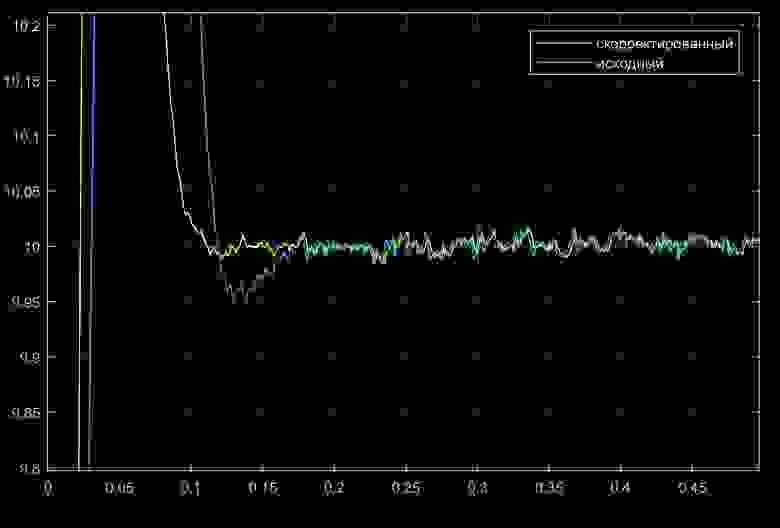
Из приведенных рисунков видно, что благодаря ПИД-регулятору, построенному с применением метода обратной задачи динамики реакция система на ступенчатый управляющий сигнал ускорилась, чего не удалось достичь применением обычного ПИД-регулятора по причине имеющейся в объекте управления нелинейности. Однако применение переменных коэффициентов ПИД-регулятора возможно решило бы эту задачу лучше и сделало бы систему более робастной. Но это уже совсем другая история.
В статье был рассмотрен метод, позволяющий построить регулятор для управления нелинейными системами, что было показано на примерах управлений осциллятором Ван дер Поля и двигателем постоянного тока.
К основным преимуществам этого метода можно отнести:
Однако данный метод также имеет ряд существенных недостатков:
В целом это довольно интересный метод, но сравнив его реализацию для управления двигателем постоянного тока (с использованием ПИД-регулятора) с двигателем, управляемым только ПИД-регулятором, стало ясно, что существенных плюшек получить от него не удастся. А вот структура управляющего устройства значительно усложняется, вынуждая в том числе бороться с шумами дифференцирования с одной стороны, и предотвращением выхода на границу устойчивости с другой. Возможно именно с этим и связано небольшое количество работ по этой теме. Одним из возможных применений метода обратной задачи динамики может быть построение эталонных (идеальных) траекторий систем для сравнения с траекториями, соответствующими различным регуляторам, к примеру линейным или линеаризованным.
1. Ким Д.П. Теория автоматического управления. Т.2. Многомерные, нелинейные, оптимальные и адаптивные системы: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2004. – 464 с.
2. Бойчук Л.М. Метод структурного синтеза нелинейных систем автоматического управления. М., «Энергия», 1971.
3. Нестационарные системы автоматического управления: анализ, синтез и оптимизация / Под ред. К.А. Пупкова и Н.Д. Егупова. – М.: Издательство МГТУ им. Н.Э. Баумана, 2007. – 632 с.

Введение
Метод обратной задачи динамики естественным образом возникает при попытке «преобразовать» одну динамическую систему в другую, когда разработчик располагает двумя уравнениями, одно из которых описывает уже имеющуюся управляемую систему, а другое выражает закон движения той самой управляемой системы, превращая её в нечто полезное. Закон может выглядеть различно, но главное чтобы он был физически реализуемым. Это может быть закон синусоидального изменения напряжения на выходе генератора или системы автоподстройки частоты, закон скорости вращения турбины или перемещения коретки принтера, или даже это могут быть координаты X, Y грифеля карандаша, которым подписывает открытки манипулятор.
Однако «навязать» свой закон управления, укладывающийся в рамки физической реализуемости и управляемости объекта можно различным образом и это зачастую не самая сложная часть разработки. А вот то, что рассматриваемый метод позволяет довольно легко учесть нелинейности и многомерность объекта на мой взгляд повышает его привлекательность. Кстати здесь можно заметить связь с методом компенсации нелинейности обратной связью [1].
Известно, что в некоторых случаях правильно сформированные нелинейные регуляторы даже при управления линейной системой дают лучшие характеристики управления, в сравнении с линейными регуляторами [2]. В качестве примера можно привести регулятор, уменьшающий коэффициент демпфирования системы при росте ошибки отработки команды и увеличивающий его по мере снижения ошибки, что приводит к улучшению качества переходного процесса.
Вообще говоря, тема управления, связанного с необходимостью учета нелинейностей давно притягивает внимание ученых и инженеров, так как большинство реальных объектов все же описывается нелинейными уравнениями. Вот некоторые примеры нелинейностей, часто встречающихся в технике:
 |
 |
 |
 |
 |
 |
 |
 |
Общая постановка задачи такова. Пусть имеется объект управления, который можно описать в виде дифференциального уравнения n-го порядка
в котором присутствует возмущение
Регулятор строится так, чтоб отработать заранее известный закон управления, который можно описать дифференциальным уравнением порядка, не ниже порядка уравнения (1), описывающего объект управления:
где
Для определения требуемого управляющего сигнала
и подставим полученное выражение вместо
Из выражения (3) становится ясно, что для создания требуемого сигнала управления необходимо измерять помимо внешних возмущений (если их влияние существенно) как саму управляемую величину
Связь регулятора и объекта управления может быть описана следующей схемой:

Управление осциллятором Ван дер Поля
Рассмотрим пример синтеза регулятора для управления автоколебательной системой. Это выдуманный пример, хорошо поясняющий суть метода. Предположим, что требуется управлять системой, уравнение которой выглядит следующим образом:
Закон управления должен быть такой:
где
Важно, чтобы входной задающий сигнал
Итак, выражаем из уравнения (5) старшую производную:
и подставляем ее в (4), выражая
Это и есть управляющий сигнал, который будет формироваться регулятором из требуемого управляющего сигнала
Автоколебания осциллятора Ван дер Поля с параметрами

Пусть у нас имеется задающий сигнал типа «ступенька»:

и мы хотим, чтобы система его повторила.
Подадим его на вход осциллятора и посмотрим отклик:

Под действием входного единичного сигнала к колебаниям осциллятора добавилось лишь небольшое постоянное смещение.
Предположим теперь, что нам необходимо получить такую реакцию осциллятора на задающий сигнал, которая соответствовала бы реакции колебательного звена (5), с постоянной времени

Теперь подадим на осциллятор сигнал управления
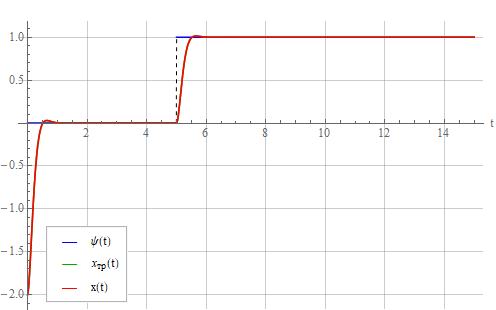
Видно что осциллятор ведет себя в соответствии с требуемым законом. Посмотрим на сигнал управления

На рисунке наблюдается значительный выброс в момент переходного процесса. В реальной системе скорее всего или система войдет в насыщение (разрушение), или, дабы это предотвратить, нам придется ограничивать входной сигнал. Учтем это, ограничив амплитуду управляющего воздействия

а выход осциллятора так:
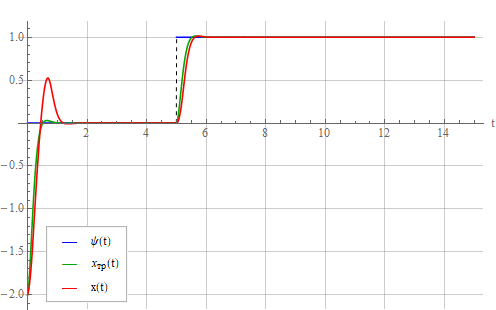
Следствие ограничения сигнала — большая ошибка переходного процесса, которая в зависимости от желаемых свойств системы может быть довольно значительной. С увеличением требуемой постоянной времени выбросы переходного процесса уменьшаются. Нужно быть внимательным, чтобы максимальный управляющий сигнал в установившемся режиме (который на данном графике начинается приблизительно с шестой секунды) не ограничивался, иначе будет бесконечный переходной процесс и система не отработает задание. Коэффициент передачи регулятора, то есть отношение управляющего сигнала
Теперь подадим на вход осциллятора вот такой линейно-меняющийся сигнал:

Реакция колебательного звена:
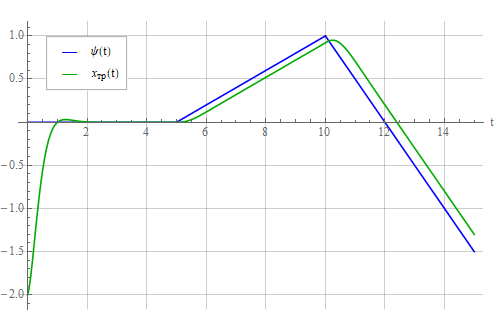
и осциллятора:
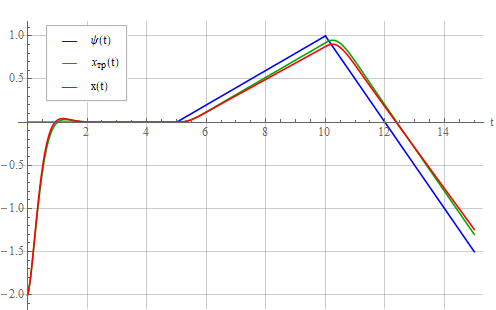
Видно, что появилось постоянное запаздывание — динамическая ошибка, потому что система спроектирована отслеживать только постоянный задающий сигнал
где
Также выразим из (7) старшую производную, подставим в уравнение объекта управления (4) и получим управляющий сигнал:
В новой структуре регулятора, соответствующего выражению (8) появилась скорость изменения задающего воздействия

Осциллятор отслеживает задающий сигнал
Но это совсем синтетический пример. В реальности будет система, структура которой возможно идентифицирована недостаточно точно — это раз. Параметры системы мы определим также с определенной погрешностью — это два. В управление входят фазовые переменные
где
Добавим 10%-ую погрешность идентификации параметров осциллятора, положив

Из рисунка видно, что появилась статическая ошибка, которая растет с ростом погрешности идентификации
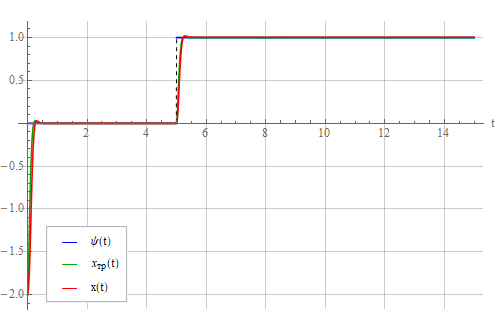
Теперь попробуем компенсировать статическую ошибку добавлением в регулятор интеграла от ошибки
где
Интеграл здесь записан формально как поясняющий общую идею, нежели математическое описание конкретного алгоритма, так как в реальном регуляторе необходимо предпринимать меры по ограничению накопленной ошибки, иначе могут возникнуть проблемы с переходным процессом. Взглянем на реакцию системы под действием получившегося регулятора, соответствующего выражению (10):

Из рисунка видно, что статическая ошибка со временем снижается, однако переходной процесс затянут. По аналогии с ПИД-регулятором можно попытаться добавить пропорциональную и дифференцирующую компоненты. Результат стал таким (коэффициенты особо тщательно не подбирались):

Естественно добавление интегральной и дифференциальной компонент не является уже частью метода обратной задачи динамики, а реализует собой некоторый метод оптимизации переходного процесса.
Проанализируем влияние шумов измерений переменных
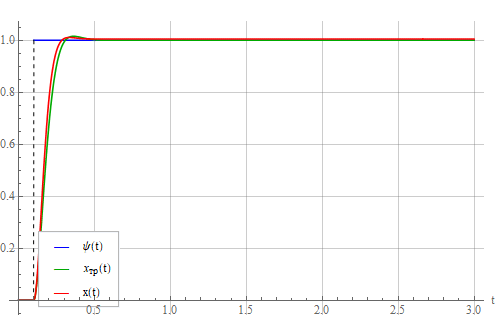
Теперь добавим к измерениям

Теперь выход системы тоже стал шуметь:

в результате зашумленного управляющего сигнала:

Взглянем на ошибку отработки задания:

Попробуем увеличить постоянные времени датчиков

Появились значительные переколебания – результат действия тех самых неучтенных малых динамических параметров [2], описывающих датчики (их инерционность). Эти динамические параметры затрудняют фильтрацию шумов, вынуждая описывать датчики с «большими» постоянными времени, что, вообще говоря, не всегда может дать положительный результат.
Управление двигателем постоянного тока с учетом нелинейного вязкого трения
Это более реальный случай применения метода обратной задачи динамики. Рассмотрим организацию управления коллекторным двигателем постоянного тока с возбуждением от постоянных магнитов (аля китайские моторчики от игрушек). В принципе тема управления такими двигателями хорошо освещена и особых сложностей не вызывает. Метод обратной задачи динамики будет использоваться по большому счету для компенсации нелинейности в уравнении динамики двигателя. Будем считать, что сам двигатель удалось описать линейными дифференциальными уравнениями, но имеется существенное влияние нелинейного вязкое трение вала, пропорционального квадрату скорости его вращения. Уравнение электромеханической системы выглядит так:
где
Попытаемся сделать такой регулятор по методу обратной задачи динамики, чтобы динамика ошибки отработки задания по скорости двигателем соответствовала таковой для колебательного звена, описываемого выражением
где
Уравнение (12) можно было бы составить, используя в качестве динамической переменной ошибку отработки команды
но тогда в уравнении появились бы члены с производными от уставки, что видно из выражения
Это в свою очередь увеличило бы и флуктуационную составляющую ошибки. А так как мы желаем, чтобы система отрабатывала лишь постоянную скачком изменяющуюся уставку (то есть считая ее скорость, ускорение и все последующие производные нулевыми), то отслеживать нам необходимо максимум ошибку по положению, без учета ее производных, или, если так проще будет понять, с занулёнными производными от ошибки, что и привело бы к выражению (12).
Чтобы получить выражение, окончательно описывающее регулятор, необходимо свести систему двух уравнений первого порядка (11) к одному уравнению второго порядка. Для этого продифференцируем первое уравнение (11) по времени (считая момент нагрузки неизменным):
и подставим в него выраженное из второго уравнения системы (11)
Подставляя в выражение (13)
Подадим на входы двух двигателей, один из которых дополнен регулятором, реализованным по принципу обратной задачи динамики, ступеньку с единичной амплитудой в соответствии со следующей схемой:
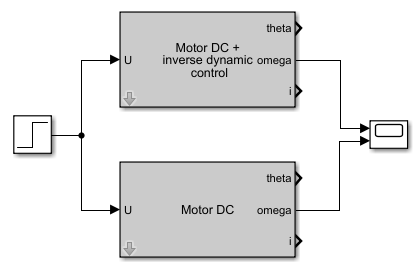
и посмотрим зависимости частот вращения валов двигателей от времени:
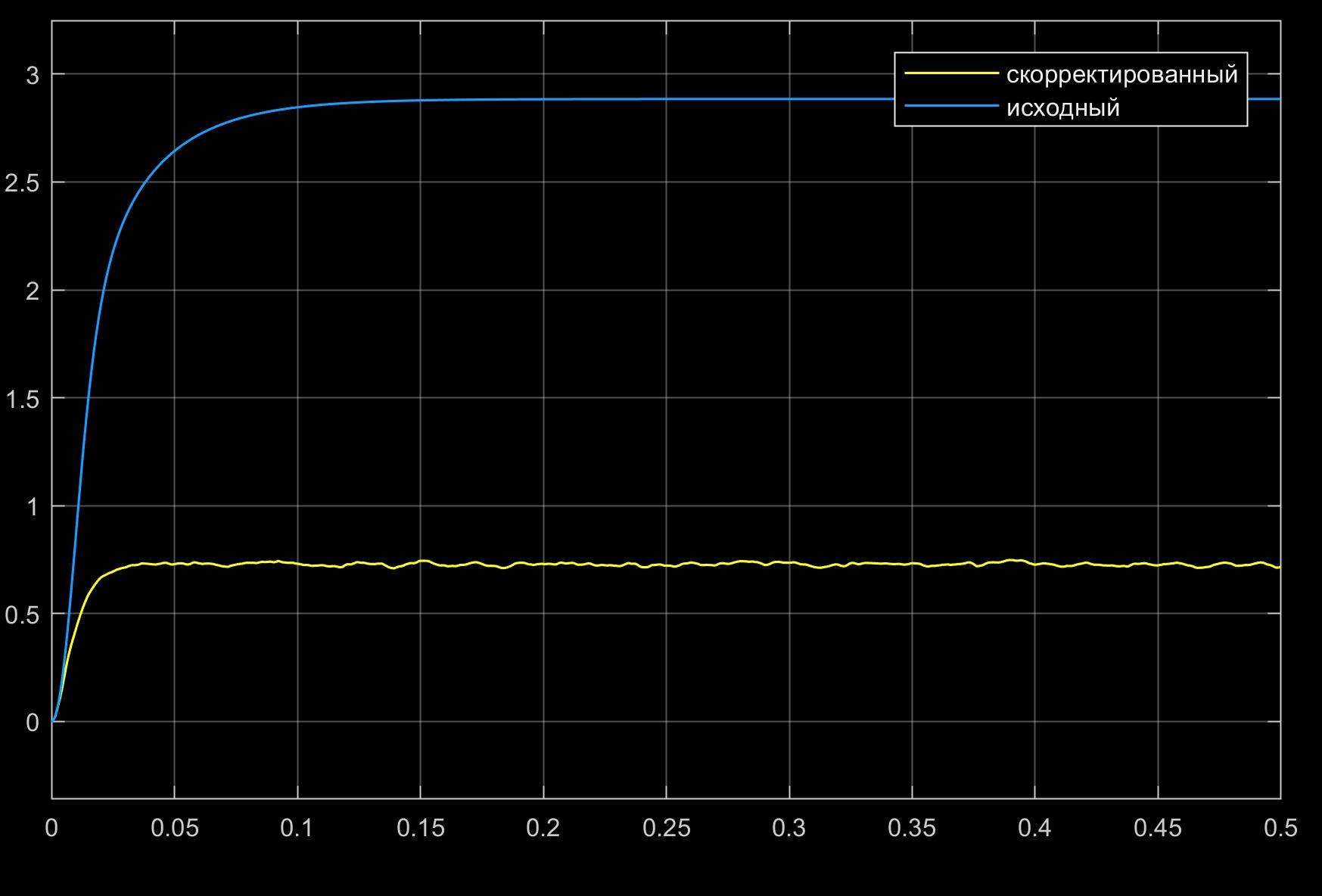
Реакция на ступеньку с амплитудой в 10 вольт:
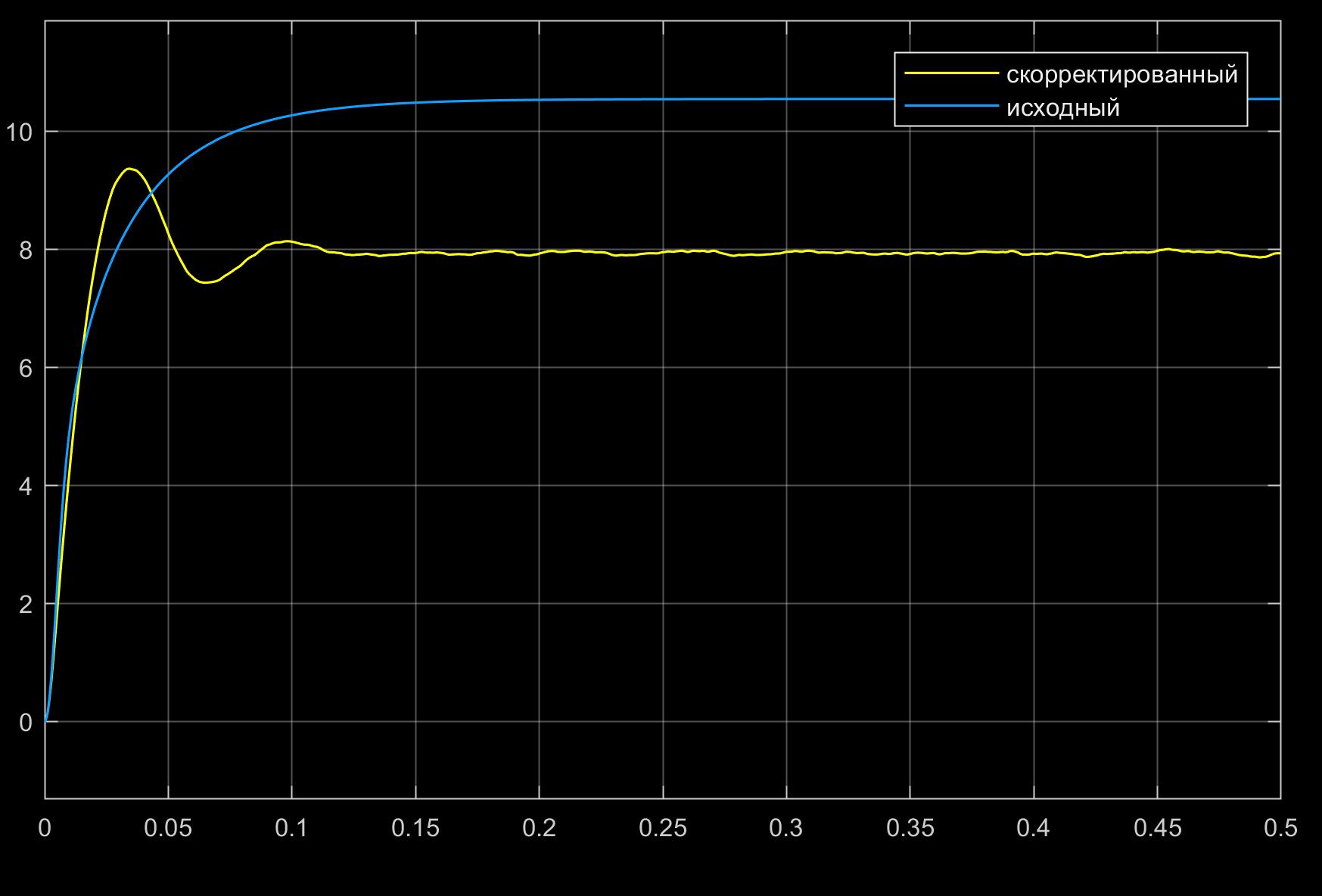
Из рисунков видна нелинейная зависимость показателя колебательности исходной системы от амплитуды входного сигнала.
Теперь сравним два двигателя с ПИД-регуляторами, структурная схема которых приведена на следующем рисунке:

Частоты вращения валов двигателей:

и более крупно:
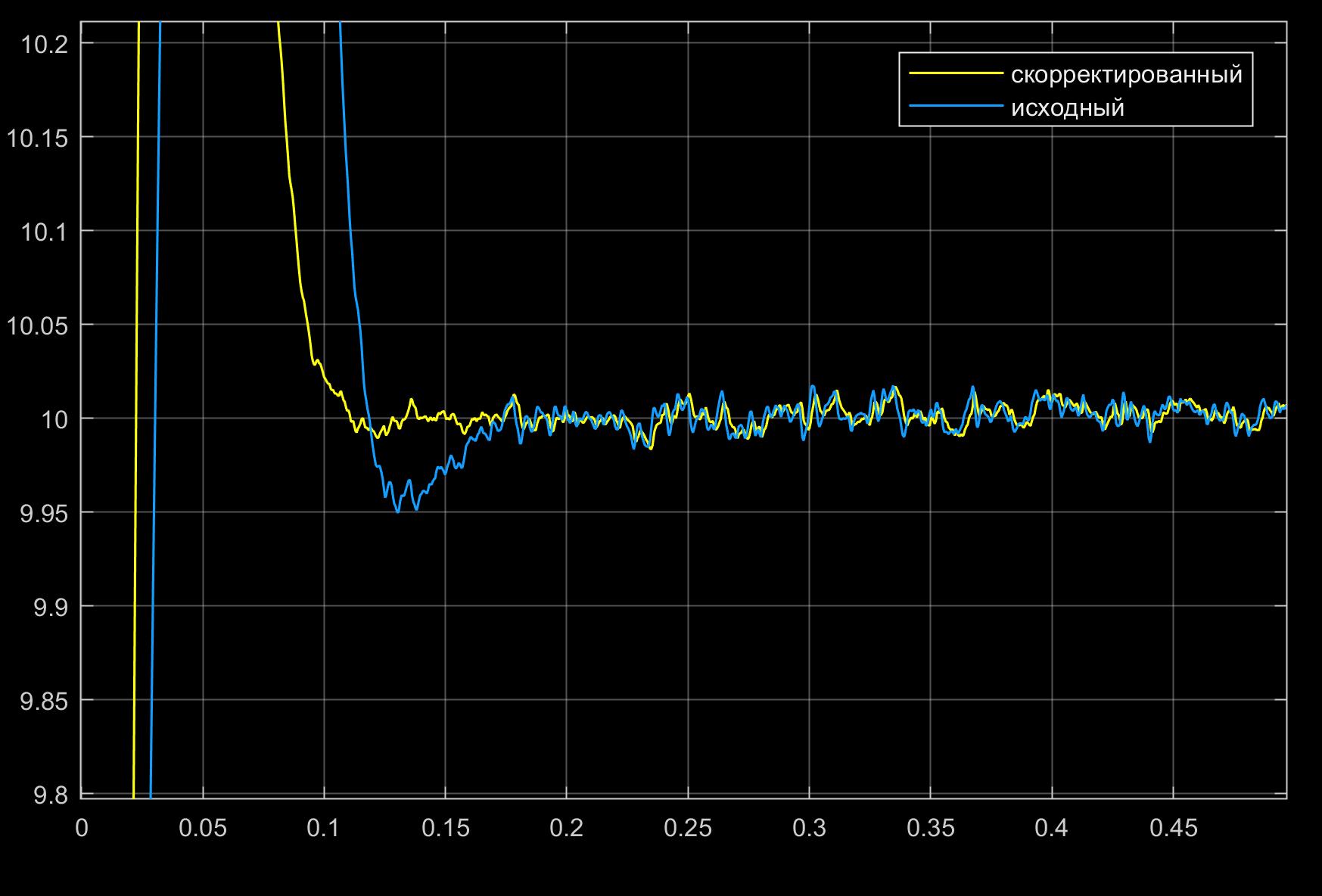
Из приведенных рисунков видно, что благодаря ПИД-регулятору, построенному с применением метода обратной задачи динамики реакция система на ступенчатый управляющий сигнал ускорилась, чего не удалось достичь применением обычного ПИД-регулятора по причине имеющейся в объекте управления нелинейности. Однако применение переменных коэффициентов ПИД-регулятора возможно решило бы эту задачу лучше и сделало бы систему более робастной. Но это уже совсем другая история.
Заключение
В статье был рассмотрен метод, позволяющий построить регулятор для управления нелинейными системами, что было показано на примерах управлений осциллятором Ван дер Поля и двигателем постоянного тока.
К основным преимуществам этого метода можно отнести:
- простота реализации требуемого закона управления (аналитически);
- возможность управления нелинейными системами;
- возможность управления нестационарными системами.
Однако данный метод также имеет ряд существенных недостатков:
- необходимость знания всего вектора состояния управляемой системы (для чего могут потребоваться операции дифференцирования, фильтрации);
- необходимость достаточно точной идентификации параметров управляемой системы, что может снизить робастность;
- необходимость исследования системы на неустойчивость, возникающую в результате совокупного действия не включенных в модель малых динамических параметров (фильтры, датчики).
В целом это довольно интересный метод, но сравнив его реализацию для управления двигателем постоянного тока (с использованием ПИД-регулятора) с двигателем, управляемым только ПИД-регулятором, стало ясно, что существенных плюшек получить от него не удастся. А вот структура управляющего устройства значительно усложняется, вынуждая в том числе бороться с шумами дифференцирования с одной стороны, и предотвращением выхода на границу устойчивости с другой. Возможно именно с этим и связано небольшое количество работ по этой теме. Одним из возможных применений метода обратной задачи динамики может быть построение эталонных (идеальных) траекторий систем для сравнения с траекториями, соответствующими различным регуляторам, к примеру линейным или линеаризованным.
Используемая литература:
1. Ким Д.П. Теория автоматического управления. Т.2. Многомерные, нелинейные, оптимальные и адаптивные системы: Учеб. пособие. – М.: ФИЗМАТЛИТ, 2004. – 464 с.
2. Бойчук Л.М. Метод структурного синтеза нелинейных систем автоматического управления. М., «Энергия», 1971.
3. Нестационарные системы автоматического управления: анализ, синтез и оптимизация / Под ред. К.А. Пупкова и Н.Д. Егупова. – М.: Издательство МГТУ им. Н.Э. Баумана, 2007. – 632 с.