Содержание
- Глава 1: использование нейросетей для распознавания рукописных цифр
- Глава 2: как работает алгоритм обратного распространения
- Глава 3:
- Глава 4: визуальное доказательство того, что нейросети способны вычислить любую функцию
- Глава 5: почему глубокие нейросети так сложно обучать?
- Глава 6:
- Послесловие: существует ли простой алгоритм для создания интеллекта?
Эмпирически мы увидели, что регуляризация помогает уменьшать переобучение. Это вдохновляет – но, к сожалению, не очевидно, почему регуляризация помогает. Обычно люди объясняют это как-то так: в каком-то смысле, менее крупные веса имеют меньшую сложность, что обеспечивает более простое и действенное объяснение данных, поэтому им надо отдавать предпочтение. Однако это слишком краткое объяснение, а некоторые его части могут показаться сомнительными или загадочными. Давайте-ка развернём эту историю и изучим её критическим взглядом. Для этого предположим, что у нас есть простой набор данных, для которого мы хотим создать модель:

По смыслу, здесь мы изучаем явление реального мира, и x и y обозначают реальные данные. Наша цель – построить модель, позволяющую нам предсказывать y как функцию x. Мы могли бы попробовать использовать нейросеть для создания такой модели, но я предлагаю нечто более простое: я попробую моделировать y как многочлен от x. Я буду делать это вместо нейросетей, поскольку использование многочленов делает объяснение особенно понятным. Как только мы разберёмся со случаем многочлена, мы перейдём к НС. На графике выше имеется десять точек, что означает, что мы можем найти уникальный многочлен 9-го порядка y = a0x9+a1x8+…+a9, абсолютно точно укладывающийся в данные. И вот график этого многочлена.

Идеальное попадание. Но мы можем получить неплохое приближение, используя линейную модель y = 2x
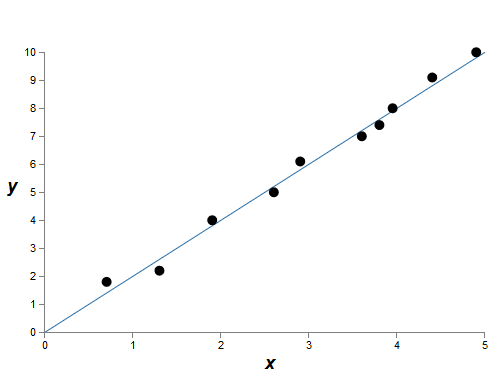
Какая из них лучше? Какая с большей вероятностью окажется истинной? Какая будет лучше обобщаться на другие примеры того же явления реального мира?
Сложные вопросы. И на них нельзя получить точные ответы, не имея дополнительной информации по поводу лежащего в основе данных явления реального мира. Однако давайте рассмотрим две возможности: (1) модель с многочленом 9-го порядка истинно описывает явление реального мира, и поэтому, обобщается идеально; (2) правильная модель – это y=2x, но у нас имеется дополнительный шум, связанный с погрешностью измерений, поэтому модель подходит не идеально.
Априори нельзя сказать, какая из двух возможностей правильная (или что не существует некоей третьей). Логически, любая из них может оказаться верной. И различие между ними нетривиально. Да, на основе имеющихся данных можно сказать, что между моделями имеется лишь небольшое отличие. Но допустим, мы хотим предсказать значение y, соответствующее какому-то большому значению x, гораздо большему, чем любое из показанных на графике. Если мы попытаемся это сделать, тогда между предсказаниями двух моделей появится огромная разница, поскольку в многочлене 9-го порядка доминирует член x9, а линейная модель линейной и остаётся.
Одна точка зрения на происходящее – заявить, что в науке нужно использовать более простое объяснение, если это возможно. Когда мы находим простую модель, объясняющую многие опорные точки, нам так и хочется закричать: «Эврика!». Ведь маловероятно, что простое объяснение появится чисто случайно. Мы подозреваем, что модель должна выдавать некую связанную с явлением правду. В данном случае модель y=2x+шум кажется гораздо более простой, чем y = a0x9+a1x8+… Было бы удивительно, если бы простота возникла случайно, поэтому мы подозреваем, что y = 2x+шум выражает некую лежащую в основе истину. С этой точки зрения модель 9-го порядка просто изучает влияние местного шума. И хотя модель 9-го порядка идеально работает для данных конкретных опорных точек, она не сможет обобщиться на другие точки, в результате чего у линейной модели с шумом предсказательные возможности будут лучше.
Давайте посмотрим, что означает эта точка зрения для нейросетей. Допустим, в нашей сети в основном имеются малые веса, как обычно бывает в регуляризированных сетях. Благодаря небольшим весам поведение сети не меняется сильно при изменении нескольких случайных входов там и сям. В итоге регуляризированной сети сложно выучить эффекты местного шума, присутствующие в данных. Это похоже на стремление к тому, чтобы отдельные свидетельства не сильно влияли на выход сети в целом. Регуляризированная сеть вместо этого обучается реагировать на такие свидетельства, которые часто встречаются в обучающих данных. И наоборот, сеть с крупными весами может довольно сильно менять своё поведение в ответ на небольшие изменения входных данных. Поэтому нерегуляризированная сеть может использовать большие веса для обучения сложной модели, содержащей много информации о шуме в обучающих данных. Короче говоря, ограничения регуляризированных сетей позволяют им создавать относительно простые модели на основе закономерностей, часто встречающихся в обучающих данных, и они устойчивы к отклонениям, вызванным шумом в обучающих данных. Есть надежда, что это заставит наши сети изучать именно само явление, и лучше обобщать полученные знания.
Учитывая всё сказанное, идея того, чтобы отдавать предпочтения более простым объяснениям, должна заставить вас нервничать. Иногда люди называют эту идею «бритвой Оккама» и рьяно применяют её, будто бы она обладает статусом общего научного принципа. Но это, разумеется, не общий научный принцип. Нет никакой априорной логической причины предпочитать простые объяснения сложным. Иногда более сложное объяснение оказывается правильным.
Позвольте описать два примера того, как более сложное объяснение оказалось правильным. В 1940-х физик Марсель Шейн объявил об открытии новой частицы. Компания, на которую он работал, General Electric, была в восторге, и широко распространила публикацию об этом событии. Однако физик Ханс Бете отнёсся к нему скептически. Бете посетил Шейна и изучил пластинки со следами новой частицы Шейна. Шейн показывал Бете пластинку за пластинкой, но на каждой из них Бете находил какую-либо проблему, говорившую о необходимости отказа от этих данных. Наконец, Шейн показал Бете пластинку, выглядевшую годно. Бете сказал, что это, возможно, просто статистическое отклонение. Шейн: «Да, но шансы на то, что это из-за статистики, даже по вашей собственной формуле, один к пяти». Бете: «Однако я уже посмотрел на пять пластинок». Наконец, Шейн сказал: «Но каждую мою пластинку, каждое хорошее изображение вы объясняли какой-то другой теорией, а у меня есть одна гипотеза, объясняющая все пластинки сразу, из которой следует, что речь идёт о новой частице». Бете ответил: «Единственное отличие между моими и вашими объяснениями в том, что ваши неправильные, а мои правильные. Ваше единое объяснение неверно, а все мои объяснения верны». Впоследствии выяснилось, что природа согласилась с Бете, и частица Шейна испарилась.
Во втором примере, в 1859 году астроном Урбен Жан Жозеф Леверье обнаружил, что форма орбиты Меркурия не соответствует теории всемирного тяготения Ньютона. Существовало крохотное отклонение от этой теории, и тогда было предложено несколько вариантов решения проблемы, которые сводились к тому, что теория Ньютона в целом верна, и требует лишь небольшого изменения. А в 1916 году Эйнштейн показал, что это отклонение можно хорошо объяснить с использованием его общей теории относительности, радикально отличающейся от ньютоновской гравитации и основанной на куда как более сложной математике. Несмотря на эту дополнительную сложность, сегодня принято считать, что объяснение Эйнштейна верно, а Ньютоновская гравитация неверна даже в модифицированной форме. Так получается, в частности, потому, что сегодня нам известно, что теория Эйнштейна объясняет многие другие явления, с которыми у теории Ньютона были сложности. Более того, что ещё более поразительно, теория Эйнштейна точно предсказывает несколько явлений, которых Ньютоновская гравитация не предсказывала вообще. Однако эти впечатляющие качества не были очевидными в прошлом. Если судить исходя из одной лишь простоты, то некоторая модифицированная форма Ньютоновской теории выглядела бы привлекательнее.
Из этих историй можно извлечь три морали. Во-первых, иногда довольно сложно решить, какое из двух объяснений будет «проще». Во-вторых, даже если бы мы и приняли такое решение, простотой нужно руководствоваться крайне осторожно! В-третьих, истинной проверкой модели является не простота, а то, насколько хорошо она предсказывает новые явления в новых условиях поведения.
Учитывая всё это и проявляя осторожность, примем эмпирический факт – регуляризированные НС обычно обобщаются лучше, чем нерегуляризированные. Поэтому далее в книге мы будем часто использовать регуляризацию. Упомянутые истории нужны лишь для того, чтобы объяснить, почему никто пока ещё не разработал полностью убедительное теоретическое объяснение тому, почему регуляризация помогает сетям проводить обобщение. Исследователи продолжают публиковать работы, где пытаются испробовать различные подходы к регуляризации, сравнивать их, смотря, что лучше работает, и пытаясь понять, почему различные подходы работают хуже или лучше. Так что к регуляризации можно относиться, как к клуджу. Когда она, довольно часто, помогает, у нас нет полностью удовлетворительного системного понимания происходящего – только неполные эвристические и практические правила.
Здесь скрывается и более глубокий набор проблем, идущих к самому сердцу науки. Это вопрос обобщения. Регуляризация может дать нам вычислительную волшебную палочку, помогающую нашим сетям лучше обобщать данные, но не даёт принципиального понимания того, как работает обобщение, и какой лучший подход к нему.
Эти проблемы восходят к проблеме индукции, известное осмысление которой проводил шотландский философ Дэвид Юм в книге "Исследование о человеческом познании" (1748). Проблеме индукции посвящена "теорема об отсутствии бесплатных обедов" Дэвида Уолперта и Уильяма Макреди (1977).
А это особенно досадно, поскольку в обычной жизни люди феноменально хорошо умеют обобщать данные. Покажите несколько изображений слона ребёнку, и он быстро научится распознавать других слонов. Конечно, он иногда может ошибиться, к примеру, перепутать носорога со слоном, но в целом этот процесс работает удивительно точно. Вот, у нас есть система – мозг человека – с огромным количеством свободных параметров. И после того, как ему показывают одно или несколько обучающих изображений, система обучается обобщать их до других изображений. Наш мозг, в каком-то смысле, удивительно хорошо умеет регуляризировать! Но как мы это делаем? На данный момент нам это неизвестно. Думаю, что в будущем мы выработаем боле мощные технологии регуляризации в искусственных нейросетях, техники, которые в итоге позволят НС обобщать данные, исходя из ещё менее крупных наборов данных.
На самом деле, наши сети и так уже обобщают куда лучше, чем можно было ожидать априори. Сеть со 100 скрытыми нейронами обладает почти 80 000 параметров. У нас есть только 50 000 изображений в обучающих данных. Это всё равно, как пытаться натянуть многочлен 80 000 порядка на 50 000 опорных точек. По всем признакам наша сеть должна ужасно переобучиться. И всё же, как мы видели, такая сеть на самом деле довольно неплохо обобщает. Почему так происходит? Это не совсем понятно. Была высказана гипотеза, что «динамика обучения градиентным спуском в многослойных сетях подвержена саморегуляризации». Это чрезвычайная удача, но и довольно тревожный факт, поскольку мы не понимаем, почему так происходит. Тем временем мы примем прагматичный подход, и будем использовать регуляризацию везде, где только можно. Нашим НС это будет на пользу.
Позвольте мне закончить этот раздел, вернувшись к тому, что я раньше не объяснил: что регуляризация L2 не ограничивает смещения. Естественно, было бы легко изменить процедуру регуляризации, чтобы она регуляризировала смещения. Но эмпирически это часто не меняет результаты каким-то заметным образом, поэтому, до некоторой степени, заниматься регуляризацией смещений, или нет – вопрос соглашения. Однако стоит отметить, что крупное смещение не делает нейрон чувствительным ко входам так, как крупные веса. Поэтому нам не нужно беспокоиться по поводу крупных смещений, позволяющим нашим сетям обучаться шуму в обучающих данных. В то же время, разрешив большие смещения, мы делаем наши сети более гибкими в их поведении – в частности, крупные смещения облегчают насыщение нейронов, чего нам бы хотелось. По этой причине обычно мы не включаем смещения в регуляризацию.
Иные техники регуляризации
Существует множество техник регуляризации, кроме L2. На самом деле, было разработано уже столько техник, что я бы при всём желании не смог кратко описать их все. В этом разделе я кратенько опишу три других подхода к уменьшению переобучения: регуляризацию L1, исключение [dropout] и искусственное увеличение обучающего набора. Мы не будем изучать их так глубоко, как предыдущие темы. Вместо этого мы просто познакомимся с ними, а заодно оценим разнообразие существующих техник регуляризации.
Регуляризация L1
В данном подходе мы изменяем нерегуляризованную функцию стоимости, добавляя сумму абсолютных значений весов:
Интуитивно это похоже на регуляризацию L2, штрафующую за большие веса и заставляющую сеть предпочитать малые веса. Конечно, член регуляризации L1 не похож на член регуляризации L2, поэтому не стоит ожидать ровно такого же поведения. Давайте попробуем понять, в чём поведение сети, обученной при помощи регуляризации L1, отличается от сети, обученной при помощи регуляризации L2.
Для этого посмотрим на частные производные функции стоимости. Дифференцируя (95), получаем:
где sgn(w) – знак w, то есть, +1, если w положительная, и -1, если w отрицательная. При помощи этого выражения мы влёгкую модифицируем обратное распространение так, чтобы оно выполняло стохастический градиентный спуск при помощи регуляризации L1. Итоговое правило обновление для L1-регуляризованной сети:
где, как обычно, ∂C/∂w можно по желанию оценить через усреднённое значение мини-пакета. Сравним это с правилом обновления регуляризации L2 (93):
В обоих выражениях действие регуляризации заключается в уменьшении весов. Это совпадает с интуитивным представлением о том, что оба типа регуляризации штрафуют большие веса. Однако уменьшаются веса по-разному. В регуляризации L1 веса уменьшаются на постоянное значение, стремясь к 0. В регуляризации L2 веса уменьшаются на значение, пропорциональное w. Поэтому когда у какого-то веса оказывается большое значение |w|, регуляризация L1 уменьшает вес не так сильно, как L2. И наоборот, когда |w| мало, регуляризация L1 уменьшает вес гораздо больше, чем регуляризация L2. В итоге регуляризация L1 стремится сконцентрировать веса сети в относительно небольшом числе связей высокой важности, а другие веса стремятся к нулю.
Я слегка сгладил одну проблему в предыдущем обсуждении – частная производная ∂C/∂w не определена, когда w=0. Это потому, что у функции |w| имеется острый «излом» в точке w=0, поэтому там её дифференцировать нельзя. Но это не страшно. Мы просто применим обычное, нерегуляризированное правило для стохастического градиентного спуска, когда w=0. Интуитивно, в этом нет ничего плохого – регуляризация должна уменьшать веса, и, очевидно, она не может уменьшить вес, уже равный 0. Точнее говоря, мы будем использовать уравнения (96) и (97) с условием, что sgn(0)=0. Это даст нам удобное и компактное правило для стохастического градиентного спуска с регуляризацией L1.
Исключение [dropout]
Исключение – совершенно другая техника регуляризации. В отличие от регуляризации L1 и L2, исключение не занимается изменением функции стоимости. Вместо этого мы изменяем саму сеть. Давайте я объясню базовую механику работы исключения, перед тем, как углубляться в тему того, почему оно работает и с какими результатами.
Допустим, мы пытаемся обучить сеть:

В частности, допустим, у нас есть обучающие входные данные x и соответствующий желаемый выход y. Обычно мы бы обучали её прямым распространением x по сети, а потом обратным распространением, чтобы определить вклад градиента. Исключение изменяет этот процесс. Мы начинаем со случайного и временного удаления половины скрытых нейронов сети, оставляя без изменений входные и выходные нейроны. После этого у нас останется примерно такая сеть. Отметьте, что исключённые нейроны, те, что временно удалены, всё равно отмечены на схеме:
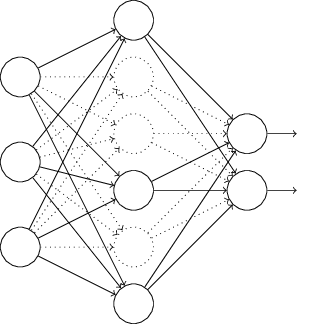
Мы передаём x прямым распространением по изменённой сети, а потом обратно распространяем результат, тоже по изменённой сети. После того, как мы проделаем это с мини-пакетом примеров, мы обновляем соответствующие веса и смещения. Потом мы повторяем этот процесс, сначала восстанавливая исключённые нейроны, потом выбирая новое случайное подмножество скрытых нейронов для удаления, оцениваем градиент для другого мини-пакета, и обновляем веса и смещения сети.
Повторяя этот процесс снова и снова, мы получим сеть, выучившую некие веса и смещения. Естественно, эти веса и смещения выучивались в условиях, при которых половина скрытых нейронов была исключена. И когда мы запускаем сеть по полной, у нас будет в два раза больше активных скрытых нейронов. Для компенсации этого мы ополовиниваем веса, исходящие от скрытых нейронов.
Процедура исключения может показаться странной и произвольной. Почему она должна помочь с регуляризацией? Чтобы объяснить происходящее, я хочу, чтобы вы на время забыли про исключение, и представили обучение НС стандартным способом. В частности, представьте, что мы обучаем несколько разных НС, используя одинаковые обучающие данные. Конечно, сети сначала могут различаться, и иногда обучение может давать разные результаты. В таких случаях мы могли бы применить какое-либо усреднение или схему голосования, чтобы решить, какой из выходов принимать. К примеру, если мы обучили пять сетей, и три из них классифицируют цифру, как «3», тогда, вероятно, это и правда тройка. А две других сети, вероятно, просто ошибаются. Такая схема усреднения часто оказывается полезным (пусть и дорогим) способом уменьшения переобучения. Причина в том, что разные сети могут переобучаться по-разному, и усреднение может помочь с устранением подобного переобучения.
Как всё это связано с исключением? Эвристически, когда мы исключаем разные наборы нейтронов, это похоже на то, как если бы мы обучали разные НС. Поэтому процедура исключения похожа на усреднение эффектов по очень большому количеству разных сетей. Разные сети переобучаются по-разному, поэтому есть надежда, что средний эффект исключения уменьшит переобучение.
Связанное с этим эвристическое объяснение пользы исключения даётся в одной из самых ранних работ, использовавших эту технику: «Эта техника уменьшает сложную совместную адаптацию нейронов, поскольку нейрон не может полагаться на присутствие определённых соседей. В итоге ему приходиться обучаться более надёжным признакам, которые могут быть полезными в совместной работе со многими различными случайными подмножествами нейронов». Иначе говоря, если представить нашу НС, как модель, делающую предсказания, то исключение будет способом гарантировать устойчивость модели к потерям отдельных частей свидетельств. В этом смысле техника напоминает регуляризации L1 и L2, стремящиеся уменьшать веса, и делающие таким способом сеть более устойчивой к потерям любых отдельных связей в сети.
Естественно, истинная мера полезности исключения – её огромные успехи в улучшении эффективности нейросетей. В оригинальной работе, где был представлен этот метод, он применялся ко множеству разных задач. Нас особенно интересует то, что авторы применили исключение к классификации цифр из MNIST, используя простейшую сеть с прямым распространением, похожую на ту, что рассматривали мы. В работе отмечается, что до тех пор наилучшим результатом для подобной архитектуры была точность в 98,4%. Они улучшили её до 98,7%, используя комбинацию исключения и изменённой формы регуляризации L2. Настолько же впечатляющие результаты были получены и для многих других задач, включая распознавание образов и речи, и обработку естественного языка. Исключение было особенно полезным в обучении крупных глубоких сетей, где часто остро встаёт проблема переобучения.
Искусственное расширение набора обучающих данных
Ранее мы видели, что наша точность классификации MNIST упала до 80 с чем-то процентов, когда мы использовали всего 1000 обучающих изображений. И неудивительно – с меньшим количеством данных наша сеть встретит меньше вариантов написания цифр людьми. Давайте попробуем обучить нашу сеть из 30 скрытых нейронов, используя разные объёмы обучающего набора, чтобы посмотреть на изменение эффективности. Мы обучаем, используя размер мини-пакета в 10, скорость обучения η = 0,5, параметр регуляризации λ=5,0, и функцию стоимости с перекрёстной энтропией. Мы будем обучать сеть 30 эпох с использованием полного набора данных, и увеличивать количество эпох пропорционально уменьшению объёма обучающих данных. Чтобы гарантировать одинаковый фактор уменьшения весов для разных наборов обучающих данных, мы будем использовать параметр регуляризации λ=5,0 с полным обучающим набором, и пропорционально уменьшать его с уменьшением объёмов данных.

Видно, что точность классификации значительно подрастает с увеличением объёмов обучающих данных. Вероятно, этот рост будет продолжаться с дальнейшим увеличением объёмов. Конечно, судя по графику выше, мы приближаемся к насыщению. Однако, допустим, что мы переделаем этот график на логарифмическую зависимость от объёма обучающих данных:

Видно, что в конце график всё равно стремится вверх. Это говорит о том, что если мы возьмём гораздо более массивный объём данных – допустим, миллионы или даже миллиарды рукописных примеров, а не 50 000 – тогда мы, вероятно, получим гораздо лучше работающую сеть даже такого небольшого размера.
Достать больше обучающих данных – прекрасная идея. К сожалению, это может обойтись дорого, поэтому на практике не всегда возможно. Однако есть и другая идея, способная сработать почти так же хорошо – искусственно увеличить набор данных. К примеру, допустим, мы возьмём изображение пятёрки из MNIST, и немного повернём его, градусов на 15:


Это явно та же цифра. Но на пиксельном уровне она сильно отличается от изображений, имеющихся в базе MNIST. Разумно предположить, что добавление этого изображения к обучающему набору данных может помочь нашей сети узнать больше о классификации изображений. Более того, мы, очевидно, не ограничены возможностью добавления всего одного изображения. Мы можем расширить наши обучающие данные, сделав несколько небольших поворотов всех обучающих картинок из MNIST, а потом использовав расширенный набор обучающих данных для увеличения эффективности сети.
Эта идея весьма мощная, и её широко используют. Посмотрим на результаты из научной работы, применившей несколько вариаций этой идеи к MNIST. Одна из архитектур рассматриваемых ими сетей была похожа на ту, что используем мы – сеть с прямым распространением с 800 скрытыми нейронами, использующую функцию стоимости с перекрёстной энтропией. Запустив эту сеть со стандартным обучающим набором MNIST, они получили точность классификации в 98,4%. Но затем они расширили обучающие данные, используя не только описанною мною выше вращение, но и перенос и искажение изображений. Обучив сеть на расширенных данных, они повысили её точность до 98,9%. Также они экспериментировали с т.н. «эластичными искажениями», особым типом искажений изображения, призванным устранить случайные колебания мускулов руки. Используя эластичные искажения для расширения данных, они достигли точности в 99,3%. По сути, они расширяли опыт их сети, выдавая ей различные вариации рукописного текста, встречающиеся в реальных почерках.
Варианты этой идеи можно использовать для улучшения показателей множества задач по обучению, не только для распознавания почерка. Общий принцип – расширить обучающие данные, применяя к ним операции, отражающие вариации, встречающиеся в реальности. Такие вариации несложно придумать. Допустим, мы создаём НС для распознавания речи. Люди могут распознавать речь даже при наличии таких искажений, как фоновый шум. Поэтому можно расширить данные, добавив фонового шума. Также мы способны распознавать ускоренную и замедленную речь. Это ещё один способ расширения обучающих данных. Эти техники используются не всегда – к примеру, вместо расширения обучающего набора через добавления шума, может оказаться более эффективным подчищать входные данные, применяя к ним фильтр шума. И всё же, стоит иметь в виду идею расширения обучающего набора, и искать способы её применения.
Упражнение
- Как мы обсудили выше, один из способов расширить обучающие данные из MNIST – использовать небольшие повороты обучающих картинок. Какая проблема может появиться, если мы допустим повороты картинок на любые углы?
Отступление, касающееся больших данных и о смысле сравнения точности классификаций
Давайте вновь взглянем на то, как точность нашей НС изменяется в зависимости от размера обучающего набора:

Допустим, что вместо использования НС мы бы использовали другую технологию машинного обучения для классификации цифр. К примеру, попробуем использовать метод опорных векторов (support vector machine, SVM), с которым мы кратко встречались в главе 1. Как и тогда, не волнуйтесь, если вы не знакомы с SVM, нам не надо разбираться в его деталях. Мы будем использовать SVM за счёт библиотеки scikit-learn. Вот, как меняется эффективность SVM в зависимости от размера обучающего набора. Для сравнения я нанёс на график и результаты работы НС.
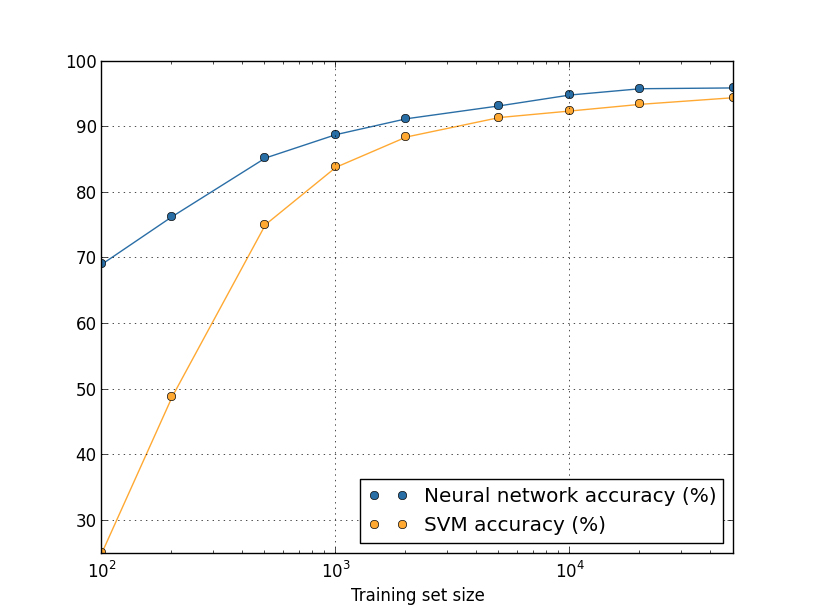
Вероятно, первое, что бросается в глаза – НС превосходит SVM на любом размере обучающего набора. Это хорошо, хотя не стоит делать из этого далеко идущих выводов, поскольку я использовал предустановленные настройки scikit-learn, а над нашей НС мы довольно серьёзно поработали. Менее яркий, но более интересный факт, следующий из графика, состоит в том, что если мы обучим наш SVM с использованием 50 000 изображений, то он сработает лучше (точность в 94,48%), чем наша НС, обученная на 5000 изображений (93,24%). Иначе говоря, увеличение объёма обучающих данных иногда компенсирует разницу в алгоритмах МО.
Может произойти ещё нечто более интересное. Допустим, мы пытаемся решить задачу с использованием двух алгоритмов МО, A и B. Иногда бывает так, что алгоритм A опережает алгоритм B на одном наборе обучающих данных, а алгоритм B опережает алгоритм A на другом наборе обучающих данных. Выше мы этого не увидели – тогда графики бы пересеклись – но такое бывает. Правильный ответ на вопрос: «Превосходит ли алгоритм A алгоритм B?» на самом деле такой: «А какой обучающий набор данных вы используете?»
Всё это необходимо учитывать, как во время разработки, так и во время чтения научных работ. Многие работы концентрируются на поиске новых трюков для выжимания лучших результатов на стандартных наборах данных для измерения. «Наша супер-пупер технология дала нам улучшение на X% на стандартном сравнительном наборе Y» – каноническая форма заявления в таком исследовании. Иногда подобные заявления на самом деле бывают интересными, но стоит понимать, что они применимы только в контексте определённого обучающего набора. Представьте себе альтернативную историю, в которой люди, изначально создавшие сравнительный набор, получили исследовательский грант покрупнее. Они могли бы использовать дополнительные деньги для сбора дополнительных данных. Вполне возможно, что «улучшение» супер-пупер технологии исчезло бы на большем наборе данных. Иначе говоря, суть улучшения может оказаться просто случайностью. Из этого в область практического применения нужно вынести следующую мораль: нам необходимо как улучшение алгоритмов, так и улучшение обучающих данных. Нет ничего плохого в том, чтобы искать улучшенные алгоритмы, но убедитесь, что вы не концентрируетесь на этом, игнорируя более лёгкий способ выиграть при помощи увеличения объёма или качества обучающих данных.
Задача
- Исследовательская задача. Как наши алгоритмы МО будут вести себя в пределе на очень больших наборах данных? Для любого заданного алгоритма естественно попытаться определить понятие асимптотической эффективности в пределе на самом деле больших данных. Дешёвый и сердитый подход к этой задаче – попытаться подобрать кривые под графики, подобные тем, что приведены выше, а потом экстраполировать кривые в бесконечность. Однако можно возразить, что разные подходы к подбору кривых могут дать разное представление об асимптотическом пределе. Сможете ли вы оправдать результаты экстраполяции для какого-то определённого класса кривых? В таком случае, сравните асимптотические пределы нескольких алгоритмов МО.
Итоги
Мы закончили наше погружение в переобучение и регуляризацию. Мы, конечно, ещё вернёмся к этим проблемам. Как я уже несколько раз упомянул, переобучение – большая проблема в области НС, особенно по мере того, как компьютеры становятся всё мощнее, и мы можем обучать всё более крупные сети. В итоге возникает насущная необходимость разработать эффективные методики регуляризации для уменьшения переобучения, поэтому данная область сегодня является весьма активной.
Инициализация весов
Когда мы создаём наши НС, нам необходимо делать выбор начальных значений весов и смещений. Пока что мы выбирали их согласно предписаниям, кратко описанным мною в главе 1. Напомню, что мы выбирали веса и смещения на основе независимого распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1. Этот подход хорошо сработал, однако он кажется довольно произвольным, поэтому стоит пересмотреть его и подумать, нельзя ли найти лучший способ назначения изначальных весов и смещений, и, возможно, помочь нашим НС учиться быстрее.
Оказывается, можно довольно серьёзно улучшить процесс инициализации по сравнению с нормализованным распределением Гаусса. Чтобы разобраться в этом, допустим, мы работаем с сетью с большим количеством входных нейронов,- скажем, с 1000. И допустим, мы использовали нормализованное распределение Гаусса для инициализации весов, соединённых с первым скрытым слоем. Пока что я сфокусируюсь только на весах, соединяющие входные нейроны с первым нейроном в скрытом слое, и проигнорирую остальную часть сети:
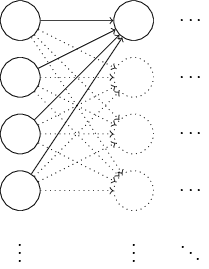
Для простоты представим, что мы пытаемся обучать сеть входом x, в котором половина входных нейронов включены, то есть, имеют значение 1, а половина – выключены, то есть, имеют значение 0. Следующий аргумент работает и в более общем случае, но вам проще будет понять его на этом особом примере. Рассмотрим взвешенную сумму z = ∑jwjxj+b входов для скрытого нейрона. 500 членов суммы исчезают, поскольку соответствующие xj равны 0. Поэтому z – это сумма 501 нормализованных гауссовых случайных переменных, 500 весов и 1 дополнительное смещение. Поэтому и само значение z имеет гауссово распределение с математическим ожиданием 0 и среднеквадратичным отклонением √501 ≈ 22,4. То есть, у z довольно широкое гауссово распределение, без острых пиков:

В частности, из этого графика видно, что |z|, скорее всего, будет довольно крупным, то есть, z ≫ 1 или z ≫ -1. В таком случае выход скрытых нейронов σ(z) будет очень близок к 1 или 0. Это значит, что наш скрытый нейрон насытится. И когда это произойдёт, как нам уже известно, небольшие изменения весов будут давать крохотные изменения в активации скрытого нейрона. Эти крохотные изменения, в свою очередь, практически не затронут остальные нейтроны в сети, и мы увидим соответствующие крохотные изменения в функции стоимости. В итоге эти веса будут обучаться очень медленно, когда мы используем алгоритм градиентного спуска. Это похоже на задачу, которую мы уже обсуждали в этой главе, в которой выходные нейроны, насыщенные на неверных значениях, заставляют обучение замедляться. Раньше мы решали эту проблему, хитроумно выбирая функцию стоимости. К сожалению, хотя это помогло с насыщенными выходными нейронами, это совсем не помогает с насыщением скрытых нейронов.
Сейчас я говорил о входящих весах первого скрытого слоя. Естественно, те же аргументы применимы и к следующим скрытым слоям: если веса в поздних скрытых слоях инициализируются с использованием нормализованных гауссовых распределений, их активации часто будут близки к 0 или 1, и обучение будет идти очень медленно.
Есть ли способ выбрать лучшие варианты инициализации для весов и смещений, чтобы мы не получали такого насыщения, и могли избежать замедления обучения? Допустим, у нас будет нейрон с количеством входящих весов nin. Тогда нам надо инициализировать эти веса случайными гауссовыми распределениями с математическим ожиданием 0 и среднеквадратичным отклонением 1/√nin. То есть, мы сжимаем гауссианы, и уменьшаем вероятность насыщения нейрона. Затем мы выберем гауссово распределение для смещений с математическим ожиданием 0 и среднеквадратичным отклонением 1, по причинам, к которым я вернусь чуть позже. Сделав такой выбор, мы вновь получим, что z = ∑jwjxj + b будет случайной переменной с гауссовым распределением с математическим ожиданием 0, однако с гораздо более выраженным пиком, чем раньше. Допустим, как и раньше, что 500 входов равны 0, и 500 равны 1. Тогда легко показать (см. упражнение ниже), что z имеет гауссово распределение с математическим ожиданием 0 и среднеквадратичным отклонением √(3/2) = 1,22… Этот график с гораздо более острым пиком, настолько, что даже на картинке ниже ситуация несколько преуменьшена, поскольку мне пришлось поменять масштаб вертикальной оси по сравнению с предыдущим графиком:
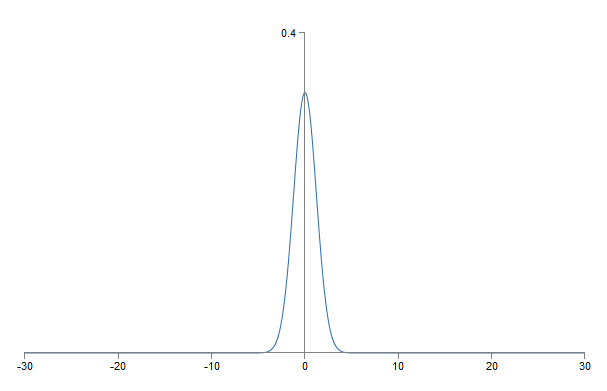
Такой нейрон насытится с гораздо меньшей вероятностью, и, соответственно, с меньшей вероятностью столкнётся с замедлением обучения.
Упражнение
- Подтвердите, что среднеквадратичное отклонение у z = ∑jwjxj + b из предыдущего параграфа равно √(3/2). Соображения в пользу этого: дисперсия суммы независимых случайных переменных равна сумме дисперсий отдельных случайных переменных; дисперсия равна квадрату среднеквадратичного отклонения.
Выше я упоминал, что мы и дальше будем инициализировать смещения, как и раньше, на основе независимого распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1. И это нормально, поскольку не сильно увеличивает вероятность насыщения наших нейронов. На самом деле инициализация смещений особого значения не имеет, если мы сумеем избежать проблемы насыщения. Некоторые даже пытаются инициализировать все смещения нулём, и полагаются на то, что градиентный спуск сможет выучить подходящие смещения. Но поскольку вероятность того, что это на что-то повлияет, мала, мы продолжим использовать ту же процедуру инициализации, что и ранее.
Давайте сравним результаты старого и нового подходов инициализации весов с использованием задачи по классификации цифр из MNIST. Как и ранее, мы будем использовать 30 скрытых нейронов, мини-пакет размером в 10, параметр регуляризации &lambda=5,0, и функцию стоимости с перекрёстной энтропией. Мы будем постепенно уменьшать скорость обучения с η=0,5 до 0,1, поскольку так результаты будут немного лучше видны на графиках. Обучаться можно с использованием старого метода инициализации весов:
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.large_weight_initializer()
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)Также можно обучаться при помощи нового подхода к инициализации весов. Это даже проще, ведь по умолчанию network2 инициализирует веса при помощи нового подхода. Это значит, что мы можем опустить вызов net.large_weight_initializer() ранее:
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True)Строим график (при помощи программы weight_initialization.py):

В обоих случаях получается точность классификации в районе 96%. Итоговая точность почти совпадает в обоих случаях. Но новая техника инициализации доходит до этой точки гораздо, гораздо быстрее. В конце последней эпохи обучения старый подход к инициализации весов достигает точности в 87%, а новый подход уже подходит к 93%. Судя по всему, новый подход к инициализации весов начинает с гораздо лучшей позиции, благодаря чему мы получаем хорошие результаты гораздо быстрее. То же явление наблюдается, если построить результаты для сети с 100 нейронами:
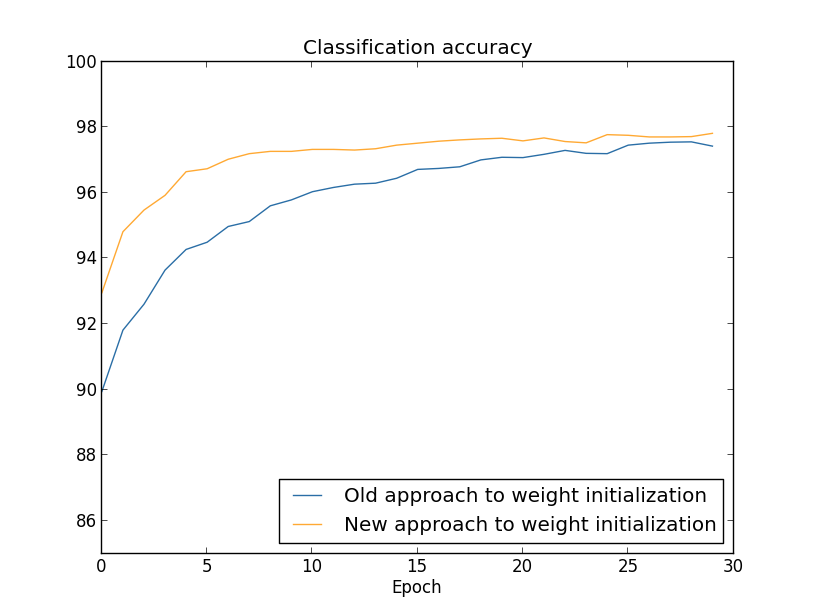
В данном случае две кривые не встречаются. Однако мои эксперименты говорят, что если добавить ещё немножко эпох, то точности начинают почти совпадать. Поэтому на базе этих экспериментов можно сказать, что улучшение инициализации весов только ускоряет обучение, но не меняет итоговой эффективности сети. Однако в главе 4 мы увидим примеры НС, у которых долгосрочная эффективность серьёзно улучшается в результате инициализации весов через 1/√nin. Поэтому, улучшается не только скорость обучения, но иногда и итоговая эффективность.
Подход к инициализации весов через 1/√nin помогает улучшать обучение нейросетей. Предлагались и другие техники инициализации весов, многие из которых основываются на этой базовой идее. Не буду рассматривать их здесь, поскольку для наших целей хорошо работает и 1/√nin. Если вам интересно, порекомендую почитать обсуждение на страницах 14 и 15 в работе от 2012 года за авторством Йошуа Бенджио.
Задача
- Объединение регуляризации и улучшенного метода инициализации весов. Иногда регуляризация L2 автоматически даёт нам результаты, похожие на новый метод инициализации весов. Допустим, мы используем старый подход к инициализации весов. Набросайте эвристический аргумент, доказывающий, что: (1) если λ будет не слишком маленькой, то в первые эпохи тренировки ослабление весов будет доминировать почти полностью; (2) если ηλ ≪ n, то веса будут ослабляться в e−ηλ/m раз в эпоху; (3) если λ будет не слишком большой, ослабление весов замедлится, когда веса уменьшатся до размера примерно 1/√n, где n – общее количество весов в сети. Докажите, что эти условия удовлетворяются в примерах, для которых в этом разделе построены графики.
Возвращаемся к распознаванию рукописных цифр: код
Давайте реализуем описанные в этой главе идеи. Мы разработаем новую программу, network2.py, улучшенную версию программы network.py, созданной нами в главе 1. Если вы уже давно не видели её код, возможно, стоит быстро пробежаться по нему. Это всего лишь 74 строчки кода, и его легко понять.
Как и в случае с network.py, звездой программы network2.py будет класс Network, который мы используем для представления наших НС. Мы инициализируем экземпляр класса списком размеров соответствующих слоёв сети, и выбором функции стоимости, по умолчанию это будет перекрёстная энтропия:
class Network(object):
def __init__(self, sizes, cost=CrossEntropyCost):
self.num_layers = len(sizes)
self.sizes = sizes
self.default_weight_initializer()
self.cost=costПервая пара строк метода __init__ совпадает с network.py, и понятны сами по себе. Следующие две строчки новые, и нам нужно подробно разобраться в том, что они делают.
Начнём с метода default_weight_initializer. Он использует новый, улучшенный подход к инициализации весов. Как мы видели, в этом подходе веса, входящие в нейрон, инициализируются на основе независимого распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1, делённого на квадратный корень из количества входящих связей в нейрон. Также этот метод будет инициализировать и смещения, используя распределение Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1. Вот код:
def default_weight_initializer(self):
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)/np.sqrt(x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]Чтобы его понять, нужно вспомнить, что np – это библиотека Numpy, занимающаяся линейной алгеброй. Мы импортировали её в начале программы. Также заметьте, что мы не инициализируем смещения в первом слое нейронов. Первый слой – входящий, поэтому смещения не используются. То же самое было network.py.
В дополнение к методу default_weight_initializer мы сделаем метод large_weight_initializer. Он инициализирует веса и смещения при помощи старого подхода из главы 1, где веса и смещения инициализируются на основе независимого распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1. Этот код, естественно, немногим отличается от default_weight_initializer:
def large_weight_initializer(self):
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]Этот метод я включил в основном потому, чтобы нам было удобнее сравнивать результаты этой главы и главы 1. Не могу представить себе какие-то реальные варианты, в которых я бы рекомендовал его использовать!
Второй новинкой метода __init__ будет инициализация атрибута стоимости. Чтобы понять, как это работает, посмотрим на используемый нами класс для представления функции стоимости с перекрёстной энтропией (директива @staticmethod сообщает интерпретатору, что данный метод не зависит от объекта, поэтому передачи параметра self в методы fn и delta не происходит).
class CrossEntropyCost(object):
@staticmethod
def fn(a, y):
return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
@staticmethod
def delta(z, a, y):
return (a-y)Давайте разберёмся. Первое, что тут видно – что, хотя перекрёстная энтропия с математической точки зрения является функцией, мы реализуем её, как класс python, а не функцию python. Почему я решил так сделать? В нашей сети стоимость играет две разные роли. Очевидная – она является мерой того, насколько хорошо выходная активация a соответствует желаемому выходу y. Эту роль обеспечивает метод CrossEntropyCost.fn. (Кстати, отметим, что вызов np.nan_to_num внутри CrossEntropyCost.fn гарантирует, что Numpy правильно обработает логарифм близких к нулю чисел). Однако функция стоимости используется в нашей сети и вторым способом. Из главы 2 вспомним, что при запуске алгоритма обратного распространения нам необходимо считать выходную ошибку сети δ L. Форма выходной ошибки зависит от функции стоимости: у разных функций стоимости будут разные формы выходной ошибки. Для перекрёстной энтропии выходная ошибка, как следует из уравнения (66), будет равна:
Поэтому я определяю второй метод, CrossEntropyCost.delta, чья цель – объяснить сети, как подсчитывать выходную ошибку. А потом мы объединяем два этих метода в один класс, содержащий всё, что нашей сети надо знать о функции стоимости.
По сходной причине в network2.py содержится класс, представляющий квадратичную функцию стоимости. Включая это для сравнения с результатами главы 1, поскольку в будущем мы в основном будем использовать перекрёстную энтропию. Код ниже. Метод QuadraticCost.fn – простое вычисление квадратичной стоимости, связанной с выходом a и желаемым выходом y. Значение, возвращаемое QuadraticCost.delta, основано на выражении (30) для выходной ошибки квадратичной стоимости, которое мы вывели в главе 2.
class QuadraticCost(object):
@staticmethod
def fn(a, y):
return 0.5*np.linalg.norm(a-y)**2
@staticmethod
def delta(z, a, y):
return (a-y) * sigmoid_prime(z)Теперь мы разобрались в основных отличиях между network2.py и network2.py. Всё очень просто. Есть и другие небольшие изменения, которые я опишу ниже, включая реализацию регуляризации L2. До этого давайте посмотрим на полный код network2.py. Подробно изучать его не обязательно, но стоит понять основную структуру, в частности, почитать комментарии, чтобы понять, что делает каждый из кусков программы. Конечно, я не запрещаю углубляться в этот вопрос, сколько вам угодно! Если потеряетесь, попробуйте прочесть текст после программы, и вернуться к коду снова. В общем, вот он:
"""network2.py
~~~~~~~~~~~~~~
Улучшенная версия network.py, реализующая алгоритм обучения со стохастическим градиентным спуском для нейросети с прямым распространением. Среди улучшений – добавление функции стоимости с перекрёстной энтропией, регуляризации, инициализация весов сети. Я сконцентрировался на упрощении кода, его читаемости и изменяемости. Он не оптимизирован, в нём не хватает многих нужных вещей.
"""
#### Библиотеке
# Стандартные
import json
import random
import sys
# Сторонние
import numpy as np
#### Определить функции стоимости, квадратичную и с перекрёстной энтропией
class QuadraticCost(object):
@staticmethod
def fn(a, y):
"""Вернуть стоимость, связанную с выходом ``a`` и желаемым выходом ``y``.
"""
return 0.5*np.linalg.norm(a-y)**2
@staticmethod
def delta(z, a, y):
"""Вернуть ошибку delta с выходного слоя."""
return (a-y) * sigmoid_prime(z)
class CrossEntropyCost(object):
@staticmethod
def fn(a, y):
"""Вернуть стоимость, связанную с выходом ``a`` и желаемым выходом ``y``. np.nan_to_num используется для численной стабильности. В частности, если у ``a`` и ``y`` в одном месте стоит значение 1.0, тогда выражение (1-y)*np.log(1-a) возвращает nan. np.nan_to_num гарантирует, что его преобразуют в правильное значение (0.0).
"""
return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
@staticmethod
def delta(z, a, y):
"""Вернуть ошибку delta с выходного слоя. Параметр ``z`` в методе не используется, и включён в список параметров для совместимости с методами delta из других классов функций стоимости.
"""
return (a-y)
#### Главный класс Network
class Network(object):
def __init__(self, sizes, cost=CrossEntropyCost):
""" Массив sizes содержит количество нейронов в соответствующих слоях. Так что, если мы хотим создать объект Network с двумя нейронами в первом слое, тремя нейронами во втором слое, и одним нейроном в третьем, то мы запишем это, как [2, 3, 1]. Смещения и веса сети инициализируются случайным образом, с использованием ``self.default_weight_initializer`` (см. его комментарии).
"""
self.num_layers = len(sizes)
self.sizes = sizes
self.default_weight_initializer()
self.cost=cost
def default_weight_initializer(self):
"""Инициализировать каждый вес случайным образом с использованием распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1, делённого на квадратный корень из количества весов, соединённых с одним и тем же нейроном. Инициализировать смещения с использованием распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1.
Первый слой считается входным, и по соглашению мы не назначаем его нейронам смещения, поскольку они используются только при подсчёте выходов с более поздних слоёв.
"""
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)/np.sqrt(x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]
def large_weight_initializer(self):
""" Инициализировать веса с использованием распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1. Инициализировать смещения с использованием распределения Гаусса с математическим ожиданием 0 и среднеквадратичным отклонением 1.
Первый слой считается входным, и по соглашению мы не назначаем его нейронам смещения, поскольку они используются только при подсчёте выходов с более поздних слоёв.
Инициализатор весов и смещений использует подход из главы 1, и включён для сравнения. Обычно лучше будет использовать инициализатор по умолчанию.
"""
self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
self.weights = [np.random.randn(y, x)
for x, y in zip(self.sizes[:-1], self.sizes[1:])]
def feedforward(self, a):
"""Вернуть выход сети, если ``a`` это вход."""
for b, w in zip(self.biases, self.weights):
a = sigmoid(np.dot(w, a)+b)
return a
def SGD(self, training_data, epochs, mini_batch_size, eta,
lmbda = 0.0,
evaluation_data=None,
monitor_evaluation_cost=False,
monitor_evaluation_accuracy=False,
monitor_training_cost=False,
monitor_training_accuracy=False):
""" Обучаем сеть при помощи мини-пакетов и стохастического градиентного спуска. ``training_data`` – список кортежей ``(x, y)``, обозначающих обучающие входные данные и желаемые выходные. Остальные обязательные параметры говорят сами за себя, как параметр регуляризации ``lmbda``. Также метод принимает ``evaluation_data``, где обычно содержатся либо проверочные, либо оценочные данные. Мы можем отслеживать стоимость и точность как на оценочных, так и на обучающих данных, выставляя соответствующие флаги. Метод возвращает кортеж с четырьмя списками: стоимость оценочных данных, для каждой из эпох, точность оценочных данных, стоимость обучающих данных и точности обучающих данных все значения вычисляются в конце каждой эпохи. К примеру, если мы обучаемся в течение 30 эпох, тогда первым элементом кортежа будет список из 30 элементов, содержащий стоимость оценочных данных в конце каждой эпохи. Если соответствующие флаги не взведены, то списки пусты.
"""
if evaluation_data: n_data = len(evaluation_data)
n = len(training_data)
evaluation_cost, evaluation_accuracy = [], []
training_cost, training_accuracy = [], []
for j in xrange(epochs):
random.shuffle(training_data)
mini_batches = [
training_data[k:k+mini_batch_size]
for k in xrange(0, n, mini_batch_size)]
for mini_batch in mini_batches:
self.update_mini_batch(
mini_batch, eta, lmbda, len(training_data))
print "Epoch %s training complete" % j
if monitor_training_cost:
cost = self.total_cost(training_data, lmbda)
training_cost.append(cost)
print "Cost on training data: {}".format(cost)
if monitor_training_accuracy:
accuracy = self.accuracy(training_data, convert=True)
training_accuracy.append(accuracy)
print "Accuracy on training data: {} / {}".format(
accuracy, n)
if monitor_evaluation_cost:
cost = self.total_cost(evaluation_data, lmbda, convert=True)
evaluation_cost.append(cost)
print "Cost on evaluation data: {}".format(cost)
if monitor_evaluation_accuracy:
accuracy = self.accuracy(evaluation_data)
evaluation_accuracy.append(accuracy)
print "Accuracy on evaluation data: {} / {}".format(
self.accuracy(evaluation_data), n_data)
print
return evaluation_cost, evaluation_accuracy, \
training_cost, training_accuracy
def update_mini_batch(self, mini_batch, eta, lmbda, n):
"""Обновить веса и смещения сети, применяя градиентный спуск с использованием обратного распространения к одному мини-пакету. ``mini_batch`` – это список кортежей ``(x, y)``, ``eta`` – скорость обучения, ``lmbda`` - параметр регуляризации, ``n`` - общий размер набора обучающих данных."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
for x, y in mini_batch:
delta_nabla_b, delta_nabla_w = self.backprop(x, y)
nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw
for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb
for b, nb in zip(self.biases, nabla_b)]
def backprop(self, x, y):
"""Вернуть кортеж ``(nabla_b, nabla_w)``, представляющий градиент для функции стоимости C_x. ``nabla_b`` и ``nabla_w`` - послойные списки массивов numpy, похожие на ``self.biases`` and ``self.weights``."""
nabla_b = [np.zeros(b.shape) for b in self.biases]
nabla_w = [np.zeros(w.shape) for w in self.weights]
# прямой проход
activation = x
activations = [x] # список для послойного хранения активаций
zs = [] # список для послойного хранения z-векторов
for b, w in zip(self.biases, self.weights):
z = np.dot(w, activation)+b
zs.append(z)
activation = sigmoid(z)
activations.append(activation)
# backward pass
delta = (self.cost).delta(zs[-1], activations[-1], y)
nabla_b[-1] = delta
nabla_w[-1] = np.dot(delta, activations[-2].transpose())
"""
Переменная l в цикле ниже используется не так, как описано во второй главе книги. l = 1 означает последний слой нейронов, l = 2 – предпоследний, и так далее. Мы пользуемся преимуществом того, что в python можно использовать отрицательные индексы в массивах.
"""
for l in xrange(2, self.num_layers):
z = zs[-l]
sp = sigmoid_prime(z)
delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
nabla_b[-l] = delta
nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
return (nabla_b, nabla_w)
def accuracy(self, data, convert=False):
"""Вернуть количество входов в ``data``, для которых НС выдаёт правильный результат. Выход НС – номер нейрона в последнем слое с наивысшей активацией.
Флажку ``convert`` назначается False, если набор данных – подтверждающий или проверочный (обычный случай) и True, если набор обучающий. Этот флаг нужен из-за того, что ``y`` по-разному представлен в разных наборах данных. Флаг отмечает, нужно ли нам преобразовывать между разными представлениями. Может показаться странной практика использования разных представлений для разных наборов данных. Почему бы не использовать одинаковые представления для всех трёх наборов? Это делается для эффективности – обычно программа считает стоимость на обучающих данных, а точность на других наборах данных. Это разные вычисления, и использование разных представлений ускоряет работу. Больше подробностей о представлениях ищите в mnist_loader.load_data_wrapper.
"""
if convert:
results = [(np.argmax(self.feedforward(x)), np.argmax(y))
for (x, y) in data]
else:
results = [(np.argmax(self.feedforward(x)), y)
for (x, y) in data]
return sum(int(x == y) for (x, y) in results)
def total_cost(self, data, lmbda, convert=False):
"""Вернуть общую стоимость для набора данных ``data``. Флажок ``convert``
устанавливается в False, если данные – обучающие (обычно), и в True, если данные –
подтверждающие или проверочные. См. комментарии по поводу похожего, но
противоположного соглашения для метода ``accuracy``, выше.
"""
cost = 0.0
for x, y in data:
a = self.feedforward(x)
if convert: y = vectorized_result(y)
cost += self.cost.fn(a, y)/len(data)
cost += 0.5*(lmbda/len(data))*sum(
np.linalg.norm(w)**2 for w in self.weights)
return cost
def save(self, filename):
"""Сохранить НС в файл ``filename``."""
data = {"sizes": self.sizes,
"weights": [w.tolist() for w in self.weights],
"biases": [b.tolist() for b in self.biases],
"cost": str(self.cost.__name__)}
f = open(filename, "w")
json.dump(data, f)
f.close()
#### Загрузка Network
def load(filename):
"""Загрузить сеть из файла ``filename``. Вернуть как экземпляр Network.
"""
f = open(filename, "r")
data = json.load(f)
f.close()
cost = getattr(sys.modules[__name__], data["cost"])
net = Network(data["sizes"], cost=cost)
net.weights = [np.array(w) for w in data["weights"]]
net.biases = [np.array(b) for b in data["biases"]]
return net
#### Разные функции
def vectorized_result(j):
""" Вернуть 10-мерный единичный вектор с 1.0 в позиции j и нулями на остальных позициях. Это используется для преобразования цифры (0..9) в соответствующие выходные данные НС.
"""
e = np.zeros((10, 1))
e[j] = 1.0
return e
def sigmoid(z):
"""Сигмоида."""
return 1.0/(1.0+np.exp(-z))
def sigmoid_prime(z):
"""Производная сигмоиды."""
return sigmoid(z)*(1-sigmoid(z))Среди более интересных изменений – включение L2 регуляризации. Хотя это большое концептуальное изменение, его настолько легко реализовать, что вы могли не заметить это в коде. По большей части, это просто передача параметра lmbda разным методам, особенно Network.SGD. Вся работа проводится в одной строчке программы, четвёртой с конца в методе Network.update_mini_batch. Там мы изменяем правило обновления градиентного спуска, чтобы оно включало ослабление веса. Изменение крохотное, но серьёзно влияющее на результаты!
Это, кстати, часто бывает при реализации новых техник в нейросетях. Мы тысячи слов потратили на обсуждение регуляризации. Концептуально это довольно тонкая и сложная для понимания вещь. Однако её можно тривиальным образом добавить к программе! Неожиданно часто сложные техники получается реализовывать с небольшими изменениями кода.
Ещё одно небольшое, но важное изменение в коде – добавление нескольких опциональных флагов к методу стохастического градиентного спуска Network.SGD. Эти флаги делают возможным отслеживание стоимости и точности либо на training_data, либо на evaluation_data, которые можно передавать в Network.SGD. Ранее в главе мы часто использовали эти флаги, но позвольте мне привести пример их использования, просто для напоминания:
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
>>> import network2
>>> net = network2.Network([784, 30, 10], cost=network2.CrossEntropyCost)
>>> net.SGD(training_data, 30, 10, 0.5,
... lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True,
... monitor_evaluation_cost=True,
... monitor_training_accuracy=True,
... monitor_training_cost=True)Мы задаём evaluation_data через validation_data. Однако мы могли бы отслеживать эффективность и на test_data, и на любом другом наборе данных. Также у нас есть четыре флага, задающие необходимость отслеживания стоимости и точности как на evaluation_data, так и на training_data. Эти флаги по умолчанию установлены в False, однако здесь они включены для отслеживания эффективности Network. Более того, метод Network.SGD из network2.py возвращает четырёхэлементный кортеж, представляющий результаты отслеживания. Использовать его можно так:
>>> evaluation_cost, evaluation_accuracy,
... training_cost, training_accuracy = net.SGD(training_data, 30, 10, 0.5,
... lmbda = 5.0,
... evaluation_data=validation_data,
... monitor_evaluation_accuracy=True,
... monitor_evaluation_cost=True,
... monitor_training_accuracy=True,
... monitor_training_cost=True)Так что, к примеру, evaluation_cost будет списком из 30 элементов, содержащим стоимость оценочных данных в конце каждой эпохи. Подобная информация чрезвычайно полезна для понимания поведения нейросети. Подобная информация чрезвычайно полезна для понимания поведения сети. Её, к примеру, можно использовать для рисования графиков обучения сети со временем. Именно так я и построил все графики из этой главы. Однако, если какой-то из флагов не взведён, соответствующий элемент кортежа будет пустым списком.
Среди других дополнений к коду – метод Network.save, сохраняющий объект Network на диск, и функция его загрузки в память. Сохранение и загрузка делаются через JSON, а не питоновские модули pickle или cPickle, которые обычно используются для сохранения на диск и загрузки в python. Использование JSON требует больше кода, чем нужно было бы для pickle или cPickle. Чтобы понять, почему я выбрал JSON, представьте, что в некий момент будущего мы решили поменять наш класс Network, чтобы там были не только сигмоидные нейроны. Для реализации этого изменения мы, скорее всего, изменили бы и атрибуте, определяемые в методе Network.__init__. А если мы просто воспользовались pickle для сохранения, наша функция загрузки не сработала бы. Использование JSON с явной сериализацией облегчает нашу задачу гарантировать, что старые версии объекта Network можно будет загружать.
В коде есть множество мелких изменений, но это просто небольшие вариации network.py. Итоговый результат – расширение нашей программы из 74 строк до гораздо более функциональной программы из 152 строк.
Задача
- Измените приведённый код, введя регуляризацию L1, и используйте её для классификации цифр MNIST сетью с 30 скрытыми нейронами. Сможете ли вы подобрать параметр регуляризации, позволяющий вам улучшить результат по сравнению с сетью без регуляризации?
- Посмотрите на метод Network.cost_derivative method в network.py. Он был написан для квадратичной стоимости. Как переписать его для стоимости с перекрёстной энтропией? Можете ли вы придумать проблему, которая может появиться в такой версии программы? В network2.py мы полностью избавились от метода Network.cost_derivative, включив его функциональность в CrossEntropyCost.delta. Как это решает найденную вами проблему?