Comments 49
По-моему там совершенно другие формулы. Похожие, но другие. Такие же формулы как у меня получены для простейших функций квадратов, кубов и так далее, без обобщения на полином со всеми ненулевым коэффициентами, с единичным интервалом.
Очевидно, что это соотношение должно быть хорошо известно, но загуглить его было непросто. Мне кажется, ближе всего написано в разделе «Polynomial sequences» статьи в английской википедии en.wikipedia.org/wiki/Constant-recursive_sequence. Там сама общая формула не указана, но проговорено, что коэффициенты берутся из биномиального преобразования значений полинома в подряд идущих точках, что в точности совпадает с формулой автора статьи.
Скажите пожалуйста, как была выведена общая формула? Потому что в приложенном файле есть подробные выкладки для 1 и 2 степени, а потом просто приводится общая формула для n-ной степени.
Когда формула известна, доказать ее — дело техники. Во-первых приведенная формула очень похожа на развернутую формулу конечной разности (n+1)-ой степени, только первый член перенесен в левую часть. Во-вторых, ключевая идея состоит в том, что конечная разность (n+1)-ой степени всегда равна нулю для полинома n-ной степени (по аналогии с (n+1)-ой производной полинома n-ной степени, которая всегда 0). Собственно, вот и все доказательство.
Относительно произвольной длины шага: если мы доказали некоторое соотношение на значения произвольных полиномов с шагом 1, то оно же будет верно с любым другим шагом. Это тривиальное следствие, но, опять же, оно очевидно только после того, как было сформулировано, спасибо автору за это.
Практическое применение этой формулы довольно узкое. Я представляю себе такой сценарий: мы рисуем график, который изображает количество пользователей в реальном времени каждый час и хотим быстро экстраполировать это число на следующий час. Обычно я явно реализую что-то типа полинома Лагранжа, что занимает десяток строк. А так можно вставить вашу формулу для второй степени в одну строчку.
Про численную устойчивость у меня большие сомнения. Мне кажется, ошибка при однократном возведении в степень гораздо меньше, чем при повторении линейной рекуррентной формулы миллиарды раз. Я проверил на python (к сожалению я не изучал внимательно Ваш репозиторий, мог что-то упустить) для случая линейной функции: если мы вычисляем 10^8 подряд идущих значений типа double, то по вашей формуле ошибка составит -0.03:
def f(x):
return x / 3 + 1 / 7
vals = {0: f(0), 1: f(1)}
for t in range(2, 10 ** 8):
vals[t] = 2 * vals[t - 1] - vals[t - 2]
vals[t] - f(t) == -0.03673642501235008
# "стандартный" способ интерполирования линейной функции
vals[0] + (vals[1] - vals[0]) * t == f(t)
Конечно, никто не заставляет нас применять эту формулу миллиарды раз, если это делать тысячу раз, погрешность пренебрежительно малая. К тому же у меня «игрушечный» пример для линейной функции, может быть при возведении в большую степень действительно будет большая ошибка при обычных методах интерполирования. Нужно аккуратно это изучить. К тому же в приложенном документе уже присутствуют функции ε во всех рассчетах.
Резюмируя: автор обратил внимание на занимательный факт из теории конечных разностей, который позволяет в одну строчку интерполировать значение полинома в следущией точке сетки по предыдущим значениям. Такая потребность возникает не очень часто, но для общего математического развития полезно.
Собственно, вот и все доказательство
А можно как-то по-подробнее — возможно и у меня получиться упростить свой вариант доказательства.
Это тривиальное следствие...
Эм, и как это тривиально доказать?
Практическое применение этой формулы довольно узкое
На самом деле подобные моим формулы используются уже очень давно и, на мой взгляд, достаточно широко. В основном в приложениях интерполяции/экстраполяции данных. Также при шаге стремящемся к нулю получаем приложение данных формул к вычислению интегралов фигур.
На самом деле целью публикации данной статьи в основном являлось получение какой-либо возможной дополнительной информации по этой тематике. Самостоятельно ничего подобного я не нашел. Доказательств моих формул где либо в литературе нет, выводов, подобных сделанным мною я тоже не нашел. По вашей ссылке приведены правильные формулы, однако доказательств там тоже нет. Кроме основной цели также было интересно донести до читателей Хабра интересные факты про полиномы — оказывается их можно полностью определить по (n+1) равноотстоящим точкам и т.д.
- Обозначение 1. Введем разностный оператор Δ. Он принимает на вход полином f и возвращает полином Δ(f) такой, что выполняется (Δ(f))(x) = f(x + 1) — f(x).
- Лемма 1. Если f имеет степень n, то Δf имеет степень n — 1, если f имеет степень 0 (константа), то Δf = 0.
- Обозначение 2. Обозначим Δ^k (f) = Δ(Δ(...Δ(f)...)) — k-кратное применение Δ.
- Следствие 1. Если f имеет степень n, то Δ^k (f) имеет степень n — k, в частности Δ^(n+1) (f) равен 0.
- Лемма 2. Δ^(n+1) (f) = вашей формуле, но внутри суммы k пробегает диапазон от 0 до n + 1 (у вас k=1..n+1).
- В итоге получаем, что 0 = Δ^(n+1) (f) = ваша формула без первого члена, равного f(x)
- Следовательно, f(x) = ваша формула
Для обобщения вашей формулы на произвольный шаг воспользуемся следующим утверждением:
- Лемма 3. Пусть мы доказали, что для любого полинома степени n выполняется некоторое соотношение на f(1), ..., f(k). Тогда для любого полинома степени n выполняется точно такое же соотношение, но на значения аргумента из любой арифметической прогрессии длины k.
- Доказательство. Допустим, мы хотим доказать соотношение для последовательности a, a + b, a + 2b,… Рассмотрим линейную функцию h(x) = a + bx. Обозначим g — полином, являющийся композицией f и h, то есть для которого выполняется g(x) = f(h(x)). Заметим, что g имеет степень n, а следовательно мы можем заключить, что для g(1), ..., g(k) выполняется то самое соотношение.
Так как g(i) = f(a + bi), мы получаем, что соотношение выполняется для f(a), f(a + b),… f(a+kb), что и требовалось доказать.
Относительно использования этой формулы для доказательства того, что полиномы степени n определяются значениями в n + 1 различных точках, есть некоторая проблема:
- Обычное доказательство следующее. Предположим противное и нашлись два полинома f и g степени n, которые совпадают в n + 1 точке. Тогда рассмотрим их разность — это тоже полином степени не больше n, у которого n + 1 корень. Но согласно следствию из основной теоремы алгебры ненулевой полином степени n может иметь не более n корней. Следовательно разность f и g тождественно равна 0 и они совпадают. Получаем, что полином степени n однозначно определяется значениями в n+1 точке.
- То есть это утверждение сводится к основной теоремы алгебры, которая в свою очередь доказывается жестким комплексным анализом.
- Проблема в том, что вся теория манипуляций с полиномами, которая применялась мною выше, основана на фундаментальном соответствии между функциями и наборами коэффициентов. А для этого соответствия необходимо доказать, что не бывает полиномов с разными коэффициентами и одинаковыми значениями, что сводится к основной теореме алгебры.
- В итоге то доказательство вашей формулы, что я привел, скорее всего где-то внутри себя уже опирается на факт о том, что полином степени n однозначно определяется значениями в n + 1 точке.
print(1.2 + 1.2 + 1.2) #3.5999999999999996
print(3*1.2) #3.5999999999999996
Именно для устранения таких псевдо-погрешностей я использовал в своём проверочном коде специализированную библиотеку.
Я не говорил, что это проблема только Python — только о том, что и в Python она тоже есть.
через (n+1) равноотстоящих точек может быть проведена одна и только одна кривая, выраженная полиномом степени n.Точки не обязательно должны быть равноотстоящими — достаточно, чтобы они не совпадали друг с другом. Равноотстоящими они должны быть только для того, чтобы использовать вашу разностную схему.
А чем метод лучше стандартных интерполяционных формул Ньютона?
Там и точки могут быть не равноотстоящими, и точка, где вычисляется следующее значение, может быть вообще абсолютно любой, и длинная арифметика для расчёта коэффициентов не нужна.
Ну, Ваш метод, очевидно, будет лучше подходить, если значения функции целочисленные, т.к. не будет делений с потерей точности, и только если нужны значения на равноотстоящих промежутках.
На практике для построения полиномов берутся обычно точки в нулях чебышёвских многочленов, т.к. интерполяция многочленами высокой степени на равномерной сетке численно неустойчива.
Для экстраполяции многочлены вообще не самый лучший выбор, лучше пользоваться рациональными функциями.

Можно взять и другие точки, не равноотстоящие — и тоже всё будет решаться:

Можете пояснить в чём смысл вашего комментария?
Насчёт интерполяционных многочленов: в первом же комментарии к данной статье это и было сказано. Там же есть и возражения. Если есть что-то добавить — пожалуйста, добавьте в ту ветку. Насчёт формулы по ссылке: там, как минимум, есть ограничение по величине «шага» — от нуля включительно до единицы включительно. И в настоящий момент я затрудняюсь из этой формулы получить какой-то «частный случай», который бы давал формулу, которая есть у меня. Если вы видите как из формулы по вышей ссылке получить мою — буду благодарен за разъяснения.

Если x константно от начальных условий, то и пересчитывать коэффициенты при y каждый раз не нужно.
А вот прямой поиск коэффициентов — это очень неустойчивый метод как раз для высоких степеней.
Если полином степени n задан последовательными равноотстоящими значениями y0,y1,y2..yn в точках x=0,1,2..n, то значение этого полинома в любой точке можно посчитать через сумму исходных значений, взятых с коэффициентами по формуле

или, если выразить её через гамма-функцию
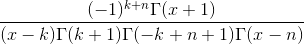
где k — порядковый номер значения, начиная от нуля.
Если в этой формуле заменить x на n+1 (следующая равноотстоящая точка), то формула сократится до

которая, собственно, и выражает биномиальные коэффициенты, о которых идёт речь в этой статье — в чём можно убедиться в Wolfram Mathematica:



Здесь мы имеем сумму полиномов одинаковой степени, каждый из которых равен 1 в одной точке и 0 во всех остальных. Таким образом, суммарный полином проходит через все эти точки и имеет ту же степень.
Символ Похгаммера обеспечивает эти самые нули в узловых точках, факториалы масштабируют значение ненулевой точки к 1 (которая затем будет умножена на конкретное значение yn).
Всё давно известно — как минимум в таких банальных вещах, как полиномиальная интерполяция. Другой вопрос, кто и в каком виде эти знания распространяет. Если учитель математики или автор статьи в википедии не понимает (или не считает нужным заострять на этом внимание) математического смысла умножения на (x-xn) — то и у ученика/читателя этого понимания возникнуть не может.
Эта статья с моей формулой, к которой также приложены доказательства. Мои доказательства очень неэлегантны, и, возможно, повторны. Поэтому мне и интересно получить более элегантные доказательства или ссылки на существующие.
По моей логике, если все шаги по выводу формулы корректны, то и формула корректна
Следовательно путь вывода — это и есть формальное доказательство.
Вы, надеюсь, его сохранили? Дайте почитать.
При выводе формул я обычно держу сразу несколько документов открытыми — так удобнее, а финальный результат уже записываю отдельно.
Суть выше описал, его достаточно, чтобы повторить вывод формулы самостоятельно, если кому интересно. Это будет всяко полезней, чем читать формальное доказательство финальной формулы, непонятно откуда взявшейся.
Эти два занятия — эквивалентны по смыслу, но второе занимает меньше времени.
Вот взять те же биномиальные коэффициенты. Сначала мы определяем их через факториал. Затем приводим к непрерывному виду через гамма-функцию. Затем по свойстве гамма функций мы можем представить их через отношение синуса и полинома. Затем мы можем разложить это в сумму sinc и даже разложить в спектр. И вроде всё корректно, и очевидно, что sinc принимает нули в целых точках кроме нуля, но — WTF? Причём тут sinc, куда делся факториал, где логика?
Представление произвольных полиномов в виде конечных разностей с произвольным шагом