
Возможно, кто-то из вас заметил, что Google на 1 апреля добавила в приложение Google Maps для Android и iOS интерактивную игру «Змейка».
Специалисты Check Point обычно заняты исследованием последних киберугроз, но здесь очень увлеклись этой игрой, правда, сильно расстраивались из-за проигрышей… поэтому возникла логичная мысль: почему бы её не взломать!
Таким образом, наши самые озорные сотрудники начали думать над обратной разработкой приложения с помощью удалённой отладки. В общем, у них получилось, и вскоре мы успешно выполнили задачу никогда не проигрывать — и даже добавили простой ИИ, который сам играет в игру.

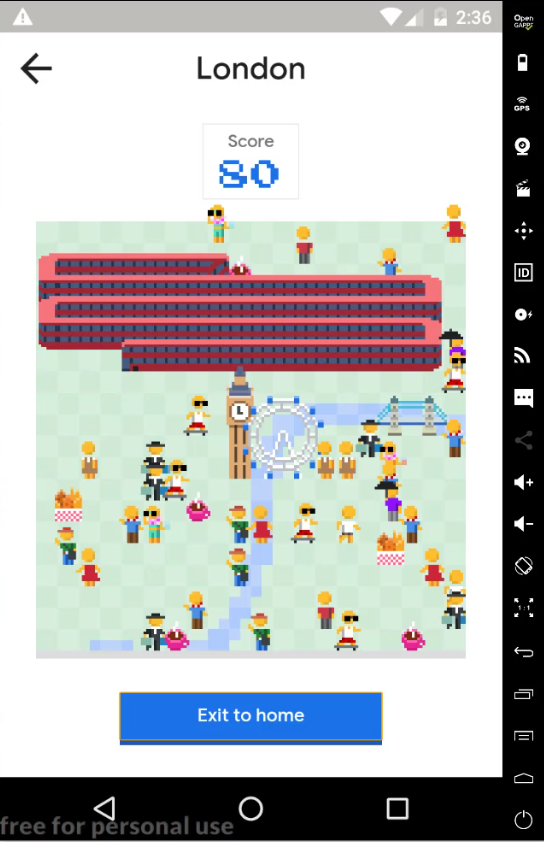
В этой заметке подробно опишем хак.
Сначала мы открыли приложение на виртуальном устройстве через Genymotion и запустили «Змейку», которая находится в меню в правом верхнем углу.
Похоже, что игра отображается в WebView, поэтому мы запустили удалённую отладку в инструментах разработчика Chrome:
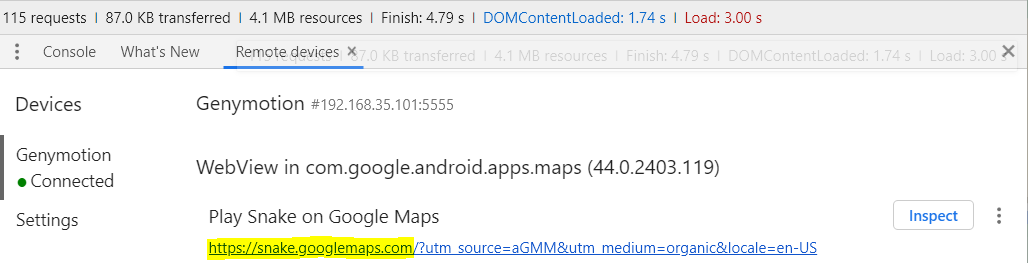
Затем перешли на сайт и нашли на вкладке с исходниками файл v18.js, а в нём несколько интересных функций.
Во-первых, функция fa() инициирует поле размером 20×20:
this.height = this.width = 20;Наша главная цель — найти и изменить функцию, которая определяет, когда змейка врезается в стену или в себя, чтобы отключить возможность проигрыша. Переменные width и height представляют размеры игрового поля, поэтому мы поискали width и height внутри исходного кода и нашли функцию F(a, b):

Похоже, F(a, b) проверяет, находятся ли координаты тела змеи в пределах поля. Один из вариантов — полностью удалить условия в функции, чтобы она всегда возвращала истину, тем самым переводя нас в «режим Бога», где мы можем проходить сквозь стены, не умирая.
Для этого мы нажали кнопку Inspect в удалённой консоли и изменили функцию F(a, b) на следующую:
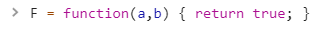
Теперь мы можем проходить сквозь стены:

Рис. 1. Режим Бога
Это всё очень хорошо, но нам по-прежнему придётся играть, самостоятельно подбирая людей, чтобы зарабатывать очки. Следующий хак решит эту проблему.
В стеке вызовов много вызовов функции wa(a). Если изучить эту функцию, то мы увидим, что она рекурсивна и отвечает за запрос кадров анимации. wa(a) вызывает функции xa(a, b) и ya(a), которые отображают игровые фигуры (поезд, люди) и поле, соответственно.
Рассмотрим функцию xa(a, b):

Она принимает два аргумента: 'a' и 'b'. Первый является частью глобальной переменной Q, которая содержит интересную информацию о нашей игре, включая массив, который представляет собой игровое поле (рис. 2), где мы видим поезд (М), людей и объекты (K). Функция также вычисляет счёт и сохраняет его в c.i, что также эквивалентно Q.b.

Рис. 2. Массив игрового поля
Данный массив соответствует такому полю:
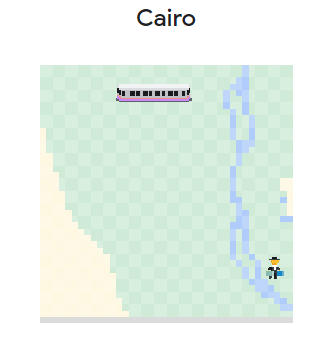
Рис. 3. Игровое поле
xa(a) также обращается к функции sa(a) на рис. 4, которая генерирует случайные координаты при каждом создании нового человека. Если вызывать функцию более одного раза, то можно создать сколько угодно людей (рис. 5).

Рис. 4. Вызов функции sa(a)
Как здесь:

Рис. 5. Вызов функции с созданием любого количества людей на карте
Обратите внимание, что даже если вызывать sa(a) более одного раза и забирать человека, счёт не меняется. При подборе пассажира вызывается функция ka(a, b) на рис. 6. Таким образом, её нужно изменить, чтобы при каждом вызове она добавляла 10 очков и обновляла счёт на экране.

Рис. 6. Обновлённая функция
Координаты каждой части поезда указаны в Q.b.o.b, где первый элемент представляет собой первый вагончик в поезде.
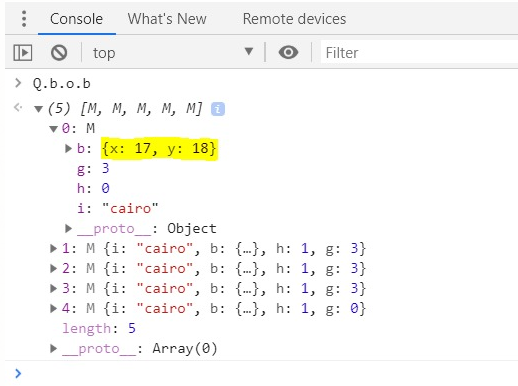
Рис. 7. Массив вагончиков
Это понадобится для создания простого ИИ. Начнём с его логики:
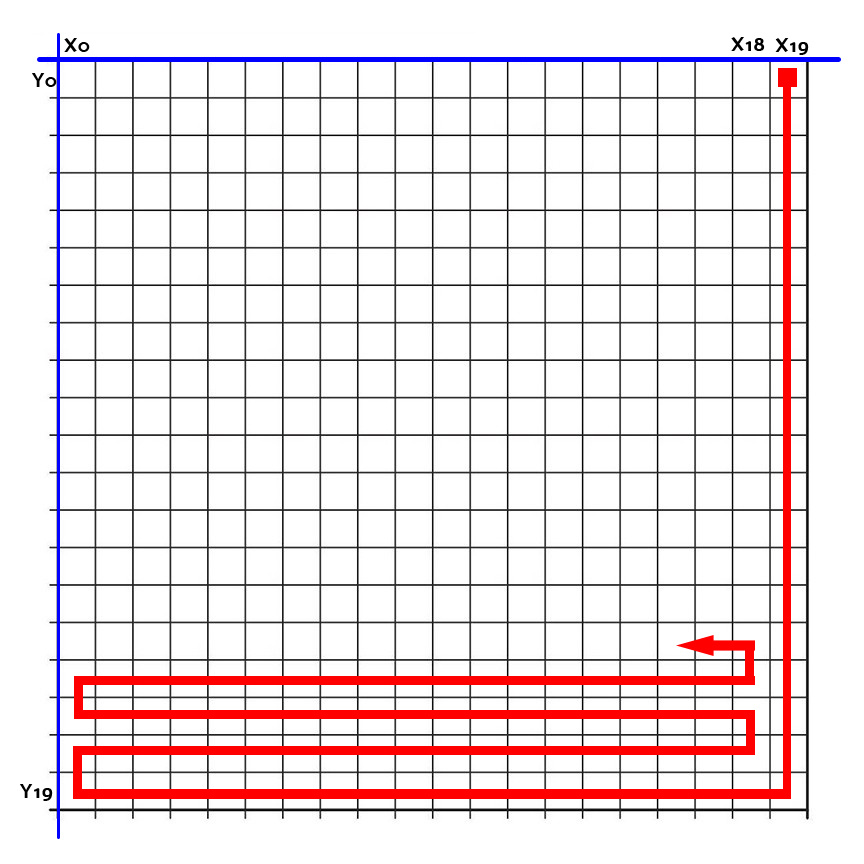
Рис. 8. Логика ИИ
Змейка представляет собой машину состояний (конечный автомат):
- На X=19 идём вниз, пока не доберёмся до Y=19.
- На X=19 и Y=19 идём влево до X=0.
- Переходим к машине состояний для зигзагов:
- Вверх на одну клетку и направо до X=18.
- Вверх на одну клетку и налево до X=0.
- Назад к шагу А.
- На Y=0 идём направо до X=19.
- Возвращаемся к шагу 1.
Полный код опубликован на GitHub.
Видео: