How to become an author
Search
Write a publication
Pull to refresh

Wolfensteiny 3D — реверс-инжиниринг 251 байтов JavaScript

Reading time5 min
Views17K
Abnormal programming*JavaScript*HTML*Canvas*Reverse engineering*
При написании кода многие не задумываются ни о чем, кроме логики самой программы. Меньшее число людей думают об оптимизации кода по времени, по памяти. Но лишь единицы доходят до последнего уровня — сжатии программы до рекордно маленького размера.

Посмотрите, например, на результат работы всего 251 байта JavaScript:


Ну, давайте разбираться, как это работает!

Откуда это?
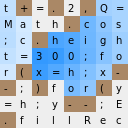
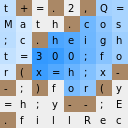
Этот код, как и то многое, к чему я обращался в этой статье, находится на сайте p01.org великолепного Mathieu 'p01' Henri, разработчика на JavaScript и не только, частенько занимающегося сжатием кода до невозможных размеров. Исходный материал этой статьи тут.

Итак, перед вами те самые 251 байт исходного кода.

<body onload=E=c.getContext("2d"),setInterval(F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,b-d?4:D/2,D/2))for(D=0;'.'<F[D*y/h-D/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1",t=h=75)><canvas id=c>

Понятно, что ничего не понятно.

Делаем код читаемым


Первым делом весь JavaScript-код я вынес в отдельный тег, для удобства.

Видно, что переменные E, h, Q, F и другие — константы, которые можно заменить их значениями/самими объектами, а также поменять названия.

var context = c.getContext("2d")
var F="t+=.2,Q=Math.cos;c.height=300;for(x=h;x--;)for(y=h;y--;E.fillRect(x*4,y*4,b-d?4:D/2,D/2))for(D=0;'.'<F[D*y/h-D/2|0?1:(d=t+D*Q(T=x/h-.5+Q(t)/8)&7)|(3.5+D*Q(T-8))<<3]&&D<8;b=d)D+=.1"
var t = 75
var size = 75

function render(){
    t += 0.2;
    c.height=300;
    for(let x = size; x--;)
        for(let y = size; y--; context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2))
            for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d)
                D += 0.1
}

setInterval(render, 75);

Здесь код из строки уже вынесен в функцию, а сама строка — нетронута, она понадобится нам в дальнейшем.

Теперь преобразуем два внешних цикла в while.

function render(){
    t += 0.2;
    c.height=300;
    let x = size;
    while(x > 0){
        let y = size;
        while(y > 0){
            for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d)
                D += 0.1
            
            context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2);
            y--;
        }
        
        x--;
    }
}

Как мы это видим?


Давайте поймём, почему мы вообще это видим. Если посмотреть на картинку ещё раз, можно понять многое.

Картинка кликабельна

Вот, что мы видим:

  1. Чем дальше объект, тем он темнее
  2. Скошенная от нас часть встречающихся препятствий залита по-другому, линиями, а не точками

В коде рисование отражено так:

//      То, что определяет, заливать с фиксированной шириной или нет
//            Координаты точки  ||    Ширина и высота точки
//                 |     |      ||        |      |
//                 ↓     ↓      ↓↓        ↓      ↓
context.fillRect(x * 4,y * 4,b - d? 4 : D / 2, D / 2);

Почему мы видим объёмные объекты в этом половодье черных точек? Ведь нам приходится довольствоваться лишь различными оттенками чёрного — размерами черных точек (менять цвет мы не можем, E.fillStyle — слишком длинно!). На самом деле, это работает просто, потому что на двумерной картинке наш глаз опирается в основном на тени и яркость освещения.

Представьте себя, идущим по тёмному коридору, у вас в руках лишь фонарик. Вы светите перед собой и видите, что одни предметы ближе и светлее (фонарик светит, препятствие яркое, нет теней), а другие дальше и темнее (свет рассеян, слаб, и видим темноту — и чувствуем расстояние). Так и здесь — чем дальше объект (больше D), тем больше по размеру мы рисуем черный квадрат на экране.
Но как мы узнаём, что надо делать ярким, а что нет?

Просчитываем пиксель


Теперь разберемся с этим монстром: 

for(var D = 0; '.' < F[D * y / size - D / 2 | 0 ? 1 : (d = t + D * Math.cos(T = x / size - 0.5 + Math.cos(t) / 8) & 7) | (3.5 + D * Math.cos(T - 8)) << 3] && D < 8; b = d)
        D += 0.1

Итак. Всё это выражение представляет собой алгоритм рендеринга (fixed step raymarching), позволяющий находить пересечение луча с блоками. Для каждого пикселя экрана мы запускаем луч, и идем по нему с фиксированным шагом 0.1, и как только встречаем препятствие — заканчиваем алгоритм, и рисуем пиксель на экране, зная дальность до препятствия.

Начнем читать этот код по частям.

Условие D * y / size - D / 2 | 0 можно представить в виде $D * (\frac{y}{size} - \frac{1}{2}) = D * (\frac{y - size/2}{size}) < 1$, тогда выражение в скобках будет показывать «отклонение» y от центра экрана (в долях экрана). Так мы пытаемся понять, находится ли луч в пределах между полом и потолком или нет. Поэтому, если мы касаемся пола (или потолка), мы выходим из цикла дальше, к отрисовке, и рисуем пиксель.
А если не касаемся, то продолжаем вычисления: ищем текущие координаты луча.

var T = x / size - .5 + Math.cos(t) / 8; // Math.cos(t) заставляет камеру 
                                         // вращаться со временем

var xcoord = t + depth * Math.cos(T);
var ycoord = 3.5 + depth * Math.cos(T - 8); //

Почему cos(T - 8)?
Так получается, что $cos(x-8) \approx sin(x)$ с точностью 0.15 радиан. Всё потому, что

$\frac{5\pi}{2} \approx 8.15 \approx 8$


, и тогда

$cos(\alpha-8) \approx cos(\alpha-\frac{5\pi}{2}) = cos(\alpha - \frac{\pi}{2})=sin(\alpha)$



Стоит поговорить, как вообще проверяется принадлежность точки в пространстве блоку. Сама карта берется из исходного кода (F) и выглядит так:
t+=.2,Q= ----> ░█░█░█░░
Math.cos ----> ░░░░█░░░
;c.heigh ----> ░░█░░░░░       А это -
t=300;fo ----> ░░░░░░░░ <---- сам проход,
r(x=h;x- ----> ░█░░░░░█       по которому летит камера
-;)for(y ----> █░█░░░█░
=h;y--;E ----> ░░░░██░░
.fillRec ----> █░░░░░░░

Так это выглядит в движении, здесь обозначена область видимости камеры.
Темными помечены те клетки, код символа которых меньше кода точки — "." — то есть символы !"#$%&'()*+,-.. Теперь мы округляем координаты луча, и пытаемся узнать — буква в данных «координатах»-индексе темная (препятствие) или нет (летим лучом дальше).

Так как индекс один, а координаты — две, то мы используем хак:

var boxIndex = xcoord & 7 | ycoord << 3;

В итоге, получаем число, отражающее номер блока (ну или пустоты).

Вернёмся к коду. Теперь он выглядит поприличнее.

Код немного потолстел
function render(){
    t += 0.2;
    c.height=300;
    let x = size;
    while(x > 0){
        let y = size;
        while(y > 0){
            var depth = 0
            while(depth < 8){
                depth += 0.1
                
                var T = x / size - .5 + Math.cos(t) / 8; // Поворот камеры
                var isFloorOrCeiling = depth * y / size - depth / 2 | 0; // Мы уперлись в потолок или пол?

                if(isFloorOrCeiling)
                    break;

                var xcoord = t + depth * Math.cos(T) & 7;
                var ycoord = 3.5 + depth * Math.sin(T); // cos - 8 -> sin
                
                boxIndex = xcoord | ycoord << 3; // Находим индекс в исходном коде,
                // своего рода карте

                if ('.' >= F[boxIndex])
                    break;
                b = xcoord; // Зачем это? Сейчас узнаем!
            }
            
            context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2)
            y--;
        }

        x--;
    }
}


Обратно в отрисовку


К чему нам всё это было? Теперь, после выполнения этого алгоритма, мы знаем дальность до объекта, и можем его нарисовать. Но один вопрос остался без ответа: как отличить потолок от отдельного блока? Ведь расстояние до потолка и до блока — числа, которые ничем не отличаются! На самом деле, мы уже ответили на этот вопрос. 

//       То, что определяет, заливать фиксированной шириной или нет
//                                 ||
//                                 ↓↓
context.fillRect(x * 4, y * 4, b - xcoord ? 4 : depth / 2, depth / 2);

В коде есть одно условие, связанное с переменной b, и влияющее на ширину «большого черного пикселя»: b - xcoord ? 4 : depth / 2. Давайте уберем это условие, и посмотрим, что будет без него:

Совсем не видно границ между блоками и потолком! (кликабельно)

Условие b - xcoord даст нам константную ширину тогда, когда изменение координаты равно 0. А когда это может не произойти? Это не происходит лишь тогда, когда мы не доходим до (2) строчки в коде:

// ....
var xcoord = t + depth * Math.cos(T) & 7; // <--- Должны побывать здесь (1)
// ...
if ('.' >= F[boxIndex]) // <--- Программа выходит здесь (3)
    break;
b = xcoord; // <--- Не должны прийти сюда (2)
// ....

Значит, программа выходит из цикла раньше, на строчке (3), когда луч идет в непрозрачный блок в направлении почти перпендикулярном её стенке, то есть попадает в «лицевую» грань блока. Таким образом, все блоки оказываются отличающимися от пола и потолка.

Вот, именно так и получается эта прекрасная 3D-картинка, которая не только радует глаз, но и заставляет думать, как и почему это работает. Посмотреть этот код в действии можно здесь (оф. сайт разработчика этого чуда).
Tags:
Hubs:
If this publication inspired you and you want to support the author, do not hesitate to click on the button
+49
Comments16
32
Karma
0
Rating
Киреев Михаил @kireevmp

Умный человек

Send message
VK

Articles

Show the best of all time
Change theme settings

Your account

Sections

Information

Services

Support
© 2006–2024, Habr