Scorobey Jan 18 2019 at 09:07

Математические модели хаоса

11 min

30K

Python*Algorithms*Mathematics*Development for Windows*Popular science

Tutorial

Введение

На Habr уже обсуждалась теория хаоса в статьях [1,2,3]. В этих статьях рассмотрены следующие аспекты теории хаоса: обобщённая схема генератора Чуа; моделирование динамики системы Лоренца; программируемые логическими интегральными схемами аттракторы Лоренца, Ресслера, Рикитаке и Нозе-Гувера.

Однако, техники теории хаоса используются и для моделирования биологических систем, которые, бесспорно, являются одними из наиболее хаотических систем из всех, что можно себе представить. Системы динамических равенств использовались для моделирования всего — от роста популяций и эпидемий, до аритмических сердцебиений [4].

В действительности, почти любая хаотическая система может быть смоделирована — рынок ценных бумаг порождает кривые, которые можно легко анализировать при помощи странных аттракторов, процесс падения капель из протекающего водопроводного крана кажется случайным при анализе невооруженным ухом, но, если его изобразить как странный аттрактор, открывается сверхъестественный порядок, которого нельзя было бы ожидать от традиционных средств.

Целью настоящей статьи является рассмотрение теории хаоса на примере роста численности биологических популяций и удвоения цикла в механических системах с графической визуализацией математических моделей основанной на простых интуитивно понятных программах, написанных на Python.

Статья написана с целью обучения, но позволит, даже не имеющему опыта программирования читателю, используя приведенные программы, самостоятельно решить большинство новых учебных задач по теме моделирования явлений хаоса.

Удвоение периода циклов и хаос на примере роста численности биологических популяций

Начнём с рассмотрения логистического дифференциального уравнения, которое моделирует ограниченный, а не экспоненциальный рост численности биологических популяций:

$\frac{dN}{dt}=aN-bN^{2},(a,b>0). (1)$

Именно это уравнение может предсказать экзотические и неожиданные модели поведения некоторых популяций. Действительно, согласно (1) при $t\rightarrow +\infty$ численность популяции приближается к граничной равной a/b.

Для численного решения логистического дифференциального решения можно использовать самый простой алгоритм, с численным значением шага времени, приняв $t_{n+1}=t_{n}+h$ , тогда решение (1) можно получить путём многократного применения следующего соотношения:

$N_{n+1}=N_{n}+(aN_n-bN{_{n}}^{2})h.$ (2)

Представим уравнение (2) в виде логистического уравнения в конечных разностях:

$N_{n+1}=rN_{n}-sN{_{n}}^{2}$ . (3),

где: r=1+ah и s=bh.
Подстановкой в (3) $N_{n}=\frac{r}{s}x_{n}$ , получим итерационную формулу:

$x_{n+1}=rx_{n}(1-x_{n})$ , (4)

Рассчитывая значения, заданные соотношением (3), можно сгенерировать последовательность $x_{1},x_{2},x_{3},.....$
максимальных значений численности популяций, которые будет поддерживать среда в заданные моменты времени $t_{1},t_{2},t_{3}.$ .

Предполагаем, что существует предельное значение дробей, выражающих часть численности популяций:

$x_{\infty }=\lim_{n \to \infty }x_{n}$ , (5).

Будем исследовать, как зависит $x_{\infty }$ от параметра роста r в уравнении (4). Для этого на Python напишем программу, которая, начиная с $x_{1}=0,5$ , вычисляет результаты при нескольких сотен итераций (n=200) для r=1,5;2,0;2,5:

Код программы

# -*- coding: utf8 -*-
from numpy import *
print("      n     r=1,5     r=2,0     r=2,5   ")
M=zeros([201,3])
a=[1.5,2.0,2.5]
for j in arange(0,3,1):
       M[0,j]=0.5
for j in arange(0,3,1):
        for i in arange(1,201,1):
                M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
for i in arange(0,201,1):
       if 0<=i<=2:
              print(" {0: 7.0f}  {1: 7.4f} {2: 7.4f}  {3: 7.4f} "
                    . format(i,M[i,0],M[i,1],M[i,2]))
       elif 2<i<=5:
              print(".")
       elif  197<=i<=200:
              print(" {0: 7.0f}  {1: 7.4f}  {2: 7.4f}  {3: 7.4f} "
                    . format(i,M[i,0],M[i,1],M[i,2]))

Результат работы программы (для сокращения вывода результатов приведены первые три и последние четыре значения):

       n   r=1,5     r=2,0     r=2,5   
       0   0.5000 0.5000   0.5000 
       1   0.3750 0.5000   0.6250 
       2   0.3516 0.5000   0.5859 
.
.
.
     197   0.3333   0.5000   0.6000 
     198   0.3333   0.5000   0.6000 
     199   0.3333   0.5000   0.6000 
     200   0.3333   0.5000   0.6000

Анализ дискретной модели показывает, что для r=1,5;2,0;2,5 с ростом количества итераций значение $x_{n}$ стабилизируется и становится практически равным предельному $x_{\infty}$ , которое определяется соотношением (5). Причём для приведенных значений r величина $x_{\infty}$ соответственно равна $x_{\infty}=0,3333;0,5000;0,6000$ .
Увеличим r=3,1;3,25;3,5 и число итераций n=1008, для этого внесём следующие изменения в программу:

Код программы


# -*- coding: utf8 -*-
from numpy import *
print("      n     r=3,1     r=3,25     r=3,5   ")
M=zeros([1008,3])
a= [3.1,3.25,3.5]
for j in arange(0,3,1):
        M[0,j]=0.5
for j in arange(0,3,1):
        for i in arange(1,1008,1):
                M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
for i in arange(0,1008,1):
        if 0<=i<=3:
                print(" {0: 7.0f}  {1: 7.4f} {2: 7.4f}  {3: 7.4f} "
                    . format(i,M[i,0],M[i,1],M[i,2]))
        elif 4<i<=7:
                print(".")
        elif  1000<=i<=1007:
                print(" {0: 7.0f}  {1: 7.4f}  {2: 7.4f}  {3: 7.4f} "
                    . format(i,M[i,0],M[i,1],M[i,2]))

Результат работы программы (для сокращения вывода результатов приведены первые четыре и последние восемь значений):

    n   r=3,1   r=3,25   r=3,5  
    0  0.5000 0.5000  0.5000 
    1  0.7750 0.8125  0.8750 
    2  0.5406 0.4951  0.3828 
    3  0.7699 0.8124  0.8269 
.
.
.
  1000  0.5580  0.4953  0.5009 
  1001  0.7646  0.8124  0.8750 
  1002  0.5580  0.4953  0.3828 
  1003  0.7646  0.8124  0.8269 
  1004  0.5580  0.4953  0.5009 
  1005  0.7646  0.8124  0.8750 
  1006  0.5580  0.4953  0.3828 
  1007  0.7646  0.8124  0.8269

Как следует из приведенных данных, вместо того, чтобы стабилизироваться возле единственной предельной численности популяции, дробная часть численности популяции колеблется между двумя дробями по мере изменения времени. По сравнению с r=3,1, период цикла для r=3,25 увеличивается вдвое, а для r=3,5 в четыре раза.

Программа для графического отображения циклов роста популяции


# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import *
M=zeros([1008,3])
a= [3.1,3.25,3.5]
for j in arange(0,3,1):
        M[0,j]=0.5
for j in arange(0,3,1):
        for i in arange(1,1008,1):
                M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
x=arange(987,999,1)
y=M[987:999,0]
y1=M[987:999,1]
y2=M[987:999,2]
plt.title('Удвоение цикла роста популяции для r=3,1;3,25;3,5') 
plt.plot(x,y, label="T=1,ymax=%s,ymin=%s"%(round(max(y),3),round(min(y),3)))
plt.plot(x,y1, label="T=2,ymax=%s,ymin=%s"%(round(max(y1),3),round(min(y1),3)))
plt.plot(x,y2, label="T=4,ymax=%s,ymin=%s"%(round(max(y2),3),round(min(y2),3)))
plt.grid()
plt.legend(loc="best")
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()

Результат выполнения программы:

Благодаря удвоению периода итерация, $x_{n+1}=rx_{n}(1-x_{n})$ стала широко известной. Когда значение скорости роста превосходит r=3,56, удвоение периода ускоряется и уже в точке r=3,57 возникает чрезвычайный хаос. Для отображения наступления хаоса воспользуемся следующей программой:

Код программы

# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import *
print("     n     r=3,57 ")
M=zeros([1041,1])
a= [3.57]
for j in arange(0,1,1):
        M[0,j]=0.5
for j in arange(0,1,1):
        for i in arange(1,1041,1):
                M[i,j]=a[j]*M[i-1,j]*(1-M[i-1,j])
for i in arange(0,1041,1):
        if 1000<=i<=1015:
                print(" {0: 7.0f} {1: 7.4f}"
          . format(i,M[i,0]))
x=arange(999,1040,1)
y=M[999:1040,0]
plt.title(' Не детерминированный хаос для r=3,57') 
plt.plot(x,y)
plt.grid()
plt.ylabel("x(n)")
plt.xlabel("n")
plt.show()

Результат выполнения программы:

   n      r=3,57 
  1000  0.4751
  1001  0.8903
  1002  0.3487
  1003  0.8108
  1004  0.5477
  1005  0.8844
  1006  0.3650
  1007  0.8275
  1008  0.5096
  1009  0.8922
  1010  0.3434
  1011  0.8050
  1012  0.5604
  1013  0.8795
  1014  0.3784
  1015  0.8397

Напишем программу для визуализации зависимости поведения итераций от параметра роста r. Для каждого значения r в интервале $a\leqslant r\leqslant b$ выполняется 1000 итераций для достижения устойчивости. Затем, каждые 250 значений, полученных в результате итераций, наносятся на график по вертикальной оси, образуя точки (r,x):

Код программы


# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import*
N=1000
y=[]
y.append(0.5)
for r in arange(2.8,4.0,0.0001):  
    for n in arange(1,N,1):       
        y.append(round(r*y[n-1]*(1-y[n-1]),4)) 
    y=y[N-250:N]
    x=[r ]*250
    plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) 
plt.title("Диаграмма ветвления при 2,8<= r<=4,0,0<=x<=1")
plt.xlabel("r")
plt.ylabel("y")
plt.axvline(x=3.01,color='black',linestyle='--')
plt.axvline(x=3.45, color='black',linestyle='--')
plt.axvline(x=3.6,color='black',linestyle='--')
plt.axvline(x=3.7,color='black',linestyle='--')
plt.axvline(x=3.8,color='black',linestyle='--')
plt.axvline(x=3.9,color='black',linestyle='--')
plt.show()

Результат в виде диаграммы:

Полученный график называется “диаграммой ветвления”, которая позволяет определить, чему соответствует данное значение r — циклу или хаосу. Единственное значение численности популяции определяется до значения $r\approx 3$ , затем цикл с периодом 2 до $r\approx 3,4$ , затем цикл с периодом 4, затем цикл с периодом 8 и далее с быстрым приближением к хаосу.

Следует отметить, что вертикальные области незаполненного пространства на графике- это области r=3,6 и r=3,7, между r=3,7 и r=3,8, между r=3,8 и r=3,9, куда возвращается циклический порядок из предыдущего хаоса.
Для рассмотрения появления цикла с периодом кратным 3 в области $3,8\leqslant r\leqslant 3,9$ внесём изменения в предыдущую программу:

Код программы


# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import*
N=1000
y=[]
y.append(0.5)
for r in arange(3.8,3.9,0.0001):  
    for n in arange(1,N,1):       
        y.append(round(r*y[n-1]*(1-y[n-1]),4)) 
    y=y[N-250:N]
    x=[r ]*250
    plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) 
plt.title("Диаграмма ветвления  при 3,8<= r<=3,9,0<=x<=1")
plt.xlabel("r")
plt.ylabel("y")
plt.axvline(x=3.83,color='black',linestyle='--')
plt.show()

Результат выполнения программы:

Цикл периода 3 появляется в окрестности точки r=3,83, а затем разбивается последовательно на циклы 6,12,24. Существование цикла с периодом 3 подразумевает наличие циклов любого другого конечного периода, а так же хаотических циклов вообще без периода.

Диаграмма ветвления позволяет проследить за развитием системы при плавном изменении параметра. При фиксированном значении параметра за орбитами точек позволяет проследить паутинная диаграмма (диаграмма Ламерея).

Построение паутинной диаграммы позволяет выявить различные эффекты, незаметные на диаграмме ветвления. Напишем программу:

Код программы


# -*- coding: utf8 -*-
import matplotlib.pyplot as plt
from numpy import *
a=2.7
x1=0.62
def ff(x):
        return a*x*(1-x)
b=a*x1*(1-x1)/x1
def fl(x):
        return b*x
x=0.1
y=0
Y=[]
X=[]
for i in arange(1,30,1):
        X.append(x)
        Y.append(y)
        y=ff(x)
        X.append(x)
        Y.append(y)
        x=y/b
plt.title('Паутинная диаграмма логистической \n функции λx(1-x) при λ = 2.7')
plt.plot(X,Y,'r')
x1=arange(0,1,0.001)
y1=[ff(x) for x in x1]
y2=[fl(x) for x in x1]
plt.plot(x1,y1,'b')
plt.plot(x1,y2,'g')
plt.grid(True)
plt.show()

Диаграмма Ламерея:

Удвоение периода в механических системах

Рассмотрим дифференциальное уравнение, которое моделирует свободные затухающие колебания материальной точки заданной массы на нелинейной пружине, при которых затухание определяется скоростью.

$mx^{''}+cx^{'}+kx+\beta x^{3}=0$ (6)

В уравнении (6) член kx представляет силу линейной пружины, приложенной к материальной точке заданной массы, а член $\beta x^{3}$ представляет фактическую нелинейность пружины.

Если на систему свободных колебаний (6) действует сила, то перемещение материальной точки массы, к которой приложена эта сила, описывается дифференциальным уравнением Дуффинга для вынужденных колебаний:

$mx^{''}+cx^{'}+kx+\beta x^{3}=F_{0}cos\omega t$ (7)

Уравнение (7) для большинства входящих в него параметров решается численным методом. Механическая система для математической модели по уравнению (7) приведена на рисунке:

Особенностью приведенной системы является то, что вместо пружины используется гибкая металлическая нить, которая колеблется в вертикальной плоскости, для которой константа Гука k отрицательна. В этой схеме точки устойчивого равновесия (а) и (с), а точка неустойчивого равновесия (b).

При смещении материальной точки из положения (b), действующая на неё сила является отталкивающей. Если периодическая сила, например, созданная осциллирующим магнитным полем частично гасится сопротивлением воздуха. Тогда, уравнение (7) является приемлемой математической моделью для горизонтального перемещения x(t) материальной точки при следующих областях параметров $k<0,c>0,\beta >0$ .

Для исследования поведения такой нелинейной системы примем $k=-1,m=c=\beta =\omega =1$ , тогда дифференциальное уравнение (7) принимает вид:

$x^{''}+x^{'}-x+x^{3}=F_{0}cos(t)$ , (8)

Напишем программу численного интегрирования уравнения (8) при начальных условиях $x(0)=1,x^{'}(0)=0$ в области $100\leqslant t\leqslant 200$ и для каждого из следующих значений амплитуды $F_{0}=0,6;0,7;0,75;0,8$ , причем в каждом случае вывести на график решения для плоскостей $x(t),x^{'}(t)$ и $inline$ :

Код программы


# -*- coding: utf8 -*-
from numpy import *
from scipy. integrate import odeint
import matplotlib.pyplot as plt
for F in [0.6,0.7,0.75,0.8]:
        def f(y,t):
                y1,y2=y
                return [y2,-y2-y1**3+y1+F*cos(t)]
        t=arange(100,200,0.001)
        y0=[1.0,0.0]
        [y1,y2]=odeint(f, y0, t, full_output=False,rtol=1e-12).T
        if F==0.6:
               plt.subplot(221)
               plt.title('Фазовая плоскость F=0.6,T=2'r'$\pi$')
               plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
                markersize=0.1)
               plt.grid(True)
               plt.subplot(222)
               plt.title('Решение x(t): F=0.6,T=2'r'$\pi$')
               plt.plot(t,y1, color='black', linestyle=' ', marker='.',
                markersize=0.1)              
               plt.grid(True)
        elif F==0.7:
                plt.subplot(223)                
                plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
                markersize=0.1, label='Фазовая плоскость \n F=0.7,T=4'r'$\pi$')
                plt.legend(loc='upper left')
                plt.grid(True)
                plt.subplot(224)
                plt.plot(t,y1, color='black', linestyle=' ', marker='.',
                 markersize=0.1, label='Решение x(t): F=0.7,T=4'r'$\pi$')
                plt.legend(loc='upper left')
                plt.grid(True)
                plt.show()
        if F==0.75:
                plt.subplot(221)
                plt.title('Фазовая плоскость F=0.75,T=8'r'$\pi$')
                plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
                 markersize=0.1)               
                plt.grid(True)
                plt.subplot(222)
                plt.title('Решение x(t): F=0.75,T=8'r'$\pi$')
                plt.plot(t,y1, color='black', linestyle=' ', marker='.',
                markersize=0.1)               
                plt.grid(True)
        elif F==0.8:
                plt.subplot(223)
                plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
                 markersize=0.1, label='Фазовая плоскость\n F=0.8,Хаос')
                plt.legend(loc='upper left')
                plt.grid(True)
                plt.subplot(224)
                plt.plot(t,y1, color='black', linestyle=' ', marker='.',
                 markersize=0.1, label='Решение x(t): F=0.8,Хаос')
                plt.legend(loc='upper left')
                plt.grid(True)
                plt.show()

Графики как результат работы программы

Этот переход от удвоения периода к хаосу показывает общий характер поведения нелинейной механической системы в ответ на изменение соответствующего физического параметра, например: $k,m,c,\beta ,\omega ,F_{0}$ . Такие явления не происходят в линейных механических системах.

Аттрактор Лоренца

Подстановка в уравнение Дуффинга для вынужденных колебаний (7) приводят к двумерной нелинейной системе дифференциальных уравнений, что и было приведено в предыдущем листинге. Трёхмерную нелинейную систему дифференциальных уравнений применительно к задачам метеорологии рассматривал Э.Н. Лоренц:

$\frac{dx}{dt}=-sx+sy,$
$\frac{dy}{dt}=-xz+rx-y,$ (9)
$\frac{dz}{dt}=xy-dz$

Решение системы (9) лучше рассматривать в проекции на одну из трёх плоскостей. Напишем программу численного интегрирования при значениях параметров b=\frac{8}{3},s=10,r=28 и начальных условиях x(0)=-8, y(0)=8, z(0)=27:

Код программы


# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
s,r,b=10,28,8/3
def f(y, t):
 y1, y2, y3 = y
 return [s*(y2-y1),
 -y2+(r-y3)*y1,
 -b*y3+y1*y2]
t = np.linspace(0,20,2001)
y0 = [-8, 8, 27]
[y1,y2,y3]=odeint(f, y0, t, full_output=False).T
plt.plot(y1,y3, color='black', linestyle=' ', marker='.',
markersize=2)
plt.xlabel('x')
plt.ylabel('z')
plt.grid(True)
plt.title("Проекция траектории Лоренца на плоскость xz")
plt.show()

Результат работы программы:

Рассматривая изображение на графике во времени, можно предположить, что точка P(x(t), y{t), z(t)) совершает случайное число колебаний то справа, то с слева. Для метеорологического приложения системы Лоренца, после случайного числа ясных дней, следует случайное число дождливых дней.

Рассмотрим программу для отображения аттрактора Лоренца в плоскости xyz для мало различающихся начальных условий:

Код программы


# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#Создаем функцию правой части системы уравнений.
s,r,b=10,25,3
def f(y, t):
 y1, y2, y3 = y
 return [s*(y2-y1),
 -y2+(r-y3)*y1,
-b*y3+y1*y2]
#Решаем систему ОДУ и строим ее фазовую траекторию
t = np.linspace(0,20,2001)
y0 = [1, -1, 10]
[y1,y2,y3]=odeint(f, y0, t, full_output=False).T
fig = plt.figure(facecolor='white') 
ax=Axes3D(fig)
ax.plot(y1,y2,y3,linewidth=2)
plt.xlabel('y1')
plt.ylabel('y2')
plt.title("Начальные условия: y0 = [1, -1, 10]")
y0 = [1.0001, -1, 10]
[y1,y2,y3]=odeint(f, y0, t, full_output=False).T
fig = plt.figure(facecolor='white') 
ax=Axes3D(fig)
ax.plot(y1,y2,y3,linewidth=2)
plt.xlabel('y1')
plt.ylabel('y2')
plt.title("Начальные условия: y0 = [1.0001, -1, 10]")
plt.show()

Результаты работы программы показаны на следующих графиках:

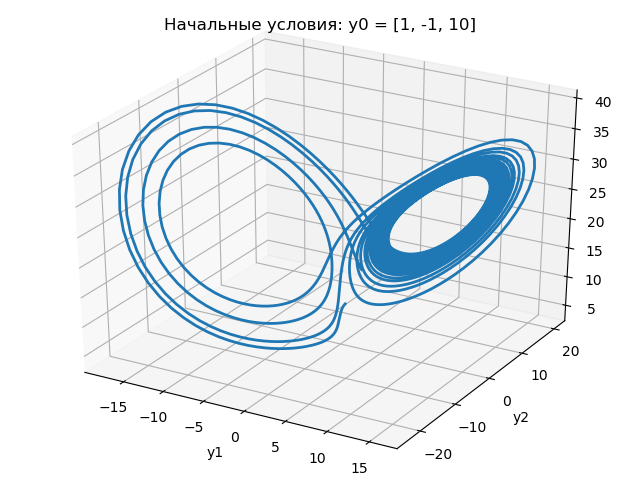
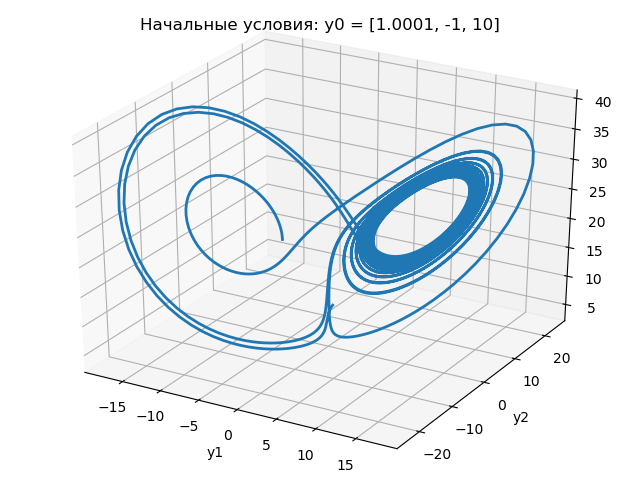
Из приведенных графиков следует, что изменение начального условия для с 1,0 до 1,0001 резко меняет характер изменения аттрактора Лоренца.

Система Росслера

Это очень интенсивно изучаемая нелинейная трехмерная система:
$\frac{dx}{dt}=-y-z,$
$\frac{dy}{dt}=x-\alpha y,$ (10)
$\frac{dz}{dt}=b+x(x-c).$

Напишем программу для численного интегрирования системы (10) для следующих параметров a=0,39, b=2, c=4 при начальных условиях x(0)=0, y(0)=0, z(0)=0:

Код программы


# -*- coding: utf8 -*-
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
a,b,c=0.398,2.0,4.0
def f(y, t):
 y1, y2, y3 = y
 return [(-y2-y3),
 y1+a*y2,
 b+y3*(y1-c)]
t = np.linspace(0,50,5001)
y0 = [0,0, 0]
[y1,y2,y3]=odeint(f, y0, t, full_output=False).T
plt.plot(y1,y2, color='black', linestyle=' ', marker='.',
markersize=2)
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.title("Проекция ленты Ройсслера на плоскость xy")
plt.show()

Результат работы программы:

График

В плоскости лента Росслера выглядит как петля, но в пространстве она оказывается перекручена подобно ленте Мебиуса.

Выводы

Для демонстрации явлений хаоса приведены простые и интуитивно понятные программы на высокоуровневом языке программирования Python, которые легко модернизировать под новые проекты по данной теме. Статья имеет учебно-методическую направленность и может быть использована в процессе обучения.

Ссылки

Немного о хаосе и о том, как его сотворить
Критический взгляд на аттрактор Лоренца
Генераторы хаоса на ПЛИС
Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB. 3-е издание.: Пер. с англ. — М.: ООО «И.Д. Вильяме», 2008. — 1104 с.: ил. — Парал. тит. англ.

Tags:

Hubs: