Продолжаю знакомить читателей Хабра с главами из своей книжки «Теория счастья» с подзаголовком «Математические основы законов подлости». Это ещё не изданная научно-популярная книжка, очень неформально рассказывающая о том, как математика позволяет с новой степенью осознанности взглянуть на мир и жизнь людей. Она для тех кому интересна наука и для тех, кому интересна жизнь. А поскольку жизнь наша сложна и, по большому счёту, непредсказуема, упор в книжке делается, в основном, на теорию вероятностей и математическую статистику. Здесь не доказываются теоремы и не даются основы науки, это ни в коем случае не учебник, а то, что называется recreational science. Но именно такой почти игровой подход позволяет развить интуицию, скрасить яркими примерами лекции для студентов и, наконец, объяснить нематематикам и нашим детям, что же такого интересного мы нашли в своей сухой науке.
Речь в этой главе пойдёт о статистике, о погоде и даже о философии. Не пугайтесь, совсем чуть-чуть. Не более того, что можно использовать для tabletalk в приличном обществе.

Как часто летом мы планируем на свои выходные дни выезд на природу, прогулку в парке или пикник, а потом дождь разбивает наши планы, заточая нас в доме! И ладно бы это случалось раз или два за сезон, порою складывается впечатление, что непогода преследует именно выходные дни, раз за разом попадая на субботу или воскресенье!
Сравнительно недавно вышла статья австралийских исследователей: «Недельные циклы пиковой температуры и интенсивность городских тепловых островов». Её подхватили новостные издания и перепечатали результаты с таким заголовком: «Вам не кажется! Учёные выяснили: погода на выходных, действительно хуже, чем в будние дни». В цитируемой работе приводится статистика температуры и осадков за много лет в нескольких городах Австралии, и вправду, выявляющая понижение температуры на в определённые часы субботы и воскресенья. После чего этому даётся объяснение, связывающее локальную погоду с уровнем загрязнённости воздуха из-за возрастающего транспортного потока. Незадолго до этого, подобное исследование проводилось в Германии и привело примерно к тем же выводам.
Согласитесь, доли градуса — это весьма тонкий эффект. Сетуя на непогоду в долгожданную субботу, мы обсуждаем, был ли день солнечным или дождливым, это обстоятельство проще зарегистрировать, а позже вспомнить, даже не обладая точными приборами. Мы проведём собственное небольшое исследование на эту тему и получим замечательный результат: можно уверенно утверждать, что мы не знаем, связаны ли на Камчатке, день недели и непогода. Исследования с отрицательным результатом обычно не попадают на страницы журналов и в новостные ленты, но нам с вами важно понять, на каком основании я, вообще, могу что-то уверенно заявлять о случайных процессах. И в этом плане отрицательный результат становится ничуть не хуже положительного.
Статистику обвиняют в массе грехов: и во лжи и в возможностях манипуляций и, наконец, в непонятности. Но мне очень хочется реабилитировать эту область знаний, показать, насколько сложна задача, для которой она предназначена и сколь непросто бывает понять ответ, который даёт статистика.
Теория вероятностей оперирует точными знаниями о случайных величинах в виде распределений или исчерпывающих комбинаторных подсчётов. Ещё раз подчеркну, что располагать точным знанием о случайной величине возможно. Но что если это точное знание нам недоступно, а единственное чем мы располагаем — это наблюдения? У разработчика нового лекарства есть какое-то ограниченное число испытаний, у создателя системы управления транспортным потоком — лишь ряд измерений на реальной дороге, у социолога – результаты опросов, причём, он может быть уверен в том, что отвечая на какие-то вопросы, респонденты попросту соврали.
Понятно, что одно наблюдение не даёт ровным счётом ничего. Два – немногим больше, чем ничего, три, четыре… сто… сколько нужно наблюдений чтобы получить какое-либо знание о случайной величине, в котором можно было бы быть уверенным с математической точностью? И что это будет за знание? Скорее всего, оно будет представлено в виде таблицы или гистограммы, дающей возможность оценить некоторые параметры случайной величины, их называют статистиками (например, область определения, среднее или дисперсия, асимметричность и т.д.). Быть может, глядя на гистограмму удастся угадать точную форму распределения. Но внимание! — все результаты наблюдений сами будут случайными величинами! Пока мы не владеем точным знанием о распределении, все результаты наблюдений дают нам лишь вероятностное описание случайного процесса! Случайное описание случайного процесса — ещё бы здесь не запутаться, а то и захотеть запутать намеренно!
Что же делает математическую статистику точной наукой? Её методы позволяют заключить наше незнание в чётко ограниченные рамки и дать вычислимую меру уверенности в том, что в этих рамках наше знание согласуется с фактами. Это язык, на котором можно рассуждать о неизвестных случайных величинах так, чтобы рассуждения имели смысл. Такой подход очень полезен в философии, психологии или социологии, где очень легко пуститься в пространные рассуждения и дискуссии без всякой надежды на получение позитивного знания и, тем более, на доказательство. Грамотной статистической обработке данных посвящена масса литературы, ведь это абсолютно необходимый инструмент для медиков, социологов, экономистов, физиков, психологов… словом, для всех научно исследующих так называемый «реальный мир», отличающийся от идеального математического лишь степенью нашего незнания о нём.
Теперь ещё раз взгляните на эпиграф к этой главе и осознайте, что статистика, которую так пренебрежительно называют третьей степенью лжи, это единственное, чем располагают естественные науки. Это ли не главный закон подлости мироздания! Все известные нам законы природы, от физических до экономических, строятся на математических моделях и их свойствах, но поверяются они статистическими методами в ходе измерений и наблюдений. В повседневности наш разум делает обобщения и подмечает закономерности, выделяет и распознаёт повторяющиеся образы, это, наверное, лучшее, что умеет человеческий мозг. Это именно то, чему в наши дни учат искусственный интеллект. Но разум экономит свои силы и склонен делать выводы по единичным наблюдениям, не сильно беспокоясь о точности или обоснованности этих выводов. По этому поводу есть замечательное самосогласованное утверждение из книги Стивена Браста «Исола»: «Все делают общие выводы из одного примера. По крайней мере, я делаю именно так». И пока речь идёт об искусстве, характере домашних любимцев или обсуждении политики, об этом можно сильно не беспокоиться. Однако при строительстве самолёта, организации диспетческой службы аэропорта или тестировании нового лекарства, уже нельзя сослаться на то, что «мне так кажется», «интуиция подсказывает» и «в жизни всякое бывает». Тут приходится ограничивать свой разум рамками строгих математических методов.
Наша книжка не учебник, и мы не будем детально изучать статистические методы и ограничимся лишь одним — техникой проверкой гипотез. Но мне хотелось бы показать ход рассуждений и форму результатов, характерных для этой области знания. И, возможно, кому-то из читателей, будущему студенту, не только станет понятно зачем его мучают матстатистикой, всеми этими QQ-диаграммами, t- и F-распределениями, но придёт в голову другой важный вопрос: а как вообще это возможно знать что-нибудь наверняка о случайном явлении? И что именно мы узнаём, используя статистические данные?
Основными столпами математической статистики являются теория вероятностей, Закон больших чисел и центральная предельная теорема.
Закон больших чисел, в вольной трактовке, говорит о том, что большое число наблюдений случайной величины почти наверняка отражает её распределение, так что наблюдаемые статистики: среднее, дисперсия и прочие характеристики, стремятся к точным значениям, соответствующим случайной величине. Иными словами, гистограмма наблюдаемых величин при бесконечном числе данных, почти наверняка стремится к тому распределению, которое мы можем считать истинным. Именно этот закон связывает «бытовое» частотное толкование вероятности и теоретическое, как меры на вероятностном пространстве.
Центральная предельная теорема, опять же, в вольной трактовке, говорит, что одной из наиболее вероятных форм распределения случайной величины является нормальное (гауссово) распределение. Точная формулировка звучит иначе: среднее значение большого числа идентично распределённых вещественных случайных величин, вне зависимости от их распределения, описывается нормальным распределением. Эту теорему обычно доказывают, применяя методы функционального анализа, но мы увидим позже, что её можно понять и даже расширить, введя понятие энтропии, как меры вероятности состояния системы: нормальное распределение имеет наибольшую энтропию при наименьшем числе ограничений. В этом смысле, оно оптимально при описании неизвестной случайной величины, либо случайной величины, являющейся совокупностью многих других величин, распределение которых тоже неизвестно.
Эти два закона лежат в основе количественных оценок достоверности наших знаний, основанных на наблюдениях. Здесь речь идёт о статистическом подтверждении или опровержении предположения, которое можно сделать из каких-то общих оснований и математической модели. Это может показаться странным, но сама по себе, статистика не производит новых знаний. Набор фактов превращается в знание лишь после построения связей между фактами, образующих определённую структуру. Именно эти структуры и связи позволяют делать предсказания и выдвигать общие предположения, основанные на чём-то, выходящем за пределы статистики. Такие предположения называются гипотезами. Самое время вспомнить один из законов мерфологии, постулат Персига:
Задача математической статистики ограничить это бесконечное число, а вернее свести их к одной, причём вовсе не обязательно верной. Для перехода к более сложной (и часто, более желанной) гипотезе, необходимо, используя данные наблюдений, опровергнуть более простую и общую гипотезу, либо подкрепить её и отказаться от дальнейшего развития теории. Часто проверяемую таким образом гипотезу называют нулевой, и в этом есть глубокий смысл.
Что может выступить в роли нулевой гипотезы? В определённом смысле, все что угодно, любое утверждение, но при условии, что его удастся перевести на язык измерения. Чаще всего, гипотезой служит ожидаемое значение какого-то параметра, который превращается в случайную величину в ходе измерения, либо отсутствие связи (корреляции) между двумя случайными величинами. Иногда предполагается вид распределения, случайного процесса, предлагается какая-то математическая модель. Классическая постановка вопроса при этом такова: позволяют ли наблюдения отвергнуть нулевую гипотезу или нет? Точнее, с какой долей уверенности мы можем утверждать, что наблюдения нельзя получить, исходя из нулевой гипотезы? При этом, если мы не смогли опираясь на статистические данные доказать, что нулевая гипотеза ложна, то она принимается истинной.
И тут можно подумать, что исследователи вынуждены совершать одну из классических логических ошибок, которая носит звучное латинское имя ad ignorantiam. Это аргументация истинности некоторого утверждения, основанная на отсутствии доказательства его ложности. Классический пример — слова, сказанные сенатором Джозефом Маккарти, когда его попросили предъявить факты для поддержки выдвинутого им обвинения, что некий человек является коммунистом: «У меня немного информации по этому вопросу, за исключением того общего заявления компетентных органов, что в его досье нет ничего, чтобы исключало его связи с коммунистами». Или ещё ярче: «Снежный человек существует, поскольку никто не доказал обратного». Выявление разницы между научной гипотезой и подобными уловками составляет предмет целой области философии: методологии научного познания. Одним из её ярких результатов является критерий фальсифицируемости, выдвинутый замечательным философом Карлом Поппером в первой половине XX века. Этот критерий призван разделять научное знание от ненаучного, и, на первый взгляд, он кажется парадоксальным:
Чем не закон подлости! Получается, что любая научная теория автоматически потенциально неверна, а теория, верная «по определению», не может считаться научной. Более того, этому критерию не удовлетворяют такие науки как математика и логика. Впрочем, их относят не к естественным наукам, а к формальным, не требующим проверки на фальсифицируемость. А если к этому добавить ещё один результат того же времени: принцип неполноты Гёделя, утверждающий, что в рамках любой формальной системы можно сформулировать утверждение, которое невозможно ни доказать, ни опровергнуть, то может стать непонятно зачем, вообще, заниматься всей этой наукой. Однако важно понимать, что принцип фальсифицируемости Поппера ничего не говорит об истинности теории, а только о том является она научной или нет. Он может помочь определить, даёт ли некая теория язык, на котором имеет смысл рассуждать о мире или нет.
Но всё же, почему, если мы не можем на базе статистических данных отвергнуть гипотезу, мы в праве принять её истинной? Дело в том, что статистическая гипотеза берётся не из желания исследователя или его предпочтений, она должна вытекать из каких-либо общих формальных законов. Например, из Центральной предельной теоремы, либо из принципа максимальной энтропии. Эти законы корректно отражают степень нашего незнания, не добавляя, без необходимости, лишних предположений или гипотез. В известном смысле, это прямое использование знаменитого философского принципа, известного как бритва Оккама:
Таким образом, когда мы принимаем нулевую гипотезу, основываясь на отсутствии её опровержения, мы формально и честно показываем, что в результате эксперимента степень нашего незнания осталась на прежнем уровне. В примере же со снежным человеком, явно или неявно, но предполагается обратное: отсутствие доказательств того, что этой загадочной твари не существует представляется чем-то, что может увеличить степень нашего знания о ней.
Вообще, с точки зрения принципа фальсифицируемости, любое утверждение о существовании чего-либо ненаучно, ибо отсутствие свидетельства ничего не доказывает. В тоже время, утверждение об отсутствии чего-либо можно легко опровергнуть предоставив экземпляр, косвенное свидетельство, либо доказав существование по построению. И в этом смысле, статистическая проверка гипотез анализирует утверждения об отсутствии искомого эффекта и может предоставить в известном смысле, точное опровержение этого утверждения. Именно этим в полной мере оправдывается термин «нулевая гипотеза»: она содержит необходимый минимум знаний о системе.
Очень важно подчеркнуть, что если статистические данные говорят о том, что нулевая гипотеза может быть отвергнута, то это не значит, что мы тем самым доказали истинность какой-либо альтернативной гипотезы. Статистику не следует путать с логикой, в этом кроется масса трудноуловимых ошибок, особенно, когда в дело вступают условные вероятности для зависимых событий. Например: очень маловероятно, что человек может быть Папой Римским ( млрд), следует ли из этого, что Папа Иоанн Павел II не был человеком? Утверждение кажется абсурдным, но, к сожалению, столь же неверным является и такой «очевидный» вывод: проверка показала, что мобильный тест на содержание алкоголя в крови даёт не более
млрд), следует ли из этого, что Папа Иоанн Павел II не был человеком? Утверждение кажется абсурдным, но, к сожалению, столь же неверным является и такой «очевидный» вывод: проверка показала, что мобильный тест на содержание алкоголя в крови даёт не более  как ложных положителых, так и ложных отрицательных результатов, следовательно, в
как ложных положителых, так и ложных отрицательных результатов, следовательно, в  случаев он верно выявит пьяного водителя. Давайте протестируем
случаев он верно выявит пьяного водителя. Давайте протестируем  водителей, и пусть
водителей, и пусть  из будут, действительно, пьяны. В результате мы получим
из будут, действительно, пьяны. В результате мы получим  ложных положительных и
ложных положительных и  ложноотрицательный результат: то есть, на одного проскочившего пьяницу придётся девять невинно обвинённых случайных водителей. Чем не закон подлости! Паритет будет наблюдаться только если доля пьяных водителей будет равна
ложноотрицательный результат: то есть, на одного проскочившего пьяницу придётся девять невинно обвинённых случайных водителей. Чем не закон подлости! Паритет будет наблюдаться только если доля пьяных водителей будет равна  , либо если отношение долей ложноположительных и ложноотрицательных результатов будет близким к реальному отношению пьяных водителей к трезвым. Причём, чем трезвее обследуемая нация, тем несправедливей будет применение описанного нами прибора!
, либо если отношение долей ложноположительных и ложноотрицательных результатов будет близким к реальному отношению пьяных водителей к трезвым. Причём, чем трезвее обследуемая нация, тем несправедливей будет применение описанного нами прибора!
Здесь мы столкнулись с зависимыми событиями. Помните, в колмогоровском определении вероятности говорилось о способе сложения вероятности объединения событий: вероятность объединения двух событий равна сумме их вероятностей за вычетом вероятности их пересечения. Однако о том, как вычисляется вероятность пересечение событий, эти определения не говорят. Для этого вводится новое понятие: условная вероятность и на передний план выходит зависимость событий друг от друга.
Вероятность пересечения событий A и B определяется как произведение вероятности события B и вероятности события , если известно, что случилось событие
, если известно, что случилось событие  :
:  и
и  независимы, если
независимы, если  , или
, или  , или
, или  .
.
Тем самым мы завершаем формальное определение вероятности, начатое в первой главе.
Пересечение — операция коммутативная, то есть . Отсюда немедленно следует теорема Байеса:
. Отсюда немедленно следует теорема Байеса:
В нашем примере с водителями и тестом на алкоголь мы имеем cобытия: — водитель пьян,
— водитель пьян,  — тест выдал положительный результат. Вероятности:
— тест выдал положительный результат. Вероятности:  — вероятность того, остановленный водитель пьян;
— вероятность того, остановленный водитель пьян;  — вероятность того, что тест выдаст положительный результат, если известно, что водитель пьян (исключается
— вероятность того, что тест выдаст положительный результат, если известно, что водитель пьян (исключается  ложноотрицателых результатов),
ложноотрицателых результатов),  — вероятность того, что тестируемый пьян, если тест дал положительный результат (исключается
— вероятность того, что тестируемый пьян, если тест дал положительный результат (исключается  ложноположительных результатов). Вычислим
ложноположительных результатов). Вычислим  — вероятность получить положительный результат теста на дороге:
— вероятность получить положительный результат теста на дороге:
Эти примеры тщательно разбираются студентами, изучающими медицинские тесты, или юридические практики. Но, боюсь, что журналистам или политикам не преподают ни математическую статистику ни теорию вероятностей, зато они охотно апеллируют к статистическим данным, вольно интерпретируют их и несут полученное «знание» в массы. Поэтому я призываю своего читателя: разобрался в математике сам, помоги разобраться другому! Другого противоядия невежеству я не вижу.
Мы рассмотрим и применим на практике только одно из множества статистических методик: проверку статистических гипотез. Для тех, кто уже связал свою жизнь с естественными или социальными науками в этих примерах не будет чего-то ошеломительно нового.
Предположим, что мы многократно измеряем случайную величину, имеющую среднее значение и стандартное отклонение
и стандартное отклонение  . Согласно Центральной предельной теореме, наблюдаемое среднее значение будет распределено нормально. Из закона больших чисел следует, что его среднее будет стремиться к
. Согласно Центральной предельной теореме, наблюдаемое среднее значение будет распределено нормально. Из закона больших чисел следует, что его среднее будет стремиться к  , а из свойств нормального распределения следует, что после
, а из свойств нормального распределения следует, что после  измерений наблюдаемая дисперсия среднего будет уменьшаться как
измерений наблюдаемая дисперсия среднего будет уменьшаться как  . Стандартное отклонение можно рассматривать как абсолютную погрешность измерения среднего, относительная погрешность при этом будет равна
. Стандартное отклонение можно рассматривать как абсолютную погрешность измерения среднего, относительная погрешность при этом будет равна  . Это весьма общие выводы, не зависящие для достаточно больших
. Это весьма общие выводы, не зависящие для достаточно больших  от конкретной формы распределения исследуемой случайной величины. Из них следуют два полезных правила (не закона):
от конкретной формы распределения исследуемой случайной величины. Из них следуют два полезных правила (не закона):
1. Минимальное число испытаний должно диктоваться желаемой относительной погрешностью
должно диктоваться желаемой относительной погрешностью  . При этом, если
. При этом, если  . При
. При  близком к нулю, относительную погрешность лучше заменить на абсолютную.
близком к нулю, относительную погрешность лучше заменить на абсолютную.
2. Пусть нулевой гипотезой будет предположение, что наблюдаемое среднее значение равно . Тогда, если наблюдаемое среднее не выходит за пределы
. Тогда, если наблюдаемое среднее не выходит за пределы  , то вероятность того что нулевая гипотеза верна, будет не менее
, то вероятность того что нулевая гипотеза верна, будет не менее  .
.
Если заменить в этих правилах на
на  , то степень уверенности вырастет до
, то степень уверенности вырастет до  , это очень сильное правило
, это очень сильное правило  , которое в физических науках отделяет предположения от экспериментально установленного факта.
, которое в физических науках отделяет предположения от экспериментально установленного факта.
Для нас полезным будет рассмотреть приложение этих правил к распределению Бернулли, описывающему случайную величину, которая принимает ровно два значения, условно называемые «успех» и «неудача», с заданной вероятностью успеха . В этом случае
. В этом случае  и
и  , так что для необходимого числа экспериментов и доверительного интервала получим
, так что для необходимого числа экспериментов и доверительного интервала получим
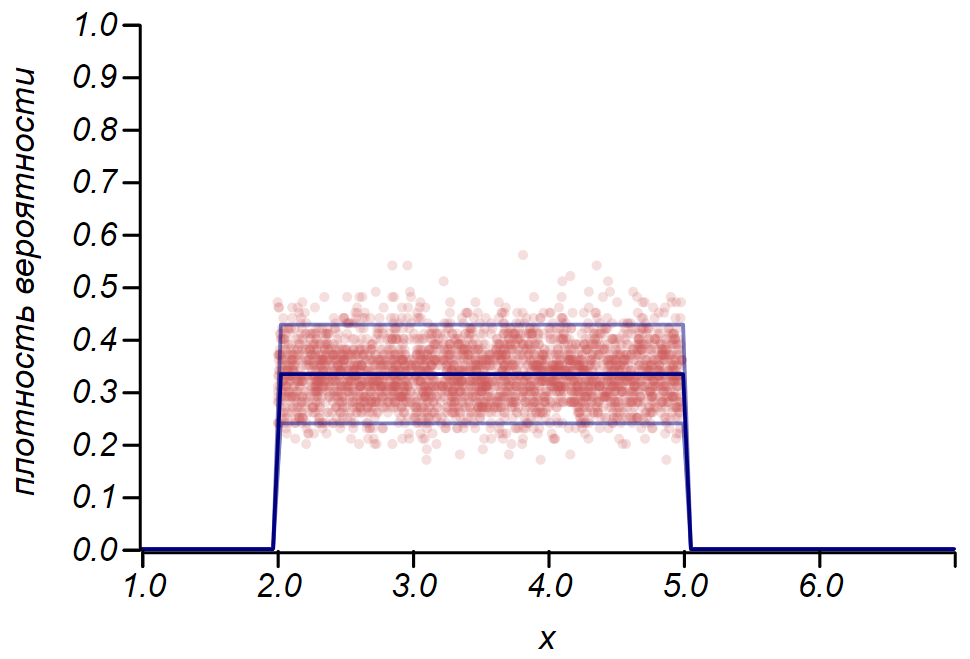
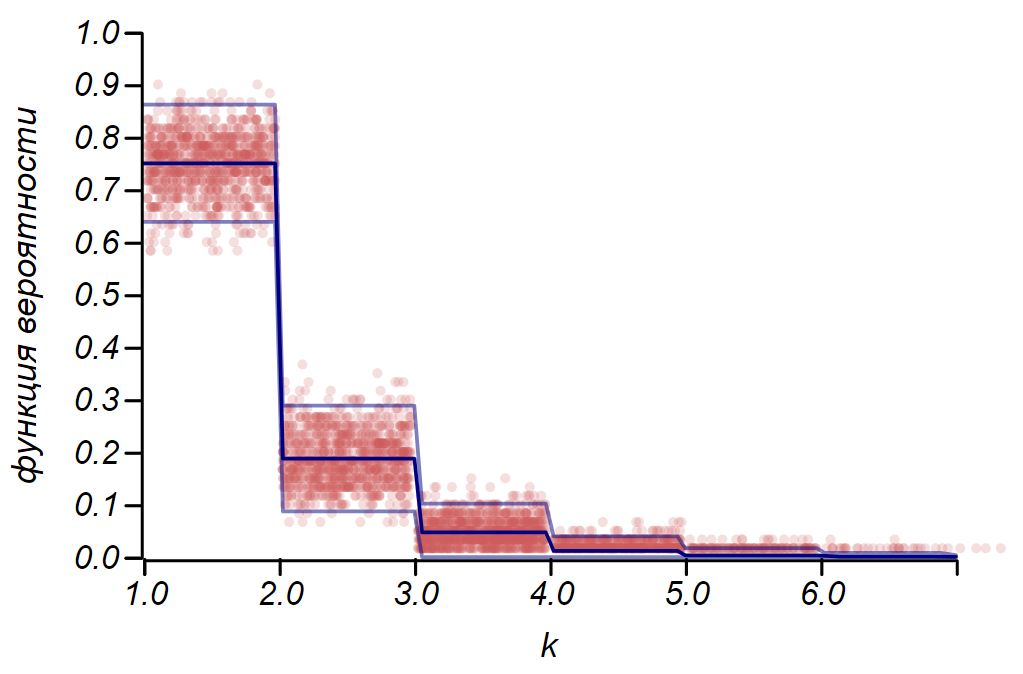
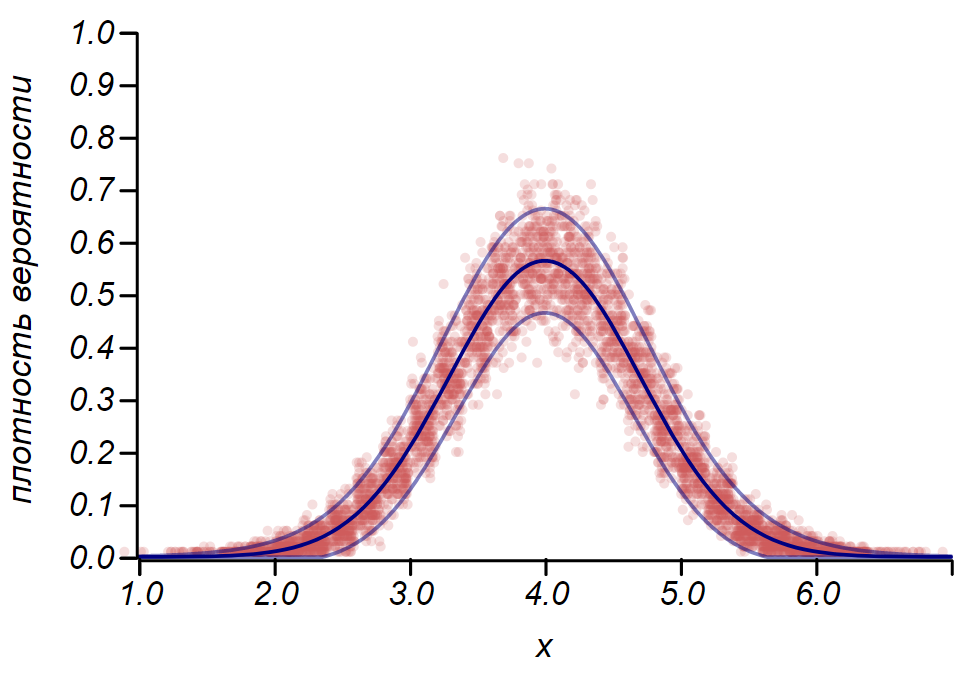
Правило для распределения Бернулли можно использовать для определения доверительного интервала при построении гистограмм. По существу, каждый столбик гистограммы представляет случайную величину с двумя значениями: «попал» – «не попал», где вероятность попадания соответствует моделируемой функции вероятности. В качестве демонстрации, сгенерируем множество выборок для трёх распределений: равномерного, геометрического и нормального, после чего сравним оценки разброса наблюдаемых данных с наблюдаемым разбросом. И здесь мы вновь видим отголоски центральной предельной теоремы, проявляющиеся в том, что распределение данных вокруг средних значений в гистограммах близко к нормальному. Однако, вблизи нуля разброс становится несимметричным и приближается к другому очень вероятному распределению – экспоненциальному. Этот пример хорошо показывает, что я имел в виду, говоря, что в статистике мы имеем дело со случайными значениями параметров случайной величины.
для распределения Бернулли можно использовать для определения доверительного интервала при построении гистограмм. По существу, каждый столбик гистограммы представляет случайную величину с двумя значениями: «попал» – «не попал», где вероятность попадания соответствует моделируемой функции вероятности. В качестве демонстрации, сгенерируем множество выборок для трёх распределений: равномерного, геометрического и нормального, после чего сравним оценки разброса наблюдаемых данных с наблюдаемым разбросом. И здесь мы вновь видим отголоски центральной предельной теоремы, проявляющиеся в том, что распределение данных вокруг средних значений в гистограммах близко к нормальному. Однако, вблизи нуля разброс становится несимметричным и приближается к другому очень вероятному распределению – экспоненциальному. Этот пример хорошо показывает, что я имел в виду, говоря, что в статистике мы имеем дело со случайными значениями параметров случайной величины.

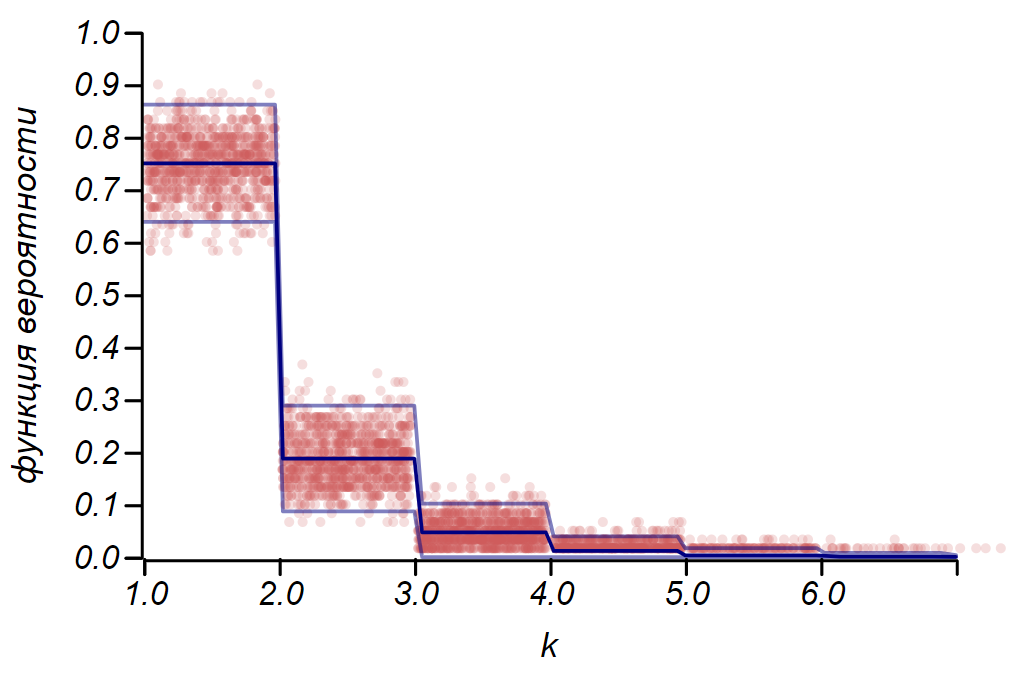
 Пример, показывающий соотношение оценки разброса, сделанной по правилу
Пример, показывающий соотношение оценки разброса, сделанной по правилу  и наблюдаемого разброса для трёх случайных величин.
и наблюдаемого разброса для трёх случайных величин.
Важно понимать, что правила и даже
и даже  не избавляют нас от ошибок. Они не гарантируют истинности какого-либо утверждения, не являются доказательствами. Статистика ограничивает степень недоверия к гипотезе, и не более того.
не избавляют нас от ошибок. Они не гарантируют истинности какого-либо утверждения, не являются доказательствами. Статистика ограничивает степень недоверия к гипотезе, и не более того.
Математик и автор прекрасного курса теории вероятностей Джиан-Карло Рота, на своих лекциях в MIT приводил такой пример. Представьте себе научный журнал, редакция которого приняла волевое решение: принимать к печати исключительно статьи с положительными результатами, которые удовлетворяют правилу или строже. При этом в редакционной колонке указано, что читатели могут быть уверены, что с вероятностью
или строже. При этом в редакционной колонке указано, что читатели могут быть уверены, что с вероятностью  читатель не встретит на страницах этого журнала неверный результат! Увы, это утверждение легко опровергнуть теми же рассуждениями, что привели нас к вопиющей несправедливости при тестировании водителей на алкоголь. Пусть
читатель не встретит на страницах этого журнала неверный результат! Увы, это утверждение легко опровергнуть теми же рассуждениями, что привели нас к вопиющей несправедливости при тестировании водителей на алкоголь. Пусть  исследователей, подвергнут опыту
исследователей, подвергнут опыту  гипотез, из которых верна лишь какая-то часть, скажем,
гипотез, из которых верна лишь какая-то часть, скажем,  . Исходя из смысла проверки гипотез, можно ожидать, что
. Исходя из смысла проверки гипотез, можно ожидать, что  из неверных гипотез ошибочно не будут отвергнуты, и войдут в журнал наряду с
из неверных гипотез ошибочно не будут отвергнуты, и войдут в журнал наряду с  верными результатами. Итого, из
верными результатами. Итого, из  результатов добрая треть окажется неверной!
результатов добрая треть окажется неверной!
Этот пример прекрасно демонстрирует наш отечественный закон подлости, который не вошёл пока в хрестоматии мерфологии, закон Черномырдина:
Легко получить общую оценку доли неверных результатов, которые войдут в выпуски журнала, при предположении, что доля верных гипотез равна и вероятность принятия ошибочной гипотезы равна
и вероятность принятия ошибочной гипотезы равна  :
:
 Оценка доли публикаций, содержащих заведомо неверные результаты при принятии различных критериев проверки гипотез. Видно, что принимать гипотезы по правилу
Оценка доли публикаций, содержащих заведомо неверные результаты при принятии различных критериев проверки гипотез. Видно, что принимать гипотезы по правилу  может быть рисковано, тогда как критерий
может быть рисковано, тогда как критерий  уже может считаться весьма сильным.
уже может считаться весьма сильным.
Конечно, мы не знаем этого , и не узнаем никогда, но оно заведомо меньше единицы, а значит, в любом случае, утверждение из редакционной колонки нельзя принимать всерьёз. Можно ограничить себя жёсткими рамками критерия
, и не узнаем никогда, но оно заведомо меньше единицы, а значит, в любом случае, утверждение из редакционной колонки нельзя принимать всерьёз. Можно ограничить себя жёсткими рамками критерия  , но он требует очень большого числа испытаний. Значит, надо увеличивать долю верных гипотез во множестве возможных предположений. На это и направлены стандартные подходы научного метода познания – логическая непротиворечивость гипотез, их согласованность с фактами и теориями, доказавшими свою применимость, опора на математические модели и критическое мышление.
, но он требует очень большого числа испытаний. Значит, надо увеличивать долю верных гипотез во множестве возможных предположений. На это и направлены стандартные подходы научного метода познания – логическая непротиворечивость гипотез, их согласованность с фактами и теориями, доказавшими свою применимость, опора на математические модели и критическое мышление.
В начале главы мы говорили о том, что выходные и непогода совпадают чаще, чем хотелось бы. Давайте постараемся завершить это исследование. Каждый дождливый день можно рассматривать как наблюдение случайной величины — дня недели, подчиняющегося распределению Бернулли с вероятностью . Примем в качестве нулевой гипотезы предположение, что все дни недели одинаковы с точки зрения погоды и дождь может пойти в любой из них равновероятно. Выходных у нас два, итого, получаем ожидаемую вероятность совпадения непогожего дня и выходного равной
. Примем в качестве нулевой гипотезы предположение, что все дни недели одинаковы с точки зрения погоды и дождь может пойти в любой из них равновероятно. Выходных у нас два, итого, получаем ожидаемую вероятность совпадения непогожего дня и выходного равной  , эта величина будет параметром распределения Бернулли. Как часто идёт дождь? В разное время года по-разному, конечно, но в Петропавловске-Камчатском, в среднем, наблюдается девяносто дождливых или снежных дней в году. Так что поток дней с осадками имеет интенсивность около
, эта величина будет параметром распределения Бернулли. Как часто идёт дождь? В разное время года по-разному, конечно, но в Петропавловске-Камчатском, в среднем, наблюдается девяносто дождливых или снежных дней в году. Так что поток дней с осадками имеет интенсивность около  . Давайте посчитаем, какое количество дождливых выходных мы должны зарегистрировать, для того, чтобы быть уверенным в том, что существует некоторая закономерность. Результаты приведены в таблице.
. Давайте посчитаем, какое количество дождливых выходных мы должны зарегистрировать, для того, чтобы быть уверенным в том, что существует некоторая закономерность. Результаты приведены в таблице.
О чем говорят эти цифры? Если вам кажется, что который год подряд «лета не было», что злой рок преследует ваши выходные, насылая на них дождь, это можно проверить и подтвердить. Однако в течение лета уличить злой рок можно лишь если больше двух пятых всех выходных окажутся дождливыми. Нулевая же гипотеза предполагает, что только четверть выходных должна совпасть с ненастной погодой. За пять лет наблюдений уже можно надеяться подметить тонкие отклонения, выходящие за пределы и, при необходимости, приступать к их объяснению.
и, при необходимости, приступать к их объяснению.
Я воспользовался школьным дневником погоды, который велся с 2014 по 2018 год, и выяснил, что за эти пять лет случилось ненастных дней из них
ненастных дней из них  пришлись на выходные. Это, действительно, больше ожидаемого числа на
пришлись на выходные. Это, действительно, больше ожидаемого числа на  дней, но значимые отклонения начинаются с
дней, но значимые отклонения начинаются с  дней, так что это, как мы говорили в детстве: «не считается». Вот как выглядит ряд данных и гистограмма, показывающая распределение непогоды по дням недели. Горизонтальными линиями на гистограмме отмечен интервал в котором может наблюдаться случайное отклонение от равномерного распределения при том же объёме данных.
дней, так что это, как мы говорили в детстве: «не считается». Вот как выглядит ряд данных и гистограмма, показывающая распределение непогоды по дням недели. Горизонтальными линиями на гистограмме отмечен интервал в котором может наблюдаться случайное отклонение от равномерного распределения при том же объёме данных.


Исходный ряд данных и распределение непогожих дней по дням недели, полученные за пять лет наблюдений.
Видно, что начиная с пятницы, действительно, наблюдается увеличение числа дней с плохой погодой. Но для поиска причины этому росту предпосылок недостаточно: такой же результат можно получать, просто перебирая случайные числа. Вывод: за пять лет наблюдения за погодой, я накопил почти две тысячи записей, но ничего нового о распределении погоды по дням недели не узнал.
При взгляде на записи в дневнике явно бросается в глаза, что непогода приходит не по одиночке, а двух-трёхдневными периодами или даже недельными циклонами. Это как-то влияет на результат? Можно попробовать принять это наблюдение во внимание, и предположить, что дожди идут в среднем по два дня (на самом деле, дней), тогда вероятность перекрыть выходные увеличивается до
дней), тогда вероятность перекрыть выходные увеличивается до  . При такой вероятности, ожидаемое число совпадений для пяти лет должно составить
. При такой вероятности, ожидаемое число совпадений для пяти лет должно составить  , то есть от
, то есть от  до
до  раз. Наблюдённая величина
раз. Наблюдённая величина  не входит в этот диапазон и значит, гипотезу об эффекте сдвоенных дней непогоды можно смело отвергать. Узнали ли мы что-то новое? Да, узнали: казалось бы, очевидная особенность процесса не влечёт за собой никакого эффекта. Об этом стоит поразмыслить, и мы это сделаем чуть позже. Но главный вывод: какие-то более тонкие эффекты рассматривать нет резона, поскольку наблюдения и, что самое главное, их количество, согласованно говорят в пользу самого простого объяснения.
не входит в этот диапазон и значит, гипотезу об эффекте сдвоенных дней непогоды можно смело отвергать. Узнали ли мы что-то новое? Да, узнали: казалось бы, очевидная особенность процесса не влечёт за собой никакого эффекта. Об этом стоит поразмыслить, и мы это сделаем чуть позже. Но главный вывод: какие-то более тонкие эффекты рассматривать нет резона, поскольку наблюдения и, что самое главное, их количество, согласованно говорят в пользу самого простого объяснения.
Но недовольство у нас вызывает не пятилетняя и даже не годовая статистика, человеческая память не столь долгая. Обидно, когда дождь идёт на выходных три или четыре раза подряд! Как часто это может наблюдаться? Особенно, если вспомнить, что гадкая погода не приходит в одиночку. Задачу можно сформулировать так: «Какова вероятность того, что выходных подряд окажутся дождливыми?» Разумно предположить, что непогожие дни образуют пуассоновский поток с интенсивностью
выходных подряд окажутся дождливыми?» Разумно предположить, что непогожие дни образуют пуассоновский поток с интенсивностью  . Это значит, что в среднем, четверть дней любого периода будет непогожей. Наблюдая только за выходными, мы не должны изменить интенсивность потока и из всех выходных непогожие должны составить, в среднем, тоже четверть. Итак, выдвигаем нулевую гипотезу: поток ненастья пуассоновский, с известным параметром, а значит, интервалы между пуассоновскими событиями описываются экспоненциальным распределением. Нас интересуют дискретные интервалы:
. Это значит, что в среднем, четверть дней любого периода будет непогожей. Наблюдая только за выходными, мы не должны изменить интенсивность потока и из всех выходных непогожие должны составить, в среднем, тоже четверть. Итак, выдвигаем нулевую гипотезу: поток ненастья пуассоновский, с известным параметром, а значит, интервалы между пуассоновскими событиями описываются экспоненциальным распределением. Нас интересуют дискретные интервалы:  дня и т. д. поэтому мы можем воспользоваться дискретным аналогом экспоненциального распределения — геометрическим распределением с параметром
дня и т. д. поэтому мы можем воспользоваться дискретным аналогом экспоненциального распределения — геометрическим распределением с параметром  . На рисунке показано, что у нас получилось и видно, что предположение о том, что мы наблюдаем пуассоновский процесс нет резона отвергать.
. На рисунке показано, что у нас получилось и видно, что предположение о том, что мы наблюдаем пуассоновский процесс нет резона отвергать.

Наблюдаемое распределение длины цепочек неудавшихся выходных и теоретическое. Тонкой линией показаны допустимые отклонения при том количестве наблюдений, что мы имеем.
Можно задаться, таким вопросом: сколько лет нужно вести наблюдения, для того, чтобы замеченную нами разницу в дней можно было бы уверенно подтвердить или отвергнуть, как случайное отклонение? Это легко посчитать: наблюдаемая вероятность
дней можно было бы уверенно подтвердить или отвергнуть, как случайное отклонение? Это легко посчитать: наблюдаемая вероятность  отличается от ожидаемой
отличается от ожидаемой  на
на  . Для фиксирования различия в сотых, требуется абсолютная погрешность, не превышающая
. Для фиксирования различия в сотых, требуется абсолютная погрешность, не превышающая  , что составляет
, что составляет  от измеряемой величины. Отсюда получаем, необходимый объём выборки
от измеряемой величины. Отсюда получаем, необходимый объём выборки  дождливых дней. Это потребует около
дождливых дней. Это потребует около  лет непрерывных метеорологических наблюдений, ведь только каждый четвёртый день идёт дождь или снег. Увы, это больше чем время, которое Камчатка находится в составе России, так что шансов выяснить, как обстоят дела «на самом деле» у меня нет. Особенно, если принять во внимание, что за это время климат успел измениться разительно — из Малого ледникового периода природа выходила в очередной оптимум.
лет непрерывных метеорологических наблюдений, ведь только каждый четвёртый день идёт дождь или снег. Увы, это больше чем время, которое Камчатка находится в составе России, так что шансов выяснить, как обстоят дела «на самом деле» у меня нет. Особенно, если принять во внимание, что за это время климат успел измениться разительно — из Малого ледникового периода природа выходила в очередной оптимум.
Так как же австралийским исследователям удалось зафиксировать отклонение температуры в доли градуса и почему имеет смысл рассматривать это исследование? Дело в том, что ими использовались часовые данные температуры, которые не были «прорежены» каким-либо случайным процессом. Таким образом, за лет метеонаблюдений удалось накопить более четверти миллиона отсчётов, что позволяет уменьшить стандартное отклонение среднего в
лет метеонаблюдений удалось накопить более четверти миллиона отсчётов, что позволяет уменьшить стандартное отклонение среднего в  раз по отношению к стандартному суточному отклонению температуры. Этого вполне достаточно, чтобы говорить о точности в десятые доли градуса. Кроме того, авторы использовали ещё один красивый метод, подтверждающий наличие временного цикла: случайное перемешивание временного ряда. Такое перемешивание сохраняет статистические свойства, такие как интенсивность потока, однако «стирает» временные закономерности, делая процесс истинно пуассоновским. Сравнение множества синтетических рядов и экспериментального позволяет убедиться в том, что замеченные отклонения процесса от пуассоновского значимы. Таким же образом сейсмологом А. А. Гусевым было показано, что землетрясения в каком-либо районе, образуют своеобразный самоподобный поток со свойствами кластеризации. Это означает, что землетрясения имеют обыкновение группироваться во времени, образуя весьма неприятные уплотнения потока. Позже выяснилось, что последовательность крупных вулканических извержений обладает таким же свойством.
раз по отношению к стандартному суточному отклонению температуры. Этого вполне достаточно, чтобы говорить о точности в десятые доли градуса. Кроме того, авторы использовали ещё один красивый метод, подтверждающий наличие временного цикла: случайное перемешивание временного ряда. Такое перемешивание сохраняет статистические свойства, такие как интенсивность потока, однако «стирает» временные закономерности, делая процесс истинно пуассоновским. Сравнение множества синтетических рядов и экспериментального позволяет убедиться в том, что замеченные отклонения процесса от пуассоновского значимы. Таким же образом сейсмологом А. А. Гусевым было показано, что землетрясения в каком-либо районе, образуют своеобразный самоподобный поток со свойствами кластеризации. Это означает, что землетрясения имеют обыкновение группироваться во времени, образуя весьма неприятные уплотнения потока. Позже выяснилось, что последовательность крупных вулканических извержений обладает таким же свойством.
Конечно же, погоду, как и землетрясения, нельзя описывать пуассоновским процессом — это динамические процессы, в которых текущее состояние является функцией предыдущих. Почему же наши наблюдения за погодой на выходных говорят в пользу простой стохастической модели? Дело в том, что мы отображаем закономерный процесс формирования осадков на множество из семи дней, или, говоря на языке математики, на систему вычетов по модулю семь. Этот процесс проекции способен порождать хаос из вполне упорядоченных рядов данных. Отсюда, к примеру, происходит видимая случайность в последовательности цифр десятичной записи большинства вещественных чисел.
Мы уже говорили о рациональных числах, тех, которые выражаются целочисленными дробями. Они имеют внутреннюю структуру, которая определяется двумя числами: числителем и знаменателем. Но при записи в десятичной форме можно наблюдать скачки от регулярности в представлении таких чисел, как , или
, или  до периодичного повторения, уже вполне беспорядочных последовательностей в таких числах как
до периодичного повторения, уже вполне беспорядочных последовательностей в таких числах как  . Иррациональные числа не имеют конечной или периодической записи в десятичной форме и в этом случае в последовательности цифр, чаще всего, царит хаос. Но это не значит, что в этих числах нет порядка! Например, первое встретившееся математикам иррациональное число
. Иррациональные числа не имеют конечной или периодической записи в десятичной форме и в этом случае в последовательности цифр, чаще всего, царит хаос. Но это не значит, что в этих числах нет порядка! Например, первое встретившееся математикам иррациональное число  в десятичной записи порождает хаотический набор цифр. Однако, с другой стороны, это число можно представить в виде бесконечной цепной дроби:
в десятичной записи порождает хаотический набор цифр. Однако, с другой стороны, это число можно представить в виде бесконечной цепной дроби:
Цепные дроби с повторяющимися коэффициентами записывают коротко, подобно периодическим десятичным дробям, например:![$\sqrt{2}=[1,\bar{2}]$](https://habrastorage.org/getpro/habr/formulas/1cc/2a9/46a/1cc2a946a36da254a3ea48722766a2dd.svg) ,
, ![$\sqrt{3}=[1,\overline{1,2}]$](https://habrastorage.org/getpro/habr/formulas/fd8/bbd/268/fd8bbd26870af7fa22d050c8eec3d162.svg) . Знаменитое золотое сечение в этом смысле представляет собой самое просто устроенное иррациональное число:
. Знаменитое золотое сечение в этом смысле представляет собой самое просто устроенное иррациональное число: ![$\varphi = [1,\bar{1}]$](https://habrastorage.org/getpro/habr/formulas/85e/85e/c93/85e85ec93313767dd395cbd64f29ef59.svg) . Все рациональные числа представляются в виде конечных цепных дробей, часть иррациональных — в виде бесконечных, но периодических, их называют алгебраическими, те же, что не имеют конечной записи даже в такой форме — трансцендентными. Самое знаменитое из трансцендентных — число
. Все рациональные числа представляются в виде конечных цепных дробей, часть иррациональных — в виде бесконечных, но периодических, их называют алгебраическими, те же, что не имеют конечной записи даже в такой форме — трансцендентными. Самое знаменитое из трансцендентных — число  , оно порождает хаос как в десятичной записи, так и в виде цепной дроби:
, оно порождает хаос как в десятичной записи, так и в виде цепной дроби: ![$\pi \approx [3, 7,15,1,292,1,1,1,2,1,3,1,14,2,1 , … ]$](https://habrastorage.org/getpro/habr/formulas/882/c53/2e9/882c532e9f2854d3a0292f7d027a1835.svg) . А вот число Эйлера
. А вот число Эйлера  , оставаясь трансцендентным, в форме цепной дроби проявляет внутреннюю структуру, скрытую в десятичной записи:
, оставаясь трансцендентным, в форме цепной дроби проявляет внутреннюю структуру, скрытую в десятичной записи: ![$e\approx[2,1,2,1,1,4,1,1,6,1,1,8,1,1,10 , … ]$](https://habrastorage.org/getpro/habr/formulas/35b/3ed/66e/35b3ed66e0f74a28cf36165bc2a84935.svg) .
.
Наверное, не один математик, начиная с Пифагора, подозревал мир в коварстве, обнаруживая, что такое нужное, такое фундаментальное число имеет столь неуловимо сложную хаотическую структуру. Конечно, его можно представить в виде сумм вполне изящных числовых рядов но эти ряды напрямую не говорят о природе этого числа и они не универсальны. Я верю, что математикам будущего откроется какое-нибудь новое представление чисел, столь же универсальное, как цепные дроби, которое позволит выявить строгий порядок, скрытых природой в числе.
имеет столь неуловимо сложную хаотическую структуру. Конечно, его можно представить в виде сумм вполне изящных числовых рядов но эти ряды напрямую не говорят о природе этого числа и они не универсальны. Я верю, что математикам будущего откроется какое-нибудь новое представление чисел, столь же универсальное, как цепные дроби, которое позволит выявить строгий порядок, скрытых природой в числе.
Результаты этой главы, по большей части, отрицательные. И как автор, желающий удивить читателя скрытыми закономерностями и неожиданными открытиями, я сомневался, стоит ли включать её в книжку. Но наш разговор о погоде ушёл в очень важную тему – о ценности и осмысленности естественнонаучного подхода.
Одна мудрая девочка, Соня Шаталова, глядя на мир сквозь призму аутизма, в десятилетнем возрасте дала очень лаконичное и точное определение: «Наука – это система знаний, основанных на сомнении». Реальный мир зыбок и норовит спрятаться за сложностью, видимой случайностью и ненадёжностью измерений. Сомнение в естественных науках неизбежно. Математика представляется царством определённости, в котором, кажется, можно забыть о сомнении. И очень заманчиво спрятаться за стенами этого царства; рассматривать вместо труднопознаваемого мира модели, которые можно исследовать досконально; считать и вычислять, благо формулы готовы переварить что угодно. Но всё же, математика является наукой и сомнение в ней – это глубокая внутренняя честность, не дающая покоя до тех пор, пока математическое построение не очистится от дополнительных предположений и лишних гипотез. В царстве математики говорят на сложном, но стройном языке, пригодном для рассуждений о реальном мире. Очень важно хоть немного познакомиться с этим языком, чтобы не давать цифрам выдавать себя за статистику, не позволять фактам притворяться знанием, а невежеству и манипуляциям противопоставлять настоящую науку.
Опубликованные главы:
• Введение в мерфологию
• Случайности случайны?
• Головокружительный полёт бутерброда с маслом
• Статистика, как научный способ чего-либо не знать
• Закон арбузной корки и нормальность ненормальности
• Закон зебры и чужой очереди
• Проклятие режиссёра и проклятые принтеры
• Термодинамика классового неравенства
• Случайности случайны?
• Головокружительный полёт бутерброда с маслом
• Статистика, как научный способ чего-либо не знать
• Закон арбузной корки и нормальность ненормальности
• Закон зебры и чужой очереди
• Проклятие режиссёра и проклятые принтеры
• Термодинамика классового неравенства
Речь в этой главе пойдёт о статистике, о погоде и даже о философии. Не пугайтесь, совсем чуть-чуть. Не более того, что можно использовать для tabletalk в приличном обществе.

Цифры обманчивы, особенно когда я сам ими занимаюсь; по этому поводу справедливо высказывание, приписываемое Дизраэли: «Существует три вида лжи: ложь, наглая ложь и статистика».
Марк Твен
Как часто летом мы планируем на свои выходные дни выезд на природу, прогулку в парке или пикник, а потом дождь разбивает наши планы, заточая нас в доме! И ладно бы это случалось раз или два за сезон, порою складывается впечатление, что непогода преследует именно выходные дни, раз за разом попадая на субботу или воскресенье!
Сравнительно недавно вышла статья австралийских исследователей: «Недельные циклы пиковой температуры и интенсивность городских тепловых островов». Её подхватили новостные издания и перепечатали результаты с таким заголовком: «Вам не кажется! Учёные выяснили: погода на выходных, действительно хуже, чем в будние дни». В цитируемой работе приводится статистика температуры и осадков за много лет в нескольких городах Австралии, и вправду, выявляющая понижение температуры на в определённые часы субботы и воскресенья. После чего этому даётся объяснение, связывающее локальную погоду с уровнем загрязнённости воздуха из-за возрастающего транспортного потока. Незадолго до этого, подобное исследование проводилось в Германии и привело примерно к тем же выводам.
Согласитесь, доли градуса — это весьма тонкий эффект. Сетуя на непогоду в долгожданную субботу, мы обсуждаем, был ли день солнечным или дождливым, это обстоятельство проще зарегистрировать, а позже вспомнить, даже не обладая точными приборами. Мы проведём собственное небольшое исследование на эту тему и получим замечательный результат: можно уверенно утверждать, что мы не знаем, связаны ли на Камчатке, день недели и непогода. Исследования с отрицательным результатом обычно не попадают на страницы журналов и в новостные ленты, но нам с вами важно понять, на каком основании я, вообще, могу что-то уверенно заявлять о случайных процессах. И в этом плане отрицательный результат становится ничуть не хуже положительного.
Слово в защиту статистики
Статистику обвиняют в массе грехов: и во лжи и в возможностях манипуляций и, наконец, в непонятности. Но мне очень хочется реабилитировать эту область знаний, показать, насколько сложна задача, для которой она предназначена и сколь непросто бывает понять ответ, который даёт статистика.
Теория вероятностей оперирует точными знаниями о случайных величинах в виде распределений или исчерпывающих комбинаторных подсчётов. Ещё раз подчеркну, что располагать точным знанием о случайной величине возможно. Но что если это точное знание нам недоступно, а единственное чем мы располагаем — это наблюдения? У разработчика нового лекарства есть какое-то ограниченное число испытаний, у создателя системы управления транспортным потоком — лишь ряд измерений на реальной дороге, у социолога – результаты опросов, причём, он может быть уверен в том, что отвечая на какие-то вопросы, респонденты попросту соврали.
Понятно, что одно наблюдение не даёт ровным счётом ничего. Два – немногим больше, чем ничего, три, четыре… сто… сколько нужно наблюдений чтобы получить какое-либо знание о случайной величине, в котором можно было бы быть уверенным с математической точностью? И что это будет за знание? Скорее всего, оно будет представлено в виде таблицы или гистограммы, дающей возможность оценить некоторые параметры случайной величины, их называют статистиками (например, область определения, среднее или дисперсия, асимметричность и т.д.). Быть может, глядя на гистограмму удастся угадать точную форму распределения. Но внимание! — все результаты наблюдений сами будут случайными величинами! Пока мы не владеем точным знанием о распределении, все результаты наблюдений дают нам лишь вероятностное описание случайного процесса! Случайное описание случайного процесса — ещё бы здесь не запутаться, а то и захотеть запутать намеренно!
Что же делает математическую статистику точной наукой? Её методы позволяют заключить наше незнание в чётко ограниченные рамки и дать вычислимую меру уверенности в том, что в этих рамках наше знание согласуется с фактами. Это язык, на котором можно рассуждать о неизвестных случайных величинах так, чтобы рассуждения имели смысл. Такой подход очень полезен в философии, психологии или социологии, где очень легко пуститься в пространные рассуждения и дискуссии без всякой надежды на получение позитивного знания и, тем более, на доказательство. Грамотной статистической обработке данных посвящена масса литературы, ведь это абсолютно необходимый инструмент для медиков, социологов, экономистов, физиков, психологов… словом, для всех научно исследующих так называемый «реальный мир», отличающийся от идеального математического лишь степенью нашего незнания о нём.
Теперь ещё раз взгляните на эпиграф к этой главе и осознайте, что статистика, которую так пренебрежительно называют третьей степенью лжи, это единственное, чем располагают естественные науки. Это ли не главный закон подлости мироздания! Все известные нам законы природы, от физических до экономических, строятся на математических моделях и их свойствах, но поверяются они статистическими методами в ходе измерений и наблюдений. В повседневности наш разум делает обобщения и подмечает закономерности, выделяет и распознаёт повторяющиеся образы, это, наверное, лучшее, что умеет человеческий мозг. Это именно то, чему в наши дни учат искусственный интеллект. Но разум экономит свои силы и склонен делать выводы по единичным наблюдениям, не сильно беспокоясь о точности или обоснованности этих выводов. По этому поводу есть замечательное самосогласованное утверждение из книги Стивена Браста «Исола»: «Все делают общие выводы из одного примера. По крайней мере, я делаю именно так». И пока речь идёт об искусстве, характере домашних любимцев или обсуждении политики, об этом можно сильно не беспокоиться. Однако при строительстве самолёта, организации диспетческой службы аэропорта или тестировании нового лекарства, уже нельзя сослаться на то, что «мне так кажется», «интуиция подсказывает» и «в жизни всякое бывает». Тут приходится ограничивать свой разум рамками строгих математических методов.
Наша книжка не учебник, и мы не будем детально изучать статистические методы и ограничимся лишь одним — техникой проверкой гипотез. Но мне хотелось бы показать ход рассуждений и форму результатов, характерных для этой области знания. И, возможно, кому-то из читателей, будущему студенту, не только станет понятно зачем его мучают матстатистикой, всеми этими QQ-диаграммами, t- и F-распределениями, но придёт в голову другой важный вопрос: а как вообще это возможно знать что-нибудь наверняка о случайном явлении? И что именно мы узнаём, используя статистические данные?
Три кита статистики
Основными столпами математической статистики являются теория вероятностей, Закон больших чисел и центральная предельная теорема.
Закон больших чисел, в вольной трактовке, говорит о том, что большое число наблюдений случайной величины почти наверняка отражает её распределение, так что наблюдаемые статистики: среднее, дисперсия и прочие характеристики, стремятся к точным значениям, соответствующим случайной величине. Иными словами, гистограмма наблюдаемых величин при бесконечном числе данных, почти наверняка стремится к тому распределению, которое мы можем считать истинным. Именно этот закон связывает «бытовое» частотное толкование вероятности и теоретическое, как меры на вероятностном пространстве.
Центральная предельная теорема, опять же, в вольной трактовке, говорит, что одной из наиболее вероятных форм распределения случайной величины является нормальное (гауссово) распределение. Точная формулировка звучит иначе: среднее значение большого числа идентично распределённых вещественных случайных величин, вне зависимости от их распределения, описывается нормальным распределением. Эту теорему обычно доказывают, применяя методы функционального анализа, но мы увидим позже, что её можно понять и даже расширить, введя понятие энтропии, как меры вероятности состояния системы: нормальное распределение имеет наибольшую энтропию при наименьшем числе ограничений. В этом смысле, оно оптимально при описании неизвестной случайной величины, либо случайной величины, являющейся совокупностью многих других величин, распределение которых тоже неизвестно.
Эти два закона лежат в основе количественных оценок достоверности наших знаний, основанных на наблюдениях. Здесь речь идёт о статистическом подтверждении или опровержении предположения, которое можно сделать из каких-то общих оснований и математической модели. Это может показаться странным, но сама по себе, статистика не производит новых знаний. Набор фактов превращается в знание лишь после построения связей между фактами, образующих определённую структуру. Именно эти структуры и связи позволяют делать предсказания и выдвигать общие предположения, основанные на чём-то, выходящем за пределы статистики. Такие предположения называются гипотезами. Самое время вспомнить один из законов мерфологии, постулат Персига:
Число разумных гипотез, объясняющих любое данное явление, бесконечно.
Задача математической статистики ограничить это бесконечное число, а вернее свести их к одной, причём вовсе не обязательно верной. Для перехода к более сложной (и часто, более желанной) гипотезе, необходимо, используя данные наблюдений, опровергнуть более простую и общую гипотезу, либо подкрепить её и отказаться от дальнейшего развития теории. Часто проверяемую таким образом гипотезу называют нулевой, и в этом есть глубокий смысл.
Что может выступить в роли нулевой гипотезы? В определённом смысле, все что угодно, любое утверждение, но при условии, что его удастся перевести на язык измерения. Чаще всего, гипотезой служит ожидаемое значение какого-то параметра, который превращается в случайную величину в ходе измерения, либо отсутствие связи (корреляции) между двумя случайными величинами. Иногда предполагается вид распределения, случайного процесса, предлагается какая-то математическая модель. Классическая постановка вопроса при этом такова: позволяют ли наблюдения отвергнуть нулевую гипотезу или нет? Точнее, с какой долей уверенности мы можем утверждать, что наблюдения нельзя получить, исходя из нулевой гипотезы? При этом, если мы не смогли опираясь на статистические данные доказать, что нулевая гипотеза ложна, то она принимается истинной.
И тут можно подумать, что исследователи вынуждены совершать одну из классических логических ошибок, которая носит звучное латинское имя ad ignorantiam. Это аргументация истинности некоторого утверждения, основанная на отсутствии доказательства его ложности. Классический пример — слова, сказанные сенатором Джозефом Маккарти, когда его попросили предъявить факты для поддержки выдвинутого им обвинения, что некий человек является коммунистом: «У меня немного информации по этому вопросу, за исключением того общего заявления компетентных органов, что в его досье нет ничего, чтобы исключало его связи с коммунистами». Или ещё ярче: «Снежный человек существует, поскольку никто не доказал обратного». Выявление разницы между научной гипотезой и подобными уловками составляет предмет целой области философии: методологии научного познания. Одним из её ярких результатов является критерий фальсифицируемости, выдвинутый замечательным философом Карлом Поппером в первой половине XX века. Этот критерий призван разделять научное знание от ненаучного, и, на первый взгляд, он кажется парадоксальным:
Теория или гипотеза может считаться научной, только если существует, пусть даже гипотетически, способ её опровергнуть.
Чем не закон подлости! Получается, что любая научная теория автоматически потенциально неверна, а теория, верная «по определению», не может считаться научной. Более того, этому критерию не удовлетворяют такие науки как математика и логика. Впрочем, их относят не к естественным наукам, а к формальным, не требующим проверки на фальсифицируемость. А если к этому добавить ещё один результат того же времени: принцип неполноты Гёделя, утверждающий, что в рамках любой формальной системы можно сформулировать утверждение, которое невозможно ни доказать, ни опровергнуть, то может стать непонятно зачем, вообще, заниматься всей этой наукой. Однако важно понимать, что принцип фальсифицируемости Поппера ничего не говорит об истинности теории, а только о том является она научной или нет. Он может помочь определить, даёт ли некая теория язык, на котором имеет смысл рассуждать о мире или нет.
Но всё же, почему, если мы не можем на базе статистических данных отвергнуть гипотезу, мы в праве принять её истинной? Дело в том, что статистическая гипотеза берётся не из желания исследователя или его предпочтений, она должна вытекать из каких-либо общих формальных законов. Например, из Центральной предельной теоремы, либо из принципа максимальной энтропии. Эти законы корректно отражают степень нашего незнания, не добавляя, без необходимости, лишних предположений или гипотез. В известном смысле, это прямое использование знаменитого философского принципа, известного как бритва Оккама:
Что может быть сделано на основе меньшего числа предположений, не следует делать, исходя из большего.
Таким образом, когда мы принимаем нулевую гипотезу, основываясь на отсутствии её опровержения, мы формально и честно показываем, что в результате эксперимента степень нашего незнания осталась на прежнем уровне. В примере же со снежным человеком, явно или неявно, но предполагается обратное: отсутствие доказательств того, что этой загадочной твари не существует представляется чем-то, что может увеличить степень нашего знания о ней.
Вообще, с точки зрения принципа фальсифицируемости, любое утверждение о существовании чего-либо ненаучно, ибо отсутствие свидетельства ничего не доказывает. В тоже время, утверждение об отсутствии чего-либо можно легко опровергнуть предоставив экземпляр, косвенное свидетельство, либо доказав существование по построению. И в этом смысле, статистическая проверка гипотез анализирует утверждения об отсутствии искомого эффекта и может предоставить в известном смысле, точное опровержение этого утверждения. Именно этим в полной мере оправдывается термин «нулевая гипотеза»: она содержит необходимый минимум знаний о системе.
Как запутать статистикой и как распутаться
Очень важно подчеркнуть, что если статистические данные говорят о том, что нулевая гипотеза может быть отвергнута, то это не значит, что мы тем самым доказали истинность какой-либо альтернативной гипотезы. Статистику не следует путать с логикой, в этом кроется масса трудноуловимых ошибок, особенно, когда в дело вступают условные вероятности для зависимых событий. Например: очень маловероятно, что человек может быть Папой Римским (
Здесь мы столкнулись с зависимыми событиями. Помните, в колмогоровском определении вероятности говорилось о способе сложения вероятности объединения событий: вероятность объединения двух событий равна сумме их вероятностей за вычетом вероятности их пересечения. Однако о том, как вычисляется вероятность пересечение событий, эти определения не говорят. Для этого вводится новое понятие: условная вероятность и на передний план выходит зависимость событий друг от друга.
Вероятность пересечения событий A и B определяется как произведение вероятности события B и вероятности события
Тем самым мы завершаем формальное определение вероятности, начатое в первой главе.
Пересечение — операция коммутативная, то есть
В нашем примере с водителями и тестом на алкоголь мы имеем cобытия:
Эти примеры тщательно разбираются студентами, изучающими медицинские тесты, или юридические практики. Но, боюсь, что журналистам или политикам не преподают ни математическую статистику ни теорию вероятностей, зато они охотно апеллируют к статистическим данным, вольно интерпретируют их и несут полученное «знание» в массы. Поэтому я призываю своего читателя: разобрался в математике сам, помоги разобраться другому! Другого противоядия невежеству я не вижу.
Измеряем нашу доверчивость
Мы рассмотрим и применим на практике только одно из множества статистических методик: проверку статистических гипотез. Для тех, кто уже связал свою жизнь с естественными или социальными науками в этих примерах не будет чего-то ошеломительно нового.
Предположим, что мы многократно измеряем случайную величину, имеющую среднее значение
1. Минимальное число испытаний
2. Пусть нулевой гипотезой будет предположение, что наблюдаемое среднее значение равно
Если заменить в этих правилах
Для нас полезным будет рассмотреть приложение этих правил к распределению Бернулли, описывающему случайную величину, которая принимает ровно два значения, условно называемые «успех» и «неудача», с заданной вероятностью успеха
Правило
Важно понимать, что правила
Математик и автор прекрасного курса теории вероятностей Джиан-Карло Рота, на своих лекциях в MIT приводил такой пример. Представьте себе научный журнал, редакция которого приняла волевое решение: принимать к печати исключительно статьи с положительными результатами, которые удовлетворяют правилу
Этот пример прекрасно демонстрирует наш отечественный закон подлости, который не вошёл пока в хрестоматии мерфологии, закон Черномырдина:
Хотели как лучше, а получилось, как всегда.
Легко получить общую оценку доли неверных результатов, которые войдут в выпуски журнала, при предположении, что доля верных гипотез равна
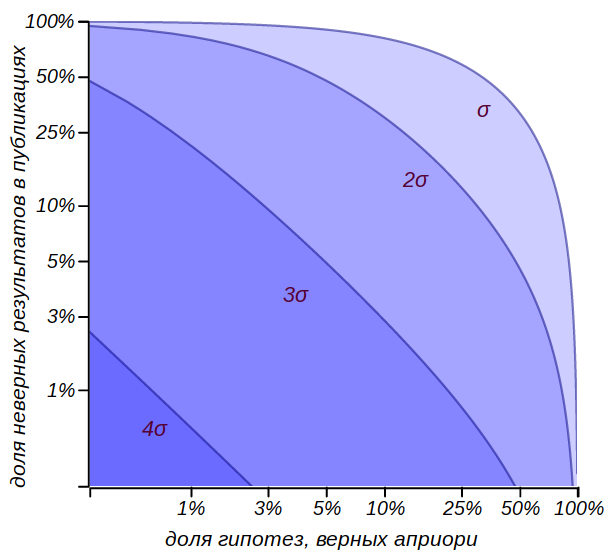
Конечно, мы не знаем этого
И снова о погоде
В начале главы мы говорили о том, что выходные и непогода совпадают чаще, чем хотелось бы. Давайте постараемся завершить это исследование. Каждый дождливый день можно рассматривать как наблюдение случайной величины — дня недели, подчиняющегося распределению Бернулли с вероятностью
| Период наблюдений | лето | год | |
|---|---|---|---|
| Ожидаемое число наблюдений | |||
| Ожидаемое число положительных исходов | |||
| Значимое отклонение | |||
| Значимая доля непогожих в общем числе выходных дней |
О чем говорят эти цифры? Если вам кажется, что который год подряд «лета не было», что злой рок преследует ваши выходные, насылая на них дождь, это можно проверить и подтвердить. Однако в течение лета уличить злой рок можно лишь если больше двух пятых всех выходных окажутся дождливыми. Нулевая же гипотеза предполагает, что только четверть выходных должна совпасть с ненастной погодой. За пять лет наблюдений уже можно надеяться подметить тонкие отклонения, выходящие за пределы
Я воспользовался школьным дневником погоды, который велся с 2014 по 2018 год, и выяснил, что за эти пять лет случилось
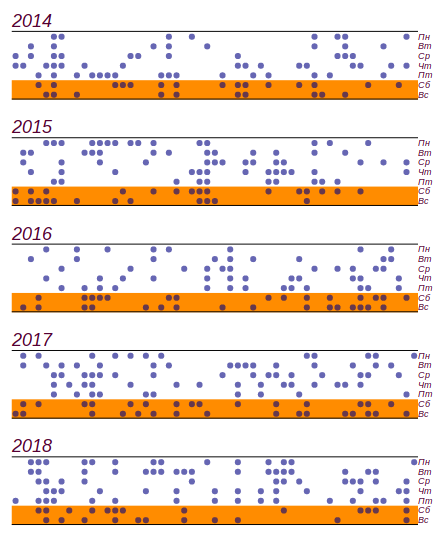
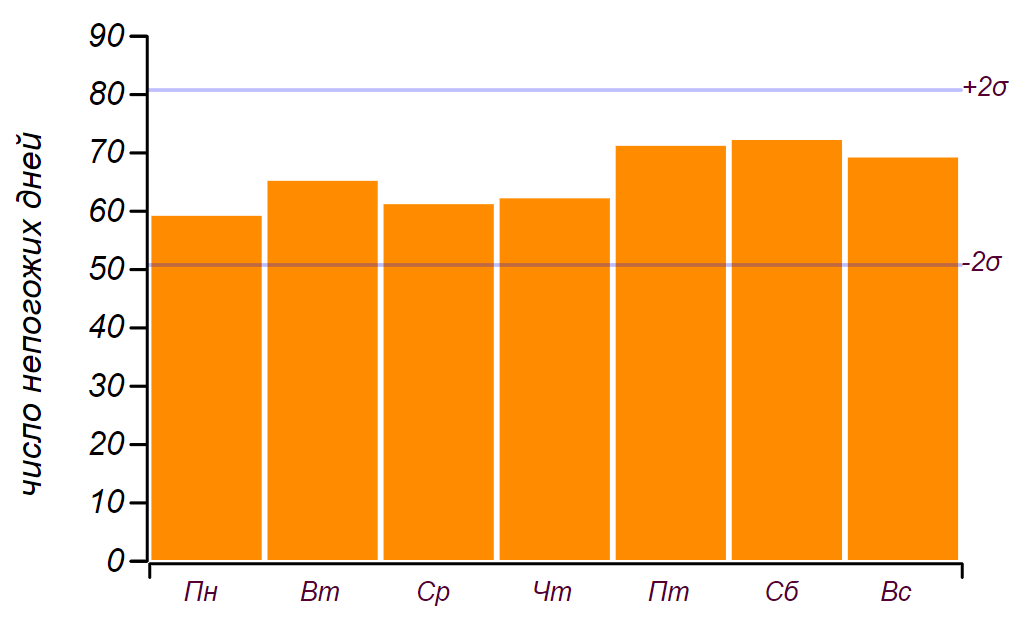
Исходный ряд данных и распределение непогожих дней по дням недели, полученные за пять лет наблюдений.
Видно, что начиная с пятницы, действительно, наблюдается увеличение числа дней с плохой погодой. Но для поиска причины этому росту предпосылок недостаточно: такой же результат можно получать, просто перебирая случайные числа. Вывод: за пять лет наблюдения за погодой, я накопил почти две тысячи записей, но ничего нового о распределении погоды по дням недели не узнал.
При взгляде на записи в дневнике явно бросается в глаза, что непогода приходит не по одиночке, а двух-трёхдневными периодами или даже недельными циклонами. Это как-то влияет на результат? Можно попробовать принять это наблюдение во внимание, и предположить, что дожди идут в среднем по два дня (на самом деле,
Но недовольство у нас вызывает не пятилетняя и даже не годовая статистика, человеческая память не столь долгая. Обидно, когда дождь идёт на выходных три или четыре раза подряд! Как часто это может наблюдаться? Особенно, если вспомнить, что гадкая погода не приходит в одиночку. Задачу можно сформулировать так: «Какова вероятность того, что
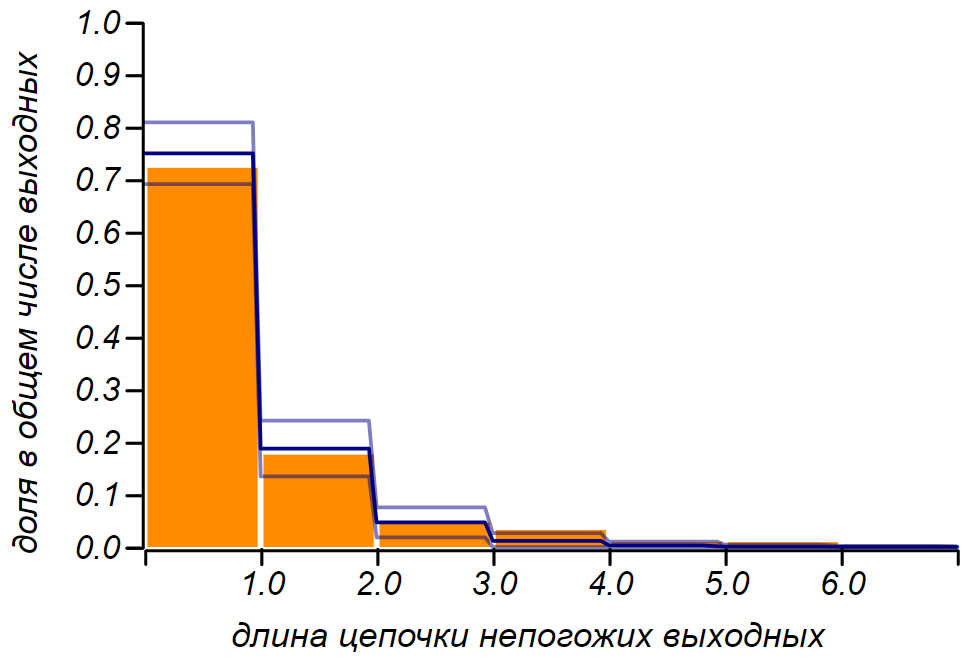
Наблюдаемое распределение длины цепочек неудавшихся выходных и теоретическое. Тонкой линией показаны допустимые отклонения при том количестве наблюдений, что мы имеем.
Можно задаться, таким вопросом: сколько лет нужно вести наблюдения, для того, чтобы замеченную нами разницу в
Так как же австралийским исследователям удалось зафиксировать отклонение температуры в доли градуса и почему имеет смысл рассматривать это исследование? Дело в том, что ими использовались часовые данные температуры, которые не были «прорежены» каким-либо случайным процессом. Таким образом, за
Ещё один источник случайности
Конечно же, погоду, как и землетрясения, нельзя описывать пуассоновским процессом — это динамические процессы, в которых текущее состояние является функцией предыдущих. Почему же наши наблюдения за погодой на выходных говорят в пользу простой стохастической модели? Дело в том, что мы отображаем закономерный процесс формирования осадков на множество из семи дней, или, говоря на языке математики, на систему вычетов по модулю семь. Этот процесс проекции способен порождать хаос из вполне упорядоченных рядов данных. Отсюда, к примеру, происходит видимая случайность в последовательности цифр десятичной записи большинства вещественных чисел.
Мы уже говорили о рациональных числах, тех, которые выражаются целочисленными дробями. Они имеют внутреннюю структуру, которая определяется двумя числами: числителем и знаменателем. Но при записи в десятичной форме можно наблюдать скачки от регулярности в представлении таких чисел, как
Цепные дроби с повторяющимися коэффициентами записывают коротко, подобно периодическим десятичным дробям, например:
Наверное, не один математик, начиная с Пифагора, подозревал мир в коварстве, обнаруживая, что такое нужное, такое фундаментальное число
Результаты этой главы, по большей части, отрицательные. И как автор, желающий удивить читателя скрытыми закономерностями и неожиданными открытиями, я сомневался, стоит ли включать её в книжку. Но наш разговор о погоде ушёл в очень важную тему – о ценности и осмысленности естественнонаучного подхода.
Одна мудрая девочка, Соня Шаталова, глядя на мир сквозь призму аутизма, в десятилетнем возрасте дала очень лаконичное и точное определение: «Наука – это система знаний, основанных на сомнении». Реальный мир зыбок и норовит спрятаться за сложностью, видимой случайностью и ненадёжностью измерений. Сомнение в естественных науках неизбежно. Математика представляется царством определённости, в котором, кажется, можно забыть о сомнении. И очень заманчиво спрятаться за стенами этого царства; рассматривать вместо труднопознаваемого мира модели, которые можно исследовать досконально; считать и вычислять, благо формулы готовы переварить что угодно. Но всё же, математика является наукой и сомнение в ней – это глубокая внутренняя честность, не дающая покоя до тех пор, пока математическое построение не очистится от дополнительных предположений и лишних гипотез. В царстве математики говорят на сложном, но стройном языке, пригодном для рассуждений о реальном мире. Очень важно хоть немного познакомиться с этим языком, чтобы не давать цифрам выдавать себя за статистику, не позволять фактам притворяться знанием, а невежеству и манипуляциям противопоставлять настоящую науку.