Comments 16
На моём ноутбуке FFTW на преобразование 65536 семплов тратит чуть более одной миллисекунды. Может, стоило оптимизировать сам алгоритм преобразования?
0
достаточно произвести преобразование только для 960 частотЕсли я правильно понял условия задачи — нет, недостаточно, так как нужно делать не преобразование 960 частот, а преобразование 960 частотных полос. А иначе получится не усреднение, а прореживание — и такой прореженный спектр будет сильно зашумлен.
Делают так:
1) выполняется прямое преобразование Фурье,
2) обнуляется отрицательная часть частот, чтобы привести сигнал к аналитическому виду — в котором мнимая часть повёрнута на 90° относительно исходного,
3) спектр разбивается на диапазоны в логарифмическом масштабе с использованием оконных функций,
4) над каждым диапазоном выполняется обратное преобразование Фурье, причём минимального размера (если в диапазон попало 8 частот, то и размер FFT также будет 8),
5) с получившего комплексного сигнала считается модуль (квадратный корень суммы квадратов действительной и мнимой части) — это и будет амплитуда.
0
Если я правильно понял условия задачи
Изначально задача была в том, чтобы исследовать передаточные характеристики звуковых систем. К счастью, они не имеют разрывов. Отсюда и было сделано допущение, что функция частоты F(w) непрерывна, а следовательно, в середине диапазона с некоторой погрешностью получим среднее значение.
Делают так
Спасибо!
0
4) над каждым диапазоном выполняется обратное преобразование Фурье, причём минимального размера (если в диапазон попало 8 частот, то и размер FFT также будет 8),
5) с получившего комплексного сигнала считается модуль (квадратный корень суммы квадратов действительной и мнимой части)
Подскажите, пожалуйста, почему возникает необходимость делать iFFT, разве нет возможности вычислить это значение из частотных компонент?
0
Потому что когда мы говорим об амплитуде, мы говорим об огибающей сигнала. Если этот сигнал — синусоида, то его огибающая константна на протяжении всего времени, поэтому её и можно получить напрямую из спектра:
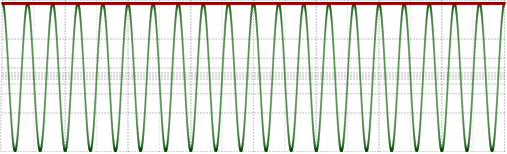
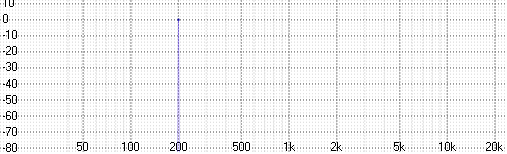
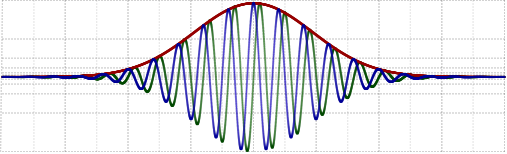
Но если сигнал состоит из полосы частот, то его огибающая уже изменяется во времени и получить её напрямую из спектра невозможно по определению:
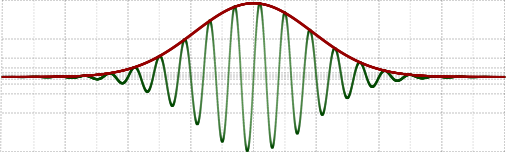
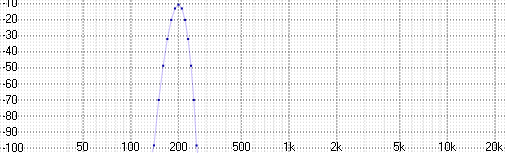
А преобразования Фурье туда-сюда нужны, чтобы выделить интересуемый частотный диапазон и привести сигнал к комплексному виду:


Но если сигнал состоит из полосы частот, то его огибающая уже изменяется во времени и получить её напрямую из спектра невозможно по определению:


А преобразования Фурье туда-сюда нужны, чтобы выделить интересуемый частотный диапазон и привести сигнал к комплексному виду:

0
Можно ссылку на мангу? (И статью оформленную в таком стиле)
+1
За исключением картинки статья никак не связана с БПФ. Более того в ней делаются странные утверждения. И еще в БПФ количество точек не обязательно должно быть кратно степени двойки, достаточно что бы раскладываться на множители (и желательно малые 2,3,5...)
+1
Мне кажется, сложность FFT можно сильно уменьшить в случае, когда предполагается представление результатов с логарифмической осью частот. Я попытался загуглить, но не смог найти по этой теме никакой информации.
Как правильно замечено в статье, на частотах порядка 10Гц и 10кГц совершенно разные минимальные требования по частотному разрешению, в то время как FFT дает одинаковое разрешение во всем диапазоне частот. И в итоге, после применения FFT большого размера, в высоких частотах происходит обычное сглаживание — т.е., мы по сути выкидываем ощутимую часть результатов.
Моя идея: уменьшить размер настолько, чтобы его было достаточно для высоких частот. А низкие — считать отдельно.
Ведь от чего зависит частотное разрешение FFT? От размера и от частоты сэмплирования. И увеличить разрешение можно как увеличение размера, так и уменьшением частоты сэмплирования.
При увеличении размера мы получаем возрастание сложности алгоритма и ухудшение временного разрешения. При уменьшении частоты сэмплирования мы получаем более узкую полосу частот для анализа — а это нам вполне подходит, если мы отдельно анализируем высокие и низкие частоты!
То есть: вместо того, чтобы, например, сделать FFT размера 4096, мы можем сделать FFT размера 1024 3 раза: один раз с изначальными данными, второй раз с вдвое меньшей частотой сэмплирования, третий раз в четверо меньшей частотой относительно начальной (или с вдвое меньшей относительно второго преобразования). В итоге получатся результаты для участков частот [0, Fs/2], [0, Fs/4], [0, Fs/8], и нам потребуется только правильно смешать их, чтобы получить примерно одинаковую точность на всех полосах. Например, от 10 до 20 Гц брать третье преобразование, от 20 до 40 брать второе, от 40 до 80 брать первое.
Эффективное разрешение по частоте получается «size * (2 ^ iters_count)», т.к. каждая итерация увеличивает точность в два раза для всех частот вплоть до уменьшенной вдвое (относительно предыдущей итерации) частоты Найквиста.
Этот алгоритм имеет целых два плюса:
1. Временное разрешение для высоких частот улучшается.
2. Сложность падает, т.к. для того же разрешения в низких частотах достаточно FFT размера в 2^iters_count меньше, чем при обычном преобразовании. При этом сложностью за счет нескольких преобразований можно пренебречь, т.к. сумма геометрической прогрессии 1/2^n, т.е. сложность от количества преобразований увеличивается не более, чем в два раза (ровно в 2 при бесконечном числе итераций).
Из минусов — необходимо хранить сигнал iters_count раз, что увеличивает потребление памяти.
Для получения сигнала с меньшей частотой сэмплирования достаточно применить фильтр низких частот вида «среднее двух значений», и его можно применять на данных предыдущей итерации, так что это почти не замедляет работу.
Я попробовал у себя реализовать это, и оно вроде как хорошо работает. Правда, не совсем очевидно, как нужно смешивать результаты нескольких итераций для полосы частот.
P.S. Никто не подскажет, какая нормировка результата FFT правильная?
Если я делаю преобразование для белого шума, то для разных размеров сумма и максимум магнитуды должны оставаться примерно одинаковыми?
А для преобразования чистого синуса — сумма и максимум магнитуды должны оставаться одинаковыми?
Как правильно замечено в статье, на частотах порядка 10Гц и 10кГц совершенно разные минимальные требования по частотному разрешению, в то время как FFT дает одинаковое разрешение во всем диапазоне частот. И в итоге, после применения FFT большого размера, в высоких частотах происходит обычное сглаживание — т.е., мы по сути выкидываем ощутимую часть результатов.
Моя идея: уменьшить размер настолько, чтобы его было достаточно для высоких частот. А низкие — считать отдельно.
Ведь от чего зависит частотное разрешение FFT? От размера и от частоты сэмплирования. И увеличить разрешение можно как увеличение размера, так и уменьшением частоты сэмплирования.
При увеличении размера мы получаем возрастание сложности алгоритма и ухудшение временного разрешения. При уменьшении частоты сэмплирования мы получаем более узкую полосу частот для анализа — а это нам вполне подходит, если мы отдельно анализируем высокие и низкие частоты!
То есть: вместо того, чтобы, например, сделать FFT размера 4096, мы можем сделать FFT размера 1024 3 раза: один раз с изначальными данными, второй раз с вдвое меньшей частотой сэмплирования, третий раз в четверо меньшей частотой относительно начальной (или с вдвое меньшей относительно второго преобразования). В итоге получатся результаты для участков частот [0, Fs/2], [0, Fs/4], [0, Fs/8], и нам потребуется только правильно смешать их, чтобы получить примерно одинаковую точность на всех полосах. Например, от 10 до 20 Гц брать третье преобразование, от 20 до 40 брать второе, от 40 до 80 брать первое.
Эффективное разрешение по частоте получается «size * (2 ^ iters_count)», т.к. каждая итерация увеличивает точность в два раза для всех частот вплоть до уменьшенной вдвое (относительно предыдущей итерации) частоты Найквиста.
Этот алгоритм имеет целых два плюса:
1. Временное разрешение для высоких частот улучшается.
2. Сложность падает, т.к. для того же разрешения в низких частотах достаточно FFT размера в 2^iters_count меньше, чем при обычном преобразовании. При этом сложностью за счет нескольких преобразований можно пренебречь, т.к. сумма геометрической прогрессии 1/2^n, т.е. сложность от количества преобразований увеличивается не более, чем в два раза (ровно в 2 при бесконечном числе итераций).
Из минусов — необходимо хранить сигнал iters_count раз, что увеличивает потребление памяти.
Для получения сигнала с меньшей частотой сэмплирования достаточно применить фильтр низких частот вида «среднее двух значений», и его можно применять на данных предыдущей итерации, так что это почти не замедляет работу.
Я попробовал у себя реализовать это, и оно вроде как хорошо работает. Правда, не совсем очевидно, как нужно смешивать результаты нескольких итераций для полосы частот.
P.S. Никто не подскажет, какая нормировка результата FFT правильная?
Если я делаю преобразование для белого шума, то для разных размеров сумма и максимум магнитуды должны оставаться примерно одинаковыми?
А для преобразования чистого синуса — сумма и максимум магнитуды должны оставаться одинаковыми?
0
Описанная вами идея действительно имеет место быть и распространена. Есть два основных подхода: изменять размер временного окна или частоту дискретизации. Встречается данный алгоритм под названием multitimewindow (MTW FFT).
0
Мне кажется, сложность FFT можно сильно уменьшить в случае, когда предполагается представление результатов с логарифмической осью частот. Я попытался загуглить, но не смог найти по этой теме никакой информации.Попробуйте погуглить "Constant-Q transform".
0
Нормировка может быть разной. Но если хочется симметрии, что бы нормы сигнала совпадали то нормируют на 1/sqrt(n)
y[k]=C*sum(x[j]*Wn^(j*k),j=0..n-1)
x[j]=C*sum(y[k]*Wn^(-k*j),k=0..n-1)
C=1/sqrt(n)
Wn=exp(-2*pi*i/n)
0
Один из способов вычисления FFT разделяет семплы на четные и нечетные, рекурсивно вычисляет для них FFT и объединяет результаты.
Поэтому ваше решение может не сработать.
0
Sign up to leave a comment.
Преобразование Фурье. The Fast and the Furious