Comments 11
Изображение Лены мы брать не будем — а возьмём что-нибудь мягкое и пушистоеА ещё лучше взять что-нибудь с огромным динамическим диапазоном (HDR), тогда работа фильтров раскроется во всей красе!
+4
Тема раскрыта не полностью.
Blur не ограничивается матрицами свёртки, при этом, являясь их частным решением.
Так же — фильтр резкости, по-сути является частной реализацией Blur, но не рассмотрен.
Более того, сами матрицы свертки суммируются с исходным изображением неправильно.
Так при наложении фильтра, блендинг выполняется не усреднением исходного значения компонент цветов, а должен выбираться из максимума цветовых компонент буфера-источника и буфера-приемника. Тогда результирующее изображение имеет более «ламповый» и реалистичный вид, избавляясь от пелены (которая, в свою очередь, является погрешностью).
В дополнении: фильтр должен применяться не сразу к буферу источнику, а считаться в отдельный буфер-приемник, после чего выполняется «Альфа-блендинг» буферов.
В противном случае, возникает вторая ошибка на этапе применения: данные полученные для текущей строки, учитывают результат предыдущей (уже вычисленной строки).
Blur не ограничивается матрицами свёртки, при этом, являясь их частным решением.
Так же — фильтр резкости, по-сути является частной реализацией Blur, но не рассмотрен.
Более того, сами матрицы свертки суммируются с исходным изображением неправильно.
Так при наложении фильтра, блендинг выполняется не усреднением исходного значения компонент цветов, а должен выбираться из максимума цветовых компонент буфера-источника и буфера-приемника. Тогда результирующее изображение имеет более «ламповый» и реалистичный вид, избавляясь от пелены (которая, в свою очередь, является погрешностью).
В дополнении: фильтр должен применяться не сразу к буферу источнику, а считаться в отдельный буфер-приемник, после чего выполняется «Альфа-блендинг» буферов.
В противном случае, возникает вторая ошибка на этапе применения: данные полученные для текущей строки, учитывают результат предыдущей (уже вычисленной строки).
-1
Тема раскрыта не полностью.Само собой — об этом сказано прямым текстом в заключении. Сама же статья является tutorial — руководством к конструированию своих собственных фильтров.
Blur не ограничивается матрицами свёртки, при этом, являясь их частным решением.Выражение «матрицами свёртки» некорректно точно так же, как и «матрица сложения» или «число свёртки»; и сама по себе матрица решением чего бы то ни было не является. Свёртка — это математическая операция, в то время как матрица — это данные, упорядоченный набор чисел. В данном случае корректно говорить «ядро свёртки» или хотя бы «матрица фильтра», потому что у нас ещё есть «матрица изображения», которые для операции свёртки совершенно равнозначны.
Так же — фильтр резкости, по-сути является частной реализацией Blur, но не рассмотрен.Фильтр резкости — sharpen — является полной противоположностью размытию и никак не может быть его частной реализацией. Линейный фильтр резкости, как и размытие, как и выделение контуров — хоть и тоже реализуется через свёртку, но это по-прежнему разные типы фильтров.
Более того, сами матрицы свертки суммируются с исходным изображением неправильно.Здесь матрицы не суммируются и не должны суммироваться. Операция свёртки != операция сложения.
Так при наложении фильтра, блендинг выполняется не усреднением исходного значения компонент цветов, а должен выбираться из максимума цветовых компонент буфера-источника и буфера-приемника. Тогда результирующее изображение имеет более «ламповый» и реалистичный вид, избавляясь от пелены (которая, в свою очередь, является погрешностью).Вы сейчас, вероятно, говорите о каком-то другом фильтре, если само прямое назначение фильтра — размытие — называете погрешностью.
Блендинг же — это совершенно отдельная операция, причём между двумя изображениями, а не изображением и ядром фильтра, и реализуются не через свёртку, а через сложение с масштабированием независимо для каждого пикселя.
В дополнении: фильтр должен применяться не сразу к буферу источнику, а считаться в отдельный буфер-приемник, после чего выполняется «Альфа-блендинг» буферов.Непонятно, откуда вы сделали вывод, что в примерах к статье буфер-приёмник не использовался. Более того — при реализации свёртки через дискретное преобразование Фурье без него вполне можно обойтись и даже — в некоторых случаях эта операция может быть обратимой.
И «Альфа-блендинг» буферов после свёртки выполняться не должен (хотя может, как и множество других операций, включая повторную свёртку).
В противном случае, возникает вторая ошибка на этапе применения: данные полученные для текущей строки, учитывают результат предыдущей (уже вычисленной строки).Фильтры с бесконечной импульсной характеристикой (рекурсивные) именно так и работает — и это не является ошибкой. В этой статье они также не рассматривались, но рассматривались, например, здесь.
+3
двумерный вариант Gaussian получен её вращением относительно оси ординат
Извините, но нет! Двумерный вариант Gaussian получается перемножением одномерных функций по двум осям, что и позволяет повсюду безболезненно использовать размытие по Гауссу.
0
Извините, но не соглашусь. То, что выполняется равенство
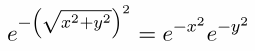
— это, конечно, интересное свойство и удобно для вычислений — но является лишь свойством самой экспоненты и на другие функции автоматически не распространяется. Физическим смыслом перехода к двум координатам здесь является именно вращение. Но за замечание спасибо — добавлю уточнение.
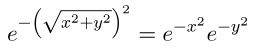
— это, конечно, интересное свойство и удобно для вычислений — но является лишь свойством самой экспоненты и на другие функции автоматически не распространяется. Физическим смыслом перехода к двум координатам здесь является именно вращение. Но за замечание спасибо — добавлю уточнение.
+1
С вашей стороны странно опустить такое удобное для вычислений свойство, учитывая что тема статьи — как раз обработка сигналов.
Вращение при потере производительности не дает никаких плюсов в вычислении гауссианы.
При этом другие представленные фильтры далеко не всегда основаны на вращении.
И поясните пожалуйста, что такое «физический смысл перехода к двум координатам», как вращение может быть физическим смыслом и причем тут физика, если статья целиком посвящена вычислительной математике.
Вращение при потере производительности не дает никаких плюсов в вычислении гауссианы.
При этом другие представленные фильтры далеко не всегда основаны на вращении.
И поясните пожалуйста, что такое «физический смысл перехода к двум координатам», как вращение может быть физическим смыслом и причем тут физика, если статья целиком посвящена вычислительной математике.
-1
Ну как минимум если мы хотим чтоб фильтр был изотропным, то есть не зависил от поворота картинки. То есть если мы повернем картинку и применим фильтр, то результат должен быть таким же, как если применить фильтр и потом повернуть результат. Вот и физический смысл. Оттуда же и вращение. Хотя тема вообще намного более глубокая, я так понимаю. Группы вращения, сферические гармоники, вот это все.
0
При повороте на угол, кратный 90 градусам, результат не зависит от порядка поворот<->фильтр для любого фильтра. При повороте на произвольный угол, будет разница для любого фильтра, так как после любой операции идет интерполяция на двумерную сетку.
Для устранения разницы, изображения должны задаваться и обрабатываться в полярных координатах, но и при этом разницы не будет только при вращении вокруг фиксированного начала координат. Или переходить на векторную графику
Для устранения разницы, изображения должны задаваться и обрабатываться в полярных координатах, но и при этом разницы не будет только при вращении вокруг фиксированного начала координат. Или переходить на векторную графику
0
А вот если бы нашей задачей стояла не равномерное размытие во всех направлениях, а разбивка изображения на перекрывающиеся блоки для сжатия с использованием модифицированного косинусного преобразования (рассматриваемое, например, в работе Rikus Muller «Applying the MDCT to Image Compression» (pdf)), вот тогда бы нам потребовалось именно перемножение одномерных оконных функций.
0
С вашей стороны странно опустить такое удобное для вычислений свойство, учитывая что тема статьи — как раз обработка сигналов.Упустил потому, что статья посвящена не фильтру Гаусса — а наоборот, всем прочим, а в терминах обработка сигналов это как раз-таки двумерная свёртка, а не две последовательных одномерных.
И поясните пожалуйста, что такое «физический смысл перехода к двум координатам», как вращение может быть физическим смыслом и причем тут физика, если статья целиком посвящена вычислительной математике.Это тоже издержки мышления. Вращение имеет понятный физический смысл, потому как встречается повсеместно в повседневной жизни. В то время как вращение математически, особенно через перемножение комплексных чисел, не всем очевидно.
+1
Sign up to leave a comment.

Нужно больше разных Blur-ов