Comments 21
прошу прощения, подпись в картинке в конце главы "что изучает теорвер" — неправильная в последнем квадратике, дважды P(a) вместо P(a) + P(b)
+2
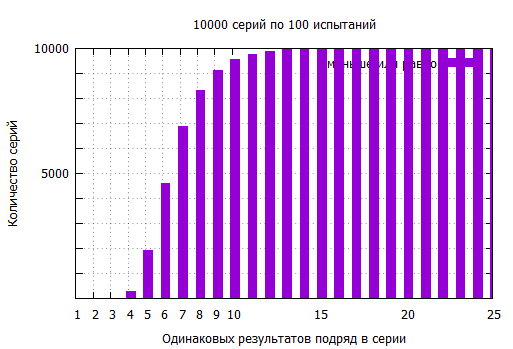
Про монетку и семь решек (или орлов) я однажды услышал другую задачку, которую потом сам распробовал «на пальцах». Проводился следующий эксперимент — две группы студентов посадили в разные аудитории и первую попросили подбросить сто раз монетку, записав последовательность результатов. А вторую попросили, не подбрасывая, придумать случайную последовательность из ста орлов и решек. Ведущий, посмотрев на результаты, определил где монетку бросали, а где рисовали из головы. Честная случайная последовательность выдавала себя длинными сериями одинаковых значений, в частности там было семь орлов (или решек, не помню уже) подряд. Товарищи, которые последовательность придумывали, старались, чтобы она выглядела послучайней, поэтому избегали длинных повторов. Максимальная серия одинаковых значений у них была всего в четыре монетки длиной. Но при ста подбрасываниях монетки вероятность получить семь или больше одинаковых значений подряд гораздо больше, чем иметь максимальную серию в четыре или меньше повторяющихся исходов.
Я сразу взялся за карандаш и клавиатуру, чтоб подсчитать эти вероятности. Вероятность в ста подбрасываниях монетки получить серию в семь или больше одинаковых значений подряд равна 54%, а вероятность получить максимальную серию в четыре или меньше всего лишь 2.83%
Я сразу взялся за карандаш и клавиатуру, чтоб подсчитать эти вероятности. Вероятность в ста подбрасываниях монетки получить серию в семь или больше одинаковых значений подряд равна 54%, а вероятность получить максимальную серию в четыре или меньше всего лишь 2.83%
+5
А с генератором случайных чисел такую штуку не пробовали повторить? Там ведь псевдослучайные числа и, возможно, тоже всплывет эффект как с написанными студентами подбрасываниями
0
Конечно, я написал пару скриптов и погонял их. Генераторы ПСЧ не настолько уж плохи, чтобы всплывали такие эффекты. Нет, все вполне соответствует расчетам. Я потом еще, специально для друзей, кто не доверяет формулам и моделированию, сделал «натурный» эксперимент. Ну реально взял мешок монеток и подбрасывал их. Мне не пришлось даже сотню раз подкидывать. У меня седьмой решкой подряд вверх упала сорок четвертая монетка. Хотя тут повезло, конечно. Под спойлером пара картинок
теория и практика
С накоплением
Вот как-то так:


С накоплением

Вот как-то так:

+1
Хорошая статья для общего обзора МНК
+1
Интересно пишете! Но кроме максимального правдоподобия часто используют максимум апостериори. Если далее упомянете, думаю будет полнее картина вопроса. Правда это уже не совсем про МНК…
0
Ну, в принципе, MAP и MLE это практически одно и то же…
0
С точностью до одного проворота ручки Байеса. В машинном обучении максимизация апостериорной вероятности позволяет получать параметры, которые лучше позволяют обобщить (и выходит экстрапллировать) данные. Лучше, значит что выбирается одна из более вероятных гипотез. MAP технически же это MLE со штрафом на параметры.
Навскидку, R-квадрат для квартета энскомба одинаковый, то и MLE тоже будет, а MAP — разный.
0
Ошибся насчёт разного MAP.
https://pste.eu/p/ZDzV.html
0
Спасибо за статью. Чтобы вспомнить о освежить в голове тервер прекрасное чтение.
Чуть-чуть попридираюсь — данная статья относится к C++, так же как и к Python, так же и к другим языкам программирования ))
Чуть-чуть попридираюсь — данная статья относится к C++, так же как и к Python, так же и к другим языкам программирования ))
0
В эволюции разум лишний элемент.
-2
В случае же когда плотность (совсем) не гауссова, МНК дают оценку, отличающуюся от оценки MLE (maximum likehood estimation)
Если по простому не для математиков… Как в случае такой плотности быть?!
0
Я когда то итерационными методами удостоверился, что что бы площать графика от формулы Бернулли по переменной p была равна единице, т.е. что бы это было распределением вероятностей, его еще нужно умножать на количество опытов. Правда на поиск максимума это не влияет.
0
Пожалуйста поясните, а почему в примерах 2-4, функция правдоподобия — произведение плотностей вероятности измерений? Разве очевидно, что измерения — независимые события, как с монеткой в первом примере? Или откуда берется это произведение?
0
Sign up to leave a comment.
В трёх статьях о наименьших квадратах: ликбез по теории вероятностей