Comments 593
Или каждый интересующийся возьмёт одну тему и аналогично согласно схеме опишет. Сначала неидеально, потом доточат
И получится Википедия.
Не получится.
На википедии вначале выпилят то что вы запостите за ОРИСС, а потом заменят на цитату из Брокгауза-Эфрона, разбавив вставками из БСЭ о том, как хорошо предмет статьи влияет на удои озимых и подтверждает верность учения Ленина-Сталина.
На википедии вначале выпилят то что вы запостите за ОРИСС, а потом заменят на цитату из Брокгауза-Эфрона, разбавив вставками из БСЭ о том, как хорошо предмет статьи влияет на удои озимых и подтверждает верность учения Ленина-Сталина.
UFO just landed and posted this here
последнее приветствуется и рекомендуется
У Вас какая-то своя особенная википедия? Потому что в обычной пока ты текст не приведёшь к виду неудобочитаемого нудного бубнения — его не примут.
UFO just landed and posted this here
Вы конечно извините, но научно-популярным на вики и не пахнет. В моем понимании, по всей видимости отличном от вашего, научно-популярное означает, что рандомный человек с минимальной теоретической подготовкой зайдя на страницу сможет хотя бы чуть-чуть понять смысл термина, а не утонуть в других терминах и гиперссылках. Да собственно по вашей ссылке примерно это и написано. Но стоит чуть дальше какого-нибудь умножения зайти, и вики уже предполагает что ты знаешь кучу всего остального. Это понятная проблема, точнее я даже не уверен что это проблема, все же максимально полно изложить суть на мой взгляд чуть более важно, но говорить что вики пишется в научно-популярном стиле такое себе.
Дурацкий вопрос — а вы английскую Википедию пробовали читать?
Там всё гораздо удобнее: неформальное описание, понятное человеку с улицы — в первой паре абзацев, дальше содержание, а уж под ним — подробный текст, который уже может требовать специальных знаний.
Русская тоже потихоньку от стиля «всё очень точно, но неподготовленный человек может застрелиться при попытке это понять» отходить начинает. Хоть и мееедленно-мееедленно.
Там всё гораздо удобнее: неформальное описание, понятное человеку с улицы — в первой паре абзацев, дальше содержание, а уж под ним — подробный текст, который уже может требовать специальных знаний.
Русская тоже потихоньку от стиля «всё очень точно, но неподготовленный человек может застрелиться при попытке это понять» отходить начинает. Хоть и мееедленно-мееедленно.
UFO just landed and posted this here
Даже среди этих статей две не хуже русской версии, а третью вообще на русский не перевели еще. Но ведь в целом английские варианты действительно более удобочитаемые. У меня вот немного другой «сходу» получился, я ткнул в «Дискриминант», раз уж он поминался в постинге. В английский статье самые первые строчки мне показались понятнее. Там ведь правда сначала в первом же предложении в двух словах дается и понятное определение и пример какая от дискриминанта может быть польза.
Давайте возьмём что-то более распространённое, например, en.wikipedia.org/wiki/Cholesky_decomposition. Тоже всё интуитивно и неформально?На все «сложные» термины есть ссылки, там же написано — зачем это нужно, есть ссылка на первооткрывателя, то есть фактически прочитав один этот абзац — вы можете удовлетворить своё любопытство.
То, что не всего понятия вырадаются через совсем уж интуитувно понятные… ну тут уж так математика устроена.
Сравните с тем, что в русской версии: теста в преамбуле, до «содержания», больше, но при этом полезной информации меньше. Написано как это понятие можно ещё больше обобщить, а нафига так делать — вообще непонятно.
Понятно только вы дочитаете-таки статью до конца и доберётесь до раздела «приложения» и там, где-то посреди этого раздела увидите-таки ответ свой жгучий вопрос «а на&&я?».
По-момему вполне хорошее подтверждение и моего тезиса и всего того, что топикстартер написал.
UFO just landed and posted this here
UFO just landed and posted this here
Зря вы так про лурк. Некоторые статьи там раскрывают суть гораздо лучше, чем Вики. Я имею ввиду именно статьи про некоторые термины и научные теории. Просто их там слишком мало.
Если одна и та же статья будет на Вики и на Лурке — я вот правда пойду читать Лурк. Там будет понятнее. Просто там значительно всего меньше.
И причем знаете почему на Лурке статьи лучше, чем на Вики? Потому что нет фимозного сообщества зашоренных людей. Вот реально, на Вики, по крайней мере русской, будто бы дух страха какого-то витает — как бы не сказать чего лишнего…
Ага. На Лурке свой фимоз.
В любом человеческом объществе это есть. И даже нечеловеческом. Банальная система опознавания «свой-чужой». Просто «своего» фимоза вы не замечаете (вы же «свой»), но человек «со стороны» его очень хорошо видит (потому что он «чужой»).
Но да, то, что русская Википедия — «чужая» для большого числа потенциальных контрибьютеров… это печально.
Но да, то, что русская Википедия — «чужая» для большого числа потенциальных контрибьютеров… это печально.
Я перестал понимать, что Вы вкладываете в слово «чужая».
Нельзя написать статью? Можно.
Нельзя дополнить статью? Тоже можно.
Если только речь не идёт про какую-нибудь околополитическую лажу или креационистские бредни.
Нельзя написать статью? Можно.
Нельзя дополнить статью? Тоже можно.
Если только речь не идёт про какую-нибудь околополитическую лажу или креационистские бредни.
Я перестал понимать, что Вы вкладываете в слово «чужая».«Политическая» и «околополитическая» лажа — это частные случаи. Но общество, вообще, пропитано подобными вещами. Это псхология — прочём касается она, как уже сказал, не только людей.
Нельзя написать статью? Можно.Вот только если она окажется «не в строку» — то её удалят. В случае с Википедией — за «недостаточную популярность» или «неакадемичность». На Лурке — за то, что «слишком похоже на педивикию».
Нельзя дополнить статью? Тоже можно.То же самое.
Но общество, вообще, пропитано подобными вещами.
Общество-то может и пропитано, но в справочнике этому не место.
Вот только если она окажется «не в строку» — то её удалят.
Ну я и говорю: надо ОЧЕНЬ постараться, чтобы оказаться «не в строку» на Википедии. Это должна быть либо какую-нибудь совсем никому неизвестная маргинальщина (не показана значимость), либо бездоказательный бред (нет АИ), либо — политика (википедия — не новости).
Я всегда руководствовался простым правилом: ссылка на источник. Если есть на что сослаться — пиши смело. Если сослаться не на что — оставь при себе. И, что характерно, этого достаточно, чтобы мои правки не удаляли.
Это должна быть либо какую-нибудь совсем никому неизвестная маргинальщина (не показана значимость)Попробуйте перенести из английской в русскую какого-нибудь Покемона и посмотрите на реакцию.
Я всегда руководствовался простым правилом: ссылка на источник.Угу. Я как-то попробовал дополнить математическую статью доказательством — его удалили, так как «не было ссылки на источник». Но если написать любую чушь на Хабр — то можно уже ссылаться и потом будет это очень сложно извести. Вот эти вот бессмысленные ссылки на написанную тобой же статью на «стороннем источнике» — это как раз вполне себе часть системы опознавания «свой-чужой» конкретно на Wikipedia.
С играми и мультфильмами — да, есть проблема. «Не показана значимость за пределами сеттинга». Т.е. если нигде кроме игры про покемонов бульбазавр не числится — русская википедия его отторгнет. По той же причине была удалена статья про зергов (со списком юнитов) из «Старкрафта».
А вот здесь я с Вами не согласен. Википедия — третичный источник, в ней должно быть только то, что есть где-то ещё.
Это побочный эффект указанной логики. Хабр — это ещё ладно, бывает, что новостные сайты за источники принимаются. С этим можно отчасти бороться шаблоном [не АИ].
Это Вас на теорию заговора пробивает. Википедия проста как три копейки, у буквального исполнения формальных правил есть побочные эффекты, всего навсего.
Я как-то попробовал дополнить математическую статью доказательством — его удалили, так как «не было ссылки на источник».
А вот здесь я с Вами не согласен. Википедия — третичный источник, в ней должно быть только то, что есть где-то ещё.
Но если написать любую чушь на Хабр — то можно уже ссылаться и потом будет это очень сложно извести.
Это побочный эффект указанной логики. Хабр — это ещё ладно, бывает, что новостные сайты за источники принимаются. С этим можно отчасти бороться шаблоном [не АИ].
системы опознавания «свой-чужой»
Это Вас на теорию заговора пробивает. Википедия проста как три копейки, у буквального исполнения формальных правил есть побочные эффекты, всего навсего.
Совершенно ужасающие в нашей Википедии тексты по математике.
Как кто-то шутил про один учебник в техникуме(!):
«Один профессор создал напоминание для другого профессора, который немного подзабыл»
Этот неловкий момент, когда раздобыл советский учебник и там понятнее изложено, чем в десятках современных и местами даже актуальнее(sic!). Актуальность достигается тем, что понятия до сих пор не устарели и более полно развернуты. У современных авторов — пропали целые разделы, зато вместо них — вода, идентичная натуральной. Максимум, что из современного учебника полезного — обзор новейших технологий.
Если что — учебник, связанный с прикладной математикой. Утерян сразу после сессии.
Еще можно упомянуть в качестве образца Детскую энциклопедию, эдакая доступная версия Википедии на десятилетия раньше.
«Один профессор создал напоминание для другого профессора, который немного подзабыл»
Этот неловкий момент, когда раздобыл советский учебник и там понятнее изложено, чем в десятках современных и местами даже актуальнее(sic!). Актуальность достигается тем, что понятия до сих пор не устарели и более полно развернуты. У современных авторов — пропали целые разделы, зато вместо них — вода, идентичная натуральной. Максимум, что из современного учебника полезного — обзор новейших технологий.
Если что — учебник, связанный с прикладной математикой. Утерян сразу после сессии.
Еще можно упомянуть в качестве образца Детскую энциклопедию, эдакая доступная версия Википедии на десятилетия раньше.
Викиучебники:
ru.wikibooks.org/wiki/Заглавная_страница
Это один из проектов википедии. Сама Википедия — это энциклопедия, а не обучающие материалы. Например, из викиучебника про квадратные уравнения:
ru.wikibooks.org/wiki/Основы_алгебры/Квадратные_уравнения
ru.wikibooks.org/wiki/Заглавная_страница
Это один из проектов википедии. Сама Википедия — это энциклопедия, а не обучающие материалы. Например, из викиучебника про квадратные уравнения:
ru.wikibooks.org/wiki/Основы_алгебры/Квадратные_уравнения
Есть ещё MathProfi, который действительно понятно всё расписывает, человеческим языком, но без потери смысла.
И что, хороший учебник типа? Всё то же самое о чём пишет автор: отсутствие введения, цели, основы, примеров.
не самый удачный пример с квадратными уравнениями: дали формулу циферки подставлсять и всё. Уж лучше бы они вообще ничего не писали, чем отвлекать людей этим информационным шумом.
Первое, что попалось на самом деле. Вопрос не в этом, а в том, что любой желающий может книгу улучшить. Считаете, что чего-то не хватает? Можете попробовать изменить формулировки, дописать. Идея именно в коллективном творчестве. И именно поэтому упрекать проект не стоит. Нельзя требовать на добровольных началах профессионального и качественного результата. Люди тратят на это личное время, не получая ничего взамен.
Людям можно только спасибо сказать.
Идея проэкта просто замечательная.
Тем более обидно, что результат не самый лучший. Это как если бы дорогой человек пек пироги, а они оказались малосъедобны.
На вики гораздо больше инфы. На английской увидел новое о кв.уравнениях.
Идея проэкта просто замечательная.
Тем более обидно, что результат не самый лучший. Это как если бы дорогой человек пек пироги, а они оказались малосъедобны.
На вики гораздо больше инфы. На английской увидел новое о кв.уравнениях.
На вики гораздо больше инфы. На английской увидел новое о кв.уравнениях.
Да, вики — более старый проект и более популярный. Проекты типы викикниг, викисловаря, викиданных и викиверситета появились позже основного. Они призваны дополнить википедию.
Например, словарные определения (статьи размером в предложение) в энциклопедии недопустимы. Но в викисловарь их добавлять можно.
В Википедию не получится добавить мануал, например, по созданию deb-пакета в Linux. Но в викикнигах ему самое место.
По сравнению с Википедией остальные её проекты очень молодые и пока развиваются медленно. Хотя бы потому, что мало кто о них знает.
Вот пример из Викикниг, который действительно полезен:
ru.wikibooks.org/wiki/Велосипед/Правила_дорожного_движения/РФ
Какие потребности, какой математики, чем не устраивают рациональные — да пес его знает
зачём вы вводите в заблуждение с самого начала, уж и Фихтенгольца (в отличие от многих других) всё это разжевывается на первой странице — невозможность извлечения квадратных корней, и как пример: ненаходимость диагонали единичного квадрата
на самом деле, единственная проблема в том, что «матан» ставят в учебные планы тех специальностей, которым он на таком уровне не нужен. это действительно проблема наших реалий, на западе это решается наличием курсов на выбор и совсем упрощенными курсами типа calculus где всё объясняется на пальцах
P.S.:
По слухам, некоторые авторы теряли листы черновиков в трамваях, а потом заменяли утерянные куски выражениями вроде «легко показать, что...»
не некоторые авторы, а Лифшиц (ибо, как известно, Ландау ничего сам не писал). но это вообще про физиков-теоретиков, к математике этот фольклор приплетать не надо, у них там была «своя атмсофера»
уж и фихтенгольца (в отличие от многих других) всё это разжевывается на первой странице
Мой косяк, спасибо, что указали. Вы абсолютно правы, разжевывается и про корень, и про корни.
К сожалению, пример с пределами по-прежнему актуален. Сам предел вводится, его назначение непонятно.
с глобальной точки зрения пределы нужны потому что весь «матан» — это учение о бесконечно малых, строго и корректно это понятие можно определить лишь с помощью предела
с практической точки зрения, фихтенгольц в том же параграфе извернулся и уже придумал для вас примеры как с помощью пределов можно считать площади и объемы
вообще, фихтенгольц — это простейшая книга по матану, где всё разжёвывается до мелочей и читателя просто закидывают разнообразными примерами, настолько приближенными к практике, насколько это возможно
с практической точки зрения, фихтенгольц в том же параграфе извернулся и уже придумал для вас примеры как с помощью пределов можно считать площади и объемы
вообще, фихтенгольц — это простейшая книга по матану, где всё разжёвывается до мелочей и читателя просто закидывают разнообразными примерами, настолько приближенными к практике, насколько это возможно
Увы. При подготовке статьи я выкинул из нее пару абзацев критики примеров к тому же пределу последовательности. Если желаете — можем обсудить в личке.
Я не спорю, Фихтенгольц хорош, но вы взгляните на учебник глазами рядового студента. На одной странице выделены курсивом понятия величина, переменная, постоянная, множество, направленная переменная, предел, последовательность, и еще пару незначительных. Примеры только в конце главы, до них еще дочитать надо. Приходится или вдумываться, или пролистывать с мыслью «да вроде все ясно». Мотивации введения термина Предел — сноска на дополнение.
Можно же было перестроить порядок подачи материала, дать несколько примеров последовательности с самого начала. Потом уже пояснить, зачем нужен предел, или просто указать на его существование, вычислить предел для последовательностей из примеров.
Что самое интересное, Фихтенгольц приблизительно это и делает: упоминает прогрессии, окружности, корни — что-то уже знакомое читателю. Верные вещи делаются в неверном порядке.
Я не спорю, Фихтенгольц хорош, но вы взгляните на учебник глазами рядового студента. На одной странице выделены курсивом понятия величина, переменная, постоянная, множество, направленная переменная, предел, последовательность, и еще пару незначительных. Примеры только в конце главы, до них еще дочитать надо. Приходится или вдумываться, или пролистывать с мыслью «да вроде все ясно». Мотивации введения термина Предел — сноска на дополнение.
Можно же было перестроить порядок подачи материала, дать несколько примеров последовательности с самого начала. Потом уже пояснить, зачем нужен предел, или просто указать на его существование, вычислить предел для последовательностей из примеров.
Что самое интересное, Фихтенгольц приблизительно это и делает: упоминает прогрессии, окружности, корни — что-то уже знакомое читателю. Верные вещи делаются в неверном порядке.
по вашему выходит, вас автор постоянно должен уговаривать прочитать очередную главу его учебника, притом ещё и (ужас!) до конца. в то, что автор неспроста вставил в книгу какие-то определения и понятия с пониманием своего дела, и их важность откроется по ходу дальнейшего изучения — вы верить отказываетесь упорно, вам нужны «подтверждения» здесь и сразу, причём непременно сразу после каждого вновь вводимого определения. эдакая «морковка», которой надо постоянно завлекать
вот здесь постоянно звучит слово «мотивация» — это на самом деле какое-то детсадовское требование. предполагается, что если человек решил изучать анализ, то пресловутая мотивация у него уже есть. если это делается из под палки, то настоящая проблема в том, зачем человека насилуют этим «матаном», а не в том, что современная математическая запись «неправильная» или учебники «плохие».
действительно, какой ужас, читая серьезную научную литературу приходится обдумывать прочитанное
в дополнении излагается «Общая точка зрения» на предел, как там написано, а не какая-то «мотивация». как вы можете предположить «общая точка зрения» будет ещё более абстрактней, чем простейшее школьное определение предела, данное в начальной главе
вот здесь постоянно звучит слово «мотивация» — это на самом деле какое-то детсадовское требование. предполагается, что если человек решил изучать анализ, то пресловутая мотивация у него уже есть. если это делается из под палки, то настоящая проблема в том, зачем человека насилуют этим «матаном», а не в том, что современная математическая запись «неправильная» или учебники «плохие».
Приходится или вдумываться
действительно, какой ужас, читая серьезную научную литературу приходится обдумывать прочитанное
Мотивации введения термина Предел — сноска на дополнение.
в дополнении излагается «Общая точка зрения» на предел, как там написано, а не какая-то «мотивация». как вы можете предположить «общая точка зрения» будет ещё более абстрактней, чем простейшее школьное определение предела, данное в начальной главе
Именно морковка. Именно подтверждения здесь и сейчас. В идеале — зацепки на уже изученные кусочки. Для читателя — идеальные условия.
Упростились тексты — сэкономилось время читателей. Больше читателей дочитало книгу. Больше читателей поняло книгу. В случае матана больше студентов не восприняло матан как насилие.
Да, не всегда у автора есть ресурсы на упрощение. Но если имеется возможность упростить материал — стоит ли ею пренебрегать?
Упростились тексты — сэкономилось время читателей. Больше читателей дочитало книгу. Больше читателей поняло книгу. В случае матана больше студентов не восприняло матан как насилие.
Да, не всегда у автора есть ресурсы на упрощение. Но если имеется возможность упростить материал — стоит ли ею пренебрегать?
Вы понимаете, что если перед каждым определением давать список каких-то «мотиваций», то это НЕ упростит понимание — это просто замусорит текст, неоправданно удлинит книгу, а действительно важные вещи просто потонут в «воде». Если что-то непонятно, то надо перечитывать и обдумывать прочитанное — по другому, к сожалению, процесс обучения не работает. Всё равно непонятно — задавать вопросы лектору. Если лектор не хочет идти на контакт и объяснять — это плохо, это уже другая проблема. Вы подошли к одногруппнику и он вам объяснил — тоже отличный способ.
И, уж придётся вам мне на слово поверить, но из всех курсов матанализа — Фихтенгольц самый простой и самый доступный, и содержит больше всего наглядных примеров и приложений. Этим объясняется, кстати, его довольно внушительный объем (2000 страниц трех томов). Правда, есть ещё Пискунов, но он больше позиционируется как для втузов, но на самом деле не для углубленного изучения — это отличный выбор.
И, уж придётся вам мне на слово поверить, но из всех курсов матанализа — Фихтенгольц самый простой и самый доступный, и содержит больше всего наглядных примеров и приложений. Этим объясняется, кстати, его довольно внушительный объем (2000 страниц трех томов). Правда, есть ещё Пискунов, но он больше позиционируется как для втузов, но на самом деле не для углубленного изучения — это отличный выбор.
По-другому процесс обучения работает.
Очень часто ситуация, когда нужно просто понять смысл определения. И в попытках понять ты читаешь определение, состоящее из кучи формальных слов, из которых тебе непонятно примерно 50%.
При этом, когда ты продолбился головой об стену, порешал практические задачи, потратил на это месяц-другой и наконец понял, ты сам можешь выдать определение, состоящее из обычных народных слов, которых тебе не хватало месяца два назад.
Тратить каждый раз по месяцу на каждый новый математический термин — могут себе позволить только математики. В жизни не всегда нужно знать всю математику, очень много айтишников работают в смежных темах, когда нужно немного копнуть.
К сожалению именно с математикой «немного» практически никогда не выходит.
Очень часто ситуация, когда нужно просто понять смысл определения. И в попытках понять ты читаешь определение, состоящее из кучи формальных слов, из которых тебе непонятно примерно 50%.
При этом, когда ты продолбился головой об стену, порешал практические задачи, потратил на это месяц-другой и наконец понял, ты сам можешь выдать определение, состоящее из обычных народных слов, которых тебе не хватало месяца два назад.
Тратить каждый раз по месяцу на каждый новый математический термин — могут себе позволить только математики. В жизни не всегда нужно знать всю математику, очень много айтишников работают в смежных темах, когда нужно немного копнуть.
К сожалению именно с математикой «немного» практически никогда не выходит.
По-другому процесс обучения работает.
обучения чему: науке или ремеслу? если науке, а конкретно матанализу, то он работает именно как я описал. учитывая, конечно, что у вас ещё будут лекции и семинары, где можно и надо задавать вопросы
В жизни не всегда нужно знать всю математику, очень много айтишников работают в смежных темах
так не зря здесь есть комментарии, что проблема больше в самой организации процесса высшего образования как целого у нас. в других странах, например, насильно матаном никто не пичкает: вы сами выбираете какие предметы слушать (но если не прослушан матан, то предметы, требующие его брать нельзя, и естественно он всё равно будет обязателен если вы поступили на математика или естественника), для не-математиков есть облегченные варианты, называемые calculus («вычисления») гдё всё просто и наглядно, «обычным народным» языком, и где вас научат решать типовые задачи. но сделать шаг в сторону после такого вы всё равно не сможете, т.к. вас просто «натаскают» на типовые примеры, без понимания самой сути теории
Тратить каждый раз по месяцу на каждый новый математический термин — могут себе позволить только математики
не надо преувеличивать. если учить матан последовательно и постепенно, то каждый термин будет вам уже знаком, останется понять как они сочетаются вместе для генерации нового определения
К сожалению именно с математикой «немного» практически никогда не выходит.
вот вы точно отобразили суть математики. там всё последовательно и строго, каждый следующий шаг должен вытекать из предыдущего, если отсутствует хоть одно промежуточное звено — рушится вся логическая цепочка, так что брать «с наскока» не получится
У меня такое ощущение, что вы обсуждаете разное. Один говорит: учебник хорош. А второй: а мне хотелось бы самоучитель!
Все эти "морковки", "тычинки" и "пестики", вполне могут быть выданы преподавателем. У меня так было. Учебник был скорее как справочник и дополнительные материалы. Интересная лекция мотивирует раз в M, а то и в N, раз лучше любого учебника, даже если он с картинками и "разговорами".
Но, тут я соглашусь: хороших лекторов наплодить, наверное, я не уверен, сложнее, чем написать один сферический всем понятный учебник.
УЧЕБНИК и должен работать как самоучитель, роль преподавателя помочь освоить учебник и если без преподавателя его освоить не возможно — это очень плохой учебник! Это я Вам говорю как человек, который очень много занимался именно самообразованием.
А справочник — это справочник, у него совсем другая структура и задачи, вот он именно дополнительные материалы.
А справочник — это справочник, у него совсем другая структура и задачи, вот он именно дополнительные материалы.
УЧЕБНИК не обязан работать как самоучитель, для самообразования он, как бы, в том числе. По определению. В то время, как самоучитель — это УЧЕБНИК для самостоятельного обучения. И нет, я не отрицаю, что кому-то лекции дополняют учебник, а кому-то наоборот. Самообразование же не отрицает возможность слушать лекции?
самоучитель — это УЧЕБНИК для самостоятельного обучения
Следует ли из этого определение:
учебник — это книга для несамостоятельного обучения
?
И воображение рисует инвалидов, которые не способны все делать самостоятельно и должны полагаться на постороннюю помощь, причем эта помощь будет очень дорогой в современном мире. В данном случае — расходы на репетиторов или преподавателей.
Попробуйте напрячь своё воображение ещё немного, и представить систему образования всю. Целиком. И подумайте над тем, что это вообще такое "система образования" и для чего вообще нужно это, якобы никому ненужное, наставничество.
Это несложно, т.к. ответ был заранее готов. «Древо технологий» аналогичная игровым, хотя такая структура в реальности больше похожа на сеть и очень сложную. Но сети две — система знаний (обычный ориентированный граф) и система образования (граф, имеющий направления и начальную точку). Система знаний — такая сеть, работа с которой требует уже наличие знаний. Система образования — это такая сеть, у которой есть некоторый «вход», который не требует знаний.
У современной системы образования есть недостаток — она не представлена в таком виде, отсюда проблема в виде «потерь входов» и прочие проблемы, затронутые в статье. А вот простые системы знаний иногда даже можно увидеть — хотя бы граф связей станиц Википедии, но более сложные системы знаний все таки разрознены.
У современной системы образования есть недостаток — она не представлена в таком виде, отсюда проблема в виде «потерь входов» и прочие проблемы, затронутые в статье. А вот простые системы знаний иногда даже можно увидеть — хотя бы граф связей станиц Википедии, но более сложные системы знаний все таки разрознены.
Следует ли из этого определение:
Нет, не следует:
Учебник — это книга для обучения, в том числе самостоятельного.
УЧЕБНИК и должен работать как самоучитель, роль преподавателя помочь освоить учебник и если без преподавателя его освоить не возможно — это очень плохой учебник!
Так учебник надо осваивать, а не прочитал и "ой, чот непонятно".
А тут где-то в камментах говорят, что препод, вместо того, чтобы объяснить, говорит «иди читай учебники».
он работает именно как я описал
Да, как вы описали, он работает. Но вы никак не обосновали, что этот способ лучший. Последовательность и строгость никак не противоречат учёту особенностей человеческого мышления. И понять от частного (от примеров и потребностей) к общему намного проще, чем от определения к частностям.
Кстати, это результат исследований, что люди строят абстракции по примерам намного проще, чем факты по абстракциям.
учёту особенностей человеческого мышления.
это хорошо, что вы отметили, что принятый в математике способ мышления отличается от обыденного. и одной из задач курса матана, как элементарнейшего введения в математику, в том числе и состоит в обучении этому способу мышления. так как если не понять его на простом курсе матана, где для каждого понятия можно подобрать осязаемый пример, то с воспритие дальнейших более продвинутых разделов станет и вовсе невозможным, ибо там уровень абстракции будет уже другой
вы отметили, что принятый в математике способ мышления отличается от обыденного
Не приписывайте, пожалуйста. Это вообще никакого отношения к моему комментарию не имеет.
Сожалею, что не смог донести мысль. Нужно отделять результат (например, понимание математики) и способ получения результата. Ваша неявная позиция, что текущий способ — единственно верный для получения нужного результата, а при других способах результат не будет достигнут — не имеет под собой оснований.
Я говорил именно про способ достижения. Способ должен лучше учитывать особенности мышления. Он и сейчас немного учитывает — и у Фихтенгольца есть примеры — но можно учитывать лучше.
потому что в математике важно понимать формулировки исходя только из внутренней логики теории. это важно, т.к. в более продвинутых разделах многие понятия уже будет не так просто соотнести с простыми физическими или геометрическими приложениями «на пальцах». та же теорема Ферма (великая) формулируется элементарно, но доказывается через сверх-абстрактные конструкции
вы читаете определение, пытаетесь его обдумать в рамках уже известных вам определений и формализма, затем переходите к примерах (которые у Фихтенгольца зачастую идут сразу после того, как дано определение — буквально несколькими строчками ниже), на которых наглядно показывается как определение работает и почему оно сформулированно именно так. и, да, это нормально — читать и перечитывать материал несколько раз и вдумываться в него, пока путём тренировки не придёт понимание формализма и соответствующего способа мышления
понимание формализма вам в любом случае нужно, если вы собираетесь быть математиком или профессионально использовать математику в своей работе. если — нет, то как я уже неоднократно говорил, именно для таких целей были придуманы курсы на выбор и облегченные варианты типа calculus — то, что у нас такого нет, это уже разговор о недостатках системы образования в целом. но Фихтенгольц — это именно учебник по анализу с математической степенью строгости
так было бы, если бы вам в институте преподаватель прочитал вводную лекцию, потом сказал — всё, встречаемся на экзамене в конце года, сидите читайте учебник, что не поняли — это ваши проблемы, спрашивать буду по всей строгости, не сдадите — вылетаете из института. так нет же, вам минимум раз в неделю читают лекции и проводят семинары, на каждом из которых можно и нужно задавать вопросы
вы читаете определение, пытаетесь его обдумать в рамках уже известных вам определений и формализма, затем переходите к примерах (которые у Фихтенгольца зачастую идут сразу после того, как дано определение — буквально несколькими строчками ниже), на которых наглядно показывается как определение работает и почему оно сформулированно именно так. и, да, это нормально — читать и перечитывать материал несколько раз и вдумываться в него, пока путём тренировки не придёт понимание формализма и соответствующего способа мышления
понимание формализма вам в любом случае нужно, если вы собираетесь быть математиком или профессионально использовать математику в своей работе. если — нет, то как я уже неоднократно говорил, именно для таких целей были придуманы курсы на выбор и облегченные варианты типа calculus — то, что у нас такого нет, это уже разговор о недостатках системы образования в целом. но Фихтенгольц — это именно учебник по анализу с математической степенью строгости
Забавно, если так учили бы плаванию. Расскажут немного теории, а потом столкнут с обрыва и вперед
так было бы, если бы вам в институте преподаватель прочитал вводную лекцию, потом сказал — всё, встречаемся на экзамене в конце года, сидите читайте учебник, что не поняли — это ваши проблемы, спрашивать буду по всей строгости, не сдадите — вылетаете из института. так нет же, вам минимум раз в неделю читают лекции и проводят семинары, на каждом из которых можно и нужно задавать вопросы
в математике важно понимать формулировки исходя только из внутренней логики теории
Формализм в математике, конечно, важен, но нельзя всё подчинять формализму, даже обучение этой математике. Иначе вы получаете молоток, с которым всё на свете становится гвоздями.
В музыке вот тоже важно уметь читать с нотного стана. Следует ли из этого, что вики-статьи или главы учебников по музыке тоже должны писаться сразу на нотном стане, без этой вашей плебейской прозы, вводных примеров, исторических экскурсов и прочих неформальных мешающих факторов? Вы бы сами стали учиться музыке по учебнику, в котором есть лишь главы из нотного стана и этюды в конце каждой главы?
Почему же, скажем, русскоязычная статья "Теория категорий" (и подобных много) сходу в карьер начинает с определения категории, написанного птичьим языком, понятным только прокачанному математику? Англоязычная хотя бы начинает с «Basic concepts», «Applications», «Utility», и только потом переходят к строгому формализму.
именно для таких целей были придуманы курсы на выбор и облегченные варианты типа calculus
Вы уже второй раз упоминаете, что calculus — это какой-то «облегчённый выриант для нематематиков». Откуда вы это взяли? Если что, по-русски calculus — это «математический анализ», а не «вычисления», что там упрощённого?
Вы уже второй раз упоминаете, что calculus — это какой-то «облегчённый выриант для нематематиков». Откуда вы это взяли?
скачайте книжки по калкулусу и убедитесь
Какие именно книжки? Calculus 101? Или что-то более углублённое по одной из тем, упомянутых тут? Я конечно не настоящий сварщик, но по мне calculus — это 100%-й классический матан. Англоязычное же «mathematical analysis» соответствует вовсе не матану, а анализу в целом, который включает в себя и матан, и функан и проч.
Забавно, если так учили бы плаванию. Расскажут немного теории, а потом столкнут с обрыва и вперед
Никто не умирает на уроках матана, поэтому и попыток что-то поменять не предпринимают в лучших традициях «Пока гром не грянет — стиль преподавания не изменится».
в обучении этому способу мышления
Никто не умирает на уроках матана, поэтому и попыток что-то поменять не предпринимают в лучших традициях «Пока гром не грянет — стиль преподавания не изменится».
Очень часто ситуация, когда нужно просто понять смысл определения.
Невозможно понять смысл определения для абстрактного объекта, просто его прочитав, как бы он ни был записан и разъяснен.
Представьте себе человека, который никогда не видел жидкостей и не представляет, что это такое. Как бы вы ему ни объясняли, как она себя ведет, и что представляет — он все равно не поймет. Это невозможно. У него нет соответствующего житейского опыта, который позволяет вам с легкостью, даже не задумываясь, ответить на вопрос: "в стакане налита вода, стакан переворачиваем, что будет?". Точно так же не существует житейского опыта, который бы вам помог понять, что такое кольцо или поле (а это совершенно базовые объекты, чего уж о том, что сложнее, говорить). Единственный способ — нарабатывать этот опыт в мысленных экспериментах.
Или на это можете взглянуть с другой стороны — вот тот же е-д формализм, это просто определенный язык, который вам позволяет рассуждать о бесконечно малых величинах и непрерывности. Можно ли изучить язык, просто почитав какие-то объяснения? Конечно, нет! Нужна полноценная речевая практика и никак иначе. Без практики вы понимать язык не начнете, не бывает так.
По-этому в учебниках никто не ставит себе целью "объяснить так, чтобы стало понятно" — это было бы просто глупостью, подобная задача неразрешима. Учебник должен предоставить достаточно точное и полное объяснение, чтобы студент потом мог по нему ставить мысленные эксперименты и, с-но, показать, как эти эксперименты следует ставить (на примере доказываемых теорем, например). А дальше дело за практикой. Именно по-этому у вас "через пару месяцев решения задачек", после наработки ассоциативных связей, и появляется понимание.
И в попытках понять ты читаешь определение, состоящее из кучи формальных слов, из которых тебе непонятно примерно 50%.
Это всего лишь означает, что нужно сначала понять эти самые непонятные слова, а потом возвращаться к определению.
математика — куча заимствований и куча непонятных слов. По сути — это больше иностранный язык (специализированный, профильный). Но никто не учит его как иностранный язык, в том числе с созданием словарей. Особенно, когда некоторые понятия могут встречаться единожды, тогда смысл запоминать и понимать, если достаточно словаря с разъяснением конкретного термина. Без разъяснения мы упускаем всё то, где этот термин встречается, а в университете таких текстов огромное количество и студенты пользуются заглушками или пустышками для этих терминов, что иногда нарушает всю логику, приводя не к пониманию, а к зубрежке.
Но никто не учит его как иностранный язык, в том числе с созданием словарейВы никогда не видели Бронштейнa и Семендяева? Мне достался от отца. Не помню какое издаение, но знаю что давно. Всё очень понятно и подробно написано.
Без разъяснения мы упускаем всё то, где этот термин встречается, а в университете таких текстов огромное количество и студенты пользуются заглушками или пустышками для этих терминов, что иногда нарушает всю логику, приводя не к пониманию, а к зубрежке.А тут больше вина школьного образования. Которое приучает людей думать, что у учителей есть задача их чему-то там научить. Нету. Учителя — помогают вам научиться, но если вы хотите потратить пять-шесть лет впостую и уйти с пустой головой… это ваше личное дело.
Самая большая проблема нашего образования не в том, как устроены учебники, а в банальном отсуствии двоек в школе и большими проблемами с ними в ВУЗе. В результате людей приучают к тому, что знания не нужны, нужно как-нибудь троечку выциганить…
К сожалению, не был знаком с «Бронштейнa и Семендяева».
Про школьное образование — тут очень много проблем:
— подбор коллектива (случайны процесс, причем с негативным отбором, т.к. успехи не поощряются и иногда ставятся даже в вину, типа "не спеши, коллектив не успевает")
— мотивации в виде «зачем учимся?»
— школьное образование запрещает самостоятельно думать, т.е. не пытайся сам делать, а делай как учитель и думай как учитель
Замечания: в ВУЗе нет учителей, 5-6 лет относится скорее к ВУЗу, но школьные 9-11 лет тоже могут потратить время в пустую и человек уйдет с пустой головой. Это еще в лучшем случае!
Отсутствие двоек? Вы серьезно? Даже в советском образовании были двойки и люди выцыганивали тройки, хоть это было тогда и сложнее. Тогда приучали к нужности образования! В результате работал на гос.предприятии и люди с советским образованием были иной раз очень большой проблемой — трудности в переквалификации и «всегда так делал» (даже если это не правильно). При кривизну рук советских сантехников и даже инженеров (особенно из автопрома) — ходили легенды.
Также из недостатков советского образования (современного и подавно):
— проблема мотивации, особенно зачем учить, если можно зазубрить в ночь перед экзаменом
— социализация людей и сексуальное воспитание (правильный подбор партнера, психология, курсы для родителей, организация групп и т.д.) — поставлено на самотек и «авось»
— финансовый менеджмент (как распоряжаться деньгами — накопление, инвестирование и т.д.) — в советское время табу, сейчас — просто игнор. И многие придумывают варианты на тему «Надо пропить!»
— скорость обучения. У всех разная, но всех под одну скорость, в итоге медлительные отстают, а быстросхватывающим — унижения
и т.д.
Я привел лишь часть проблем. Может, не в двойках дело? Перечисленные проблемы в большинстве случаев даже другие действующие и старые системы не решают.
Про школьное образование — тут очень много проблем:
— подбор коллектива (случайны процесс, причем с негативным отбором, т.к. успехи не поощряются и иногда ставятся даже в вину, типа "не спеши, коллектив не успевает")
— мотивации в виде «зачем учимся?»
— школьное образование запрещает самостоятельно думать, т.е. не пытайся сам делать, а делай как учитель и думай как учитель
Замечания: в ВУЗе нет учителей, 5-6 лет относится скорее к ВУЗу, но школьные 9-11 лет тоже могут потратить время в пустую и человек уйдет с пустой головой. Это еще в лучшем случае!
Отсутствие двоек? Вы серьезно? Даже в советском образовании были двойки и люди выцыганивали тройки, хоть это было тогда и сложнее. Тогда приучали к нужности образования! В результате работал на гос.предприятии и люди с советским образованием были иной раз очень большой проблемой — трудности в переквалификации и «всегда так делал» (даже если это не правильно). При кривизну рук советских сантехников и даже инженеров (особенно из автопрома) — ходили легенды.
Также из недостатков советского образования (современного и подавно):
— проблема мотивации, особенно зачем учить, если можно зазубрить в ночь перед экзаменом
— социализация людей и сексуальное воспитание (правильный подбор партнера, психология, курсы для родителей, организация групп и т.д.) — поставлено на самотек и «авось»
— финансовый менеджмент (как распоряжаться деньгами — накопление, инвестирование и т.д.) — в советское время табу, сейчас — просто игнор. И многие придумывают варианты на тему «Надо пропить!»
— скорость обучения. У всех разная, но всех под одну скорость, в итоге медлительные отстают, а быстросхватывающим — унижения
и т.д.
Я привел лишь часть проблем. Может, не в двойках дело? Перечисленные проблемы в большинстве случаев даже другие действующие и старые системы не решают.
Отсутствие двоек? Вы серьезно? Даже в советском образовании были двойки и люди выцыганивали тройки, хоть это было тогда и сложнее.Даже в советском образовании люди получали диплом об окончании 8го (а кто и 10го класса) с пометками «удовлетворительно» (и выше) во всех графах обладая при этом знаниями на уровне начальной школы.
Я ровно это и имею в виду. Нет двоек — это не обозначает, что их не ставят. Это обозначает, что есть целая система, которая заставляет учащихся и учителей ставить, в конце-концов, тройку «за красивые глаза». За годы обучения в школе человек сознательно или не сознательно подводится к выводу о том, что его задача — не научиться что-то делать, а «выцыганить» тройку.
Перечисленные проблемы в большинстве случаев даже другие действующие и старые системы не решают.Проблема мотивации, как минимум, напрямую зависит от феномена отсуствия двоек. Если система, так или иначе, не допускает появления людей, которые получили неуд (за то, что у них реально нет знаний), то отсюда и получается зубрёжка в ночь перед экзаменом и прочее. То же самое со скоростью обучения: если у вас нет возможности разделить людей на быстро обучаемых и медленно обучаемых, а главное, нельзя вынести «за скобки» совсем необучаемых (неважно — не могут они обучаться или не хотят), то отсюда возникают запреты за самостоятельное мышление и прочее — потому что для педагага не очеь важно, сколько людей научатся что-то делать хорошо — зато черезвычайно важно не допустить, чтобы кто-то «отпал совсем».
Ну это всё равно как если бы вас заставили мясо варить, не давая снять пену и выкинуть её. В результате будет получен большой котёл… «мутной хрени». Вместо прозрачного бульона.
Тут скорее проблема отсутствия реального и осознаваемого наказания, нежели эфемерные двойки, которые сами по себе наказанием не являются.
Под осознаваемым наказанием — здесь и сейчас, а не когда-нибудь с кучей условностей.
Проще на RPG объяснить. Если персонажу поставить дебаф (метка об получении со временем отрицательного урона), то в зависимости от свойств дебафа:
1) дебаф не наносит урон. Или нанесет через 1-6 месяцев и более. Обычно игнорируется из-за свойств человеческой памяти и психологии.
2) дебаф наносит урон сразу и немного. Также может быть проигнорирован, если урон терпимый
3) дебаф наносит случайный урон несколько раз в случайное время. По бихевиоризму — самый идеальный вариант, но обычно не реализуется из-за сложности.
Но в школе ни дебафы, ни бафы (положительные бонусы) не наносятся. Вариант применения бафа — еда в столовой, билеты в кино и т.д.
Максимальный дебаф — двойка. Максимальный баф — пятерка. И они абсолютно ничего не значат и в школе, и в реальном мире, т.к. не делают человека успешным или неудачником. Полно историй, как отличники становились неудачниками и гораздо больше, как двоечники-троечники становились успешными людьми.
Под осознаваемым наказанием — здесь и сейчас, а не когда-нибудь с кучей условностей.
Проще на RPG объяснить. Если персонажу поставить дебаф (метка об получении со временем отрицательного урона), то в зависимости от свойств дебафа:
1) дебаф не наносит урон. Или нанесет через 1-6 месяцев и более. Обычно игнорируется из-за свойств человеческой памяти и психологии.
2) дебаф наносит урон сразу и немного. Также может быть проигнорирован, если урон терпимый
3) дебаф наносит случайный урон несколько раз в случайное время. По бихевиоризму — самый идеальный вариант, но обычно не реализуется из-за сложности.
Но в школе ни дебафы, ни бафы (положительные бонусы) не наносятся. Вариант применения бафа — еда в столовой, билеты в кино и т.д.
Максимальный дебаф — двойка. Максимальный баф — пятерка. И они абсолютно ничего не значат и в школе, и в реальном мире, т.к. не делают человека успешным или неудачником. Полно историй, как отличники становились неудачниками и гораздо больше, как двоечники-троечники становились успешными людьми.
Вы опять не поняли, что я имею в виду под «отсутствием двоек».
Двойка — это не наказание. Двойка — это констатация факта: материал не усвоен, рассказывать что-то дальше — бессмысленно.
Ну вот посмотрите куда-нибудь, где диплома нет, а дают реальные знания. Скажем курсы иностранного языка. Там есть уровни и если вы не пройдёте тест — то вас не допустят в группу рассчитанную на соотвествующий уровень. Это не наказание и не поощрение — это просто способ учить только людей, которые обладают, примерно, одинаковым уровнем знаний.
Вот этот механизм в школе и в огромном количестве ВУЗов выключен нафиг.
Двойка — это не наказание. Двойка — это констатация факта: материал не усвоен, рассказывать что-то дальше — бессмысленно.
Ну вот посмотрите куда-нибудь, где диплома нет, а дают реальные знания. Скажем курсы иностранного языка. Там есть уровни и если вы не пройдёте тест — то вас не допустят в группу рассчитанную на соотвествующий уровень. Это не наказание и не поощрение — это просто способ учить только людей, которые обладают, примерно, одинаковым уровнем знаний.
Вот этот механизм в школе и в огромном количестве ВУЗов выключен нафиг.
Несколько ремарок:
— У нас таки пятибалльная система. Т.е. есть ещё и колы, но они в дискуссии не упоминаются
— Для того, чтобы к оценкам относились серьёзнее, как к констатации факта, а не как к бафу\дебафу, должна быть унифицированная и понятая система выставления оценок, т.е. должно быть понятно, чего и сколько (не)сделать, чтобы получить соответствующую оценку. В любом классе, на любом предмете — одинаковая система. Сейчас это в лучшем случае похоже на систему скидок в магазинах.
— Подкрепление должно быть мгновенным и неизбежным, случайным оно быть не должно, или не работает, или психику портит. При этом оно должно быть в обе стороны, любой дрессировщик подтвердит, что похвалы без наказаний работают плохо.
— «Баф» должен быть материальным и желанным. Например, в школе моя учительница по географии давших ответ за пределами учебника угощала конфетами. Да, «Умница, на сахарок», но все ученики старались, и принцип работает на всех возрастах.
— Место родителей в школьном образовании… В принципе, всё, что связано с воспитанием, а не обучением, должны брать на себя родители. И мотивацию, и базовую философию науки, и бафы-дебафы. Но этого мало что (по усреднению) нет, так и полностью отдать школе не готовы.
— У нас таки пятибалльная система. Т.е. есть ещё и колы, но они в дискуссии не упоминаются
— Для того, чтобы к оценкам относились серьёзнее, как к констатации факта, а не как к бафу\дебафу, должна быть унифицированная и понятая система выставления оценок, т.е. должно быть понятно, чего и сколько (не)сделать, чтобы получить соответствующую оценку. В любом классе, на любом предмете — одинаковая система. Сейчас это в лучшем случае похоже на систему скидок в магазинах.
— Подкрепление должно быть мгновенным и неизбежным, случайным оно быть не должно, или не работает, или психику портит. При этом оно должно быть в обе стороны, любой дрессировщик подтвердит, что похвалы без наказаний работают плохо.
— «Баф» должен быть материальным и желанным. Например, в школе моя учительница по географии давших ответ за пределами учебника угощала конфетами. Да, «Умница, на сахарок», но все ученики старались, и принцип работает на всех возрастах.
— Место родителей в школьном образовании… В принципе, всё, что связано с воспитанием, а не обучением, должны брать на себя родители. И мотивацию, и базовую философию науки, и бафы-дебафы. Но этого мало что (по усреднению) нет, так и полностью отдать школе не готовы.
Ремарки на ремарки:
— У нас тоже, хотя до войны была 12-бальная система, а когда я учился — также была 5-бальная система.
— Помимо выставления оценок еще и система образования должна быть унифицирована. Иначе получается, что даже между двумя классами есть разница в образовании, особенно из-за праздников и прочего выпадение учебных дней. Между школами есть разница, про университеты вообще молчу — каждый год отличается от предыдущего по многим параметрам и чаще всего новые идут в худшую сторону.
— про подкрепление не соглашусь. Ибо бихевиоризм разделяет время (в) и размер (р) подкрепления в виде константного (к) и случайного (с). Итого 4 вида — кв+кр; св+кр; кв+ср; св+ср. Так вот — для случайного времени и случайного размера получены наилучшие результаты в дрессировке дельфинов (у одной из сторонниц бихевиоризма). У людей это еще называется азартом, который подкрепляется непредсказуемостью получения выигрыша. Если в казино будут вместо денег требовать сдачи норм ГТО или иных физ.культ.показателей, тогда все участники будут брать все новые и новые высоты!
— Ваш «Баф» интересен, но не универсален. Одноклассница с сахарным диабетом и все — эта идея вредна. Опять же — мобильные игры предлагают не конфеты, а средства индивидуализации (скрины, темы оформления и т.д.)
Родители и мотивация. Сложное совмещение, если чаще всего окружающий мир неплохо демотивирует и строится на активном потреблядстве. А родительский голос в современном мире еще и нивелируется, т.к. в западной модели мировоззрения родителям уготован дом престарелых для освобождения жил.площади. Да и сами родители могут не уделить своему чаду достаточно времени, ибо работа 40ч в неделю + проезд, т.к. при капитализме «Кто не работает — тот не ест».
— У нас тоже, хотя до войны была 12-бальная система, а когда я учился — также была 5-бальная система.
— Помимо выставления оценок еще и система образования должна быть унифицирована. Иначе получается, что даже между двумя классами есть разница в образовании, особенно из-за праздников и прочего выпадение учебных дней. Между школами есть разница, про университеты вообще молчу — каждый год отличается от предыдущего по многим параметрам и чаще всего новые идут в худшую сторону.
— про подкрепление не соглашусь. Ибо бихевиоризм разделяет время (в) и размер (р) подкрепления в виде константного (к) и случайного (с). Итого 4 вида — кв+кр; св+кр; кв+ср; св+ср. Так вот — для случайного времени и случайного размера получены наилучшие результаты в дрессировке дельфинов (у одной из сторонниц бихевиоризма). У людей это еще называется азартом, который подкрепляется непредсказуемостью получения выигрыша. Если в казино будут вместо денег требовать сдачи норм ГТО или иных физ.культ.показателей, тогда все участники будут брать все новые и новые высоты!
— Ваш «Баф» интересен, но не универсален. Одноклассница с сахарным диабетом и все — эта идея вредна. Опять же — мобильные игры предлагают не конфеты, а средства индивидуализации (скрины, темы оформления и т.д.)
Родители и мотивация. Сложное совмещение, если чаще всего окружающий мир неплохо демотивирует и строится на активном потреблядстве. А родительский голос в современном мире еще и нивелируется, т.к. в западной модели мировоззрения родителям уготован дом престарелых для освобождения жил.площади. Да и сами родители могут не уделить своему чаду достаточно времени, ибо работа 40ч в неделю + проезд, т.к. при капитализме «Кто не работает — тот не ест».
Про «баф» — это были 90е, какие мобильные игры… Но про принцип, как я понял, Вы согласны?
Приведите, пожалуйста, определение «случайного подкрепления». Я опираюсь в первую очередь на книги по дрессировке, краткий смысл: тыкать щенка/кота носом в лужу имеет смысл только пока пахнет, иначе он сам не поймёт, за что его наказывают.
Про родителей и воспитание: нельзя накладывать обязательства, не давая полномочий. Сейчас фактически нельзя отобрать у играющего на уроке школьника телефон или выставить его из класса, родители очень против. Но требуют, чтобы школа воспитывала их детей, поскольку сами они работают целыми днями и общаются с детьми менее часа в день.
Приведите, пожалуйста, определение «случайного подкрепления». Я опираюсь в первую очередь на книги по дрессировке, краткий смысл: тыкать щенка/кота носом в лужу имеет смысл только пока пахнет, иначе он сам не поймёт, за что его наказывают.
Про родителей и воспитание: нельзя накладывать обязательства, не давая полномочий. Сейчас фактически нельзя отобрать у играющего на уроке школьника телефон или выставить его из класса, родители очень против. Но требуют, чтобы школа воспитывала их детей, поскольку сами они работают целыми днями и общаются с детьми менее часа в день.
тыкать щенка/кота носом в лужу имеет смысл только пока пахнет, иначе он сам не поймёт, за что его наказывают.
Считаю это очень глупым занятием. Иногда до анекдотических ситуаций доходит, когда котенок наложит кучу, пару раз в нее потыкается мордой и пойдет себе дальше. Ведь вы учите его тыкаться мордой туда и все. Котенок должен телепатически догадаться, чего вы хотите от него на самом деле?
Пример случайного подкрепления в случайный отрезок времени — обычное казино.
По теме — книга «Прайор Карен. Не рычите на собаку».
Перечитываю книгу, чтобы найти удачный пример. Многие примеры занимаются страницы и указывают только на какой-то один аспект. И вся книга из таких примеров. Вот удачное:
Вариативное подкрепление
Действенность вариативного подкрепления лежит в основе всех азартных игр. Если каждый раз, опустив в автомат 5 центов, будете получать десять, то скоро вы потеряете к этому интерес.
Да, вы будете делать деньги, но какой это нудный способ! Людям нравится играть с автоматом именно потому, что невозможно предугадать заранее, то ли ничего не получишь, то ли какую-то мелочь, то ли сразу кучу денег, и когда именно будит это подкрепление (это может быть только один самый первый раз). Почему одни люди втягиваются в азартную игру, а другие могут поиграть
и бросить, это уже другой вопрос, но для тех, кто попался на крючок, этим крючком стал вариативный режим положительного подкрепления.
Чем длительнее интервалы между подкреплениями в вариативном режиме, тем сильнее
он стимулирует поведение. Однако режимы с длительными интервалами работают против вас, когда вы пытаетесь угасить поведение. Если поведение не подкреплять совсем, то скоро появится тенденция к его угасанию; но если оно все-таки время от времени подкрепляется — неважно сколь эпизодично — одна сигарета, одна рюмка, одна поблажка ворчуну или нытику —
и поведение вместо того, чтобы угаситься, может быть значительно усилено режимом с длительными интервалами между подкреплениями.
Всё, что вы описываете — это уже эффекты второго порядка. Если бы переход на следующую ступень не был бы автоматическим (или почти автоматическим) — то можно было бы разрабатывать системы поощрений, «бафы»/«дебаффы» и прочее.
Но если учащиеся (и, главное, родители) твёрдо уверены в том, что «ну рано или поздно троячок-то сделают, пожурят только чуток» — то всё это не работает.
Но если учащиеся (и, главное, родители) твёрдо уверены в том, что «ну рано или поздно троячок-то сделают, пожурят только чуток» — то всё это не работает.
Знаете, так можно опять упереться в табуированную в Европе тему «лишних людей». Вот, допустим, есть у умственно полноценного человека, не в экстремальных условиях возможность по своей вине не получить обязательное среднее образование, вопросы:
1. Будут ли учителя этим шантажировать? А радикальные родители («девочкам школа лишнее» / «я с 10 лет работал, и ты пойдёшь»)?
2. Сможет ли он найти работу, с которой можно не помереть с голода? Если фактически нет, то это противоречит декларируемой социальной политике.
UPD Подумал, всё ещё проще: у нас нет формализации, что такое и зачем нужна школа, каким в исчислимых проверяемых величинах, должен быть школьник на первой линейке и на последней. Конечно, если пофиг, куда идти, то не заблудишься, но и школьное образование будет для государства больше декоративным объектом, а не функциональным.
1. Будут ли учителя этим шантажировать? А радикальные родители («девочкам школа лишнее» / «я с 10 лет работал, и ты пойдёшь»)?
2. Сможет ли он найти работу, с которой можно не помереть с голода? Если фактически нет, то это противоречит декларируемой социальной политике.
UPD Подумал, всё ещё проще: у нас нет формализации, что такое и зачем нужна школа, каким в исчислимых проверяемых величинах, должен быть школьник на первой линейке и на последней. Конечно, если пофиг, куда идти, то не заблудишься, но и школьное образование будет для государства больше декоративным объектом, а не функциональным.
Можно упереться. Как и всякое табу — данное разрушает общество. Но это можно сделать гораздо более мягкими способами. Если у нас есть проблемы с тем, что работодатели не берут людей без среднего образования, но берут людей с «корочками» и без знаний — то эти знания нужно сделать опциональными. Официально. Чтобы незнание какой-нибудь географии не приводило к тому, что человек выпускался без «корочек» — но чтобы можно было полагаться на то, что если уж у человека написано «знает Географию в объёме 8 классов», то он после этого Австрию и Австралию не путал бы.
Вот не охать не ухать на тему «он вообще не знает чем Акртика от Антарктики отличаются и белых медведей на южном полюсе рисует» (притом что аттестат-то есть!), а официально признать что для того, чтобы разносить пиццу — этих знаний не требуется.
Попытка же решать социальные вопросы за счёт превращения школы из места, где получают знания, в «клуб по интересам» — ничем хорошим кончится не может.
Вот не охать не ухать на тему «он вообще не знает чем Акртика от Антарктики отличаются и белых медведей на южном полюсе рисует» (притом что аттестат-то есть!), а официально признать что для того, чтобы разносить пиццу — этих знаний не требуется.
Попытка же решать социальные вопросы за счёт превращения школы из места, где получают знания, в «клуб по интересам» — ничем хорошим кончится не может.
Тут мы упираемся в 2 классических вопроса: кому это нужно и в чём выгода. Иначе говоря, кто формулирует требования и следит за исполнением, и за чей счёт банкет, вопросы не методические, а политические и управленческие. Нужно будет построить skillwheel/дерево знаний, унифицировать и реформировать образование, убедить работодателей и родителей, и при этом не поломать то, что ещё работает… Ради чего?
при этом не поломать то, что ещё работает…Оно уже не работает.
Ради чего?Ради того, чтобы аттестат и диплом имели какой-то смысл. Потому что сегодня, де-факто, они никакого смысла не имеют и при приёме на работу никак не учитываются. А где учитываются — принимают не любые дипломы, а вполне определённые, система образования в целом — попросту не работает так, как задумано.
Оно уже не работает.В виде малочисленных устоявшихся коллективов, где действительно стараются обучить с учётом личных особенностей и психологии — работает. Но да, скорее вопреки, и коллективы строятся в основном на социальных связях.
они никакого смысла не имеют и при приёме на работу никак не учитываютсяРаботодатели часто не могут очертить круг задач работника, вот и ищут человека-оркестр. Так что, если начинать реформу от формулировки целей, государству следует начать с создания удобного бесплатного аналога НН, хотя бы для госучреждений, с проверяемой формой должностных требований (может, вообще с формочками, а не текстовой).
Бронштейн И.Н., Семендяев К.А.
Справочник по математике для инженеров и учащихся втузов
mexalib.com/view/20254
Справочник по математике для инженеров и учащихся втузов
mexalib.com/view/20254
Ок, я поверил вам, Фихтенгольц самый простой. В том числе, благодаря примерам и приложениям. И 2000 страниц вы не считаете «водой», не так ли?
Я уверен, что можно добавить примеров и «мотиваций» еще на 100 страниц. Немного перемешать существующие абзацы. И тогда моментов, когда что-то непонятно, станет в два раза меньше. Как итог, скорость чтения «средним» студентом вырастет в полтора раза.
Работы — на несколько человеко-лет, плюс еще 5 лет экспериментов. Признаюсь, лично я не смогу выполнить эту работу в ближайшее десятилетие, но такой «апдейт» Фихтенгольца вполне возможен силами «среднего» университета (один математик, два методиста, пара аспирантов, плюс преподаватели для экспериментов). Надеюсь, вы поверите мне на слово.
Я уверен, что можно добавить примеров и «мотиваций» еще на 100 страниц. Немного перемешать существующие абзацы. И тогда моментов, когда что-то непонятно, станет в два раза меньше. Как итог, скорость чтения «средним» студентом вырастет в полтора раза.
Работы — на несколько человеко-лет, плюс еще 5 лет экспериментов. Признаюсь, лично я не смогу выполнить эту работу в ближайшее десятилетие, но такой «апдейт» Фихтенгольца вполне возможен силами «среднего» университета (один математик, два методиста, пара аспирантов, плюс преподаватели для экспериментов). Надеюсь, вы поверите мне на слово.
я написал, что фихтенгольц самый простой, наверное, потому что я сравнивал с другими учебниками, но я вас ни к чему не принуждаю. вы можете открыть любой другой, например, Зорича, Никольского, Кудрявцева, или курсы НМУ (упоминание которого весьма забавно в вашей статье, по соседству с жалобами на «сложноту» понятия предела) и сравнить наглядно. вы же предлагаете «поверить вам на слово» исходя из умозрительного эксперимента
теперь, вы пишите про добавление примеров и мотиваций на «100 страниц». это заниженная оценка. одних параграфов у фихтенгольца 762 штуки. добавление хотя бы одной страницы к каждому, добавит минимум 762 страницы. но ведь там бывает в одном параграфе вводится и по несколько определений
ну во-первых, «апдейтить» таким образом Фихтенгольца вам, к счастью, не дадут, просто из-за авторских прав. проводить подобные эксперименты с лекционным курсом, основываясь на «апдейте», просто бессмысленно, по той простой причине, что целиком Фихтенгольца на лекциях не дают никогда — он просто слишком объемный — энциклопедичный, как сказано в предисловии. стандартный трехсеместровый курс анализа покрывает в лучшем случае всего лишь 30, а то и только 20 процентов всего материала. Фихтенгольц — как вам справедливо и неоднократно отмечали здесь в комментариях, всего лишь часть учебного процесса, в который входят и лекции, и семинары, и возможность непосредственного общения с преподавателями
а теперь представьте, сколько удастся изложить, если ещё и тратить время на «мотивирование» каждого термина. фактически, вы требуете, чтобы вам читали не анализ, а историю математики — какие задачи привели к пределу, какие к производной, к дифференциалам и т.д. и самое забавное, что в начале своего развития анализ как раз не имел точных формулировок, все понятия формулировались очень туммано и пространно, зато «простым народным языком». читать тексты и какие-то доказательства того времени — затруднительно, из-за обилия воды и непонятных рассуждений ни о чём, т.к. без отсутсвия строгих формулировок каждый был волен обращаться с пределами как ему хотелось. естественно, что куча полученных результатов тех времен оказывалась либо ошибочной, либо имела ограниченную область применимости
теперь, вы пишите про добавление примеров и мотиваций на «100 страниц». это заниженная оценка. одних параграфов у фихтенгольца 762 штуки. добавление хотя бы одной страницы к каждому, добавит минимум 762 страницы. но ведь там бывает в одном параграфе вводится и по несколько определений
но такой «апдейт» Фихтенгольца вполне возможен силами «среднего» университета
ну во-первых, «апдейтить» таким образом Фихтенгольца вам, к счастью, не дадут, просто из-за авторских прав. проводить подобные эксперименты с лекционным курсом, основываясь на «апдейте», просто бессмысленно, по той простой причине, что целиком Фихтенгольца на лекциях не дают никогда — он просто слишком объемный — энциклопедичный, как сказано в предисловии. стандартный трехсеместровый курс анализа покрывает в лучшем случае всего лишь 30, а то и только 20 процентов всего материала. Фихтенгольц — как вам справедливо и неоднократно отмечали здесь в комментариях, всего лишь часть учебного процесса, в который входят и лекции, и семинары, и возможность непосредственного общения с преподавателями
а теперь представьте, сколько удастся изложить, если ещё и тратить время на «мотивирование» каждого термина. фактически, вы требуете, чтобы вам читали не анализ, а историю математики — какие задачи привели к пределу, какие к производной, к дифференциалам и т.д. и самое забавное, что в начале своего развития анализ как раз не имел точных формулировок, все понятия формулировались очень туммано и пространно, зато «простым народным языком». читать тексты и какие-то доказательства того времени — затруднительно, из-за обилия воды и непонятных рассуждений ни о чём, т.к. без отсутсвия строгих формулировок каждый был волен обращаться с пределами как ему хотелось. естественно, что куча полученных результатов тех времен оказывалась либо ошибочной, либо имела ограниченную область применимости
я написал, что фихтенгольц самый простой, наверное, потому чтоДруг, я не спорю, что он простой. Я лишь утверждаю, что его можно сделать проще.
НМУ (упоминание которого весьма забавно в вашей статье, по соседству с жалобами на «сложноту» понятия предела)Сложность материала, и сложность подачи материала — это разные вещи. Можно сложение 2+3 запутать коммутативностью (см Арнольда). В НМУ (в том числе судя по комментариям) умели хорошо подавать сложный материал.
целиком Фихтенгольца на лекциях не дают никогдаБез проблем. Можно поработать над теми частями, которые дают чаще всего.
Фихтенгольц — как вам справедливо и неоднократно отмечали здесь в комментариях, всего лишь часть учебного процесса, в который входят и лекции, и семинары, и возможность непосредственного общения с преподавателямиКак отмечали здесь же в комментариях, далеко не всегда можно положиться на преподавателей.
одних параграфов у фихтенгольца 762 штуки. добавление хотя бы одной страницы к каждому, добавит минимум 762 страницы.О, понял вас. Мы по разному трактуем понятие «мотивация». Не нужно писать длинных мотивирующих постов. Часто можно просто перестроить уже имеющийся материал, с добавлением буквально пары приложений. Пример.
В НМУ (в том числе судя по комментариям) умели хорошо подавать сложный материал
А можно пример такого комментария? Пока что, выходит совсем наоборот и НМУ это лучший пример принципа «учить плавать — скинув в воду с обрыва». Оттуда выпускается максимум 2-3 человека со всего набора на первый курс, при том что поступают туда уже сверхмотивированные люди с отличной школьной подготовкой (которые материал Фихетнгольца или его эквивалент освоили уже в школе, наряду с введением в несколько других разделов математики на уровне как минимум одгого семестра обычного ун-та). Это просто потому, что математика развита уже настолько, что материал уже некуда впихнуть. И именно поэтому сейчас новые доказательства каких-нибудь знаменитых теорем понимает лишь десяток человек во всем мире, и они годами разбирают и выверяют доказательство, параллельно делая его доступным для других математиков.
Я лишь утверждаю, что его можно сделать проще.
Я не спорю, что можно проще, но не путём добавления «мотиваций». Ну и про сами мотивации вам внизу написали несколько отличных комментариев, не вижу смысла повторяться. Добавлю лишь, что примеры в Фихтенгольце идут после определений, т.к. они их демонстрируют — невозможно демонстрировать примером определение, которого ещё нет.
Пример.
В вашем примере используется слово «сходится» которое не имеет смысла, пока оно не сформулировано чётким определением. и эти же самые примеры идут в оригинальной книге, сразу после самого определения предела, а не где-то там в конце параграфа
Как отмечали здесь же в комментариях, далеко не всегда можно положиться на преподавателей.
А вот здесь мы опять возвращаемся к уже сформулированному многими другими людьми замечанию, что ваша статья касается проблем преподавания и проблем высшего образования, чем вопросам непосредственно математики.
Интересное у вас представление о НМУ.
НМУ не заканчивают не потому что это так сложно, а потому что это мало кому нужно. Сравните с количеством заканчивающих матфак ВШЭ, программа и преподаватели те же.
Про сверхмотивированных людей, прошедших в школе три курса мехмата, тоже не совсем правда: таких людей не то чтобы очень много.
Наконец, про подход «учить плавать, скинув в воду» не совсем точно. Зависит. Что-то такое есть, да, но вообще-то главное, почему НМУ может научить так хорошо понимать математику, — потому что любой курс сопровождается задачами (если и вовсе не состоит из них).
Как в обычном институте? Ты можешь послушать рассказ лектора, ничего не понять и пойти домой. Потом тебе, может быть, выпадет билет на экзамене с этим, и ты, возможно, что-нибудь сообразишь и запомнишь.
В НМУ тебя после лекции ждёт десяток задач от простых до сложных, и даже если ты что-то не понял в теме, в процессе их решения или же сдачи ты всё поймёшь. Более того, задачи дают большую часть понимания, а лекция — лишь маленькое предисловие к ним, вводящее в курс дела.
НМУ не заканчивают не потому что это так сложно, а потому что это мало кому нужно. Сравните с количеством заканчивающих матфак ВШЭ, программа и преподаватели те же.
Про сверхмотивированных людей, прошедших в школе три курса мехмата, тоже не совсем правда: таких людей не то чтобы очень много.
Наконец, про подход «учить плавать, скинув в воду» не совсем точно. Зависит. Что-то такое есть, да, но вообще-то главное, почему НМУ может научить так хорошо понимать математику, — потому что любой курс сопровождается задачами (если и вовсе не состоит из них).
Как в обычном институте? Ты можешь послушать рассказ лектора, ничего не понять и пойти домой. Потом тебе, может быть, выпадет билет на экзамене с этим, и ты, возможно, что-нибудь сообразишь и запомнишь.
В НМУ тебя после лекции ждёт десяток задач от простых до сложных, и даже если ты что-то не понял в теме, в процессе их решения или же сдачи ты всё поймёшь. Более того, задачи дают большую часть понимания, а лекция — лишь маленькое предисловие к ним, вводящее в курс дела.
программа и преподаватели те же.
далеко не факт. но и ВШЭ появилось не так давно
НМУ не заканчивают не потому что это так сложно, а потому что это мало кому нужно
зачем тогда туда вообще идут?
В НМУ тебя после лекции ждёт десяток задач от простых до сложных, и даже если ты что-то не понял в теме, в процессе их решения или же сдачи ты всё поймёшь
вот видите. лектор не сидит и не разжевывает каждую мелочь в виде какой должна быть епсилон больше 0. а даёт задачи, которые надо решать самому и прорабатывать
Как в обычном институте?
внезапно в обычном институте тоже есть задачи. только уровень их от НМУ отличается кардинально. и вы программу того же первого семестра матана НМУ и обычного универа сравнивали?
далеко не факт. но и ВШЭ появилось не так давно
Матфак ВШЭ создан на базе НМУ. В годы моего обучения в НМУ к нам приходили ребята из вышки, потому что у НМУ и ВШЭ был взаимозачёт листков и экзаменов.
зачем тогда туда вообще идут?
Во-первых, у каждого свои цели.
Во-вторых, идут на 1 курс, где изучаются вполне стандартные анализ, алгебра, топология / геометрия, а не на 5, где даже комбинаторику расскажут на категорном языке и на стыке с алггеомом. Что, конечно, тоже классно, но нужно и понятно куда меньшему числу людей. Полистайте список спецкурсов в этом году, если хотите удостовериться (а после 2 курса, кажется, обучение продолжается именно в форме спецкурсов).
В-третьих, если уж на то пошло, всё зависит не только от сложности или нужности, а от отношения сложность / нужность, которое не столь велико для большинства.
вот видите. лектор не сидит и не разжевывает каждую мелочь в виде какой должна быть епсилон больше 0. а даёт задачи, которые надо решать самому и прорабатывать
Причём тут это вообще? Вообще не вижу, что вы этим доказываете.
Про эпсилон разговор в другой ветке. Да, я всё ещё придерживаюсь тезиса, что если на 1 курсе целый год нужно думать над определениями, чтобы их понять, то курс читают как-то неправильно.
В случае НМУ это пофиксилось бы просто: несколько задачек на понимание эпсилон, и если у тебя ну совсем никак не выходит понять, что же такое эпсилон, то принимающий задаёт тебе какой-нибудь наводящий вопрос. Да и сами задачи являются наводящими вопросами в конце концов.
внезапно в обычном институте тоже есть задачи. только уровень их от НМУ отличается кардинально. и вы программу того же первого семестра матана НМУ и обычного универа сравнивали?
Нет никакой программы НМУ. Всё зависит от преподавателя. Например, на алгебре в 16 году была в основном общая алгебра, в 17 что-то околомехматское, в 18, как и в 15 — категории и что-то околоалггеомное (и это на 1 курсе!).
ium.mccme.ru/f16/f16-algebra-program.pdf
ium.mccme.ru/f17/f17-Elagin_program.pdf
ium.mccme.ru/f18/Shabat_program_IUM.pdf
Матан немножко труднее читать разнообразно, но можно, можно.
И да, естественно, я сравнивал все курсы, что знаю. Но я тут тоже потерял нить спора, к чему вы это?
потому что у НМУ и ВШЭ был взаимозачёт листков и экзаменов.
часть курсов — возможно, но чтобы прям все 1-в-1, тем более, когда, как вы говорите, на нму нет «программы»…
в любом случае, я полагал, что не оканчивают потому что сложно, вы уточнили, что потому что соотношение сложность/нужность — очень высокое, пусть так
Нет никакой программы НМУ.
ну как же, есть на текущий год программа матана ium.mccme.ru/f18/f18-analiz1.html, другие можно найти в прошлых годах. да, они отличаются от препода к преподу, но их общий уровень — на порядок, или я бы даже сказал на два порядка, превышает уровень программы обычного университета. и для того, чтобы освоить всё это за семестр, надо точно также на порядок больше затратить время над самостоятельную работу над книгами и задачами (и иметь при этом на два порядка больше мотивации), чем просто почитать и разобрать материал одной лекции обычного университета, чтобы понять что же такое эпсилон
В случае НМУ это пофиксилось бы просто: несколько задачек на понимание эпсилон, и если у тебя ну совсем никак не выходит понять, что же такое эпсилон, то принимающий задаёт тебе какой-нибудь наводящий вопрос. Да и сами задачи являются наводящими вопросами в конце концов.
так, и в обычных университетах так делают на семинарах
Не возражаю кроме последнего. В обычных университетах копаются в практике, забывая про теорию. Ну то есть если в НМУ всё на заданиях вроде доказать эквивалентность пары определений или теорему, то в обычных университетах это время предпочтут потратить на решение интегралов, пределов, СЛАУ (если мы всё ещё говорим о первом курсе) и т.п.
В итоге эпсилон-дельта так и останутся непознанными, зато мы научимся в столь нужное аналитическое интегрирование.
В итоге эпсилон-дельта так и останутся непознанными, зато мы научимся в столь нужное аналитическое интегрирование.
самые первые задания на практиках, когда даются пределы последовательностей — доказывать что такая-то последовательность имеет предел
вот сидят и ковыряются, вычисляя эти эпсилон-дельта для всяких элементарных вещей
вот сидят и ковыряются, вычисляя эти эпсилон-дельта для всяких элементарных вещей
Ну то есть если в НМУ всё на заданиях вроде доказать эквивалентность пары определений или теорему
А теоремы и эквивалентность определений доказывают на лекциях.
Как в обычном институте? Ты можешь послушать рассказ лектора, ничего не понять и пойти домой. Потом тебе, может быть, выпадет билет на экзамене с этим, и ты, возможно, что-нибудь сообразишь и запомнишь.
В НМУ тебя после лекции ждёт десяток задач от простых до сложных
Чего-то вы выдумываете, по всем предметам же практические занятия есть.
Во-первых, не по всем (кажется, из всех математических предметов отдельно выделенные практические занятия у нас были только по матану и линалу, остальным же приходилось выделять время от лекций). Возможно, потому что я инженер.
Во-вторых, задачи другие же.
Во-вторых, задачи другие же.
кажется, из всех математических предметов отдельно выделенные практические занятия у нас были только по матану и линалу
А какие у вас еще были математические предметы? Теорвер ятп — по нему, думаю, была практика. Диффуры — по ним тоже наверняка была практика. Численные методы — практика тоже точно была, потому что чм без практики это вообще странно. Еще что?
Во-вторых, задачи другие же.
В каком смысле другие? Что изучаете на лекциях, об том и задачи, а как по-другому может быть?
Вот например по анализу у нас оба семестра в расписании было несколько лекций в неделю и несколько семинаров. По лин. алгебре так же. По ОДУ ещё.
А вот функан, вар. исчисление, умф, тензорный анализ и дифгем, тфкп, тервер и слупы, численные и их допглавы и кто помнит что ещё значились в расписании как просто занятия (причём большинство — 1 раз в неделю), и преподавателям приходилось либо из и так небольшого количества лекций выделять практические занятия (а какая об этом может идти речь, если у тебя 1 или 0.5 занятия в неделю, в которые даже лекции не все помещаются?), либо же отделять первую половину лекции под лекцию, а вторую под практику.
Не по всему так было, я сейчас понимаю, что начинаю забывать уже, могу наврать в чём-то, но тем не менее, случай очень частый.
Ха. Вот так и может. На лекции, конечно, расскажут таблицу интегралов в общих определениях, но трюки типа «вот тут прибавим и отнимем x, чтобы взять интеграл» будут именно на практических занятиях.
Я выше об этом говорил. После лекции про предел последовательности в НМУ вас попросят доказать разные факты о пределах и последовательностях, а в обычном институте научат 10 трюкам, как найти какой-нибудь странный предел, не используя Лопиталь или ряд Тейлора. Иными словами, в НМУ задачи теоретические, именно потому люди из НМУ отлично понимают теорию (на которой ведь и базируется всё). В обычных институтах задачи больше практические (хотя где на практике нужно брать предел без Лопиталя, ума не приложу, даже в доказательствах это не нужно). Поэтому студент может, как обезьянка, дифференцировать и интегрировать, не понимая смысла этой операции.
А вот функан, вар. исчисление, умф, тензорный анализ и дифгем, тфкп, тервер и слупы, численные и их допглавы и кто помнит что ещё значились в расписании как просто занятия (причём большинство — 1 раз в неделю), и преподавателям приходилось либо из и так небольшого количества лекций выделять практические занятия (а какая об этом может идти речь, если у тебя 1 или 0.5 занятия в неделю, в которые даже лекции не все помещаются?), либо же отделять первую половину лекции под лекцию, а вторую под практику.
Не по всему так было, я сейчас понимаю, что начинаю забывать уже, могу наврать в чём-то, но тем не менее, случай очень частый.
В каком смысле другие? Что изучаете на лекциях, об том и задачи, а как по-другому может быть?
Ха. Вот так и может. На лекции, конечно, расскажут таблицу интегралов в общих определениях, но трюки типа «вот тут прибавим и отнимем x, чтобы взять интеграл» будут именно на практических занятиях.
Я выше об этом говорил. После лекции про предел последовательности в НМУ вас попросят доказать разные факты о пределах и последовательностях, а в обычном институте научат 10 трюкам, как найти какой-нибудь странный предел, не используя Лопиталь или ряд Тейлора. Иными словами, в НМУ задачи теоретические, именно потому люди из НМУ отлично понимают теорию (на которой ведь и базируется всё). В обычных институтах задачи больше практические (хотя где на практике нужно брать предел без Лопиталя, ума не приложу, даже в доказательствах это не нужно). Поэтому студент может, как обезьянка, дифференцировать и интегрировать, не понимая смысла этой операции.
А вот функан, вар. исчисление, умф, ...
Как-то странно у вас было, если честно.
После лекции про предел последовательности в НМУ вас попросят доказать разные факты о пределах и последовательностях
Но это же везде так. После определения предела вы проходите теоремы об этих пределах.
Как-то странно у вас было, если честно
Не возражаю. Но судя по всему, более-менее везде так кроме пары не совсем скатившихся мест (мехмат там).
Но это же везде так. После определения предела вы проходите теоремы об этих пределах
Нет. В НМУ студент САМ доказывает эти теоремы. У него есть только формулировки. В обычном универе эти теоремы рассказывают студенту на лекциях. Ну камон, это как если бы одни программировали сами, а другие смотрели на ютубе, как пишут код — кто быстрее научится? Даже не так: кто вообще научится?
Нет. В НМУ студент САМ доказывает эти теоремы. У него есть только формулировки. В обычном универе эти теоремы рассказывают студенту на лекциях.
Потому что от студента НМУ ожидается, что он и так все это, вообще говоря, знает.
А как вы будете от человека, который впервые услышал определения, чего-то там доказывать — не совсем ясно. С-но теоремы и имеют целью показать, как это делается. Обучение по подобию.
Заметьте, подавляющее большинство-то в итоге и повторить рассуждения из теоремы не может. А вы предлагаете этим людям его с нуля выдумывать.
Ну камон, это как если бы одни программировали сами, а другие смотрели на ютубе, как пишут код — кто быстрее научится? Даже не так: кто вообще научится?
Так во время обучения людям же дают примеры кода.
Потому что от студента НМУ ожидается, что он и так все это, вообще говоря, знает.
более того, в предисловии к тем же лекциям Львовского это прямо и упоминается
поэтому, все упоминания НМУ в контексте содержания данной статьи и большинства комментариев к ней, мне представляются какой-то сверх-тонкой иронией
большинство и так жалуется на сложность, непонятность и «недомотивированность» обычного курса анализа по Фихтенгольцу. дай им курс НМУ и требования НМУ — большинство далее первых страниц бы не осилило. нет, была бы пара-тройка человек, которые бы справились и выплыли, но мы же не этого хотим?
Druu, вам ответ сюда же.
Так. Для начала давайте разграничим эти два треда — про НМУ и про недостатки образования. Иначе получается довольно странно: в одном месте я топлю за НМУ, где образование довольно непростое, в другом говорю, что образование слишком сложно и надо упрощать (на самом деле нет, ничего такого).
Сперва должен озвучить интересный факт: полтора семестра НМУ мне дали гора-аздо больше в плане математики, чем все матпредметы в МАИ вместе взятые. Я сейчас не про какие-то частные знания вроде «10 трюков, как взять интеграл» или «как решать интегральные уравнения», а именно про общие вещи, про основу, про понимание математики и так далее. МАИ, кажется, вообще инсайтов или внезапных озарений, которые бы затрагивали вообще всю математику, не принёс.
Если вы хотите сказать, что, задавая доказательство теоремы как задачу, ожидается услышать от студента пересказ из учебника — нет, это абсолютная неправда. Если, что студент должен помнить принцип доказательства из учебника, и построить какое-то доказательство на этом самом принципе — нет, это тоже неправда.
Многие задачи вовсе придумываются лектором, и в учебниках отсутствуют.
Лол. Вы не поверите, но так НМУ и работает.
Я проходил курс дискретной математики для школьников (матшкольников, естессно) в НМУ, вот этот вот: ium.mccme.ru/s17/s17-MSkopenkov.html, знаете, как он был устроен?
Все занятия были практическими с паруминутными вкраплениями лекции. Рассказывались определения, а потом в качестве задач задавались различные теоремы и факты об этих определениях, которые нужно было доказать. Сидишь за партой и решаешь самостоятельно. Решил — подзываешь кого-нибудь принять. Время от времени кого-то вызывали к доске, но вообще довольно редко. Или вот книги есть — скажем, Топология от Вербицкого или «Теорема Абеля в задачах» Алексеева, там то же самое.
На большинстве других предметов лекции есть, но тот же самый принцип работает.
Ну блин, ну посмотрите вы пример какой-нибудь. Вот например в этом году вторая лекция по алгебре ium.mccme.ru/postscript/f18/algebra1-lect02.pdf, а вот задачи к ней ium.mccme.ru/postscript/f18/algebra1-list02.pdf. Я вам гарантирую, что на лекции не были рассказаны способы решать эти задачи, их нужно самому придумать.
Подождите. Это вот как раз про разграничение тредов. Нигде и не утверждалось, что лекции НМУ простые. Однако должен сказать, они как правило хорошо мотивированные и вот это вот всё.
Должен сказать, что в НМУ вполне обычно слышать фразу вроде «ну вы все в школе проходили, как брать интегралы через вычеты», всё рассчитано на матшкольников и т.п. И вот пререквизиты ко Львовскому в принципе вполне подходят к программе 57 школы, например www.mccme.ru/~merzon/v14.
Теперь про сложность и непонятность. Я ни в коем случае не считаю, что программа по любому математическому предмету, скажем, сложная, и её нужно упрощать. Или что наоборот надо во все вузы ввести задачи из НМУ (хотя на самом деле было бы круто, но я пока затрудняюсь сказать, как это сделать). Нет. Я считаю, что хромает именно подача материала, например, те же мотивации.
Вот давайте например возьмём стандартную программу по матанализу 1 семестра, как она выглядит?
1. Действительные числа, множества, етс.
2. Последовательность и её предел.
3. Функция и её предел.
4. Производная, дифференциал, ряд Тейлора.
5. Интеграл.
Ну как-то плюс-минус так. Заглядываем внутрь, и видим гору ничем не мотивированных определений, доказательств ничем не мотивированных фактов и так далее. Например, возьмите первокурсника и спросите, зачем нужны последовательности в программе по матану. Лично по-моему, последовательности нужны а) чтобы определить предел функции, т.к. предел последовательности определяется гораздо проще и естественнее; б) через них можно определить действительные числа (хотя это и не делают). Но вам никакой первокурсник этого не скажет. Непонятно зачем они нужны.
Или вот про платоновский мир идей или про систему Евклида «постулаты/аксиомы — определения — доказательства» никто не рассказывает. Да, предполагается, что все это знают со школы, но на самом деле не знают ведь.
Как должна выглядеть программа по моему мнению?
1. Ставим задачу о нахождении касательной, площади, длины, объёма. Замечаем, что если ввести «очень маленькую величину», эти задачи можно решить. Рассказываем про Архимеда, Ньютона, етс. Доказываем, что очень маленькой величины нет и показываем пару парадоксов на эту тему. Анонс: дальше мы расскажем, как посмотреть на эти задачи с другой стороны и решить парадоксы.
2. Рассказываем про предел последовательности и замечаем, что можно определить площадь, касательную, длину, объём и етс как предел этой самой последовательности. Рассказываем про предел функции по Гейне.
3. и так далее.
…
n. Ну и в самом конце можно рассказать про формализацию фундамента, определения чисел и так далее. Когда люди уже понимают, зачем это нужно и что формализация полезна и вообще необходима, ибо см. Евклид.
Напоминаю, что это чисто моё видение, а я про анализ даже 1 семестра знаю и понимаю ну далеко не всё. Уверен, здесь можно намного-намного больше.
Иии… можно продолжать. К предложенному автором «интуитивное понимание — парадоксы — формализация» я пришёл в своё время сам, и из этого делаю вывод, что для других людей тоже должно работать. Сейчас же программа предлагает самому отыскать интуицию за формализацией, а затем ещё и найти, зачем вообще формализация нужна. Можно конечно сказать, что это тоже своеобразное упражнение, но, боюсь, оно в итоге приводит к тому самому «пара-тройка человек выплывает, остальные не поймут анализ никогда».
Так. Для начала давайте разграничим эти два треда — про НМУ и про недостатки образования. Иначе получается довольно странно: в одном месте я топлю за НМУ, где образование довольно непростое, в другом говорю, что образование слишком сложно и надо упрощать (на самом деле нет, ничего такого).
Сперва должен озвучить интересный факт: полтора семестра НМУ мне дали гора-аздо больше в плане математики, чем все матпредметы в МАИ вместе взятые. Я сейчас не про какие-то частные знания вроде «10 трюков, как взять интеграл» или «как решать интегральные уравнения», а именно про общие вещи, про основу, про понимание математики и так далее. МАИ, кажется, вообще инсайтов или внезапных озарений, которые бы затрагивали вообще всю математику, не принёс.
Потому что от студента НМУ ожидается, что он и так все это, вообще говоря, знает.
Если вы хотите сказать, что, задавая доказательство теоремы как задачу, ожидается услышать от студента пересказ из учебника — нет, это абсолютная неправда. Если, что студент должен помнить принцип доказательства из учебника, и построить какое-то доказательство на этом самом принципе — нет, это тоже неправда.
Многие задачи вовсе придумываются лектором, и в учебниках отсутствуют.
А как вы будете от человека, который впервые услышал определения, чего-то там доказывать — не совсем ясно.
Лол. Вы не поверите, но так НМУ и работает.
Я проходил курс дискретной математики для школьников (матшкольников, естессно) в НМУ, вот этот вот: ium.mccme.ru/s17/s17-MSkopenkov.html, знаете, как он был устроен?
Все занятия были практическими с паруминутными вкраплениями лекции. Рассказывались определения, а потом в качестве задач задавались различные теоремы и факты об этих определениях, которые нужно было доказать. Сидишь за партой и решаешь самостоятельно. Решил — подзываешь кого-нибудь принять. Время от времени кого-то вызывали к доске, но вообще довольно редко. Или вот книги есть — скажем, Топология от Вербицкого или «Теорема Абеля в задачах» Алексеева, там то же самое.
На большинстве других предметов лекции есть, но тот же самый принцип работает.
Ну блин, ну посмотрите вы пример какой-нибудь. Вот например в этом году вторая лекция по алгебре ium.mccme.ru/postscript/f18/algebra1-lect02.pdf, а вот задачи к ней ium.mccme.ru/postscript/f18/algebra1-list02.pdf. Я вам гарантирую, что на лекции не были рассказаны способы решать эти задачи, их нужно самому придумать.
более того, в предисловии к тем же лекциям Львовского это прямо и упоминается
Подождите. Это вот как раз про разграничение тредов. Нигде и не утверждалось, что лекции НМУ простые. Однако должен сказать, они как правило хорошо мотивированные и вот это вот всё.
Должен сказать, что в НМУ вполне обычно слышать фразу вроде «ну вы все в школе проходили, как брать интегралы через вычеты», всё рассчитано на матшкольников и т.п. И вот пререквизиты ко Львовскому в принципе вполне подходят к программе 57 школы, например www.mccme.ru/~merzon/v14.
Теперь про сложность и непонятность. Я ни в коем случае не считаю, что программа по любому математическому предмету, скажем, сложная, и её нужно упрощать. Или что наоборот надо во все вузы ввести задачи из НМУ (хотя на самом деле было бы круто, но я пока затрудняюсь сказать, как это сделать). Нет. Я считаю, что хромает именно подача материала, например, те же мотивации.
Вот давайте например возьмём стандартную программу по матанализу 1 семестра, как она выглядит?
1. Действительные числа, множества, етс.
2. Последовательность и её предел.
3. Функция и её предел.
4. Производная, дифференциал, ряд Тейлора.
5. Интеграл.
Ну как-то плюс-минус так. Заглядываем внутрь, и видим гору ничем не мотивированных определений, доказательств ничем не мотивированных фактов и так далее. Например, возьмите первокурсника и спросите, зачем нужны последовательности в программе по матану. Лично по-моему, последовательности нужны а) чтобы определить предел функции, т.к. предел последовательности определяется гораздо проще и естественнее; б) через них можно определить действительные числа (хотя это и не делают). Но вам никакой первокурсник этого не скажет. Непонятно зачем они нужны.
Или вот про платоновский мир идей или про систему Евклида «постулаты/аксиомы — определения — доказательства» никто не рассказывает. Да, предполагается, что все это знают со школы, но на самом деле не знают ведь.
Как должна выглядеть программа по моему мнению?
1. Ставим задачу о нахождении касательной, площади, длины, объёма. Замечаем, что если ввести «очень маленькую величину», эти задачи можно решить. Рассказываем про Архимеда, Ньютона, етс. Доказываем, что очень маленькой величины нет и показываем пару парадоксов на эту тему. Анонс: дальше мы расскажем, как посмотреть на эти задачи с другой стороны и решить парадоксы.
2. Рассказываем про предел последовательности и замечаем, что можно определить площадь, касательную, длину, объём и етс как предел этой самой последовательности. Рассказываем про предел функции по Гейне.
3. и так далее.
…
n. Ну и в самом конце можно рассказать про формализацию фундамента, определения чисел и так далее. Когда люди уже понимают, зачем это нужно и что формализация полезна и вообще необходима, ибо см. Евклид.
Напоминаю, что это чисто моё видение, а я про анализ даже 1 семестра знаю и понимаю ну далеко не всё. Уверен, здесь можно намного-намного больше.
Иии… можно продолжать. К предложенному автором «интуитивное понимание — парадоксы — формализация» я пришёл в своё время сам, и из этого делаю вывод, что для других людей тоже должно работать. Сейчас же программа предлагает самому отыскать интуицию за формализацией, а затем ещё и найти, зачем вообще формализация нужна. Можно конечно сказать, что это тоже своеобразное упражнение, но, боюсь, оно в итоге приводит к тому самому «пара-тройка человек выплывает, остальные не поймут анализ никогда».
Если вы хотите сказать, что, задавая доказательство теоремы как задачу, ожидается услышать от студента пересказ из учебника — нет, это абсолютная неправда.
Я говорю о том, что те вещи что мы обсуждаем студент НМУ знает еще до того, как их начали изучать. В случае же любого другого случайного заведения — он их не знает. Логично, что обучение тому, что знаешь, отличается от обучения тому, чего не знаешь. Так ведь?
Или вот книги есть — скажем, Топология от Вербицкого или «Теорема Абеля в задачах» Алексеева, там то же самое.
Задачи после параграфов практически во всех учебниках есть.
Как должна выглядеть программа по моему мнению?
Проблема в том, что то, что вы описываете, возможно только в очень ограниченном числе случаев для очень ограниченного числа объектов.
Я говорю о том, что те вещи что мы обсуждаем студент НМУ знает еще до того, как их начали изучать.
Это тоже неправда. Во-первых, нет. Никакой матшкольник не знает категории (да и выпускник мехмата наверное далекоо не каждый) — а вон они, на первом курсе НМУ. Вещи, которые студент и так знает, скажем, комплексные числа, изучать нет никакого смысла, и такой фигнёй в НМУ никто не занимается.
Во-вторых, студенты разные, и на 1 курсе НМУ бывают люди с разными знаниями. Встречаются и аспиранты, которые те же категории знают, таких единицы; встречаются и 10-11-классники.
Задачи после параграфов практически во всех учебниках есть.
Это такой троллинг что ли? Вы рассуждаете о том, что не знаете, пытаясь попасть в точку?
Откройте, да посмотрите: www.mccme.ru/free-books/pdf/alekseev.pdf
Возьмём, например, 4 главу «Циклические группы» — 7 строк в начале главы это определение, что такое порядок элемента. А дальше — задачи. Теория даётся в задачах, слышите? В обычном учебнике какой-нибудь факт вроде «a^i != a^j для элемента бесконечного порядка» будет доказываться автором в тексте, а в задачах будет что-нибудь вроде «выпишите элементы группы симметрий квадрата». Здесь такие факты даются в качестве задач читающему.
Проблема в том, что то, что вы описываете, возможно только в очень ограниченном числе случаев для очень ограниченного числа объектов.
Во-первых, докажите. Я не понимаю, почему вы так считаете.
Во-вторых, что мешает так читать хотя бы те предметы, в которых это возможно? Тот же анализ.
Это тоже неправда. Во-первых, нет. Никакой матшкольник не знает категории
При чем тут категории если мы говорим конкретно о теории пределов?
Во-вторых, студенты разные, и на 1 курсе НМУ бывают люди с разными знаниями.
Конечно с разными, но программа НМУ устроена так, что теория пределов предполагается известной для студента.
Во-первых, докажите. Я не понимаю, почему вы так считаете.
Потому что подавляющее большинство мат. объектов вводятся без какой-либо мотивировки и оказывается полезным постфактум. Пределы, производные и прочую элементарщину вы сможете так вот на пальцах" пояснить, что-то чуть более сложное — уже нет.
Это такой троллинг что ли?
Какой троллинг? Еще раз — задачи после параграфа есть в любом нормальном учебнике. Офк, бывает что нет — но это исключение.
Здесь такие факты даются в качестве задач читающему.
Ну и так практически в любом учебнике происходит. Непонятно, где вы тут что-то особенное увидели.
При чем тут категории если мы говорим конкретно о теории пределов?Вы утверждаете, что студенты НМУ уже плюс-минус знакомы с темой, на которую рассказывается лекция. И говорите, что не понимаете, как студент может доказать что-то про объект, определение которого услышал 5 минут назад.
Я привёл пример. Чем категории принципиально отличаются от пределов?
Потому что подавляющее большинство мат. объектов вводятся без какой-либо мотивировки и оказывается полезным постфактум. Пределы, производные и прочую элементарщину вы сможете так вот на пальцах" пояснить, что-то чуть более сложное — уже нет.Во-первых, вы говорите что-то странное. Да, математики чисто по приколу придумывают объекты и что-то про них доказывают, но нет, мы говорим не об этом. Когда вы составляете программу «чему учить первокурсников в 1 семестре на анализе», у вас должна быть конкретная причина, зачем туда включать ту или иную тему. Это и есть мотивировка.
Какой троллинг? Еще раз — задачи после параграфа есть в любом нормальном учебнике. Офк, бывает что нет — но это исключение.Ещё раз: это не учебник, это задачник. Задачи после параграфа, как правило, не такие сложные, но даже если вдруг и так, их количество не может конкурировать с количеством задач в задачнике.
Ну вот вам например бауманский учебник:
Спойлер
Не такие задачи в НМУ по сложности, не такие.
Я привёл пример. Чем категории принципиально отличаются от пределов?
Категории от теории пределов отличаются тем, что их студенту НМУ знать (наверное) не требуется, а теорию пределов — знать требуется.
Когда вы составляете программу «чему учить первокурсников в 1 семестре на анализе», у вас должна быть конкретная причина, зачем туда включать ту или иную тему.
Так еще раз, теорию пределов студент НМУ уже знает.
Ещё раз: это не учебник, это задачник.
А при чем тут задачник, если речь про учебник? Вы потеряли нить разговора.
Не такие задачи в НМУ по сложности, не такие.
А какая разница, какие они по сложности? Задачи на понимание теории есть? Есть. Ч. Т. Д.
Конечно, в НМУ все на порядок сложнее — на то он и НМУ. Именно по-этому программа НМУ на порядок менее понятна и более сложна.
Однако должен сказать, они как правило хорошо мотивированные и вот это вот всё.
ну, не знаю… в рамках того требования к «мотивировке», которое задал автор настоящей статьи (чтобы всё подкреплялось практическими примерами и чуть ли сразу не приложениями), про лекции того же Львовского я бы так не сказал. сразу вводит кучу абстракций типа топ.пространств и фигачит дальше со страшной силой.
у меня всё-таки впечатление, что это ориентированно именно на мотивированного студента
И вот пререквизиты ко Львовскому в принципе вполне подходят к программе 57 школы, например www.mccme.ru/~merzon/v14.
ну, собственно, про это я и писал в этом комментарии, например: habr.com/post/427345/#comment_19348158 — в НМУ на порядок выше требования к школьной подготовке, с чем вы тогда не согласились. отмечу лишь, что я там имел ввиду именно обычный средний университет, а не топ-уровень навроде мехмата. ибо в топы тоже поступают с неслабой подготовкой и проблем с мотивацией (по крайней мере матана) там тоже возникать не должно
Рассказывались определения, а потом в качестве задач задавались различные теоремы и факты об этих определениях, которые нужно было доказать. Сидишь за партой и решаешь самостоятельно
так, ну то, что в НМУ высокие требования к школьной подготовке студентов мы уже выяснили. вы в пример приводите школьный кружок, но опять таки тоже для матшкольников. но в обычном случае, проблема в том, что для того чтобы быть способными что-то доказать самостоятельно, необходимо достичь некоторого «критического уровня». такой уровень поставят в матшколе, но в случае с обычными выпускниками — скорее всего он у них будет отсутствовать. и такие студенты, какую прекрасную лекцию им не прочитай, всё равно не будут способны что-то доказывать — они просто не умеют. чтобы научились и приходится давать элементарные доказательства на лекциях
Заглядываем внутрь, и видим гору ничем не мотивированных определений, доказательств ничем не мотивированных фактов и так далее
не знаю, почему у вас сложилось такое мнение. видимо, вам очень неудачно прочитали курс по стандартной программе. я же, например, открывая Фихтенгольца, вижу достаточно элементарное и разжёванное изложение, простое до такой степени, что в нём может разобраться выпускник обычной (не математической!) школы, при понимании важности самостоятельной работы и необходимости прорабатывать материал.
и, считаю, что именно это элементарное понимание концепции «самостоятельной работы» у многих отсутствует: люди просто не понимают, что лекции надо перечитывать и разбирать, точно так же, как и учебник надо читать с ручкой в руках и продёлывать все выкладки, по несколько раз, до полного понимания. в идеале, потом ещё и открывать Демидовича и прорешивать задачи по пройденному разделу (а помимо просто вычислительных, там хватает и задач на понимание определений, и даже задач на доказательство/интерпретацию теории)
Но вам никакой первокурсник этого не скажет. Непонятно зачем они нужны
ну здесь не надо так обобщать. учивший студент — ответит, неучивший — не ответит
Как должна выглядеть программа по моему мнению?
на самом деле, вполне неплохая программа, которая возможно и даст свои плоды. тем не менее, проблема с неспособностью самостоятельно доказывать утверждения, всё равно сохранится и с ней, так что все те же самые теоремы, что и в обычном курсе — всё равно надо будет показывать как доказывать, только в другом порядке
основная же загвоздка в том, что нет таких учебников по вашей программе (или я не знаю). так что имеется, с одной стороны, Фихтенгольц и его вариации в сторону упрощений (тот же Пискунов). или «новомодные» учебники типа Зорича, где с самого начала гонят ещё больше абстракций, которые требуют и более высокого порога вхождения, и десятикратно большего объема самостоятельной работы, чем простой фихтенгольц
Сперва должен озвучить интересный факт: полтора семестра НМУ мне дали гора-аздо больше в плане математики, чем все матпредметы в МАИ вместе взятые
ну, на самом деле, это очевидно, для специализированного университета уровня НМУ. но вы не думали, что вы так много получили в НМУ, именно благодаря тому, что до этого у вас была подготовка МАИ, где вам набили руку на рутинных задачах и задали общий уровень? потом вы смогли углубиться и отшлифовать детали в НМУ, но именно благодаря тому что вы уже имели общение представление о математике и знали куда и где копать
Львовский это сильно своеобразное чтиво, например, я его даже будучи в НМУ не очень понимал, а начал сильно после. Это совсем никак не учебник для начинающих (в любом смысле), а скорее шпаргалка для тех, кто уже знаком со всеми мотивациями. Как и Бурбаки или Кнут, например.
Курсы НМУ не мотивированы на том уровне, на котором предложил автор статьи. На таком уровне вообще не очень много что объясняется, увы.
Но курсы НМУ мотивированы сильно лучше, чем многое другое, в частности, большинство моих маткурсов в МАИ.
Я лишь хотел а) развеять миф о том, что НМУ не заканчивают только потому что это очень сложно — нет, не только; б) развеять миф, что крутой уровень студентов обуславливается лишь очень сложной программой, которая обеспечивает не столько подготовку, сколько отбор. Есть такое, да, программа действительно сложнее и отбор действительно есть, но нет, там именно подготовка, а не отбор. Ну и в) объяснить, за счёт чего такой эффект.
Вообще тут хорошо бы начать делить, а про какую программу мы говорим, т.к. например, анализ, читаемый гуманитариям, инженерам, физикам и математикам — это, по-хорошему, 4 разных анализа. С соответственными задачами и так далее. Кому-то доказательства совсем не сдались (хотя было бы классно научить и их доказывать, но давайте двигаться шажками), кому-то же это жизненно необходимо.
Анализ, читаемый математикам, я видел только в НМУ, и он был хорошим. Но я предполагаю, что читаемое математикам в более-менее остальных местах сильно напоминает мою программу для инженеров в МАИ, а значит, отстой.
Скажите, для чего нужны последовательности в анализе 1 семестра? Я своё мнение озвучил, но я ещё не уверен, что оно верно. Это пока просто результат обдумывания, который мне ещё никто не аппрувил. Если ваше такое же, вы же так думали об этом и до меня (странный вопрос, но я его должен спросить)?
Ну и — откуда об этом узнаёт студент, в результате долгого обдумывания программы матана и задавания себе вопросов «а зачем нам рассказали вот это»? Я не помню мотивировки к их вводу ни в Зориче, ни в Фихтенгольце, ни в Кудрявцеве, ни, кажется, ещё где-либо.
Кроме того, как минимум нигде не указанными пререквизитами к тому же Фихтенгольцу будет понимание, что математика устроена как евклидова геометрия (постулаты, определения, теоремы, етс) и наверное ещё что математика это не про реальный мир. Без этого нормально понять анализ не получится.
Лично мне с домашкой в 500-600 интегралов-пределов было просто не до Демидовича :)
Но — нет. У меня не было представления о математике и куда копать.
Например, на моей самой первой лекции в НМУ, это была лекция по геометрии, рассказали про попытки доказать 5 постулат и про Лобачевского. Так совпало, что я эту же историю читал парой дней раньше в какой-то научпоп-книжке.
История была увлекательной, она (особенно после второго прослушивания) осталась у меня в памяти, и довольно скоро я понял, что так в общем и устроена вся математика.
Ещё я где-то прочитал про идею Гильберта «мы можем вместо точек, прямых и окружностей рассуждать о пивных кружках, столах и стульях, дав им такие же определения, и результаты не изменятся».
Это всё привело к внезапному пониманию, как же всё-таки устроена математика. Почему всё всегда доказывается. Почему обозначения не важны, и об определениях спорить бессмысленно. И так далее.
На первой алгебре был интересный рассказ про числа и уравнения. И на первом анализе тоже, надо же.
Тут ещё стоит сделать отступление и сказать, что школьники после школы в большинстве случаев не знают, что такое иррациональные числа, а помнят лишь вызубренный факт, что пи, е и корни из 2, 3, 5, 7 иррациональны. Много раз проверял. Сам уже не помню, откуда это узнал, но точно не из школы.
Так вот, на анализе рассказывали определения натуральных чисел, затем целых через натуральные, рациональных через целые и, кажется, целых через действительные. Кстати про упомянутую сложность НМУ — слов вроде «факторизация по отношению эквивалентности» ещё не звучало, было просто «считаем такие пары одинаковыми, если...». Про факторизацию я узнал и вовсе сильно позже, читая и разбирая Лорана Шварца.
Ещё интересный факт, мне и до этого рассказывали эти определения — преподаватель по алгебре в МАИ, весьма увлечённый человек, во время экзамена разговор зашёл в это русло, и удалось дознаться у него, что натуральные числа это, оказывается, множества. Правда, смысла этого я тогда не понял.
На алгебре же рассказывали про различные уравнения, которые внезапно оказались мотивировкой ко вводу новых видов чисел. В натуральных не решается уравнение x + 1 = 0, в целых 2x = 1, в рациональных x^2 = 2, в действительных x^2 + 1 = 0. Можно продолжать.
А вот ещё вспомнилась за несколько месяцев до НМУ старая (2012 что ли) скачанная лекция оттуда по алгебре (читал Смирнов). Там тоже никаких фактормножеств не вводилось. Он захотел определить кольцо вычетов, и рассказал так: «Давайте поделим все числа на n с остатком. И сложим разные числа в разные корзины. Вот эти корзины и будем считать числами и научимся их складывать и умножать.». Причём там было гораздо проще и многословнее, я укорачиваю в расчёте, что вы это знаете. Ох уж это непонятное и сложное НМУ :)
Курсы НМУ не мотивированы на том уровне, на котором предложил автор статьи. На таком уровне вообще не очень много что объясняется, увы.
Но курсы НМУ мотивированы сильно лучше, чем многое другое, в частности, большинство моих маткурсов в МАИ.
в НМУ на порядок выше требования к школьной подготовке, с чем вы тогда не согласились.Ээ, нет, не было такого. Я специально поискал, может ошибаюсь, но вроде нет, не говорил я такого.
Я лишь хотел а) развеять миф о том, что НМУ не заканчивают только потому что это очень сложно — нет, не только; б) развеять миф, что крутой уровень студентов обуславливается лишь очень сложной программой, которая обеспечивает не столько подготовку, сколько отбор. Есть такое, да, программа действительно сложнее и отбор действительно есть, но нет, там именно подготовка, а не отбор. Ну и в) объяснить, за счёт чего такой эффект.
что для того чтобы быть способными что-то доказать самостоятельно, необходимо достичь некоторого «критического уровня»Согласен.
такой уровень поставят в матшколе, но в случае с обычными выпускниками — скорее всего он у них будет отсутствовать.Согласен.
чтобы научились и приходится давать элементарные доказательства на лекцияхНе согласен, что этого достаточно, чтобы научиться доказывать. Хотя это да, разумеется, даст некоторое представление, как доказательства выглядят, но чтобы научиться доказывать, нужно доказывать. Могу ошибаться, но по моему опыту нет никакого плавного входа в доказательства — нужно пытаться, и в какой-то момент будет первый качественный скачок.
Вообще тут хорошо бы начать делить, а про какую программу мы говорим, т.к. например, анализ, читаемый гуманитариям, инженерам, физикам и математикам — это, по-хорошему, 4 разных анализа. С соответственными задачами и так далее. Кому-то доказательства совсем не сдались (хотя было бы классно научить и их доказывать, но давайте двигаться шажками), кому-то же это жизненно необходимо.
Анализ, читаемый математикам, я видел только в НМУ, и он был хорошим. Но я предполагаю, что читаемое математикам в более-менее остальных местах сильно напоминает мою программу для инженеров в МАИ, а значит, отстой.
видимо, вам очень неудачно прочитали курс по стандартной программе.Да, это так. Но подождите, давайте обсудим Фихтенгольца.
Скажите, для чего нужны последовательности в анализе 1 семестра? Я своё мнение озвучил, но я ещё не уверен, что оно верно. Это пока просто результат обдумывания, который мне ещё никто не аппрувил. Если ваше такое же, вы же так думали об этом и до меня (странный вопрос, но я его должен спросить)?
Ну и — откуда об этом узнаёт студент, в результате долгого обдумывания программы матана и задавания себе вопросов «а зачем нам рассказали вот это»? Я не помню мотивировки к их вводу ни в Зориче, ни в Фихтенгольце, ни в Кудрявцеве, ни, кажется, ещё где-либо.
Кроме того, как минимум нигде не указанными пререквизитами к тому же Фихтенгольцу будет понимание, что математика устроена как евклидова геометрия (постулаты, определения, теоремы, етс) и наверное ещё что математика это не про реальный мир. Без этого нормально понять анализ не получится.
Лично мне с домашкой в 500-600 интегралов-пределов было просто не до Демидовича :)
ну здесь не надо так обобщать. учивший студент — ответит, неучивший — не ответитСюда же — откуда он об этом узнает?
тем не менее, проблема с неспособностью самостоятельно доказывать утверждения, всё равно сохранится и с ней, так что все те же самые теоремы, что и в обычном курсе — всё равно надо будет показывать как доказывать, только в другом порядкеДа, это правда, но перегруппировывать темы, рассказывать историю и мотивировки имеет под собой другую цель — подать курс не как кучу разрозненных фактов, непонятно зачем собранных вместе, а как законченную логичную историю, в которой всё на своём месте. Каждый будет понимать, зачем последовательности, зачем предел, зачем дифференциал.
основная же загвоздка в том, что нет таких учебников по вашей программеЭто правда, да, увы. На самом деле когда я думал про сегодня эту программу, мне в ней почудился Курант-Роббинс, у них, кажется довольно научно-популярный учебник. И наверное неформальный.
ну, на самом деле, это очевидно, для специализированного университета уровня НМУ. но вы не думали, что вы так много получили в НМУ, именно благодаря тому, что до этого у вас была подготовка МАИ, где вам набили руку на рутинных задачах и задали общий уровень? потом вы смогли углубиться и отшлифовать детали в НМУ, но именно благодаря тому что вы уже имели общение представление о математике и знали куда и где копатьДумал, и это отчасти верно. Когда я пришёл в НМУ, мне действительно было проще, потому что я уже понимал эпсилон-дельта, интеграл и предел, всякие там бесконечно малые (я тогда ещё считал, что величины), матрицы, векторы, вот это всё, имел кое-какой опыт с комплексными числами и так далее. И даже знал, что такое доказательство. Это куда лучше, чем если бы я пришёл после школы.
Но — нет. У меня не было представления о математике и куда копать.
Например, на моей самой первой лекции в НМУ, это была лекция по геометрии, рассказали про попытки доказать 5 постулат и про Лобачевского. Так совпало, что я эту же историю читал парой дней раньше в какой-то научпоп-книжке.
История была увлекательной, она (особенно после второго прослушивания) осталась у меня в памяти, и довольно скоро я понял, что так в общем и устроена вся математика.
Ещё я где-то прочитал про идею Гильберта «мы можем вместо точек, прямых и окружностей рассуждать о пивных кружках, столах и стульях, дав им такие же определения, и результаты не изменятся».
Это всё привело к внезапному пониманию, как же всё-таки устроена математика. Почему всё всегда доказывается. Почему обозначения не важны, и об определениях спорить бессмысленно. И так далее.
На первой алгебре был интересный рассказ про числа и уравнения. И на первом анализе тоже, надо же.
Тут ещё стоит сделать отступление и сказать, что школьники после школы в большинстве случаев не знают, что такое иррациональные числа, а помнят лишь вызубренный факт, что пи, е и корни из 2, 3, 5, 7 иррациональны. Много раз проверял. Сам уже не помню, откуда это узнал, но точно не из школы.
Так вот, на анализе рассказывали определения натуральных чисел, затем целых через натуральные, рациональных через целые и, кажется, целых через действительные. Кстати про упомянутую сложность НМУ — слов вроде «факторизация по отношению эквивалентности» ещё не звучало, было просто «считаем такие пары одинаковыми, если...». Про факторизацию я узнал и вовсе сильно позже, читая и разбирая Лорана Шварца.
Ещё интересный факт, мне и до этого рассказывали эти определения — преподаватель по алгебре в МАИ, весьма увлечённый человек, во время экзамена разговор зашёл в это русло, и удалось дознаться у него, что натуральные числа это, оказывается, множества. Правда, смысла этого я тогда не понял.
На алгебре же рассказывали про различные уравнения, которые внезапно оказались мотивировкой ко вводу новых видов чисел. В натуральных не решается уравнение x + 1 = 0, в целых 2x = 1, в рациональных x^2 = 2, в действительных x^2 + 1 = 0. Можно продолжать.
А вот ещё вспомнилась за несколько месяцев до НМУ старая (2012 что ли) скачанная лекция оттуда по алгебре (читал Смирнов). Там тоже никаких фактормножеств не вводилось. Он захотел определить кольцо вычетов, и рассказал так: «Давайте поделим все числа на n с остатком. И сложим разные числа в разные корзины. Вот эти корзины и будем считать числами и научимся их складывать и умножать.». Причём там было гораздо проще и многословнее, я укорачиваю в расчёте, что вы это знаете. Ох уж это непонятное и сложное НМУ :)
Не согласен, что этого достаточно, чтобы научиться доказывать
ну так я и не утверждал, что это достаточное условие — но необходимое, безусловно
в идеальном случае, вообще, надо бы хотя бы семестр, а лучше два, читать какой-то подготовительный курс на уровне фихтенгольца (или по вашей программе), дабы закрыть школьные пробелы, а потом делать качественный скачок. но, увы, на такое просто никакая программа не расчитана, и всё-таки некоторым подоготовленным студентам этот курс был бы скучен. идеальных выходом, опять же, была бы модель западных университетов, когда все курсы идут по выбору, и те кто не уверен в своих силах, выбирали бы подготовительный курс, а с хорошей подготовкой — продвинутый. но, т.к. такого нет и не предвидится, то читают исходя из расчёта на самых слабых
Вообще тут хорошо бы начать делить, а про какую программу мы говорим, т.к. например, анализ, читаемый гуманитариям, инженерам, физикам и математикам — это, по-хорошему, 4 разных анализа
и об этом я тоже неоднократно говорил, когда опять приводил примеры с calculus — упрощенным курсом анализа для инженеров, который тоже решал бы подавляющее число проблем, сформулированных здесь. не всем нужен анализ со строгим последовательным изложениям с доказательствами
в исходной статье «критикуют» Фихтенгольца, поэтому речь и идёт об обычном курсе, на нём построенном (естественно, с сильными сокращениями). такой занимает три семестра, если грубо, то 1 — дифференцирование, 2 — интегрирование + дифф нескольких переменных, 3 — интегрирование по нескольким переменным. такой курс анализа принят в большинстве обычных (не топовых!) университетах на математических и физ-мат специальностях (зачастую вообще читают вместе всему потоку)
Если ваше такое же, вы же так думали об этом и до меня (странный вопрос, но я его должен спросить)?
ну и вы правильно написали, разумеется, и я уже отвечал на этот вопрос даже до вашего сообщения: в первую очередь последовательности нужны для того, чтобы определить предел функции и на основе его — непрерывность. потом — доказать непрерывность элементарных функций. вывести число Е
Сюда же — откуда он об этом узнает?
внимательный студент — прямо на лекциях, тем более лектор всё равно будет эту взаимосвязь подчеркивать. если лектор тарабнит определения как машина, и не добавляет ничего кроме формального минимума (и то, определение Е входит в их число), то есть ещё и семинары, где после задачек на пределы, последует тема непрерывных функций и семинарист скажет: а помните сколько мы задач нарешали на разные пределы последовательностей, вот теперь они нам понадобятся доказать непрерывность элементарных функций. если уж и с семинарами туго — это, вообще-то уже будет систематическая проблема курса анализа в этом универе. но даже при этом, как минимум при подготовке к экзамену, когда надо будет перечитывать все лекции целиком, откроется полная картина, где всё взаимосвязано и подогнано (если студент эту картину не открывал по кусочкам во время семестра, перечитывая и сопоставляя лекции). если уж и лекции были прочитаны хаотично — то, да, неоткуда :) тогда остается лишь брать книжку и разбираться самому
Лично мне с домашкой в 500-600 интегралов-пределов было просто не до Демидовича :)
500 интегралов это перебор, 100 достаточно. но интегралы задают в середине второго семестра, пределы последовательностей идут в начале первого. и, что, у вас основной задачник на практиках не Демидович был?
Я не помню мотивировки к их вводу ни в Зориче, ни в Фихтенгольце, ни в Кудрявцеве, ни, кажется, ещё где-либо.
ну а как мотивируют в НМУ? или насколько понимаю, никак — предполагается что уже все и так должны знать?
математика устроена как евклидова геометрия (постулаты, определения, теоремы, етс) и наверное ещё что математика это не про реальный мир. Без этого нормально понять анализ не получится.
не, ну это уже к вопросам философии. например про отсылку к евклиду я только что от вас услышал, поэтому не считаю что «Без этого нормально понять анализ не получится»
Много раз проверял. Сам уже не помню, откуда это узнал, но точно не из школы.
ну, не знаю. по-моему всё-таки школьники знают, что ирррациональные числа — это такие, которые нельзя представить в виде дроби, как минимум. если не знают, то на 1й лекции это напоминается с классической демонстрацией иррациональности корня из двух.
и удалось дознаться у него, что натуральные числа это, оказывается, множества
вы имеете ввиду, всё множество натуральных чисел, или то что каждое число — множество? если последнее, то для курса анализа это не надо, и, пожалуй, введение в такие дебри наоборот сделает курсу хуже. обычно рациональные числа воспринимаются как данные, потому что они «естественные»
Про факторизацию я узнал и вовсе сильно позже, читая и разбирая Лорана Шварца.
вообще, у вас интересный путь. насколько я понимаю, в НМУ вы уже пошли даже после окончания МАИ — так оказывается можно вообще? и, что вас заставило начинать изучать математику на таком высоком уровне аж до НМУ и Шварца, всё-таки, насколько я понимаю, в МАИ люди идут изначально не за математикой… и пригодились ли полученные знания в вашей непосредственной работе, или это всё-таки осталось на уровне хобби?
Да, я тоже обо всём этом думаю (про первые 2 пункта).
Ну я не совсем правильно выразился, видимо.
Школьнику (не матшкольнику, а обычному) в школе ничего не доказывают, как правило, он не знаком вообще с понятием «доказательство теоремы», считает, что аксиома это аналог теоремы, но без доказательства… ну и так далее. Могу ошибаться, но Евклид первым заложил идею «вводим определения / аксиомы, доказываем о них что-то» и вот это вот всё. А рассказ о том, что при отрицании 5 постулата получается неевклидова геометрия, неплохо помогает понять, зачем аксиомы нужны и почему от них зависит всё.
Действительные, кажется, тоже вполне воспринимаются как «естественные», поскольку мы всё-таки интуитивно воспринимаем мир как R^3 (по крайней мере, моя картинка в голове даже не Q^3), хоть это и не так.
И определения чисел вовсе не очень нужны в курсе анализа, однако же если вернуться к моей предлагаемой программе, я предлагаю двигаться от интуиции к формализации, и в самом конце этой самой программы в качестве бонуса будет венец формализации — мы введём определения чисел.
Но — да, согласен, это не очень нужно. Тут я скорее просто делюсь своей историей, как я начал хоть как-то понимать математику.
Я об определении натуральных чисел. Когда мы уже ввели множества, мы можем определить натуральное число как класс эквивалентности равномощных множеств.
Да, я весьма смело сказал, что все маткурсы МАИ мне ничего не дали, это скорее потому что отлично знаю, на каком уровне математика у одногруппников :)
Да, в НМУ свободный проход всем. На любую лекцию можно прийти и 10-класснику и аспиранту. Если вы об этом.
Ну в первую очередь я пришёл как раз за этим самым «хочу начать понимать математику». Да, сейчас мне уже сложно представить, как можно это не понимать, это же обычная логика, однако раньше действительно было совершенно непонятно примерно всё, и оба семестра анализа я сдал на 3, вынеся оттуда больше понимание, как решать интегралы, чем что-либо ещё.
Потом увлёкся… и вот. В итоге дошёл до Рудина, Лорана Шварца, Львовского, Дьедонне… ну в смысле, до книжек такой вот сложности. Даже Бурбаки читал, но не очень много.
Зачем я пошёл в МАИ, да ещё и на инженера — вообще отдельный вопрос, но вкратце, это не то, чем я хотел бы заниматься, и не то, чем в итоге занимаюсь. Плохое школьное образование, плохо сданное ЕГЭ… и вот это вот всё. Например, в 11 классе я вовсе перестал посещать школьные уроки математики, предпочтя готовиться самостоятельно, в итоге я сдал с огромным отрывом от всего класса… но даже не то чтобы хорошо, просто не настолько отстойно, как все остальные :)
Математика так и осталась по большей частью хобби. Ещё её понимание неплохо помогает в других хобби, например, статьи по геймдеву читать теперь гораздо проще. Но в работе вроде бы пока не пригождалось.
и, что, у вас основной задачник на практиках не Демидович был?Честно, не помню. Интегралы-пределы были не из Демидовича, но мне к зачёту оттуда задавали несколько задач.
ну а как мотивируют в НМУ? или насколько понимаю, никак — предполагается что уже все и так должны знать?Да, в НМУ, кажется, именно последовательности тоже не мотивировали. Хотя не уверен, я мог просто пропустить. Я там много пропускал в своё время, поэтому я до сих пор и не умею нормально в математику.
не, ну это уже к вопросам философии. например про отсылку к евклиду я только что от вас услышал, поэтому не считаю что «Без этого нормально понять анализ не получится»
Ну я не совсем правильно выразился, видимо.
Школьнику (не матшкольнику, а обычному) в школе ничего не доказывают, как правило, он не знаком вообще с понятием «доказательство теоремы», считает, что аксиома это аналог теоремы, но без доказательства… ну и так далее. Могу ошибаться, но Евклид первым заложил идею «вводим определения / аксиомы, доказываем о них что-то» и вот это вот всё. А рассказ о том, что при отрицании 5 постулата получается неевклидова геометрия, неплохо помогает понять, зачем аксиомы нужны и почему от них зависит всё.
ну, не знаю. по-моему всё-таки школьники знают, что ирррациональные числа — это такие, которые нельзя представить в виде дроби, как минимум. если не знают, то на 1й лекции это напоминается с классической демонстрацией иррациональности корня из двух.Ну вот в том и дело, что я неоднократно спрашивал школьников и первокурсников, что такое иррациональное число, и они в основном не знали :)
вы имеете ввиду, всё множество натуральных чисел, или то что каждое число — множество? если последнее, то для курса анализа это не надо, и, пожалуй, введение в такие дебри наоборот сделает курсу хуже. обычно рациональные числа воспринимаются как данные, потому что они «естественные»
Действительные, кажется, тоже вполне воспринимаются как «естественные», поскольку мы всё-таки интуитивно воспринимаем мир как R^3 (по крайней мере, моя картинка в голове даже не Q^3), хоть это и не так.
И определения чисел вовсе не очень нужны в курсе анализа, однако же если вернуться к моей предлагаемой программе, я предлагаю двигаться от интуиции к формализации, и в самом конце этой самой программы в качестве бонуса будет венец формализации — мы введём определения чисел.
Но — да, согласен, это не очень нужно. Тут я скорее просто делюсь своей историей, как я начал хоть как-то понимать математику.
Я об определении натуральных чисел. Когда мы уже ввели множества, мы можем определить натуральное число как класс эквивалентности равномощных множеств.
вообще, у вас интересный путь. насколько я понимаю, в НМУ вы уже пошли даже после окончания МАИ — так оказывается можно вообще?Нет, я пришёл в НМУ на 2 курсе МАИ. Задержался там на ~полтора семестра.
Да, я весьма смело сказал, что все маткурсы МАИ мне ничего не дали, это скорее потому что отлично знаю, на каком уровне математика у одногруппников :)
Да, в НМУ свободный проход всем. На любую лекцию можно прийти и 10-класснику и аспиранту. Если вы об этом.
и, что вас заставило начинать изучать математику на таком высоком уровне аж до НМУ и Шварца, всё-таки, насколько я понимаю, в МАИ люди идут изначально не за математикой… и пригодились ли полученные знания в вашей непосредственной работе, или это всё-таки осталось на уровне хобби?
Ну в первую очередь я пришёл как раз за этим самым «хочу начать понимать математику». Да, сейчас мне уже сложно представить, как можно это не понимать, это же обычная логика, однако раньше действительно было совершенно непонятно примерно всё, и оба семестра анализа я сдал на 3, вынеся оттуда больше понимание, как решать интегралы, чем что-либо ещё.
Потом увлёкся… и вот. В итоге дошёл до Рудина, Лорана Шварца, Львовского, Дьедонне… ну в смысле, до книжек такой вот сложности. Даже Бурбаки читал, но не очень много.
Зачем я пошёл в МАИ, да ещё и на инженера — вообще отдельный вопрос, но вкратце, это не то, чем я хотел бы заниматься, и не то, чем в итоге занимаюсь. Плохое школьное образование, плохо сданное ЕГЭ… и вот это вот всё. Например, в 11 классе я вовсе перестал посещать школьные уроки математики, предпочтя готовиться самостоятельно, в итоге я сдал с огромным отрывом от всего класса… но даже не то чтобы хорошо, просто не настолько отстойно, как все остальные :)
Математика так и осталась по большей частью хобби. Ещё её понимание неплохо помогает в других хобби, например, статьи по геймдеву читать теперь гораздо проще. Но в работе вроде бы пока не пригождалось.
Скажите, для чего нужны последовательности в анализе 1 семестра?
Проблема том, что это бессмысленный вопрос. Потому что:
- большинство мат. объектов не нужны ни для чего кроме фана
- даже если они для чего-то нужнЫ, то нельзя это объяснить, пока человек не научится с объектом соответствующим работать. Студент НМУ уже умеет работать с пределами просто поступив в НМУ, по-этому ему можно объяснять что-то из разряда зачем и почему. Если же вы попытаетесь объяснять мотивировку пределов обычному студенту обычного матфака — это будет просто hurr durr. Никто просто не поймет, что вы пытаетесь задвигать.
А вот функан, вар. исчисление, умф, тензорный анализ и дифгем, тфкп, тервер и слупы, численные и их допглавы и кто помнит что ещё значились в расписании как просто занятия
это всё изучается на протяжении 4х лет. и не знаю как было у вас, может очередные «инновации», но в обычных универах и лекции и практики на всё это дело есть
После лекции про предел последовательности в НМУ вас попросят доказать разные факты о пределах и последовательностях
так прикол в том, что эти «факты» в обычных универах на лекциях тщательно разжевывают и доказывают
именно потому люди из НМУ отлично понимают теорию (на которой ведь и базируется всё)
сами ведь написал " (на которой ведь и базируется всё)" — люди, которые идут в нму это понимают и теорию разбирают и учат. студенты в обычных университетах — зачастую не понимают, потому что «скучно», «недостаточно мотивировано», «не применяется» и прочие отмазки. хотя, чтобы понять теорию надо не таки сильно напрячься — просто взять и перечитать лекцию, вдумчиво разбирая каждый момент. вот и весь секрет «сложности матана»
Часто можно просто перестроить уже имеющийся материал, с добавлением буквально пары приложений. Пример.
Так ваш пример не работает. Ваша "перестройка" ничем не лучше оригинала абсолютно.
UFO just landed and posted this here
А зачем эти интегралы нужны?Интеграл — это просто перемножение двух величин, например умножение скорости на время для нахождения пройденного расстояния. Только теперь скорость может меняться.
UFO just landed and posted this here
Видимо, я не совсем четко сформулировал. Сейчас я знаю, зачем нужны интегралы. Знаю, что они выводятся через верхние\нижние суммы, и пониманию назначение пределов.
Первокурсники не знают про интегралы, верхние и нижние суммы и прочие ништяки. Соответственно, само понятие предела им не особо и нужно. Необходимость этого понятия желательно обосновать, хоть как-то.
Первокурсники не знают про интегралы, верхние и нижние суммы и прочие ништяки. Соответственно, само понятие предела им не особо и нужно. Необходимость этого понятия желательно обосновать, хоть как-то.
Первокурсники не знают про интегралы, верхние и нижние суммы и прочие ништяки. Соответственно, само понятие предела им не особо и нужно.
Так извините, а что вы предлагаете? Дать сперва какое-то определение через пределы, когда люди еще совсем не знают, что такое пределы, и сказать: "вот вам нужны пределы чтобы понять это определение"? Так это определение для них будет полный hurrdurr.
Так извините, а что вы предлагаете?Конкретно Фихтенгольц приводит примеры иррационального числа, и периметр вписанного правильного многоугольника. Соответственно, можно заявить: у некоторых последовательностей значения x_n «приближаются» к некоторому числу с ростом n.
1, 1.4, 1.41,… приближается («сходится») к корню их двух (этот пример у Фихта есть). Последовательности периметров правильных вписанных\описанных многоугольников (тут должны быть формула и рисунок) «сходятся» к длине окружности, приближая число Pi. Последовательность 1
1 -1/2
1 -1/2 + 1/3
1 -1/2 + 1/3 -1/4 сходится к…
Сходящиеся последовательности являются необходимой базой для дальнейших тем (эти темы могут быть указаны в оглавлении) и обладают собственными любопытными свойствами.
Далее вводим предел, даем примеры и контрпримеры типа (-1)^n, поясняем определение...
Собственно, я добавил буквально пару предложений к материалам Фихтенгольца. При этом минимальные изменения в порядке абзацев дают более плавный ввод терминов, простейшие примеры перекинуты ближе к определению, не заставляя читателя переворачивать страницы туда-обратно. На лекции можно мельком упомянуть «условно-сходящийся ряд», при изучении рядов студенты его «вспомнят» как нечто смутно знакомое.
Конкретно Фихтенгольц приводит примеры иррационального числа, и периметр вписанного правильного многоугольника.
Это все совершенно примитивные вещи, которые возможны исключительно на уровне введения в дисциплину. Дальше не получится. Не будет у вас просто таких вот житейских "приближается", которые достаточно близко описывают происходящее.
Ну и да, то что вы описали особо никакого профита не дает, вся та же самая информация содержится просто в самих словах: "предел", "стремится", "сходится" — и так понятно что что-то там к чему-то там как-то приближается, без отдельных пояснений. Проблема исключительно в том, чтобы набить руку на самом формализме — так, чтобы интуитивно думать на языке е-д, в определенных терминах, определенным способом.
с интегралом вроде ж оно попроще? Вот есть у тебя длина, есть площадь, есть объем — это же все очень похожие штуки в нашем чудесном евклидовом пространстве точек. Если студент понимает, что кроме него бывают другие пространства и они тоже очень полезны — ему можно объяснить, что в них понятие объема/площади тоже может пригодиться.
Угу. Площадь. Почему тогда интеграл от 0 до +бесконечности от 1/х не считается в школьных рамках, при том площадь очевидно (из симметрии графика) равна 1+(интеграл от 1 до бесконечности)*2 ( а вот выражение в скобках уже считается легко)
Он же расходится, разве нет?
Интеграл расходится, а площадь легко считается из симметрии.
В силу симметрии площадь гиперболы от 0 до 1 минус 1 равно площади гиперболы от 1 до бесконечности, в этом я согласен.
Но эта пл-дь (1..inf) бесконечна. Ее можно приблизить (причем снизу) прямоугольникаи ширины 1 и высоты 1/2, 1/3,1/4,1/5 и т.д. А сумма этого ряда бесконечна
Ваше утверждение фактически неверно, ввиду того, что сей график симметричен относительно прямой Y=X, а вовсе не вертикали X=1.
Ну. Симметрия относительно У=Х. Фигура под графиком состоит из квадрата 1*1 и двух «треугольников»: горизонтального Х=1 и до бесконечности и такого же по форме, но вертикального. У=1 и до бесконечности.
Значит площадь равна 1+2*«треугольник»
Вдоль икса мы посчитать можем, значит итоговая площадь тоже должна сходиться.
Значит площадь равна 1+2*«треугольник»
Вдоль икса мы посчитать можем, значит итоговая площадь тоже должна сходиться.
расходится у вас хоть «вдоль Y», хоть «вдоль X», интеграл расходящийся от любой «стартовой точки»
Вдоль икса мы посчитать можемМожем, да. Ответ — ∞.
значит итоговая площадь тоже должна сходиться.Это с какого-такого перепугу? Площади обоих треугольников превосходят любое наперёд заданное число — и это легко доказать. Если вы уж так любите геометрию: засуньте туда сначала квадратик 1x1, потом, правее, ½ x 1, ¼ x 2, ⅛ x 4,… они все лежат под графиком, площадь каждого — ½… и их бесконечно много.
Вот есть у тебя длина, есть площадь, есть объем
А что такое длина, площадь и объем? Если вы попробуете это определить, то окажется что можно, с-но, многими способами неэквивалентными это сделать, единственность получается только при совпадении нескольких условий, причем для объема искомой меры не существует в принципе и надо пожертвовать либо геометрической инвариантностью, либо "всюду определенностью".
это все так, но я не на этом делаю акцент, а на том, что площадь, длина и объем студенту точно известны, и он явно нутром догадывается, что они очень похожи — вот от этого и надо отталкиваться
А вот в том-то и дело, что они не «очень похожи». Или вы про сапог Шварца ничего не слышали?
ваши предложения?
Перед тем, как что-то предлагать нужно вначале понять чего мы хотим получить. Если специалистов — то нужно прежде всего дать преподавателям возможность отсеивать тех, кто ни фига не знает и не умеет. Что создаст главное: мотивацию. Желание учиться.
А дальше — уже можно думать на тему: как сделать, чтобы человек, который хочет учиться смог бы более просто разобраться с пределами и интегралами.
А дальше — уже можно думать на тему: как сделать, чтобы человек, который хочет учиться смог бы более просто разобраться с пределами и интегралами.
Почему вы думаете, что отчисление неуспевающих будет кого-то мотивировать?
По моему опыту, желание учиться появляется тогда, когда человек понимает зачем применять изучаемый материал и у него получается его осваивать.
Почему вы думаете, что отчисление неуспевающих будет кого-то мотивировать?
Никого мотивировать и не надо не надо, надо просто отчислить немотивированных и работать с оставшимися. Не хочет человек учится — пусть не учится. Почему его кто-то заставлять должен?
Сперва его в школе мотивируют, потом в институте мотивируют, потом на работе мотивируют: "ну давай, ну поработай немного".
Прекратите этот инфантилизм уже. Дайте людям возможность быть взрослыми и нести ответственность.
У нас бы на матфаке тогда осталось бы со всемго потока человека 3-4, староста, профорг и пара людей которые учить не хотят но им это дается. После чего возникли бы вопросы к факультету, уменьшили бы финансирование и т.д.
У нас бы на матфаке тогда осталось бы со всемго потока человека 3-4, староста, профорг и пара людей которые учить не хотят но им это дается.
И в чем тут проблема?
После чего возникли бы вопросы к факультету, уменьшили бы финансирование и т.д.
Это отдельный вопрос, который к теме обсуждения уже не относится.
И в чем тут проблема?
Проблемы нет. Только скорее вопросы к преподу неже ли к ученикам.
Проблемы нет. Только скорее вопросы к преподу неже ли к ученикам.
Почему к преподу, если не учатся ученики? Препод все, что должен, делает.
Задача препода, донести свой предмет до большинства. Если большинство не усваивает его — значит препод делает что то не верно.
Конкретно в моем случае, дебильных лекторов чаще всего хорошо компенсировал препод ведущий практику.
От препода всегда очень многое зависит. У нас был препод, и вот только у него такое случалось, что со всего потока экзамен сдавал 1 человек. Потом уже на очередной пересдаче деканат сам менял препода который принимал бы, или уже комиссия. Они сами знали что проблемый препод. Но считался типа «сильный», «крутой» и такой должен быть в ВУЗе.
Ну и зачем отчислять? У нас после первого курса половина потока сами ушли, а ко второму курсу еще половина. Из нашей группы, конкретно прям отчислили за все время обучения 3 человека. А доучилось из 30 человек в группе, только 10. Но это скорее объяснялось только тем, что оценки за «просто так» ставились только старостам/профоргам/спортсменам. Во всех остальных случаях автоматы были большой редкостью.
Так что при нормально выстроеной системе обучения люди сами осознают что стезя не их.
Конкретно в моем случае, дебильных лекторов чаще всего хорошо компенсировал препод ведущий практику.
От препода всегда очень многое зависит. У нас был препод, и вот только у него такое случалось, что со всего потока экзамен сдавал 1 человек. Потом уже на очередной пересдаче деканат сам менял препода который принимал бы, или уже комиссия. Они сами знали что проблемый препод. Но считался типа «сильный», «крутой» и такой должен быть в ВУЗе.
Ну и зачем отчислять? У нас после первого курса половина потока сами ушли, а ко второму курсу еще половина. Из нашей группы, конкретно прям отчислили за все время обучения 3 человека. А доучилось из 30 человек в группе, только 10. Но это скорее объяснялось только тем, что оценки за «просто так» ставились только старостам/профоргам/спортсменам. Во всех остальных случаях автоматы были большой редкостью.
Так что при нормально выстроеной системе обучения люди сами осознают что стезя не их.
Задача препода, донести свой предмет до большинства.
Нету у него такой задачи. Препод вообще не занимается донесением чего-то там. Задача препода — это направить студента к требуемой информации. Усвоение информации — задача студента.
Отличное оправдение для любого препода-разгельдяя. Не я плохой, студенты не усваивают. Збс.
Похоже мне с преподами в свое время повезло что они были не такого мнения как Вы.
Похоже мне с преподами в свое время повезло что они были не такого мнения как Вы.
Отличное оправдение для любого препода-разгельдяя. Не я плохой, студенты не усваивают.
Почему же препод — разгильдяй?
Еще раз — препод выполняет свои обязательства, т.к. передает студенту требуемую им информацию.
А вот если студент вместо того, чтобы приложить усилия и разобраться читает учебник наискосок и потом жалуется "не понимаю" — то этот студент и есть разгильдяй.
И одно дело если к преподавателю приходит мотивированный студент, и совсем другое — когда такой вот разгильдяй (поверьте, по уровню вопросов элементарно определить, человек действительно пытался разобраться и у него затык, или он просто лентяй и остановился, прочитав текст пару раз). Какой интерес преподавателю вообще тратить на него свое время?
Если человек не готов трудиться — пусть идет лесом.
Нормальная скорость усваивания математического текста — порядка страницы в часы (мы, конечно, говорим именно об обучении, а не о чтении специалистом). Сколько из тех, кто тут вопит про "не понимаю" самостоятельно тратил по паре-тройке часов на разбор страничной теоремы?
Ну такие ученики всегда есть. Да, это это далеко не все у кого не заходит материал. И преподы тоже есть такие, что ппц. У нас вот был «уравнения в частных производных», там все задачки в пару строк, а потом выкладок на пару листов. Преподу надо было сдавать решеные задачи чтоб зачет получить. А вся его проверка сводилась только к сверке ответа со своим. И если не верно отправлял перерешиватьа когда так с самого начала, довольно проблематично найти где же твои рассуждения пошли не туда.
Его предмет не знали 99% студентов которые через него проходили… Предыдущие потоки сдавали одни и те же варианты в разное время, пока он не начал записывать кому что выдал. С одной стороны у тебя затык, а другой стороны препод которому нет дела ни до чего. Только из за него при мне на 3 курсе отчислили 5 человек.
Ну и смысл такого препода?
Его предмет не знали 99% студентов которые через него проходили… Предыдущие потоки сдавали одни и те же варианты в разное время, пока он не начал записывать кому что выдал. С одной стороны у тебя затык, а другой стороны препод которому нет дела ни до чего. Только из за него при мне на 3 курсе отчислили 5 человек.
Ну и смысл такого препода?
И если не верно отправлял перерешиватьа когда так с самого начала, довольно проблематично найти где же твои рассуждения пошли не туда.
Так все верно, место ошибки студенту нельзя сообщать, он сам его найти должен. Решил неправильно — иди перерешивай, пока не решишь правильно.
А вы какой-то халявы хотите — неправильно сделал, за тебя нашли ошибку, ты ее изи исправил. Ну это же несерьезно, как в таком стиле можно вообще чему-то научиться? Поиск и исправление собственных ошибок — неотъемлемая часть обучения.
У вас если баг в программе, то вам же не будут указывать где он? Сами найти должны, разве не так?
Предыдущие потоки сдавали одни и те же варианты в разное время, пока он не начал записывать кому что выдал. С одной стороны у тебя затык, а другой стороны препод которому нет дела ни до чего. Только из за него при мне на 3 курсе отчислили 5 человек.
Ну и смысл такого препода?
Очевидно, ему следовало лучше следить за тем, чтобы никто ничего не списывал и одни варианты не сдавал. Тогда бы отчислили не 5 человек, а 25. Какой смысл? Ну тот смысл, чтобы заниматься образованием — то есть давать знания тем, кто хочет их получать, а остальных отчислять.
С какой стати давать диплом людям, которые не способны свою ошибку в задаче найти? Это специалисты что ли? Нет.
А то наплодилось странных людей, которые вроде проходили матанализ, сдали его, но при этом не в состоянии объяснить разницу между интегралом Римана и интегралом Лебега (пусть неформально офк, когда был тот матанализ, но хотя бы на пальцах). С какой стати у них вообще есть диплом? Его надо выкинуть на помойку.
Мда…
Т.е. списывание это проблема? У нас у нормальных преподов это проблемой не являлось. Просто списать
всегда было мало.
Самое смешное, очень часто на матфаке от преподов встречал такое: «вам не нужно сейчас понимать, просто учите, понимать начнете уже после универа», а сами при этом спрашивали именно понимание лол.
Собсно мне вот стало интересно, и я стал нормально учиться, только на последних курсах.
Вы так радикально настроены, как я понимаю, вы просто за то, чтоб на матфаке учились математике только те кто хочет ей фундаментально заниматься? :) так этого никогда небыло и не будет. Да и сейчас матфак по большей части свалка, куда поступают те, кто не прошел «на модные» специальности из-за конкурса типа КБ. А отучитсья чтоб пойти тем же преподом, это надо быть именно больным математикой).
У нас нашу специальность закрыли, сделали бакалавров и обозвали более модно, хотя программа обучения никак не изменилась, только последний год «отрезали» (представляю разочарование тех кто туда попадает не глянув программа. Да и глянув, что они так сходу поймут). А если всех отчислять как вы хотите, начнутся большие вопросы к преподам и не только. Скорее всего весь деканат сменится.
Т.е. списывание это проблема? У нас у нормальных преподов это проблемой не являлось. Просто списать
всегда было мало.
Самое смешное, очень часто на матфаке от преподов встречал такое: «вам не нужно сейчас понимать, просто учите, понимать начнете уже после универа», а сами при этом спрашивали именно понимание лол.
Собсно мне вот стало интересно, и я стал нормально учиться, только на последних курсах.
Вы так радикально настроены, как я понимаю, вы просто за то, чтоб на матфаке учились математике только те кто хочет ей фундаментально заниматься? :) так этого никогда небыло и не будет. Да и сейчас матфак по большей части свалка, куда поступают те, кто не прошел «на модные» специальности из-за конкурса типа КБ. А отучитсья чтоб пойти тем же преподом, это надо быть именно больным математикой).
У нас нашу специальность закрыли, сделали бакалавров и обозвали более модно, хотя программа обучения никак не изменилась, только последний год «отрезали» (представляю разочарование тех кто туда попадает не глянув программа. Да и глянув, что они так сходу поймут). А если всех отчислять как вы хотите, начнутся большие вопросы к преподам и не только. Скорее всего весь деканат сменится.
Мда…
Т.е. списывание это проблема?
А с чего бы нет? Студент пытается обмануть преподавателя. Конечно же, это проблема!
Он не только лентяй и никакой специалист, но еще и человек непорядочный.
Вы так радикально настроены, как я понимаю, вы просто за то, чтоб на матфаке учились математике только те кто хочет ей фундаментально заниматься?
Я за то, что если у человека есть с дипломе курс матана или линейной алгебры — то, значит, он знает матан или линейную алгебру. Это же разумно, разве нет? В противном случае — что этот диплом показывает?
Вы так радикально настроены, как я понимаю, вы просто за то, чтоб на матфаке учились математике только те кто хочет ей фундаментально заниматься?
Очевидно, на любой специальности должны учиться те, кто хочет там учиться.
А отучитсья чтоб пойти тем же преподом, это надо быть именно больным математикой).
Преподы идут в педагогический.
Да и сейчас матфак по большей части свалка, куда поступают те, кто не прошел «на модные» специальности из-за конкурса типа КБ.
Ну логично же всех "свалочных" отчислять, нет?
У нас нашу специальность закрыли, сделали бакалавров
Это сейчас почти везде так, специалитет заменен бакалавриатом + магистратурой.
. А если всех отчислять как вы хотите, начнутся большие вопросы к преподам и не только.
Значит, не надо количество отчисленных студентов считать какой-то полезной метрикой.
Еслиб от нас это зависило. Ректорат тоже тасует студентов как ему удобнее. Я поступал на ПМИ и ПМ, Поступил на Прикладную Математику. А зачислили меня потом, после своих уже разбирательств на Математику, о чем я узнал когда выдавали студенческие в первый учебный день. И что, после этого мне отчисляться и бросать потому что не то что я хотел? Я учился просто в том объеме который был мне нужен, а не гнался за объемом курса который мне был не очень то интересен. С переводом были сложнее, ПМ добили платниками в тот раз. А на курс ниже и терять еще год — нет спасибо.
Что специалистов заменили на бакалавров это я вкурсе, я хотел акцентировать на переименовании специальности. А так у бакалавров курс совсем дибильно построен, просто сделали обрубок.
Что специалистов заменили на бакалавров это я вкурсе, я хотел акцентировать на переименовании специальности. А так у бакалавров курс совсем дибильно построен, просто сделали обрубок.
И что, после этого мне отчисляться и бросать потому что не то что я хотел?
А есть какие-то причины поступить в данном случае иначе?
А так у бакалавров курс совсем дибильно построен, просто сделали обрубок.
Да там в любом случае на 5 курсе уже написание диплома, а по предметам ничего важного обычно нет.
А есть какие-то причины поступить в данном случае иначе?
Отчислиться из принципа, пойти в армию (так как отчисление и отсрочка сразу сгорает), потерять время, возможно здоровье и потом уже никуда не поступить? лол.
И только потому что название специальности чуть не то, 80% пар у нас были вместе.
Спокойно отучиться, для работы — нет разницы что у меня в дипломе М или ПМ.
передает студенту требуемую им информацию
У акта передачи информации в данном случае есть вполне конкретная характеристика качества передачи. Качество определяется тем, насколько много информации, вылетев из-под мела и изо рта преподавателя, было усвоено в голове студента.
У акта передачи информации в данном случае есть вполне конкретная характеристика качества передачи.
Качество передачи практически во всех случаях идеальное. Это же математика. Главное, чтобы не было опечаток
Качество определяется тем, насколько много информации, вылетев из-под мела и изо рта преподавателя, было усвоено в голове студента.
Вы сейчас говорите не об информации, а о навыке. Навык — не информация, его нельзя просто "передать и все". Навык требуется тренировать. А это уже зависит от студента — тренируется он или нет.
Качество передачи практически во всех случаях идеальное. Это же математика. Главное, чтобы не было опечаток
Почитайте работы Галуа, и вы поймете, почему из французской академии наук ему сказали следующее:
"Дорогой месье Галуа!
Ваша рукопись была послана для ознакомления месье Пуассону. Он возвратил её нам с отзывом, который мы здесь и приводим:
… Мы приложили все усилия, чтобы понять доказательства месье Галуа. Его рассуждения недостач точно ясны, недостаточно развёрнуты и не дают возможности судить, насколько они точны..."
Это «месье Пуассон», который в день математике посвящает часов 13-16. Уж то, что 17-тилетний месье Иванов что-то может не понять, тем более ясно.
Почитайте работы Галуа, и вы поймете, почему из французской академии наук ему сказали следующее:
Ну не надо сравнивать с временами Галуа. Тогда, во-первых, математика была еще недостаточно строгой, с-но не было выработано четких и ясных критериев, что "все передано ок", а во-вторых — Галуа, например, просто пропускал некоторые доказательства.
С рассматриваемой темой все это никак не соотносится, в учебниках все корректно и полно излагается.
зачем все эти пределы нужны, ведь интегральные суммы снизу и сверху вводятся после пределов
Вообще интегралы это уже следующий семестр. Непосредственно после теории пределов идут производные, которые без пределов как-то тоже не особо.
Ну, это вот кстати вопрос подачи материала. В НГУ, к примеру, было принято сначала рассказать о линейных операторах, потом ввести для них матричное представление, и оттуда же вытащить умножение матриц.
В результате всё довольно сильно зависит от преподавателей. и пока преподавание (на всех уровнях) не станет профессией востребованной, хорошие преподаватели (а следовательно и хорошие учебники) так и будут скорее случайностью, чем закономерностью.
В результате всё довольно сильно зависит от преподавателей. и пока преподавание (на всех уровнях) не станет профессией востребованной, хорошие преподаватели (а следовательно и хорошие учебники) так и будут скорее случайностью, чем закономерностью.
в то, что автор неспроста вставил в книгу какие-то определения и понятия с пониманием своего дела, и их важность откроется по ходу дальнейшего изучения — вы верить отказываетесь упорно, вам нужны «подтверждения» здесь и сразу, причём непременно сразу после каждого вновь вводимого определения. эдакая «морковка»
Да не так, не в «вере» дело — просто вот читаешь текст, настолько перегруженный новыми для тебя и глубоко абстрактными понятиями — и ты его не то что не понимаешь, ты даже не понимаешь, понимаешь ты его или не понимаешь. Особенно заметно, когда читаешь с целью немедленной практической реализации: прочитал раз — не понял. Перечитал — не понял. Медленно, вдумчиво прожевал каждый параграф, пропустил через себя, актуализировал и абсорбировал материал — во, вроде, понял. Начинаешь программу писать, сразу становится ясно, что «понял» ты какой-то бред, не имеющий отношения к реальности. И это ещё хорошо, что ты хотя бы понял, что не понял — а если материал не предполагает незамедлительной практической реализации, так даже этого не поймёшь, уйдёшь дальше в жизнь с иллюзией понимания.
UFO just landed and posted this here
Иногда мозг запоминает совершенно бесполезные вещи. Например нафига я до сих пор помню формулу этил-с2-диизопропиламиноэтилметилфосфонотиолата? Видел один раз лет 15 назад. Запомнилось железно.
Воистину, по современным представлениям психологической науки, все именно так. Почему это до академической среды так медленно доходит, не знаю, наверное из-за инертности системы.
Вспомнилось, как в какой-то книге Фейнман описывал, как он приехал в Бразилию, что ли, и увидел, что студенты там совершенно не понимают смысла формул, которые они заучили и кое-как применяют в стандартных кейсах (которые они тоже заучили), но чуть шаг в сторону, и они впадают в ступор. Это когда его попросили высказать мнение, что не так в системе образования в этой стране. Он потом отвечал на это, что главное не формулы заучивать, а создавать понимание, что эти формулы означают (а также как их получить и почему они именно такие).
Оставлю вот еще ссылку на сайт, который понравился: BetterExplained — Math lessons that click. Например, там есть статья про формулу Эйлера
Вспомнилось, как в какой-то книге Фейнман описывал, как он приехал в Бразилию, что ли, и увидел, что студенты там совершенно не понимают смысла формул, которые они заучили и кое-как применяют в стандартных кейсах (которые они тоже заучили), но чуть шаг в сторону, и они впадают в ступор. Это когда его попросили высказать мнение, что не так в системе образования в этой стране. Он потом отвечал на это, что главное не формулы заучивать, а создавать понимание, что эти формулы означают (а также как их получить и почему они именно такие).
Оставлю вот еще ссылку на сайт, который понравился: BetterExplained — Math lessons that click. Например, там есть статья про формулу Эйлера
UFO just landed and posted this here
выходит, вас автор постоянно должен уговаривать прочитать очередную главу его учебника, притом ещё и (ужас!) до конца
предполагается, что если человек решил изучать анализ, то пресловутая мотивация у него уже есть
Это очень неправильный подход.
Во-первых, потому что от него один шаг до «читаю лекции как вздумается, доказываю как хочется, не забочусь о понятности, верности, актуальности и так далее, потому что если человек решил изучать мой предмет, то озаботиться пониманием, верностью и актуальностью материалов это его проблема».
Иными словами, вы предлагаете выбросить педагогику напрочь на свалку истории, потому что понятность материала не нужна, это проблемы самого учащегося.
Во-вторых, у вас совершенно неверное представление, что каждый человек знает, что он хочет, почему, и знает, каково в действительности то, что он хочет. Читая интересно, можно самый скучный предмет заставить любить, и наоборот.
действительно, какой ужас, читая серьезную научную литературу приходится обдумывать прочитанное
Хорошо, когда приходится обдумывать действительно что-то нужное, а не например косноязычие автора.
«Мотивацией» называются причины, по которым автор вводит новое понятие. Мотивацией ко вводу матриц может быть более простая запись СЛАУ или необходимость расширения понятия числа для линейных отображений в R^n для n > 1 (в R линейное это f(x) = ax, в R^n это f(X) = AX, где A матрица, а X вектор).
Мотивацией ко вводу дифуров может быть то, что для меняющегося во времени физ. процесса проще написать дифур, чем что-то ещё.
Мотивацией ко вводу предела может быть… нет, вовсе не необходимость интегрировать и дифференцировать. Найти площадь или касательную можно абсолютно спокойно без пределов — придумываешь оченьочень большую величину, подставляешь в выражение, вуаля. Такой себе трюк, которыми в большом разнообразии пользуются физики.
Мотивацией ко вводу предела будет именно формализация этого трюка и устранение внутренних противоречий этого самого трюка.
«Мотивацией» называются причины, по которым автор вводит новое понятие.
Ну видите ли, тут проблема. Мотивация для ввода 99% математичеаких понятий будет в итоге — "автору так по приколу", если быть до конца честным.
И либо вы разделяете эстетические взгляды автора, тогда вам тоже это по приколу, либо не разделяете.
Такой себе трюк, которыми в большом разнообразии пользуются физики.
Математики при виде такого трюка обычно превращаются в огромного зеленого монстра и начинают крушить все вокруг.
Математики при виде такого трюка обычно превращаются в огромного зеленого монстра и начинают крушить все вокруг.В XIX веке математики тоже так делали. Наполучали идиотских результатов — перестали.
Мотивация для ввода 99% математичеаких понятий будет в итоге — «автору так по приколу», если быть до конца честным
Почему? Можно пример?
Математики при виде такого трюка обычно превращаются в огромного зеленого монстра и начинают крушить все вокруг.
Отлично понимаю, мне очень хотелось крушить всё вокруг во время физических доказательств.
я сейчас жене так и объясняю. «Видишь матрицу? Короче, если надо будет что-либо крутить, увеличивать или сдвигать в компьютерной графике — самая удобная штука, вот спроси у моего друга, сделавшего редактор мультиков на андроид, который его уже шесть лет кормит. Видишь множество и всякие их пересечения и объединения? Ну вот, в SQL есть всякие JOIN'ы, отлично объясняются через множества, плюс в некоторых языках они есть в стандартной библиотеке. Видишь булевые операции? В каждом if'е у тебя будут такие.»
Это очень неправильный подход.
Во-первых, потому что от него один шаг до «читаю лекции как вздумается,
обратите внимание, что я писал это в ответ на критику и предложения по «улучшению» конкретного учебника, а не лекций
Во-вторых, у вас совершенно неверное представление, что каждый человек знает, что он хочет, почему, и знает, каково в действительности то, что он хочет
ну по крайней мере если человек поступил на специальность, в названии которой есть слово «математика», он должен понимать, что ему не зря поставили в программу матан и значит знать его необходимо. точно также и со многими смежными науками — матан является для них всех базой, элементарной азбукой без понимания которой дальнейшее продвижении в своих областях невозможно. чем плохая мотивация?
«Мотивацией» называются причины, по которым автор вводит новое понятие.
мотивация одна — это необходимо для внутреннего развития теории. куча ништяков, в том же матане, из этого полезет сразу как начинаются те же интегралы. и, да, возможно в матане ещё можно мотивировать большую часть понятий, тратя на это и так не резиновое время лекций. но, в более продвинутых разделах — вы так явно ненамотивируете
ну и, возвращаясь к Фихтенгольцу, у того уж с подобными мотивациями — всё в порядке. те же последовательности он мусолит пару страниц, перед тем как ввести определение предела. потом ещё страницу расписывает что эпсилон может быть сколь угодно малым.
перед тем как ввести производную приводит примеры с необходимостью измерения мгновенной скорости. перед тем как ввести функцию — примеры функциональных зависимостей, для функций многих переменных — то же. и ещё во многих случах разжевывает материал. но требовать «мотиваций» прям перед каждым определением каждого параграфа — это перебор
ну и, учитывая нашу с вами беседу в соседенй ветки комментариев, не могу не спросить: а как с мотивациями на лекциях НМУ, тем более вы их, как понимаю, вживую слушали? я не сомневаюсь, что там мастерские лекторы, которые действительно могут увлечь своим изложением предмета — ведь они лучшие из всей страны, но вот что мне крайне сомнительно, что они делают это таким примитивным способом как «морковка» перед носом каждого студента и упрашиванием его послушать очередную теорему, сразу суля золотые горы в виде незамедлительного «практического» результата ее применения
Мотивацией ко вводу предела может быть… нет, вовсе не необходимость интегрировать и дифференцировать. Найти площадь или касательную можно абсолютно спокойно без пределов — придумываешь оченьочень большую величину, подставляешь в выражение, вуаля. Такой себе трюк, которыми в большом разнообразии пользуются физики.
вот только не надо путать причину со следствием. причина, почему физики могут себе позволить делать это так вольготно — в том, что они прекрасно в курсе, что в математике это всё строго доказано, и поэтому можно опустить скучные и долгие выкладки и оговорки, и сделать всё напрямик. и в принципе это оправдано. НО не в курсе математики, ибо там «грязную» работу по построению непротиворечивого формализма свалить уже не на кого
а пределы используюся сразу уже при формулировке понятия непрерывности функции
он должен понимать, что ему не зря поставили в программу матан и значит знать его необходимо
Из этого и можно запросто извлечь утверждение, что читать что-либо понятно не очень нужно. Потому что знать предмет — это проблема учащегося, а преподавателя. Это мне и не нравится.
Про Фихтенгольца не спорю, что он понятнее наверное всех классических учебников по анализу, однако же согласен с автором статьи, что он мог бы быть ещё понятнее.
Да, лекции НМУ я слушал вживую, и с мотивациями там всё было куда лучше, чем где-либо ещё, где я слушал (включая и мой институт). Лекторы действительно стараются читать интересно и хорошо. Сложно != скучно ведь. Могу сейчас вспомнить очень много примеров, когда лекторы плавно подводили к тому, что новое определение совершенно естественно появляется само собой.
Именно это я (и наверное автор) и называю мотивацией, никак не могу понять, зачем вы думаете про морковку и упрашивание послушать теорему. Мотивация — это объяснение, зачем нужен новый термин.
А мои первые 2 лекции там были просто-напросто экскурсом в историю, после которого тем не менее внезапно начинаешь понимать очень многое, что знал, но не понимал раньше.
Ньютон с Лейбницем, кажется, без этого обходились.
Ну и на самом деле — вот не знаю. У нас в курсе УМФ в МАИ были ну очень грязные доказательства, буквально состоящие из хаков, пихания физики внутрь математики и наоборот и так далее. Вероятно, нам просто поленились доказывать прям строго, но у меня периодически появлялось ощущение, что их просто проверили на практике и забили.
Можно и наоборот — предел определить через непрерывные функции.
Могу сейчас вспомнить очень много примеров, когда лекторы плавно подводили к тому, что новое определение совершенно естественно появляется само собой.
А с точки зрения кого-то другого — ничего плавного там не было.
Можно и наоборот — предел определить через непрерывные функции.
Нет, нельзя, потому что предел — он у последовательности, функций там просто нет.
А с точки зрения кого-то другого — ничего плавного там не было.
Почему вы так считаете? Это гипотеза или у вас есть объективные причины так считать?
Нет, нельзя, потому что предел — он у последовательности, функций там просто нет.
Определяем топологические пространства, топологию и т.п.
f непрерывно, если прообраз открытого множества открыт. (или какое-нибудь эквивалентное определение)
А дальше что-нибудь такое:
Определяем топологические пространства, топологию и т.п.
и вы действительно считаете, что это проще и будет лучше пониматься, и будет «лучше мотивировано», чем определение через эпсилон?
Почему вы так считаете?
Вопрос в том, почему вы считаете обратное. То, что вам что-то показалось — это ваш личный опыт, который распространять на остальных нельзя.
А дальше что-нибудь такое:
Так это предел функции f, а не предел последовательности.
Так это предел функции f, а не предел последовательности.
последовательность определяется как функция (отображение)
так что прокатит. правда то определение выше не покрывает, как раз, нужный случай , но думаю там как-то изгаляются и для него
последовательность определяется как функция (отображение)
так что прокатит.
Да? И какая топология на N?
Да?
ага, про это даже Фихтенгольц писал (есстественно, без всяких топологий и отображений)
И какая топология на N?
ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D0%BA%D1%80%D0%B5%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE
ru.wikipedia.org/wiki/%D0%94%D0%B8%D1%81%D0%BA%D1%80%D0%B5%
То, что в дискретной топологии на N все подмножества открыты, и, с-но, все ф-и из N — непрерывны, а значит предел в любой точке будет любым числом — вас не смущает?
так нам не в любой точке нужен предел, а в бесконечности
То есть у вас пространство N + Inf, а не N. И какая на нем топология? Дискретная не подходит, уже выяснили.
нет, вы правы насчёт N+Inf
вот нашёл как это делается vyshka.math.ru/pspdf/f08/calculus-1/l20.pdf
вот нашёл как это делается vyshka.math.ru/pspdf/f08/calculus-1/l20.pdf
Так там про метрические пространства написано. Но у N+Inf нет метрики.
Так там про метрические пространства написано. Но у N+Inf нет метрики.
Не, все ок.
Там хитрая топология задается, в которой множество { Inf } закрытое, а мн-ва вида {n, n+1, n+2..., Inf} — открытые. В итоге если вы в качестве предела попытаетесь взять малую окрестность точки, которая пределом не является, то ее прообразом будет { inf } либо { inf } и числа от n до inf с дырками (если например последовательность вида 0 1 0 1 0 1...) — закрытое мн-во, с-но такая точка не сможет быть пределом. И, наоборот, если точка будет пределом то в прообраз малой окрестности вместе с Inf попадут все натуральные с какого-то номера, то есть {n, n+1, n+2..., Inf} => прообраз открыт.
Спасибо, я знаю как это делается (кстати, Inf не может быть в прообразе потому что не входит в область определения функции). Но по ссылке этого всего нет.
на стр.4 всё есть
Спасибо, я знаю как это делается (кстати, Inf не может быть в прообразе потому что не входит в область определения функции).
Там ф-я доопределяется в той точке, в которой мы ищем предел, с-но Inf входит.
То етсь мы берем последовательность, говорим что "пусть в Inf значение будет А" и тогда полученная ф-я либо будет непрерывна (и тогда А есть предел нашей последовательности) либо не будет (и тогда А не предел).
Но по ссылке этого всего нет.
определение 20.9 и то, что непосредственно за ним
Отнюдь. Можно вначале ввести понятие топологии. Потом, опираясь на него, понятие непрерывной функции. И на основании него ввести предел. См., например, лекции Львовского по матанализу (кстати, из НМУ).
я дал как раз сылку выше уже на них. вообще, интересная штука, давно про них слышал, но никак руки не доходили, а счас как раз повод появился посмотреть
но, строго говоря, Львовский сперва пределы функции и последовательности вводит по-обычному, как полагается. и только потом, в самом конце, показывает «как можно было бы»
кстати, это тот же Львовский, что книжку по латеху написал (инициалы те же), или просто совпадение?
но, строго говоря, Львовский сперва пределы функции и последовательности вводит по-обычному, как полагается. и только потом, в самом конце, показывает «как можно было бы»
кстати, это тот же Львовский, что книжку по латеху написал (инициалы те же), или просто совпадение?
Скорее всего тот же. НМУ для вёрстки изначально TeX и LaTeX использовала
не, ну это не аргумент. в математике латех с 90х годов юзают
Это понятно. Но вряд ли в НМУ работают так уж много Львовских.
книжку по латеху изначально ничто не связывало с НМУ, по крайней мере в моем пдф с сайта автора
но погуглил немного, и, да: один и тот же
www.livelib.ru/author/30182-sergej-lvovskij?PageSpeed=noscript
но погуглил немного, и, да: один и тот же
www.livelib.ru/author/30182-sergej-lvovskij?PageSpeed=noscript
> строго говоря, Львовский сперва пределы функции и последовательности вводит по-обычному, как полагается. и только потом, в самом конце, показывает «как можно было бы»
В том Львовском, которого вы цитировали (определение 2.4), предел введен так, как я сказал. После чего вводится предел последовательности как пример (в соседней ветке обсудили механизм).
Кстати, это не самый общий способ введения предела. Можно еще взять сходимостные пространства, определенные с помощью сетей или фильтров. Тут в качестве источника рекомендую Dolecki «Convergence foundations of topology». Он использует фильтры.
Кстати, Зорич в своем учебнике пределы тоже интересно вводит (базы, которые базы фильтров). Вообще Зорич — лучший учебник матана для первого курса, который я видел. Перед ним хорошо почитать Зельдович «Высшая математика для начинающих и ее приложения к физике» (желательно еще в школе).
В том Львовском, которого вы цитировали (определение 2.4), предел введен так, как я сказал. После чего вводится предел последовательности как пример (в соседней ветке обсудили механизм).
Кстати, это не самый общий способ введения предела. Можно еще взять сходимостные пространства, определенные с помощью сетей или фильтров. Тут в качестве источника рекомендую Dolecki «Convergence foundations of topology». Он использует фильтры.
Кстати, Зорич в своем учебнике пределы тоже интересно вводит (базы, которые базы фильтров). Вообще Зорич — лучший учебник матана для первого курса, который я видел. Перед ним хорошо почитать Зельдович «Высшая математика для начинающих и ее приложения к физике» (желательно еще в школе).
В том Львовском, которого вы цитировали (определение 2.4), предел введен так, как я сказал.
это не я цитировал. в тех лекциях, на которые я ссылку давал — предел вводится по-старинке
Вообще Зорич — лучший учебник матана для первого курса, который я видел
для тех, кто прочитал Фихтенгольца в школе (или усвоил эквивалентный материал любым другим способом) — да. попробуйте так давать на 1м курсе обычного универа обычным вчерашним школьникам — усвояемость будет на нуле (кроме, возможно, 1-2 человек)
«выделены курсивом понятия величина, переменная, постоянная, множество, направленная переменная, предел, последовательность».
Хоть для школьников, хоть для студентов начинаю объяснения с одной идеи: математика это сказка. Любая математическая теория неявно начинается со слов: «Представим себе мир, в котором существуют такие-то объекты с такими-то свойствами и действуют такие-то законы. И посмотрим, что в таком мире возможно, а что нет». Когда-то математики заботились о том, чтобы придумываемый мир напоминал реальный. Потом поняли, что это абсолютно не важно. Удастся ли поставить в соответствие математической теории какие-то явления реального мира — дело физиков и прочих естественников.
В школьной программе этот подход не приветствуется, считается, что на примерах из реального мира разбирать математику проще. В вузе для физиков или инженеров тоже полезны примеры. И их стараются приводить. Но при подготовке профессиональных математиков это уже не обязательно. А может быть и вредно.
Хоть для школьников, хоть для студентов начинаю объяснения с одной идеи: математика это сказка. Любая математическая теория неявно начинается со слов: «Представим себе мир, в котором существуют такие-то объекты с такими-то свойствами и действуют такие-то законы. И посмотрим, что в таком мире возможно, а что нет». Когда-то математики заботились о том, чтобы придумываемый мир напоминал реальный. Потом поняли, что это абсолютно не важно. Удастся ли поставить в соответствие математической теории какие-то явления реального мира — дело физиков и прочих естественников.
В школьной программе этот подход не приветствуется, считается, что на примерах из реального мира разбирать математику проще. В вузе для физиков или инженеров тоже полезны примеры. И их стараются приводить. Но при подготовке профессиональных математиков это уже не обязательно. А может быть и вредно.
Математикам НЕЛЬЗЯ давать ПРИДУМЫВАТЬ примеры из жизни. Задачу про бассейн и трубы через которые втекает и вытекает помните? Для начальных класов вроде…
А ничего что скорость вытекания зависит от высоты столба жидкости? Да еще там зависимость степенная, сколько помню. Там интеграл брать самый раз, я так думаю.
А ничего что скорость вытекания зависит от высоты столба жидкости? Да еще там зависимость степенная, сколько помню. Там интеграл брать самый раз, я так думаю.
Вы очень трудную тему затронули) Такая ошибка была даже у авторов задачи для международной (СНГшной) олимпиады по гидравлике. Там предлагалось посчитать (с интегралом) за сколько жидкость выливается из одного и другого отверстия вращающегося сосуда по отдельности, а потом определить время опорожнения из двух отверстий по школьной формуле для общей работы (не учитывая, что там вообще-то будет взаимовлияние).
а что за задачка, можно ссылки?
В интернетах, к сожалению, не нашёл, а оригинал утрачен при переездах. Речь об олимпиаде по гидравлике в Одессе при Институте холода в 2008-м году, если мне не изменяет память.
Суть задачи заключается в том, что есть вращающийся сосуд, в дне которого на разном расстоянии от центра просверлены отверстия, через которые выливается жидкость. Нужно определить время максимального опорожнения для каждого из отверстий и для двух отверстий вместе. Ну и по-моему, сколько жидкости останется в каждом из этих случаев.
В случае отдельных отверстий всё просто: строится поверхность жидкости (парабола) и через интеграл считается время, когда парабола коснётся отверстия. А для двух отверстий интеграл аналитически не берётся. Авторами задачи в «правильном» решении предлагалось посчитать время по общей работе. Уже после олимпиады наша кафедра (гидравлики, МГТУ им. Баумана) повозмущалась, но, понятное дело, ни к чему это не привело. Через пару лет вообще разругались с организаторами, и вроде до сих пор МГТУ им. Баумана в этих олимпиадах не участвует)
Суть задачи заключается в том, что есть вращающийся сосуд, в дне которого на разном расстоянии от центра просверлены отверстия, через которые выливается жидкость. Нужно определить время максимального опорожнения для каждого из отверстий и для двух отверстий вместе. Ну и по-моему, сколько жидкости останется в каждом из этих случаев.
В случае отдельных отверстий всё просто: строится поверхность жидкости (парабола) и через интеграл считается время, когда парабола коснётся отверстия. А для двух отверстий интеграл аналитически не берётся. Авторами задачи в «правильном» решении предлагалось посчитать время по общей работе. Уже после олимпиады наша кафедра (гидравлики, МГТУ им. Баумана) повозмущалась, но, понятное дело, ни к чему это не привело. Через пару лет вообще разругались с организаторами, и вроде до сих пор МГТУ им. Баумана в этих олимпиадах не участвует)
хех, помню само мгту проводило олимпиаду по физике (как раз вроде в 2008) где в условиях механической задачи предполагалось не учитывать трение, хотя это делало условие физически некорректным (без трения указанный процесс просто не мог осуществиться). при этом, решение с учетом трения было элементарным, пусть и немного хитрым — но его организаторы не засчитывали, настаивая на своем неправильном (притом ответы совпадали)
так что такое сплошь и рядом
так что такое сплошь и рядом
Ну я о том и говорю, что когда сплошь и рядом встречаешь такие косяки авторов задач на университетских всероссийских олимпиадах, школьные задачки с трубами и бассейном уже и не кажутся такими уж бредовыми)
В конце концов, все задачки с «правильным ответом» призваны продемонстрировать владение конкретным методом и умением действовать в определённой ситуации по определённому лекалу. Это тоже в целом неплохой навык, а уж тренировать креативность лучше в рамках какой-то проектной работы.
В конце концов, все задачки с «правильным ответом» призваны продемонстрировать владение конкретным методом и умением действовать в определённой ситуации по определённому лекалу. Это тоже в целом неплохой навык, а уж тренировать креативность лучше в рамках какой-то проектной работы.
Математики всегда будут рассматривать сферического коня в вакууме. Особенно, если речь идет о примерах для школьников.
Велосипедист из пункта А в пункт Б не будет ехать с постоянной скоростью. Землекоп не выкопает за 8-й час работы столько же, сколько за первый.
Все примеры из задачника по математике имеют к жизни косвенное отношение.
Это просто способ представить условия задачи наглядно.
Даже яблоки подсчитать можно только условно — они же разные.
-У тебя было шесть яблок, половину отдал другу, сколько осталось?
-Пять с половиной.
Первая фраза из парижской лекции известного математика «математические основы конструирования одежды»: для простоты представим, что человеческое тело имеет форму шара.
Велосипедист из пункта А в пункт Б не будет ехать с постоянной скоростью. Землекоп не выкопает за 8-й час работы столько же, сколько за первый.
Все примеры из задачника по математике имеют к жизни косвенное отношение.
Это просто способ представить условия задачи наглядно.
Даже яблоки подсчитать можно только условно — они же разные.
-У тебя было шесть яблок, половину отдал другу, сколько осталось?
-Пять с половиной.
Первая фраза из парижской лекции известного математика «математические основы конструирования одежды»: для простоты представим, что человеческое тело имеет форму шара.
UFO just landed and posted this here
Популярный в СССР учебник теорвера Елены Вентцель тоже переполнен практическими примерами. В основном они затрагивают теорию бомбометания, баллистические задачи, системы распознавания "свой-чужой" и прочие, не менее актуальные прикладные вопросы.
вообще, фихтенгольц — это простейшая книга по матану, где всё разжёвывается до мелочей и читателя просто закидывают разнообразными примерами, настолько приближенными к практике, насколько это возможно
Подтверждаю. Я на втором курсе перечитывал этот учебник (начались диффуры, хотелось ещё раз подтянуть матчасть). Он читается как художественная литература. У меня до сих пор дома тома стоят, так и тянет ещё раз почитать.
Но часть критики в статье я всё же считаю верной. Например, зачастую в учебниках не хватает бэкграунда, процесса становления. Математику в учебниках описывают от общего к частному, а ведь развивается она в обратном направлении: есть конкретные задачи, люди придумывают методы их решения, а потом потихоньку обобщают. Если показываешь сразу готовое комплекстное решение, понять его гораздо сложнее, потому что непонятно, как ко всему этому пришли.
Особенно полезно самому выводить формулы, после этого их уже не нужно помнить, можно помнить только ключевую идею. Более того, вывод формул может приносить огромное удовольствие, ведь каждый раз это как маленькое открытие.
Давайте глубже копнем. «Это учение о бесконечно малых». А зачем нам бесконечно малые, почему они полезны или интересны?
А зачем нам бесконечно малые, почему они полезны или интересны?
Чтобы это нормально объяснить придется заходить еще с апорий Зенона. И самое печальное, что даже если все это студенту объяснить — пониманию это никак способствовать не будет. Наоборот, он скажет — нахрена вы еще какой-то лишней хренью мне мозг грузите.
Нельзя ли начать с аналогии про молекулы и атомы? Ну вот есть у нас какие-то крайне малые сущности, которые мы не видим, но которые формируют окружающий мир и влияют на свойства вещей.
Нельзя ли начать с аналогии про молекулы и атомы?
Вообще не вижу, каким образом можно молекулы и атомы притянуть к бесконечно малым.
Ну если вы хотите человека полностью и окончательно запутать — тогда вперёд.
Ибо если использовать классическую физику и начать с молекул и атомов — то вы получите мир, который и близко не похож на реальный (именно поэтому его так сложно моделировать на компьютерах… они ж у нас классические — нолики и единички).
Чтобы физику и молекулы/атомы сдружить вам нужна квантовая механика и Уравнение Шрёдингера. Как вы это вообще собрались рассказывать человеку, которые ни о пределех, ни о производной понятия не имеет?
Ибо если использовать классическую физику и начать с молекул и атомов — то вы получите мир, который и близко не похож на реальный (именно поэтому его так сложно моделировать на компьютерах… они ж у нас классические — нолики и единички).
Чтобы физику и молекулы/атомы сдружить вам нужна квантовая механика и Уравнение Шрёдингера. Как вы это вообще собрались рассказывать человеку, которые ни о пределех, ни о производной понятия не имеет?
Почему вы думаете, что молекулы, атомы нам нужны для формулирования непротиворечивых теорий?
Я же предлагаю такую аналогию только для того, чтобы донести до студентов ответ "Почему нам важно обращать внимание на бесконечно малые значения?".
Извините, но вот я уже знаю матан, работа с пределами и е-д формализмом мне не доставляет проблем, кроме того я могу работать с бм при помощи нестандартного анализа (альтернативный вариант).
И мне ваша аналогия ну совсем непонятна и ничего до меня не доносит. Искренне сомневаюсь, что она что-то в принципе до кого-то могла бы донести.
Было бы странно ожидать, что аналогия, предназначенная для ничего не понимающих студентов, донесла бы вам что-то новое.
Что, впрочем, не исключает негодности аналогии. Мне еще не приходилось объяснять пределы.
Было бы странно ожидать, что аналогия, предназначенная для ничего не понимающих студентов, донесла бы вам что-то новое.
Так дело не в том что она нового не доносит, дело в том, что я вообще не вижу какое она отношение имеет к предмету обсуждения. То есть если вы ее используете с человеком, который не знает предмета, она вообще никакой пользы ему не принесет. А скорее всего — еще и навредит.
ну, можно с зенона, а я уверен, что можно еще как-нибудь. Вот например через те же самые треугольнички из статьи — ведь чем они меньше по размеру, тем вычисление у нас точнее.
Знаете, вот именно так и получается в википедии. Вместо того, чтобы подумать и пояснить на простых примерах, зачем нам вечно малые, начинают рассказывать что это очень сложно.
Ну вот проблему бесконечно малого отрезка времени объяснить очень легко — когда тебе нужно засечь время, ты нажимаешь кнопку на секундомере, а потом нажимаешь второй раз и все.
А если тебе нужно засечь гораздо меньший отрезок, чем ты можешь нажать — у тебя возникают проблемы. И есть промежутки, которые не успевает засечь даже процессор.
Проблема бесконечно малых вещей объяснить легко — когда у тебя предмет примерно сопоставим с размером фотона, ты его физически увидеть не можешь, как бы ты не увеличивал.
Видите как в физике все просто.
Почему же в математике начинают эту лишнюю хрень?
Ну вот проблему бесконечно малого отрезка времени объяснить очень легко — когда тебе нужно засечь время, ты нажимаешь кнопку на секундомере, а потом нажимаешь второй раз и все.
А если тебе нужно засечь гораздо меньший отрезок, чем ты можешь нажать — у тебя возникают проблемы. И есть промежутки, которые не успевает засечь даже процессор.
Проблема бесконечно малых вещей объяснить легко — когда у тебя предмет примерно сопоставим с размером фотона, ты его физически увидеть не можешь, как бы ты не увеличивал.
Видите как в физике все просто.
Почему же в математике начинают эту лишнюю хрень?
Проблема бесконечно малых вещей объяснить легко — когда у тебя предмет примерно сопоставим с размером фотонаУ фотона нет размера. Возможно вы имеете в виду длину волны?
ты его физически увидеть не можешь, как бы ты не увеличивал.И наоборот, нельзя «нарисовать» картинку, с характерным размером меньше, чем длина волны, да? А ничего, что вы вот этим вот строки набираете на «невозможном» компьютере, в котором используется «невозможный» процессор? Напомню, что в современной литограции используется 193нм лазер, а техпроцессы с такими огромными транзисторами — это «прошлый век». Буквально.
Почему же в математике начинают эту лишнюю хрень?Потому что для физика нормально сказать «если A и B, то C, мамой клянусь»… а потом, оп-па, взять — и забрать свои слова обратно. Как в ваших рассказах про «размеры фотона» и «предменты».
А в математике — нет. Если теорема верна и в доказательстве нет ошибок — то она таки верна.
У фотона нет размера. Возможно вы имеете в виду длину волны?
Вот именно в этом заключается проблема.
Мы сейчас не обсуждаем что такое фотон, я пытался привести пример простым языком, почему нельзя сделать оптический микроскоп, который увидит бесконечно малое.
Любой школьник, примерно слышавший о фотоне, поймет.
А вы тут же хотите все усложнить, довести до формального, то есть сделать собственно то о чем речь в статье.
Понимаете какая история — пока у вас нет «формального» у вас нет математики. Это, собственно, выяснили развивая матанализ. Пока с ним общались «неформально», так, как предалагает вы — в XIX веке — то «надоказывали» кучу всякой чуши.
Почему? А очень просто. Математика — это многоэтажнлое здание где одни утверждения базируютс на других. Очень многоэтажное. Иногда в цепочках «многоуровневых лемм» тысячи ярусов бывают, а уж сотни — так это вообще норма.
А что будет если мы выстроим цепочку из 1000 лемм, из которых каждая иногда врёт? Ну, скажем, в 1% случаем? А очень просто: 99.9999% брака будет. Испечёте вы на основе этой «новейшей» технологии процессор — а из тиража в миллион штук… один годный.
Извините, но базисом ни для «чтения книги природы», ни для рассчётак чего-либо такая математика не годится. Нужно сстрогость — и, стало быть, формальность.
P.S. Вы не сможете в оптическом микроскопе увидеть транзисторы, так как они слишком малы. Но сделав достаточно много снимков и потом немного посчитав — вы сможете все транзисторы различить. Именно потому что фотон — это не частица и именно потому что к нему имеет отношение матан. Работа же с дискретными числами, на которую выводит ваш пример — ещё сложнее и запутаннее, чем работа с непрерывными, хотите вы в это верить или нет. Недаром теория чисел — читается после матана, а не до. И базируется, собственно, на нём.
Почему? А очень просто. Математика — это многоэтажнлое здание где одни утверждения базируютс на других. Очень многоэтажное. Иногда в цепочках «многоуровневых лемм» тысячи ярусов бывают, а уж сотни — так это вообще норма.
А что будет если мы выстроим цепочку из 1000 лемм, из которых каждая иногда врёт? Ну, скажем, в 1% случаем? А очень просто: 99.9999% брака будет. Испечёте вы на основе этой «новейшей» технологии процессор — а из тиража в миллион штук… один годный.
Извините, но базисом ни для «чтения книги природы», ни для рассчётак чего-либо такая математика не годится. Нужно сстрогость — и, стало быть, формальность.
P.S. Вы не сможете в оптическом микроскопе увидеть транзисторы, так как они слишком малы. Но сделав достаточно много снимков и потом немного посчитав — вы сможете все транзисторы различить. Именно потому что фотон — это не частица и именно потому что к нему имеет отношение матан. Работа же с дискретными числами, на которую выводит ваш пример — ещё сложнее и запутаннее, чем работа с непрерывными, хотите вы в это верить или нет. Недаром теория чисел — читается после матана, а не до. И базируется, собственно, на нём.
Недаром теория чисел — читается после матана, а не до. И базируется, собственно, на нём.
До сих пор помню, как в 10 классе, дочитав школьный учебник, решил вперед перейти, по универской программе. Посмотрел последнюю тему в учебнике — там диффуры. Ну скачал учебник по диффурам — начал читать, понял, что что-тол тут не так. Ну, акей, думаю, надо начинать тогда с основ. Видимо, в школе нам чего-то не договаривают. С-но сперва с основами разобраться — а потом уже диффуры. А основы что? Ну теория чисел, конечно, что может быть проще чисел, правда? Они же в самом начале. Скачал учебник, прочитал введение, где ни одной формулы нет. Не понял ни фразы, расстроился.
> Почему же в математике начинают эту лишнюю хрень?
вы, наверное, просто не знаете как в физике определяют фотон — не для популярных обзоров, а именно для того чтобы реально с ним работать и выдавать какие-то результаты для применения на практике или в экспериментах. эта «хрень» будет в сто раз сложнее курса матана
вы, наверное, просто не знаете как в физике определяют фотон — не для популярных обзоров, а именно для того чтобы реально с ним работать и выдавать какие-то результаты для применения на практике или в экспериментах. эта «хрень» будет в сто раз сложнее курса матана
Проблема бесконечно малых вещей объяснить легко — когда у тебя предмет примерно сопоставим с размером фотона, ты его физически увидеть не можешь, как бы ты не увеличивал.
Нет, проблема не в этом.
на самом деле, единственная проблема в том, что «матан» ставят в учебные планы тех специальностей, которым он на таком уровне не нужен. это действительно проблема наших реалий, на западе это решается наличием курсов на выбор и совсем упрощенными курсами типа calculus где всё объясняется на пальцах
Позвольте не согласиться с «ненужностью» матана. Считаю, что в текущих реалиях первые пару курсов технического универа (пусть и обрезанные) необходимы всем. Чтобы даже самый гуманитарный гуманитарий знал что такое индукция и умел её применять, владел каким-то базовым пониманием теории вероятностей и статистики. С текущей модой на демократию каждый человек должен иметь возможность критически воспринимать информацию, иначе мы получим то, что имеем.
Чтобы даже самый гуманитарный
Нет, гуманитарию не надо ни интегралы, ни матрицы, ни индукции. Математику у гуманитариев надо выкинуть, а вместо нее добавить историю математики, с кратким обзором направлений, парадоксами "на пальцах", и прочими интересными вещами. Ну это как на уроках литературы вас не учат писать стихи, вам рассказывают про тех, кто их писал и приводят примеры стихов. Аналогичная ситуация, не надо учить гуманитариев заниматься математикой, надо просто рассказывать — про математику и людей, которые ей занимаются.
с кратким обзором направлений, парадоксами «на пальцах», и прочими интересными вещами
Потом это «на пальцах» легко превращается в непонимание, а то и в лженауку. Поэтому-то и воду заряжали (и заряжают) от телевизора — людей научили, что есть какие-то лучи, а что это и на каких принципах оно работает не объяснили.
Ну это как на уроках литературы вас не учат писать стихи
Я думаю, если бы можно было научить писать стихи, то этому бы учили. Это то же самое, что обучить рисовать картины. Можно обучиться технике, но нельзя (на данный момент) научиться быть хорошим художником.
Я и предлагаю учить не решать проблемы тысячелетия (рисовать картины), а учить базовым вещам (технике рисования).
Можно обучиться технике, но нельзя (на данный момент) научиться быть хорошим художником.
Если бы учили хотя бы технике — глядишь и хороших художников было бы побольше. Из-за того, что не учат — кто-то просто не попробовал…
Потом это «на пальцах» легко превращается в непонимание, а то и в лженауку.
Конечно же не превращается, есть вещи, которые можно достаточно строго изложить, не предполагая у слушателя математической подготовки выше самой базовой (основы алгебры, арифметики, геометрии). Штука в том что это именно отдельные примеры — что и нужно гуманитариям.
Я и предлагаю учить не решать проблемы тысячелетия (рисовать картины), а учить базовым вещам (технике рисования).
Технике надо учить того, кто потом ей будет пользоваться. Учительница английского будущая — не будет. Ей нужна не техника, а культура.
Зачем учить меня каким-то хитрым мазкам или способам смешивания краски, если я рисовать картины не хочу и вообще это дело ненавижу? А вот рассказать об истории живописи, дать обзор существующих направлений, рассмотреть конкретные картины и дать их анализ — это вполне ок.
Есть разница между писателем и читателем, понимаете? Учить писать надо того, кто будет писать.
Только разница между рисованием и математикой в том, что технику мазков может нигде больше и не получится использоваться, а вот на основах математики построен мир. Может учительнице английского никогда и не пригодится непосредственно понимание определения предела, но уж точно лишним не может и строгости мысли добавит.
Только разница между рисованием и математикой в том, что технику мазков может нигде больше и не получится использоваться, а вот на основах математики построен мир.
Это все замечательно, но, еще раз, техника математики (и вообще чего угодно) нужна тем и только тем кто потом будет заниматься математикой (или чем угодно). Вот и все.
Может учительнице английского никогда и не пригодится непосредственно понимание определения предела, но уж точно лишним не может и строгости мысли добавит.
Ничего оно ей не добавит кроме головной боли.
Учительница английского будущая — не будет.
А может будет? Вы сперва научите.
А может будет? Вы сперва научите.
А она того хочет? Вы ее спросили? Она же решила стать учительницей английского. Если бы она хотела быть математиком — она бы пошла учиться на математика, а не на учительницу английского.
Давайте мб вас силой заставим учиться писать картины, петь, играть на балалайке, танцевать твист и играть в го?
А она того хочет?
А откуда она знает, пока не попробовала?
Она же решила стать учительницей английского.
И жить на работе?
Давайте мб вас силой заставим учиться писать картины, петь, играть на балалайке, танцевать твист и играть в го?
Если Вы найдёте мне для этого время — то я от этого точно не умру. Потом половину забуду как страшный сон, другой половиной буду пользоваться всю жизнь. Проблема в том, что заранее неизвестно, что к какой половине относится.
А откуда она знает, пока не попробовала?
Видите ли в чем дело, чтобы попробовать все — надо не есть не спать и только пробовать лет эдак тыщу. Причем за эту тыщу лет появиться еще куча занятий, на попробовать которые надо будет потратить еще две тыщи лет.
Почему вы предлагаете пробовать матан? Почему бы ей не попробовать писать скандинавские саги?
И жить на работе?
Откуда вы это взяли? Вы предлагаете ей выбрать матан в качестве хобби? Ну так тем более не надо ей брать интегралы и считать определители, а надо давать историю и обзорные лекции.
Если Вы найдёте мне для этого время — то я от этого точно не умру.
Но вы же в данном случае не предлагаете учительнице "если найдете время", это обязательный предмет.
Меньше спите, не поешьте разок, не отдохнете. Зато картины порисуете.
другой половиной буду пользоваться всю жизнь
Скорее всего, ничем не будете пользоваться.
Нет, гуманитарию не надо ни интегралы, ни матрицы, ни индукции.
И чем же он сможет заниматься без всего этого? Я сегодня утром задумался: придумал две профессии с высшим образованием, но без математики: переводчик и врач (и то не всякий).
Сможете ещё придумать?
не надо учить гуманитариев заниматься математикой
Пока не заставишь человека попробовать заниматься математикой — не поймёшь, гуманитарий он или нет.
UFO just landed and posted this here
Я специально сказал «с высшим образованием». Вот я — учился на инженера, работаю программистом. Пригождается мне высшее образование? Как бы не так! Занимаюсь ремеслом! А чтобы почувствовать себя программистом — академической математики не хватает.
Менеджер, юрист. Согласен. Переводчика — сам назвал, это моя жена. Её сестра — архитектор, если бы ей не давали сопромат, то что бы тогда осталось?
Ещё одна моя знакомая — инженер-конструктор изделий из кожи. У них была настоящая теплотехника, я даже удивился (сам с ужасом вспоминаю тройные интегралы от гауссинады).
Менеджер, юрист. Согласен. Переводчика — сам назвал, это моя жена. Её сестра — архитектор, если бы ей не давали сопромат, то что бы тогда осталось?
Ещё одна моя знакомая — инженер-конструктор изделий из кожи. У них была настоящая теплотехника, я даже удивился (сам с ужасом вспоминаю тройные интегралы от гауссинады).
а весь сопромат и утечки тепла программа на комплюктере у них там считаетА потом мосты рушатся, так как «архитекторы с дипломом» не понимают, когда выходят за рамки применимости заложенных в эти программы моделей.
Есть конкретные примеры мостов, которые разрушились от того, что архитекторы с дипломом вышли за рамки применимости моделей?
Разумеется. Вот мостик. Вот домик. Вот школа.
Это то, что навскидку нашлось. А так — это, увы, типичное явление.
Это то, что навскидку нашлось. А так — это, увы, типичное явление.
И чем же он сможет заниматься без всего этого?
ДА практически чем угодно, в 99% профессий ни интегралы ни матрицы вам не понадобятся.
в 99% профессий ни интегралы ни матрицы вам не понадобятся.
И высшее образование тоже. Ну, разве что «для галочки».
И высшее образование тоже.
окей
в 99% профессий где нужно высшее образование игтегралы тоже не понадобятся. С-но, кому понадобятся интегралы:
- математики, физики, прочие ученые-технари и их обслуживающие
- инженеры
- конец списка
математики, физики, прочие ученые-технари и их обслуживающие
инженеры
Забыли учёных-естественников, которым математика год от года всё нужнее.
Ну, вероятно, вы сумеете доказать, что всё это вместе — процент от числа профессий, где нужно высшее образование.
Потому что если считать по моим знакомым с высшим образованием — одних только инженеров процентов 20%.
Забыли учёных-естественников
Ну я сказал — ученые технари
Ну, вероятно, вы сумеете доказать, что всё это вместе — процент от числа профессий, где нужно высшее образование.
Это фактически две профессии.
Потому что если считать по моим знакомым с высшим образованием — одних только инженеров процентов 20%.
Вы кого именно подразумеваете под инженерами? Давайте сразу оговоримся — программисты и прочие итшники это не инженеры. Инженеры — это которые строят самолеты, проектируют двигатели и атомные электростанции.
Давайте сразу оговоримся — программисты и прочие итшники это не инженеры.
О-кей. Тогда 5%.
А остальные 15% — это такие ITшники, которым нужна математика.
А остальные 15% — это такие ITшники, которым нужна математика.
Математика нужна только тем итшникам, которые непосредственно обслуживают науку (работают в НИИ, работают с учеными, которые потом пишут статьи в журналы, или сами являются таковыми и пишут статьи в журналы), либо инженеров (но тут уже в существенно меньшей степени). То есть — практически никому. Я бы сказал, что из всех программистов хорошо если одному из ста нужна математика. И, думаю, это значительно завышенная оценка, на самом-то деле.
НИИ мертвы уже лет 25. Сейчас все двигают частные фирмы.
Математика нужна везде чуть глубже разработки интерфейсов. От видео и прочих кодеков до протоколов.
PS: И это я даже про криптографию не вспомнил.
Математика нужна везде чуть глубже разработки интерфейсов. От видео и прочих кодеков до протоколов.
PS: И это я даже про криптографию не вспомнил.
НИИ мертвы уже лет 25.
Я подразумевал любое учреждение, которое занимается научными исследованиями. Конкретная форма не существенна.
Математика нужна везде чуть глубже разработки интерфейсов. От видео и прочих кодеков до протоколов.
ДА нет, практически нигде не нужна. Вот чтобы разработать кодек — нужна, будут методы в научной статье изложены. А потом реализовать — уже не нужна, кроме базовой.
PS: И это я даже про криптографию не вспомнил.
Конечно, ученым, которые занимаются криптографией, математика нужна. А программисты — просто реализуют алгоритмы, созданные учеными. Для этого достаточно на порядки меньшего уровня знаний.
Сейчас научными исследованиями каждый второй стартап занимается. Не говоря уже о всех монстрах. Нет (или почти нет) чистых ученых в computer science. Все пишут код.
После разработки кодек надо понять, улучшить, оптимизировать под железо, протестировать. Реализовать с учетом особенностей платформ подо все. Для RFC документы написать. Работы море. И вся она знания математики требует.
Ну-ну. Не понимая как и почему оно работает будет все печально. Дыра? Где дыра? Вы о чем вообще? Вот брутфорсом не подбирается, а оптимизировать перебор я не умею.
После разработки кодек надо понять, улучшить, оптимизировать под железо, протестировать. Реализовать с учетом особенностей платформ подо все. Для RFC документы написать. Работы море. И вся она знания математики требует.
Ну-ну. Не понимая как и почему оно работает будет все печально. Дыра? Где дыра? Вы о чем вообще? Вот брутфорсом не подбирается, а оптимизировать перебор я не умею.
Сейчас научными исследованиями каждый второй стартап занимается.
Нет, не занимается.
После разработки кодек надо понять, улучшить, оптимизировать под железо, протестировать.
И для всего этого математика не нужна.
Ну-ну. Не понимая как и почему оно работает будет все печально.
Ну так люди, кто это все пишет, они и не понимают. И ничего печального, представьте себе.
Дыра? Где дыра? Вы о чем вообще?
Вообще никак с математикой не связано. Это вопрос реализации.
CRC32 дыряв принципиально, MD5 тоже.
CRC32 дыряв принципиально
Что значит "дыряв"? Если правильно реализован — то гарантированно не "дыряв".
Представим что есть алгоритм ЭЦП подписывающий CRC32 хэш. Алгоритм абсолютно правильно реализованный. За сколько времени вы сможете подделать такую ЭПЦ?
Для упрощения алгоритм аналогичен ГОСТУ, во всем кроме функции хеширования. У вас есть подписанный файлик. Допустим тот же pdf и открепленная подпись. Надо поменять содержимое файлика и сохранить валидность подписи.
Для упрощения алгоритм аналогичен ГОСТУ, во всем кроме функции хеширования. У вас есть подписанный файлик. Допустим тот же pdf и открепленная подпись. Надо поменять содержимое файлика и сохранить валидность подписи.
Представим что есть алгоритм ЭЦП подписывающий CRC32 хэш. Алгоритм абсолютно правильно реализованный. За сколько времени вы сможете подделать такую ЭПЦ?
А какое это отношение имеет к дырявости? Если алгоритм правильно реализован, то вы получаете все гарантии, которые этот алгоритм дает.
Что именно вы требуется от алгоритма — это уже ваш выбор. Если вы не требуете от хеша криптографической стойкости — ну ее и нет, но это же не хеш дырявый, это требования дырявые.
И для понимания того, что подпись должна быть стойкой ко взлому (то есть для способности сформулировать требования) — математика не нужна, нужен мозг.
Надо уметь понимать криптостойкий ли хэш. CRC32 я привел как пример некриптостойкого.
Еще разные разделы математики нужны создателям чертежных систем, графических движков, аналитикам данных, геймдевщикам. Еще «редким» кастам: ИТ-медикам, безопасникам, автоматизаторам производств…
Лично я пару математических трюков использовал в вебе, хотя казалось бы…
Лично я пару математических трюков использовал в вебе, хотя казалось бы…
Еще разные разделы математики нужны создателям чертежных систем, графических движков, аналитикам данных, геймдевщикам.
Слушайте, ну вы про какие-то совершенно элементарные вещи говорите уровня 2*2=4. По такой логике математика всем нужна, сдачу в магазине-то надо считать. Или зарплату, которую вам на работе выдали.
Вы очень лихо записали математику, необходимую специалистам выше, в «элементарную». Можете чуть подробнее обосновать такую категоричность?
Вы очень лихо записали математику, необходимую специалистам выше, в «элементарную».
А какая она?
Можете чуть подробнее обосновать такую категоричность?
Обосновать что именно? Что базовые понятия считаются элементарными? Ну это вроде как очевидно, все упомянутые навыки не требуют никаких пререквизитов, вы можете им обучать любого человека с улицы, ergo они по определению элементарны.
С-но именно потому и незачем им учить — если человеку для написания 3ддвижка понадобятся базовые навыки линейной алгебры (в пределах первых 10 страничек учебника) — он их за недельку разберет и проблема решена.
Элементарная математика: это 2+2=4. Думаю, математику средней российской школы можно считать элементарной.
По поводу упомянутых навыков (это разделы математики нужны создателям чертежных систем, графических движков, аналитикам данных, геймдевщикам). В статье я упоминал учебник для создателя чертежных систем: он уже требовал ЛинАла, АнГема, немного матана и приближенных вычислений. Аналитикам данных и прочим DS надо знать теорвер и статистику (а есть еще нейросетевики, математику которых я просто не могу оценить). У геймдевщиков свои заморочки с балансом, рандомом генерацией карт, расчетов оценочных функций для AI, отдельные задачи оптимизцации из предметной области; короче, может всплыть любая математика, пускай и не на самом хардкорном уровне. И да, всю эту математику надо прикладывать к оборудованию, а это отдельный цимес.
P.S. Если мои (дилетантские) аргументы вам кажутся неубедительными — можно призвать в ветку топ-авторов соответствующих хабов.
По поводу упомянутых навыков (это разделы математики нужны создателям чертежных систем, графических движков, аналитикам данных, геймдевщикам). В статье я упоминал учебник для создателя чертежных систем: он уже требовал ЛинАла, АнГема, немного матана и приближенных вычислений. Аналитикам данных и прочим DS надо знать теорвер и статистику (а есть еще нейросетевики, математику которых я просто не могу оценить). У геймдевщиков свои заморочки с балансом, рандомом генерацией карт, расчетов оценочных функций для AI, отдельные задачи оптимизцации из предметной области; короче, может всплыть любая математика, пускай и не на самом хардкорном уровне. И да, всю эту математику надо прикладывать к оборудованию, а это отдельный цимес.
P.S. Если мои (дилетантские) аргументы вам кажутся неубедительными — можно призвать в ветку топ-авторов соответствующих хабов.
Элементарная математика: это 2+2=4. Думаю, математику средней российской школы можно считать элементарной.
Элементарная — эта та, что не требует каких-то пререквизитов кроме базовых (того, что проходится в общей школе). Теория пределов — элементарна, основы линейной алгебры — элементарны, основы общей алгебры — элементарны, начала общей топологии — элементарны.
То есть вы можете взять любого человека с улицы и ему спокойно все это объяснять.
Все о чем вы говорите — это совершенно базовые вещи, еще раз, если человеку для задачи нужны основы линейной алгебры в рамках первых 10 страничек учебника — он просто возьмет и прочитает.
Теория пределов — элементарна, основы линейной алгебры — элементарны, основы общей алгебры — элементарны, начала общей топологии — элементарны.А, понятно. У нас разные определения «элементарности». В ваших терминах математика выше элементарной действительно нужна лишь крайне малой доле программистов.
То есть вы можете взять любого человека с улицы и ему спокойно все это объяснять.На вашей улице живут очень хорошие люди. Вы на Вернадского или на Воробьевых? На моей улице далеко не каждый осознавал тот же дискриминант.
В ваших терминах математика выше элементарной действительно нужна лишь крайне малой доле программистов.
ну о том и речь. эти курсы объединяются в calculus и в доступной форме читаются не_математически-ориентированным специальностям, которым нужны только элементарные приложения
за такой подход и надо ратовать
На моей улице далеко не каждый осознавал тот же дискриминант.
Так на подобном уровне его осознавать не надо, надо просто понимать что в формуле написано, и как его посчитать, разве нет? А это не требует каких-то особых знаний, там только умножение и сложение применяется.
а я вот до сих пор не понимаю, почему он так называется и почему он из всей формулы выделяется в отдельную букву. Что он дискриминирует? У него есть самостоятельный смысл?
Кстати, то же самое про детерминант у матриц. Что он детерминирует, то бишь определяет?
Кстати, то же самое про детерминант у матриц. Что он детерминирует, то бишь определяет?
Что он дискриминирует?
Уравнение по характеру решения (наличие совпадающих/комплексных корней ) :)
Кстати, то же самое про детерминант у матриц. Что он детерминирует, то бишь определяет?
Опять же — определенные свойства матриц.
Именование подобных объектов сродни именованию переменных при программировании. Во время выкладок у кого-то когда получилось какое-то важно число, которое вычислялось по соответствующей формуле, его как-то назвали, чтобы в дальнейшем было удобнее ссылаться, вот и все.
В какой конкретно задаче оно так было именовано — обычно совсем неинтересно и никакого понимания вам не придаст, поверьте. Скорее, наоборот запутает.
Давайте сразу оговоримся — программисты и прочие итшники это не инженеры. Инженеры — это которые строят самолеты, проектируют двигатели и атомные электростанции.
А это почему так кстати? В самолетах, двигателях и электростанциях много разных программ. Их кто разрабатывает? Специалисты в области программной инженерии, разве нет?
А то ведь по вашей логике вообще никаких инженеров и нету вовсе — есть схемотехники, они только схемы рисуют, есть конструктора — они только конструируют. Куда ни кинь — никто непосредственно за все эти станции и двигатели не отвечает, так что ли?
В самолетах, двигателях и электростанциях много разных программ. Их кто разрабатывает?
программисты, которым при этой разработке знания математики не требуются.
они только схемы рисуют, есть конструктора — они только конструируют
Есть те, кто их считает. Вот им математика — нужна. Ну, чтобы считать. А тем, кто рисует и конструирует (если это другие люди) — конечно, не нужна. Потому что зачем? За них уже все посчитано, с-но самим считать ничего не требуется. А если не надо считать — не нужна и математика.
Обождите, вы не поняли — я не утверждал, что всем этим людям нужна математика (хотя я готов был бы это и утверждать в отношении at least части их, но это неважно). Меня коробило и коробит отделение инженеров-программистов от остальной части инженеров, ровно о чем я и высказался.
Но если уж зашла речь, то вопрос такой — а где по-вашему зона раздела между «математика нужна» и «математика не нужна»? Банальный апериодический фильтр посчитать — это нужна, или не нужна? Ядро фильтра для обработки изображения определить — нужна, или не нужна?
Но если уж зашла речь, то вопрос такой — а где по-вашему зона раздела между «математика нужна» и «математика не нужна»? Банальный апериодический фильтр посчитать — это нужна, или не нужна? Ядро фильтра для обработки изображения определить — нужна, или не нужна?
Но если уж зашла речь, то вопрос такой — а где по-вашему зона раздела между «математика нужна» и «математика не нужна»?
Для того, чтобы подставить числа в готовую формулу — не нужна. Нужна чтобы придумать эту формулу.
Для того, чтобы подставить числа в готовую формулу — не нужна. Нужна чтобы придумать эту формулу.
Опять непонятно. Вот предположим вывел я формулу для расчета коэффициента усиления в каком-то хитровымудренном измерительном усилителе, и потом использовал ее для подбора параметров — это уже формула, или еще нет?
Опять непонятно. Вот предположим вывел я формулу для расчета коэффициента усиления в каком-то хитровымудренном измерительном усилителе, и потом использовал ее для подбора параметров — это уже формула, или еще нет?
А какие средства вы использовали для ее вывода?
Ну и да, 99 из 100 программистов с такого рода задачами никогда не столкнется, т.к. с железом не работает.
А какие средства вы использовали для ее вывода?
Ну, базовые средства само собой — законы Ома и Кирхгофа. Дальше уже из знаний схемотехники все проистекает. То есть конечно тут больше физики, чем математики, но вторая есть язык первой. И в итоге ведь формула получается.
Ну и да, 99 из 100 программистов с такого рода задачами никогда не столкнется, т.к. с железом не работает
Вы преувеличиваете (или преуменьшаете, смотря с какой стороны смотреть).
Я согласен с тем, что тождественность программирования и математики является ошибкой, и когда абстрактная толпа программистов дистанцирует себя от остального общества по принципу «мы математики, а вы нет» — это выглядит смешно. Но это не повод утверждать, что математиков среди программистов ровно 1%.
Ну, базовые средства само собой — законы Ома и Кирхгофа.
Я говорю о математических средствах. Какой формализм использовался для выкладок?
Но это не повод утверждать, что математиков среди программистов ровно 1%.
Ну допустим не ровно 1%, пусть будет 2%, или 2.1111%. Это что-то поменяло?
Смысл в том, что их очень мало, практически нет.
Я говорю о математических средствах. Какой формализм использовался для выкладок?
Будучи знакомым (шапочно) с понятием математического формализма, тем не менее не могу ответить на ваш вопрос, т.к. видимо его совсем не понимаю. Скажу так — предложите варианты? :)
Смысл в том, что их очень мало, практически нет
Вот я как раз полагаю, что их не «очень мало», а «просто мало».
Скажу так — предложите варианты?
Ну вы могли применять к формулам какие-то базовые преобразования (сложение, умножение,
элементарные ф-и, простейшие замены), могли использовать дифференциальное интегральное исчисление, могли использовать аппарат аналитической геометрии, аппарат тензорного исчисления, функциональный анализ, могли использовать в рамках вывода какие-то алгебраические соображения (тут уже, с-но, вам пришлось бы работать с алгебраическими структурами), топологические (общая топология и более сложные — в сторону алгебраической топологии, дифференциальной топологии) и т.д..
То есть можно переформулировать так: "что нужно знать, чтобы понять ваши выкладки?"
Тенденции сейчас такие, что программисты, которым не нужна математика, скоро сами станут никому не нужны, т.к. их труд относительно легко автоматизируется.
Например, раньше инженеру, чтобы получить результаты расчёта мат. модели, нужно было идти к программисту, которые переводил его уравнения в код и выдавал перфокарты с результатами. Уже лет 20 как вид таких программистов полностью вымер.
Трудно автоматизировать творческий процесс, а людям, занятым такими процессами в технике, как правило, нужна математика. При этом, каждый технический специалист сейчас хоть немного, но и программист. Конечно, есть ещё большой пласт людей, которые просто пишут код, но это уже скорее становится профессией средне-специального образования. Конечно, выпускникам техникумов математика практически в работе не нужна.
Например, раньше инженеру, чтобы получить результаты расчёта мат. модели, нужно было идти к программисту, которые переводил его уравнения в код и выдавал перфокарты с результатами. Уже лет 20 как вид таких программистов полностью вымер.
Трудно автоматизировать творческий процесс, а людям, занятым такими процессами в технике, как правило, нужна математика. При этом, каждый технический специалист сейчас хоть немного, но и программист. Конечно, есть ещё большой пласт людей, которые просто пишут код, но это уже скорее становится профессией средне-специального образования. Конечно, выпускникам техникумов математика практически в работе не нужна.
Тенденции сейчас такие, что программисты, которым не нужна математика, скоро сами станут никому не нужны, т.к. их труд относительно легко автоматизируется.
Ну вот когда автоматизируются — тогда автоматизируются. Пока что мы даже по направлению к этому не идем.
Трудно автоматизировать творческий процесс, а людям, занятым такими процессами в технике, как правило, нужна математика.
Ну это кому конкретно?
Ну вот когда автоматизируются — тогда автоматизируются. Пока что мы даже по направлению к этому не идем.
Ну как же не идём? Уже сейчас профессия «программист» сместилась в сегмент средне-специального образования, хотя раньше требовала глубокого знания различных разделов высшей математики. В очень многих областях техники программисты уже были вытеснены CAE-софтом. По-моему, вектор развития вполне явно проглядывается.
Ну это кому конкретно?
Ну я, например, работаю в инженерном отделе частной фирмы, которая как раз занимается созданием софта для моделирования динамики технических систем. Для того, чтобы создавать модели, мне иногда нужно и дифференциальные уравнения на листочке решить, преобразовав по Лапласу и интеграл взять аналитически. Про численные методы вообще молчу. При этом, разумеется, программы я пишу сам на языке Modelica, ну и совсем немного C++, программист со мной рядом не сидит. Основная часть технических специалистов фирмы — инженеры, физики, математики. Есть программисты, которые отвечают за лицензирование, билды проекта, тестсеты, которым, вероятно, математика не очень нужна, но таких наверное несколько человек на всю фирму.
Ну как же не идём?
Ну так.
Уже сейчас профессия «программист» сместилась в сегмент средне-специального образования, хотя раньше требовала глубокого знания различных разделов высшей математики.
А это не потому что кто-то идет в сторону автоматизации, это потому что раньше программисты решали только те задачи, для которых требовалась математика, а теперь в дополнение к ним решают и другие. То есть класс задач только расширяется. Так что вектор развития, действительно, очевиден, но направлен он строго противоположно тому, о котором вы говорите.
Ну я, например, работаю в инженерном отделе частной фирмы, которая как раз занимается созданием софта для моделирования динамики технических систем.
То есть вы попадаете в группу "обслуживают ученых и инженеров".
Штука в том, что очень мало программистов попадает в эту группу.
Штука в том, что очень мало программистов попадает в эту группу.
Штука в том, что я вообще в Ваши группы не попадаю, потому что я в той же степени программист, в которой и «оператор ЭВМ». Я — инженер и для решения своих задач использую программирование.
Вообще, дискуссия переходит в плоскость «среднее образование против высшего». Я не буду спорить с тем, что глобально большинству специалистов для работы достаточно среднего образования с прицелом на практику, вместо обременения себя матаном. Если Вы говорите о том, что для того, чтобы научиться писать код, не нужно идти в ВУЗ, я полностью с Вами согласен.
По поводу того, будет ли на рынке труда место людям, которые умеют только писать код или их вытеснят кодогенераторы с дружественным для профильных специалистов (будь то инженеры, дизайнеры или специалисты по бизнес-процессам) интерфейсом, конечно, дискуссионный. Но в качестве предмета для дискуссии я вижу здесь только вопрос «когда?».
Я — инженер
То есть попадаете в группу "инженер". Непонятно, с чем вы спорите.
По поводу того, будет ли на рынке труда место людям, которые умеют только писать код или их вытеснят кодогенераторы с дружественным для профильных специалистов (будь то инженеры, дизайнеры или специалисты по бизнес-процессам) интерфейсом, конечно, дискуссионный.
Не будет такого, пока сильный ИИ не изобретете.
Вот смотрите, были раньше модными всякие WYSIWYG для хтмля — и то в итоге не взлетело.
Не будет такого, пока сильный ИИ не изобретете.
Вот смотрите, были раньше модными всякие WYSIWYG для хтмля — и то в итоге не взлетело.
Когда сильный ИИ изобретут, тогда и инженерам придётся придумывать чем заниматься. А автоматизация кодогенерации — это уже давно свершившийся факт во многих отраслях промышленности. Вопрос только в том, когда автоматизация захватит все отрасли.
А автоматизация кодогенерации — это уже давно свершившийся факт во многих отраслях промышленности.
Только то, что мы обсуждаем, к кодогенерации никакого отношения не имеет.
Когда сильный ИИ изобретут, тогда и инженерам придётся придумывать чем заниматься.
Так а содержательно работа кодера от работы инженера ничем не отличается.
Только то, что мы обсуждаем, к кодогенерации никакого отношения не имеет.
Тогда попрошу расшифровать какой ещё круг обязанностей Вы видите у программиста, которому не нужна математика (кроме перевода чётко сформулированных пожеланий клиента в код).
Вы видите у программиста, которому не нужна математика
Решать задачи бизнеса :)
(кроме перевода чётко сформулированных пожеланий клиента в код)
Это в инженерных дисциплинах есть более-менее четкое ТЗ (хотя и тоже с оговорками иногда), которое надо в код перевести. А основная часть индустрии работает с плавающим ТЗ, которое меняется на ходу и которое вообще из заказчика извлечь — уже отдельное искусство. И методы разработки используются соответствующие, учитывающие этот факт. С-но сформулировать пожелания клиента — и есть значительная часть работы программиста.
Потому что когда человек не программист — он обычно не в состоянии адекватным образом сформулировать свои хотелки :)
То что Вы перечислили — часть рутины вообще любого специалиста. Круг задач скорее относится к проект-менеджеру, но в принципе, их может решать и инженер и программист и дизайнер.
Я думаю, Вы хотите сказать, что хороший программист должен быть глубоко погружен в проблему клиента, т.е. желательно быть специалистом в той области, чьи проблемы он решает. Это именно то, о чём говорю я. Уже сейчас гораздо важнее разбираться в бизнес-процессах, в дизайне, в технических науках, а умение писать код — лишь хорошее дополнение к квалификации.
Я думаю, Вы хотите сказать, что хороший программист должен быть глубоко погружен в проблему клиента, т.е. желательно быть специалистом в той области, чьи проблемы он решает. Это именно то, о чём говорю я. Уже сейчас гораздо важнее разбираться в бизнес-процессах, в дизайне, в технических науках, а умение писать код — лишь хорошее дополнение к квалификации.
Уже сейчас гораздо важнее разбираться в бизнес-процессах, в дизайне, в технических науках, а умение писать код — лишь хорошее дополнение к квалификации.
Так умение писать ТЗ — это и есть умение писать код :)
Любое полное ТЗ эквивалентно коду. И, действительно, если таковое ТЗ компьютеру предоставить (допустим, в формате программы на с++), то он по этому ТЗ сгенерирует код на языке ассемблера соответствующей архитектуры :)
"профессиональные писцы ТЗ" — это программисты и есть. Люди, которые способны зафиксировать ТЗ полностью и формально строго.
И эту задачу без сильного ИИ вам савтоматизировать не выйдет никак.
Да, умение со слов клиента сформировать ТЗ — неотъемлемая часть квалификации любого специалиста. Если Вы настаиваете на том, что любой специалист, по сути в душе — программист, то я с этим в целом согласен. Единственное, нужно понимать, что это лишь базовый навык, поверх которого лежит специализация.
Да, умение со слов клиента сформировать ТЗ — неотъемлемая часть квалификации любого специалиста.
Но никто кроме программистов, по факту, формированием ТЗ не занимается (по крайней мере если речь о ТЗ, которые сможет понять компьютер — т.е. полных и формально строгих). Не говоря уже о том, чтобы заниматься этим профессионально :)
Так что непонятно при чем тут любые специалисты.
Не понимаю, откуда у Вас такая уверенность в том, что Вы всё знаете о рабочем процессе специалистов других отраслей?
Моя работа по инженерным проектам заключается в том, что я формализую пожелания клиента по части имитационной модели его устройства, обрабатываю поступившие данные, обобщаю и дополняю их так, что компьютер выдаёт однозначное решение проблемы клиента.
Моя жена работает 3Д-визуализатором, и её работа заключается в том же самом: она берёт пожелания клиента по части того как должна выглядеть картинка, формализует их в ТЗ, «объясняет» задание компьютеру и получает однозначный результат, который после ряда итераций полностью удовлетворяет запрос клиента.
Вы пытаетесь вложить в профессию программиста значение творца. Отчасти это так и есть, но творец — это не только (и не столько) программист. Профессий-творцов очень много, а программист — это прежде всего человек, который пишет код.
Моя работа по инженерным проектам заключается в том, что я формализую пожелания клиента по части имитационной модели его устройства, обрабатываю поступившие данные, обобщаю и дополняю их так, что компьютер выдаёт однозначное решение проблемы клиента.
Моя жена работает 3Д-визуализатором, и её работа заключается в том же самом: она берёт пожелания клиента по части того как должна выглядеть картинка, формализует их в ТЗ, «объясняет» задание компьютеру и получает однозначный результат, который после ряда итераций полностью удовлетворяет запрос клиента.
Вы пытаетесь вложить в профессию программиста значение творца. Отчасти это так и есть, но творец — это не только (и не столько) программист. Профессий-творцов очень много, а программист — это прежде всего человек, который пишет код.
Не понимаю, откуда у Вас такая уверенность в том, что Вы всё знаете о рабочем процессе специалистов других отраслей?
Потому что я вижу результат работы. Вам не обязательно быть пекарем, чтобы посмотреть на хлеб и сделать выводы о работе пекаря.
программист — это прежде всего человек, который пишет код.
Хорошо, давайте определимся. Что такое "код"? Является ли "кодом" то, что вы (или ваша жена) передаете компьютеру с целью получить результат? Если (не)является, то почему?
Потому что я вижу результат работы.
Ну так и судите результат, а не впадайте в заблуждения, пытаясь делать выводы о процессах.
Хорошо, давайте определимся. Что такое «код»? Является ли «кодом» то, что вы (или ваша жена) передаете компьютеру с целью получить результат? Если (не)является, то почему?
Конечно, это в конечном итоге код. Но пишется этот код автоматически при помощи специально адаптированных для этого интерфейсов.
Там где процесс трансформации «ТЗ» специалиста в язык, понятный компьютеру (пока) не автоматизирован, требуется прибегать к ручному программированию.
Конечно, это в конечном итоге код. Но пишется этот код автоматически при помощи специально адаптированных для этого интерфейсов.
Погодите, так вы пишите код, который компьютер исполняет, или за вас компьютер пишет код, который он потом исполняет?
Если второе — значит, ТЗ пишет компьютер, тогда почему вы сказали, что ТЗ пишете вы?
В процессе работы задаются такие параметры, что у компьютера есть только один вариант создания кода.
Когда я перетаскиваю элемент системы на форму, генерятся соответствующие строчки кода. Конкретно в нашей программе их можно и руками писать, но перетаскивать элемент-таки быстрее.
Собственно, вы когда на c++ пишете, тоже не напрямую с регистрами работаете, выходит, компьютер вам тоже помогает ТЗ «писать».
Когда я перетаскиваю элемент системы на форму, генерятся соответствующие строчки кода. Конкретно в нашей программе их можно и руками писать, но перетаскивать элемент-таки быстрее.
Собственно, вы когда на c++ пишете, тоже не напрямую с регистрами работаете, выходит, компьютер вам тоже помогает ТЗ «писать».
Так вы (и ваша жена) программисты или нет?
Ну я же говорю — мы по специальности ровно в той же степени программисты, в какой и операторы ЭВМ. В наших и многих других областях часть работы программиста была давно и успешно автоматизирована в полном объёме.
В наших и многих других областях часть работы программиста была давно и успешно автоматизирована в полном объёме.
Погодите, как же она автоматизирована, если вы сами говорите, что свой "код" руками пишете?
Смотря о чём вы конкретно. Когда я работаю над инженерными проектами, я пользуюсь преимущественно готовыми элементами, выступая пользователем нашей программы. В этом случае я описываю техническую систему через графический интерфейс и параметризую её. Код создаётся автоматически.
Пишу код руками я для создания новых элементов. Но и в этом случае решающую роль играет владение математикой и физикой, нежели программированием т.к. в программе символьный анализ и процесс приведения уравнений к удобной для численного решения форме тоже автоматизирован. Т.е. основное время занимает творческая работа по выбору допущений и способов описания физических процессов.
Пишу код руками я для создания новых элементов. Но и в этом случае решающую роль играет владение математикой и физикой, нежели программированием т.к. в программе символьный анализ и процесс приведения уравнений к удобной для численного решения форме тоже автоматизирован. Т.е. основное время занимает творческая работа по выбору допущений и способов описания физических процессов.
Автоматизация кодогенерации — это эвфемизм для языка более высокого уровня, это ж классика, Брукс.
К сожалению, математику надо еще подружить с физикой.
Учусь на один из подвидов экономиста и тут изучают математику без физики, поэтому иногда математически верные расчеты при физическом сопоставлении с задачей превращается в непроходимый бред. А еще у нас(экономистов) математика преподается слабее и в учебниках по экономики даются входные данные, диф.ур. и сразу результат без вывода и преобразований, в стиле «поверьте на слово». Дали математикам пересчитать — их результат с результатом из учебника не сошелся.
Вроде экономист должен быть ближе к инженерам по подготовке, т.к. от экономиста зависит проект иной раз больше, чем от инженера. Например, инженер сообщает: — мы может сделать такую деталь в 4-х вариантах, в каждом упор на такие-то свойства.
И уже экономист считает альтернативные расходы, экономическую эффективность и прочие показатели, на базе которых находит сбалансированное решение. Но современные экономисты ищут не сбалансированное решение, а «правильное», которое в реальном мире может не существовать. Я молчу про привычку экономистов все переводить в деньги, что приводит к «эффективному менеджменту»: «деньги за каждую строчку кода» и стилю кода «индусский код».
Учусь на один из подвидов экономиста и тут изучают математику без физики, поэтому иногда математически верные расчеты при физическом сопоставлении с задачей превращается в непроходимый бред. А еще у нас(экономистов) математика преподается слабее и в учебниках по экономики даются входные данные, диф.ур. и сразу результат без вывода и преобразований, в стиле «поверьте на слово». Дали математикам пересчитать — их результат с результатом из учебника не сошелся.
Вроде экономист должен быть ближе к инженерам по подготовке, т.к. от экономиста зависит проект иной раз больше, чем от инженера. Например, инженер сообщает: — мы может сделать такую деталь в 4-х вариантах, в каждом упор на такие-то свойства.
И уже экономист считает альтернативные расходы, экономическую эффективность и прочие показатели, на базе которых находит сбалансированное решение. Но современные экономисты ищут не сбалансированное решение, а «правильное», которое в реальном мире может не существовать. Я молчу про привычку экономистов все переводить в деньги, что приводит к «эффективному менеджменту»: «деньги за каждую строчку кода» и стилю кода «индусский код».
UFO just landed and posted this here
Конкретная математика стр. 20.
Там на примере Ханойской башни. Если уж это не понять, то ой.
Заголовок спойлера
Математическая индукция — это общий способ доказательства, что некоторое утверждение о целом числе n справедливо
при любом n >= n0. Сначала данное утверждение доказывается,
когда n принимает свое наименьшее значение, n0; это называется
базой или основанием. Затем данное утверждение доказывается
для n > n0, в предположении, что оно уже доказано для всех n
между n0 и n — 1 включительно; это называется индукцией или
индуктивным переходом. Такого рода доказательство позволяет получить бесконечное число результатов при конечном объеме работы.
при любом n >= n0. Сначала данное утверждение доказывается,
когда n принимает свое наименьшее значение, n0; это называется
базой или основанием. Затем данное утверждение доказывается
для n > n0, в предположении, что оно уже доказано для всех n
между n0 и n — 1 включительно; это называется индукцией или
индуктивным переходом. Такого рода доказательство позволяет получить бесконечное число результатов при конечном объеме работы.
Там на примере Ханойской башни. Если уж это не понять, то ой.
UFO just landed and posted this here
Принцип математической индукции. Показанный на целых числах. На простом практическом (и классическом) примере. Кому нужно дальше, больше, выше — найдёт, я уверен.
Заголовок спойлераСужать область применения математики пользоваться числами всего лишь для того, чтобы посчитать зарплату — нормально.
ользоваться числами всего лишь для того, чтобы посчитать зарплату — нормально.
Нормально, только индукция для этого не нужна.
*Очень терпеливо*
Если ТЗ состоит в том, «Чтобы даже самый гуманитарный гуманитарий знал что такое индукция и умел её применять», то я привёл пример, где оная в двух словах разжёвана. Пользоваться частным случаем целых чисел для этого — не «почти преступление».
Чтобы даже самый гуманитарный гуманитарий знал что такое индукция и умел её применять
Как бы вы объясняли математическую индукцию для гуманитариев?
Конкретная математика стр. 20.
Математическая индукция применима далеко не только для целых чисел, сужать область её применимости до них — почти преступление.
Если ТЗ состоит в том, «Чтобы даже самый гуманитарный гуманитарий знал что такое индукция и умел её применять», то я привёл пример, где оная в двух словах разжёвана. Пользоваться частным случаем целых чисел для этого — не «почти преступление».
Статья называется «Проблемы современной записи математических текстов» но весь текст посвящен проблеме преподавания. Это сбивает с толку.
1) Хочу защитить Фихтенгольца. Его учебник, один из выдающихся, является частью образовательного процесса в котором должны быть и лекции и семинары, и тут талант автора учебника вполне может быть испорчен безаталанностью лектора.
2) Про «реальные проблемы». В рамках семинара или лекции с небольшим числом слушающих можно прощупывать почву и подгонять материал под аудиторию. При написании учебника для широкой аудитории это невозможно и лучше как раз оставлять стерильные формулировки, которые на местах уже адаптируют.
Вот например лет десять назад Питер издали классную Дискретную Математику для программистов (это я как программист с преподавательским опытом оцениваю). Но для не программистов я бы рекомендовал другой учебник.
3) «У профессоров математики хватает своих задач, чтобы писать учебники.»
Не достаточно быть талантом в своей профессии что бы писать хорошие учебники.
Нужно что бы талант в математике совпал с талантом в педагогике и писательстве. Это на столько редкое явление что даже слабые приближения к идеалу не сходят с полок годами.
Но всё это меркнет с общей проблемой ВО в России — многим было бы достаточно для счастливой жизни и училища но традиция, общество и военкомат влекут всех в стены ВУЗов, где боль, страдания и скрежет зубовный.
1) Хочу защитить Фихтенгольца. Его учебник, один из выдающихся, является частью образовательного процесса в котором должны быть и лекции и семинары, и тут талант автора учебника вполне может быть испорчен безаталанностью лектора.
2) Про «реальные проблемы». В рамках семинара или лекции с небольшим числом слушающих можно прощупывать почву и подгонять материал под аудиторию. При написании учебника для широкой аудитории это невозможно и лучше как раз оставлять стерильные формулировки, которые на местах уже адаптируют.
Вот например лет десять назад Питер издали классную Дискретную Математику для программистов (это я как программист с преподавательским опытом оцениваю). Но для не программистов я бы рекомендовал другой учебник.
3) «У профессоров математики хватает своих задач, чтобы писать учебники.»
Не достаточно быть талантом в своей профессии что бы писать хорошие учебники.
Нужно что бы талант в математике совпал с талантом в педагогике и писательстве. Это на столько редкое явление что даже слабые приближения к идеалу не сходят с полок годами.
Но всё это меркнет с общей проблемой ВО в России — многим было бы достаточно для счастливой жизни и училища но традиция, общество и военкомат влекут всех в стены ВУЗов, где боль, страдания и скрежет зубовный.
Статья называется «Проблемы современной записи математических текстов» но весь текст посвящен проблеме преподавания. Это сбивает с толку.Вы во многом правы. Увы, большая часть виденных мною «профессиональных» работ по понятности была хуже учебников. Плюс, школьная\университетская литература известна большинству на хабре, а «профессиональная» — процентам.
Хочу защитить Фихтенгольца. Его учебник, один из выдающихся, является частью образовательного процесса в котором должны быть и лекции и семинарыФихт крут, не спорю. Но учебный процесс предполагает наличие лектора, который, скорее всего, не обладает талантом\подготовкой педагога. Плюс, в наше время хайпится самообразование, и рассчитывать на помощь лектора не приходится.
Уверен, Фихтенгольц написал один из лучших учебников своего времени, но времена меняются.
При написании учебника для широкой аудитории… лучше как раз оставлять стерильные формулировки, которые на местах уже адаптируют.Опять-таки, мы живем во времена стартапов. Одно из сопутствующих поверий: лучше удовлетворить потребности одной группы пользователей на 100%, чем потребности трех групп на 80%. Дискретная Математика Для Программистов зайдет одной группе, Дискретная Математика Для Лириков — другой. В идеале, хотелось бы иметь большой учебник, из которого относительно легко вырывались бы куски для целевых групп. Вопрос цены и усилий на несколько учебников вместо одного остается открытым, да.
Нужно что бы талант в математике совпал с талантом в педагогике и писательстве. Это на столько редкое явлениеПолностью и абсолютно согласен. Поэтому и упомянул про командную работу. Лучше иметь отличный учебник от трех авторов, чем три посредственных от каждого.
Уверен, Фихтенгольц написал один из лучших учебников своего времени, но времена меняются.Я с матаном после второго курса (давно это было) очень мало сталкивался — много больше с «линейкой», комбинаторикой, графами. Поэтому любопытно: есть сегодня современный учебник по матану, который сильно превосходит Фихтенгольца? (Дайте, пожалуйста, ссылку — полистаю из интереса).
Нужно что бы талант в математике совпал с талантом в педагогике и писательстве.Совершенно необязательно. Более того — человек, которому «хорошо даётся» что-то скорее всего напишет хреновый учебник. Он напишет «очевидно» не потому, что потеряет две страницы выкладок в трамвае, а потому, что ему — действительно очевидно!
Есть профессионалы, которые умеют ещё и объяснять (Фейнман, к примеру), но вообще — для написания хорошего учебника нужно быть скорее хорошим педагогом, чем хорошим математиком…
О, да!
С преподаванием математики — проблем куча. Вставлю пять копеек.
1. Обычно это преподавание математики для… математиков. Физическая, экономическая, жизненная, философская подоплека остается за кадром. В результате мотивация страдает дичайшим образом. Но… чтобы всё донести нужно время и заинтересованность преподавателя и студентов. По наблюдениям — какому-то проценту умненьких студентов понятно и так, а оставшимся — бесполезно и не пригодится.
2. Обучение решению стандартных задач стандартными методами. Т.е. увы — математика не очень-то учит думать. Разные курсы физики в этом смысле у нас лучше — там надо все же модели строить.
3. Обратная связь — в школе есть ежедневная проверка тетрадей. В институте — нет. Реально хорошую работу со студентами — с въедливыми правками в каждом пункте студенческих поползновений наблюдал только на семинарах мехмата МГУ.
4. Наверное могли бы помочь книги типа «Высшая математика для гиперчайников», или «Высшая математика человеческим языком» — и в принципе не так сложно это сделать — просто по тому же Фихтенгольцу пройтись и переписать в забавном виде. Хотя может оно уже и есть.
5. Но не всё просто — те же математические определения они СТРОГИЕ — это архиважно. И после понимания смысла на пальцах, надо расшифровывать строгое определение и соотносить его с реальностью.
6-я копейка.
Кто не читал «Плач математика» Пола Локхарда — стоит прочитать.
С преподаванием математики — проблем куча. Вставлю пять копеек.
1. Обычно это преподавание математики для… математиков. Физическая, экономическая, жизненная, философская подоплека остается за кадром. В результате мотивация страдает дичайшим образом. Но… чтобы всё донести нужно время и заинтересованность преподавателя и студентов. По наблюдениям — какому-то проценту умненьких студентов понятно и так, а оставшимся — бесполезно и не пригодится.
2. Обучение решению стандартных задач стандартными методами. Т.е. увы — математика не очень-то учит думать. Разные курсы физики в этом смысле у нас лучше — там надо все же модели строить.
3. Обратная связь — в школе есть ежедневная проверка тетрадей. В институте — нет. Реально хорошую работу со студентами — с въедливыми правками в каждом пункте студенческих поползновений наблюдал только на семинарах мехмата МГУ.
4. Наверное могли бы помочь книги типа «Высшая математика для гиперчайников», или «Высшая математика человеческим языком» — и в принципе не так сложно это сделать — просто по тому же Фихтенгольцу пройтись и переписать в забавном виде. Хотя может оно уже и есть.
5. Но не всё просто — те же математические определения они СТРОГИЕ — это архиважно. И после понимания смысла на пальцах, надо расшифровывать строгое определение и соотносить его с реальностью.
6-я копейка.
Кто не читал «Плач математика» Пола Локхарда — стоит прочитать.
Согласен со всеми пятью копейками. По поводу четвертой: есть книги для чайников. В моем случае для меня одного экзамена зашли конспекты Письменного (дополняемые Фихтенгольцем). Для следующего экзамена, правда, уже не зашли.
UFO just landed and posted this here
4. Наверное могли бы помочь книги типа «Высшая математика для гиперчайников», или «Высшая математика человеческим языком» — и в принципе не так сложно это сделать — просто по тому же Фихтенгольцу пройтись и переписать в забавном виде. Хотя может оно уже и есть.
Видел матан в комиксах.
Ха, вот вам отдельные математические манги
1. Син, Т. Занимательная статистика. Факторный анализ. Манга
2. Митио, С. Занимательная математика. Анализ Фурье. Манга
3. Син, Т. Занимательная статистика. Регрессионный анализ.
4. Тахакаси, С. Занимательная статистика. Манга
5. Хироюки Кодзима, Cин Тогами, Занимательная математика. Производные и интегралы. Манга
6. Минору С., Занимательная математика. Дифференциальные уравнения. Манга
7. Син Такахаси, Иноуэ Ироха, Занимательная математика. Линейная алгебра. Манга
Кому надо по физике?
1. Нитта, Х. Занимательная физика. Механика. Манга
2. Томохиро, Х. Занимательная физика. Термодинамика. Манга
3. Ёсикадзу, И. Занимательная физика. Электрические цепи. Манга
4. Фудзитаки, К. Занимательная физика. Электричество. Манга
5. Такэи, М. Занимательная физика. Гидродинамика. Манга
6. Исикава, К. Занимательная физика. Квантовая механика. Манга
7. Ямамото, М. Занимательная физика. Теория относительности. Манга
8. Суэмасу, Х. Занимательная физика. Сопротивление материалов. Манга
Кому чуть-чуть информатики и программирования?
1. Мана, Т. Занимательное программирование. Базы данных. Манга
2. Сибуя, М. Занимательная информатика. Центральный процессор. Манга
3. Митани Масааки, Сато Синъити, Хиноки Идэро, Занимательная информатика. Криптография. Манга
И это далеко не все…
1. Син, Т. Занимательная статистика. Факторный анализ. Манга
2. Митио, С. Занимательная математика. Анализ Фурье. Манга
3. Син, Т. Занимательная статистика. Регрессионный анализ.
4. Тахакаси, С. Занимательная статистика. Манга
5. Хироюки Кодзима, Cин Тогами, Занимательная математика. Производные и интегралы. Манга
6. Минору С., Занимательная математика. Дифференциальные уравнения. Манга
7. Син Такахаси, Иноуэ Ироха, Занимательная математика. Линейная алгебра. Манга
Кому надо по физике?
1. Нитта, Х. Занимательная физика. Механика. Манга
2. Томохиро, Х. Занимательная физика. Термодинамика. Манга
3. Ёсикадзу, И. Занимательная физика. Электрические цепи. Манга
4. Фудзитаки, К. Занимательная физика. Электричество. Манга
5. Такэи, М. Занимательная физика. Гидродинамика. Манга
6. Исикава, К. Занимательная физика. Квантовая механика. Манга
7. Ямамото, М. Занимательная физика. Теория относительности. Манга
8. Суэмасу, Х. Занимательная физика. Сопротивление материалов. Манга
Кому чуть-чуть информатики и программирования?
1. Мана, Т. Занимательное программирование. Базы данных. Манга
2. Сибуя, М. Занимательная информатика. Центральный процессор. Манга
3. Митани Масааки, Сато Синъити, Хиноки Идэро, Занимательная информатика. Криптография. Манга
И это далеко не все…
Кстати, у того же Пола Локхарта есть, собственно, та самая «Математика для гиперчайников» — ru.b-ok.org/book/2474364/ab5400
Русского перевода пока нет, к сожалению. Но она написана настолько простым языком, что и Google Translate хватает.
Русского перевода пока нет, к сожалению. Но она написана настолько простым языком, что и Google Translate хватает.
Обычно это преподавание математики для… математиков.
Математику в вузах преподают математики. Поэтому часто копируют стиль собственных преподавателей.
Но хороший преподаватель математики строит курс с учетом аудитории. Ее подготовки и ЦЕЛЕЙ.
Для школьников я бы начал говорить о пределах с парадоксов Зенона. Мол был такой очень древний грек, пудривший согражданам мозги. Большинство его логических фокусов сводилось к тому, что если величину разбить на бесконечное число частей, то она кажется бесконечной. Целое состоит из половины и половины половины и еще половины половины половины и так до бесконечности. Так вот, лет триста назад математики научились считать все эти кусочки мал мала меньше и строго показали, когда сумма оказывается бесконечной, а когда нет. Сейчас мы с этим будем разбираться.
Для инженеров я бы начал с рядов Тейлора и Фурье. С того, что в инженерном деле часто встречаются функции с которыми работать крайне неудобно. Но есть довольно универсальный способ заменить такую функцию суммой бесконечного ряда ясных и привычных степенных функций. И тогда мы можем вести расчеты по привычным формулам с любой нужной точностью. Но для этого нужно научиться работать с бесконечными рядами. И начнем мы не с суммы функций, а, для простоты, с суммы чисел.
Для статистиков придется искать понятную задачу в теорвере и т.д.
Просто вы читаете плохие книги.
Сработает. Редко, когда в математике что-то появляется совсем с потолка. А даже если и появляется, то попадает на всеобщее обозрение не просто так.
Наверняка в высших разделах математики подход «сначала пример, потом абстракция» не сработает.
Сработает. Редко, когда в математике что-то появляется совсем с потолка. А даже если и появляется, то попадает на всеобщее обозрение не просто так.
Во-первых, название статьи совершенно не связано с её содержанием.
Во-вторых, касательно претензий образованию.
По-моему, в школьном курсе действительно есть места, где следовало, во-первых, дать понимание того, откуда это взялось (пример с формулой дискриминанта) а во-вторых — доходчивее объяснить зачем это нужно (конкретный пример привести затрудняюсь, но такое точно было).
Но вот в вузовском курсе подобные претензии, по-моему, уже совершенно необоснованы. Он, с одной стороны, и так хорошо структурирован (потому как нет необходимости уместить кучу разнородных мелочей в один краткий курс), а, с другой, предназначен для уже сформировавшихся интеллектуально личностей, и тащить туда объяснения для, грубо говоря, идиотов — лишняя потеря времени и места в учебнике.
Ну и с фразой, вами упомянутой
Дай вопрошающему грош, если он ищет выгоды, а не математики
полностью согласен.
Дай вопрошающему грош, если он ищет выгоды, а не математики
Как отметили выше, вы описали проблемы преподавания матана, а не проблемы с записью математических выражений. Прошу прощения за высокомерный снобизм, но у вас просто нет достаточного опыта судить об удобстве записи в математике. Проблемы с записью особо громоздких конструкций есть, и они вполне себе решаются. К примеру, в ML вполне себе рисуют картинки вместо явной записи свёртки десятка тензоров с двадцатью индексами. В физике та же фигня: используют бра-кет запись, диаграммы и тому прочее наравне с обычной записью. Это всё есть (правильные и вполне рабочие) уровни абстракций.
Ну а проблемы преподования — да, они есть. Универсального курса матана, идельного и понятного всем не существует. Преподователь, лектор или автор учебника обязан делать допущения относительно интересов аудитории. Во время курса он должен решать проблемы, знакомые его слушателям/читателям. А проблемы у всех нас разные. Поэтому и учебники и курсы разные: для математиков, для физиков, для химиков, для экономистов и т.п.
Ну а проблемы преподования — да, они есть. Универсального курса матана, идельного и понятного всем не существует. Преподователь, лектор или автор учебника обязан делать допущения относительно интересов аудитории. Во время курса он должен решать проблемы, знакомые его слушателям/читателям. А проблемы у всех нас разные. Поэтому и учебники и курсы разные: для математиков, для физиков, для химиков, для экономистов и т.п.
Ну а проблемы преподования — да, они есть. Универсального курса матана, идельного и понятного всем не существует. Преподователь, лектор или автор учебника обязан делать допущения относительно интересов аудитории. Во время курса он должен решать проблемы, знакомые его слушателям/читателям
всё-таки дело обстоит с точностью до наоборот. матан читают на самом первом курсе, когда у потенциальнах химиков, физиков, экономистов и прочих ещё нет никакого конструктивного понимания о проблемах своих наук (ну, кроме школьных представлений). кроме того, читают его на первом курсе не просто так. матан — по сути элементарный раздел математики, введение в математический язык. естественно, необходимо как можно скорее научить студентов этому языку, чтобы те как можно быстрее смогли понимать его внутри своих областей и пользоваться им для решения специализированных задач. это можно сравнить с элементарной азбукой, которой нужно овладеть, чтобы научиться читать, и как-то странно полагать, что для физиков, химиков или экономистов нужно каждому по специализированному букварю
всё-таки дело обстоит с точностью до наоборот. матан читают на самом первом курсе, когда у потенциальнах химиков, физиков, экономистов и прочих ещё нет никакого конструктивного понимания о проблемах своих наук (ну, кроме школьных представлений)Почему бы не предположить обратное: если юное дарование специально выбрало ту или иную науку, то оно имеет хоть какое-то представление о проблемах в области. Вот лично я постоянно слышал в школе, что ту или иную задачу можно решить гораздо проще с помощью дифференциального исчисления. Т.е. я пришел в ВУЗ изначально заинтересованным, и это — нормально.
это можно сравнить с элементарной азбукой, которой нужно овладеть, чтобы научиться читать, и как-то странно полагать, что для физиков, химиков или экономистов нужно каждому по специализированному букварюИМХО сравнение с изучением языка особенно точное (и мне оно нравится). Есть английские курсы для детей, для взрослых, для технарей, для китайцев и т.п. — каждому нужен свой подход, не смотря на то, что предмет один и тот же.
Вот лично я постоянно слышал в школе, что ту или иную задачу можно решить гораздо проще с помощью дифференциального исчисления. Т.е. я пришел в ВУЗ изначально заинтересованным, и это — нормально.
это нормально, но до того как приступить непосредственно к решению задачи, вам нужно изучить основы — которые абсолютно одинаковые для всего, они более элементарны и находятся над (или «под») этими задачами — отличная аналогия с кирпичиками выше
потому что более-менее реальные задачи — это как минимум дифференциальные уравнения, которые идут далеко после курса матана
каждому нужен свой подход, не смотря на то, что предмет один и тот же.
да, язык может специализироваться потом, но база — она одинаковая во всех курсах: алфавит, произношение, времена (прошлое, настоящее и т.п.), основной набор начальных слов, формы глагола «to be» и т.д. когда база получена, начинается специализация с разучиванием конкретных тем и конкретных наборов слов для них, но базовая грамматика — везде одна
также и с матаном, он даёт элементарную базу, которую потом уже используют в курсах физики, химии и прочего для решения конкретных задач
Я перестал вас понимать. Задача — это, к примеру, почему планеты движутся по почти замкнутым орбитам в плоскости. В формулировке нет никаких кирпичиков от матана в том смысле, что даже семиклассник сможет понять в чём вообще проблема. Ну а препод по матану может взять эту задачу на вооружение и рассказать о бесконечно малых, о рядах, о пределах, о производных и их разновидностях (что есть азбука матана) на примере этой задачи.
Относительно языков — у вас явно нет положительного опыта. Я пытаюсь учить свой четвёртый язык и, на текущий момент, я ещё не знаю всех тонкостей алфавита, но могу спросить почём велик в магазине или какая сегодня погода. Да и всех форм «to be» я тоже не знаю. Заставить всё это учить до базовых фраз — это всё равно, что давать определение пределов по Коши и определение производной на первой лекции, а потом сказать, что tan' = 1/cos^2 следует очевидным образом, попутно заставив студентов заполнять таблицу производных дома. Да, это — последовательно и строго, но не имеет никакого отношения к обучению.
Относительно языков — у вас явно нет положительного опыта. Я пытаюсь учить свой четвёртый язык и, на текущий момент, я ещё не знаю всех тонкостей алфавита, но могу спросить почём велик в магазине или какая сегодня погода. Да и всех форм «to be» я тоже не знаю. Заставить всё это учить до базовых фраз — это всё равно, что давать определение пределов по Коши и определение производной на первой лекции, а потом сказать, что tan' = 1/cos^2 следует очевидным образом, попутно заставив студентов заполнять таблицу производных дома. Да, это — последовательно и строго, но не имеет никакого отношения к обучению.
ну смотрите, движение планет — второй закон ньютона. а что там у нас в правой части, dp/dt — производная. и — всё. чтобы дойти до этого надо начинать с последовательностей (на самом деле с вещественных чисел, ну ладно, их введем аксиоматически), потом пределы, обобщить пределы на функцию, ввести производные, потом дифференциалы, и наконец доказать теорему о постоянной функции (и то, это будет такой лайфхак, чтобы получить постоянную для движения, а по чесноку уравнения надо интегрировать, а это — пилить ещё больше семестра до определенных интегралов и формулы Ньютона-Лейбница) — итого больше чем полсеместра чистого матана. но на самом деле прикол в том, что параллельно матану у вас уже будет идти физика, где вы будете решать эту и много других замечательных задач и где от вас уже будут требовать в полной мере владения дифференциальным и интегральным аппаратом, только посмеиваясь над попытками школьных оправданий вроде «а по матану мы ещё до этого не дошли». на самом деле в этом нет ничего страшного, ибо дифференцировать и интегрировать учат в школе, но там именно натаскивают на решение типовых задач и ставят технику, а вот полного понимая теории и всех ньюансов у вас до курса матана не будет. так что приложением матана к задачам физики вы будете заниматься непосредственно в курсе физики, так как сама физика внезапно целиком и полностью написана на языке матана, а вот учить матан и восполнять школьные пробелы будет именно на парах матана.
не знаю какой язык, в изначальном сообщении вы упомянули английский вот давайте на нем и остановимся. «я ещё не знаю всех тонкостей алфавита» — серьёзно, какие тонкости алфавита? алфавит просто надо знать, 26 букв
«Да и всех форм «to be» я тоже не знаю» — серьёзно, I am, he is, we are?
«базовые фразы» — это My name is Vasya и London is the capital of Great Britain
вы серьезно полагаете, что в какой-то методике изучения языка можно избежать знания такой элементарщины?
хотя, конечно могут быть разные, в том числе и экзотические методы изучения языков — всё таки там простор для творчества почти не ограничен и аналогия с матаном всё-таки условная. в нём же широко не разгуляешь, т.к. есть очень жёсткая и последовательная логическая структура
Я пытаюсь учить свой четвёртый язык и, на текущий момент
не знаю какой язык, в изначальном сообщении вы упомянули английский вот давайте на нем и остановимся. «я ещё не знаю всех тонкостей алфавита» — серьёзно, какие тонкости алфавита? алфавит просто надо знать, 26 букв
«Да и всех форм «to be» я тоже не знаю» — серьёзно, I am, he is, we are?
«базовые фразы» — это My name is Vasya и London is the capital of Great Britain
вы серьезно полагаете, что в какой-то методике изучения языка можно избежать знания такой элементарщины?
хотя, конечно могут быть разные, в том числе и экзотические методы изучения языков — всё таки там простор для творчества почти не ограничен и аналогия с матаном всё-таки условная. в нём же широко не разгуляешь, т.к. есть очень жёсткая и последовательная логическая структура
Вы написали много, мягко говоря, противоречивых вещей. Я безоговорочно капитулирую в этом «споре». На вопросы отвечаю.
какие тонкости алфавита?Я имел ввиду конкретно диактрику, которой в английском языке нет.
вы серьезно полагаете, что в какой-то методике изучения языка можно избежать знания такой элементарщины?Нет.
Почему бы не предположить обратное: если юное дарование специально выбрало ту или иную науку, то оно имеет хоть какое-то представление о проблемах в области. Вот лично я постоянно слышал в школе, что ту или иную задачу можно решить гораздо проще с помощью дифференциального исчисления. Т.е. я пришел в ВУЗ изначально заинтересованным, и это — нормально.Будущему инженеру или физику применение математики в его сфере вполне очевидно еще в школе. А вот даже олимпиаднику биологу места применения математики в его науке станут видны только ближе к концу обучения. Вот где химию применять в биологии да, понятно еще в школе, а вот то что многие процессы описываются сложными мат.моделями — это далеко не так очевидно даже очень увлеченному биологией школьнику.
Вы-то за всех биологов-олимпиадников не говорите. К примеру, можно сделать проект на конкурс, собрать данные, скажем, о распространении тли, обработать их, смоделировать что-то там и в процессе познакомиться с элементами из матана. Даже чтобы просто представить какой-то объем данных по любой дисциплине на красивом слайде может понадобиться матан. А статистика, которую в СНГ вообще не учат, на Западе (да и на Востоке) вообще считается маст-хэв для всех и учится в школе.
Конечно, не имеет смысла говорить что прямо все школьники должны этим интересоваться. Но если интересуются — то это нормально, что я и написал.
Конечно, не имеет смысла говорить что прямо все школьники должны этим интересоваться. Но если интересуются — то это нормально, что я и написал.
Вы-то за всех биологов-олимпиадников не говорите.А я за всех и не говорю, но знал реальные примеры реальных людей очень увлеченных биологией и с нулевой математикой и непониманием ее необходимости.
Я тоже считаю статистику и основы теор.вера маст хевом и даже считаю что именно их надо изучать в школе для понимания очень многих жизненных вещей вместо интегрирования с диференцированием, которые все равно большинству из тех кто не пойдет в ВУЗ вообще никак в жизни не пригодятся.
Но, из необходимости статистики необходимость матана кстати для многих совсем не очевидна до глубокого погружения в тему.
Вот эта фраза:
Вопросы о том, нужно ли его изучать в принципе можете обсудить с противниками высшего образования как такового. Я считаю, что высшее образование — вещь, по большому счёту, статусная (= необязательная), и если тебе этот статус не нужен — можешь самостоятельно учить то, что интересно и в любом порядке. Это как купить Феррари: ты же не будешь просить сделать салон из кожзама просто потому, что он дешевле? Если нужно дешевле — есть другие автомобили, а если хочешь Феррари — будь добр брать то, что продают и по той цене, которой продают. Так и с высшим образованием: либо иди и соответствуй, не задавая лишних вопросов, либо учи сам. При этом никто не исключает, что покупая фордик или штудируя онлайн курсы ты будешь счастливее, умнее, быстрее или успешнее чем если бы вбухал своё время/деньги в статусную вещь. Утрирую совсем чуть-чуть.
А вот даже олимпиаднику биологу места применения математики в его науке станут видны только ближе к концу обучениязвучит именно так, как будто вы говорите за всех. В любом случае, я не агитировал заставлять всех учить матан и не пойму, зачем вы вообще оставили ваш комментарий под моим. Речь шла о том, учить раньше или позже, ну так вот: я не вижу смысла откладывать тот или иной предмет по той причине, что некоторым он может не понадобиться. Это абсолютно неконструктивно. Так можно откладывать всё. Предметы идут по повышению сложности и матан — один из самых легких. Поэтому, его изучают на первом курсе. Всё.
Вопросы о том, нужно ли его изучать в принципе можете обсудить с противниками высшего образования как такового. Я считаю, что высшее образование — вещь, по большому счёту, статусная (= необязательная), и если тебе этот статус не нужен — можешь самостоятельно учить то, что интересно и в любом порядке. Это как купить Феррари: ты же не будешь просить сделать салон из кожзама просто потому, что он дешевле? Если нужно дешевле — есть другие автомобили, а если хочешь Феррари — будь добр брать то, что продают и по той цене, которой продают. Так и с высшим образованием: либо иди и соответствуй, не задавая лишних вопросов, либо учи сам. При этом никто не исключает, что покупая фордик или штудируя онлайн курсы ты будешь счастливее, умнее, быстрее или успешнее чем если бы вбухал своё время/деньги в статусную вещь. Утрирую совсем чуть-чуть.
Не математик. Читал недавно книжку, название (по памяти) «Идеи (или теории) которые должны умереть». Это сборник статетей участников некоего научного сообшества (не рускоязычного). В этой книге запомнилась статья про матан. Там два вывода: 1) Матан реально нужен ОЧЕНЬ маленькому числу учёных -ИССЛЕДОВАТЕЛЕЙ. 2) Бесконечная глупость читать матан на первом курсе.
Можно бесконечно растягивать и, соответственно, удорожать образование отодвигая предметы на потом. Не удивлюсь, если некое научное сообщество в этом прямо заинтересовано.
Посмотрите, пожалуйста, оно? www.labirint.ru/books/605779
Если да, про ученых-исследователей в каких областях идет речь в соответствующем эссе?
Чем ближе наука к практике, чем нужнее там математический аппарат, тем преступнее продавать такую книгу за деньги.
Если да, про ученых-исследователей в каких областях идет речь в соответствующем эссе?
Чем ближе наука к практике, чем нужнее там математический аппарат, тем преступнее продавать такую книгу за деньги.
Это оно. Мне очень понравилась. Кругозор развивет очень здорово.
Я извиняюсь, сказано это было про подготовку програмистов. Основная идея — матан на первом курсе отсеивает кучу народа, убивая уверенность в собственных силах и отвращает от професии
Я извиняюсь, сказано это было про подготовку програмистов. Основная идея — матан на первом курсе отсеивает кучу народа, убивая уверенность в собственных силах и отвращает от професии
Что характерно, книга написана учёными из США и Канады, где (как и в России) какая-то зашкаливающая доля людей с высшим образованием (т.н. Grade inflation). Если в стране «высшее образование» у 50% населения, этот уровень можно смело принимать за средний, а «высший» уровень присваивать тому меньшинству, которому для работы требуются сложные для освоения большинством методы (например, математика в случае технического образования).
Тогда не будет таких проблем, что программиста пичкают матаном, потому что программиста будут учить в образовательных учреждениях среднего специального образования (как например, в немецкоязычных странах), и он будет справляться с большинством задач, которые сегодня решает средний программист.
В ВУЗах же должны учить математиков, физиков и инженеров, для которых программирование является лишь одним из инструментов, который облегчает использование в своей работе математических методов.
Тогда не будет таких проблем, что программиста пичкают матаном, потому что программиста будут учить в образовательных учреждениях среднего специального образования (как например, в немецкоязычных странах), и он будет справляться с большинством задач, которые сегодня решает средний программист.
В ВУЗах же должны учить математиков, физиков и инженеров, для которых программирование является лишь одним из инструментов, который облегчает использование в своей работе математических методов.
Не помню, кто сказал, что в ближайшие годы страны мира НАВСЕГДА поделятся на развитые и неразвитые. «Развивающихся» не будет. И перейти из неразвитых в развитые будет НЕВОЗМОЖНО (обратно — запросто). Те правительства, которые серьёзно относятся к будущему своих стран, прилагают все усилия чтобы мотивировать людей учится. За Штаты не скажу, а в Канаде в последние годы, во многих провинциях, для людей с низким доходом, высшее образование практически бесплатно. Правительство выделяет гранты на образование. Именно гранты а не ссуды.
В Германии в большинстве земель за первое образование никому из своего кармана не нужно платить (в т.ч. иностранцам). Не нужно клянчить никакие гранты, просто поступаешь в гос. университет/училище/техникум и учишься. Но высшее образование всё равно у подавляющего меньшинства трудоспособного населения, что и логично.
Если говорить о программистах, то разработчик приложений, игр, интерфейсов — это всё крепкое среднее образование, и людей там как раз не грузят матаном, давая только самые его основы, необходимые для практики. Т.е. по сути здесь уже реализована описанная выше мечта не грузить среднего специалиста теорией.
А в России, США и Канаде, я так понимаю, если человек не разгружает навоз лопатой, а давит кнопки перед монитором, то это уже точно высшее образование, а если ещё и программу может написать, то это уже учёная степень магистра.
Общество быстро развивается, технологии идут в массы, и если раньше операторами ЭВМ были только учёные, то сейчас компьютерами разве что домашние животные не пользуются (пока). Но это не значит, что всем нужно раздать учёную степень. Высшее образование — это по определению набор знаний навыков, которым обладает меньшинство трудоспособного населения.
Если говорить о программистах, то разработчик приложений, игр, интерфейсов — это всё крепкое среднее образование, и людей там как раз не грузят матаном, давая только самые его основы, необходимые для практики. Т.е. по сути здесь уже реализована описанная выше мечта не грузить среднего специалиста теорией.
А в России, США и Канаде, я так понимаю, если человек не разгружает навоз лопатой, а давит кнопки перед монитором, то это уже точно высшее образование, а если ещё и программу может написать, то это уже учёная степень магистра.
Общество быстро развивается, технологии идут в массы, и если раньше операторами ЭВМ были только учёные, то сейчас компьютерами разве что домашние животные не пользуются (пока). Но это не значит, что всем нужно раздать учёную степень. Высшее образование — это по определению набор знаний навыков, которым обладает меньшинство трудоспособного населения.
Ясно, спасибо. Не видели авторы R&D-инженеров, которые используют матан и иже с ним каждый день. Бывает. Разработчиков игр с алгеброй и геометрией на завтрак и обед тоже не видели. Тоже бывает.
На мой взгляд математика — это наука о том как из отдельных «кирпичиков» складывать по определенным правилам большие «здания» доказательств. Математика принципиально «конструктивна» — мы не «разбираем» здание на кирпичики а строим его из них. При этом практическую пользу обычно несет именно «здание» а не «кирпичик» что и порождает нежелание возиться с «бесполезными кирпичами» которое Вы описываете. Поверх этого идет необходимость строить здание по строго определенным правилам. Что тоже порождает протест — почему это я не могу построить здание которое я хочу и как я хочу? Зачем мне эти дурацкие правила? Но вот без правил этих ничего толкового построить на практике, увы, не удастся. И хотя «общий обзор» возможных зданий куда интереснее, но, увы, толком не приближает нас к пониманию того как же эти здания надо строить.
Демонстрация «общего» — это неплохой способ а) заинтересовать слушателя («о, какую классную вещь можно сделать») и б) дать ему в руки «кирпичик» большего размера (давайте будем собирать типовые хрущовки из панелей вместо того чтобы возиться с кирпичами"). Но и только. Вот писал я, к примеру, на Хабр статью про преобразование Фурье. Именно с позиций «рассказать об общей картине». И все бы хорошо — но это не математика. И если человек захочет серьезно разобраться в ПФ то ему все равно придется нырять в (зверски непростой и далеко не очевидный) матан. Моя же статья никак, увы, этому не учит. В лучшем случае — показывает как пользоваться ПФ в «бытовых» целях.
Возвращаясь к вопросу «как учить математику»: у нас есть два компонента которым следует научить. Показать «кирпичики» и показать «правила» по которым они складываются а затем натренировать человека чтобы у него в памяти отложились а) список наиболее полезных кирпичиков, б) доведенные до автоматизма правила их складывания и в) типовые полезные чертежи которые легко можно адаптировать под конкретный частный проект дабы не делать его с нуля. Для чего мы берем студента и заставляем его а) учить список кирпичиков и правил и б) строить, строить, строить и еще раз строить на практике из них разнообразные дома. От простых к сложным — пока руку не набьет. Но это, собственно, ровно то как процесс преподавания математике сейчас и организован. По крайней мере в ФМШ и на мехмате МГУ где я учился. При этом простые задачи часто будут не интересные и скучные — условно говоря, «сложите из кирпичей колонну в два кирпича на два высотою 3 метра». Но это — работает. А вот попытавшись разок разобрать здание на кирпичики Вы вряд ли научитесь как его строить. Особенно при попытках разобрать здание сложное (а именно такие представляют наибольший практический интерес) — просто завязните в деталях или упустите массу важных моментов. Интересных задач в математике вообще не так уж много и руку только на них одних набить, увы, не получится.
Демонстрация «общего» — это неплохой способ а) заинтересовать слушателя («о, какую классную вещь можно сделать») и б) дать ему в руки «кирпичик» большего размера (давайте будем собирать типовые хрущовки из панелей вместо того чтобы возиться с кирпичами"). Но и только. Вот писал я, к примеру, на Хабр статью про преобразование Фурье. Именно с позиций «рассказать об общей картине». И все бы хорошо — но это не математика. И если человек захочет серьезно разобраться в ПФ то ему все равно придется нырять в (зверски непростой и далеко не очевидный) матан. Моя же статья никак, увы, этому не учит. В лучшем случае — показывает как пользоваться ПФ в «бытовых» целях.
Возвращаясь к вопросу «как учить математику»: у нас есть два компонента которым следует научить. Показать «кирпичики» и показать «правила» по которым они складываются а затем натренировать человека чтобы у него в памяти отложились а) список наиболее полезных кирпичиков, б) доведенные до автоматизма правила их складывания и в) типовые полезные чертежи которые легко можно адаптировать под конкретный частный проект дабы не делать его с нуля. Для чего мы берем студента и заставляем его а) учить список кирпичиков и правил и б) строить, строить, строить и еще раз строить на практике из них разнообразные дома. От простых к сложным — пока руку не набьет. Но это, собственно, ровно то как процесс преподавания математике сейчас и организован. По крайней мере в ФМШ и на мехмате МГУ где я учился. При этом простые задачи часто будут не интересные и скучные — условно говоря, «сложите из кирпичей колонну в два кирпича на два высотою 3 метра». Но это — работает. А вот попытавшись разок разобрать здание на кирпичики Вы вряд ли научитесь как его строить. Особенно при попытках разобрать здание сложное (а именно такие представляют наибольший практический интерес) — просто завязните в деталях или упустите массу важных моментов. Интересных задач в математике вообще не так уж много и руку только на них одних набить, увы, не получится.
О, хорошая аналогия. Несколько риторических вопросов: сможет ли такой строитель разработать принципиально новый кирпич, если текущих не хватает? Насколько часто возникают ситуации, что текущих кирпичей не хватает? Кого запоминают больше: разработчиков новых кирпичей? Кто нужен чаще, укладчик стандартных кирпичей, или разработчик новых?
Вопросы актуальные: если обзор каждого кирпичика позволит быстрее довести до автоматизма «правила складывания» — есть ли резон обозревать каждый кирпичик? Если обзор каждого кирпичика упростит процесс обновления знаний в будущем — есть ли резон обозревать каждый кирпичик?
Вопросы актуальные: если обзор каждого кирпичика позволит быстрее довести до автоматизма «правила складывания» — есть ли резон обозревать каждый кирпичик? Если обзор каждого кирпичика упростит процесс обновления знаний в будущем — есть ли резон обозревать каждый кирпичик?
«Новые кирпичи» появляются исключительно редко, это по сути рождение целых новых областей в математике. Обычное математическое образование даже не ставит перед собой задачи создать людей способных на это. Но сила математики в том что сравнительно небольшого числа существующих кирпичиков хватает на громадный пласт практических и теоретических построений.
Математика принципиально «конструктивна»Опасное утверждение в случае математики:
Конструктивная математика — близкое к интуиционизму течение в математике, изучающее конструктивные построения. Согласно критерию конструктивности — «существовать — значит быть построенным».[17] Критерий конструктивности — более сильное требование, чем критерий непротиворечивости.[18] (Вики)
(Мне показалось, что «Конструктивная математика» не имелась в виду? — Уточнил на всякий случай.)
В любой математике доказательства конструктивны.
Конструктивная же математика о которой Вы пишете (более правильное название — «математический конструктивизм») — это попытка обобщить эту идею дальше, потребовав чтобы не только доказательства но и объекты с которыми они оперируют строились конструктивно.
Конструктивная же математика о которой Вы пишете (более правильное название — «математический конструктивизм») — это попытка обобщить эту идею дальше, потребовав чтобы не только доказательства но и объекты с которыми они оперируют строились конструктивно.
Ну вообще можно доказать, что доказательство существует, но само его не предъявлять :)
UFO just landed and posted this here
Это неоднозначный вопрос.
Смотрите, если у вас есть конкретный вывод, то утверждение "вывод существует" (= "теорема доказана") не просто выводимо — оно явно истинно.
Если же вы вывели утверждение о существовании вывода, не предъявляя самого вывода, то вопрос истинности, вообще говоря, еще открыт. Да, обычно у нас soundness и выводимое утверждение истинно в любой интерпретации, но что если нет? Допустим, метатеория противоречива — в этом случае утверждение о существовании вывода в теории может оказаться ложным. Ложной будет и теорема. Если же вы доказали теорему предоставив вывод — то теорема доказана вне зависимости от противоречивости любой метатеории.
Так что, по логике, явно эти случаи должны быть разделены.
Готовое доказательство конструктивно в том смысле, что к выводу доказательства есть конечный путь из логических следствий начиная от определения «вещественное число это ...» Однако придумывание доказательства штука очень неконструктивная. Это скорее прохождение бесконечномерного лабирита в темноте. Конструкнивность это скорее про программирование: там именно собирают кирпичи вместе и делают конструкции совершенно офигительной высоты. Интуиция там как правило не участвует.
На мой взгляд математика — это наукаМатематика — это не наука. крите́рий По́ппера она проваливает с треском. Математика — это инструмент, которым пользуется наука. Любая. Много вы видели программистов, которым никогда не требовалось складывать строки? А ведь там нас ждёт Маляр Шлемиэль, пределы и O большое. Потому идея «не преподавать матан» заставляет задумать о том, являются ли авторы этой идеи вообще учёными или нет.
Сила и слабость математики вообще (и матана в частности) — ровно в том, что это не наука, и стало быть, с реальными миром она никак не связана.
А вот желания конкретного индувидуума — с реальным миров очень даже связаны… но у разных людей — разные цели. Потому очень сложно сделать самоучитель математики, которй был бы интересен всем.
Критерий фальсификации Поппера, на который начали молиться в постсоветское время — не единственный критерий научности в философии науки, и тем более, не самый лучший. Вы посмотрите на этот абсурд — математика по нему не является наукой, разве это не лучшая демонстрация несостоятельности самого термина «науки-по-попперу»?
Вы посмотрите на этот абсурд — математика по нему не является наукой, разве это не лучшая демонстрация несостоятельности самого термина «науки-по-попперу»?Нет. Я хорошо помню курс «философия математики» и хорошо помню как там у самых разных философов были самые разные подходы — и у большинства математика «выпадала».
Именно потому, что математика — не наука. Там невозможны эксперименты, там новые знания не могут ограничить область применимости старых и т.д. и т.п.
Как тут уже писали: математика — это язык, на котором написана «книга природы», но к самой этой книге математика — отнощения не имеет.
Это одновременно и самое сильное и самое ужасное свойство математики…
Математика — способ описания явлений и связей между явлениями. Способ со внутренней структурой, которую можно проверять на целостность только относительно себя самой. Верность самой реальной связи между явлениями, например, не может быть подтверждена внутренней верностью описания этой связи. Скажем, математическая формула из ньютоновской механики не дает никакого намёка на более общую формулу из релятивистской механики, хотя и является ее вырожденным случаем.
UFO just landed and posted this here
Потому что эксперимент, в науке, предназначен для проверки наших знаний об окружающем мире. Математика ничего «не знает» об окружающем мире: аксиомы истинны по определению, а любые, сделанные на их основе выводы, либо абсолютно верны (если нет ошибок), либо, так же абсолютно неверны (если ошибки есть).
Критерий Поппера предназначен для ЕСТЕСТВЕННЫХ наук.
А общего критерия для всех наук — не существует.
А общего критерия для всех наук — не существует.
Помню я спрашивал у нашего философа, является ли «Наука Логики» Гегеля наукой по Попперу. Только недавно понял, насколько неправильным был этот вопрос и насколько сильно мы инфицированы религиозным попперианством.
Причём тут религоизность? Наука — это просто такая область деятельности, где мы строим часть картины мира на основе опытов. Всё. Это просто определение, не больше, не меньше. Вот прямо в первом абзаце: Нау́ка — область человеческой деятельности, направленная на выработку и систематизацию объективных знаний о действительности. А математика никаких знаний о действительности нам не даёт — ни объективных, ни субъективных, никаких! Какая ж это, нафиг, наука?
Заметьте: это не означает что всем, что не наука, не нужно заниматься! Написание каких-нибудь романов и написания поэм, скажем, ни разу не наука ни по какому критерию — но жить в мире, где нет ни писателей, ни поэтов будет невыносимо скучно.
Заметьте: это не означает что всем, что не наука, не нужно заниматься! Написание каких-нибудь романов и написания поэм, скажем, ни разу не наука ни по какому критерию — но жить в мире, где нет ни писателей, ни поэтов будет невыносимо скучно.
«Наука Логики» Гегеля
Кстати говоря, Гегель эту книгу на полном серьёзе писал, или чтобы поржать над теми, кто поведётся? Учитывая его собственное отношение к словоблудию, которое он высказывал в некоторых письмах…
Математика — это инструмент, которым пользуется наука.
Мы, вроде, с вами уже это обсуждали. В математике ученые формулируют утверждения вида: "из последовательности символов А при помощи последовательного применения правил преобразования Х можно получить последовательность символов В". Это вполне фальсифицируемо — просто берешь А, выполняешь указанные преобразования и смотришь, что получилось. Если получилось не В — утверждение сфальсифицировано.
Никаких нефальсифицируемых утверждений в математике не формулируется.
Вы, конечно, можете какие-то последовательности символов интерпретировать как некие утверждения, и эти утверждения, действительно, могут оказаться нефалльсифицируемыми. Только математика тут уже не при чем, это же вы интерпретациями занимались.
В математике ученые формулируют утверждения вида: "из последовательности символов А при помощи последовательного применения правил преобразования Х можно получить последовательность символов В".
Это только в конструктивной математике. Вообще говоря, много утверждений вида "существует объект, обладающий свойством P" или, выражаясь вашими словами "как не крути правила X, последовательность B из A ты получить не сможешь" (обычно эти теоремы самые важные и сложные).
Примеры:
- У любого полинома n-степени с комплексными коэффициентами (n≥1) существует хотя бы один комплексный корень (ни слова про то, как его найти).
- Для любого n ≥ 5 не существует формулы, которая бы выражала корни любого полинома степени n в радикалах.
- Всякое n-мерное многообразие гомотопически эквивалентно n-мерной сфере тогда и только тогда, когда оно гомеоморфно ей (когда я наконец понял разницу между гомотопиями и гомеоморфизмами, мне это крышу снесло).
Это только в конструктивной математике.
Нет, это абсолютно в любой.
Вообще говоря, много утверждений вида "существует объект, обладающий свойством P"
Так это утверждение является просто последовательностью символов. Которую нам надо получить из другой последовательности символов (условий теоремы). В качестве доказательства теоремы — у вас конечная последовательность правил вывода, которые из последовательности символов, описывающей условия теоремы, делают последовательность символов, описывающих результат теоремы.
Примеры:
Ну и все ваши примеры — это те самые пары последовательностей А и В. А доказательства этих теорем — конечные последовательности правил, которые путем своего применения А превращают в В.
А доказательства этих теорем — конечные последовательности правил
Нет, правила — это логика + набор аксиом. Доказательства — это последовательные применения законов логики к аксиомам для получения требуемого результата.
Только вот в современной математике док-ва стали настолько сложными, что проверить их абы кто не может, нужны другие супер-математики. И даже если всё проверили, не исключена вероятность, что где-нибудь ошибка сидит. Воеводский не от хорошей жизни гомотопической теорией типов занялся.
Когда-нибудь всё везде будет строго доказываться на аналоге Coq, вот тогда ваш тезис будет совсем верным.
Нет, правила — это логика + набор аксиом.
Вы забыли про правила вывода. С-но аксиомы можно рассматривать как частный случай правил вывода с пустой левой частью. Законы логики — тоже состоят из аксиом и правил вывода.
Только вот в современной математике док-ва стали настолько сложными, что проверить их абы кто не может, нужны другие супер-математики.
А это ничего не меняет, фальсифицирующий эксперимент не перестает им быть от того, что его сложно провести. В итоге все равно у вас есть вывод, который можно формально проверить на валидность.
Вы забыли про правила вывода.
Под "законами логики" я имел ввиду исчисление предикатов и логика высших порядков, о каких именно "правилах вывода" вы говорите? Мат. индукция? Это частный случай исчисления предикатов.
Мат. индукция? Это частный случай исчисления предикатов.Не совсем так. Исчисление предикатов может «покрыть» лишь счётный набор множеств. А в реальной науке часто приходится рассуждать о несчётных наборах.
То есть когда вы вот в том самом матане написали ∀х∈ℝ — всё, вы вылетели за рамки «исчисления предикатов». Потому что оных ℝ — несчётное множество.
Не совсем так. Исчисление предикатов может «покрыть» лишь счётный набор множеств. А в реальной науке часто приходится рассуждать о несчётных наборах.
Нет, вы вполне можете рассуждать о несчетных наборах, проблема в том, что вы, неформального говоря, не сможете в явном виде "пощупать" более чем счетное подмножество этого набора. То есть вы можете говорить об R, можете говорить об элементах R, но если вы попытаетесь говорить об отдельных конкретных элементах R, как об отдельных числах, явно их обозначая — вот тогда и возникнет проблема.
Еще вы можете в теорию явно насовать все требуемые константы, но тогда у вас будет несчетная сигнатура.
Нет, вы вполне можете рассуждать о несчетных наборах, проблема в том, что вы, неформального говоря, не сможете в явном виде «пощупать» более чем счетное подмножество этого набора.Я — могу. А «исчисление предикатов» (вернее логика первого порядка) — не может.
Она оперирует с формулами, коих, как несложно понять, счётное число, а не с множествами — которых несчётно. Отсюда и знаменитая теорема.
Я — могу. А «исчисление предикатов» (вернее логика первого порядка) — не может.
Подразумевалось "не можете при помощи исчисления предикатов".
Она оперирует с формулами, коих, как несложно понять, счётное число, а не с множествами — которых несчётно.
Но это не мешает вам внутри исчисления предикатов работать с несчетными множествами и даже с множествами большими, чем несчетные (например, с множеством всех ф-й из R в R). И теорему Кантора доказать не мешает.
Отсюда и знаменитая теорема.
Нет, терема Геделя тут не при делах, вы говорите про https://ru.wikipedia.org/wiki/%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%9B%D1%91%D0%B2%D0%B5%D0%BD%D0%B3%D0%B5%D0%B9%D0%BC%D0%B0_%E2%80%94_%D0%A1%D0%BA%D1%83%D0%BB%D0%B5%D0%BC%D0%B0 и соответствующий парадокс https://ru.wikipedia.org/wiki/%D0%9F%D0%B0%D1%80%D0%B0%D0%B4%D0%BE%D0%BA%D1%81_%D0%A1%D0%BA%D1%83%D0%BB%D0%B5%D0%BC%D0%B0
Под "законами логики" я имел ввиду исчисление предикатов и логика высших порядков, о каких именно "правилах вывода" вы говорите?
И я говорю про исчисление предикатов (логика первого порядка). В ней два правила вывода — modus ponens и обобщение. Индукция (когда она содержится в аксиоматике) — это обычно аксиома (или схема).
логика высших порядков
Ну ей де-факто никто не пользуется (исключения есть, в пределах стат. погрешности).
И тем не менее, проэктирования здания начинается с общего вида. Чертежи кладки кирпичей — много позже.
Вопрос с «реальными проблемами» (прикладными, на самом деле) не так очевиден, как вам кажется.
Если человек пытается вникнуть в суть абстракции, но у него никак не получается, и он ищет практический пример (являющийся, как это чаще всего бывает, в той или иной степени вырожденным случаем), а найдя его — удовлетворяется, у этого человека, вероятнее всего, просто недостаточно развиты навыки абстрактного мышления. Потому что вырожденный пример хоть и может иллюстрировать абстракцию, но не может ее полностью описывать (просто по определению). Уверенность в понимании, которая возникает после знакомства с такими примерами — ложная. Решение частных задач помогает укрепить понимание абстрактной концепции, на которой они основаны, то есть является хорошим упражнением, но не может заменить само понимание. Понимание возникает при анализе связей между частями абстракции, при попытках группировать фрагменты абстракции на основе этих связей, при попытках поиска связей. А не при мысленном сравнении и установлении тождества (операции конкретно-предметного мышления, а не абстрактного).
Если человек пытается вникнуть в суть абстракции, но у него никак не получается, и он ищет практический пример (являющийся, как это чаще всего бывает, в той или иной степени вырожденным случаем), а найдя его — удовлетворяется, у этого человека, вероятнее всего, просто недостаточно развиты навыки абстрактного мышления. Потому что вырожденный пример хоть и может иллюстрировать абстракцию, но не может ее полностью описывать (просто по определению). Уверенность в понимании, которая возникает после знакомства с такими примерами — ложная. Решение частных задач помогает укрепить понимание абстрактной концепции, на которой они основаны, то есть является хорошим упражнением, но не может заменить само понимание. Понимание возникает при анализе связей между частями абстракции, при попытках группировать фрагменты абстракции на основе этих связей, при попытках поиска связей. А не при мысленном сравнении и установлении тождества (операции конкретно-предметного мышления, а не абстрактного).
Это кстати интересный вопрос, о том как разные люди себе представляют математику. Вот например когда вы читаете про «компактное множество», что вы предствляете? Или например пространство интегрируемых по лебегу фукнций? Если в первом случае я вижу такую кучу непонятно чего с «чёткими» границами, то во втором случае это такая непонятная каша и честнее будет сказать, что я на самом деле никак это пространство не представляю.
Хотел ответить, что я лично ничего не представляю. Но нет. Я представляю себе что-то вроде псевдокода. Каждая математическая сущность — это либо объект либо интерфейс (выражаясь в терминах ООП).
В контексте владения абстрактным мышлением, это совершенно не важно, какой визуальный, слуховой или иной образ вызывает у человека упоминание той или иной концепции. Более того, этот образ может быть просто побочным продуктом мыслительного процесса.
Но если этих примеров он изучает много-премного, то он начинает замечать общее в них, что и приводит его к более глубокому понимаю самой абстракции.
Вы проецируете математические операции на мыслительные. Это так, на самом деле, работает крайне редко. В смысле, это может так работать, но если человек способен проанализировать множество частных случаев и сделать верный вывод о механизме, он способен понять и абстрактное описание механизма. Если неспособен — ему ни то, ни другое не подходит.
Ну это вы как-то очень быстро сдались. Что значит неспособен? Неспособен — это значит, что преподаватель с неправильной стороны подошел.
Вот тут я объясняю, что сходу винить только способ преподавания, исходя из того, что дисциплине, требующей высоко развитого абстрактного мышления — безосновательно. Не существует подтверждения, что высшую математику может успешно освоить и применять вне учебных условий каждый.
Неспособен — это значит, что преподаватель с неправильной стороны подошел.
При чем тут вообще преподаватель? Учится-то не он, а студент. Если студент не научился, то это вина студента, у него же были абсолютно все возможности. Почему преподаватель виноват в том, что студент из-за своей лини не стал ими пользоваться?
Зависит от того, с какой вы стороны баррикад. Я вот со стороны преподавателей в основном и вижу, что образование работает на десятую часть своей возможной мощности. Раз я с этой стороны, я и фокусируюсь на том, что могу изменить.
Это может прозвучать смешно в контексте этой дискуссии, но ваша точка зрения — по большому счету — марксизм, который делит всё на классы «угнетателей» и «угнетаемых». На самом деле, если даже точно известно, что преподаватель — идиот, это вовсе не означает, что все его студенты не понимают материал только из-за этого, а изменив подачу материала, можно их всех или даже просто какую-то часть вдруг сделать понимающими материал. Это ложная дихотомия уровня детского сада.
Я не понял, где вы нашли это в моих рассуждениях. Конечно, факторов, по которым студенты не понимают материал много. Однако они отлично делятся на две группы — факторы, на которые я, преподаватель, повлиять могу, и те, на которые повлиять не могу. Подача материала и повышения качества преподавания — в первой группе, поэтому на них и надо лично мне сосредотачиваться.
Вы говорите о каких-то баррикадах и сторонах. Рассматривать эту проблему однобоко — просто бессмысленно. Да, российская система образования работает не лушим образом, и для улучшения результата это нужно менять. Но в равной степени на результат влияет личный уровень развития каждого конкретного обучаемого. Который может быть недостаточен для освоения предмета. И если преподаватель начнет вытягивать тех, у кого он недостаточен, те, у кого он достаточен, будут автоматически обойдены вниманием.
Я вот со стороны преподавателей в основном и вижу, что образование работает на десятую часть своей возможной мощности.
Что это значит? Нам, очевидно, не нужно в десять раз больше людей с ВО, у нас и так их переизбыток. Может, стоит усилия перевести с экстенсивного пути на интенсивный? Поотчислять нафиг тех, кто не учится, и сфокусировать усилия на тех, кто учится?
Миллион плюсов автору.
Особенно за тервер обидно. Ну самая жизненная математика. От покера до рулетки с блекджеком.
А на лекциях треш какой-то рассказывают. И люди потом не могут простейшие вещи на пальцах прикинуть.
А на лекциях треш какой-то рассказывают. И люди потом не могут простейшие вещи на пальцах прикинуть.
«Тервер на пальцах» дает опасно ошибочные построения. Там как раз очень легко ошибиться действуя исходя из здравого смысла и аналогий. Отсюда крайняя важность осознания там фундаментальных основ тервера и способности аккуратно их применять. Так что без трэша обойтись, увы, не получится.
Так из-за треша средний студент и не осваивает. Его пичкают непонятной теорией, вместо интереснейшего практичного знания.
Нормальный студент такое забывает на следующий день после сдачи экзамена.
Тервер имеет практическую ценность только когда он посчитан верно. От неверно посчитанного тервера как бы вреда не было больше чем пользы. А «без трэша» Вы в тервере черта с два что посчитаете правильно. Прикладной (да и не только прикладной) тервер вообще на мой взгляд печально славится уныло-скучными и порою зубодробительными выкладками которые надо проделывать правильно и аккуратно.
Естественно это совершенно не означает что интересных задач на тервере не надо давать. Надо. Просто решать их как ни крути придется используя «трэш».
Естественно это совершенно не означает что интересных задач на тервере не надо давать. Надо. Просто решать их как ни крути придется используя «трэш».
Я ровно про это и говорю. Сейчас начинают с очень сложно воспринимаемого, но зато точного определения. Продолжают еще более плохо воспринимаемой формулой. И заканчивают зубодробительными выкладками. А зачем и почему это все могут даже не сказать. Студенты все это забывают на утро после экзамена.
А можно начать с объяснения и расчета кто из 3 игроков в русскую рулетку скорее всего умрет и каким игроком быть выгоднее всего. И уже продолжить формулами и строгими определениями используемыми для этих расчетов. Студенты все это скорее всего запомнят и поймут как и зачем применять.
А можно начать с объяснения и расчета кто из 3 игроков в русскую рулетку скорее всего умрет и каким игроком быть выгоднее всего. И уже продолжить формулами и строгими определениями используемыми для этих расчетов. Студенты все это скорее всего запомнят и поймут как и зачем применять.
Студенты все это скорее всего запомнят и поймут как и зачем применять.Полезнее всего привести несколько примеров, где правильный ответ резко отличается от интуитивного (типа парадокса Монти Холла), показать что там всё отлично считается (если правильно считать) — и таки практика совпадает с теорией, а не со «здравым смыслом».
Вот только точно ли всё это нужно пихать в учебник?
Да про те задачи что я говорю интуитивно тоже сложно сказать решение. На пальцах это не интуитивно, а посчитать примерно. На уровне больше-меньше и порядок разницы.
Классические задачи? Конечно надо.
Реальные задачи для которых все это и было придумано? Конечно надо.
Учебники пишутся для живых людей. Живому человеку очень сложно воспринимать формальный текст. Лекторы бывают разные. Лучше подстраховаться и написать.
Классические задачи? Конечно надо.
Реальные задачи для которых все это и было придумано? Конечно надо.
Учебники пишутся для живых людей. Живому человеку очень сложно воспринимать формальный текст. Лекторы бывают разные. Лучше подстраховаться и написать.
А тут уместен вопрос к методу.
Действительно ли все те, кто не понимают абстрактное объяснение, способны вообще понять эту концепцию до уровня свободного ее применения? Может так быть, что какие методы обучения не применяй, только те, кто особенно способен к абстрактному мышлению (меньшинство) способны это понять и использовать. А остальным стоит ограничиться эмпирическим применением прикладных шаблонных решений и умением верно выбирать из этих шаблонов. Вместо того, чтобы всех пытаться тянуть к высшему уровню, а когда они плохо тянутся — винить лектора, а не их самих за неверный выбор программы обучения, например.
Никого же не удивляет, что одни люди идут заниматься наукой и становятся учеными, а другие ограничиваются инженерией, то есть чисто прикладным применением. Это нормально, и для этого, в общем случае, есть все средства. Основная проблема — в том, чтобы как можно раньше понять, что больше подходит тому или иному индивидууму и концентрировать на этом усилия. А не растрачивать их на одних, тормозя других.
Действительно ли все те, кто не понимают абстрактное объяснение, способны вообще понять эту концепцию до уровня свободного ее применения? Может так быть, что какие методы обучения не применяй, только те, кто особенно способен к абстрактному мышлению (меньшинство) способны это понять и использовать. А остальным стоит ограничиться эмпирическим применением прикладных шаблонных решений и умением верно выбирать из этих шаблонов. Вместо того, чтобы всех пытаться тянуть к высшему уровню, а когда они плохо тянутся — винить лектора, а не их самих за неверный выбор программы обучения, например.
Никого же не удивляет, что одни люди идут заниматься наукой и становятся учеными, а другие ограничиваются инженерией, то есть чисто прикладным применением. Это нормально, и для этого, в общем случае, есть все средства. Основная проблема — в том, чтобы как можно раньше понять, что больше подходит тому или иному индивидууму и концентрировать на этом усилия. А не растрачивать их на одних, тормозя других.
Это разделение людей на сорта очень преждевременно. Давайте мыслить как исследователи. Попался вам такой ученик у которого «плохо с абстрактным мышлением». Мы ведь можем если не измерить, то хотя бы прикинуть, в каких местах у него возникают проблемы в абстрагировании? По-моему, можем.
Моя задача как учителя — понять, в какой момент ученик не справляется с тем, чтобы отбросить ненужное, сосредоточившись на общем. В какой момент его мыслительная машина заклинивает? В каком месте в ее механизме лежит камушек, как его вытащить? Очень часто бывает, что после преодоления затыка ученик начинает прямо-таки блистать — оказывается, что у него не общий «уровень абстрактного мышления» (ох уж и заносчивое словосочетание!) был низок, а просто была одна конкретная проблема с пониманием одной конкретной важной штуки.
- Он не понимает, что общего у трех сосен, трех лисиц и трех тюбиков зубной пасты? Ему неясно понятие числа? Ничего страшного, многие этого не понимали много лет, но сейчас большинство людей это освоило.
- Он не понимает, что общего у футбольного мячика и купола церкви, ему неясно понятие формы? Это тоже лечится.
- Он не понимает определение предела или неподвижной точки или компактного множества? А вы, как учитель, способны положа руку на сердце утверждать, что если вас с ним запереть на неделю в комнате, он все еще его не поймет?
- он не способен держать в голове длинные цепочки рассуждений? Ну дык, а какой его предел — два звена цепочки, пять? Можно ли помочь ему дорасти с пяти звеньев до шести?
Моя задача как учителя — понять, в какой момент ученик не справляется с тем, чтобы отбросить ненужное, сосредоточившись на общем. В какой момент его мыслительная машина заклинивает? В каком месте в ее механизме лежит камушек, как его вытащить? Очень часто бывает, что после преодоления затыка ученик начинает прямо-таки блистать — оказывается, что у него не общий «уровень абстрактного мышления» (ох уж и заносчивое словосочетание!) был низок, а просто была одна конкретная проблема с пониманием одной конкретной важной штуки.
Все ваши утверждения о «это все поправимо» — о сферическом коне в вакууме. То есть ваше стремление все поправить — необходимо. Но не существует никакого, ни практического, ни теоретического доказательства или объяснения, как и почему это возможно в отношении каждого конкретного индивидуума, да еще и уже практически взрослого. Существуют системы образования, где индивидуальным особенностям уделяется на порядок больше внимания, чем в других системах (например, это финская система). Но даже в них основная часть проходящих через эту систему все равно остаются на довольно среднем уровне. Основной результат применения таких систем — уменьшение левой части распределения (сдвиг в среднюю, сведение к минимуму тех, кто раньше считался вообще неспособным к обучению), а не уменьшение средней в пользу правой. Правая остается практически столь же мала, как была.
В констатации факта, что не каждый может стать ученым, нет абсолютно ничего оскорбительного. Люди не рождены и не вырастают равными. Утверждение обратного — идеология, которая не основана ни на каких реальных научных фактах.
В констатации факта, что не каждый может стать ученым, нет абсолютно ничего оскорбительного. Люди не рождены и не вырастают равными. Утверждение обратного — идеология, которая не основана ни на каких реальных научных фактах.
Вузовская математика нужна не только ученым. Она нужна инженерам (в самом широком понимании этого слова), экономистам, биологам, химикам. Да в общем всем негуманитариям.
Система образования плохо выполняет эту функцию. И это точно можно улучшить. Как минимум сняв барьер «Я не понимаю зачем все это вообще нужно?»
Исходные данные у нас неплохие. Приходят люди неплохо сдавшие достаточно сложный ЕГЭ по математике. То есть они как минимум не тупые и мотивированные на обучение. Надо им помогать, а не ставить стену из непробиваемых определений.
Система образования плохо выполняет эту функцию. И это точно можно улучшить. Как минимум сняв барьер «Я не понимаю зачем все это вообще нужно?»
Исходные данные у нас неплохие. Приходят люди неплохо сдавшие достаточно сложный ЕГЭ по математике. То есть они как минимум не тупые и мотивированные на обучение. Надо им помогать, а не ставить стену из непробиваемых определений.
Вузовская математика нужна не только ученым. Она нужна инженерам (в самом широком понимании этого слова), экономистам, биологам, химикам. Да в общем всем негуманитариям.
Им не математика нужна, а ее приложения. Проблема в том, что им дают математику как обычную, но только обгрызенную. А желательно бы давать математику 18 века. Она тогда цельная, но при этом с минимальным количеством абстрактной чепухи.
Это разделение людей на сорта очень преждевременно.
Почему же преждевременно? Вот один человек может пожать 100кг от груди, а другой — не может. Если не может вы говорите — иди качайся, Вася, и не берете его в свою группу, пока он не предоставит вам доказательства выполнения пререкизитов. Где тут вы видите проблему?
А вы, как учитель, способны положа руку на сердце утверждать, что если вас с ним запереть на неделю в комнате, он все еще его не поймет?
Конечно, не поймет. Теория пределов изучается половину первого семестра, минимум по две пары теории и практики в неделю + занятия дома, то есть порядка 2+ часов ежедневно. И значительная часть студентов начинает понимать формализм достаточно хорошо только к концу первого курса, то есть можно оценить примерно как ~500 часов тренировок, требуемых для того, чтобы "прокачать" навык понимания до требуемого уровня.
В неделе всего-навсего 24*7 = 168 часов тренировок, если не спать, не есть и т.д.
Ваше предположение о возможности решения этой проблемы "если закрыть" выгльдит странно, вы же не предполагаете что если дрыща 50кг закрыть на неделю с тренером, то он через неделю выйдет 100кг качком? Это физиологически невозможно.
Приходят люди неплохо сдавшие достаточно сложный ЕГЭ по математике.
ЕГЭ по математике никакого отношения вообще не имеет к математике. Это совершенно другой предмет. Человек, который сдал ЕГЭ по математике на 100, вообще говоря, не имеет каких-то ощутимых преимуществ перед тем, который его сдал на какой-то минимум, который ему позволят базовые знания арифметики и алгебры.
А я не говорю о теории пределов. Я говорю только об определении предела (для любого эпсилон существует дельта, блабла), о преодолении синдрома ослепленного фарами оленя при виде жуткого нечитаемого набора формул. Я сейчас свою жену учу читать книжку по мат.анализу, например, переписывать сложноподчиненные предложения вроде вот такого:
… в последовательность шагов и тонну примеров. Замечательный кстати пример невнятного бормотания на странице 29 учебника по введению в анализ, рождающий целый куст вопросов:
… в последовательность шагов и тонну примеров. Замечательный кстати пример невнятного бормотания на странице 29 учебника по введению в анализ, рождающий целый куст вопросов:
- что означают скобочки в формуле 1.9? Вроде только что определение было без скобочек. (читаем вместе доказательство, понимаем, что это просто умножение). Почему не дописать перед формулой 1.9 её текстовую формулировку?
- откуда взялась буква i, ее раньше нигде не было? Вроде это обычно индекс, да? А в каких он пределах меняется? Вот что, трудно было сказать подробнее, ввести все обозначения?
- зачем нужно сложное предложение, со скобочками и союзами-вставками? Давайте перепишем это в виде последовательности шагов.
- n и k, а уж тем более смысл выражения n-k в голове держать сложновато. Давайте параллельно выписывать примеры, положа n за 5, а k за 2.
так учебники разные бывают, то что вы нашли неудачно написанный учебник — не является открытием
если вы человека впервые обучаете матану зачем-то, то лучше смените учебник
и в учебники, конечно много чего пихают, но приведенный вами фрагмент больше относится к комбинаторике, а не к матану. и непонятно, что там доказывают, если число размещений, то не проще сперва доказать его равенство биномиальным коэффициентам, откуда это формула следует автоматически. или это и доказывают?
если вы человека впервые обучаете матану зачем-то, то лучше смените учебник
и в учебники, конечно много чего пихают, но приведенный вами фрагмент больше относится к комбинаторике, а не к матану. и непонятно, что там доказывают, если число размещений, то не проще сперва доказать его равенство биномиальным коэффициентам, откуда это формула следует автоматически. или это и доказывают?
Я тоже немного удивился, когда увидел комбинаторику в учебнике по матану. Л.Д. Кудрявцев, курс мат.анализа, 2003 год, переработка учебника 1988-1989. Пока ползем по нему, ей задают по главам на уроках, но впоследствие конечно надо переходить на что-то более приличное.
Насчет биномиальных коэффициентов — по-моему это было бы неправильным требовать их помнить из курса элементарной математики и что-то из них выводить. Я вот лично не помню.
Ну вот потому комбинаторика и появилась в учебнике по матану. По хорошему-то это всё вы бы должны были знать ещё до того, как начнёте изучать матан… но ведь не знаете же?
Хуже того, ваши вопросы показывают, что вы и начальную-то математику из школьного курса плохо знаете («что означают скобочки в формуле 1.9» — это просто десять баллов из пять позможных). И «Вот что, трудно было сказать подробнее, ввести все обозначения?» — вы придираетесь к обозначениям, которые должны были видеть сто раз в задачках на алгебру и геометрию? Это не шутка, не издевательство?
И дальше — всё упирается в то, что авторы книг по матану не знают чего читатели знают, чего нет.
Хуже того, ваши вопросы показывают, что вы и начальную-то математику из школьного курса плохо знаете («что означают скобочки в формуле 1.9» — это просто десять баллов из пять позможных). И «Вот что, трудно было сказать подробнее, ввести все обозначения?» — вы придираетесь к обозначениям, которые должны были видеть сто раз в задачках на алгебру и геометрию? Это не шутка, не издевательство?
И дальше — всё упирается в то, что авторы книг по матану не знают чего читатели знают, чего нет.
Ну в нашем случае я закончил прикладную математику лет восемь назад, а математическими задачами в программировании не занимался где-то года четыре, а жена закончила школу лет семь назад и разумеется ничего не помнит. Поэтому не издеваюсь, я искренне сначала смотрел на эту A со скобочками и думал, как же скаляр стал внезапно функцией, что за бардак.
Я не думаю, что введение абсолютно всех обозначений, из школьного курса, которые будут использоваться в рассуждениях, ну или ссылки на соответствующие школьные учебники повредили бы данному изданию. Тут к вопросу нужно подходить как программистам — если хоть одна переменная не объявлена или не импортирована явно из другого модуля — учебник не должен «скомпилироваться».
Я не думаю, что введение абсолютно всех обозначений, из школьного курса, которые будут использоваться в рассуждениях, ну или ссылки на соответствующие школьные учебники повредили бы данному изданию. Тут к вопросу нужно подходить как программистам — если хоть одна переменная не объявлена или не импортирована явно из другого модуля — учебник не должен «скомпилироваться».
Тут к вопросу нужно подходить как программистам — если хоть одна переменная не объявлена или не импортирована явно из другого модуля — учебник не должен «скомпилироваться».Великолепная аналогия, кстати! И решается так же, как в программировании. Там в предисловнии к книжке написано обычно — какие вещи вы должны знать перед тем, как её начать читать. Элементарную математику, в частности, в объёме школьной программы.
математическими задачами в программировании не занимался где-то года четыре, а жена закончила школу лет семь назад и разумеется ничего не помнит.Ну то есть это вы «потеряли» кучу библиотек, а не авторы учебника.
Я не думаю, что введение абсолютно всех обозначений, из школьного курса, которые будут использоваться в рассуждениях, ну или ссылки на соответствующие школьные учебники повредили бы данному изданию.А давайте я вас попрошу написать хотя бы он проект на оригинальном Паскале без модулеи и include'ов, а? Вот вам системные функции POSIX — а дальше всё должно быть в одном файле. Много вы при таком подходе напрограммируете? А почему авторы учебников должны так работать?
по-моему это было бы неправильным требовать их помнить из курса элементарной математики
здрасьте, зачем их требовать знать, когда они элементарно выводятся из задачи по размещении элементов по ячейкам
ну и, всё-таки, бином Ньютона — это школьная программа и полезная формула, которая часто используется в анализе. так что если забыли ее неплохо было бы повторить, тем более много времени это не займёт — и заодно в индукции человек потренируется. а то с подобной логикой можно договориться и до того, что «было бы неправильно» требовать помнить как дроби складывать
на уроках
«на уроках»??? это в школе что ли O_O
ей задают по главам на уроках
вот это, кстати, реально жесткая система — вместо того чтобы читать лекции и распинаться, препод просто задает и требует, причем по не самому очевидному учебнику
ну или ссылки на соответствующие школьные учебники повредили бы данному изданию
не, это уже перебор. вы же должны понимать, что этот учебник расчитан на людей, которые только закончили школу и поступили в институт. а если у вас всё забылось из школьной программы давно, то ясное дело сперва будет трудновато. причём этот учебник заточен под математические специальности, т.е. явно предполагается высокая математическая подготовка из школы с соответствующим уклоном. вы посмотрите примеры вступительных экзаменов годов написания учебника для университетов его назначения
А я не говорю о теории пределов. Я говорю только об определении предела (для любого эпсилон существует дельта, блабла)
А теория пределов — это и есть определение предела + несколько очевидных теорем, весь смысл которых — в умении использовать это определение. Если вы понимаете определение предела — вы знаете теорию пределов.
что означают скобочки в формуле 1.9?
Это же стандартная нотация
откуда взялась буква i, ее раньше нигде не было? Вроде это обычно индекс, да? А в каких он пределах меняется? Вот что, трудно было сказать подробнее, ввести все обозначения?
Я уверен, что где-то во введении были изложены правила работы с индексами. По крайней мере, обычно это делается.
Он ни в каких пределах не меняется. меняется индекс индекса — его пределы известны, это от 1 до k, а сам индекс (i) просто какой-то элемент из произвольного индексирующего множества которое, скорее всего, было задано до этого.
зачем нужно сложное предложение, со скобочками и союзами-вставками? Давайте перепишем это в виде последовательности шагов.
И как там у вас это выглядит с последовательностью шагов?
n и k, а уж тем более смысл выражения n-k в голове держать сложновато. Давайте параллельно выписывать примеры, положа n за 5, а k за 2.
То есть вы предлагаете к n и k запомнить еще и пару конкретных чисел, чтобы сложнее стало и совсем всех запутать?
Это же стандартная нотация
она стандартная и для функций (аргументы пишутся в скобочках) и для умножения (знак умножения пропускается). Парсер студента ломается и его клинит, ему надо разрешать неоднозначность, добавлять много контекста. Чтобы парсер не клинило, пишем перед формулой фразу, в которой будет слово «произведение».
И как там у вас это выглядит с последовательностью шагов?
Ну, примерно так:
- Возьмем все размещения из n по k элементов. Каждое из таких размещений — это множество, и всего у нас их будет Ank штук.
- Обозначим их так: xi1, xi2, …, Xik, где i-индекc, номер размещения, меняющийся от 1 до Ank.
- Добавим в каждое из этих размещений Xi по одному элементу xik+1, причем этот элемент не должен входить в Xi. Обратите внимание, что таких элементов xik+1 будет ровно n-k.
А потом тоже самое продемонстрировать для примера размещений из четырех по два для множества {1,2,3,4}.
Это же классический chunking, студент оперирует маленькими кусочками знаний, а преподаватель — большими. Задача преподавателя или автора учебника — в зависимости от целевой аудитории уменьшать размер кусочка.
Парсер студента ломается и его клинитЗначит нужно прокачивать парсер.
ему надо разрешать неоднозначность, добавлять много контекстаЕму не нужно добавлять «много контекста». Ему нужно всего лишь знать — вот это вот буквочка обозначает функцию или нет. Как для парсинга C++ нужно знать — является ли последовательность букв именем типа или нет, так и для парсинга матформул нужно знать — чем явдяется та или иная буква. Ибо одна и та же записть для объектов разной природы может обозначать сильно разные вещи.
Задача преподавателя или автора учебника — в зависимости от целевой аудитории уменьшать размер кусочка.Абсолютно верно. Но при этом нужно учитивыть что тот же Фихтенгольц — это 2'000 страниц. Если вы его превратите в то, что вы предлагает — будет 20'000 страниц (хорошо если не 200'000).
Практически это обозначает, что полезнее не превращать учебник в 100-томник (который никто и никогда не прочёт), а учить читателей понимать более-менее сжатое изложние.
Да даже 2'000'000 страниц не проблема, если
1) Учебник электронный
2) Читать нужно не все, а только то что непонятно.
2 ГБ — почти ни о чем.
2) Читать нужно не все, а только то что непонятно.А вот с этим будут проблемы. Как в куче воды найти зёрна того, что вам нужно?
2 ГБ — почти ни о чем.Взять того же Фихтенгольца и добавить к каждому абзацу примеров, задач и прочего… для тех, кто «не понял»… интересная штука может получиться — вот только кто это всё будет оплачивать?
До сих пор страдаю. Интеграл. Не умею. До сих пор.
Матмех СПбГу, 97 год.
Стыдно сказать, но в аналитическом виде я брать интегралы не умею до сих пор. В цифровом виде — столбиками, трапециями, кривыми — сколько угодно (еще в 8 классе умел). Ну ок, 20 лет этого не делал, но там же просто все…
Но в аналитическом виде — для меня это реально тёмный лес. Какие-то фундаментальные основы, какой-то кирпичик выпал — и здание математики держится на честном слове.
:(
Матмех СПбГу, 97 год.
— Совершенно очевидно, что… <.....> Ч
Через 20 слов я уже совершенно перестаю понимать о чем речь и переспрашиваю:
— Вы не могли бы объяснить…
— Не мог бы. Это вам должны были рассказывать на алгебре. Что, не рассказали? Спросите преподавателя. Кто у вас препод? Имярёк? Ааа… — глубокомысленно, — понятно.
Прихожу к преподу по алгебре.
— Вы не могли бы объяснить…
Препод поднимает на меня больные усталые похмельные глаза и сипло отвечает:
— Не мог бы. Читайте учебник, там все есть.
— Но я не понимаю, объясните пожалуйста.
— Если вы не понимаете учебник, зачем вы поступали?
Стыдно сказать, но в аналитическом виде я брать интегралы не умею до сих пор. В цифровом виде — столбиками, трапециями, кривыми — сколько угодно (еще в 8 классе умел). Ну ок, 20 лет этого не делал, но там же просто все…
Но в аналитическом виде — для меня это реально тёмный лес. Какие-то фундаментальные основы, какой-то кирпичик выпал — и здание математики держится на честном слове.
:(
Взятие интеграла в аналитическом виде — это набор трюков, а не теория. Тут надо не понимать, а практиковаться.
UFO just landed and posted this here
Там всё просто как раз. Первое что надо знать: никто не знает как считать интегралы в аналитическом виде. Есть несколкьо известных приёмов: ну там «взять интеграл по частям», «угадать первообразную» и т.д. Интеграл берётся так: пробуем применить приём 1 — не работает, приём 2 — не работает, приём 3 — работает, применяем, повторяем. Это как собирать кубик рубика: никто (ну кроме тех кто постиг дзен) не знает как его собирать, но есть 5-6 известных трюков и их более-менее методом тыка применяют пока кубик не соберётся. Я бы ещё сравнил это с прохождением лабиринта: вы примерно предствляете куда хотите попасть, но не знаете как. У вас каждый раз есть несколько вариантов: идти вправо, влево и т.д. Вы эти варианты перебираете пока не найдёте выход или пока не надоест (возможно выхода нет — это «неберущийся» интеграл, и таких большинство).
Препод поднимает на меня больные усталые похмельные глаза и сипло отвечает:
— Не мог бы. Читайте учебник, там все есть.
Так все верно говорит. Вот возьмем человека, который на гитаре играет — вас же не удивляет, что нельзя просто прочитать какой-то хитрый самоучитель и стать хорошим гитаристом? Надо практиковаться, ежедневно, на протяжении многих лет. И если что-то не получается — значит, надо идти и заниматься соответствующими упражнениями. Тут все то же самое, вы когда к преподавателю приходите и говорите "я учебник прочитал и не понял", то тут вывод один — вы хреново читали, значит, надо читать еще. Один раз, второй, пятидесятый. Почитайте с недельку, рано или поздно дойдет.
вас же не удивляет, что нельзя просто прочитать какой-то хитрый самоучитель и стать хорошим гитаристом
Не удивляет. Но, по вашей логике, получается так:
Вы приходите в музыкальную школу на класс гитары и говорите преподавателю:
— У меня не получается играть, помогите мне.
А он вам в ответ:
— Читайте учебник, там все есть. Если вы не понимаете, что там написано — зачем вы сюда поступали.
И это хреновый преподаватель. Потому что хороший скажет:
— Бери гитару и показывай, как ты играешь. Нет, пальцы не так ставишь. Смотри как надо. Держи. Попробуй сам. Вот так. Нет, не так, левее, крепче держи, ага. Теперь другая рука. Теперь давай еще раз повторим. Видишь, начало же получаться?
К сожалению, методика «кинь его в воду и пускай пытается выплыть, а утонет — да хер бы с ним» крайне плохо работает, особенно для ментальных дисциплин.
Не удивляет. Но, по вашей логике, получается так:
Нет, не так. В математике чтение учебника — это и есть выполнение упражнений (в том числе). По-этому отправить читать учебник — это равносильно тому, что преподаватель по гитаре покажет набор упражнений и отправит вас домой их выполнять.
Нет, пальцы не так ставишь. Смотри как надо. Держи.
И, опять же, в учебнике в виде доказательств теорем вам как раз и дана идеальная расстановка. Смотрите и учитесь сколько угодно.
Потом вы придете на практическое занятие, попробуете там что-то подоказывать — и вам как раз расскажут, что вы "руки ставите неправильно" (если неправильно).
К сожалению, методика «кинь его в воду и пускай пытается выплыть, а утонет — да хер бы с ним» крайне плохо работает, особенно для ментальных дисциплин.
Ментальные дисциплины изучаются точно так же как нементальные — путем тренировки.
Просто люди ленивы и трудиться не хотят, а хотят серебряной пули, какого-то фантастического текста, который прочитал — и все понял!
Нет, в математике "понял" — это результат той самой тренировки. Понимание — это не знания, это навык. А с навыками все просто: no pain — no gain. Никакого способа считерить нет, как бы лентяям ни хотелось.
В математике чтение учебника — это и есть выполнение упражнений
Нет.
Я прочитал много книжек по математике и программированию, и совершенно уверен, что просто чтение не работает, в голове не остаётся совершенно ничего.
Кмк, лучше всего начинать сразу с задач, и читать учебник, чтобы понять в чём заключается проблема и как её решить.
Недавно пробовал такой подход с топологией. Берёшь задачи-теоремы, которые нужно доказать, и читаешь ровно столько учебника, сколько нужно, чтобы всё доказать/решить.
Вот тогда реально хорошо понимаешь материал.
Я прочитал много книжек по математике и программированию, и совершенно уверен, что просто чтение не работает, в голове не остаётся совершенно ничего.
Так надо не просто читать а разбирать текст. Естественно, по принципу "смотрю в книгу — вижу фигу" результат будет нулевой. Надо усилия прикладывать. Чтобы мышцы росли, надо брать вес, который даст стресс вашим мышцам. Иначе они расти не будут. Тут то же самое.
Кмк, лучше всего начинать сразу с задач, и читать учебник, чтобы понять в чём заключается проблема и как её решить.
Как именно вы будете работать с текстом — это уже ваше дело. Как удобно — так и работаете, это личное.
Берёшь задачи-теоремы, которые нужно доказать, и читаешь ровно столько учебника, сколько нужно, чтобы всё доказать/решить.
Только обычно до чтения соответствующей главы даже формулировка этих задач будет вам непонятна. Т.к. в них будут входить неизвестные термины. Смысл тогда эти задачи читать?
этот ваш махмет — это ж вроде игра на выживание, совершенно адские условия естественного отбора, чтобы из миллиона прошедших его дятлов, выпустились один-два Колмогорова.
Мда, только час ночи может быть мне оправданием за это:
взгляд, конечно же взгляд! Больной, усталый и похмельный взгляд.
больные усталые похмельные глаза
взгляд, конечно же взгляд! Больной, усталый и похмельный взгляд.
Тут, мне кажется, всё просто: непонятно на лекции — спрашивайте преподавателя, непонятно после лекции — идите в библиотеку, непонятно в книжке — меняйте книжку, ищите статьи и первоисточники. Читайте зарубежные учебники (не потому что они лучше, а потому что они все разные). Сами устраивайте семинары среди студентов. Ставьте собственные задачи. И очень скоро вы поймёте: это вам вообще надо? У вас не будет потребительского отношения к математике, если она часть вашей жизни. Люди творили математику в войну, в голод, в юности и в старости, даже в психушке. И вовсе не из-за пользы, а потому что это была их жизнь, их понимание прекрасного. Таких всегда немного. Эйлеры, Гильберты, Фихтенгольцы, Фейнманы и Савватеевы всегда дефицит. И наконец, математика никому ничего не должна. Она не должна быть полезной. Не должна быть понятной. Только непротиворечивой. Её результатами можно пользоваться, и опыт показывает, что практически всё от абстрактных алгебр до теории кос, паркетов или категорий находит своё применение. Причём, не по отдельности, а в совокупности. Забавно наблюдать, как народ, ожидая год от года появления новых технологий, усиления мощности смартфонов, развития интеллектуальных сервисов, капризно возмущается: "Зачем нам все эти сложности с функциональным программированием — оно не практично, с коллайдерами — они дорогие и бесполезные, с теорией категорий и гомологической теорией типов — очередная фигня, которую понимает полторы сотни человек… эллиптические кривые, abc-гипотеза, вы что серьёзно считаете, что на них можно потратить жизнь?" Так что, по-моему, нет какой-то "проблемы современных математических текстов", которую можно было бы решить., как нет, скажем, "проблемы современного театра (потому что я в нём ничерта не смыслю)".
Так что, по-моему, нет какой-то «проблемы современных математических текстов»ИМХО есть принципиальные проблемы. Кратко для примера можно назвать 3:
1) Многие авторы отмечают тенденцию к усложнению доказательств новых теорем — есть опасение, что скоро появятся задачи, которые будут нерешаемы по причине сложности для любого человека (слишком сложные тексты);
2) Системы ИИ автоматического доказательства теорем пока справляются только с тривиальными задачами. Ни одному математику не удается научить (сделать текст для) ИИ делать нетривиальные доказательства. Есть опасение, что не удастся.
3) Машинное решение задачи 4х красок (текст) остается непонятным для математиков. Это методологическая проблема: можно ли в принципе признавать такое решение?
Перечисленные вами проблемы, действительно реальны, важны и интересны, но обсуждаемая статья, к сожалению, не про них.
2) И не надо. Точно также у нас нет ИИ который бы мог написать программу, однако есть методы написания программ которые позволяют глупым человекам собирать необозримые по сложности программы. Например линукс можно было бы сравнить с библиотекой томов того самого Тейхмюллера, т.е. никто даже близко не пытается разобраться во сём досконально, как это делают с проверкой доказательств. Однако ни у кого не возникает вопросов работает линукс и есть ли там фундаментальные ошибки которые делают его неработоспособным. Когда я учился в универе, я попробовал записать доказательство простой теоремы в виде программы: ну там каждая лемма это функция и т.д. Не получилось потому что все «строгие» математические определения на самом деле не такие уж строгие. Типичный пример: «Рассмотрим множество функций A.» Нормальная фраза для математика, но совершенно бессмысленная для программиста. Какое множество? Конечное? Открытое? Счётное? Какие функции? Любые? Интегрируемые? Непрерывные? Сколько аргументов у них? Какого типа аргументы? Математики такие подробности всегда пропускают, потому что подразумевают контекст. По этой же причине «теорию тейхмюллера» проверяют уже много лет: автор подразумевает контекст, а другие математики пытаются догадаться, что там подразумевалось.
Точно также у нас нет ИИ который бы мог написать программу, однако есть методы написания программ которые позволяют глупым человекам собирать необозримые по сложности программы.К сожалению все эти методы работают только если мы миримся с тем, что результирующая программа будет с ошибками и иногда будет делать не то, что нужно.
Для математики такое не подходит.
Однако ни у кого не возникает вопросов работает линуксИменно так. Ни у кого никаких вопросов не возникает ибо всем прекрасно известно: не работает. Вопрос только в том, что некоторые люди могут «завалить его» за пару дней, а некоторым потребуется неделя.
Но завалить его могут все — тут даже вопросов нету.
Математики такие подробности всегда пропускают, потому что подразумевают контекст.Да — это известная беда.
Какое множество? Конечное? Открытое? Счётное? Какие функции? Любые? Интегрируемые? Непрерывные? Сколько аргументов у них? Какого типа аргументы?Это всё вопросы, на которые для каждой теоремы можно ответить. И, более того, сложность многих теорем варьируется от тривиальных до многотомно-доказываемых в зависимости от ответа на эти вопросы.
UFO just landed and posted this here
Типичный пример: «Рассмотрим множество функций A.» Нормальная фраза для математика
Какие-то у вас странные математики и странная математика. В моей математике всегда указывается, что это конкретно за множество.
Вот это «подразумевание контекста» реально выбешивает, когда речь идет о преподавании.
Вот это «подразумевание контекста» реально выбешивает, когда речь идет о преподавании.
Слушайте, ну никто ничего не подразумевает, все явно оговаривается. Вот беру я учебник Ленга по алгебре — и там сразу указывается, какие конкретные знания должны иметься у читателя и далее вводятся все обозначения, базовые определения вроде "отображения" или "отношения", описание правил использования индексов, базовые вещи вроде леммы Цорна.
Есть, конечно, исключения — но они именно исключения.
В 9 случаях из 10 проблема "подразумевается из контекста" является результатом невнимательности читателя.
Ужасный текст. Какие-то обрывочные мысли. Случайные примеры. Ничего не понятно. Неужели вы преподаёте?!
Ну, набежали…
Вот обьяснили предел на пальцах, бОльшее количество студентов быстрее поняло. Кому от этого стало хуже? При этом строгое определение никуда не делось.
А у нас на матанализе было всё просто. Пришёл преподаватель — и давай строчить на доске формулы. Понимание, примеры — не, не слышали. Да чего ж тут непонятного? всё очевидно… С трудом удавалось поспевать за ним хотя бы переписывать хотя бы текст (то есть мне удавалось поспевать… многие и на этом сдувались), а дома уже строчка за строчкой нужно было разбираться (конспекты получались удобные — сама суть без лишних слов). Мужик молодой был и невероятно головатый (сейчас он уже зав.кафедры стал), ещё и брат у него такой же… Ему всё казалось очевидным и даже не представлял, что кому-то что-то может быть непонятно. И требовал на экзаменах неплохо так (причём не денег, а именно знаний). Хотя итоговую оценку на третьем курсе (которая пошла в диплом) всем поставил автоматом.
«Математика. Утрата определённости» (англ. Mathematics: The Loss of Certainty) — Мо́рис Клайн (англ. Morris Kline)
https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0._%D0%A3%D1%82%D1%80%D0%B0%D1%82%D0%B0_%D0%BE%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D1%91%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D0%B8
(немного юмора)
и всё это — бутылкой пива!
:)
Попросил однокурсника о помощи с вычислением длины кривой через интеграл. Тот взял бутылку пива, нарисовал рандомную кривую, спрямил бесконечно малыми отрезками...
и всё это — бутылкой пива!
:)
Я не знаю, можно ли массово использовать подход общий обзор => контрпримеры => формализм.
Можно. В своих дисциплинах я так и делаю. Но коллеги, преподающие смежные области и обеспечивающие мои дисциплины базой — в большинстве своем так не делают. К сожалению
Добавлю нытья. Очень часто кажется, что некоторые математики специально запутывают свои тексты, чтобы менее сведущему в математике человеку было сложнее разобраться.
Приведу конкретный пример. Пишу библиотеку для вычислений с повышенной точностью и дошла очередь до вычисления логарифмов. Поиск в интернете вывел на статью «A New Method for Approximating Logarithms with k-th Order» (pdf) — но даже после 20 прочтений так и не смог ничего понять. Там вводятся леммы, доказываются неравенства, даже есть глава с названием «The Algorithm», но вот самого алгоритма с формулой, где слева — логарифм, а справа — вычисления, обнаружить не смог. В конце там есть таблица с результатами и упоминается MATLAB, посредством которого сделаны вычисления, но самого кода — нет. Им что, жалко? Мне попадались работы, где код на фортране занимал больше места, чем математическое описание, и за такие работы отдельное спасибо авторам (хотя код у математиков обычно получается не очень) — как минимум его можно отдебажить и понять суть хотя бы алгоритмически.
И ладно если бы я был дебил — но в итоге, плюнув на всё, смог вывести алгоритм вычисления логарифма самостоятельно (и это не метод Ньютона). И даже после этого я не смог до конца понять ту работу — в частности, откуда ограничение в r≤½, и почему m должно быть обязательно целым — т.к. у меня и с нецелым всё прекрасно считается.
Приведу конкретный пример. Пишу библиотеку для вычислений с повышенной точностью и дошла очередь до вычисления логарифмов. Поиск в интернете вывел на статью «A New Method for Approximating Logarithms with k-th Order» (pdf) — но даже после 20 прочтений так и не смог ничего понять. Там вводятся леммы, доказываются неравенства, даже есть глава с названием «The Algorithm», но вот самого алгоритма с формулой, где слева — логарифм, а справа — вычисления, обнаружить не смог. В конце там есть таблица с результатами и упоминается MATLAB, посредством которого сделаны вычисления, но самого кода — нет. Им что, жалко? Мне попадались работы, где код на фортране занимал больше места, чем математическое описание, и за такие работы отдельное спасибо авторам (хотя код у математиков обычно получается не очень) — как минимум его можно отдебажить и понять суть хотя бы алгоритмически.
И ладно если бы я был дебил — но в итоге, плюнув на всё, смог вывести алгоритм вычисления логарифма самостоятельно (и это не метод Ньютона). И даже после этого я не смог до конца понять ту работу — в частности, откуда ограничение в r≤½, и почему m должно быть обязательно целым — т.к. у меня и с нецелым всё прекрасно считается.
некоторые математики специально запутывают свои тексты, чтобы менее сведущему в математике человеку было сложнее разобраться
В ходе изучения нескольких математических дисциплин пришёл к тому же выводу. К сожалению, в реальной жизни, гений и злодейство — вещи вполне совместимые.
1) Некоторые искренне не понимают — что тут такого может быть непонятного.
2) Некоторыми движет некоторый «научный» снобизм: Я в свое время поломал над этим голову, постиг, так сказать, всю глубину наших глубин, а теперь поломайте голову вы. Этакая математическая «дедовщина».
3) Случай описанный вами самый щепетильный: вопрос научного первенства и признания. Когда человек намеренно запутывает свой текст, не даёт всех выкладок, это говорит о том что он боится так называемой «кражи идеи», когда основываясь на его научном материале посторонние создают себе имя в научном мире («забывая» при этом упомянуть того кто проделал первоначальную черновую работу).
PS Вообще было отвратительно узнать, что среди математиков были склоки не хуже чем травля генетиков во времена лысенковщины.
http://cyclowiki.org/wiki/Пощёчина_Колмогорова_Лузину
Вставлю пять копеек про научные статьи в ответ на комментарии выше, и на утверждения ТС в конце публикации о том, что
Приведу выдержку о том, как принято доносить информацию до читателя в высокорейтинговых статьях.
— Относитесь к читателю вашей работы как к гостю в вашем доме. Спросите, чего угодно гостю, может быть что-то выпить или перекусить? Не угодно ли гостю отдохнуть?
Вот источник целиком — billf.mit.edu/sites/default/files/documents/cvprPapers.pdf
Мне он в свое время очень помог начать писать хорошие статьи.
большая часть виденных мною «профессиональных» работ в плане подачи материала не отличается от учебников.
Приведу выдержку о том, как принято доносить информацию до читателя в высокорейтинговых статьях.
Treat the reader as you would a guest in your house. Anticipate their needs: would you like something to drink? Something to eat? Perhaps now, after eating, you’d like to rest?
— Относитесь к читателю вашей работы как к гостю в вашем доме. Спросите, чего угодно гостю, может быть что-то выпить или перекусить? Не угодно ли гостю отдохнуть?
Вот источник целиком — billf.mit.edu/sites/default/files/documents/cvprPapers.pdf
Мне он в свое время очень помог начать писать хорошие статьи.
Нам препод по диффурам рекомендовал попробовать Уолтера Рудина читать, если Фихтенгольц не идёт. Кое-что действительно становилось понятнее…
Как вы думаете, стоит ли на хабр написать цикл статей, что-то типо «Курс Математического Анализа для программистов» с использованием примеров и практики?
Предствьте себе, что у вас есть СУБД. Вы хотите понять, как она работает. Но в вашем распоряжении только содержимое базы данных. Возможно, основываясь только на них, понять, как работает СУБД, как взаимодействует с другими программами, зачем вообще нужно всё это хозяйство? Нет.
Так и с преподаванием математики. Это попытка скопировать данные из головы лектора в головы студентов. А у них и структура-то совсем другая, несовместимая.
Так и с преподаванием математики. Это попытка скопировать данные из головы лектора в головы студентов. А у них и структура-то совсем другая, несовместимая.
Когда я изучал высшую математику в универе, то активно пользовался сайтом mathprofi. Изложение довольно доступное и примеры понятные.
Не отрицая наличие проблем в российской системе образования, хочется заметить следующее. У подхода с разжёвыванием материала по математике до мелкодисперсной массы, которую можно вводить через трубочку, есть проблема: для абстрактных и сложных понятий можно придумать десятки объяснений «на пальцах» и десятки примеров. И то, которое покажется ясным одному студенту, другого может поставить в тупик. Суть в том, что любой пример описывет только один какой-то аспект рассматриваемого понятия, и никто не знает, какой именно аспект будет непонятен очередному студенту. Это не говорит о том, что приводить примеры и давать упрощённые объяснения бесмысленно. Да и не вспомню я ни одного курса, где бы препы не давали бы примеров. Это говорит о том, что без обратной интерактивной связи со стороны студентов (которая вообще отсутствует, если речь идёт о книге) преподаватель может даже не знать, чего именно им не понятно.
Тут мы подходим к другой проблеме. Человека невозможно научить. Но человеку можно помочь научиться. Иными словами, никакого другого обучения, кроме самообучения, не бывает. Универ, просто, сильно упрощает этот процесс тем, что там есть программа, которая, если выстроена разумно, даёт представление о том, в какой последовательности надо изучать предметы. И там есть люди, которые (предположительно) являются специалистами в своих областях и могут ответить на большинство вопросов. Но если студент сам не будет продумывать материал, хотя бы для того, чтобы сформулировать конкретные вопросы (примеры, контрпримеры и т.п.), то можно какие угодно суперучебники писать, какие угодно суперпедагогичные лекции читать — всё будет бестолку. В России, к сожалению, школьное образование построено так, что он приучает к тотальному контролю сверху, когда за тебя уже всё решили, тебе надо только как попугаю всё повторить. Это, естественно, мало способствует формированию правильных навыков самообучения. Однако, в хороших вузах как раз и пытаются эти навыки привить. Хороших вузов, только вот, мало…
Тут мы подходим к другой проблеме. Человека невозможно научить. Но человеку можно помочь научиться. Иными словами, никакого другого обучения, кроме самообучения, не бывает. Универ, просто, сильно упрощает этот процесс тем, что там есть программа, которая, если выстроена разумно, даёт представление о том, в какой последовательности надо изучать предметы. И там есть люди, которые (предположительно) являются специалистами в своих областях и могут ответить на большинство вопросов. Но если студент сам не будет продумывать материал, хотя бы для того, чтобы сформулировать конкретные вопросы (примеры, контрпримеры и т.п.), то можно какие угодно суперучебники писать, какие угодно суперпедагогичные лекции читать — всё будет бестолку. В России, к сожалению, школьное образование построено так, что он приучает к тотальному контролю сверху, когда за тебя уже всё решили, тебе надо только как попугаю всё повторить. Это, естественно, мало способствует формированию правильных навыков самообучения. Однако, в хороших вузах как раз и пытаются эти навыки привить. Хороших вузов, только вот, мало…
Вы упускаете момент доверия к авторитету. Университетское образование рассчитано на то, что всякий приходящий в институт сознательно и подсознательно верит в авторитет университета и его преподавателей — именно это склонение перед авторитетом может позволить ему, скажем, не сильно задумываться о том, а действительно ли нужно интегральное исчисление будущему программисту. «Это не мое дело — подвергать сомнению программу, ее писали очень умные люди, а мое дело — прилежно ее изучать. Чем лучше изучу, тем лучшим я буду специалистом».
В современном мире я очень сомневаюсь, что у нас есть такой высокий уровень доверия.
В современном мире я очень сомневаюсь, что у нас есть такой высокий уровень доверия.
Ну, это проблемы отдельно взятых студентов. Разумный подход (который, к сожалению, возникает после): учи пока преподают, всё, что изучишь — можешь когда-нибудь применить, или не применить, а то, что не изучишь — точно никогда не применишь.
Я, вот, очень жалею, что слаб в математике.
Я, вот, очень жалею, что слаб в математике.
Вот у меня была такая проблема — я всегда старался распределять свои силы разумно, всегда задавал себе вопрос «а зачем тебе заниматься вот этой дисциплиной?», и в свои 18 лет уж точно знал, что могу себе расставить приоритеты. Понимаете, я чувствовал себя сознательным индивидом, а не наивным ботаном!
Каково же было мое удивление через семь лет после выпуска из института, когда я понял, что был я тупым кретином, который не доверял программе обучения из идиотского нон-конформизма замешанного на мутных суждениях типа «раз это государственный институт — то все там неэффективно и устарело», «мы живем в эпоху перемен, и что было верно вчера не будет верным даже сегодня» и коронное «я пришел программировать зергов, а вы мне тут показываете каких-то дурацких ферзей». За эти семь лет мне успела пригодиться почти каждая из дисциплин, и каждую пришлось заново самостоятельно изучать. Оказывается, тупые ботаны, положившиеся на авторитет зарабатывающих три копейки преподов (господи, какой там мог быть авторитет для пупа земли?!) были гораздо более умными чем я, думавший, что расставляю приоритеты!
Вопрос дня — как донести эту мысль до сегодняшнего студента, похожего на меня из прошлого?
Каково же было мое удивление через семь лет после выпуска из института, когда я понял, что был я тупым кретином, который не доверял программе обучения из идиотского нон-конформизма замешанного на мутных суждениях типа «раз это государственный институт — то все там неэффективно и устарело», «мы живем в эпоху перемен, и что было верно вчера не будет верным даже сегодня» и коронное «я пришел программировать зергов, а вы мне тут показываете каких-то дурацких ферзей». За эти семь лет мне успела пригодиться почти каждая из дисциплин, и каждую пришлось заново самостоятельно изучать. Оказывается, тупые ботаны, положившиеся на авторитет зарабатывающих три копейки преподов (господи, какой там мог быть авторитет для пупа земли?!) были гораздо более умными чем я, думавший, что расставляю приоритеты!
Вопрос дня — как донести эту мысль до сегодняшнего студента, похожего на меня из прошлого?
За эти семь лет мне успела пригодиться почти каждая из дисциплин, и каждую пришлось заново самостоятельно изучать.
Присоединяюсь. Тоже во время учёбы смело отметал матан как что-то ненужное, а в итоге просто потратил на его усвоение больше времени уже во время работы.
Вопрос дня — как донести эту мысль до сегодняшнего студента, похожего на меня из прошлого?
Думаю, доносить что-то вовсе необязательно. В худшем случае усвоение произойдёт методом последовательных приближений по мере надобности. В лучшем случае человек так ничего и не поймёт, устроится работать по рабочей специальности, будет рассказывать всем, что он разработчик, матан ему вообще ни разу не пригодился и будет при этом абсолютно счастлив и уверен в себе.
Думаю, доносить что-то вовсе необязательно.
Ну тут у нас с вами целеполагание разное — я все же к коммунистическому идеалу «всестороннего развития всех членов общества» склонен, чтобы каждый ребенок смог раскрыться настолько, насколько возможно.
А по-моему, у нас почти одинаковое целеполагание. Нужно дать возможность каждому освоить любую специальность, но заставлять ни к чему. И обманом заманивать тоже никого не нужно. А то люди будут поступать в университет ради непрекращающихся развлечений, а потом в лекционном зале вместо клоуна с медведями столкнутся с предельно абстрактными задачами и формулами.
Для мотивации я бы добавил разве, что крепкая математическая подготовка — это то, за что очень ценят специалистов из бСССР на Западе (где как раз распространена манера преподавать матан любой сложности посредством шоу и примитивных шуточных задачек).
Для мотивации я бы добавил разве, что крепкая математическая подготовка — это то, за что очень ценят специалистов из бСССР на Западе (где как раз распространена манера преподавать матан любой сложности посредством шоу и примитивных шуточных задачек).
А никто и не утверждал, что матан и другие дисциплины не нужны.
В статье говорится, что при обучении преподы, учебники, и многие доступные материалы (википедия), приводит объяснения без привязки к реальным практическим задачам.
Слишком часто объяснения идут излишне формальным языком, который перегружен другими формальными определениями.
Возможно в энциклопедиях и справочниках для продвинутых математиков и полезно использовать полный формализм, чтобы учесть все нюансы, но не в общедоступных википедии и школьных учебниках.
Особенно часто встречаются резкие переходы типа «берем один апельсин и одно яблоко, как вы видите все несложно, теперь очевидно что из этого получается )@K$&%H@#JK$H#@$*@#%$HJ@#%(@#JK» выглядит как-то так.
В статье говорится, что при обучении преподы, учебники, и многие доступные материалы (википедия), приводит объяснения без привязки к реальным практическим задачам.
Слишком часто объяснения идут излишне формальным языком, который перегружен другими формальными определениями.
Возможно в энциклопедиях и справочниках для продвинутых математиков и полезно использовать полный формализм, чтобы учесть все нюансы, но не в общедоступных википедии и школьных учебниках.
Особенно часто встречаются резкие переходы типа «берем один апельсин и одно яблоко, как вы видите все несложно, теперь очевидно что из этого получается )@K$&%H@#JK$H#@$*@#%$HJ@#%(@#JK» выглядит как-то так.
Я тоже не утверждал, что кто-то утверждал) Просто ответил на комментарий выше.
По поводу школьников, я вообще не понимаю, зачем им нужен матан. Детей как раз важно просто заинтересовать какой-то специальностью. Даже в случае с техническими специальностями, на мой взгляд, для этой цели больше подходит обществознание, чем математика или физика. А уж как запускать ракеты посредством матана их научат уже в ВУЗах.
А Википедию вообще можно править самостоятельно, насколько я понимаю.
По поводу практических примеров, я тоже очень этого хотел на младших курсах. Но сейчас я понимаю, что если бы вместо абстрактных задачек мне на 2-м, 3-м курсе стали бы объяснять как рассчитать при помощи комплексных чисел гидравлический четвертьволновой газитель пульсаций, я бы точно психанул или ушёл в глубокую депрессию.
По поводу школьников, я вообще не понимаю, зачем им нужен матан. Детей как раз важно просто заинтересовать какой-то специальностью. Даже в случае с техническими специальностями, на мой взгляд, для этой цели больше подходит обществознание, чем математика или физика. А уж как запускать ракеты посредством матана их научат уже в ВУЗах.
А Википедию вообще можно править самостоятельно, насколько я понимаю.
По поводу практических примеров, я тоже очень этого хотел на младших курсах. Но сейчас я понимаю, что если бы вместо абстрактных задачек мне на 2-м, 3-м курсе стали бы объяснять как рассчитать при помощи комплексных чисел гидравлический четвертьволновой газитель пульсаций, я бы точно психанул или ушёл в глубокую депрессию.
Доверие, безусловно нужно, иначе вообще непонятно, зачем идти в универ. Но честно говоря, не очень понятно, какое это отношение имеет к проблеме качества университетского образования. Университетские программы составляются в расчёте на определённую специальность. Например, специальность прикладная математика будет подразумевать, сюрприз, много разной математики.
Не знаю, кого Вы подразумеваете под «программистом». Сейчас это понятие размылось настолько, что это может означать и как человека, разрабатывающего с нуля ОС реального времени для новой архитектуры, так и мальчика, меняющего катриджи в принтерах. Если смотреть в официальные документы, то есть специальность 09.02.03 «Программирование в компьютерных системах». Она относится к среднему профобразованию, по ней готовят 2 года в ПТУ (или, как они сейчас себя называют, в «коллЕджах»). Там, действительно, вряд ли нужно интегральное исчисление, но его там вряд ли и преподают.
С другой стороны, то, что в России компании от любого эникейщика ожидают чуть ли не кандидатской степени, относится к ещё одной проблеме, связанной с девальвацией высшего образования как такового. «Если уж у нас даже уборщица факультет машиностроения с красным дипломом закончила, то Вы, товарищ системный администратор, не можете у нас со своим среднеспециальным дипломом работать.»
Но всё это — совершенно другая тема, и к делу преподавания математики никак не относится.
Не знаю, кого Вы подразумеваете под «программистом». Сейчас это понятие размылось настолько, что это может означать и как человека, разрабатывающего с нуля ОС реального времени для новой архитектуры, так и мальчика, меняющего катриджи в принтерах. Если смотреть в официальные документы, то есть специальность 09.02.03 «Программирование в компьютерных системах». Она относится к среднему профобразованию, по ней готовят 2 года в ПТУ (или, как они сейчас себя называют, в «коллЕджах»). Там, действительно, вряд ли нужно интегральное исчисление, но его там вряд ли и преподают.
С другой стороны, то, что в России компании от любого эникейщика ожидают чуть ли не кандидатской степени, относится к ещё одной проблеме, связанной с девальвацией высшего образования как такового. «Если уж у нас даже уборщица факультет машиностроения с красным дипломом закончила, то Вы, товарищ системный администратор, не можете у нас со своим среднеспециальным дипломом работать.»
Но всё это — совершенно другая тема, и к делу преподавания математики никак не относится.
Получив профильное образование, вспоминая свои лекции на первых курсах, заметила, что у многих преподавателей как будто психологический барьер: категорически не хотят объяснять на пальцах. Как будто студенты подумают, что перед ними не очень продвинутый математик или это как-то ещё погубит их самооценку. Классический сценарий повествования на лекциях: сразу вводятся определения, появляющиеся из неоткуда, потом формулируется теорема с огромным количеством ограничений, а доказательство пишется исключительно языком формул, с минимумом рисунков и пояснений. И ни в коем случае нельзя упустить ни одну мелочь, даже если в прикладных задачах все замысловатые условия теоремы выполняются всегда. Обычно это дословно (точнее, доформульно или даже досимвольно) повторяет учебник. Но, пожалуй, больше всего мне не хватало примеров прикладных задач или хотя бы областей.
И только лектор по матанализу на первом курсе (что было очень к стати) сначала рассказывал доказательства очень неформально, «размахивая руками», как говорится. И когда уже основные шаги в общих чертах были понятны, формализовал всё сказанное, делая акцент на том, где какое ограничение из условий используется, можно ли без него обойтись и в каких случаях.
На лекциях по линейной алгебре и теорверу творился мрак: ни одного слова на доске, чистое повторение формул без дополнительных объяснений. Ну нельзя так читать первокурсникам! А потом на старших курсах часто звучала фраза «это должно быть вам известно из курса линейной алгебры», а ты сидишь и смутно вспоминаешь, что такие слова где-то слышал, но сути объекта не понимаешь. Пробелы пришлось самостоятельно восполнять, используя альтернативные ресурсы.
При этом я не уверена, что неформальным объяснениям место в учебниках. Конечно, там должны быть примеры, чем больше, тем лучше, но степень формальности должна оставаться высокой. Идеально было бы, если бы на лекциях рассказывали всё неформально и на пальцах, больше уделяя внимание вопросам «откуда это взялось, зачем нужно и где используется?». А за формальной записью того же самого уже нужно лезть в учебник, и после человеческих объяснений оно воспримется куда лучше. Но это тоже субъективное мнение, основанное на собственных ощущениях. Конечно, классические учебники не должны быть единственной литературой по предмету. Книжки «для чайников» пригодятся и тем же студентам, которые пропустили объяснения на лекциях, и желающим освоить предмет самостоятельно вне ВУЗа.
Дополнительные проблемы возникают, когда учебников несколько, и все авторы читают лекции по предмету по-своему. Отличия могут быть минимальны: один в определении пишет знак «больше», а другой — «больше или равно», или изложение идёт в разном порядке. Из-за этого разгорается методическая гражданская война. А потом на экзамене только попробуй сказать определение из учебника профессора Х, отвечая билет профессору У.
Сначала думала, что пост будет про нотацию математических выражений. Там хоть и есть свои сложности, без неё было бы гораздо хуже :)
И только лектор по матанализу на первом курсе (что было очень к стати) сначала рассказывал доказательства очень неформально, «размахивая руками», как говорится. И когда уже основные шаги в общих чертах были понятны, формализовал всё сказанное, делая акцент на том, где какое ограничение из условий используется, можно ли без него обойтись и в каких случаях.
На лекциях по линейной алгебре и теорверу творился мрак: ни одного слова на доске, чистое повторение формул без дополнительных объяснений. Ну нельзя так читать первокурсникам! А потом на старших курсах часто звучала фраза «это должно быть вам известно из курса линейной алгебры», а ты сидишь и смутно вспоминаешь, что такие слова где-то слышал, но сути объекта не понимаешь. Пробелы пришлось самостоятельно восполнять, используя альтернативные ресурсы.
При этом я не уверена, что неформальным объяснениям место в учебниках. Конечно, там должны быть примеры, чем больше, тем лучше, но степень формальности должна оставаться высокой. Идеально было бы, если бы на лекциях рассказывали всё неформально и на пальцах, больше уделяя внимание вопросам «откуда это взялось, зачем нужно и где используется?». А за формальной записью того же самого уже нужно лезть в учебник, и после человеческих объяснений оно воспримется куда лучше. Но это тоже субъективное мнение, основанное на собственных ощущениях. Конечно, классические учебники не должны быть единственной литературой по предмету. Книжки «для чайников» пригодятся и тем же студентам, которые пропустили объяснения на лекциях, и желающим освоить предмет самостоятельно вне ВУЗа.
Дополнительные проблемы возникают, когда учебников несколько, и все авторы читают лекции по предмету по-своему. Отличия могут быть минимальны: один в определении пишет знак «больше», а другой — «больше или равно», или изложение идёт в разном порядке. Из-за этого разгорается методическая гражданская война. А потом на экзамене только попробуй сказать определение из учебника профессора Х, отвечая билет профессору У.
Сначала думала, что пост будет про нотацию математических выражений. Там хоть и есть свои сложности, без неё было бы гораздо хуже :)
Перед математиками стоят такие же проблемы, как и перед программистами.
Три основных проблемы — и все сложные.
1. Разобраться в какой-либо области (вопросе, проблеме).
2. Зафиксировать понимание, описав эту область (вопрос, проблему) так, чтоб тебя поняли другие.
3. Реализовать область (вопрос, проблему) в виде набора инструментов (программ), чтобы можно было «руками пощупать».
Три основных проблемы — и все сложные.
1. Разобраться в какой-либо области (вопросе, проблеме).
2. Зафиксировать понимание, описав эту область (вопрос, проблему) так, чтоб тебя поняли другие.
3. Реализовать область (вопрос, проблему) в виде набора инструментов (программ), чтобы можно было «руками пощупать».
Встречался с таким заблуждением — сначала будем строить простую модель, потом будем дополнять её деталями и все больше приближаться к реальности. В реальности, так можно делать с линейными зависимостями. Когда есть нелинейные зависимости, то простое добавление деталей приводит к тому, что модель сильно уходит в сторону от реальности.
Когда моделировал поведение плазмы встречался с таким. Добавляешь в программу обработку еще одного физического эффекта и модель просто рушится и программа производит какую-то ерунду. Поэтому простые модели рулят, а добавление параметров и адаптация к реальности — это особое искусство.
Когда моделировал поведение плазмы встречался с таким. Добавляешь в программу обработку еще одного физического эффекта и модель просто рушится и программа производит какую-то ерунду. Поэтому простые модели рулят, а добавление параметров и адаптация к реальности — это особое искусство.
Спасибо за длину кривой. Это прекрасно!
UFO just landed and posted this here
Раз уж зашла речь о математике в массы — порекомендую всем серию лекций Алексея Савватеева — математика для гуманитариев. Человек на пальцах объясняет важные математические понятия, приводит конкретные примеры, и учит людей думать. Он преподает математику в школах, но не уверен, воспримут ли таких людей в обычной школе.
На первом занятии, например, на пальцах доказал, что невозможно собрать пятнашки, если поменять местами 14 и 15.
На первом занятии, например, на пальцах доказал, что невозможно собрать пятнашки, если поменять местами 14 и 15.
У Владимира Итенберга хорошие беседы о математике, для начинающих самое то.
Кстати, по этим лекциям Савватеев выпустил книгу. Так вот — она абсолютно нечитаемая! Если сравнивать книгу и сами лекции (видео) — это день и ночь в плане понятности. Это я к тому, что писать «учебники» действительно надо уметь, и это не зависит от умения объяснять…
Дубль
При подсчете на бумажке слишком много внимания\времени уходит непосредственно на вычисления. Даже если берутся малые числа вроде (13, 19).
Плюс, если кто-то считает на доске — часть внимания слушателей уходит на проверку арифметики. Если же аудитория считает раздельно: кто-то заканчивает сильно быстрее, а кто-то сильно медленнее, и разброс достаточно серьезен.
С другой стороны, при самообучении таких проблем не возникает, так ручной счет может быть актуальным.
Плюс, если кто-то считает на доске — часть внимания слушателей уходит на проверку арифметики. Если же аудитория считает раздельно: кто-то заканчивает сильно быстрее, а кто-то сильно медленнее, и разброс достаточно серьезен.
С другой стороны, при самообучении таких проблем не возникает, так ручной счет может быть актуальным.
Так, примеры «на бумажке» никак не помогают осознать RSA
Вот как раз наоборот. RSA идеален для обьяснения на пальцах, а замороченные поточные типа AES — нет, хотя в AES идеи более интуитивное и менее "математичные"
Мне эта статья напомнила картинку с какими то американскими тестами где всё предельно практично: на счету 100 денег, процент в банке такой то, сколько будет через 5 лет. Вообще если вам нужны такие кондовые примеры для понимания картины и если определение предела вызывает у вас трудности, то математика не для вас и в этом нет ничего плохого: кто то не видит смысла общаться с людьми, а кого то от этого прёт. Как только вступление с определением предела пройдёт и начнётся настоящая математика с псевдогильбертовыми бесконечномерными компактными подмножествами конечномерных многообразий, примеры из реальной жизни не помогут. математикой занимаются как мне кажется ради достижения такого состояния «ощущения полноты картины» — кто то курит косят ради особых ощущений, монах медитирует свою медитацию для такого ощущения, а математик дотошно разбирается в особо абстрактной и такой же бесполезной теореме и тащится от ощущения понимания всей картины. Проблема математики вовсе не в том, что её мало кто может осилить, а в том язык математики застрял в эпохе античности: одни почтенные старцы пишут доказательство теоремы руками на пергаменте, а другие не менее почтенные старцы потом это 10 лет проверяют.
UFO just landed and posted this here
Вот этот пример с баром, Анжелиной Джоли и девушками очень жизненный и понятный, да. Вообще математики это такие люди, которые известны своей способностью зажигать в барах и отрываться на вечеринках а также клеить моделей. Да что там математикам, вообще большинству молодёжи это близко и знакомо.
В отличие от примеров, допустим, с компьютерными играми, где у танка есть какая-то вероятность пробить броню другого танка, зависящая от многих параметров. Ну, или в Старкрафте где так-то тоже есть что поанализировать или там ещё огромная куча MMO, где надо уметь собрать экипировнку и команду. Это всё, конечно, не очень примеры, они молодёжи не близки.
Да что там ВУЗ! Вы давно открывали школьный учебник? Вспоминаю, как у сестры началось деление. Так там сразу с порога что-то вроде: «частное это результат деления делимого на делитель». И всё. Только цитата была посложнее, на уровне очень правильной формальной математики учитывающей деление на 0. И разбирайся дальше как хочешь, решай задачи. Честно говоря я сам сразу с порога не понял, и был просто в шоке, что так сложно объясняется деление…
Вместо того, чтобы просто написать что-то вроде этого:
Вместо того, чтобы просто написать что-то вроде этого:
Сколько раз 3 содержится в 14?
Повторяя операцию вычитания 3 из 14, мы находим, что 3 содержится в 14 четыре раза, и ещё «остаётся» число 2.
Полагаю, что в соответствии с научным подходом автору было бы не плохо ознакомиться с предшественниками, которые критиковали современные подходы к преподаванию математики. Начать можно с www.google.ru/search?newwindow=1&ei=u1DlW-zwB8SOmgXq-YuADA&q=%D0%B0%D1%80%D0%BD%D0%BE%D0%BB%D1%8C%D0%B4+%D0%BE+%D0%BF%D1%80%D0%B5%D0%BF%D0%BE%D0%B4%D0%B0%D0%B2%D0%B0%D0%BD%D0%B8%D0%B8+%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B8&oq=%D0%B0%D1%80%D0%BD%D0%BE%D0%BB%D1%8C%D0%B4+%D0%BF%D1%80%D0%B5%D0%BF%D0%BE%D0%B4%D0%B0%D0%B2%D0%B0&gs_l=psy-ab.3.0.0i22i30k1.48957.53779.0.55124.17.16.0.1.1.0.70.973.16.16.0....0...1c.1.64.psy-ab..0.17.976...0j0i131k1j0i67k1j0i10i67k1.0.MOcRmurZlw4
В свое время я офигел от учебника 50-х годов по уравнениям в частных производных, который читался почти как художественная литература. Там было ВСЕ понятно. На фоне всех остальных учебников он смотрелся дико:).
В свое время я офигел от учебника 50-х годов по уравнениям в частных производных, который читался почти как художественная литература. Там было ВСЕ понятно. На фоне всех остальных учебников он смотрелся дико:).
Если я не указал список литературы, это еще не значит, что я не читал Арнольда. Предлагаю обмен: я вам ссылку на Фейнмана (читайте про образование в Бразилии, поиск по "Что касается образования в Бразилии, то у меня был очень интересный опыт."), в вы ссылку на УрЧаПы. Тогда у нас будет по две ссылки.
В сети не могу найти. По моим воспоминаниям (25+ лет уже прошло) это была книжка Петровский И.Г. «Уравнения в частных производных» (возможно дифференциальные). Точно помню, что за нее дана Сталинская премия, о чем было в ней упоминание. Умопомрачительная полиграфия. За 40 лет, сколько было на момент моего знакомства с этой книжкой, она практически не истрепалась.
Я про математику могу сказать одно — 1Blue3Brown.
www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw
Более зажигающего видео про линейную алгебру (и матанализ) я не видел.
www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw
Более зажигающего видео про линейную алгебру (и матанализ) я не видел.
Могла бы плюсануть, обязательно бы это сделала! Только они «3Blue1Brown», но не суть. По линейной алгебре из видео поняла больше, чем после годового курса в университете. Тоже кидала этот канал в комменты к недавнему посту с советами первокурсникам. ИМХО, вот примерно так и нужно рассказывать на лекциях.
Добавлю Welch Labs.
youtu.be/T647CGsuOVU?list=PLiaHhY2iBX9g6KIvZ_703G3KJXapKkNaF
За весь ТФКП нам не рассказывали, что график f(x) = x^2 + 1 можно нарисовать так (заодно и видно, что i это корень уравнения x^2 + 1).
youtu.be/T647CGsuOVU?list=PLiaHhY2iBX9g6KIvZ_703G3KJXapKkNaF
За весь ТФКП нам не рассказывали, что график f(x) = x^2 + 1 можно нарисовать так (заодно и видно, что i это корень уравнения x^2 + 1).
Мне не видно. Где это видно? Почему график объемный? Что означает цветовое кодирование? Что у нас по оси z вообще? Почему все перевернуто? Помогите, я хочу проникнуться прекрасностью этого примера.
заодно и видно, что i это корень уравнения x^2 + 1
вся шутка в том, что на самом деле на картинке этого НЕ видно, т.к. пересечение поверхности с плоскостью даёт кривую , содержащую бесконечно много точек вида . чтобы найти на этой кривой точки, которые будут соответствовать решению исходного уравнения, надо дополнительно учитывать условие , получаемое из равенства для мнимой части
А вас не смущает, что в ТФКП это должен быть график в 4 мерном пространстве?
П.С. В видео встречается квадратный корень из минус единицы, это сразу неуд.
П.С. В видео встречается квадратный корень из минус единицы, это сразу неуд.
П.С. В видео встречается квадратный корень из минус единицы, это сразу неуд.
Это же чисто вопрос записи, не влияющий никак на выкладки. Чего сразу неуд?
Начните читать ТФКП. Узнайте откуда берётся мнимая единица. Почему она в квадрате равна -1. Узнайте почему можно писать a+bi и что это означает. У вас сразу отпадут вопросы типа «Это же чисто вопрос записи, не влияющий никак на выкладки.»
Это не вопрос записи, это определение «свой-чужой». Если вы пишете что мнимая единица это квадратный корень из -1, это сразу показывает, что вы ни чего не знаете про ТФКП, а понахватались всякого где не попади.
Это не вопрос записи, это определение «свой-чужой». Если вы пишете что мнимая единица это квадратный корень из -1, это сразу показывает, что вы ни чего не знаете про ТФКП, а понахватались всякого где не попади.
Начните читать ТФКП.
Спасибо, читал. Как человек, изучавший ТФКП, уверенно вам заявляю — нет никаких проблем с обозначением i как sqrt(-1). Если кто-то вам сказал иное — вас обманули, Не верьте на слово, изучайте сами.
Это не вопрос записи, это определение «свой-чужой». Если вы пишете что мнимая единица это квадратный корень из -1
То есть, по-вашему, мнимая единица не является квадратным корнем из -1? Интересное мнение.
Давайте по порядку:
- что такое квадратный корень из -1?
- что такое мнимая единица?
Видимо у нас с вами было разное ТФКП.
Ответы на ваши вопросы можно найти в википедии, или других математических ресурсах.
1. ru.wikipedia.org/wiki/Квадратный_корень
2. ru.wikipedia.org/wiki/Мнимая_единица
В общем-то, по ссылке на мнимую единицу, даже есть параграф, про запись мнимой единицы через квадратный корень из -1, и к чему это приводит.
Ответы на ваши вопросы можно найти в википедии, или других математических ресурсах.
1. ru.wikipedia.org/wiki/Квадратный_корень
2. ru.wikipedia.org/wiki/Мнимая_единица
В общем-то, по ссылке на мнимую единицу, даже есть параграф, про запись мнимой единицы через квадратный корень из -1, и к чему это приводит.
В общем-то, по ссылке на мнимую единицу, даже есть параграф, про запись мнимой единицы через квадратный корень из -1, и к чему это приводит.
Ни к чему это не приводит, если внимательно прочитать.
Ответы на ваши вопросы можно найти в википедии, или других математических ресурсах.
Отлично!
Давайте посмотрим на ваши определения:
Мнимая единица — это число, квадрат которого равен −1. Т.е. i — это одно из решений уравнения x^2+1=0 или x^2=-1.
Квадратный корень из числа a — это число x, дающее a при возведении в квадрат. Равносильное определение: квадратный корень из числа a — это решение уравнения x^2=a.
Итак, я беру второе определение квадратного корня (решение уравнения x^2=a) и подставляю туда -1, в результате получаю "решение уравнения x^2=-1", но это как раз определение мнимой единицы.
Как же так?
и к чему это приводит
это приводит к возможности ошибиться в расчетах, если по привычке обращать с комплексными корнями как с вещественными
в остальном же, вопрос о или — чисто вопрос соглашения, на самом деле не важный для теории. это как с чего начинать нумерацию массива с 0 или 1
Видимо у нас с вами было разное ТФКП.
видимо вам препод попался, который заморачивался на вопрос знания каких-то внутренних догм, не имеющих отношения к математике, а служащих именно для выделения «свой-чужой» и проверки посещаемости лекций. есть такие, к сожалению. ещё излюбленный приём у них это спрашивать какой характер разрыва у гиперболы при
Когда вы пишете i=sqrt(-1), вы подразумеваете что из определения i^2=-1, вы делаете переход к i=sqrt(-1), но почему-то не объясняете правомерность этого перехода.
Можно ввести вместо определения i^2=-1 другое определение. Например пусть i=sqrt(-1), но тогда не понятно причем тут ТФКП и причем тут запись a+bi и как она связана со всем остальным.
Можно ввести вместо определения i^2=-1 другое определение. Например пусть i=sqrt(-1), но тогда не понятно причем тут ТФКП и причем тут запись a+bi и как она связана со всем остальным.
но тогда не понятно причем тут ТФКП и причем тут запись a+bi и как она связана со всем остальным.
Можете спокойно везде вместо a+bi писать a+b*sqrt(-1), ничего не изменится кроме более громоздкой записи. Я вам больше скажу — до того, как явно ввели i, именно так и писали.
Не могли бы вы дать ссылку на научную работу в которой бы было написано так громоздко?
вот по-быстрому даже книжечку нашёл вам: Г. Эдвардс, «Последняя теорема Ферма», M.: Мир, 1980 (перевод с английского)
html-версия ega-math.narod.ru/Books/Edwards.htm, там же можете скачать скан
автор воспроизводит аргументы Эйлера, там испольуются числа вида
html-версия ega-math.narod.ru/Books/Edwards.htm, там же можете скачать скан
автор воспроизводит аргументы Эйлера, там испольуются числа вида
так никто и не говорит, что теорию надо начинать строить с соотношения , пусть так оно и было исторически
но когда мы построили теорию, и ввели там корни, то внезапно оказывается, что , откуда можно приписать любой — и ничего от этого не изменится, всегда будет , а больше и не надо!
обычно разграничивают с по нескольким причинам:
1) аксиомы требуют только — это надо помнить
2) так просто короче писать :)
3) можно заиграться и начать применять свойства радикалов из положительных чисел, которые в ТФКП уже несправедливы, типичная ошибка начинающих типа:
но когда мы построили теорию, и ввели там корни, то внезапно оказывается, что , откуда можно приписать любой — и ничего от этого не изменится, всегда будет , а больше и не надо!
обычно разграничивают с по нескольким причинам:
1) аксиомы требуют только — это надо помнить
2) так просто короче писать :)
3) можно заиграться и начать применять свойства радикалов из положительных чисел, которые в ТФКП уже несправедливы, типичная ошибка начинающих типа:
Ни разу не встречал такой аксиоматике. Везде дают по определению без объяснения что происходит, или таки объясняют почему и что, а аксиоматика совсем другая.
Хотелось бы посмотреть на книги в которых исторически описано i=sqrt(-1), а то ещё не одной не видел. Не дадите ссылку на такой раритет?
Хотелось бы посмотреть на книги в которых исторически описано i=sqrt(-1), а то ещё не одной не видел. Не дадите ссылку на такой раритет?
Ни разу не встречал такой аксиоматике
аксиоматика везде одинаковая и начинается с «комплексными числами называются пары действительных чисел, для которых сложение и умножение определены как...». и всё вышенаписанное из этого следует. аксиомы ничего не говорят о знаке при корне из -1, т.к. это было бы избыточно и не нужно. можно срезюмировать:
1) говорить что не является — неверно (таки будет являться, одним из двух)
2) говорить что определяется как — тоже неверно, формально определение иное
3) тем не менее, по ходу дела действительно оказывается, что можно написать и ни на что это не повлияет. и тем более так можно и нужно делать в научно-популярных видео для облегчения понимания
Не дадите ссылку на такой раритет?
это вам надо искать работы времен Эйлера где-нибудь в крутых библиотеках или их оцифровки, для исторического интереса
без объяснения что происходит
ну например в той же википедии вам объяснили:
«−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «-i» и «-i» на «i».
Странный спор.
По всей видимости вы знаете что к i^2=-1 можно прийти двумя способами.
1. Дать определение i^2=-1 без объяснения почему и как.
2. Ввести аксиоматику над парой вещественных чисел и вывести что (0,1)*(0,1)=(-1,0), после чего показать что (a,0), это полностью соответствует a, и дать обозначение для пары (0,1), в итоге получить i^2=-1.
Ни в одном из этих случаев нельзя сделать правомерный переход от i^2=-1 к i=sqrt(-1). Но это вам не мешает спорить об этом.
Странно.
По всей видимости вы знаете что к i^2=-1 можно прийти двумя способами.
1. Дать определение i^2=-1 без объяснения почему и как.
2. Ввести аксиоматику над парой вещественных чисел и вывести что (0,1)*(0,1)=(-1,0), после чего показать что (a,0), это полностью соответствует a, и дать обозначение для пары (0,1), в итоге получить i^2=-1.
Ни в одном из этих случаев нельзя сделать правомерный переход от i^2=-1 к i=sqrt(-1). Но это вам не мешает спорить об этом.
Странно.
Ни в одном из этих случаев нельзя сделать правомерный переход от i^2=-1 к i=sqrt(-1). Но это вам не мешает спорить об этом.
в обоих случаях вводятся корни и показывается, что . вы просто не хотите читать, что вам пишут и игнорируете ту же википедию, ссылки на которую помпезно раздавали в начале спора, как на «опровержение»
В том то и проблема что нет. Когда комплексное число представляется в виде a+bi четко оговаривается, что a и b это вещественные числа, а в области вещественных чисел нельзя брать квадратный корень из отрицательного числа. Операция sqrt(-1) неопределенна ни в вещественной, не в комплексной области.
Когда вы пытаетесь взять квадратный корень из минус единицы по формуле Муавра, то изначально делаете недопустимое действие. Нельзя слева писать sqrt(-1).
Приведённый вами пример обычно получается из решения уравнения x^2+1=0. Почему-то выбрасывают начало уравнения и пишут то что пишете вы, но это в корне не верно, потому что плюс-минус i, это решение квадратного уравнения, а не корень из минус единицы.
И да, во всех моих ссылках на википедию написано "не надо писать sqrt(-1)=i, это плохая идея, будет много проблем", но почему-то вы это активно игнорируете.
Операция sqrt(-1) неопределенна ни в вещественной, не в комплексной области.
вы издеваетесь?
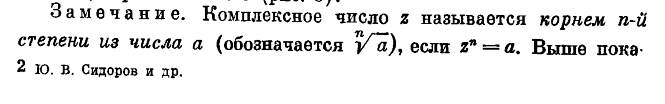
И да, во всех моих ссылках на википедию написано «не надо писать sqrt(-1)=i, это плохая идея, будет много проблем», но почему-то вы это активно игнорируете.
там написано, дословно:
Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i {\displaystyle i} i через радикал
какие могут быть ошибочные выкладки — я уже написал, когда для свойств комплексных корней неявно предполагается справедливость свойств вещественных
что a и b это вещественные числа, а в области вещественных чисел нельзя брать квадратный корень из отрицательного числа. Операция sqrt(-1) неопределенна ни в вещественной, не в комплексной области.
Я верно понимаю, что если написать i = sqrt(-1 + 0*i) — это вас устроит? Ведь в данном случае мы извлекаем корень в явном виде из комплексного числа, так?
потому что плюс-минус i, это решение квадратного уравнения, а не корень из минус единицы.
А корень из минус единицы — это решение соответствующего уравнения по определению корня.
Вы почему-то упорно игнорируете этот факт.
Напишите +-i = sqrt(0 + 1*i^2) и это меня устроит. Тут не будет извлечения корня из отрицательного вещественного числа.
В общем я понял что спор бессмысленный. Вы хотите видеть магию извлечения корня из отрицательного вещественного числа с переходом в комплексную плоскость. С моей точки зрения тут нет ни какой магии и переход из одной области в другую осуществляется строго по необходимости. Нет смысла искать решение квадратного уравнения с отрицательным дискриминант, как это любят делать в школе, если на этом всё решение квадратного уравнения заканчивается. И наоборот, имеет смысл выйти в комплексную плоскость если это лишь небольшая часть большой задачи, возможно в итоге получится вещественный ответ.
В общем я понял что спор бессмысленный. Вы хотите видеть магию извлечения корня из отрицательного вещественного числа с переходом в комплексную плоскость. С моей точки зрения тут нет ни какой магии и переход из одной области в другую осуществляется строго по необходимости. Нет смысла искать решение квадратного уравнения с отрицательным дискриминант, как это любят делать в школе, если на этом всё решение квадратного уравнения заканчивается. И наоборот, имеет смысл выйти в комплексную плоскость если это лишь небольшая часть большой задачи, возможно в итоге получится вещественный ответ.
Напишите +-i = sqrt(0 + 1*i^2) и это меня устроит.
Да подождите, вы сказали что из -1 в вещественных числах корень не извлекается, я предложил извлекать из комплексного. Из комплексного тоже не извлекается? Он что, вообще не извлекается, или как?
Чем формально i = sqrt(-1) отличается от 2 = sqrt(4)? Точно так же же можно заявить, что надо писать +-2 = sqrt(4), а остальное от лукавого, нет?
И наоборот, имеет смысл выйти в комплексную плоскость если это лишь небольшая часть большой задачи, возможно в итоге получится вещественный ответ.
Далеко не только, ответ может получиться и комплексный, и при этом это будет иметь физический смысл, как в задачах обтекания крыла или электродинамике.
ТФКП — это вообще не алгебра, это матан для комплексных чисел, у которого есть свое содержание из-за условия Коши-Римана.
Напишите +-i = sqrt(0 + 1*i^2) и это меня устроит. Тут не будет извлечения корня из отрицательного вещественного числа.
мда…
особенно забавно сравнить с более ранним замечанием:
вы ни чего не знаете про ТФКП, а понахватались всякого где не попади
И да, во всех моих ссылках на википедию написано "не надо писать sqrt(-1)=i
Там написано, что надо делать это с осторожностью. Точно с такой же осторожностью, с которой надо производить операцию деления — учитывать возможность нуля.
Сама по себе такая запись математически корректна, вы не сможете получить из нее противоречие.
Операция sqrt(-1) неопределенна ни в вещественной, не в комплексной области.
Простите?..
Вы говорите, что корни из комплексных чисел брать нельзя?
Вернее, давайте для начала вернёмся к правильным терминам. «sqrt(-1)» это не операция, а число. Операция это «sqrt». Так вы утверждаете, что операция «sqrt» не определена для пары действительных чисел (-1, 0), называющейся комплексным числом и коротко записываемой как -1?
Ни в одном из этих случаев нельзя сделать правомерный переход от i^2=-1 к i=sqrt(-1).
Вы уже объяснили, как так выходит, что определения sqrt(-1) и i совпадают?
Примеры хорошие, но по сути это приводится именно рафинированный прикладной подход, а не фундаментальный. Не скажу, что такая система плоха, но она просто иная — ей мы готовим инженера, но не готовим ученого, даже выжигаем зачатки склонности. Это аналог тестовых ЕГЭ по литературе — проверить, что человек читал материал, это поможет, но не покажет, анализировал ли он его. В идеале конечно хорошо бы знать возможности ребенка и при отсутствии склонности к умозрительному подходу обучать чисто эмпирически, но это только мечта. Поэтому в советской школе давали всем фундаментальных вариант (насколько хороша давали — это уже другой вопрос), а далее или переобучали на прикладника или уже развитие продолжалось в университете. В западной же системе почти всем дают прикладную бузу, а элиту сразу учат по фундаментальной методике.
Кстати, слова Евклида можно трактовать по-разному. Александрийская школа объединяла вавилонскую (после аккадского завоевания) и египетскую систему счета, поэтому совмещала полупозиционное счисление в совокупности с рядами. В итоге часть расчетов велось пропорциями (фактическая тригонометрия), а часть — взаимными переводами между рядами и системой вавилонских дробей (дробь первого порядка со знаменателем 60, второго — со знаменателем 602).
Для текста, формул и чисел использовались одни и те же буквы (тогда еще 29 было символов — первыми 9 буквами алфавита греки обозначали первые девять чисел; вторые девять букв обозначали первые девяти целым кратным числа десять; и последние девять символов — первым девяти целым кратным числа 100. Для обозначения первых девяти целых кратных числа 1000 те же первые 9 букв снабжались штрихами слева).
Так что говоря о царской дороге он все де подразумевал систему обозначений чисел, отличную от букв, но не связанную с аттической фигурной записью, без этого действительно в научных текстах разобраться было довольно сложно
Кстати, слова Евклида можно трактовать по-разному. Александрийская школа объединяла вавилонскую (после аккадского завоевания) и египетскую систему счета, поэтому совмещала полупозиционное счисление в совокупности с рядами. В итоге часть расчетов велось пропорциями (фактическая тригонометрия), а часть — взаимными переводами между рядами и системой вавилонских дробей (дробь первого порядка со знаменателем 60, второго — со знаменателем 602).
Для текста, формул и чисел использовались одни и те же буквы (тогда еще 29 было символов — первыми 9 буквами алфавита греки обозначали первые девять чисел; вторые девять букв обозначали первые девяти целым кратным числа десять; и последние девять символов — первым девяти целым кратным числа 100. Для обозначения первых девяти целых кратных числа 1000 те же первые 9 букв снабжались штрихами слева).
Так что говоря о царской дороге он все де подразумевал систему обозначений чисел, отличную от букв, но не связанную с аттической фигурной записью, без этого действительно в научных текстах разобраться было довольно сложно
А насколько передовая теоретическая математика сейчас оторвана хоть от каких-то прикладных областей?
Я к тому, что даже самые передовые вещи же наверное доказывают не «потому что мы смогли», а еще и потому что это как-то можно будет использовать в вычислениях чего-то прикладного?
Я к тому, что даже самые передовые вещи же наверное доказывают не «потому что мы смогли», а еще и потому что это как-то можно будет использовать в вычислениях чего-то прикладного?
по правде говоря — когда как.
Кеплер ведь изначально строил модель солнечной системы по принципу вложения правильных многоугольников. Теория не подтвердилась, но сейчас об этом мало кто помнит. Однако тот же Субботин реинкарнировал эту теорию немного с другой стороны, приняв, что система является соединением 2 систем — классической (от Юпитера) и аномальной (до Земли). И теория видимо достаточно близка к истине. Хотя есть и неприятный момент — приход в равновесие (согласование) этих систем станет концом нашей солнечной системы.
За базу взята реальная модель, но абсолютно оторванная от практической применимости- тут скорее спортивный интерес )
Кеплер ведь изначально строил модель солнечной системы по принципу вложения правильных многоугольников. Теория не подтвердилась, но сейчас об этом мало кто помнит. Однако тот же Субботин реинкарнировал эту теорию немного с другой стороны, приняв, что система является соединением 2 систем — классической (от Юпитера) и аномальной (до Земли). И теория видимо достаточно близка к истине. Хотя есть и неприятный момент — приход в равновесие (согласование) этих систем станет концом нашей солнечной системы.
За базу взята реальная модель, но абсолютно оторванная от практической применимости- тут скорее спортивный интерес )
Я к тому, что даже самые передовые вещи же наверное доказывают не «потому что мы смогли», а еще и потому что это как-то можно будет использовать в вычислениях чего-то прикладного?
Именно "потому что мы смогли", математикой ведь занимаются по фану, а не ради какой-то пользы. Естественно, есть исключения.
«Я просто читал теорему, выделял главное, писал/решал тривиальные примеры, потом разбирался с формализмом — и реально понимал, о чем идет речь. » -кстати да, сам так делал.
А учебники действительно так себе. Ради 1% случае, запудривают объяснение так, чтобы никому не было понятно. Зато да, математические выверено.
А учебники действительно так себе. Ради 1% случае, запудривают объяснение так, чтобы никому не было понятно. Зато да, математические выверено.
кстати да, сам так делалОткрою вам «страшную» тайну: все так делают. Потому что так и задумывалось :)
А учебники действительно так себе.То, что вам попадались не лучшие (для вас) учебники, говорит скорее о неудачном выборе литературы (а её много разной, не стоит останавливаться на одном учебнике даже самого популярного автора).
Математическая нотация создана с целью достижения максимально однозначной «читаемости», а не для того, чтобы её можно было как художественную литературу или музыку читать и понимать «с листа».
У меня схожие проблемы были с русским языком в школе.
Тебе просто говорят «жи/ши пиши через и» и всё. Просто набор догм.
А потом я почитал, например, «Слово о словах» и узнал, что у всех правил есть история и какие-то причины и стало как-то гораздо интереснее.
Сейчас сам немного преподаю и всегда при подготовке материала готовлюсь ответить на вопросы вида «а нафига это вообще?» и, что немаловажно, регулярно этот вопрос задают. И вижу у студентов интерес к предмету, что чертовски приятно.
Тебе просто говорят «жи/ши пиши через и» и всё. Просто набор догм.
А потом я почитал, например, «Слово о словах» и узнал, что у всех правил есть история и какие-то причины и стало как-то гораздо интереснее.
Сейчас сам немного преподаю и всегда при подготовке материала готовлюсь ответить на вопросы вида «а нафига это вообще?» и, что немаловажно, регулярно этот вопрос задают. И вижу у студентов интерес к предмету, что чертовски приятно.
Как можно улучшить подачу материала в математических текстах
В текущих (российских) реалиях — никак. Энтузиасты есть, профессионалы есть, мотивации нет.
Надо просто поднимать время от времени хайп по поводу того, что математик — уважаемый человек, аналогично и к учёному. Когда учёные поймут, что их могут полюбить массы за то, что те доступным языком описали какие-то сложные вещи, или даже выложили такое описание на ютуб, мотивация сразу появится, я гарантирую.
Но пока у нас прививается только любовь к западным учёным, к западным космическим агенствам, а любые отечественные начинания несправедливо охаяны и высмеяны с ног до головы, мало какому учёному или профессору захочется после этого ради этих людей что-то нормальное писать. И поделом. Так что сам факт этой статьи — это уже хайп в правильном направлении, надо просто немного оптимизма и уважения добавить.
Помните школу? А формулу дискриминанта? А как она доказывается/выводится?Дискриминант в школах Германии не в ходу. Школьники знают «pq-формулу», которая подходит для решения приведённых квадратных уравнений. Выводится при помощи дополнения квадрата, формул сокращённого умножения и эквивалентных преобразований.
…
«abc-формула» (та самая, с дискриминантом) выводится аналогично. Если не ошибаюсь, популярна в Австрии ну и в СНГ. Было бы любопытно узнать, чем пользуются «соседи».
Я вот еще один аспект затрону — слабая техническая составляющая современных учебников. Большинство электронных учебников 21-го века ничем не отличаются от таковых 17-го века. Почему я не могу кликнуть по абсолютно каждому слову во фразе или по буковке в формуле и хотя бы перейти по гиперссылке или увидеть попап с кратким пояснением того? Особенно для тех разделов математики, где у нас вводится очень много определений, понятий и дополнительных буковок.
В итоге читаешь-читаешь книжку — и внезапно появляется перевернутый треугольничек, с двумя индексом — и ты начинаешь листать и листать книжку назад, находишь, где автор ввел треугольничек, через пять страниц — где он записал эти индексы. А проблема простая, на написание электрических учебников у нас распиливается невероятное количество денег, мааленькую порцию которых можно было бы выделить на то, чтобы скажем html-изировать Фихтенгольца.
В итоге читаешь-читаешь книжку — и внезапно появляется перевернутый треугольничек, с двумя индексом — и ты начинаешь листать и листать книжку назад, находишь, где автор ввел треугольничек, через пять страниц — где он записал эти индексы. А проблема простая, на написание электрических учебников у нас распиливается невероятное количество денег, мааленькую порцию которых можно было бы выделить на то, чтобы скажем html-изировать Фихтенгольца.
Это вообще совсем отдельная история. И в США и в России и, похоже, во всём мире выпуск учебников — это очень доходный бизнес. Которому не нужны хорошие учебники. Ему нужны новые учебники!
Помните у Фейнмана?
Помните у Фейнмана?
Очередь дошла до книги, которая была частью трехтомного сборника, выпускаемого одним издательством, и меня спросили, что я о ней думаю.Это, правда, по подходам в США — но я сильно что-то сомневаюсь, что в России ситуация сильно лучше.
Я сказал: «Эту книгу мне не прислали со склада, но две другие были хорошие».
Кто-то попытался повторить вопрос «Что Вы думаете об этой книге?». — Я уже сказал, что мне ее не прислали. Так что я не могу о ней судить. Работник книжного склада был здесь же и сказал: «Извините, я могу все объяснить. Я не прислал Вам эту книгу, так как она не была еще закончена. По правилам мы должны иметь каждую книгу к определенному сроку, а издатель задержался с ней на несколько дней. Поэтому нам прислали макет книги с обложкой и пустыми страницами внутри. Компания приносит свои извинения и надеется, что трехтомник будет обсужден, несмотря на задержку третьего тома».
Оказалось, что этот пустой макет был оценен некоторыми членами комиссии! Они не могли поверить, что книги не было, ведь оценки-то были. Более того, оценки у несуществующей книжки были выше, чем у двух других. То обстоятельство, что книги не было, ничуть не помешало ее оценке.
«Я могу научить дифференцировать любого. Дайте только розгу. Дайте розгу, и вот этот… нет, лучше — этот, будет дифференцировать. Дайте только розгу. И свяжите ему руки. А потом руки развяжут, и он будет дифференцировать.»
© И.А.Борачинский, МФТИ
Очень крутая статья.
Вспомнился мой матан первого курса. Предел по эпсилон-дельта. Никто не понимал, все просто зубрили, и всё. Я сам несколько дней (то ли в ноябре, то ли уже в декабре) ходил и думал, и в какой-то миг внезапное озарение: а давай считать эпсилон каким-то очень маленьким числом! Тогда всё неожиданно встаёт на свои места.
Потом уже узнал, что похожим подходом (с очень маленькими числами) руководствовались Ньютон и Лейбниц, изобретая анализ, а потом пришёл Коши, наприводил контрпримеров и усложнил, чтоб всё формально и логично.
Потом уже не так сложно: определение производной (как delta_y / delta_x, delta_x -> 0) быстро понялось само, интеграл Римана интуитивно понятен из гифки в Википедии (благо, аппроксимировать площади я умел ещё в 8 классе как минимум), а через какое-то время ещё и узнал, что ∫ это просто запись для lim sum(...), а dx для delta_x внутри суммы.
Пример из статьи с интегралом по контуру я узнал во втором семестре на вариационном исчислении. Очень крутой препод, очень классно рассказывал, походя проливая свет и на другие предметы. Даже жаль, что не хватало знаний, чтобы понимать, о чём он говорит, полностью, хотя логику рассуждений вроде бы прослеживали. Но звучало всё равно как магия. Горестно взмахивал руками, узнавая, что мы не умеем в дифуры и ТФКП, и зачем нам вообще вариационное исчисление и функан на 1 курсе.
Он же и сказал, что dx это просто очень маленький кусочек x, и по теореме Пифагора получается интеграл по контуру. Тогда не полностью это получилось понять и осознать, и только физика в следующем семестре, где подход типа «порежем тело на маленькие кусочки dx» является совершенно обычным, наконец сделала нас хоть что-то понимать.
Вспомнился мой матан первого курса. Предел по эпсилон-дельта. Никто не понимал, все просто зубрили, и всё. Я сам несколько дней (то ли в ноябре, то ли уже в декабре) ходил и думал, и в какой-то миг внезапное озарение: а давай считать эпсилон каким-то очень маленьким числом! Тогда всё неожиданно встаёт на свои места.
Потом уже узнал, что похожим подходом (с очень маленькими числами) руководствовались Ньютон и Лейбниц, изобретая анализ, а потом пришёл Коши, наприводил контрпримеров и усложнил, чтоб всё формально и логично.
Потом уже не так сложно: определение производной (как delta_y / delta_x, delta_x -> 0) быстро понялось само, интеграл Римана интуитивно понятен из гифки в Википедии (благо, аппроксимировать площади я умел ещё в 8 классе как минимум), а через какое-то время ещё и узнал, что ∫ это просто запись для lim sum(...), а dx для delta_x внутри суммы.
Пример из статьи с интегралом по контуру я узнал во втором семестре на вариационном исчислении. Очень крутой препод, очень классно рассказывал, походя проливая свет и на другие предметы. Даже жаль, что не хватало знаний, чтобы понимать, о чём он говорит, полностью, хотя логику рассуждений вроде бы прослеживали. Но звучало всё равно как магия. Горестно взмахивал руками, узнавая, что мы не умеем в дифуры и ТФКП, и зачем нам вообще вариационное исчисление и функан на 1 курсе.
Он же и сказал, что dx это просто очень маленький кусочек x, и по теореме Пифагора получается интеграл по контуру. Тогда не полностью это получилось понять и осознать, и только физика в следующем семестре, где подход типа «порежем тело на маленькие кусочки dx» является совершенно обычным, наконец сделала нас хоть что-то понимать.
а давай считать эпсилон каким-то очень маленьким числом
Эээ… А разве теорема Коши не звучит как "… для сколь угодно малого эпсилон ..."?
В суть теоремы я тоже тяжело врубался, и врубился только после экзамена (каким чудом я его сдал?..)
Нет. Она звучит как «для любого эпсилон», слова вроде «сколь угодно малого» это именно пояснение, более того, формальными знаками их не запишешь. Только «для любого».
так поэтому теоремы и даются в виде текста, а не записываются одними значками, пусть запись и означает что может быть и сколько угодно малым, и сколько угодно большим, подробно расписать это в тексте не повредит:
плюс потом про малость эпсилон в тексте ещё несколько раз размусоливается и повторяется на нескольких примерах, дабы было совсем понятно
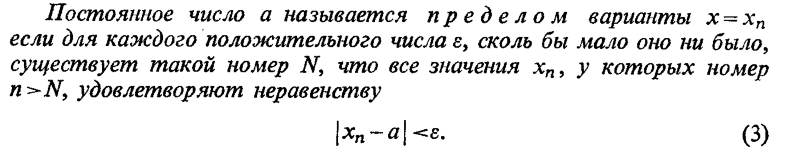
плюс потом про малость эпсилон в тексте ещё несколько раз размусоливается и повторяется на нескольких примерах, дабы было совсем понятно
Разве эпсилон не принят обозначением «чего то очень маленького»? Нам так вводили, и потому запись одними значками всегда сразу воспринималась как полностью аналогичная данному тексту.
Разве эпсилон не принят обозначением «чего то очень маленького»?
Конечно, принят, просто кое-кто спит на лекциях, а потом вместо внимательного чтения учебника его наискось просматривает. И потом рассказывает, как все непонятно в этой вашей матеше.
Я спал, все мои одногруппники спали, автор статьи спал, половина комментаторов здесь спала. Вы не спали, вы молодец!
Или же всё-таки у нас с вами разный опыт, мы были на разных лекциях, которые читали нам разные люди.
Впервые слышу, что эпсилон принят обозначением чего-то маленького. Встречал его в такой роли тысячу раз, но явно написанным / сказанным встречаю впервые.
Или же всё-таки у нас с вами разный опыт, мы были на разных лекциях, которые читали нам разные люди.
Впервые слышу, что эпсилон принят обозначением чего-то маленького. Встречал его в такой роли тысячу раз, но явно написанным / сказанным встречаю впервые.
Или же всё-таки у нас с вами разный опыт, мы были на разных лекциях, которые читали нам разные люди.Нам по Камынину читали — и это была та ещё… вещь. Слов там было примерно вдвое меньше, чем у вас тут, кванторов — побольше.
Сейчас книжки под рукой нет, но выглядело это примерно так:
«Определение: a — предел последовательности xn, если ∀ε>0 ∃n0 ∀n>n0 |xn-a|<ε»
Всё просто, понятно, логично. Одна строчка. Чего обсуждать-то.
Я спал, все мои одногруппники спали, автор статьи спал, половина комментаторов здесь спала.
Так и есть. Подавляющее большинство людей на первом курсе матфака страдает херней вместо того, чтобы учиться. Это просто факт.
Или же всё-таки у нас с вами разный опыт, мы были на разных лекциях, которые читали нам разные люди.
А при чем тут лекции? Основная часть обучения происходит дома, когда вы разбираете учебник, или тот же текст лекций.
Вспомнился мой матан первого курса. Предел по эпсилон-дельта. Никто не понимал, все просто зубрили, и всё. Я сам несколько дней (то ли в ноябре, то ли уже в декабре) ходил и думал, и в какой-то миг внезапное озарение: а давай считать эпсилон каким-то очень маленьким числом! Тогда всё неожиданно встаёт на свои места.
А что, где-то не дают эквивалентное определение предела по Гейне?
У нас было. Не сказал бы, что понять его было проще. Да, оно действительно элементарно: давайте возьмём последовательность, стремящуюся к x, обернём каждый член в функцию, и оно будет стремиться к lim f(x). Если бы мне кто-нибудь так сказал, да ещё и пример привёл, я бы сразу всё понял.
Только вот у нас было что-то сложное с окрестностями, выколотыми точками и т.п., мало что-либо объясняющее и ещё больше запутывающее. Из этого можно получить что-то нормальное человеческое, как у меня выше, только вот первокурсники обычно так ещё не умеют.
Только вот у нас было что-то сложное с окрестностями, выколотыми точками и т.п., мало что-либо объясняющее и ещё больше запутывающее. Из этого можно получить что-то нормальное человеческое, как у меня выше, только вот первокурсники обычно так ещё не умеют.
Да, оно действительно элементарно: давайте возьмём последовательность, стремящуюся к x, обернём каждый член в функцию, и оно будет стремиться к lim f(x).
Ну вообще говоря оно именно так и звучит: пределом функции в x_lim называется Y такое, что для любой последовательности x_n -> x_lim (forall i: x_i != x_lim) соответствующая последовательность f(x_n) -> Y
Окрестность там может встречаться только раз (условие в скобках на то, что последовательность не должна содержать саму точку-предел, нужная для кейза, в котором ф-я в точке не определена, но предел в ней имеет).
У вас с окрестностями, наверное, была альтернативная формулировка по Коши, которая вообще не знаю зачем нужна.
Есть разные мнения, чем занимается и чем является математика. Изложу (в вольном виде) немного мыслей из книги "Апология математика" Г. Харди, с которыми, впрочем, я не вполне согласен.
Есть 2 (как минимум) реальности — наша и математическая. В "нашей" находимся мы, атомы, физические законы — то, чем занимается физика, то, что мы видим и ощущаем. В "математической" находятся абстрактные математические объекты — числа, отношения, структуры и т.д. Когда математик описывает новый объект (например, кватернион, или тензор, или теорему), он не придумывает и не конструирует его, а открывает существующий в математической реальности объект. Настоящая математика — она про изучение другой, математической реальности, а не нашей.
Иногда случается, что абстрактные математические объекты находят применение в описании нашей реальности. Бывает, что от математика даже требуется, чтобы он описал математические объекты "на заказ", под нужды например физиков. Поэтому другое, более прикладное и "приземлённое" толкование сущности математики — математик конструирует, придумывает математические объекты. Но эта "инженерная" математика (в частности, интегралы), хотя и несёт в себе огромную пользу, не настоящая. Настоящая, абстрактная математика полностью бесполезна.
Какого толкования придерживаться — вопрос веры. Вот тут и начинаются срачи, нашедшие отражение даже в рассказах WH40k.
По одну сторону "чистые" математики, которые обитают в своём мире и которым плевать, нужно ли студентам то, что они рассказывают.
По другую — студенты, школьники, которые пытаются понять то, что рассказывают математики, но за неимением практического применения абстрактных вещей рассказанное понять не могут. Потом они говорят "Зачем мне в жизни синусы?" и "Я на следующий день после экзамена всё забыл, и за 20 лет ничего не пригодилось".
Где-то между полюсами находятся инженеры (+ экономисты и прочие), которые поняли матан и имеют с этого наибольший профит; и прикладные математики, которые объяснили инженерам.
Основная проблема обучения (инженеров) математике в том, что проще и эффективнее обучать их именно абстрактным вещам — это даёт им возможность гибко применять абстрактные вещи, если сами осилят найти применение. Другой полюс — обучение чисто на примерах, без теории, показал свою неэффективность где-то пару веков назад.
Но учить абстрактные вещи сложно и часто ненужно, поэтому соблюдают некоторый баланс между абстрактной математикой и прикладной, например дают абстрактное определение матрицы и определителя матрицы, а о применениях студенты узнают сильно позже (совсем же абстрактные вещи инженерам вовсе не дают). Вот в эти моменты и бывает непонятно, зачем нужна математика и почему её объясняют так ненаглядно. Конечно, хороший преподаватель и/или хорошая программа обучения могут сгладить эти моменты, но так бывает не всегда.
Вот и получается, что учат абстрактным вещам, не говоря заранее о применениях. И это как-то работает.
Если тебе не понятно, иди гоняй танчики или еще какие безделицы.
Если говорить о преподавании математики, то характер проблемы на мой взгляд точно сформулировал в своё время (1981) В.А.Рохлин:
В наше время можно окончить среднюю школу и не решить, в действительности, ни одной математической задачи. Даются шаблоны, примеры, подражая которым дети и справляются со своими школьными обязанностями.Я бы то же самое добавил и про физику. И собственно, тем же макаром большинство успешно продолжают учиться в институтах. (И мне вспоминаются ещё слова В.И. Арнольда о том, что математика — это та часть физики, в которой эксперименты дёшевы.)
Автору, да и всем очень рекомендую прочесть книгу
М.Клайн «Математика Утрата определенности» Москва «Мир» 1984
М.Клайн «Математика Утрата определенности» Москва «Мир» 1984
Как-то пробежала книга Статистика и котики:
iknigi.net/avtor-vladimir-savelev/154442-statistika-i-kotiki-vladimir-savelev.html
Местами занятно.
iknigi.net/avtor-vladimir-savelev/154442-statistika-i-kotiki-vladimir-savelev.html
Местами занятно.
Вот наконец-то эволюция высшей школы дошла до этого этапа, когда наука должна быть «sexy». Повторила тот путь, который западная наука прошла в 20м веке, буквально за 30 лет.
От почета науки, ни черта не осталось, только как еще один способ получить материальную выгоду, или очередное шоу, для избранных.
От почета науки, ни черта не осталось, только как еще один способ получить материальную выгоду, или очередное шоу, для избранных.
Написано очень хорошо, но, увы, совсем не ново. Как минимум сразу же вспоминается Фейнман с полностью аналогичной темой по физике, когда студенты отлично решают абстрактные теоретические задачи, которые просто заучили на память, но абсолютно не в состоянии применить полученные знания на практике, т.к. не понимают смысла того, что они запомнили (выделение мое).
lib.ru/ANEKDOTY/FEINMAN/feinman.txt
Вот цитата, чтобы не ходить по ссылке.
lib.ru/ANEKDOTY/FEINMAN/feinman.txt
Вот цитата, чтобы не ходить по ссылке.
Я обнаружил очень странное явление: я задавал вопрос, и студенты
отвечали, не задумываясь. Но когда я задавал вопрос еще раз — на ту же тему
и, как мне казалось, тот же самый вопрос, они вообще не могли ответить!
Например, однажды я рассказывал о поляризации света и раздал им всем кусочки
поляроида.
Поляроид пропускает свет только с определенным направлением
поляризации. Поэтому я объяснил, как определить направление поляризации
света по тому, темный поляроид или светлый.
Сначала мы взяли две полоски поляроида и вращали их до тех пор, пока
они не пропустили максимум света. Теперь мы могли сказать, что две полоски
пропускают свет, поляризованный в одном направлении: что пропускает один
поляроид, может пройти и через второй. Но потом я спросил, можно ли, имея
всего один кусок поляроида, определить, в каком направлении он поляризует
свет. Они совершенно не представляли себе.
Я знал, что это требует известной доли находчивости, поэтому я
подсказал: «Посмотрите на залив. Как от него отражается свет?»
Все молчат. Тогда я сказал:
— Вы когда-нибудь слышали об угле Брюстера?
— Да, сэр. Угол Брюстера — это угол, отражаясь под которым от
преломляющей среды, свет полностью поляризуется.
— В каком направлении свет поляризуется при отражении?
— Свет поляризуется перпендикулярно плоскости падения, сэр.
Даже теперь я не могу этого понять. Они знали все наизусть. Они знали
даже, что тангенс угла Брюстера равен показателю преломления!
Я сказал: «Ну?»
По-прежнему, ничего. Они только что сказали мне, что свет, отражаясь от
преломляющей среды, как, например, воды в заливе, поляризуется. Они даже
сказали, в каком направлении он поляризуется.
Я сказал: «Посмотрите на залив через поляроид. Теперь поворачивайте
поляроид».
— О-о-о, он поляризован! — воскликнули они.
После длительного расследования я, наконец, понял, что студенты все
запоминали, но ничего не понимали.
>После длительного расследования я, наконец, понял, что студенты все
>запоминали, но ничего не понимали.
Зря Фейнман не сказал, что отвечали не все студенты, а лишь некоторые (те, что с хорошей памятью, а их увы единицы на группу).
В общем в многословии аудитории отказать нельзя. Поговорили, и что? Все останется как было? От автора хотелось бы заключительное резюме.
>запоминали, но ничего не понимали.
Зря Фейнман не сказал, что отвечали не все студенты, а лишь некоторые (те, что с хорошей памятью, а их увы единицы на группу).
В общем в многословии аудитории отказать нельзя. Поговорили, и что? Все останется как было? От автора хотелось бы заключительное резюме.
Проблемы современной записи математических текстов