Представляю вашему вниманию вторую часть статьи о поиске подозреваемых в мошениничестве на основе данных из Enron Dataset. Если вы не читали первую часть, ознакомиться с ней можно здесь.
Сейчас речь пойдет про процесс построения, оптимизации и выбора модели, которая даст ответ: стоит ли подозревать человека в мошеничестве?

Ранее мы проанализировали один из открытых датасетов, дающий информацию о подозреваемых по делу о компании Enron и мошенничестве в ней. Также было исправлено смещение в исходных данных, заполнены пробелы(NaN), после чего данные были нормализованы и прошли отбор признаков.
В результате получились привычные многим:
- X_train и y_train — выборка, используемая для обучения(111 записей );
- X_test и y_test — выборка, на которой будет проверена корректность предсказаний наших моделей (28 записей).
Кстати о моделях… Для того, чтобы правильно предсказать, стоит ли подозревать человека, исходя из каких-то признаков, характеризующих его деятельность, мы будем использовать классификацию. Основные типы моделей, используемые для решения задач в этом сегменте, можно взять из Sklearn:
- Naive Bayes (наивный байесовский классификатор);
- SVM (машина опорных векторов);
- K-nearest neighbors (метод поиска ближайших соседей);
- Random Forest (случайный лес);
- Neural Network (нейронные сети).
Также есть картинка, достаточно хорошо иллюстрирующая их применимость:

Среди них присутствует знакомое многим Decision Tree (дерево решений), но, пожалуй, нет смысла в одной задаче использовать этот метод вместе с Random Forest, который является ансамблем из решающих деревьев. Поэтому заменим его на Logistic Regression (логистическая регрессия), что способна выступать в качестве классификатора и выдавать один из ожидаемых вариантов (0 или 1).
Начало
Инициализируем все упомянутые классификаторы с дефолтными значениями:
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
from sklearn.ensemble import RandomForestClassifier
random_state = 42
gnb = GaussianNB()
svc = SVC()
knn = KNeighborsClassifier()
log = LogisticRegression(random_state=random_state)
rfc = RandomForestClassifier(random_state=random_state)
mlp = MLPClassifier(random_state=random_state)Также сгруппируем их, чтобы было удобнее работать с ними как с совокупностью, а не писать код для каждого в отдельности. Например, можем обучить их все сразу:
classifiers = [gnb, svc, knn, log, rfc, mlp]
for clf in classifiers:
clf.fit(X_train, y_train)После того, как модели были обучены, пришло время первой проверки их качества предсказания. Дополнительно визуализируем наши результаты используя Seaborn:
from sklearn.metrics import accuracy_score
def calculate_accuracy(X, y):
result = pd.DataFrame(columns=['classifier', 'accuracy'])
for clf in classifiers:
predicted = clf.predict(X_test)
accuracy = round(100.0 * accuracy_score(y_test, predicted), 2)
classifier = clf.__class__.__name__
classifier = classifier.replace('Classifier', '')
result = result.append({'classifier': classifier, 'accuracy': accuracy}, ignore_index=True)
print('Accuracy is {accuracy}% for {classifier_name}'.format(accuracy=accuracy, classifier_name=classifier))
result = result.sort_values(['classifier'], ascending=True)
plt.subplots(figsize=(10, 7))
sns.barplot(x="classifier", y='accuracy', palette=cmap, data=result)Поглядим на общее представление о точности работы классификаторов:
calculate_accuracy(X_train, y_train) 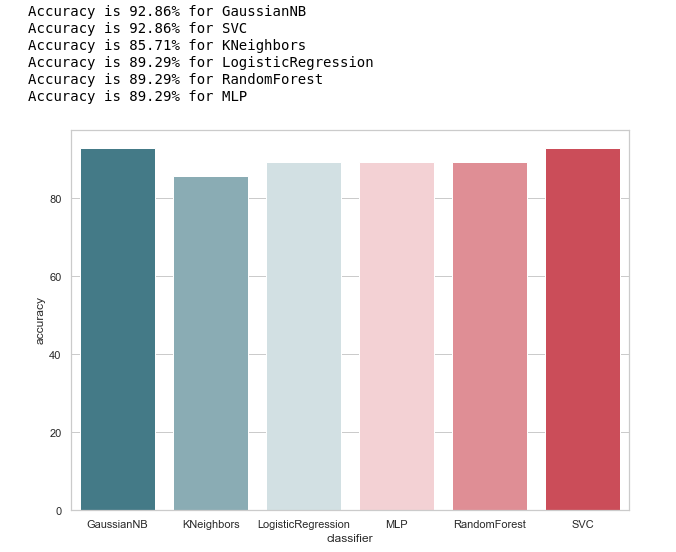
На первый взгляд выглядит весьма неплохо, точность предсказаний на тестовой выборке колеблется около 90%. Кажется, задача выполнена блестяще!
Высокая точность не гарантия правильности предсказаний. В нашей тестовой выборке 28 записей, 4 из которых связаны с подозреваемыми, а 24 с теми, кто вне подозрения. Представим, что мы создали какой-то алгоритм вида:
def QuaziAlgo(features):
return 0После чего отдали ему на вход нашу тестовую выборку, и получили, что все 28 человек невиновны. Какова будет точность (accuracy) алгоритма в данном случае?
Интересно, что у KNeighbors такая же точность предсказания...
Но всё таки, прежде чем обольщаться, давайте построим матрицу ошибок (confusion matrix) для результатов предсказания:
from sklearn.metrics import confusion_matrix
def make_confussion_matrices(X, y):
matrices = {}
result = pd.DataFrame(columns=['classifier', 'recall'])
for clf in classifiers:
classifier = clf.__class__.__name__
classifier = classifier.replace('Classifier', '')
predicted = clf.predict(X_test)
print(f'{predicted}-{classifier}')
matrix = confusion_matrix(y_test,predicted,labels=[1,0])
matrices[classifier] = matrix.T
return matricesПосчитаем матрицы ошибок для каждого классификатора и вместе с этим посмотрим, что они предсказывали:
matrices = make_confussion_matrices(X_train,y_train)
Даже текстового представления результата работы классификаторов хватит, чтобы понять, что что-то явно пошло не так.
Метод ближайших соседей вообще не выявил ни одного подозреваемого в тестовой выборке. Возникает два вопроса:
- В чем причина такого поведения классификатора KNeighbors?
- Зачем мы построили матрицы ошибок, если не используем их, а просто смотрим на результаты предсказания?
Заглянем глубже
Начнем со второго вопроса. Попробуем визуализировать наши матрицы ошибок, и представим данные в графическом формате, чтобы понять, где происходит ошибка классификации:
import itertools
from collections import Iterable
def draw_confussion_matrices(row,col,matrices,figsize = (16,12)):
fig, (axes) = plt.subplots(row,col, sharex='col', sharey='row',figsize=figsize )
if any(isinstance(i, Iterable) for i in axes):
axes = list(itertools.chain.from_iterable(axes))
idx = 0
for name,matrix in matrices.items():
df_cm = pd.DataFrame(
matrix, index=['True','False'], columns=['True','False'],
)
ax = axes[idx]
fig.subplots_adjust(wspace=0.1)
sns.heatmap(df_cm, annot=True,cmap=cmap,cbar=False ,fmt="d",ax=ax,linewidths=1)
ax.set_title(name)
idx += 1Отобразим их в 2 строки и 3 столбца:
draw_confussion_matrices(2,3,matrices)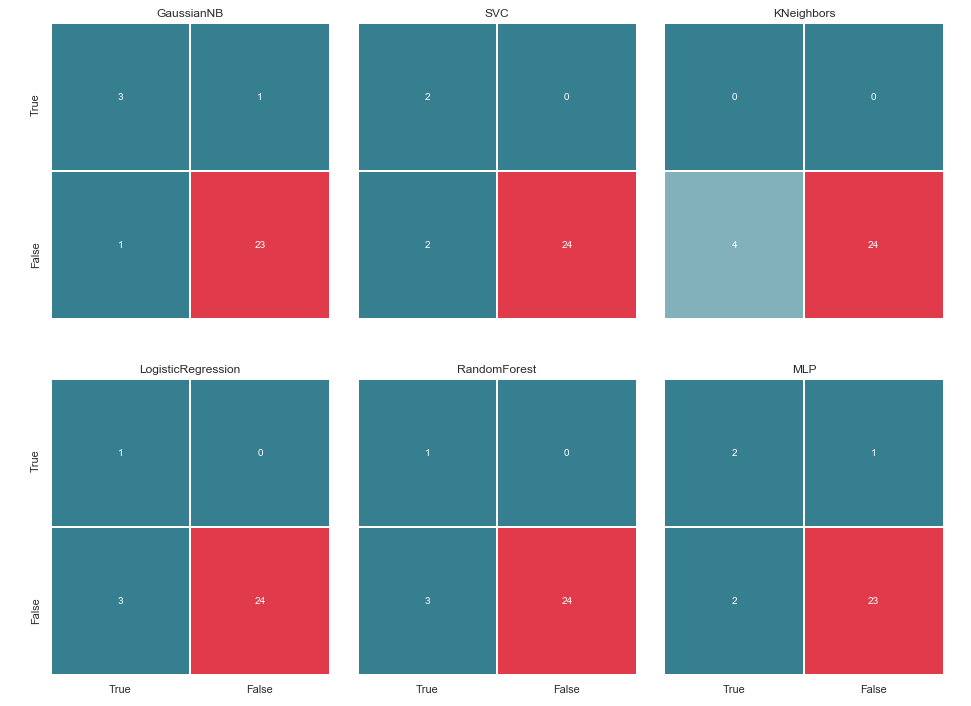
Прежде чем продолжать, стоит дать некоторые пояснения. Обозначение True, что расположено слева от матрицы ошибок конкретного классификатора, означает, что классификатор посчитал человека подозреваемым, значение False — что человек вне подозрения. Аналогично True и False внизу изображения дает нам реальное положение дел, которое может не совпадать с решением классификатора.
Например, мы видим, что решения KNeighbors с точностью предсказания в 85.71% совпало с реальным положением дел, когда 24 человека, что были вне подозрения, были внесены в аналогичный список со стороны классификатора. Но 4 человека из списка подозреваемых тоже были внесены в этот список. Если бы данный классификатор принимал решения, возможно кому-то удалось бы избежать суда.
Таким образом, матрицы ошибок очень хороший инструмент для понимания, что пошло не так в задачах классификации. Их основное преимущество в наглядности, и поэтому мы обращаемся к ним.
Метрики
В общем виде это можно проиллюстрировать следующей картинкой:

А что такое TP, TN, FP и какой-то FN в данном случае?
Иными словами, мы стремимся к тому, чтобы ответы классификатора и реальное положение дел совпадали. То есть к тому, чтобы все цифры были распределены между ячейками TP и TN (истинные решения) и не попадали в FN и FP(ложные решения).
Например в каноническом случае с дигностированием рака, FP предпочтительнее чем FN, ибо в случае ложного вердикта о раке, пациенту пропишут лекарства и будут его лечить. Да, это повлияет на его здоровье и кошелек, но всё-таки это считается менее опасным, нежели FN и пропущенный период, на котором рак можно победить малыми средствами.
Что насчет подозреваемых в нашем случае? Наверное, FN не так страшен, как FP. Впрочем об этом далее…
И раз речь зашла об аббревиатурах, самое время вспомнить о метриках точности (Precision) и полноты (Recall).
Если отступить от формальной записи, то Precision можно выразить как:
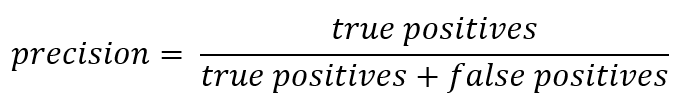
Иными словами, ведётся счёт, сколько полученных от классификатора положительных ответов являются правильными. Чем больше точность, тем меньше число ложных попаданий (точность равна 1, если не было ни одного FP).
Recall же в общем виде представлен как:
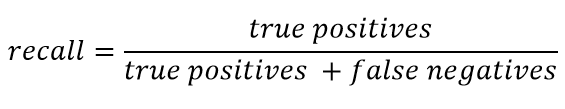
Recall характеризует способность классификатора «угадывать» как можно большее число положительных ответов из ожидаемых. Чем выше полнота — тем меньше было FN.
Обычно стараются балансировать между этими двумя, но в данном случае приоритет будет полностью отдан Precision. Причина: более гуманистический подход, желание минимизировать число ложно-положительных срабатываний и, как следствие, избежать того, чтобы подозрение падало на невиновного.
Посчитаем Precision для наших классификаторов:
from sklearn.metrics import precision_score
def calculate_precision(X, y):
result = pd.DataFrame(columns=['classifier', 'precision'])
for clf in classifiers:
predicted = clf.predict(X_test)
precision = precision_score(y_test, predicted, average='macro')
classifier = clf.__class__.__name__
classifier = classifier.replace('Classifier', '')
result = result.append({'classifier': classifier, 'precision': precision}, ignore_index=True)
print('Precision is {precision} for {classifier_name}'.format(precision=round(precision,2), classifier_name=classifier))
result = result.sort_values(['classifier'], ascending=True)
plt.subplots(figsize=(10, 7))
sns.barplot(x="classifier", y='precision', palette=cmap, data=result)
calculate_precision(X_train, y_train)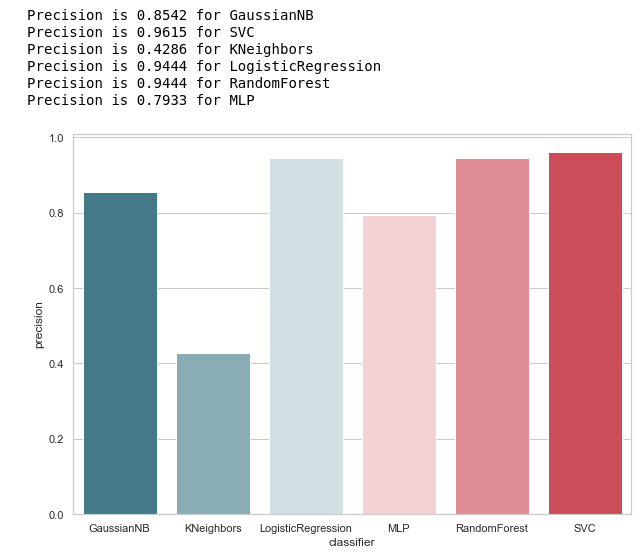
Как следует из рисунка, вышло вполне ожидаемо: точность KNeighbors оказалась ниже всех, ибо значение TP у него самое меньшее.
В тоже время на хабре есть хорошая статья о метриках, и тем, кто хочеть погрузиться в данную тему поглубже, стоит с ней ознакомиться.
Подбор гипер-параметров
После того, как мы нашли метрику, что наиболее подходит к выбранным условиям (уменьшаем число FP), можно вернуться к первому вопросу: В чем причина такого поведения классификатора KNeighbors?
Причина кроется в параметрах по умолчанию, с которыми была создана данная модель. И, скорее всего, к этому этапу многие могли бы воскликнуть: зачем обучать на дефолтных парметрах? Есть же специальные средства для подбора, например, часто используемый GridSearchCV.
Да, оно так, и настало время прибегнуть к нему,
Но перед этим уберем байессовский классификатор из нашего списка. Он допускает один FP, и вместе с тем данный алгоритм не принимает никаких изменяемых параметров, вследствие чего результат не изменится.
classifiers.remove(gnb)Подстройка
Зададим сетку параметров для каждого классификатора:
parameters = {'SVC':{'kernel':('linear', 'rbf','poly'), 'C':[i for i in range(1,11)],'random_state': (random_state,)},
'KNeighbors':{'algorithm':('ball_tree', 'kd_tree'), 'n_neighbors':[i for i in range(2,20)]},
'LogisticRegression':{'penalty':('l1', 'l2'), 'C':[i for i in range(1,11)],'random_state': (random_state,)},
'RandomForest':{'n_estimators':[i for i in range(10,101,10)],'random_state': (random_state,)},
'MLP':{'activation':('relu','logistic'),'solver':('sgd','lbfgs'),'max_iter':(500,1000), 'hidden_layer_sizes':[(7,),(7,7)],'random_state': (random_state,)}}Дополнительно хотелось обратить внимание на число слоев/нейронов в MLP.
Решено задавать их не перебором всех возможных значений, а всё-таки основываться на формуле:
Хочется сказать сразу, обучение и кросс-валидация будут производиться только на обучающей выборке. Я допускаю, что существует мнение, что можно делать это на всех данных как в примере с Iris Dataset. Но, на мой взгляд, такой подход не совсем оправдан, поскольку нельзя будет доверять результатам проверки на тестовой выборке.
Проведем оптимизацию и заменим наши классификаторы на улучшенную их версию:
from sklearn.model_selection import GridSearchCV
warnings.filterwarnings('ignore')
for idx,clf in enumerate(classifiers):
classifier = clf.__class__.__name__
classifier = classifier.replace('Classifier', '')
params = parameters.get(classifier)
if not params:
continue
new_clf = clf.__class__()
gs = GridSearchCV(new_clf, params, cv=5)
result =gs.fit(X_train, y_train)
print(f'The best params for {classifier} are {result.best_params_}')
classifiers[idx] = result.best_estimator_
После того, как мы выбрали метрику для оценки и выполнили GridSearchCV, мы готовы подвести финальную черту.
Подводим итоги
Матрица ошибок v.2
matrices = make_confussion_matrices(X_train,y_train)
draw_confussion_matrices(1,2,first_row,figsize = (10.5,6))
draw_confussion_matrices(1,3,second_row,figsize = (16,6))
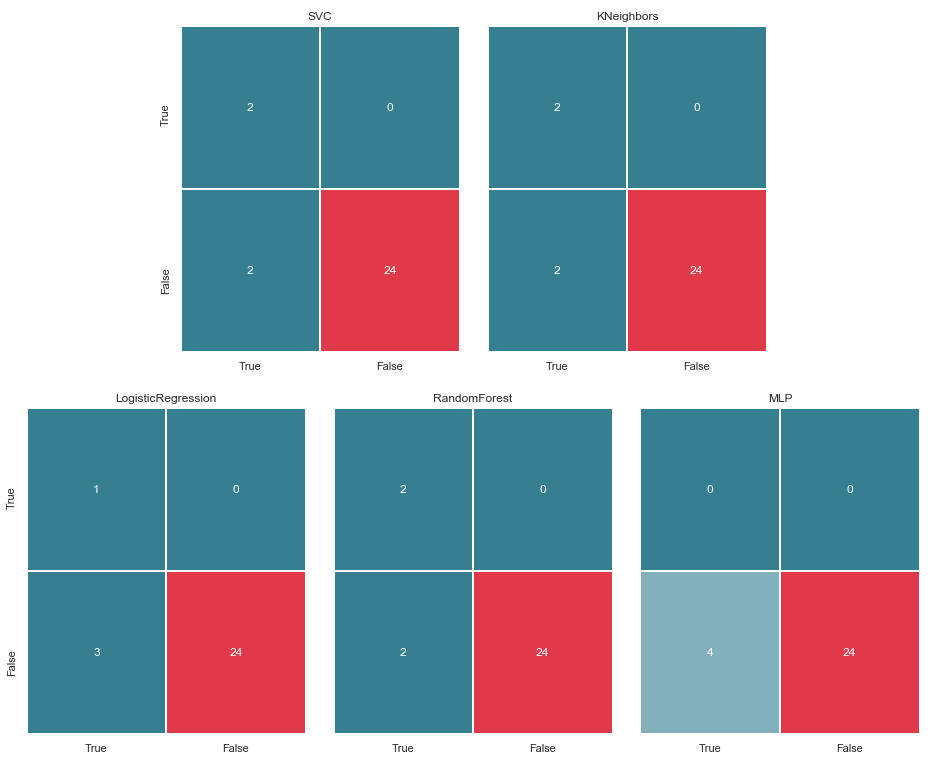
Как видно из матрицы, MLP проявил деградацию и посчитал что в тестовой выборке нет подозреваемых. Random Forest добрал точности и исправил параметры по False Negative и True Positive. А KNeighbors проявил улучшение в предсказании. Прогноз по другим не изменился.
Точность v.2
Теперь ни один из наших текущих классификаторов не имеет ошибок с False Positive, что не может не радовать. Но, если выразить всё языком цифр, мы получим следующую картину:
calculate_precision(X_train, y_train) 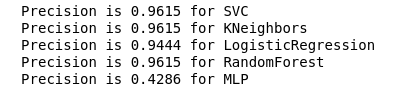
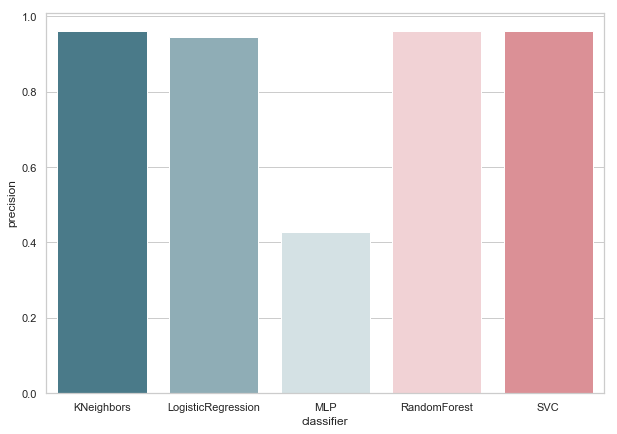
Выявлено 3 классификатора с самым высоким показателем Precision. И у них одинаковые значения, исходя из матрицы ошибок. Какой классификатор выбрать?
Кто же лучше?
Мне кажется, это достаточно непростой вопрос, на который не существует универсального ответа. Тем не менее, моя точка зрения в данном случае выглядела бы примерно так:
1.Классификатор должен быть настолько простым по своей технической реализации, насколько возможно. Тогда у него будет меньше риск переобучения (наверное, это и произошло с MLP). Поэтому это не Random Forest, поскольку данный алгоритм является ансамблем 30 деревьев и, как следствие, зависит от них. Созвучно одной из идей Python Zen: простое лучше, чем сложное.
2.Неплохо, когда алгоритм был интуитивно понятен. То есть KNeighbors воспринимается проще, чем SVM c потенциальным многомерным пространством.
Что в свою очередь похоже на другое высказывание: явное лучше, чем неявное.
Поэтому KNeighbors с 3 соседями, на мой взгляд, лучший кандидат.
Это конец второй части, описывающей использование Enron Dataset в качестве примера задачи классификации в машинном обучении. За основу взяты материалы из курса Introduction to Machine Learning на Udacity. Также есть python notebook, отражающий всю описаную последовательность действий.