Обзор градиентных методов в задачах математической оптимизации

Идея данного метода в том, что поиск происходит в направлении покоординатного спуска во время новой итерации. Спуск осуществляется постепенно по каждой координате. Количество координат напрямую зависит от количества переменных.
Для демонстрации хода работы данного метода, для начала необходимо взять функцию z = f(x1, x2,…, xn) и выбрать любую точку M0(x10, x20,…, xn0) в n пространстве, которая зависит от числа характеристик функции. Следующим шагом идет фиксация всех точек функции в константу, кроме самой первой. Это делается для того, чтобы поиск многомерной оптимизации свести к решению поиска на определенном отрезке задачу одномерной оптимизации, то есть поиска аргумента x1.
Для нахождения значения данной переменной, необходимо производить спуск по этой координате до новой точки M1(x11, x21,…, xn1). Далее функция дифференцируется и тогда мы можем найти значение новой следующий точки с помощью данного выражения:



После нахождения значения переменной, необходимо повторить итерацию с фиксацией всех аргументов кроме x2 и начать производить спуск по новой координате до следующей новой точке M2(x11,x21,x30…,xn0). Теперь значение новой точки будет происходить по выражению:



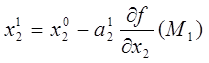
И снова итерация с фиксацией будет повторяться до тех пор, пока все аргументы от xi до xn не закончатся. При последней итерации, мы последовательно пройдем по всем возможным координатам, в которых уже найдем локальные минимумы, поэтому целевая функция на последний координате дойдет до глобального минимума. Одним из преимуществ данного метода в том, что в любой момент времени есть возможность прервать спуск и последняя найденная точка будет являться точкой минимума. Это бывает полезно, когда метод уходит в бесконечный цикл и результатом этого поиска можно считать последнюю найденную координату. Однако, целевая установка поиска глобального минимума в области может быть так и не достигнута из-за того, что мы прервали поиск минимума (см. Рисунок 1).


Рисунок 1 – Отмена выполнения покоординатного спуска

Исследование данного метода показали, что каждая найденная вычисляемая точка в пространстве является точкой глобального минимума заданной функции, а функция z = f(x1, x2,…, xn) является выпуклой и дифференцируемой.
Отсюда можно сделать вывод, что функция z = f(x1, x2,…, xn) выпукла и дифференцируема в пространстве, а каждая найденная предельная точка в последовательности M0(x10, x20,…, xn0) будет являться точкой глобального минимума (см. Рисунок 2) данной функции по методу покоординатного спуска.


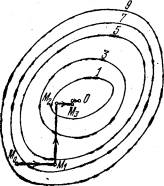
Рисунок 2 – Локальные точки минимума на оси координат

Можно сделать вывод о том, что данный алгоритм отлично справляется с простыми задачами многомерной оптимизации, путём последовательно решения n количества задач одномерной оптимизации, например, методом золотого сечения.

Ход выполнения метода покоординатного спуска происходит по алгоритму описанного в блок схеме (см. Рисунок 3). Итерации выполнения данного метода:
• Изначально необходимо ввести несколько параметров: точность Эпсилон, которая должна быть строго положительной, стартовая точка x1 с которой мы начнем выполнение нашего алгоритма и установить Лямбда j;
• Следующим шагом будет взять первую стартовую точку x1, после чего происходит решение обычного одномерного уравнения с одной переменной и формула для нахождения минимума будет, где k = 1, j=1:

• Теперь после вычисления точки экстремума, необходимо проверить количество аргументов в функции и если j будет меньше n, тогда необходимо повторить предыдущий шаг и переопределить аргумент j = j + 1. При всех иных случаях, переходим к следующему шагу.
• Теперь необходимо переопределить переменную x по формуле x (k + 1) = y (n + 1) и попытаться выполнить сходимость функции в заданной точности по выражению:

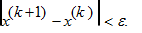
Теперь от данного выражения зависит нахождение точки экстремума. Если данное выражение истинно, тогда вычисление точки экстремума сводится к x*= xk + 1. Но часто необходимо выполнить дополнительные итерации, зависящие от точности, поэтому значения аргументов будет переопределено y(1) = x(k + 1), а значения индексов j =1, k = k + 1.


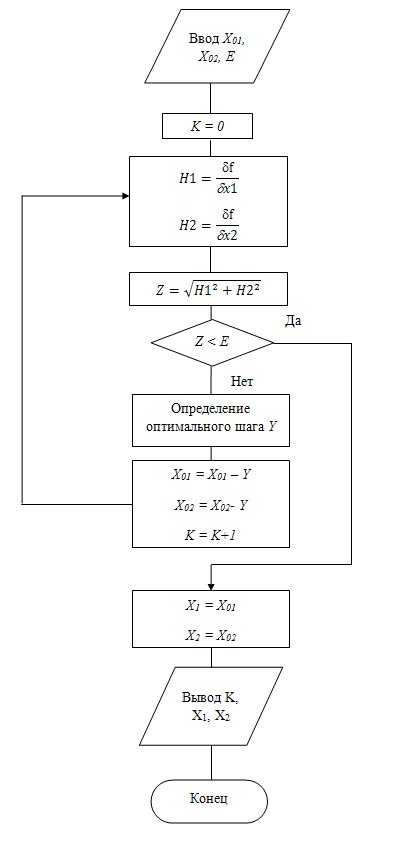
Рисунок 3 – Блок схема метода покоординатного спуска

Итого, у нас имеется отличный и многофункциональный алгоритм многомерной оптимизации, который способен разбивать сложную задачу, на несколько последовательно итерационных одномерных. Да, данный метод достаточно прост в реализации и имеет легкое определение точек в пространстве, потому что данной метод гарантирует сходимость к локальной точке минимума. Но даже при таких весомых достоинствах, метод способен уходить в бесконечные циклы из-за того, что может попасть в своего рода овраг.
Существуют овражные функции, в которых существуют впадины. Алгоритм, попав в одну из таких впадин, уже не может выбраться и точку минимума он обнаружит уже там. Так же большое число последовательных использований одного и того же метода одномерной оптимизации, может сильно отразиться на слабых вычислительных машинах. Мало того, что сходимость в данной функции очень медленная, поскольку необходимо вычислить все переменные и зачастую высокая заданная точность увеличивает в разы время решения задачи, так и главным недостатком данного алгоритма – ограниченная применимость.
Проводя исследование различных алгоритмов решения задач оптимизации, нельзя не отметить, что огромную роль играет качество данных алгоритмов. Так же не стоит забывать таких важных характеристик, как время и стабильность выполнения, способность находить наилучшие значения, минимизирующие или максимизирующие целевую функцию, простота реализации решения практических задач. Метод покоординатного спуска прост в использовании, но в задачах многомерной оптимизации, чаще всего, необходимо выполнять комплексные вычисления, а не разбиение целой задачи на подзадачи.

Стоит отметить известность данного алгоритма среди исследователей методов многомерной оптимизации. Метод Нелдера – Мида один из немногих методов, который основанный на концепции последовательной трансформации деформируемого симплекса вокруг точки экстремума и не используют алгоритм движения в сторону глобального минимума.
Данный симплекс является регулярным, а представляется как многогранник с равностоящими вершинами симплекса в N-мерном пространстве. В различных пространствах, симплекс отображается в R2-равносторонний треугольник, а в R3 — правильный тетраэдр.
Как упоминалось выше, алгоритм является развитием метода симплексов Спендли, Хекста и Химсворта, но, в отличие от последнего, допускает использование неправильных симплексов. Чаще всего, под симплексом подразумевается выпуклый многогранник с числом вершин N+1, где N – количество параметров модели в n -мерном пространстве.
Для того, чтобы начать пользоваться данным методом, необходимо определиться с базовой вершиной всех имеющихся множества координат с помощью выражения:



Самым замечательным в этом методе то, что у симплекса существуют возможности самостоятельно выполнять определенные функции:
• Отражение через центр тяжести, отражение со сжатием или растяжением;
• Растяжение;
• Сжатие.
Преимуществу среди этих свойств отдают отражению, поскольку данный параметр является наиболее опционально – функциональным. От любой выбранной вершины возможно сделать отражение относительно центра тяжести симплекса по выражению:.



где xc — центр тяжести (см. Рисунок 1).


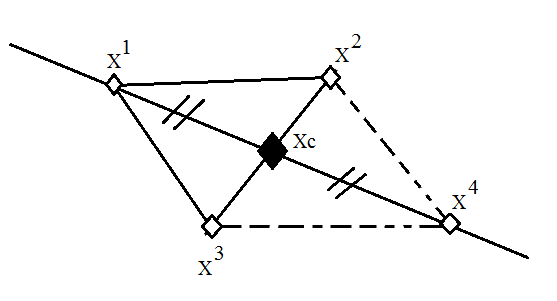
Рисунок 1 – Отражение через центр тяжести

Следующим шагом необходимо провести расчет аргументов целевой функции во всех вершинах отраженного симплекса. После этого, мы получим полную информацию о том, как симплекс будет вести себя в пространстве, а значит и информацию о поведении функции.
Для того чтобы совершить поиск точки минимума или максимума целевой функции с помощью методов использующих симплексы, необходимо придерживаться следующей последовательности:
• На каждом шаге строиться симплекс, в каждой точке которого, необходимо произвести расчет всех его вершин, после чего отсортировать полученные результаты по возрастанию;
• Следующий шаг – это отражение. Необходимо провести попытку получить значения нового симплекса, а путём отражения, у нас получиться избавиться от нежелательных значений, которые стараются двигать симплекс не в сторону глобального минимума;
• Чтобы получить значения нового симплекса, из полученных отсортированных результатов, мы берем две вершины с наихудшими значениями. Возможны такие случаи, что сразу подобрать подходящие значения не удастся, тогда придется вернуться к первому шагу и произвести сжатие симплекса к точке с самым наименьшим значением;
• Окончанием поиска точки экстремума является центр тяжести, при условии, что значение разности между функциями имеет наименьшие значения в точках симплекса.

Алгоритм Нелдера – Мида так же использует эти функции работы с симплексом по следующим формулам:

• Функция отражения через центр тяжести симплекса высчитывается по следующему выражению:


Данное отражение выполняется строго в сторону точки экстремума и только через центр тяжести (см. Рисунок 2).


Рисунок 2 – Отражение симплекса происходит через центр тяжести

• Функция сжатия вовнутрь симплекса высчитывается по следующему выражению:


Для того, чтобы провести сжатие, необходимо определить точку с наименьшим значением (см. Рисунок 3).


Рисунок 3 – Сжатие симплекса происходит к наименьшему аргументу.

• Функция отражения со сжатием симплекса высчитывается по следующему выражению:


Для того, чтобы провести отражение со сжатием (см. Рисунок 4), необходимо помнить работу двух отдельных функций – это отражение через центр тяжести и сжатие симплекса к наименьшему значению.


Рисунок 4 — Отражение со сжатие

• Функция отражения с растяжением симплекса (см. Рисунок 5) происходит с использованием двух функций – это отражение через центр тяжести и растяжение через наибольшее значение.


Рисунок 5 — Отражение с растяжением.

Чтобы продемонстрировать работу метода Нелдера – Мида, необходимо обратиться к блок схеме алгоритма (см. Рисунок 6).
Первостепенно, как и в предыдущих примерах, нужно задать параметр искаженности ε, которая должна быть строго больше нуля, а также задать необходмые параметры для вычисления α, β и a. Это нужно будет для вычисления функции f(x0), а также для построения самого симплекса.


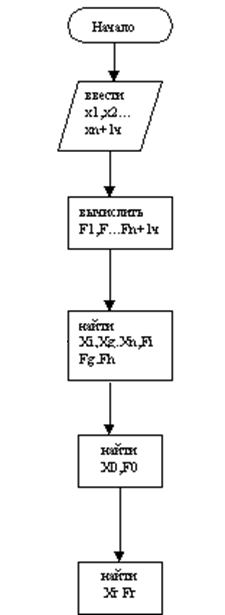
Рисунок 6 — Первая часть метода Нелдера — Мида.

После построения симплекса необходимо произвести расчет всех значений целевой функции. Как и было описано выше про поиск экстремума с помощью симплекса, необходимо рассчитать функцию симплекса f(x) во всех его точках. Далее производим сортировку, где базовая точка будет находиться:


Теперь, когда базовая точка рассчитана, а также и все остальные отсортированы в списке, мы производим проверку условия достижимости по ранее заданной нами точности:


Как только данное условие станет истинным, тогда точка x(0) симплекса будет считаться искомой точкой экстремума. В другом случае, мы переходим на следующий шаг, где нужно определить новое значение центра тяжести по формуле:


Если данное условие выполняется, тогда точка x(0) будет являться точкой минимума, в противном случае, необходимо перейти на следующий шаг в котором необходимо произвести поиск наименьшего аргумента функции:


Из функции необходимо достать самую минимальное значение аргумента для того, что перейти к следующему шагу выполнения алгоритма. Иногда случается проблема того, что несколько аргументов сразу имеют одинаковое значение, вычисляемое из функции. Решением такой проблемы может стать повторное определение значения аргумента вплоть до десятитысячных.
После повторного вычисления минимального аргумента, необходимо заново сохранить новые полученные значения на n позициях аргументов.


Рисунок 7 — Вторая часть метода Нелдера — Мида.

Вычисленное из предыдущей функции значение необходимо подставить в условие fmin < f(xN). При истинном выполнении данного условия, точка x(N) будет являться минимальной из группы тех, которые хранятся в отсортированном списке и нужно вернуться к шагу, где мы рассчитывали центр тяжести, в противном случае, производим сжатие симплекса в 2 раза и возвращаемся к самому началу с новым набором точек.
Исследования данного алгоритма показывают, что методы с нерегулярными симплексами (см. Рисунок 8) еще достаточно слабо изучены, но это не мешает им отлично справляться с поставленными задачами.
Более глубокие тесты показывают, что экспериментальным образом можно подобрать наиболее подходящие для задачи параметры функций растяжения, сжатия и отражения, но можно пользоваться общепринятыми параметрами этих функций α = 1/2, β = 2, γ = 2 или α = 1/4, β = 5/2, γ = 2. Поэтому, перед тем как отбрасывать данный метод для решения поставленной задачи, необходимо понимать, что для каждого нового поиска безусловного экстремума, нужно пристально наблюдать за поведением симплекса во время его работы и отмечать нестандартные решения метода.


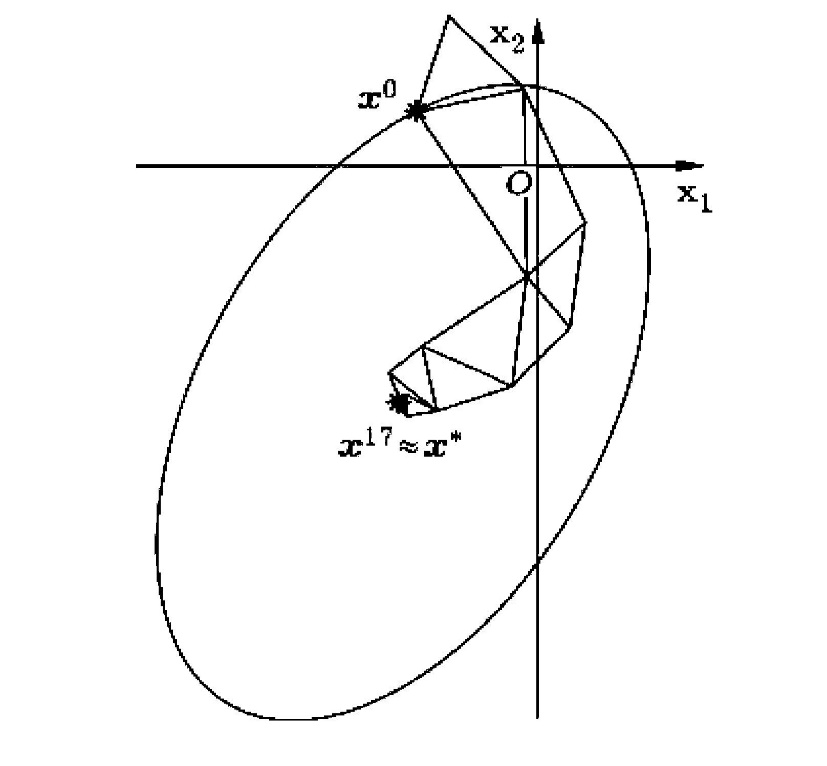
Рисунок 8 — Процесс нахождения минимума.

Статистика показала, что в работе данного алгоритма существует одна из наиболее распространенных проблем – это вырождение деформируемого симплекса. Это происходит, когда каждый раз, когда несколько вершин симплекса попадают в одно пространство, размерность которого не удовлетворяет поставленной задачи.
Таким образом, размерность во время работы и заданная размерность закидывают несколько вершин симплекса в одну прямую, запуская метод в бесконечный цикл. Алгоритм в данной модификации еще не оснащен способом выйти из такого положения и сместить одну вершину в сторону, поэтому приходится создать новый симплекс с новыми параметрами, чтобы такого в дальнейшем не происходило.
Еще одной особенностью обладает данный метод – это некорректной работой при шести и более вершинах симплекса. Однако, при модификации данного метода, можно избавиться от этой проблемы и даже не потерять при этом скорости выполнения, но значение выделяемой памяти заметно повысится. Данный метод можно считать циклическим, поскольку он полностью основан на циклах, поэтому и замечается некорректная работа при большом количестве вершин.
Алгоритм Нелдера – Мида по праву можно считать одним из наилучших методов нахождения точки экстремума с помощью симплекса и отлично подходит для использования его в различные рода инженерных и экономических задачах. Даже не смотря на цикличность, количество памяти он использует очень малое количество, по сравнение с тем же методом покоординатного спуска, а для нахождения самого экстремума требуется высчитывать только значения центра тяжести и функции. Небольшое, но достаточное, количество комплексных параметров дают этому методу широкое использование в сложных математических и актуальных производственных задачах.
Симплексные алгоритмы – это край, горизонты которого еще мы не скоро раскроем, но уже сейчас они значительно упрощают нашу жизнь своей визуальной составляющей.