Comments 29
В колодце тонули камень и ножницы а бумага его накрывала. Потом я только узнал что классическая игра состоит из 3 элементов.
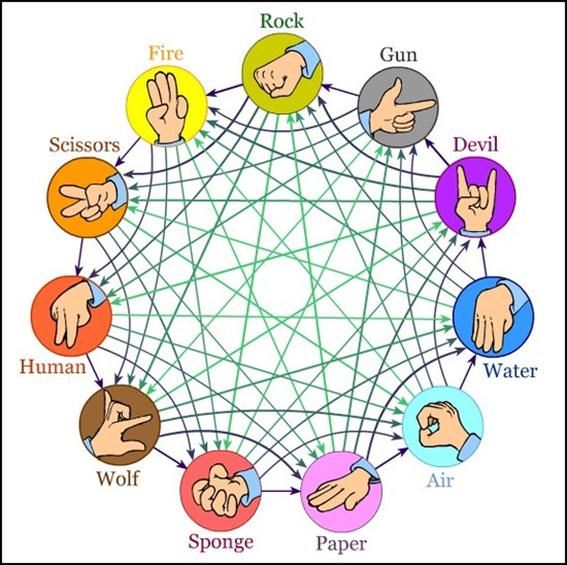



Чем больше элементов, тем меньше вероятность ничьей.
Повышение количества опций ведёт к понижению шансов ничьей лишь в том случае, когда все эти опции будут Парето-оптимальны, и игра останется симметричной :) Вот для картинок в комментах это верно, поскольку все вершины имеют одинаковое число входящих и исходящих рёбер.
Бумага и колодец побеждают 2-х «противников» и проигрывают одному, а камень и ножницы — побеждают только 1-го «противника» и проигрывают 2-м.
Но и с колодцем было аналогично: где-то он полностью заменял ножницы — камень-бумага-колодец при этом также правила не были однозначны — то бумага накрывала колодец, то колодец мочил бумагу. То камень тонул в колодце, то камень затыкал колодец. Про связь бумага-камень — в первом абзаце.
А когда существовали одновременно и ножницы и колодец… то тут выходило совсем непотребство… все что написано выше применялось и менялось одновременно.
Впрочем была одна комбинация, которая не давала других интерпритаций — Колодец-ножницы-бумага. Т.е выброшен камень, а не ножницы. И если связи ножницы-бумага еще можно реверсировать относительно друг-друга, то для связи колодец-ножницы все однозначно, как не выдумывай, а необходимость в признаке «бьет одного, бьется одним», фиксируются связи колодец-бумага, и ножницы-бумага.
Потому именно в таком варианте играли в большинстве компаний в моем детстве.
Описанная вами версия ничем не отличается от классической, и вот почему.
В обычной игре каждый вариант не лучше и не хуже другого. В вашей игре колодец однозначно лучше камня — оба одинаково проигрывают бумаге и побеждают ножницы, но при встрече друг с другом преимущество за колодцем. Таким образом, у игрока нет стимула когда-либо использовать камень, потому что если он вместо него покажет колодец, его шансы гарантированно вырастут при любом ходе соперника. Значит, никто из игроков никогда не будет использовать камень, и в игре снова остаётся три варианта с классическим балансом, — колодец, ножницы, бумага.
Если сформулировать это более формально, то в обычной игре все три опции Парето-оптимальны; в вашей версии одна из четырёх опций строго доминируется другой, поэтому остаются всё те же три Парето-оптимальных.
На первом уровне анализа кажется что это «камень», как формально наиболее старшая комбинация (аналог туза в карточных играх, где двойка/шестёрка бьют этого туза). Маленькие дети чаще всего выберут «камень».
Более глубокий уровень анализа подсказывает что надо контрить «наиболее очевидную комбинацию» — камень. Поэтому чаще всего в игре встречается «бумага».
И вот именно эту, наиболее часто встречаемую комбинацию, и должны контрить «ножницы».
Дальнейшая рекурсия уровней анализа лишена практического смысла.
То есть какую бы вы стратегию вы не выбрали, вы всегда проиграете в долгой игре.
Поэтому можно надеяться, что «игры» наподобие экономических пакетов стимулирования, налоговых кодексов, условий договоров и конструкций сетей приведут к равновесиям Нэша, при которых отдельные лица, действующие в собственных интересах, придут к устраивающему всех результату и системы станут стабильными.
Равновесие по нэшу разработано для игр с нулевой суммой.
Применять его к играм с положительной суммой — не корректно.
А из игр с нулевой суммой, где достигнуто равновесие — нужно немедленно уходить, тк заниматься тем, что не дает прибыли на дистанции просто глупо.
Бизнес например, это игра с положительной суммой.
Тк доход превышает совместные вложения всех сторон.
Налоговый кодекс это сделка государства с бизнесом, общая идея которой — вы нам платите, а мы вам позволяем работать. И тут все в плюсе, и бизнес себе что то заработал и государство собрало налоги.
Траффик на дорогах я склонен рассматривать не как сделку между всем участниками движения, а как набор сделок участник-государство.
И это также игра с положительной суммой, если участник не имеет стабильного профита от перемещению по транспортной системе, он просто не будет ей пользоваться. Правила тоже государство устанавливает, а не другие участники.
«Камень-ножницы-бумага» и теория игр