Comments 58
и вообще открыли, что иррациональных чисел больше, чем рациональных
Это неправда: и тех, и других – бесконечное количество. Другое дело, что мощность множества иррациональных чисел больше, чем рациональных.
Ну и забавляет вот это:
Как находить рациональные решения для полиномов со степенью 2, таких, как x^2 + y^2 = 1
Конкретно у этого полинома рациональные решения находятся очевидным перебором: (0,1) и (1,0). Непонятно, что мешает автору привести общий вид полинома, или хотя бы написать n вместо 1?
Э… а как же (3/5, 4/5)? Уже не рациональное решение? :)
А понятие «счётное множество» означает, что все элементы множества можно пронумеровать натуральными числами (1, 2, 3, 4, ...).
P.S. Кстати, любое бесконечное подмножество любого счётного множества также является счётным. Прикольно, правда?) Математика это красиво.
и тех, и других – бесконечное количествоага, только одни можно пересчитать, а другие нет. Множество рациональных чисел — счётно (и при этом бесконечно, да), множество иррациональных — континуально. То есть иррациональных больше.
В Википедии написано, что его репрессировали за разглашение математических тайн, а вовсе не за их открытие. Напишите туда свою версию, указав источник.
> поиска прямоугольных треугольников с рациональными длинами сторон и одновременно рациональной площадью.
Если катеты прямоугольного треугольника рациональны, то площадь тоже рациональна. Гипотенуза вообще не влияет и м.б. иррациональной.
1. Это, всё же, перевод англоязычной статьи, которая, похоже, ссылается на англоязычную вики, в которой источником указана книга "The life of Pythagoras".
2. В оригинале сказано следующее:
And rational solutions to elliptic curves are at the heart of certain geometry problems in the Pythagorean style, such as figuring out which right triangles have both rational side lengths and rational area.На сколько я понимаю, здесь говорится, о поиске правильных(равносторонних) треугольников у которых длина стороны и площадь являются рациональными числами.
Хотя, в наше время, очевидно, что таких треугольников не существует(за исключением вырожденного случая), потому что, площадь правильного треугольника через длину его стороны выражается следующим отношением:
 (где S — площадь, а — длина стороны)
(где S — площадь, а — длина стороны)Согласно одной из версий истории, Гиппас сделал это открытие, находясь в море, и его коллеги, потрясённые этим открытием, сбросили его за борт.
Скорее, он достал команду своим постоянным умничанием, что пришлось его выкинуть за борт, чтобы заткнулся.
"Иррациональное число 0,(9)" — это как? Почему вы решили, что оно иррациональное? И почему вы решили, что это вообще число?
И при чем тут вообще вера? существование иррациональных чисел было доказано давным-давно и от веры в них ничего не зависит.
На матане нас учили, что это вторая запись единицы.
Почему вы решили, что оно иррациональное?
По определению иррациональных чисел.
И почему вы решили, что это вообще число?
ЭЭЭ… потому, что это такое число как и число Пи, только у него вот такая запись, а не

Такие числа могут существовать только в воображении как пределы, но в реальности нет объектов, которые бы им соответствовали — это вопрос веры, как не смотри.
0,(9) — рациональное число, но сама его запись в десятичной форме подразумевает использование предела, что как минимум несовершенно, как максимум недопустимо.
Вообще-то все строго наоборот. В реальности существуют лишь иррациональные числа, а рациональные — лишь неточные приближения к ним.
Нас в школе ещё учили как такие "иррациональные" числа представлять в виде рациональной дроби (10^k*x — x)/(10^k-1) в данном случае будет (9.(9)-0.(9))/9
Нельзя так считать. Бесконечно малых чисел не бывает. Бывают только бесконечно малые последовательности и бесконечно малые функции.
Ты не ведаешь могущества темной стороны (https://ru.m.wikipedia.org/wiki/Нестандартный_анализ)
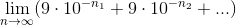
 , где ряд соответственно является пределом частичных сумм. Имхо бесконечные дроби обычно трактуются именно так.
, где ряд соответственно является пределом частичных сумм. Имхо бесконечные дроби обычно трактуются именно так. Вообще в анализе сначала определяются именно рациональные числа, и действия над ними, потом это множество дополняется до действительных чисел для замкнутости (сечениями, десятичными дробями или как-то иначе), для действительных чисел уже определяются все арифметические действия, доказываются снова все свойства этих действий, показывается, что рациональные числа можно считать подмножеством всех действительных.
После этого проблем с пониманием иррациональных чисел в анализе нет.
Нет, действительных чисел с названными вами свойствами не существует.
ну ладно, тогда посчитайте разность 1 — 0.(9)
нет, там в конце нет 1, (0) — вот это бесконечное повторение, после бесконечности нет ничего…
1 — 0.(9) = 0.(0) = 0
1 — 0.(0) = 1
1 — 0.(0)1 = 0.(9)
Если можно точно указать первую цифру числа и бесконечную последовательность цифр после нее, то почему нельзя указать последнюю цифру числа и бесконечную последовательность цифр перед ней. Бесконечный не в том смысле что у него нет конца, а в том что его нельзя достигнуть. Здесь 1 в 0.(0)1 — это недостижимая позиция, но это не значит что она несуществующая.
0.(0)123(4)567(89)
А чем они хуже 0.(0)1?
Это у вас какая-то альтернативная логика. По нормальной логике, если десятичная (или двоичная) дробь чем-то оканчивается, то она конечная, и это число рациональное. Вы утверждаете, что пи — рациональное число?
Рациональные решения эллиптических кривых находятся в самом центре различных геометрических задач пифагорейского стиля, к примеру, поиска прямоугольных треугольников с рациональными длинами сторон и одновременно рациональной площадьюЕсли a,b — катеты (рациональные), то площадь S=ab/2 — тоже рациональная. В чём проблема?
Легко видеть, что у полиномиального уравнения, в котором степень переменных не превышает 1, типа y = 3x + 4, есть бесконечное число рациональных решений. Любое рациональное значение x даёт рациональное значение y, и наоборот.
Простите, что? Корнем этого уравнения (как и любого линейного уравнения) будет являться одна и только одна точка. Никак не их бесконечное множество. Ну и да, статья написана несколько грубовато
Очень просто использовать две разные рациональные точки для генерации третьей, но очень сложно сделать наоборот – взять одну рациональную точку и найти две других рациональных точки, которые бы сгенерировали её.
Ну вот в такой формулировке вторая часть утверждения — неправильная. Сложно найти порядок точки.
Гипотеза говорит, что статистически, примерно у половины эллиптических кривых ранг равен 0 (то есть, у них есть либо конечное количество рациональных точек, или нулевое), а у другой половины – 1 (то есть, их бесконечное количество рациональных точек можно сгенерить из одной).
Выше ранг был определён через соединение точек между собой. Возникает очевидный вопрос, как можно сгененрировать бесконечное множестов рациональных точек, начав с одной, ведь её не с чем соединять? В статье Википедии про эллиптические кривые находим ответ: групповой закон для пары совпадающих точек определяется через касательную. Почему этого нельзя было написать в статье?!
Далее, понятие статистики на множестве кривых очевидно не имеет смысла. Вот какая доля рациональных чисел, по статистике, превышает 10?
Хотя в тексте указано «но если брать всё более крупные коллекции эллиптических кривых...» это не сильно проясняет ситуацию, если заранее не знать правильный ответ.
В результате гугления, я выяснил примерно следующее: все эллиптические кривые можно оценивать некоторой величиной — алгбераической высотой (naive height ), при этом множество кривых с высотой меньше заданной — конечно. Таким образом, можно рассматривать асимптотику по высоте для доли кривых с различным рангом, не превышающим заданной высоты.
Интересно, что меня побудила потратить время на выяснение этих вопросов не любовь к эллиптическим кривым и не замечаетельная статья, а очевидные, раздражающие нестыковки.
На мой взгляд, неплохо было бы в правила публикаций ввести пункт о защите здравого смысла: если что-то ему противоречит, то нужно либо давать пояснения, либо не переводить.
Хорошо бы не забыть, что вместе и рядом с ними стоят взрастившие и финансирующие их университеты и воспитавшие стремление к знаниям учителя. Жены дарящие любовь и коллеги не жалеющие поддержки. «Соперники» не дающие расслабится и журналисты которые любят крутых математиков.
Мы — социум. Мы продолжаемся.
Математики проливают свет на минималистскую гипотезу