Comments 11
Спасибо за статью.
Эх… когда-то, когда компьютеры были большие и доступ у ним был не у всех — пытался для себя решить аналитически простую вроде бы задачку:
«Тело брошено под углом к горизонту с начальной скоростью V0 так, что точка падения отличается то точки бросания на выстоту h (в плюс или минус). Найти угол, при котом дальность броска максимальна. (Воздухом, размерами тела, кривизной Земли и т.п. пренебречь)» (исходник — прыжок вдаль с тумбочки, но решение должно по идее годится много для чего).
Не осилил — задачка при всей кажущейся простоте оказалась не по зубам. Ностальжи…
Эх… когда-то, когда компьютеры были большие и доступ у ним был не у всех — пытался для себя решить аналитически простую вроде бы задачку:
«Тело брошено под углом к горизонту с начальной скоростью V0 так, что точка падения отличается то точки бросания на выстоту h (в плюс или минус). Найти угол, при котом дальность броска максимальна. (Воздухом, размерами тела, кривизной Земли и т.п. пренебречь)» (исходник — прыжок вдаль с тумбочки, но решение должно по идее годится много для чего).
Не осилил — задачка при всей кажущейся простоте оказалась не по зубам. Ностальжи…
0
Да ладно! Вероятно, «не по зубам» она Вам была классе в 7-м? В 8 или 9, наверно решили бы, если бы вспомнили?
0
Попробуйте на досуге. листок-бумажка. Мне на 4-м курсе не самого последнего технического ВУЗ-а пачки бумаги и недели вечерами не хватило, хотя это конечно не показатель сложности самой задачи да…
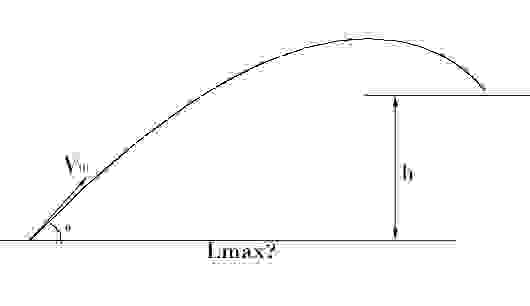
даны V0 и h, найти афльфа (т.е. формулу а(v,h)), при котором L максимально. (h может быть отрицательным, так же очевидно, что не все сочетания V и h имеют решение. Так же очевидно что при h=0 альфа 45гр., а при h=«минус-бесконечность» альфа = 0). Сейчас пакеты символьной математики конечно решают это влёт.

даны V0 и h, найти афльфа (т.е. формулу а(v,h)), при котором L максимально. (h может быть отрицательным, так же очевидно, что не все сочетания V и h имеют решение. Так же очевидно что при h=0 альфа 45гр., а при h=«минус-бесконечность» альфа = 0). Сейчас пакеты символьной математики конечно решают это влёт.
0
«карандаш+бумага», конечно, зарапартовался, извиняюсь.
0
Эх, много раз зарекался — не делать ничего на ночь глядя… 1-пиксельную линию где-то по пути съело… Вот:

0
Ища ноль производной Lmax по a, вышел на уравнение с cos2a, которое свелось к неполному кубическому.
Кубические я решать не умею, придётся научиться. Спать пора. Завтра дорешаю.
Кубические я решать не умею, придётся научиться. Спать пора. Завтра дорешаю.
0
Сейчас посчитал, но общая формула очень сложна как мне кажется для практического использования: там вроде не только кубическое уравнение, но еще и квадратный корень из выражения, в котором тоже есть альфа. Мне кажется, этот тот случай, когда понимание использования формул это лучше вывода аналитической формулы =)
0
Не осилил — задачка при всей кажущейся простоте оказалась не по зубам.
угол броска для максимального расстояния без разницы высоты, то есть " на полу" будет 45%. Для изображённой высоты h будет примерно то же — хотите аналитически, хотите просто по смыслу прикиньте что расстояние на высоте h увеличивается когда расстояние на полу увеличивается, за исключением когда угол броска изначально не позволит попасть над высотой, тогда кидаем так чтобы обьект поднимаясь вплотную пролетел к границе на высоте h.
0
Sign up to leave a comment.
Моделирование динамических систем: решение нелинейных уравнений