
Как бы вы подошли к симуляции дождя, ну или любого другого продолжительного физического процесса?
Симуляцию, будь это дождь, поток воздуха над крылом самолёта или же падающий по ступенькам слинки (помните игрушку-пружинку радугу из детства?), можно представить, если знать следующее:
- Состояние всего в момент начала симуляции.
- Как это состояние меняется из одного момента времени в другой?
Под «состоянием всего» я подразумеваю любые переменные данные, которые либо определяют как выглядит окружение, либо же изменения, происходящие с течением времени. Как пример состояния можно привести положение капли дождя, направление ветра, либо же скорость каждой части пружинки слинки.
Если положить, что всё наше состояние окружения это один большой вектор
- Найти значение
, удовлетворяющее
?
- Найти функцию
такую, что
.
Зачем нам надо хранить состояние всего в одном векторе, я объясню чуть позже. Это один из тех случаев, когда кажется что мы перебарщиваем с обобщением задачи, но я обещаю, в таком подходе есть свои интересности.
Теперь взглянем как можно хранить всю информацию об окружении в одном векторе на простом примере. Допустим, у нас есть 2 объекта в 2D симуляции. Каждый объект определяется своим положением

Таким образом, чтобы получить вектор
Если вас смущает, почему мы хотим найти
Начальное состояние
Чтобы определить начальное состояние симуляции, нужно определить вектор
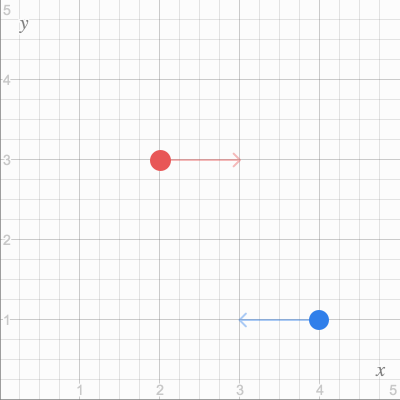
То в векторном виде это можно представить следующим образом:
Если объединить это всё в один вектор, мы получим нужный нам
Производная функция
Для этого, решим уравнение
Ого! Высокая получилась формула! Но можно привести её в более читаемый вид, если разобьём наш вектор
От определения этих двух производных и зависит качество симуляции, именно в них вся сила. И чтобы симуляция не походила на программу где всё случается хаотичным образом, можно обратиться к физике за вдохновением.
Кинематика и динамика
Кинематика и динамика — необходимые ингредиенты для создания интересной симуляции. Начнём с самых основ на нашем примере.
За положение в пространстве отвечает
Может показаться, что мы уже нашли нужную нам функцию
И в самом деле мы блестяще справились с
Тут нам поможет второй закон Ньютона:
Так, погодите ка,
Предположим, что в нашем простом примере, единственной силой, которая воздействует на объекты является гравитационное притяжение. В таком случае, мы можем определить
Где
Для создания самой симуляции, также нам понадобится направление и как то указать
Подытожим. Изменение состояний в нашей системе из двух объектов полностью выражено через переменные
Теперь у нас есть всё, что отличает нашу симуляцию от всех других симуляций:
Но как, имея строго определённую симуляцию, превратить её в красивую анимацию?
Если у вас был опыт написания симуляции или игры, то возможно вы предложите нечто такое:
x += v * delta_t
v += F/m * delta_tНо давайте чуть остановимся и разберём почему это сработает.
Дифференциальные уравнения
Прежде чем мы приступим к реализации, нужно определиться, какая информация у нас уже имеется и что нам нужно. У нас есть значение
Имея это ввиду и приглядевшись к
Задача нахождения
Численное интегрирование
Для некоторых примеров задач Коши можно легко найти ответ аналитическим методом, но в сложных симуляциях аналитический подход может оказаться очень сложным. Поэтому попробуем найти способ поиска аппроксимированного решения задачи.
Для примера возьмём простую задачу Коши.
Дано:
Рассмотрим задачу с геометрической точки зрения и посмотрим на значение и касательную в точке
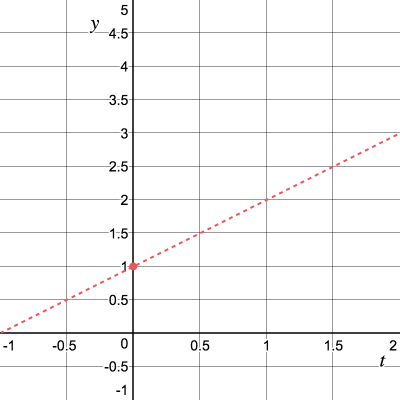
Мы пока не знаем как выглядит
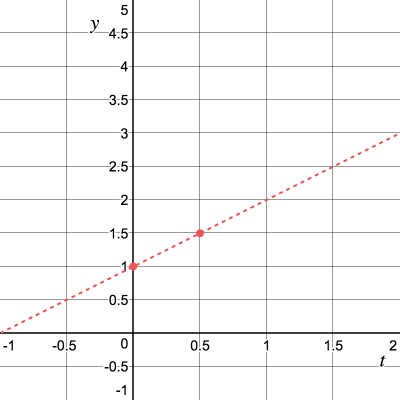
Если расписать, то мы приближаем значение
Так, для
Теперь мы можем продолжить вычислять для других точек. Хотя, конечно, мы нашли не точное значение
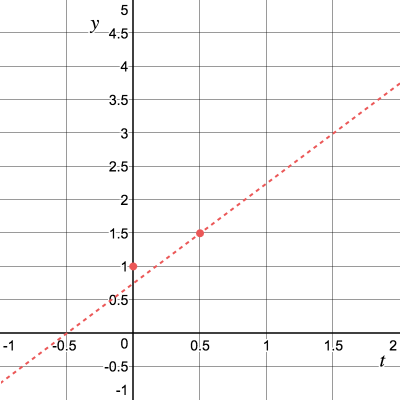
Далее, продвинемся ещё на
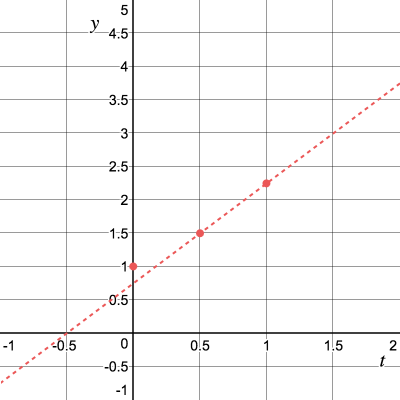
Повторим процесс и получим угловой коэффициент касательной
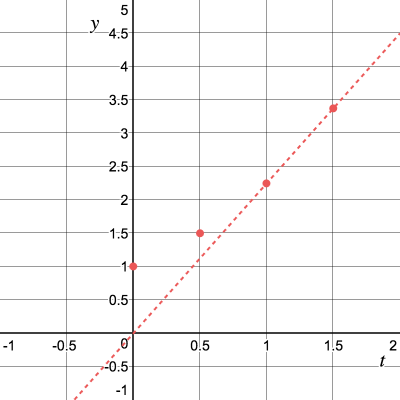
Процедуру можно проводить рекурсивно и для этого выведем формулу:
Данный численный метод решения дифференциальных уравнений называется методом Эйлера. Для общего случая шаг
x += v * delta_t.В нашем конкретном случае, пошаговое решение выглядит так:
Используя данный метод, результаты удобно представлять в виде таблицы:
Оказывается, у нашей задачи есть красивое аналитическое решение

Как вы думаете, что произойдёт, если в методе Эйлера уменьшить шаг?
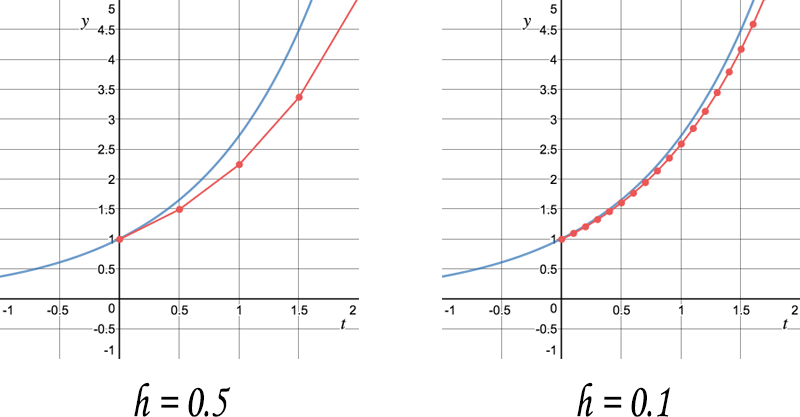
Разница между аппроксимированным и точным решениями уменьшается с уменьшением
Настало время кодить!
С таким же успехом как мы вывели математическое представление описания симуляции, мы можем написать реализацию симуляции программно.
Т.к. я больше всего знаком с JavaScript, и мне нравится ясность, которую добавляют в код аннотации, все примеры будут написаны на TypeScript.
А начнём мы с версии, в которой подразумевали, что
function runSimulation(
// y(0) = y0
y0: number[],
// dy/dt(t) = f(t, y(t))
f: (t: number, y: number[]) => number[],
// показывает текущее состояние симуляции
render: (y: number[]) => void
) {
// Шаг вперёд на 1/60 секунды за тик
// Если анимация будет 60fps то это приведёт к симуляции в рельном времени
const h = 1 / 60.0;
function simulationStep(ti: number, yi: T) {
render(yi)
requestAnimationFrame(function() {
const fi = f(ti, yi)
// t_{i+1} = t_i + h
const tNext = ti + h
// y_{i+1} = y_i + h f(t_i, y_i)
const yNext = []
for (let j = 0; j < y.length; j++) {
yNext.push(yi[j] + h * fi[j]);
}
simulationStep(tNext, yNext)
}
}
simulationStep(0, y0)
}Оперировать с одномерными массивами не всегда удобно, можно абстрагировать функции сложения и умножения процесса симуляции в интерфейс и получить краткую обобщённую реализацию симуляции используя TypeScript Generics.
interface Numeric<T> {
plus(other: T): T
times(scalar: number): T
}
function runSimulation<T extends Numeric<T>>(
y0: T,
f: (t: number, y: T) => T,
render: (y: T) => void
) {
const h = 1 / 60.0;
function simulationStep(ti: number, yi: T) {
render(yi)
requestAnimationFrame(function() {
// t_{i+1} = t_i + h
const tNext = ti + h
// y_{i+1} = y_i + h f(t_i, y_i)
const yNext = yi.plus(f(ti, yi).times(h))
simulationStep(yNext, tNext)
})
}
simulationStep(y0, 0.0)
}Положительной стороной данного подхода является возможность сконцентрироваться на основе симуляции: что именно эту симуляцию отличает от любой другой. Используем пример симуляции с двумя объектами, упомянутыми выше:
Код симуляция двух объектов
// Состояние симуляции двух объектов в один тик времени
class TwoParticles implements Numeric<TwoParticles> {
constructor(
readonly x1: Vec2, readonly v1: Vec2,
readonly x2: Vec2, readonly v2: Vec2
) { }
plus(other: TwoParticles) {
return new TwoParticles(
this.x1.plus(other.x1), this.v1.plus(other.v1),
this.x2.plus(other.x2), this.v2.plus(other.v2)
);
}
times(scalar: number) {
return new TwoParticles(
this.x1.times(scalar), this.v1.times(scalar),
this.x2.times(scalar), this.v2.times(scalar)
)
}
}
// dy/dt (t) = f(t, y(t))
function f(t: number, y: TwoParticles) {
const { x1, v1, x2, v2 } = y;
return new TwoParticles(
// dx1/dt = v1
v1,
// dv1/dt = G*m2*(x2-x1)/|x2-x1|^3
x2.minus(x1).times(G * m2 / Math.pow(x2.minus(x1).length(), 3)),
// dx2/dt = v2
v2,
// dv2/dt = G*m1*(x1-x1)/|x1-x2|^3
x1.minus(x2).times(G * m1 / Math.pow(x1.minus(x2).length(), 3))
)
}
// y(0) = y0
const y0 = new TwoParticles(
/* x1 */ new Vec2(2, 3),
/* v1 */ new Vec2(1, 0),
/* x2 */ new Vec2(4, 1),
/* v2 */ new Vec2(-1, 0)
)
const canvas = document.createElement("canvas")
canvas.width = 400;
canvas.height = 400;
const ctx = canvas.getContext("2d")!;
document.body.appendChild(canvas);
// Текущее состояние симуляции
function render(y: TwoParticles) {
const { x1, x2 } = y;
ctx.fillStyle = "white";
ctx.fillRect(0, 0, 400, 400);
ctx.fillStyle = "black";
ctx.beginPath();
ctx.ellipse(x1.x*50 + 200, x1.y*50 + 200, 15, 15, 0, 0, 2 * Math.PI);
ctx.fill();
ctx.fillStyle = "red";
ctx.beginPath();
ctx.ellipse(x2.x*50 + 200, x2.y*50 + 200, 30, 30, 0, 0, 2 * Math.PI);
ctx.fill();
}
// Запускаем!
runSimulation(y0, f, render)Если подшаманить с числами, то можно получить симуляцию орбиты Луны!
Симуляция орбиты Луны, 1 пикс. = 2500 км. 1 сек. симуляции равна 1 дню на Земле. Пропорция Луны к Земле увеличена в 10 раз
Столкновения и ограничения
Приведённая математическая модель и в самом деле симулирует физический мир, но в некоторых случаях метод численного интегрирования, к сожалению, ломается.
Представьте симуляцию прыгающего на поверхности мячика.
Состояние симуляции можно описать так:
Где
Если изобразить график
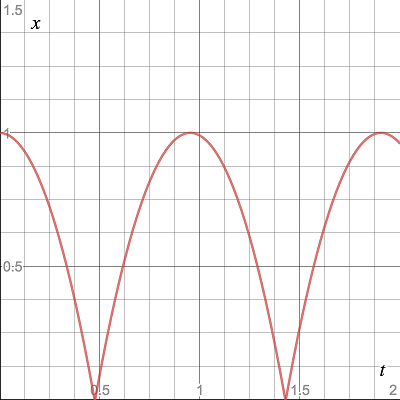
Во время падения мяча производная функции
С ускорением свободного падения,
Но что произойдёт, когда мяч коснётся поверхности? То, что мяч достиг поверхности мы можем узнать по
Можно было бы решить эту задачу путём определения момента столкновения
Можно, конечно, определить столкновение в ограниченном промежутке времени и применить другую силу
А чтобы уменьшить величину проницания мячом поверхности, можно за один тик вычислять сразу несколько шагов симуляции. В совокупности с этим, код нашей симуляции изменится так:
function runSimulation<T extends Numeric<T>>(
y0: T,
f: (t: number, y: T) => T,
applyConstraints: (y: T) => T,
iterationsPerFrame: number,
render: (y: T) => void
) {
const frameTime = 1 / 60.0
const h = frameTime / iterationsPerFrame
function simulationStep(yi: T, ti: number) {
render(yi)
requestAnimationFrame(function () {
for (let i = 0; i < iterationsPerFrame; i++) {
yi = yi.plus(f(ti, yi).times(h))
yi = applyConstraints(yi)
ti = ti + h
}
simulationStep(yi, ti)
})
}
simulationStep(y0, 0.0)
}И теперь уже можно написать код нашего прыгающего мячика:
Код прыгающего мячика
const g = -9.8; // m / s^2
const r = 0.2; // m
class Ball implements Numeric<Ball> {
constructor(readonly x: number, readonly v: number) { }
plus(other: Ball) { return new Ball(this.x + other.x, this.v + other.v) }
times(scalar: number) { return new Ball(this.x * scalar, this.v * scalar) }
}
function f(t: number, y: Ball) {
const { x, v } = y
return new Ball(v, g)
}
function applyConstraints(y: Ball): Ball {
const { x, v } = y
if (x <= 0 && v < 0) {
return new Ball(x, -v)
}
return y
}
const y0 = new Ball(
/* x */ 0.8,
/* v */ 0
)
function render(y: Ball) {
ctx.clearRect(0, 0, 400, 400)
ctx.fillStyle = '#EB5757'
ctx.beginPath()
ctx.ellipse(200, 400 - ((y.x + r) * 300), r * 300, r * 300, 0, 0, 2 * Math.PI)
ctx.fill()
}
runSimulation(y0, f, applyConstraints, 30, render)
Внимание разработчикам!
Хоть у такой модели есть свои плюсы, она не всегда ведёт к производительным симуляциям. По мне, такой фреймворк полезен для представления поведения симуляции, даже если в ней происходит много чего лишнего.
Например, симуляция дождя в начале этой статьи [прим. В оригинальной статье, в начале вставлена красивая интерактивная симуляция дождя, рекомендую посмотреть воочию] не была создана с использованием, описанного в статье, шаблона. Это был эксперимент с использованием Entity–component–system. Исходники симуляции можно найти тут: симуляция дождя на GitHub.
До скорого!
Я нахожу пересечение математики, физики и программирования чем-то действительно впечатляющим. Создание работающей симуляции, её запуск и рендеринг это некий особенный вид чего-то из ничего.
На всё изложенное меня вдохновили материалы лекции SIGGRAPH, точно так же как и в симуляции жидкости. Если хотите найти более исчерпывающую информацию о вышеизложенном, то взгляните на материалы курса SIGGRAPH 2001 «Введение в физическое моделирование». Привожу ссылку на курс 1997 года, т.к. Pixar похоже удалила версию 2001.
Хочу поблагодарить Maggie Cai за чудесную иллюстрацию пары под зонтом и за терпение при кропотливом подборе цветов, в то время как я не могу отличить синее от серого.
А если вас интересует, то иллюстрации были созданы в Figma.
Only registered users can participate in poll. Log in, please.
Переводить ли статью «симуляция жидкости» (ссылка дана в заключении статьи)
97.11% Да168
2.89% Нет5
173 users voted. 22 users abstained.