Comments 28
Наконец-то серьезная статья, спасибо! Отличный метод. Использую его в работе. Работает действительно надежно.
+1
Хорошая статья. Помню, в университете при написании дипломной работы использовал этот алгоритм для обучения многослойных сетей — при ограниченных ресурсах LMA является хорошей альтернативой другим методам. Еще можно добавить, что μ можно рассматривать как параметр регуляризации, и иногда его сомножитель I заменяют на diag(JTJ) для улучшения сходимости.
+4
Спасибо, прочитал с удовольствием, словно в университет обратно вернулся.
У меня такой вопрос — а почему Python? Есть же куча средств, где всё это реализовано библиотеками.
Ну вот, скажем, на LabVIEV Levenberg-Marquardt прямо из коробки.
Смотрите, как симпатично получается:
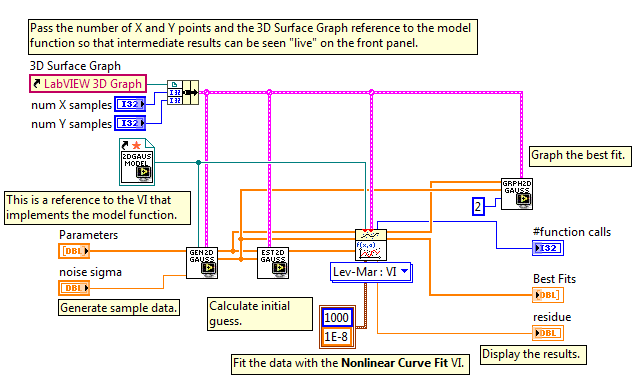

Я вовсе не холивара ради, просто это экономит огромную кучу времени. Даже с применением Anaconda (спасибо за наводку) вам пришлось написать некоторое количество обвязки плюс код для рисования графиков… Ну или Matlab как-то больше ожидаешь увидеть для решения подобных задач.
У меня такой вопрос — а почему Python? Есть же куча средств, где всё это реализовано библиотеками.
Ну вот, скажем, на LabVIEV Levenberg-Marquardt прямо из коробки.
Смотрите, как симпатично получается:
Я вовсе не холивара ради, просто это экономит огромную кучу времени. Даже с применением Anaconda (спасибо за наводку) вам пришлось написать некоторое количество обвязки плюс код для рисования графиков… Ну или Matlab как-то больше ожидаешь увидеть для решения подобных задач.
0
Matlab, например, платный. В Python есть замечательный пакет SciPy, в котором как раз реализовано множество оптимизационных алгоритмов — глобальных/локальных, условных/безусловных…
+1
- Целью статьи было собрать всё в 1 месте. Разъяснить теорию, предоставить работающий код, показать на графике. На мой взгяд, так материал воспринимается гораздо проще и эффектнее. Если бы я просто вызывал методы готовой библиотеки, то согласитесь, что это было бы не так интересно(и понятно)
- Как отметил kxx, в Python есть пакет SciPy (который кстати входит в Anaconda), в котором есть всё для наших целей
+2
Извините, а чем Вас не устроила реализация метода в scipy.optimize?
0
Спасибо большое автору за интересную статью! Давно пользуюсь этим методом.
Важное отличие Левенберга — Марквардта, из-за которого я перешел на него с квазиньютоновского Limited-memory BFGS, это возможность Л-М корректно работать в пространстве переменных разного масштаба. LBFGS очень удобен тем, что экономит итерации и ограниченно потребляет память на задачах локальной оптимизации в пространствах большой размерности. Мы удачного использовали его в задачах размерности 30 000, 100 000 и более, например в оптимизации атомных структур больших молекул — там все координаты и их изменения одинакового масштаба, например ангстремы.
Однако, в иных задачах, таких как фиттинг модели под экспериментальные данные, варьируемые параметры модели могут оказаться сильно разных масштабов. Варианты вроде искать оптимум в пространстве логарифмов параметров не всегда разумны. А при введении скалирующих коэффициентов Левенберг — Марквардт по моему опыту оказывается более толерантен к ошибкам скалирования, чем LBFGS, который начинает давать разные оптимумы в зависимости от конкретного выбора скалирования.
Насколько я понял в SciPy сейчас отсутствует реализация Левенберга — Марквардта, мне кажется автор этой статьи вполне дозрел добавить этот метод в SciPy, это был бы очень серьезный вклад.
Однажды столкнулся с необходимостью проводить глобальный фиттинг, пришлось писать собственную реализацию на С++ с использованием оптимизатора Л-М из библиотеки ALGLIB, так как в SciPy этот метод отсутствовал, в Mathematica он формально есть, но заставить его работать в моей задаче мне не удалось — в Mathematica несколько оптимизаторов, метод оптимизации L-M задается как параметр и поддерживается только одним из оптимизаторов, как раз тем, в который нельзя передать в качестве функции свой код. В Matlab тоже оптимизация хромает.
Важное отличие Левенберга — Марквардта, из-за которого я перешел на него с квазиньютоновского Limited-memory BFGS, это возможность Л-М корректно работать в пространстве переменных разного масштаба. LBFGS очень удобен тем, что экономит итерации и ограниченно потребляет память на задачах локальной оптимизации в пространствах большой размерности. Мы удачного использовали его в задачах размерности 30 000, 100 000 и более, например в оптимизации атомных структур больших молекул — там все координаты и их изменения одинакового масштаба, например ангстремы.
Однако, в иных задачах, таких как фиттинг модели под экспериментальные данные, варьируемые параметры модели могут оказаться сильно разных масштабов. Варианты вроде искать оптимум в пространстве логарифмов параметров не всегда разумны. А при введении скалирующих коэффициентов Левенберг — Марквардт по моему опыту оказывается более толерантен к ошибкам скалирования, чем LBFGS, который начинает давать разные оптимумы в зависимости от конкретного выбора скалирования.
Насколько я понял в SciPy сейчас отсутствует реализация Левенберга — Марквардта, мне кажется автор этой статьи вполне дозрел добавить этот метод в SciPy, это был бы очень серьезный вклад.
Однажды столкнулся с необходимостью проводить глобальный фиттинг, пришлось писать собственную реализацию на С++ с использованием оптимизатора Л-М из библиотеки ALGLIB, так как в SciPy этот метод отсутствовал, в Mathematica он формально есть, но заставить его работать в моей задаче мне не удалось — в Mathematica несколько оптимизаторов, метод оптимизации L-M задается как параметр и поддерживается только одним из оптимизаторов, как раз тем, в который нельзя передать в качестве функции свой код. В Matlab тоже оптимизация хромает.
0
Здравствуйте. Как отметил Andy_U, Scipy уже содержит алгоритм Левенберга — Марквардта. Вот ссылка. А вот для задачи curve_fitting
0
В случае, если требуется Левенберг — Марквардт не для минимизации «в общем», а для подгона модели к данным (метод наименьших квадратов), то можно взять «обёртку» над scipy — lmfit, которая значительно удобнее для такого применения (хотя и не идеальна), а также содержит дополнительные функции.
+1
Статья оказалась полезной для меня, спасибо.
Хотелось бы узнать Ваше мнение о методе Нелдера-Мида.
Хотелось бы узнать Ваше мнение о методе Нелдера-Мида.
0
Главное преимущество в методе Нелдера-Мида, на мой взягляд, является отсутствие ограничения на гладкость функции(т.е. существования производных в каждой точке функции). Ещё он даёт высокую хорошую оптимизацию на первых итерациях, хотя на это способны и рассмотренные методы.
Минусом является плохая сходимость в конце оптимизации, а то и вообще отсутствие сходимости.
Я читал, что его используют, когда не нужна хорошая точность результатов, например для оценки параметров в методе опорных векторов
Минусом является плохая сходимость в конце оптимизации, а то и вообще отсутствие сходимости.
Я читал, что его используют, когда не нужна хорошая точность результатов, например для оценки параметров в методе опорных векторов
+1
Отличная статья! Отличная анимация!
Вопрос. Такой метод будет нормально работать в условиях многочисленных локальных минимумов, гребней, оврагов и т.д.? То есть на очень сложной поверхности?
Вопрос. Такой метод будет нормально работать в условиях многочисленных локальных минимумов, гребней, оврагов и т.д.? То есть на очень сложной поверхности?
0
Посоветуйте либу на С++ реализующую этот алгоритм. Начать изучать (и использовать в простых задачах) ceres-solver. Что скажите о ней?
0
К сожалению, не работал с библиотеками на C++
0
Было дело использовал библиотеку CppNumericalSolvers Только заголовочные файлы, небольшая и хорошо расширяема. Автор быстро отвечает на тикеты :)
+1
Отличная статья! Радует глаз такая качественная работа! 5+
0
Спасибо за статью, вынудила залезть в книжки.
У Вас в предисловии к методу Ньютона разделяется (возможно, ненамеренно) метод решения нелинейных уравнений и метод одноименный оптимизации. Фактически это один и тот же метод, если свести задачу поиска минимума функции к решению уравнения «градиент равен нулю».
Зачем в алгоритме Ньютона делать проверку на положительную определенность гауссиана, ведь она требуется только в точке минимума и совершенно не обязательно присутствует в окрестности этой точки?
Откуда взята рекомендованное значение 0.05 на шаг в МНС?
Вопросы вызвал метод Гаусса-Ньютона (ранее не встречал), формулировка мне показалась странноватой. Фактически оптимизирующей последовательностью в данном случае (при \alpha = 1) является последовательность минимумов тейлоровых приближений первого порядка целевой функции. Это кажется странным, ведь остаточный член формулы Тейлора может считаться пренебрежимо малым лишь в достаточно малой окрестности точки разложения, а в данном случае искомый минимум может быть от нее сколь угодно далеко. Такую быструю сходимость для функции Розенброка, по-видимому, можно связать с достаточно «хорошим» поведением ее производных. В литературе, на кторую Вы ссылаетесь, утверждается, что если такая последовательность сходится, то она сходится к стационарной точке. Но я не нашел никаких упоминаний того, при каких условиях гарантируется, либо хотя-бы имеет смысл надеяться, что последовательность сойдется. Встречали ли Вы упоминания чего-либо подобного? Также в данном случае не очень понятен смысл и критерий выбора значения параметра «шага» алгоритма.
У Вас в предисловии к методу Ньютона разделяется (возможно, ненамеренно) метод решения нелинейных уравнений и метод одноименный оптимизации. Фактически это один и тот же метод, если свести задачу поиска минимума функции к решению уравнения «градиент равен нулю».
Зачем в алгоритме Ньютона делать проверку на положительную определенность гауссиана, ведь она требуется только в точке минимума и совершенно не обязательно присутствует в окрестности этой точки?
Откуда взята рекомендованное значение 0.05 на шаг в МНС?
Вопросы вызвал метод Гаусса-Ньютона (ранее не встречал), формулировка мне показалась странноватой. Фактически оптимизирующей последовательностью в данном случае (при \alpha = 1) является последовательность минимумов тейлоровых приближений первого порядка целевой функции. Это кажется странным, ведь остаточный член формулы Тейлора может считаться пренебрежимо малым лишь в достаточно малой окрестности точки разложения, а в данном случае искомый минимум может быть от нее сколь угодно далеко. Такую быструю сходимость для функции Розенброка, по-видимому, можно связать с достаточно «хорошим» поведением ее производных. В литературе, на кторую Вы ссылаетесь, утверждается, что если такая последовательность сходится, то она сходится к стационарной точке. Но я не нашел никаких упоминаний того, при каких условиях гарантируется, либо хотя-бы имеет смысл надеяться, что последовательность сойдется. Встречали ли Вы упоминания чего-либо подобного? Также в данном случае не очень понятен смысл и критерий выбора значения параметра «шага» алгоритма.
0
опечатался, положительную определенность гессиана, конечно.
0
- «У Вас в предисловии к методу Ньютона разделяется (возможно, ненамеренно) метод решения нелинейных уравнений и метод одноименный оптимизации. Фактически это один и тот же метод, если свести задачу поиска минимума функции к решению уравнения «градиент равен нулю» „
Я не отрицаю общей идеи методов, но решения уравнений будут разные. В методе для поиска корня предполагается дополнительно, что f(x*)=0 и используется только линейная аппроксимация - “Зачем в алгоритме Ньютона делать проверку на положительную определенность гауссиана, ведь она требуется только в точке минимума»
Вы думаете в верном направлении, только смотрите в чём фокус: мы на каждом шаге аппроксимируем квадратичной функцией в окресности. А далее — ищем минимум этой аппроксимации. И это на Каждой итерации. - «Откуда взята рекомендованное значение 0.05 на шаг в МНС», например отсюда 14 стр. Вообще рекомендуют использовать шаги 0.005, 0.01, 0.05, и 0.10
- «Вопросы вызвал метод Гаусса-Ньютона (ранее не встречал), формулировка мне показалась странноватой. Фактически оптимизирующей последовательностью в данном случае (при \alpha = 1) является последовательность минимумов тейлоровых приближений первого порядка целевой функции. Это кажется странным, ведь остаточный член формулы Тейлора может считаться пренебрежимо малым лишь в достаточно малой окрестности точки разложения, а в данном случае искомый минимум может быть от нее сколь угодно далеко»
Согласен, однако это рекомендованное значение. Тут можно принять во внимание, что целевая функция неотрицательна, на практике я читал метод работает хорошо с таким коэффициентом.
- " Но я не нашел никаких упоминаний того, при каких условиях гарантируется, либо хотя-бы имеет смысл надеяться, что последовательность сойдется"
Стр. 21 «The method with line search can be shown to have guaranteed
convergence» при выполнении условий. Про полный ранг J я писал в статье. Про ограничение F(x)<=F(x_0) можно было добавить
0
1. Ну правильно, решается уравнение F(x) = 0 с нелинейной функцией F. Для этого оно приводится к форме задачи о поиске неподвижной точки путем умножения слева на несигнулярную матрицу (-A) (выбираемую в принципе произвольно и в общем отличающуюся на каждой итерации) и прибавления к обеим частям x, из чего имеем:
x — A*F(x) = x.
В классическом методе Ньютона в качестве A берется обратная к F'(x) = J(x) и вводится итерационная последовательность
%5E%7B-1%7D%20%5Ccdot%20F(x_%7Bk%7D))
А чтобы исключить необходимость обращения якобиана, можно это привести в неявной формуле относительно приращения:
%20(x_%7Bk%2B1%7D%20-%20x_%7Bk%7D)%20%3D%20-%20F(x_%7Bk%7D))
Теперь для задачи оптимизации функции F имеем уравнение%20%3D%200) его якобиан = гессиан целевой функции. Итого имеем
его якобиан = гессиан целевой функции. Итого имеем
%20(x_%7Bk%2B1%7D%20-%20x_%7Bk%7D)%20%3D%20-%20%5Cbigtriangledown%20F(x_%7Bk%7D)) .
.
Сравните это с написанным у Вас.
2. Вы не ответили на вопрос зачем в Вашем случае требовать положительность гессиана. Вы действительно движетесь на каждой итерации в направлении наивысшей кривизны, но делать трудоемкую проверку на положительную определенность-то зачем? Это, конечно, не криминал, и даже объяснимо, поскольку в случае положительной определенности матрицы A поправка (x_{k+1} — x{k}) определяет т.н. «направления спуска» и оказываются применимы классические теоремы сходимости методов прямого поиска. Но в таком случае нужно накладывать ограничения на выбор последовательности значений «шага» — иначе это требование бессмысленно. А в приведенной формулировке об этом не упоминается. Я, честно сказать, не видел применения к реальным задачам модифицированных методов Ньютона с проверкой и коррекцией определенности гессиана. Возможно, Вы видели?
3. На странице 14 приведены результаты вычислительных экспериментов при минимизации конкретной функции, с чего Вы решили, что это рекомендуемые значения? Меня смутило вот что. Из теории градиентных методов известно, что при выборе постоянного на протяжении всего оптимизирующего процесса «шага» есть порог значения, при котором процесс теряет устойчивость. Этот порог сильно зависит от вида целевой функции. Откуда могут взяться такие рекомендации? Единственное, что мне приходилось видеть, это замечания вроде: «попробуйте значение на-вскидку, разошлось — уменьшите, сходится но медленно — прервите и уменьшите шаг». А так, чтоб конкретные значения…
4 и 5. Действительно, не слишком внимательно изучил материал. При более подробном изучении увидел, что определяемое поправкой направление оказывается направлением спуска, а значит есть классы функций, для которых гарантированно существует последовательность «шагов», приводящая к стационарной точке. Но, например, здесь подтверждают мое предположение о том, что для сходимости с произвольным шагом функция должна быть достаточно гладкой и достаточно пологой. А здесьше доказательно показывается, что применяемых обыкновенно условий Гольдштейна и Вульфа для шага итерации не достаточно для сходимости.
x — A*F(x) = x.
В классическом методе Ньютона в качестве A берется обратная к F'(x) = J(x) и вводится итерационная последовательность
А чтобы исключить необходимость обращения якобиана, можно это привести в неявной формуле относительно приращения:
Теперь для задачи оптимизации функции F имеем уравнение
Сравните это с написанным у Вас.
2. Вы не ответили на вопрос зачем в Вашем случае требовать положительность гессиана. Вы действительно движетесь на каждой итерации в направлении наивысшей кривизны, но делать трудоемкую проверку на положительную определенность-то зачем? Это, конечно, не криминал, и даже объяснимо, поскольку в случае положительной определенности матрицы A поправка (x_{k+1} — x{k}) определяет т.н. «направления спуска» и оказываются применимы классические теоремы сходимости методов прямого поиска. Но в таком случае нужно накладывать ограничения на выбор последовательности значений «шага» — иначе это требование бессмысленно. А в приведенной формулировке об этом не упоминается. Я, честно сказать, не видел применения к реальным задачам модифицированных методов Ньютона с проверкой и коррекцией определенности гессиана. Возможно, Вы видели?
3. На странице 14 приведены результаты вычислительных экспериментов при минимизации конкретной функции, с чего Вы решили, что это рекомендуемые значения? Меня смутило вот что. Из теории градиентных методов известно, что при выборе постоянного на протяжении всего оптимизирующего процесса «шага» есть порог значения, при котором процесс теряет устойчивость. Этот порог сильно зависит от вида целевой функции. Откуда могут взяться такие рекомендации? Единственное, что мне приходилось видеть, это замечания вроде: «попробуйте значение на-вскидку, разошлось — уменьшите, сходится но медленно — прервите и уменьшите шаг». А так, чтоб конкретные значения…
4 и 5. Действительно, не слишком внимательно изучил материал. При более подробном изучении увидел, что определяемое поправкой направление оказывается направлением спуска, а значит есть классы функций, для которых гарантированно существует последовательность «шагов», приводящая к стационарной точке. Но, например, здесь подтверждают мое предположение о том, что для сходимости с произвольным шагом функция должна быть достаточно гладкой и достаточно пологой. А здесьше доказательно показывается, что применяемых обыкновенно условий Гольдштейна и Вульфа для шага итерации не достаточно для сходимости.
+1
Подскажите почему траектория поиска в трех методах из четырех летит в начале поиска в воздухе, а не ползет по поверхности функции.
0
Нет сравнительного анализа погрешности аппроксимации
0
Sign up to leave a comment.
Алгоритм Левенберга — Марквардта для нелинейного метода наименьших квадратов и его реализация на Python