Comments 77
Если вас интересует введение, можете попробовать посмотреть здесь.
Сейчас я понимаю что там вейвлеты были бы очень в помощь. К сожалению не знаю ни одной библиотеки общего назначения включающей вейвлет-преобразование, все только про изображения. То же самое с литературой.
Лекция — Преобразование Гильберта-Хуанга
Спектральный анализ на ограниченном интервале времени. Оконные функции
Но, честно говоря, не знаю, как оконные функции использовать в данной ситуации. Можно же просто менять длительность измерения, чтобы укладывалось целое число периодов составляющих сигнала. Зачем оконные функции?
Увеличение и подбор периода измерения возможно только в частных случаях, когда мы например измеряем качество напряжения в бытовой сети — частота сигнала известна с высокой точностью, нас интересуют только гармоники.
А если стоит задача измерить спектральное распределение в шумоподобном сигнале? Где там брать период сигнала?
Главная особенность этих функций — они плавно уменьшают амплитуду обрабатываемого сигнала в начале и конце до нуля, поэтому краевые эффекты исчезают.
Соответствующая картинка с сайта выше:

Или электродвигатель вращает передаточный механизм с известной скоростью и т.д.
А с какой целью необходимо получить спектральное распределение? Чтобы посмотреть как энергия распределяется по частоте? Так это одна задача. А выделить составляющие сигнала — это другая задача.
… а применительно к сигналам из реального мира, само преобразование фурье тривиально, а самые ништяки кроются в особенностях нарезки оных тайлов…

Длительность 4,5 сек
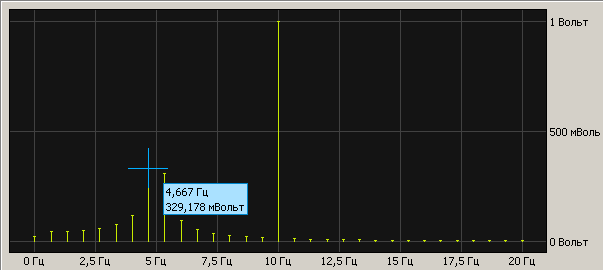
Длительность 1,5 сек

Длительность 11,5 сек
Хм… Интуитивно мне казалось, что амплитуда гармоники 5Гц с увеличением длительности измерения будет стремиться к реальной 0.5 В.
Про артефакты, маскировку частот.
Про конечность выборки.
Про фильтры и окна.
Маткадовские примеры (старый Mathcad).
«По самому определению дискретного Фурье-преобразования, исходная функция и так предполагается равной
нулю за пределами расчетного интервала». Это для интеграла Фурье.
Для рядов Фурье за пределами интервала измерений исходная функция продлевается периодически, что позволяет найти «неискаженный правильный» спектр, даже если сигнал ограничен.
Собственно пафос данной статьи в этом и заключался ))
Хотя, если в пределах окна уложится целое число периодов сигнала — спектр все равно будет «искаженный»?
— не верно Ряд Фурье не сходится поточечно. Здесь более тонкие вещи происходят. (см. эффект Гипса, и определение сходимости функций)
2. «Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. »
— Не иногда, а ВСЕГДА. Очень громоздкая нотация с sin-ми и cos-ми. Вы с этой нотацией далеко не уедете! Преобразование Фурье применяется для очень сложных математических и физических задач. Нечего создавать исскусственную сложность накачивая выражения лишними латинскими буквами.
3. «Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда)
тригонометрических функций (синусоид и\или косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.»
У вас всё перемешалось в голове или вы описались.
— Преобразование Фурье не определено (в классическом понимании функций) для функции равной константе. Вы не до конца понмиаете ряды Фурье, так что преобразование лучше и не трогайте.
— То что функция определена на периоде [0,T] это не означает, что она периодическая если вы говорите о ряде Фурье.
— Существует ли преобразование Фурье для функции которая определена и непрерывна [0,T] ЗАВИСИТ от поведения на концах этой функции. Для функций некоторых классов это преобразование существует.
Если вы считаете, что вы не описались, тогда — ну не можете Вы комбинирую гармонические функции сложением получить не периодическую функцию.
4. «Преобразование Фурье — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
— Не очень глубокая фраза. И более того, вообще-то преобразование Фурье определено и для функций нескольких аргументов. Это стоит подчеркнуть. Т.к. не все методы обобщаются на R^n (e.g. поиска нуля функции в отрезке [a, b] для f(a)f(b)<0)
Про то что вы писали:
«что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать.»
— да так надо делать, потому что это единственный способ что-то выводить и писать компактно. Если чувствуете дискомфорт, то вам просто рано трогать эту темы в полной мере. Для математиков ДПФ, Преобр. Фурье, Ряд Фурье — разные вещи для вас — судя по статье одинаковые. Нету никаких математиков! Есть инженеры и всё. Все те люди которые причастны к этому преобразованию Хевисайд, Лауренц Шварц, Фурье — они не только математики.
«ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле,...»
— что же такое спектр, и каковы его составляющие вопрос остался открытым…
И на последок от себя:
1. Преобразование Фурье не определено для sin,cos, единицы.
2. Ряд Фурье сходится только для функций которые относятся к класс L2 в смысле что сходится площадь охватываемой изначальной функции и вашим разложением.
Могу посоветовать, не торопится… И когда вы увидите основные Теоремы такие как (Reiz-Fisher Theorem).
2. Это зависит от задачи. С тем же успехом моно сказать, что «не надо забивать себе голову комплексными величинами, когда амплитуды и частоты — реальные»
3.>Если вы считаете, что вы не описались, тогда — ну не можете Вы комбинирую гармонические функции сложением получить не периодическую функцию.
Ну вот из-за подобного я и писал статью. И все равно…
Комбинируя гармонические функции мы получим функцию, совпадающую с нашим измеренным сигналом на отрезке измерения. Это все что надо. А вне этого отрезка функция будет периодически продолжена. Но в нашем конкретном случае это не важно.
И кто тут что не понимает ..))
4. Рассматривалось применение преобразование Фурье в сигналам. Поэтому. А так конечно, математическая теория гораздо шире.
Я в своих ограниченных задачах дискомфорта уже не чувствую. А люди которые, начинают изучать эту тему и у которых в голове смешались ряды Фурье и для периодических функций и преобразование — для непериодических, и много чего еще — конечно чувствуют дискомфорт.
>Преобразование Фурье не определено для sin,cos, единицы.
Ох… Еще раз — пафос статьи был в том, чтобы обратить внимание на ряды Фурье, как способ анализа сигналов.
Зачем сюда притягивать преобразование Фурье? Вот и получается каша ((
A: В статье, как мне показалось очень свободно эти термины меняются местами.
У меня есть вопрос. Т.е. получает так, то что вы предлагаете:
1. Мы берём функцию
2. Умножаем её на прямогольник, который принимает 1 в отрезке [0,T]
3. Периодизруете функцию с шагом T (сворачиваете с Ш шагом в T)
4.a. Делааете разложением в Ряд Фурье.
4.б Умножаете функцию 4.a на коробку с шага 2
И в результате вы получаете, что 4.б есть аппроксимация 2.?
По поводу вопроса.
1. Берем непериодическую функцию, определенную на всей оси X, от -беск до +беск.
2. Вырезаем из нее кусок от 0 до Т
3. Разлагаем этот кусок в ряд Фурье — представляем этот кусок в виде суммы ряда Фурье
Да, рядом Фурье будет представлена периодическая(!) ф-ция, представленная повторением вырезанного куска.
4. Если ее рассмотреть только на отрезке 0… Т (умножить на коробку), то, да, 4Б есть аппроксимация 2.
4.
За пределами [0,T] можно не «добивать» функцию нулями, а размножить периодически-чётно, и тогда всё хорошо будет, получится дискретный действительнозначный спектр из дельта-функций. А если добивать нулями, то должен получиться гадкий непрерывный, да ещё и с комплексной частью.
Почему из дельта-функций? Просто амплитуды гармоник. Конечные величины.
Потому что $f(x) = \sum{n=-\infty}^{\infty} A(n) e^{2i\pi n x} = \int{-\infty}^{\infty} (\sum_{n=-\infty)^{\infty}\delta( \xi — n)) e^{2i\pi \xi x}d\xi$
Слева у вас стоит ряд Фурье по комплексным экспонентам, а справа — обратное преобразование Фурье по комплексным экспонентам (плюс коэффициент я где-то потерял).
$\delta(\xi — x) = <e^{ix\xi},e^{ix\xi}>$
Приведенная вами формула означает то же самое?
Ну, проинтегрируйте преобразование Фурье, которое у меня справа, то и получите.
Ряд Фурье — это просто частный случай преобразования Фурье, когда функция периодическая и действительнозначная. Тогда преобразование даст гребёнку из дельт, а формула для обратного как раз и даст коэффициенты ряда. А всякие гадкие мнимые части уйдут.
Хармут_Теория секвентного анализа Основы и применения_1980.djvu
Я так понимаю, с их помощью удобно синтезировать произвольные сигналы сложением прямоугольных функций.
«Чтобы увеличить разрешение в 2 раза до 0,5 Гц — надо увеличить длительность измерения в 2 раза — до 2 сек. Сигнал длительностью 10 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 0,1 Гц. Других способов увеличить разрешение по частоте нет.»
Казалось бы, два Фурье-разложения, полностью сходящихся на интервале, должны сходится всюду? Почему нельзя, достаточно точно измерив сигнал в 1 сек, расширить его на 10 сек?
после оцифровки превращается в сигнал низкой частотыА какой именно частоты? Правильно ли, что: T_observed = T_sample%T_signal?
10%21=10=-11
10%11=10=-1
10%9=1
график 10%x в wolframalpha
Еще интересно, возникает ли аналогичный эффект, когда сигнал имеет больший период, чем период окна?
Что-то наподобие: T_observed = T_sample%T_signal%T_frame?
frame_rate < freq0 < sample_rate,
где < — отношение делимости,
то разложив размер окна на простые множители, и взяв оригинальные подмножества, получим количество возможных частот без искажений:
window=2*2*2*2*3*5*5*5*11 gives (1+4)*(1+1)*(1+3)*(1+1) frequencies
window=60=2*2*3*5 gives (1+2)*(1+1)*(1+1)*(1+1)=24 frequencies
window=4096=2^12 gives (1+12)=13 frequencies
А sample_rate говорит о том, сколько вообще гармоник может быть в спектре, то есть задает их количество.
А для высших гармоник, я так понимаю, играет роль то, что за время измерения уложится много их периодов. Поэтому, хотя на один период ВЧ гармоники придется например 5 точек (некратность может быть в пределах 1\5 периода ВЧ гармоники), но за время измерения произойдет усреднение и размазывание уменьшится. Но это надо смотреть. (Студентам лабораторная работа :-)
А вот с амплитудой все хуже, она сильно уменьшается.
— не верно Ряд Фурье не сходится поточечно. Здесь более тонкие вещи происходят. (см. эффект Гипса, и определение сходимости функций)
2. «Иногда при работе с рядами Фурье бывает удобнее использовать вместо синусов и косинусов экспоненты мнимого аргумента, то есть использовать преобразование Фурье в комплексной форме. »
— Не иногда, а ВСЕГДА. Очень громоздкая нотация с sin-ми и cos-ми. Вы с этой нотацией далеко не уедете! Преобразование Фурье применяется для очень сложных математических и физических задач. Нечего создавать исскусственную сложность накачивая выражения лишними латинскими буквами.
3. «Преобразование Фурье позволяет представить непрерывную функцию f(x) (сигнал), определенную на отрезке {0, T} в виде суммы бесконечного числа (бесконечного ряда)
тригонометрических функций (синусоид и\или косинусоид) с определёнными амплитудами и фазами, также рассматриваемых на отрезке {0, T}. Такой ряд называется рядом Фурье.»
У вас всё перемешалось в голове или вы описались.
— Преобразование Фурье не определено (в классическом понимании функций) для функции равной константе. Вы не до конца понмиаете ряды Фурье, так что преобразование лучше и не трогайте.
— То что функция определена на периоде [0,T] это не означает, что она периодическая если вы говорите о ряде Фурье.
— Существует ли преобразование Фурье для функции которая определена и непрерывна [0,T] ЗАВИСИТ от поведения на концах этой функции. Для функций некоторых классов это преобразование существует.
Если вы считаете, что вы не описались, тогда — ну не можете Вы комбинирую гармонические функции сложением получить не периодическую функцию.
4. «Преобразование Фурье — операция, сопоставляющая одной функции вещественной переменной другую функцию, также вещественной переменной.»
— Не очень глубокая фраза. И более того, вообще-то преобразование Фурье определено и для функций нескольких аргументов. Это стоит подчеркнуть. Т.к. не все методы обобщаются на R^n (e.g. поиска нуля функции в отрезке [a, b] для f(a)f(b)<0)
Про то что вы писали:
«что математикам бывает удобнее представить спектр в комплексной форме с использованием отрицательных частот не значит, что «так правильно» и «так всегда надо делать.»
— да так надо делать, потому что это единственный способ что-то выводить и писать компактно. Если чувствуете дискомфорт, то вам просто рано трогать эту темы в полной мере. Для математиков ДПФ, Преобр. Фурье, Ряд Фурье — разные вещи для вас — судя по статье одинаковые. Нету никаких математиков! Есть инженеры и всё. Все те люди которые причастны к этому преобразованию Хевисайд, Лауренц Шварц, Фурье — они не только математики.
«ДПФ ограниченного во времени сигнала дает его «настоящий» спектр, в том смысле,...»
— что же такое спектр, и каковы его составляющие вопрос остался открытым…
И на последок от себя:
1. Преобразование Фурье не определено для sin,cos, единицы.
2. Ряд Фурье сходится только для функций которые относятся к класс L2 в смысле что сходится площадь охватываемой изначальной функции и вашим разложением.
Могу посоветовать, не торопится… И когда вы увидите основные Теоремы такие как (Reiz-Fisher Theorem) то уже тогда присутпайте к изучению преобразования Фурье.
Преобразование Фурье не определено для sin, cos, единицы
Прекрасно определено и представляет из себя дельта-функции Дирака. Wolfram Alpha в помощь.
Ряд Фурье сходится только для функций которые...
От того, что ряд Фурье не сходится для некоторых функций, он не перестаёт быть рядом Фурье и даже не перестаёт быть однозначно обратимым.
"На рис. 5 красная синусоида высокой частоты" — думаю, здесь по-факту шла речь о рисунке 11 ибо предложение по смыслу и по георафии относится именно к нему :)
Существует ли простой ASIC чип, который с одной стороны получает I2S/PDM интерфейс и аппаратно вычисляет FFT после каждого семпла на линии LR?
То есть вычислять FFT непрерывно в потоковом режиме по скользящему окну.
Чтобы можно было по SPI вычитывать результат работы FFT (массив мощности/ фазы для каждой частоты в спектре входного аудио сигнала).
Скорее всего это какой-то аппаратный аудиокодек с функцией аппаратного FFT. Очень не хотелось бы делать это с нуля на FPGA.
Кто-нибудь сталкивался с подобными микросхемами?
Зачем, какую задачу вы решаете? Скользящее FFT реализуется точно так же, как и скользящее среднее через рекурсивный фильтр, только дополнительно помножается на комплексную синусоиду.
Зачем, какую задачу вы решаете?
Хочу демодулировать FSK сигнал. И передавать бинарные данные звуком. Обновлять прошивку через микрофон.
Там же модуляция вроде только по двум частотам делается? Тогда и для демодуляции полноценное FFT избыточно, по идее двух частот должно быть достаточно.
Если сделать 16 частот, то можно будет передавать log2(16)=4 бита за раз.
Если сделать 32 частоты, то можно будет передавать log2(32)=5 бит за раз.
Если сделать 64 частоты, то можно будет передавать log2(64)=6 бит за раз.
Скорость передачи в любом случае будет ограничена несущей частотой - все эти погони за гигагерцами в сетях WI-FI совсем не случайны. Не получится на частоте в 1Гц передавать данных больше, чем 1 бит в секунду. Близко расположить несущие частоты друг к другу тоже не получится - потому что модуляция расширяет спектр несущей частоты, и чем выше скорость передачи, тем шире полоса. Ну и - при передаче "по воздуху" уровень шума значительно выше, чем по проводам или радиоволнам, прежде всего за счёт акустической реверберации. Фазы будут "уплывать".
таааа ладно? давно уже в эзернет используют 1024 уровневую модуляцию, передавая 10 бит на БОД, конечно же в идеальных условиях. WiFi при этом комбинирует ЧМ и ФМ, получая дополнительные биты на БОД.
Так-то берёте АЦП 4 битное, выдаёте ЦАП-ом на 4 бита напряжение каждую секунду, и получаете скорость передачи 4 бита в секунду, а не ваш 1 максимальный. При этом, конечно в протокол нужно ввести преамбулу, для синхронизации в том числе и по амплитуде.
Что значит "таааа ладно"? Эзернет по проводам передаётся, на чем специально было заострено внимание, и QAM с вариациями - это совсем другие протоколы, чем обсуждаемый здесь FSK.
Передача данных через звук тема не новая и не оригинальная, и куча публикаций, и готовые решения есть. Ну а если вы сможете по факту, а не в мысленном эксперименте превзойти существующие решения - то я буду только рад, эта тема меня тоже интересует.
Если на входе чистая синусоида - то для точного вычисления её частоты достаточно 4-х отчётов. Правда, для этого нужно погрузиться в теорию чуть глубже, чем она описана в типовых учебниках по ЦОС - и выяснить, почему "размытие спектра" выглядит именно так, а не иначе, и какой именно математической функцией она описывается.
Практическое применение преобразования Фурье для анализа сигналов. Введение для начинающих