Comments 11
Все же конечно сюда зашли из-за интереса к метрикам Минковского
пришлось даже свой пост перечитать, а то забыл уже о чем там -)
мне кажется ваша ошибка в рассуждениях где то вот тут; естественно для дискретного объекта, коем является людое изображение, минимальным разбиением будет вообще один единственный пиксель, тогда размерность такого объекта будет максимальной размерностью из множеств разбиения, верно?
вообще говоря верно, но совсем бесполезно
на много полезнее представить что у нас не дискретный объект, а какой то действительно фрактальноподобный (а не просто объединение пикселей, или как вы предположили — отрезков), и предположить что мы можем box-count'ингом аппроксимировать только до определенного момента, а далее уже экстраполировать разбиения, в этом и суть алгоритма
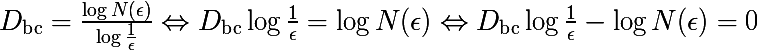
далее обычный подход из машинного обучения:
1 — собрать датасет (как раз аппроксимирование боксами и подсчет их)
2 — обобщить (решить задачу линейной регрессии)
таких предположений там нет, мой пост не о предположения и не гипотезах моих личных, я не ученый, я практик, мой пост о фактах, фактах которые доказаны и приняты
у меня там есть цитата которая имхо отражает, что такое фрактальная размерность
литература
Т.к. контур мы представляем прямыми, то у нас площадь разбивается либо на треугольник, либо квадрат.
мне кажется ваша ошибка в рассуждениях где то вот тут; естественно для дискретного объекта, коем является людое изображение, минимальным разбиением будет вообще один единственный пиксель, тогда размерность такого объекта будет максимальной размерностью из множеств разбиения, верно?
вообще говоря верно, но совсем бесполезно
на много полезнее представить что у нас не дискретный объект, а какой то действительно фрактальноподобный (а не просто объединение пикселей, или как вы предположили — отрезков), и предположить что мы можем box-count'ингом аппроксимировать только до определенного момента, а далее уже экстраполировать разбиения, в этом и суть алгоритма
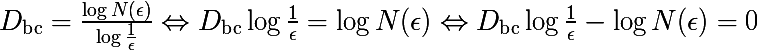
далее обычный подход из машинного обучения:
1 — собрать датасет (как раз аппроксимирование боксами и подсчет их)
2 — обобщить (решить задачу линейной регрессии)
Как не странно, но тоже два. Это, кстати, разбивает предположение в исходной статье, что фрактальная размерность отражает негладкость кривой.
таких предположений там нет, мой пост не о предположения и не гипотезах моих личных, я не ученый, я практик, мой пост о фактах, фактах которые доказаны и приняты
у меня там есть цитата которая имхо отражает, что такое фрактальная размерность
дробная размерность — это своего рода плотность самоподобия
литература
Начну с конца:
У вас там есть такая фраза:
«Фрактальная размерность в районе единицы сообщает нам о том, что фигура действительно без особенностей, и вполне гладкая.»
Вот за нее я зацепился.
>>на много полезнее представить что у нас не дискретный объект, а какой то действительно фрактальноподобный
Вот моя последняя часть как раз об этом. На примере теоретического значений для круга квадрата и треугольника, а также того наблюдения, как банальный поворот банального квадрата вносит ошибку и как это ошибка убывает я длеаю заключение, что натравливать алгоритм на распознавание изображений или другого ряда данные, не будучи уверенным, что это фрактал, практически бесполезно.
У вас там есть такая фраза:
«Фрактальная размерность в районе единицы сообщает нам о том, что фигура действительно без особенностей, и вполне гладкая.»
Вот за нее я зацепился.
>>на много полезнее представить что у нас не дискретный объект, а какой то действительно фрактальноподобный
Вот моя последняя часть как раз об этом. На примере теоретического значений для круга квадрата и треугольника, а также того наблюдения, как банальный поворот банального квадрата вносит ошибку и как это ошибка убывает я длеаю заключение, что натравливать алгоритм на распознавание изображений или другого ряда данные, не будучи уверенным, что это фрактал, практически бесполезно.
а что в реальном мире фрактал?
Очень много что. Облака, горы, деревья, лес, человеческий мозг, раковые образования и т.д… Например, статья, ссылку на которую вы даете ниже — это исследование компьютерных методов в маммографии. И тут я не удивлен.
гугл легко с вами не согласится по поводу того полезная ли фича box-count размерность или нет, вот одна из первых ссылок
Зачем заниматься тем, что невозможно посчитать (Хаусдорф), и тем, что дает оценку только с одной стороны (Минковский), когда есть куча алгоритмов для вычисления Херста. Тут есть свои проблмы (в основном завышение результата), но это хотя бы не безнадежно.
Пример
Пример
Sign up to leave a comment.
Об ограничениях в применимости метрики Минковского в цифровой обработке данных