How to become an author
Search
Write a publication
Pull to refresh

Comments 57

Вообще забавно, но на практике, эффективнее использовать что-то типа
function getDays(month)
{
    switch (month) {
    case 1:
    case 3:
    case 5:
    case 7:
    case 8:
    case 10:
    case 12:
       days = 31;
       break;
    case 4:
    case 6:
    case 9:
    case 11:
       days = 30;
       break;
    case 2:
       days = 28;
       break;
    default:
        days = -1;
    }
    return days;
}

при этом, в февральской ветке можно добавить проверку на високосность.
Total votes 8: ↑4 and ↓40
или [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31][month — 1]
Total votes 22: ↑22 and ↓0+22
Можно ещё 28 + ((0x2eeeecc >> (2*month)) & 3). Ваш вариант выиграет на x86-64, мой — на x86 просто, хотя разница там копеечная.

А вышеупомянутый вариант со switch'ом будет всё-таки разика в полтора медленнее… хотя так ли это всё важно?
Total votes 10: ↑10 and ↓0+10
Почему это switch будет медленный? Ныне компиляторы оптимизируют switch только в путь. В данном случае свитч скорее всего будет оптимизирован в таблицу и соответственно будет иметь константную сложность.
This comment wasn’t rated yet0
Не будет тут switch оптимизирован в таблицу. Обработку defaut'а в таблицу всё равно не засунешь, её всё равно придётся отдельно делать, в с учётом того, что вариантов немного компилятор, скорее всего, сгенерирует одно-два сравнения сверх этого.

Ни до моего варианта, ни до варианта deNULL'а ни один известных мне компилятор не додумался.
This comment wasn’t rated yet0
Ваш вариант самый крутой, умножение заменить сдвигом еще. Вариант с массивом чисел самый очевидный, но закодировать количества дней в 32-битное число — просто и гениально, в стиле олдскульной оптимизации, когда каждый байт был на счету.
Total votes 4: ↑4 and ↓0+4
Умножение я предоставил оптимизировать компилятору. Умножения на константу — это то, что они делают прекрасно. В большинстве случаев компилятор заменит его на сложение и задействует при этом LEA, чтобы регистр не портить.
Total votes 2: ↑2 and ↓0+2
Почему-то никто не обратил внимания на ошибку в константе.
days = 28 + ((0x3bbeecc >> (month * 2)) & 3);
И таки идеальный вариант!
Total votes 5: ↑5 and ↓0+5

Я пытался понять это самостоятельно и нашёл несколько упоминаний подобного метода на других сайтах, но к своему невежеству так и не выяснил: откуда взялось число 0x3bbeecc?

This comment wasn’t rated yet0

К 28 надо прибавить 0, 2 или 3 — это занимает два бита. Отсюда получается 2 в множителе и 3 в маске.
А дальше просто упаковать все добавки в одно целое:


12 11 10 09 08 07 06 05 04 03 02 01 00 - номер месяца
11 10 11 10 11 11 10 11 10 11 00 11 00 - перечисляем количество дней для добавки

И получаем 0x3bbeecc

This comment wasn’t rated yet0
Если не учитывать високосность, то для практики проще всего что-то такое:
function getDays(m){
 return m === 2 ? 28 : 30 + (m > 7 ? m+1 : m) % 2;
}
This comment wasn’t rated yet0
Требую вариант с преобразованием Фурье ))
Total votes 17: ↑17 and ↓0+17
Как-же вы запарили… Да читают, читают ваши теги!
Total votes 28: ↑28 and ↓0+28
Самый простой способ запомнить (без всяких костяшек и мнемонических правил) — помнить о двух цезарях.
При Юлие Цезаре всё было просто: все нечётные месяцы были по 31 дню. Потом пришёл Август; в августе стало 31 день, и начиная с августа чётные месяцы стали по 31 дню.
Total votes 3: ↑3 and ↓0+3
Занятно, но сам с детства использовал «правило костяшек». Если считать костяшки пальцев на руках и выемки между ними слева направо, то костяшка будет указывать на 31 день, а выемка на 30(или 28 в феврале). При этом переход с левой руки на правую как раз попадет на июль-август.
Total votes 6: ↑6 and ↓0+6
А теперь открытие — костяшки можно считать и справа налево и вообще только на одной руке, потому что они симметричны :)
Total votes 7: ↑7 and ↓0+7
Ещё можно помнить о Тиберие, который — по легенде* — пресёк традицию переименования месяцев в честь императоров.

* Когда к Тиберию пришёл сенат с заискивающим предложением назвать в его честь месяц в календаре, тот, засмеявшись, бросил им в ответ:
— Глупцы! Что же вы предложите 13-му императору?!
Total votes 3: ↑3 and ↓0+3
И вы действительно считаете что это запомнить проще чем костяшки?
Total votes 2: ↑2 and ↓0+2
Проведите эксперимент: нужно определить сколько дней в ноябре. Ноябрь -> 11-й месяц -> нечётный и больше 7 => 30 дней. В уме быстрее выйдет, чем все костяшки пересчитывать.
This comment wasn’t rated yet0
Каждый по своему это считает. Для меня есть четыре с половиной «реперные» точки: январь и декабрь (все знают что начинает и кончается год «длинными» месяцами) и вышеупомянутые «июль» и «август» (которые тоже оба длинные потому что император Август не хотел, чтобы его месяц был короче, чем у предшественника). Ну и февраль, как «очень особый» случай (там и от года количество дней зависит). Ну и чего там осталось? 2-3 шага от любой реперной точки — и мы добираемся до любого месяца.

Ваш метод хорош, если помнить какой по номеру каждый месяц, но я таких людей немного знаю. Особенно если учесть что названия врут (судя по названию тот же Ноябрь как бы должен бы быть девятым, да? правда на чётность это не влияет, но всё же...). Всё равно считать нужно откуда-то, а «реперных точек» меньше (что январь первый и декабрь последний, двенадцатый, все знают, а вот что посредине — уже нужно «на пальцах» считать).

Так-то самый быстрый способ — просто запомнить где сколько дней, но если мы тут что-то обсуждаем, то, похоже, что с запоминаем у нас всё не слишком хорошо, не так ли?
Total votes 1: ↑1 and ↓0+1
Можно также воспользоваться интерполяцией Лагранжа:
sage: PolynomialRing(QQ, 'x').lagrange_polynomial(zip(range(1, 13), (31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31)))

-11/907200*x^11 + 163/181440*x^10 - 37/1260*x^9 + 13481/24192*x^8 - 2055371/302400*x^7 + 240683/4320*x^6 - 28268521/90720*x^5 + 85774775/72576*x^4 - 446998571/151200*x^3 + 46351537/10080*x^2 - 221017/56*x + 1416
Total votes 11: ↑11 and ↓0+11
Или, если смущают дроби, можно сделать по модулю например 37:

sage: PolynomialRing(GF(37), 'x').lagrange_polynomial(zip(range(1, 13), (31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31)), algorithm="neville")[-1]

16*x^11 + 12*x^10 + 4*x^8 + 21*x^7 + 29*x^6 + 10*x^5 + 12*x^4 + 34*x^3 + 26*x^2 + 5*x + 10
Total votes 6: ↑6 and ↓0+6
О! спасибо! Очевидным ответом был «интерполяционый полином». Я всё ждал, когда кто-то запостит формулу.
Total votes 3: ↑3 and ↓0+3
Так не честно! :)
У вас информации в формуле заметно больше, чем в самом ряду. В статье более компактный вариант.
Total votes 1: ↑1 and ↓0+1
А теперь посчитайте с учетом високосного года :)
This comment wasn’t rated yet0
Интересно, насколько хорошо справится с задачей генетический алгоритм, если скормить ему достаточно квадратных скобок, операций взятия остатка и небольших целых чисел
Total votes 1: ↑1 and ↓0+1
Другой механизм описан в книге Романовского «Микрокалькуляторы в рассказах и играх». Пара «месяц-год» переводится к нумерации «с марта» (март = 1, февраль = 12), а затем [30,59*месяц] + день − 30.

Правда, ПМК — зверь особый, ветвление там работает медленнее и расходует больше команд, чем умножение. А целую часть даже на Б3-34 можно вычислить через КИПr; r — любой свободный регистр памяти не менее 7 (0…3 автодекрементные, 4…6 автоинкрементные).
Total votes 3: ↑3 and ↓0+3
Немного офтопа. Я ухитрялся на МК-61 на экзамене обращать матрицу 3×3. Заняло это всю память, для вычисления миноров по-чёрному использовались автоинкремент и автодекремент — поэтому матрица вписывалась не в логичные регистры 1…9, а в 7, 8, 9, 1, 2, 3, A, B, C.
Total votes 1: ↑1 and ↓0+1
Насколько я помню, существовали и алгоритмы и для матриц 4x4. Только они были уже интерактивные — эпизодически запрашивали ввод данных, не умещавшихся в памяти. Для МК-52 были возможны и ещё более сложные алгоритмы, не влезающие в 104 (вроде) ячейки оперативной памяти — там была возможность ручной подгрузки программ из энергонезависимой памяти. Были также и библиотеки программ и во внешних ПЗУ. Также можно было сохранять/восстанавливать данные оперативной памяти. Но необходимость делать это вбивая адреса вручную, ручное переключение режимов записи и чрезвычайно долгий процесс сохранения/восстановления убивал все желание работать. Старались обходится более отзывчивыми алгоритмами, разбиением задач на части и записью/восстановлением данных с помощью карандаша и бумаги.
This comment wasn’t rated yet0
Давно думал написать статью на Хабр в духе «как сделать вычисление дня недели по дате на советском программируемом калькуляторе в 40-50 шагов памяти», но посчитал, что мелко и никому не интересно. А тут только из одного месяца такое развели :-)
Total votes 1: ↑1 and ↓0+1
Ну теперь-то вы сделаете статью?
Total votes 3: ↑3 and ↓0+3
Красиво!
На шарпе можно скобки убрать: 
30 ^ m & 1 ^ m / 8 ^ 4 / m & 2;
This comment wasn’t rated yet0
Для сравнения, в предложенной в статье формуле 9 операций
28 + (m + m / 8) % 2 + 2 % m + 1 / m * 2;
а у вас только 7. Интересно, можно ли компактнее?
Total votes 1: ↑1 and ↓0+1
Есть несколько вариантов с 6 действиями:

((m+m/8)|30)-(4/m&2)
31-(102/m&1)-(4/m&2)
((~8)>>m&30)|(3-102/m&5)

Соптимизировать до пяти ни один не удалось.
~8 за действие не считается — это константа.
Total votes 1: ↑1 and ↓0+1
Может я чего не понимаю в колбасных обрезках, но в предложенной мною (и исправленной withkittens) формуле всего четыре действия… или там как-то по другому считать нужно?
Total votes 1: ↑1 and ↓0+1
Я тоже не понимаю. В формуле со сдвигом их действительно четыре. Возможно, смущает слишком магическая константа?
This comment wasn’t rated yet0
Я думаю тут скорее психология: мы тут думаем над всякими чётностями/нечётностми, цезарями и прочим, а оказывается что самый оптимальный вариант — «спресовать» данные о длинах и всё, думать ни о чём не нужно. Обидна, да?
Total votes 1: ↑1 and ↓0+1
Ваше решение хорошее. Но, решение включает полную таблицу, пусть и свернутую в 32битную константу. Поиск альтернативных функций интересен сам по себе, как реализация переборных алгоритмов.
Total votes 1: ↑1 and ↓0+1
Самое красивое и эстетичное из всех =)
Total votes 3: ↑1 and ↓2-1
Можно вот так еще:
31
-
(3) * (m == 2)
+
(1) * (m == 2) * ((y % 4 == 0) - (y % 100 == 0) + (y % 400 == 0))
-
(1) * (m == 4 || m == 6 || m == 9 || m == 11)
Total votes 1: ↑1 and ↓0+1
Вы уверены, что хорошо проверили свои выкладки?

Функция
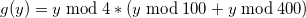
image
Спокойно утверждает 2100 год как високосный, не смотря на оговорку о том, что это не так.

И далее, функция
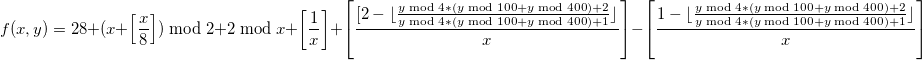
image
Ведет себя так же некорректно:
f(2,2100)===29 //true
Total votes 2: ↑2 and ↓0+2
Вы правы, я вижу ошибку. Я поспешно воспользовался этой формулой. Вместо неё следовало использовать следующую формулу:

(1 - (y % 4 + 2) % (y % 4 + 1)) * ((y % 100 + 2) % (y % 100 + 1)) + (1 - (y % 400 + 2) % (y % 400 + 1))



ideone.com/VDHV3z

Я внесу соответствующие исправления в пост.
This comment wasn’t rated yet0
Благодаря комментарию keksmen исправлена ошибка в формуле определения високосного года (g(y)) и исправлена итоговая формула.
This comment wasn’t rated yet0
С високосным годом (для C/C++):

31-(102/m&1)-((4/m&2)>>((!y%4)-(!y%100)+(!y%400)))

Операция !y — это не условный переход. В зависимости от желания компилятора он компилируется либо в
    neg ecx
    sbb eax,eax
    inc eax

либо в
    xor eax,eax
    test ecx,ecx
    sete al
This comment wasn’t rated yet0
Удостоверьтесь, что не допустили ошибки. Когда я выполняю ваш код, в феврале всегда 28 дней.

ideone.com/QaTplf
This comment wasn’t rated yet0
Да, скобки не там.

31-(102/m&1)-((4/m&2)>>(!(y%4)-!(y%100)+!(y%400)))
Total votes 1: ↑1 and ↓0+1
Date.prototype.isLeapYear = function () {
    var y = this.getFullYear();
    return !(y % 4) && !!(y % 100) || !(y % 400)
};

Date.prototype.getDaysInMonth = function () {
    // adapted from ZX-Spectrum BIOS :-)
    return 28 + ((this.isLeapYear() << 2 | 15662003) >> (this.getMonth() << 1) & 3)
};
This comment wasn’t rated yet0
Sign up to leave a comment.

Articles

Show the best of all time

Your account

Sections

Information

Services

Support
© 2006–2024, Habr