Эта примечательная гипотеза связывает поведение функции L там, где в настоящее время неизвестно, определена ли она, и порядок группы Ш, про которую неизвестно, конечна ли она!
J.T.Tate, The arithmetic of elliptic curves, Inventiones mathematicae 23 (1974)
Оригинал
(Краткая справка насчёт актуальности цитаты 40-летней давности: после Уайлса и Ко таки стало известно, что функцию L можно определить на всей комплексной плоскости. Конечность группы Ш в общем случае остаётся неизвестной.)This remarkable conjecture relates the behaviour of a function L at a point where it is not at present known to be defined to the order of a group Ш which is not known to be finite!
Остаётся обсудить возможность ошибки. В качестве предосторожности против внутренних ошибок компьютера можно прогнать все вычисления дважды или делать проверки внутри программы. Более того, компьютеры — в отличие от людей — устроены так, что их ошибки обычно чересчур велики, чтобы их не заметить. Мы уверены, что в наших результатах нет подобных ошибок. С другой стороны, при кодировании замысловатой схемы вычислений в компьютерную программу неизбежны программистские ошибки. Большинство из них обнаруживаются ещё до основных запусков, из-за того, что программа виснет или выдаёт нелепые результаты. Но программа, которую считается работающей, всё ещё может содержать логические ошибки, проявляющиеся при редких стечениях обстоятельств: и действительно, большинство компьютеров подвержено аномалиям, из-за которых те иногда ведут себя не так, как должны по спецификациям. В сущности, наша программа для этапа (ii) оказалась неточной и пропустила очень небольшое количество эквивалентностей, которые должна была найти.
По этим причинам мы считаем, что не стоит автоматически доверять результатам, полученным на компьютере. В некоторых случаях их можно проверить за счёт свойств, которые по существу не были задействованы в вычислениях и которые вряд ли пережили бы возможную ошибку. (Например, таблицу значений гладкой функции, полученную без использования интерполяции, можно проверить вычислением разностей соседних значений.) Но если подобные проверки недоступны, не стоит полностью доверять результатам, пока они не были независимо подтверждены другим программистом на другом компьютере. Мы не думаем, что это задаёт чрезмерный стандарт во время, когда компьютеры становятся столь широко доступны; и мы уверены, что низкие стандарты уже привели к публикации и вере в неверные результаты.
B.J.Birch and H.P.F.Swinnerton-Dyer, Notes on elliptic curves. I, Journal für die reine und angewandte Mathematik 212 (1963)
Оригинал
It remains to discuss the question of error. One can take precautions against machine errors either by running all the calculations twice or by checks included in the program. Moreover, machines — unlike human beings — are so designed that the errors they make are usually too gross to be overlooked. We are satisfied that there are in our results no undetected errors of this sort. On the other hand, in translating an elaborate scheme of calculation into a machine program one is bound to make mistakes. Most of these are found before the program is used for production runs; they show up because the program grinds to a halt or produces ridiculous results. But a program which is believed to work may still contain logical errors which only have an effect in rare circumstances: and indeed most computers have anomalies which cause them occasionally not to behave in the way that their specifications suggest. In fact, our program for stage (ii) was imperfect in that a very few equivalences were missed by the machine.
For these reasons we believe that results obtained from a computer should not be automatically trusted. In some cases they can be checked because they have properties which were not essentially used in the course of the calculation and which would be unlikely to survive if an error had been made. (For example, if a table of a smooth function has been calculated without the use of interpolation, it can be checked by differencing.) But if checks of this sort are not available, results should not be fully trusted until they have been independently reproduced by a different programmer using a different machine. We do not think this sets an unreasonable standard, now that computers are becoming so widely available; and we are satisfied that lower standards have already led to a number of untrue results being published and believed.
For these reasons we believe that results obtained from a computer should not be automatically trusted. In some cases they can be checked because they have properties which were not essentially used in the course of the calculation and which would be unlikely to survive if an error had been made. (For example, if a table of a smooth function has been calculated without the use of interpolation, it can be checked by differencing.) But if checks of this sort are not available, results should not be fully trusted until they have been independently reproduced by a different programmer using a different machine. We do not think this sets an unreasonable standard, now that computers are becoming so widely available; and we are satisfied that lower standards have already led to a number of untrue results being published and believed.

Под катом не будет формулировки гипотезы; знающие выражения вроде «Euler product» и «holomorphic continuation» (и в смысле языка, и в смысле обозначаемых понятий) могут прочитать пятистраничный pdf с сайта института Клэя. Под катом — некоторая попытка пояснить, на каком направлении развития математической мысли вообще находится гипотеза Бёрча — Свиннертон-Дайера. А также — как можно досчитать до больших чисел вроде тех, что показаны на КДПВ, менее чем за секунду.
Речь пойдёт о поиске рациональных решений уравнений с двумя переменными.
Линейные и квадратичные уравнения
Простейший случай — линейные уравнения: ax+by+c=0 (где a, b, c — рациональные). Здесь решение просто: если исключить вырожденные случаи с a=b=0, одна из переменных может принимать любое рациональное значение, а другая однозначно вычисляется по первой.
Следующий случай — квадратичные уравнения. Здесь разных случаев уже больше, но если вычеркнуть те, где всё и так понятно (y-x²=0, y²-x²=0), то оставшиеся линейной заменой переменных сводятся к виду ax²+by²+c=0, где a, b, c ненулевые рациональные. Возьмём три характерных примера:

Очевидно, что первый пример не имеет рациональных решений, потому что левая часть всегда не меньше единицы и не может быть равна нулю. Можно сказать по-другому: первый пример не имеет даже вещественных решений, а рациональные числа — подмножество вещественных, так что и рациональных решений нет.
Менее очевидно, что второй пример не имеет рациональных решений. Приведём x и y к наименьшему общему знаменателю, пусть x=k/n, y=m/n, где k, m, n целые и взаимно простые в совокупности (то есть нет числа, большего единицы, которое одновременно делило бы все три). Тогда уравнение преобразуется к виду
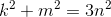 .
.Рассмотрим его по модулю 3. Квадрат целого числа по модулю 3 может быть равен либо 0, либо 1; сумма двух квадратов по модулю 3 может быть нулём, только если оба числа делятся на 3. Значит, k и m должны делиться на 3.
Возьмём теперь модуль 9=3². Левая часть делится на 9, отсюда 3n² должно делиться на 9 и n должно делиться на 3. Значит, решений, где k, m, n целые и взаимно простые в совокупности, не существует, и у исходного уравнения нет рациональных решений, как и было обещано.

У третьего уравнения несколько решений указать легко: например, x=1, y=0. Когда известно одно решение квадратичного уравнения, не составляет труда найти все методом, восходящим ещё к Диофанту: прямая, проходящая через точку (1,0), пересекает окружность ещё ровно в одной точке, и эта точка будет рациональной тогда и только тогда, когда угловой коэффициент прямой рационален. Конкретно для окружности, если обозначить угловой коэффициент через -t, прямая имеет вид y=(1-x)t, и вторая точка пересечения с окружностью x²+y²=1 имеет координаты
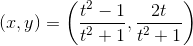 — это и есть общее решение третьего примера (за исключением самой точки (1,0), которая в некотором смысле соответствует
— это и есть общее решение третьего примера (за исключением самой точки (1,0), которая в некотором смысле соответствует 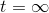 ).
).Принцип Хассе
Идея приводить уравнения с целыми или рациональными коэффициентами по модулю какого-нибудь простого числа, а также степеней этого же числа, исключительно плодотворна. Специальная конструкция «давайте скажем, что нас интересует только то, что происходит по модулю p, p² и всех остальных степеней p сразу, а прочие арифметические свойства мы игнорируем» называется "p-адические числа" (здесь могла бы быть ссылка на Википедию, но там иногда попадаются страшные слова); p-адические числа, как и вещественные, содержат в себе рациональные числа и добавляют много других (например, квадратный корень из 2 извлекается по модулю 7 и всех степеней семёрки, так что он есть среди 7-адических чисел; с другой стороны, он же не извлекается ни по модулю 4, ни по модулю 3, так что среди 2- и 3-адических чисел его нет). Рассуждения по поводу второго примера дословно переносятся на 3-адические числа, и можно сказать: второй пример не имеет даже 3-адических решений, а рациональные числа — подмножество 3-адических, так что и рациональных решений нет.
Работать с одним простым числом часто легко и приятно. В конце концов, все варианты по модулю простого числа можно перебрать. С другой стороны, работа более чем с одним простым числом имеет тенденцию быть намного сложнее — проблема Гольдбаха и проблема простых-близнецов тому яркие свидетельства.
 Переход к вещественным и p-адическим числам хорошо помогает доказывать, что решений нет. И наоборот, принцип Хассе говорит, что если есть вещественные и p-адические решения для всех p, то обязательно есть и рациональные решения. (Конечно, простых чисел бесконечно много, и проверка всех может затянуться. Но можно доказать, что если p не делит ни числители, ни знаменатели a, b, c и больше 2, то p-адические решения всегда есть, а для делителей abc можно эффективно проверить существование решений с помощью закона квадратичной взаимности.)
Переход к вещественным и p-адическим числам хорошо помогает доказывать, что решений нет. И наоборот, принцип Хассе говорит, что если есть вещественные и p-адические решения для всех p, то обязательно есть и рациональные решения. (Конечно, простых чисел бесконечно много, и проверка всех может затянуться. Но можно доказать, что если p не делит ни числители, ни знаменатели a, b, c и больше 2, то p-адические решения всегда есть, а для делителей abc можно эффективно проверить существование решений с помощью закона квадратичной взаимности.)К большому сожалению, принцип Хассе не выполняется для уравнений более высокой степени. Например, можно доказать, что уравнение 3x3+4y3+5=0 имеет вещественные и p-адические решения для всех p, но не имеет рациональных решений.
Эллиптические кривые
Уравнение третьей степени, если, опять же, вычеркнуть разные вырожденные случаи вроде y(x²-1)=x3-1 и y²=x3+x², задаёт кривую рода 1 (это не определение, бывают и другие кривые рода 1). На кривой может и не быть точек (решений уравнения). Если точки есть и если выделить одну из них, получится эллиптическая кривая; в случае эллиптической кривой всегда можно заменой переменных отправить выделенную точку на бесконечность и получить уравнение стандартного вида y²=x3+ax+b, a, b рациональные (и даже целые, от знаменателей всегда можно избавиться ещё одной заменой переменных), что мы и сделаем: дальше будут только эллиптические кривые (над рациональными числами).
Неформально говоря, насколько именно принцип Хассе нарушается для отдельно взятой эллиптической кривой и связанных с ней сущностей, характеризует группа Тейта — Шафаревича кривой, с подачи Тейта традиционно обозначаемая кириллической Ш даже в статьях, где большинство букв — английские. Предполагается, что она конечна. Гипотеза Бёрча — Свиннертон-Дайера задействует порядок этой группы.
 В отличие от квадратичных уравнений, после нахождения одной точки (и отправки её на бесконечность) всё только начинается. Хорошо известно, что точки на эллиптической кривой можно складывать. Если взять одну точку и начать её складывать с самой собой (P, P+P=2P, P+P+P=3P, ...), то возможны два варианта: либо через какое-то число шагов получится бесконечно удалённая точка (после чего следующий шаг даст снова P и процесс зациклится), либо все получаемые точки будут различны (и тогда имеет смысл взять ещё и -P, -2P и так далее). В первом случае точка называется точкой кручения; для отдельно взятой кривой таких может быть от 1 до 12, исключая 11 (всегда существующая бесконечно удалённая точка — тоже точка кручения). Теорема Морделла — Вейля гласит, что всегда можно найти конечное число (возможно, 0) точек второго типа P1, ..., Pr так, что любая точка кривой единственным образом записывается в виде n1P1+...+nrPr+Q, где Q — какая-то точка кручения, а ni — целые числа. Число r называется рангом кривой. Например, кривая y²=x3+877x, нарисованная на КДПВ, имеет ранг 1 и две точки кручения; любая (рациональная) точка кривой есть либо nP, либо nP+(0,0), где координаты P подписаны на картинке.
В отличие от квадратичных уравнений, после нахождения одной точки (и отправки её на бесконечность) всё только начинается. Хорошо известно, что точки на эллиптической кривой можно складывать. Если взять одну точку и начать её складывать с самой собой (P, P+P=2P, P+P+P=3P, ...), то возможны два варианта: либо через какое-то число шагов получится бесконечно удалённая точка (после чего следующий шаг даст снова P и процесс зациклится), либо все получаемые точки будут различны (и тогда имеет смысл взять ещё и -P, -2P и так далее). В первом случае точка называется точкой кручения; для отдельно взятой кривой таких может быть от 1 до 12, исключая 11 (всегда существующая бесконечно удалённая точка — тоже точка кручения). Теорема Морделла — Вейля гласит, что всегда можно найти конечное число (возможно, 0) точек второго типа P1, ..., Pr так, что любая точка кривой единственным образом записывается в виде n1P1+...+nrPr+Q, где Q — какая-то точка кручения, а ni — целые числа. Число r называется рангом кривой. Например, кривая y²=x3+877x, нарисованная на КДПВ, имеет ранг 1 и две точки кручения; любая (рациональная) точка кривой есть либо nP, либо nP+(0,0), где координаты P подписаны на картинке.Все точки кручения найти сравнительно несложно. Например, в случае целых коэффициентов a и b все точки кручения (исключая бесконечно удалённую) сами имеют целые координаты, причём y-координата либо равна нулю, либо y² делит 4a3+27b². Вычисление ранга и поиск порождающих точек Pi намного сложнее.
Пора что-нибудь вычислить
Можно искать точки на кривой, просто перебирая числитель и знаменатель x-координаты в порядке возрастания и проверяя, получается ли рациональное y. Нетрудно сообразить, что в случае целых коэффициентов кривой знаменатель x должен быть точным квадратом, а знаменатель y — кубом того же числа (знаменатели на КДПВ равны 78841535860683900210 в квадрате и в кубе), что немного облегчает жизнь. Впрочем, кривая на КДПВ специально выбрана так, чтобы взгляд на неё пресекал подобные мысли в зародыше (P — точка с наименьшим знаменателем, не считая (0,0)).
В принципе, существует общая процедура n-спуска (n — натуральное число, не меньшее 2), которая позволяет вычислить r и найти r независимых точек, если группа Тейта-Шафаревича не имеет элементов порядка n, и получить верхнюю и нижнюю оценку на r и найти сколько-то независимых точек в общем случае. (В последнем случае можно повторить спуск, выбирая в качестве n растущие степени какого-нибудь простого числа; если группа Тейта-Шафаревича таки конечна, то через конечное время процесс сойдётся.) Но на практике выполнять её крайне неудобно. Бёрч и Свиннертон-Дайер в первой из двух своих статей предложили метод для 2-спуска, не выходящий за рамки вещественной арифметики. Желающие точного описания могут заглянуть в исходники mwrank, а конкретно в mwrank1.cc, здесь будут некоторые результаты для y²=x3+877x.
На первом этапе метод ищет квартики — кривые вида
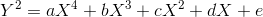 , — из которых есть отображение на исходную кривую, путём перебора a, b, c в определённых диапазонах, вычисления d и e, проверки, что d и e получаются целыми, и отбрасывания тех квартик, на которых нет вещественных точек или p-адических точек для хоть какого-нибудь p.
, — из которых есть отображение на исходную кривую, путём перебора a, b, c в определённых диапазонах, вычисления d и e, проверки, что d и e получаются целыми, и отбрасывания тех квартик, на которых нет вещественных точек или p-адических точек для хоть какого-нибудь p.После первого этапа некоторые квартики могут оказаться эквивалентными (переходить друг в друга дробно-линейной заменой X). На втором этапе метод оставляет по одной квартике из каждого класса эквивалентности. После этого остаётся 2m+k-1 квартик, где множитель 2k равен 1,2 или 4, если на исходной кривой есть соответственно 0,1,3 точек порядка 2 (которые характеризуются y=0), а m — верхняя оценка на ранг. На кривой y²=x3+877x есть одна точка порядка 2, а ранг равен единице, так что получаются три квартики.
Первая:
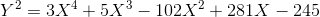
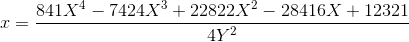
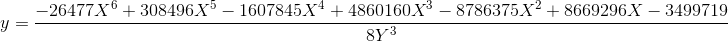
(Формат Хабра не располагает к выписыванию формул для всех коэффициентов, но тем не менее они есть: все коэффициенты в преобразовании координат вычисляются через a,b,c,d,e, например, 12321 получается как d²-8ec/3.)
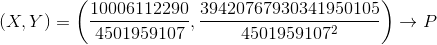
Вторая:
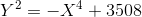
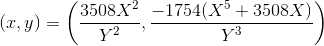

Третья:
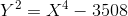
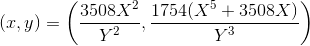
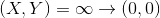
(На квартике могут быть 0 либо 2 бесконечно удалённые точки в зависимости от того, является ли a точным квадратом; на первых двух квартиках таких не было, здесь их целых две, обе переходят в (0,0). Замена
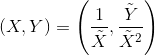 сводит их к обычным точкам.)
сводит их к обычным точкам.)На третьем этапе метод ищет рациональную точку на квартиках, оставшихся после второго этапа. Числитель и знаменатель x-координаты на исходной кривой по порядку примерно равны четвёртой степени числителя и знаменателя X-координаты на квартике (умножение на n на эллиптической кривой — операция степени n², для 2-спуска получается степень 4). Если точку удалось найти, то по ней можно вычислить точку на исходной кривой. Если же точку не удалось найти, то возникает проблема: это может означать либо, что её действительно нет (а есть нетривиальные элементы группы Тейта-Шафаревича), либо, что плохо искали. Теоретическое решение — параллельно запускать спуск высшего порядка и поиск точек с большими числителями и знаменателями. Хорошего практического решения неизвестно.
Для случая кривой y²=x3+877x координаты на квартиках выглядят менее внушительными, чем координаты точек исходной кривой, но всё равно слишком велики для прямого перебора. Тем не менее, с квартикой
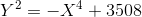 можно спуститься дальше. (С первой квартикой дальше работать сложно, но и не нужно: одной порождающей точки вполне хватит.) Правая часть биквадратична, то есть выражается через X²; так бывает всегда, когда на исходной кривой есть точка второго порядка (с y=0). Если взять в качестве переменных пару (X², Y), то получится квадратичное уравнение, которое уже можно решить:
можно спуститься дальше. (С первой квартикой дальше работать сложно, но и не нужно: одной порождающей точки вполне хватит.) Правая часть биквадратична, то есть выражается через X²; так бывает всегда, когда на исходной кривой есть точка второго порядка (с y=0). Если взять в качестве переменных пару (X², Y), то получится квадратичное уравнение, которое уже можно решить: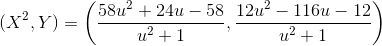
Далее, любой общий делитель числителя и знаменателя выражения для X² должен также делить
 ; их частное может быть квадратом, только если они оба имеют вид "d умножить на квадрат", где d — делитель 3508, свободный от квадратов, то есть одно из чисел 1,2,877,1754 (отрицательные d исключены, ибо знаменатель всегда положителен). Числитель не может быть точным квадратом в 2-адических (и тем более в рациональных) числах. Пробуем d=2:
; их частное может быть квадратом, только если они оба имеют вид "d умножить на квадрат", где d — делитель 3508, свободный от квадратов, то есть одно из чисел 1,2,877,1754 (отрицательные d исключены, ибо знаменатель всегда положителен). Числитель не может быть точным квадратом в 2-адических (и тем более в рациональных) числах. Пробуем d=2: 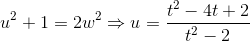 . Подставляя полученное выражение для u в числитель и требуя, чтобы числитель был удвоенным квадратом, получаем новую квартику
. Подставляя полученное выражение для u в числитель и требуя, чтобы числитель был удвоенным квадратом, получаем новую квартику  .
.На ней уже есть точка, доступная для перебора:
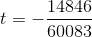 .
.Перебор на квартиках можно ещё сократить, используя всё ту же идею о рассмотрении уравнения по модулю простых чисел и степеней простых. При поиске целых k, m таких, что
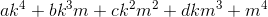 — точный квадрат, для каждого простого числа p примерно половина из p² возможных пар остатков (k, m) даёт не квадрат по модулю p. (Вместо 2 и 3 лучше смотреть на их степени 16 и 9; для больших p увеличение степени ничего не даёт.) Значит, «хороших» пар остатков по модулю, например, 16*9*5*7, примерно 1/16 от общего количества возможных пар; достаточно вести перебор только пар (k,m) с «хорошими» остатками. Вышеупомянутый mwrank, используя подобные соображения, находит точку P с КДПВ менее, чем за секунду.
— точный квадрат, для каждого простого числа p примерно половина из p² возможных пар остатков (k, m) даёт не квадрат по модулю p. (Вместо 2 и 3 лучше смотреть на их степени 16 и 9; для больших p увеличение степени ничего не даёт.) Значит, «хороших» пар остатков по модулю, например, 16*9*5*7, примерно 1/16 от общего количества возможных пар; достаточно вести перебор только пар (k,m) с «хорошими» остатками. Вышеупомянутый mwrank, используя подобные соображения, находит точку P с КДПВ менее, чем за секунду.Гипотеза Бёрча — Свиннертон-Дайера

 В первой статье «Notes on elliptic curves. I» Бёрч и Свиннертон-Дайер собрали статистику по рангам пары тысяч эллиптических кривых. Во второй статье «Notes on elliptic curves. II» пришло время анализа накопленной статистики, там же и предложена титульная гипотеза.
В первой статье «Notes on elliptic curves. I» Бёрч и Свиннертон-Дайер собрали статистику по рангам пары тысяч эллиптических кривых. Во второй статье «Notes on elliptic curves. II» пришло время анализа накопленной статистики, там же и предложена титульная гипотеза.Работа с эллиптической кривой над рациональными числами бывает проблематична: координаты точек быстро растут, процедура вычисления ранга не всегда даёт ответ. С другой стороны, имея уравнение с целыми коэффициентами, можно рассмотреть его по модулю разных простых чисел. Число точек по модулю небольших простых чисел легко посчитать непосредственно, но совсем непонятно, какое отношение полученные числа имеют к рациональным точкам.
Если для каждого простого числа посчитать число точек на кривой по модулю этого простого числа, получится некоторый бесконечный набор целых чисел. Дзета-функция Хассе — Вейля эллиптической кривой, традиционно обозначаемая буквой L, получается, если определённым образом «склеить» этот набор в одну функцию комплексной переменной. Поскольку она содержит информацию о поведении по модулю сразу всех простых чисел, про неё бывает проблематично что-нибудь доказать. (В этом она похожа на дзета-функцию Римана — и гипотеза Римана, касающаяся свойств дзета-функции Римана, является ещё одной из «задач тысячелетия».) Гипотеза Бёрча — Свиннертон-Дайера идёт дальше и связывает поведение кривой над рациональными числами (конкретно, ранг) со свойствами дзета-функции, вычисляемой исключительно по поведению кривой по конечным модулям.