How to become an author
Search
Write a publication
Pull to refresh

Comments 88

Сразу вспомнился фильм «Классик» где как раз говорилось про крутое разбитие пирамиды при котором два крайних шара закатываются в лунки.
Total votes 16: ↑16 and ↓0+16
В фильме немного пофантазировали :) Что бы при идеальном разбое, который тут посчитали, на русском бильярде угловые шары упали в лузы, нужно что бы пирамида стояла ближе к центру стола, где угловые лузы были на траектории дивжения.
Total votes 6: ↑3 and ↓30
UFO just landed and posted this here
Таким образом, шаг за шагом, можно рассчитать «идеальную партию»
Total votes 2: ↑1 and ↓10
А если у поверхности нет трения, то идеальная партия будет состоять из одного—самого первого—удара, потому что шарики будут кататься бесконечно. Более того, все они рано или поздно закатятся в лузы. Дело в том, что если траектория шарика не периодическая, он рано или поздно столкнется с любой точкой стенки, а значит, и с какой-то лузой. Некоторые периодические траектории тоже столкнутся с лузой (а некоторые—нет). Можно показать, что периодические траектории бывают только когда тангенс угла движения шарика (отн. горизонтальной или вертикальной оси) рационален. Но рациональных чисел намного меньше, чем иррациональных (точнее, мощность иррациональных чисел больше мощности рациональных, рациональные—счетные, иррациональные—несчетные), так что рациональные тангенсы почти никогда не будут получены. Хотя было бы интересно проверить численно или аналитически.
Total votes 44: ↑41 and ↓3+38
Это тоже трение и вязкость / неупругость стенок.
Total votes 4: ↑4 and ↓0+4
Если у поверхности не будет трения, то в пуле будет невозможно выиграть, т.к. рано или поздно биток тоже закатится в лузу, а это будет фол, если при этом все остальные шары тоже закатятся, то выиграет соперник.
Total votes 12: ↑12 and ↓0+12
В идеальной системе будет также сохраняться симметрия, т.е. биток будет всегда двигаться по осевой
Кстати, это же верно как минимум еще для трех шаров. К сожалению идеальная партия не кончится никогда.
Total votes 3: ↑3 and ↓0+3
>> все они рано или поздно закатятся в лузы
Не факт, если предположить что один оставшийся шар двигается перпендикулярно бортам о которые ударяется, то он никогда не закатится в лузу.
Total votes 6: ↑5 and ↓1+4
Предположить можно, но вероятность того, что шар будет двигаться перпендикулярно борту равна нулю.
Total votes 3: ↑2 and ↓1+1
Как вы лихо посчитали, что ситуация невозможная. Есть множество циклических траекторий, которые не приведут к закатыванию в лунку. Например самая простая. Шар под углом 90 градусов ударяется о борт, отскакивает, катится в противоположный борт и т д. Так как мы рассматриваем идеальный случай то и все неровности поверхности из за которых траектория будет меняться нет. И это самый простой случай, возможны и более сложные варианты, вот например.
Image #2098152, 181.5 KB
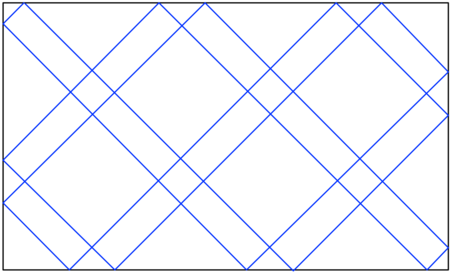
Total votes 9: ↑6 and ↓3+3
Я совсем не спорю, что такие траектории есть. Но вероятность каждой из этих траекторий, и в частности катание шара по одной линии, перпендикулярной бортам, равна нулю :) Собственно я написал только это.
Total votes 13: ↑9 and ↓4+5
Ну смотри, такие траектории, которые могут бесконечно зациклить шар есть. Причем такая траектория не одна а целое множество (я сейчас несколько таких нарисовал, несмотря на то что та программа в которой я это делал не приспособлена для черчения и там сложно отсчитывать углы). А значит уже вероятность не может быть равна нулю, как существуют положительные исходы.
Total votes 4: ↑1 and ↓3-2
В этих рассуждениях есть довольно тонкий момент: исходы есть, их множество бесконечное (но счетное), а вероятность их получить все равно равна нулю. Это называется множество меры нуль (в смысле теории меры, не путать с нульмерным множеством; хотя рациональные числа нульмерны тоже). Почему множество счетное, написано вот тут, а почему оно намного меньше множества действительных чисел, и почему намного легче получить иррациональное число, вот тут и тут (но довольно скупо).
Total votes 10: ↑10 and ↓0+10
Наверное корректнее в этом случае говорить, что «вероятность стремится к нулю»?
Total votes 2: ↑0 and ↓2-2
Не стремится, а именно равна. Чтобы было корректно говорить «стремится», нужно иметь какую-то динамику, какой-нибудь изменяемый параметр, от которого зависит характеристика системы и который тоже куда-нибудь стремится; тут же такого нет.

Вероятность того, что случайно выбранное (вещественное) число от 0 до 1 окажется равным 0.5 (или даже рациональным) — строго равна нулю.
Total votes 7: ↑7 and ↓0+7
Интеграл от строго нуля на любом отрезке равен нулю, нет?
Немного расходится с тем фактом, что какое-то число будет выбрано с вероятностью единица )
Total votes 1: ↑1 and ↓0+1
Если вы переходите к интегралу, то вы уже оперируете не вероятностью, а плотностью вероятности. В этом случае последняя, конечно, не равна нулю, и интеграл от нее действительно должен дать 1.
Тут, конечно, можно было бы сказать, что сумма вероятностей выбора всех чисел должна дать единицу; но писать такого рода суммы (с индексом, пробегающим несчётное множество) даже математики боятся — для этого и придумали интеграл :)
Total votes 3: ↑3 and ↓0+3
Вообще-то Поль Дирак придумал функцию, которую можно использовать в качестве плотности вероятности, такую, что любой её интервал (сколь угодно малый), содержащий точку 0, будет равен единице. И вообще, предыдущее предложение — и есть определение функции Дирака :)

Тут можно считать, что как бы вероятность нуля равна единице, а вероятность остальных любых чисел, хотя бы и близких к нулю — равна нулю. Ну или что f(0)=1/0.

Но в природе такие распределения, конечно, не встречаются.
Total votes 1: ↑1 and ↓0+1
Как, в общем, отсутствие трения и сам по себе «идеальный удар».
О чём тогда речь?
This comment wasn’t rated yet0
Отсутствие трения и идеальный удар — просто модель; и речь о том, что в рамках этой модели при более или менее слуайном ударе все шары закатятся в лунки с вероятностью 1. :)
This comment wasn’t rated yet0
Ну это и сам Bas1l написал:
Можно показать, что периодические траектории бывают только когда тангенс угла движения шарика (отн. горизонтальной или вертикальной оси) рационален.

Такие траектории существуют и их бесконечно много даже — это факт.
Но если эта приведенная цитата верна, то вероятность таких траекторий — ноль. Ниже там написано почему.
Total votes 1: ↑1 and ↓0+1
Ну почему же? Если взялись допустить полное отсутствие трения и абсолютную упругость шаров и стенок — то идеальный удар (о котором статья) заставит биток, а также шары 1, 5 и 13 двигаться по одной линии перпендекулярно бортам. И это будет вечно.
This comment wasn’t rated yet0
В приведённом выше идеальном разбитии целых три шара двигаются перпендикулярно борту. Если им на пути не встретятся другие шары, то ни в какую лузу они не закатятся.
This comment wasn’t rated yet0
В примере да, всё так. Только мы перешли к «реальной» игре уже.
Total votes 1: ↑0 and ↓1-1
Не встретятся. Точнее, если встретятся — то с двух сторон одновременно (ввиду симметрии), а потому на направление их движения никак не повлияют, только на скорость.
Total votes 1: ↑1 and ↓0+1
А можно в студию доказательство равенства нулю, а не какому-нибудь бесконечно малому числу?
Total votes 1: ↑0 and ↓1-1
Единицу делим на бесконечное кол-во возможных траекторий и получаем бесконечно малый ноль для вероятности какой либо одной траектории :)
Total votes 1: ↑0 and ↓1-1
бесконечно малое это не тоже самое что и ноль.
Total votes 2: ↑2 and ↓0+2
Только обратите внимание, что здесь как раз не «невозможное событие», а просто событие с нулевой вероятностью. Это совсем не одно и то же. Т.е. каждая траектория ведь явно же лежит в пространстве элементарных событий эксперимента, но вероятность каждой нулевая. Тут с одной стороны всё верно. С другой сомневаюсь, что корретно так говорить, т.к. изначальное событие (идеальное разбитие пирамиды) у нас по самому условию задачи совсем не случайное. Потому не очень понятно какие случайные траектории тут обсуждаются и откуда они взялись)
Total votes 2: ↑2 and ↓0+2
Ну я начало треда то и сам нашёл как раз) Но всё равно наличие бесконечного кол-ва траекторий не очень понятно, т.к. траекторий будет по количеству шаров и они будут при каждом опыте одинаковы в случае идеальных условий. А идеальные условия у нас по условию задачи. Траектории в таком случае даже по определению не могут быть случайны, нет? И посылка, сформулированная как
вероятность каждой из этих траекторий, и в частности катание шара по одной линии, перпендикулярной бортам, равна нулю
вообще никак не корректна. Т.к. вероятностей здесь нет вообще. Т.к. при симметричной фигуре и при заранее заданных условиях шары вполне могут отлететь строго перпендикулярно бортам. Биток и три шара на оси (жёлтый и два оранжевых) именно так и отлетают на анимации — строго вертикально.
This comment wasn’t rated yet0
От условий задачи автор комментария вообще ушёл к обычной игре в бильярд без трения
This comment wasn’t rated yet0
В общем, вы правы. Тут только надо различать несколько сторон «идеальности»: наличие диссипации энергии (трение, неупругие столкновения) и «неидеальность» направлений (по сути—наличие тепловых флуктуаций, которые слегка искажают углы при столкновениях). Про отсутствие трения было явно сказано, про флуктуации—нет. Конечно, если все углы супер-идеальны, то как минимум два шарика будут бесконечно долго двигаться (вдоль вертикальных линий, если не столкнутся с другими—но даже при столкновениях траектории могут остаться периодическими). Но самое незначительное искажение траектории (физической природой которого может быть смещение хотя бы одного атома в шарике при столкновении) испортит идеальную картину.

Обычно в физике, насколько я знаю, предполагается, что такая «идеальность» намного «жестче», чем простое отсутствие диссипации энергии, и ее нельзя добиться. И действительно, избежать значимых потерь энергии на довольно большом промежутке времени вполне можно (т. е., чтоб ни один шар не остановился, пока не закатится), а вот флуктуаций избежать тяжело. В квантовых системах это вообще точные утверждения: потери можно сделать строго равными нулю (сверхпроводимость, сверхтекучесть), а флуктуации не исчезают даже при абсолютном нуле температур.

Математически говорят, что система неустойчива (в смысле Ляпунова).
Total votes 1: ↑1 and ↓0+1
Я ждал, когда упомянут Ляпунова. И ещё надо упомянуть Синая. Всё-таки про биллиард говорим и про неустойчивость.

Вот если бы математик из статьи что-нибудь интересное посчитал по поводу биллиарда Синая, вот это было бы круто. А так — рутина…
Total votes 2: ↑2 and ↓0+2
Очень просто. Бесконечно малых чисел не существует :)
Total votes 2: ↑1 and ↓10
Чисел вообще не существует, они все придуманные.
Total votes 1: ↑0 and ↓1-1
Ну, это уже демагогия пошла — смотря что считать существующим. Нас вон, может, тоже не существует и мы снимся Будде :)

Нет, я имел в виду, что математика (ну, не считая нестандартного анализа, про который сказано выше) попросту не оперирует бесконечно малыми числами, и всё.
This comment wasn’t rated yet0
В таких случаях строгое равенство нулю доказывается от противного. Допустим, что вероятность (p) движения по некоторой траектории (i) не равна нулю, то есть pi > 0. Поскольку по условию вероятность выбора траекторий одинакова, то есть pi = pj = p для любых траекторий i и j, то всего возможно не более 1/p разных исходов (сумма-то вероятностей равна 1 по определению). А это противоречит условию бесконечости количества траекторий. Значит p = 0.
Total votes 1: ↑0 and ↓1-1
А это противоречит условию бесконечости количества траекторий. Значит p = 0.


Количество циклических траекторий как раз бесконечное.

Но вероятность циклической траектории все равно нуль.

Подробнее вот в этом коменте: habrahabr.ru/post/211324/#comment_7274092
Total votes 2: ↑1 and ↓10
Количество циклических траекторий как раз бесконечное.

Именно в этом и суть доказательства от противного. Мы пришли к противоречию с изначальной (правильной) предпосылкой о бесконечности количества траекторий.

Подробнее вот в этом коменте: habrahabr.ru/post/211324/#comment_7274092

Все верно в этом комменте, я с ним не спорю. В своем комментарии я объяснил, почему именно нуль, а не «бесконечно малое».
Total votes 1: ↑0 and ↓1-1
Это и есть частный случай периодической траектории — угол 90° имеет рациональный тангенс. Если угол будет хоть чуть-чуть другим, шар рано или поздно докатится до лузы.
This comment wasn’t rated yet0
Простите, уточню: угол в 90 градусов не имеет тангенса :)
Он имеет рациональный котангенс, чего тоже достаточно.
Total votes 2: ↑2 and ↓0+2
Когда-то в детстве на Sega Mega Drive играл в биллиард, и там можно было установить силу трения. Однажды, поставив 0, прождал ооочень долго, но 1 шарик так и катался :) так сказать, попал в «рациональное» число.
Total votes 1: ↑1 and ↓0+1
К слову, числа, записываемые конечным кол-вом цифр (а на компах используются только такие) — все рациональные.
Total votes 5: ↑5 and ↓0+5
Строго говоря, на компах бывают не только такие. То есть, в численной арифметике с плавающей точкой — да, а в символьной — можно использовать объекты вида sqrt(2) и это «точный корень из двух», а не его приближение с точностью до 53 двоичных порядков.
This comment wasn’t rated yet0
А почему из не периодичности траектории вытекает что шарик коснется всех точек стенок?
Total votes 1: ↑1 and ↓0+1
Не всех; но он коснётся сколь угодно близко к какой угодно точке.
Доказательство примерно такое: сперва периодически повторим наш бильярдный стол; когда шарик отражается от стенки — мы будем трактовать так, будто шарик просто прокатился в «соседний стол» (эдакое «зазеркалье»). Таким образом можно считать траекторию шарика просто прямой.
Введем теперь систему координат, так чтобы вершины «начального стола» имели координаты (0,0), (1,0), (0,1), (1,1). Тогда пересечения прямой траектории с линиями сетки дадут нам координаты точек столкновения со столом; таким образом, мы получаем, что, скажем, координата X m-того столкновения шарика со стеной будет равна {m*tan(alpha)} ( {} — значит дробная часть). Осталось показать, что это множество (при иррациональных тангенсах) всюду плотно.
А это уже — содержание теоремы Кронекера; доказательство приведено в выпуске журнала Квант от 1986 года по ссылке, и понять его можно :)
Total votes 6: ↑6 and ↓0+6
Да-да, именно это и имелось в виду!
This comment wasn’t rated yet0
Я бы добавил, что рациональный тангенс даст периодическое движение только если отношение сторон a/b стола рационально; в общем случае тангенс должен быть линейно зависим с a/b над полем рациональных чисел.
Увы, не знаю, каково отношение сторон стола в идеальном бильярде.
This comment wasn’t rated yet0
1-й, 5-й и 13-й, а также биток будут бесконечно кататься вдоль осевой, и ни в какую лузу никогда не попадут.
This comment wasn’t rated yet0
В идеальной партии всегда будет выигрывать первый игрок, потому что он не допустит ни единого промаха.
This comment wasn’t rated yet0
Для начала нужно было их расставить правильно, что ли?
Total votes 7: ↑2 and ↓5-3
На столе есть такой маленький кружочек.
Total votes 4: ↑2 and ↓20
Осталось, чтобы кто-то опробовал на практике данную модель
This comment wasn’t rated yet0
Эм, а в ректоре в 3D Max это сделать нельзя, нужно считать уравнения?
Total votes 28: ↑2 and ↓26-24
Там ведь не будет корректная физическая симуляция; там будет какая-то симуляция, которая выглядит нормально.
Total votes 3: ↑3 and ↓0+3
Эм, ну как бы физический движок, койм является Reactor, моделирует физические законы реального мира.
Total votes 1: ↑0 and ↓1-1
Судя по описанию с википедии (увы, с движком я не знаком), тех законов, что он моделирует — недостаточно; тут основная проблема — закон взаимодействия шаров, для которого нужна нормальная теория упругости, с которой Reactor, похоже, не знаком.

На самом деле, даже если бы Reactor это все умел, то, мне кажется, что вбить решение нескольких диффуров в Mathematica было даже проще, чем нарисовать такую же сценку в 3DS Max. Особенно в смысле извлечения таблички со скоростями и направлениями.
This comment wasn’t rated yet0
Согласен про табличку со скоростями.
This comment wasn’t rated yet0
Ну, система неголономная, так что не всё так тривиально с диффурами. Но да, рассчёты в математике, рендеринг в максе — выглядит разумно.
This comment wasn’t rated yet0
Желаемое: идеальный удар раскидывает все шарики по лункам.

Реальность: идеальный удар — простой биток по центру, причём с кучей допущений.
Total votes 6: ↑6 and ↓0+6
Дык наука же. Тут идеальный удар — сферический и в вакууме.
Total votes 1: ↑1 and ↓0+1
Кстати, было бы интересно просчитать всю физику и математику бильярда, а потом открыть школу фокусов, подобных тому что делает этот чел:
Фокусник

Интересно, он тоже математик?
Total votes 14: ↑14 and ↓0+14
Посмотрите практически любой обучающий фильм по бильярду, там эта физика объясняется.
Даже после понимания, что такое тангенсная линия уже сможете часть фокусов делать.
Total votes 1: ↑1 and ↓0+1
можете порекомендовать конкретный?
This comment wasn’t rated yet0
Меня больше интересует то, как он смог уговорить свою девушку принять столько поз за один вечер… завиду…
Total votes 6: ↑4 and ↓2+2
UFO just landed and posted this here
> Теорема Пуанкаре о возвращении.

Фантастически крутая теорема. Это прямо праздник. Вкратце примерно так: если некая замкнутая система когда-то проходила через определённое состояние, то когда-нибудь она непременно пройдёт сколь угодно близко от этого состояния.
Total votes 1: ↑1 and ↓0+1
Вот если бы показали как лучше разбить пирамиду, чтобы залетело как можно больше шаров(сплошных или полосатых)…
Total votes 1: ↑1 and ↓0+1
В восьмерке это непредсказуемо и даже опасно. Потому как вам нельзя:
1 забивать шары оппонента
2 забивать черный шар
This comment wasn’t rated yet0
Интересно, что 7 шаров движутся хоть как-то по направлению удара битка, а остальные 9, включая биток в обратном направлении. Теперь понятно, почему при хорошем разбитии пирамиды, шары скатываются больше к центру.
This comment wasn’t rated yet0
На самом деле я могу отправить биток очень сильно в центр пирамиды после соударения, или наоборот оттянуть его на себя к ближайшему борту, все зависит от точки соударения кия и битка. Кий специально сделан утончающимся к концу, что бы можно было придавать крутящий момент шара и менять его поведение в зависимости от ситуации игры.
This comment wasn’t rated yet0
В данном случае никаких крутящих моментов нет. Суть лишь в том, что шар летит к пирамиде, при этом после удара большая часть шаров летит в обратном направлении, хоть и с маленькой скоростью. Не сенсационное открытие конечно, но интересный факт.
This comment wasn’t rated yet0
Почему цвета шариков, имеющих симметричные траектории движения, разные?
This comment wasn’t rated yet0
Трехмерный бильярд — моя курсовая, первая большая программа, которую я написал. Прям, ностальгия накатила. Спасибо за статью! :)
Total votes 1: ↑1 and ↓0+1
А у вас код сохранился для тех, кому любопытно? :)
Я бы губу раскатал и на мат. модель или теорию, но курсовая есть курсовая.

Буду искренне признателен.
Total votes 1: ↑1 and ↓0+1
К сожалению, код почил с одним из хардов. Да и к лучшему, наверное, программу я писал лет 10 назад (это была курсовая учебного центра по программированию), сейчас мне было бы просто страшно смотреть в исходники :)

А что с мат. моделью? Там ничего сложного нет, если физика в двухмерном пространстве (у меня трехмерной была только визуальная часть). Единственное, что нужно сделать — рассчитать новые векторы скоростей шаров, после их столкновения. Я тогда не смог самостоятельно расписать формулу, но нагуглил её достаточно быстро.

Реализация была «в лоб»: удар кием — придаём шару вектор скорости, по таймеру обрабатываем изменения положений шаров и, если столкнутся, их новые векторы скоростей.
Total votes 1: ↑1 and ↓0+1
Реквестирую четырехмерный и n-мерный бильярд.
Total votes 2: ↑2 and ↓0+2
Одним из вариантов курсовой был трёхмерный тетрис. Кто-то пошутил, что надо добавить вариант с четырёхмерным тетрисом. Преподаватель, не растерявшись, начал рассказывать, что сложного в этом ничего нет: фактически, вся математика будет той же самой, только для четырёх измерений: четыре координаты у точки и т.д. Визуально такой тетрис тоже можно показать: в трёхмерном варианте вы проецируете результат на двухмерную плоскость — монитор. Точно так же на двухмерную плоскость можно спроецировать четырехмерное пространство.

Так что и четырехмерный бильярд вполне можно сделать. Только, наверное, ничего понятно не будет.
This comment wasn’t rated yet0
Ощущаю себя на острие науки
Total votes 8: ↑2 and ↓6-4
Sign up to leave a comment.

Articles

Show the best of all time
Change theme settings

Your account

Sections

Information

Services

Support
© 2006–2024, Habr