Comments 37
Сколько итераций было сделано для получения результата на второй картинке?
+2
Не могли бы вы добавить в статью сравнение этого метода с генетическим алгоритмом? Плюсы и минусы этих методов относительно друг-друга.
Ведь в целом они похожи, но хотелось бы увидеть, когда какой следует применять.
Я вот несколько раз применял ген. алг для различных задач, в частности для обучения многослойного перцептрона — получил весьма интересные результаты, но с методом из вашей статьи знаком только понаслышке и не знаю его преимуществ и недостатков относительно ген. алга (в частности, в вопросе обучения НС)
Upd: не увидел ваше заключение, прошу прощения. Но вопрос остается открытым, и, на мой взгляд, ответ на него даже важнее реализации метода имитации отжига в матлабе.
Ведь в целом они похожи, но хотелось бы увидеть, когда какой следует применять.
Я вот несколько раз применял ген. алг для различных задач, в частности для обучения многослойного перцептрона — получил весьма интересные результаты, но с методом из вашей статьи знаком только понаслышке и не знаю его преимуществ и недостатков относительно ген. алга (в частности, в вопросе обучения НС)
Upd: не увидел ваше заключение, прошу прощения. Но вопрос остается открытым, и, на мой взгляд, ответ на него даже важнее реализации метода имитации отжига в матлабе.
+2
Большое спасибо за интересную статью!
С радостью почитаю обзор различных методов оптимизации. Сам занимаюсь целочисленным программированием (точнее 0-1), но, боюсь, фундамента моих знаний недостаточно для столь понятного и отличного описания. Оптимизация — очень широкая область, но на Хабре, к сожалению, почти нет материалов по ней.
С радостью почитаю обзор различных методов оптимизации. Сам занимаюсь целочисленным программированием (точнее 0-1), но, боюсь, фундамента моих знаний недостаточно для столь понятного и отличного описания. Оптимизация — очень широкая область, но на Хабре, к сожалению, почти нет материалов по ней.
+2
Интересный метод. Спасибо за наглядное описание.
Надо бы попробовать его приспособить к задачам решения нелинейных уравнений. Иногда, вместо решения сложной системы многих переменных f(x_1..x_n) = 0 можно попытаться минимизировать каким-нибудь образом построенную из этих уравнений функцию, например, сумму их квадратов (что абсолютно естественно для комплексных чисел — минимизация квадрата модуля). Возможно, этот метод себя сможет хорошо проявить, в отличие от многомерных секущих (плохо сходятся) или Ньютона-Рафсона (жутко долго писать и неудобно вычислять производные, если функция не задана аналитически).
Надо бы попробовать его приспособить к задачам решения нелинейных уравнений. Иногда, вместо решения сложной системы многих переменных f(x_1..x_n) = 0 можно попытаться минимизировать каким-нибудь образом построенную из этих уравнений функцию, например, сумму их квадратов (что абсолютно естественно для комплексных чисел — минимизация квадрата модуля). Возможно, этот метод себя сможет хорошо проявить, в отличие от многомерных секущих (плохо сходятся) или Ньютона-Рафсона (жутко долго писать и неудобно вычислять производные, если функция не задана аналитически).
+2
Следует также отметить, что метод имитации отжига — это слега адаптированный алгоритм Метрополиса (Metropolis algorithm), который, в свою очередь, является примером метода Markov Chain Monte Carlo (MCMC). А MCMC, по мнению нескольких научных изданий, входит в 10-ку наиболее важных для инженерии алгоритмов 20-ого столетия (для примера, туда же обычно включают быструю сортировку).
Спасибо за прекрасное описание! Жирный плюс в карму, и будет ждать следующих статей!
Спасибо за прекрасное описание! Жирный плюс в карму, и будет ждать следующих статей!
+4
Супер!
Поиск кратчайшего пути по «бразильской» системе!
Очень напоминает как много-много стартапов 99% из которых проваливается в итоге рождают что-нибудь в духе эппл или макрософт!
Конечно в реальной жизни множество особенностей, но метод отжига заполнил очень большой кусок в картине того, как реальный человек (или структура состоящая из людей) взаимодействует с миром!
И прямо так руки к чешутся взять и применить этот алгоритм к какой-нибудь олимпиадной задачке из школьных времен. Такое чувство, что множество хитрых задачек сведутся к одному алгоритму и будут проходить 90% тестов :)
Поиск кратчайшего пути по «бразильской» системе!
Очень напоминает как много-много стартапов 99% из которых проваливается в итоге рождают что-нибудь в духе эппл или макрософт!
Конечно в реальной жизни множество особенностей, но метод отжига заполнил очень большой кусок в картине того, как реальный человек (или структура состоящая из людей) взаимодействует с миром!
И прямо так руки к чешутся взять и применить этот алгоритм к какой-нибудь олимпиадной задачке из школьных времен. Такое чувство, что множество хитрых задачек сведутся к одному алгоритму и будут проходить 90% тестов :)
0
При словосочетании «олимпиадная задача» надолго завис, размышляя о задаче траты средств на олимпиаду 2014 в Сочи. Ох, что за времена.
+1
Такое чувство, что множество хитрых задачек сведутся к одному алгоритму и будут проходить 90% тестов :)
Только вот скорее всего (в олимпиадах, проводящихся по правилам ACM) за это дадут 0 баллов :) Нужно пройти все тесты.
0
А о самом интересном-то и не написали. Почему вероятность перехода именно
exp(-dE/T)?+4
Собственно, в этом и сидит физический аспект алгоритма.
Чистая термодинамика и никакой магии.
Вероятность пребывания системы в состоянии с энергией E при температуре T равна C*exp(-E/T), где С — нормировочный множитель. Это свойство общее для любых макроскопических систем и известно под названием распределения Гиббса. Вероятность состояния с энергией повыше равна, соответственно, C*exp(-(E+dE)/T).
А вероятность перехода между двумя этими состояниями равна экспоненте, в которой вместо энергии стоит dE — если условно принять нижний уровень за основное состояние (считать, что для него E=0 — в случае с потенциальной энергией именно это и можно сделать), как раз и получим, что вероятность попасть в состояние с энергией dE равна exp(-dE/T), только нормировка C здесь будет пересчитана.
Чистая термодинамика и никакой магии.
Вероятность пребывания системы в состоянии с энергией E при температуре T равна C*exp(-E/T), где С — нормировочный множитель. Это свойство общее для любых макроскопических систем и известно под названием распределения Гиббса. Вероятность состояния с энергией повыше равна, соответственно, C*exp(-(E+dE)/T).
А вероятность перехода между двумя этими состояниями равна экспоненте, в которой вместо энергии стоит dE — если условно принять нижний уровень за основное состояние (считать, что для него E=0 — в случае с потенциальной энергией именно это и можно сделать), как раз и получим, что вероятность попасть в состояние с энергией dE равна exp(-dE/T), только нормировка C здесь будет пересчитана.
+10
Очень интересная и крайне доступно написанная статья! Спасибо!
Что можете сказать про скорость такого алгоритма и точность относительно других методов?
Я занимался подобными изысканиями для поиска лучших торговых стратегий в трейдинге. Мне нужно было найти не только глобальный экстремум, но и максимально исследовать все локальные экстремумы! Разработал новый алгоритм, который не стремится к глобальному экстремуму, а удаляет из пространства исследования все минимумы и сходится ко всем экстремумам.
Метод оказался эффективнее и удобнее по сравнению с теми, которые я ранее использовал. Буду рад, если вы как эксперт оцените мой алгоритм, а то я прямых аналогов ему пока не нашел.
Удачи!
Что можете сказать про скорость такого алгоритма и точность относительно других методов?
Я занимался подобными изысканиями для поиска лучших торговых стратегий в трейдинге. Мне нужно было найти не только глобальный экстремум, но и максимально исследовать все локальные экстремумы! Разработал новый алгоритм, который не стремится к глобальному экстремуму, а удаляет из пространства исследования все минимумы и сходится ко всем экстремумам.
Метод оказался эффективнее и удобнее по сравнению с теми, которые я ранее использовал. Буду рад, если вы как эксперт оцените мой алгоритм, а то я прямых аналогов ему пока не нашел.
Удачи!
0
Понимаю, что было бы интересно взглянуть на сравнение «имитации отжига» с другими методами оптимизации, например, генетическими алгоритмами или динамическим программированием; привести примеры из интересных областей вроде machine learning; указать на связь с Марковскими моделями и много чего ещё. Однако, в рамках одной статьи всего не объять.
жду продолжения
+2
Спасибо, отличная статья!
+1
Спасибо за статью.
А можно выложить куда-то полные исходники?
А можно выложить куда-то полные исходники?
0
Конечно, последняя версия с комментариями.
+2
Спасибо, статья пришлась кстати.
Попробую «метод отжига» (MO) при случае на своих реальных данных.
На практике приходится работать с оптимизацией и еще один метод не помешает.
Пользуясь случаем, хотелось бы обсудить пару моментов. На правоту не претендую, скорее рассуждаю вслух.
Главное, на что я хочу обратить внимание: предпочтение одного метода другому определяется в первую очередь характером ваших данных. Это из личного опыта.
Так, например, может и не быть большого смысла применять МО в задаче коммивояжера с простым (как в примере) — равномерным распределением городов по некоторой плоскости.
Здесь вполне прилично справится метод монотонного спуска (ММС). Ну или преимущества МО еще прийдется поискать и доказать. Проблема возможной сходимости к локальным максимумам (что призван преодолеть МО), по моему мнению, возникнет тогда, когда в расположении городов будет присутствовать выраженная кластеризация.
Другая возможность — если функция генерации нового состояния почему-то из каких-то тактических соображений работает не затрагивает весь набор «городов.
Вид и свойствацелевой функции (как вычисляется „энергия“) тоже будут влиять.
Захотелось поиграться с МО самому.
Начал с ММС, чтоб потом сравнить.
Вот здесь под спойлер положил на скорую руку сооруженный R код для МНС и пару картинок.
Не совсем прозрачно пока для меня вопрос «температуры».
Выдастся время на еще один подзод — попробую довести реализацию своего кода до МО.
Будем думать.
Попробую «метод отжига» (MO) при случае на своих реальных данных.
На практике приходится работать с оптимизацией и еще один метод не помешает.
Пользуясь случаем, хотелось бы обсудить пару моментов. На правоту не претендую, скорее рассуждаю вслух.
Главное, на что я хочу обратить внимание: предпочтение одного метода другому определяется в первую очередь характером ваших данных. Это из личного опыта.
Так, например, может и не быть большого смысла применять МО в задаче коммивояжера с простым (как в примере) — равномерным распределением городов по некоторой плоскости.
Здесь вполне прилично справится метод монотонного спуска (ММС). Ну или преимущества МО еще прийдется поискать и доказать. Проблема возможной сходимости к локальным максимумам (что призван преодолеть МО), по моему мнению, возникнет тогда, когда в расположении городов будет присутствовать выраженная кластеризация.
Другая возможность — если функция генерации нового состояния почему-то из каких-то тактических соображений работает не затрагивает весь набор «городов.
Вид и свойствацелевой функции (как вычисляется „энергия“) тоже будут влиять.
А если без извлечения корня?...
Вот тут, кстати, возникает вопрос… А не лучше ли будет обойтись без извлечения корня?..
Сумма квадратов разностей имеет более „энергетический“ вид с точки зрения меня, как физика…
Ок, еще один вопрос для „поиграться на досуге.
Сумма квадратов разностей имеет более „энергетический“ вид с точки зрения меня, как физика…
Ок, еще один вопрос для „поиграться на досуге.
Захотелось поиграться с МО самому.
Начал с ММС, чтоб потом сравнить.
Вот здесь под спойлер положил на скорую руку сооруженный R код для МНС и пару картинок.
R код для монотонного спуска, для любителей
Может кого заинтересует, например, в порядке знакомства с R.
А то я все собираюсь написать пост с примерами практического использования.
Заодно можно сравнить с авторским матлабовским кодом.
Код не идеален, но рабочий.
Руки не дошли рассмотреть с “отжигом».
Картинки:
«Города» и случайный маршрут обхода.
В шапке — значение «энергии» — полной длины данного маршрута.

16 попыток

А то я все собираюсь написать пост с примерами практического использования.
Заодно можно сравнить с авторским матлабовским кодом.
Код не идеален, но рабочий.
####### Init
n.cities=100
## Матрица координат
coors=data.frame(cbind(x=runif(n.cities), y=runif(n.cities)))
## Случайно выбранный маршрут -- вектор индексов городов в случайной последовательности
s0=sample(1:n.cities)
######## Functions ##############
plot.s<-function(s=s0) {
crs=rbind(coors[s,], coors[s[1],])
plot(crs$x,crs$y,type="b",axes=F)
}
E<-function(s=s0){
crs=rbind(coors[s,], coors[s[1],])
sum(sqrt(diff(crs$x)^2+diff(crs$y)^2))
}
next.s<-function(s=s0){
ii=sample(1:length(s),2)
s[ii[1]:ii[2]]<-s[ii[2]:ii[1]]
return(s)
}
runOnce<-function(s=s0, n.iter=100000, plo=T) {
Es=E(s)
for (i in 1:n.iter){
ns=next.s(s)
Ens=E(ns)
cat(i, Es,Ens,"\n")
if (Ens<Es){
s=ns
Es=Ens
if (plo){
plot.s(s)
title(paste("i=",i,"E=",signif(Es,3)))
}
}
}
return(s)
}
######## End of Functions #######
## Main ##
plot.s(s0)
title(paste("Randomly generated route,",n.cities," cities, E=",signif(E(s0),3)))
### Один "сеанс"
runOnce()
## Результаты 16 попыток
op<-par(mfcol=c(4,4),mar=c(0,0,2,0))
for (j in 1:16){
s=runOnce(plo=F,n.iter=100000)
plot.s(s)
title(paste("E=",signif(E(s),3)))
}
Руки не дошли рассмотреть с “отжигом».
Картинки:
«Города» и случайный маршрут обхода.
В шапке — значение «энергии» — полной длины данного маршрута.

16 попыток

Не совсем прозрачно пока для меня вопрос «температуры».
Выдастся время на еще один подзод — попробую довести реализацию своего кода до МО.
Будем думать.
+1
Почему-то не видны картинки, залитые на hfbrastorage…
Перевставил.
Перевставил.
Скрытый текст
Картинки:
«Города» и случайный маршрут обхода.
В шапке — значение «энергии» — полной длины данного маршрута.
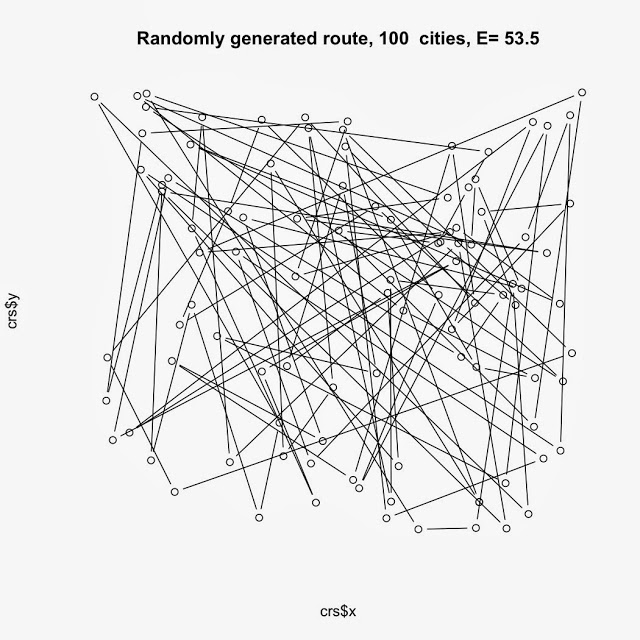
16 попыток, монотонный спуск.
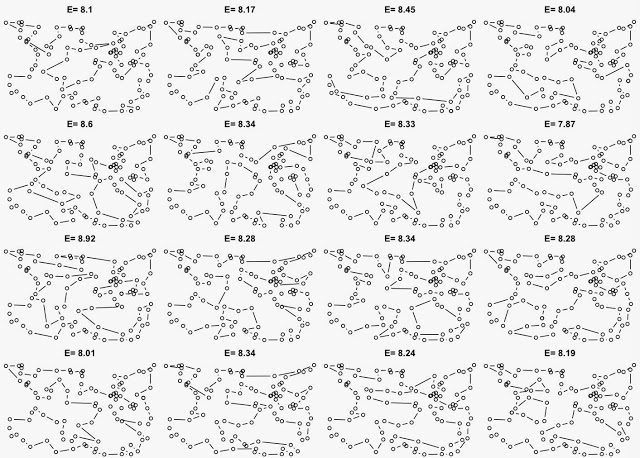
«Города» и случайный маршрут обхода.
В шапке — значение «энергии» — полной длины данного маршрута.

16 попыток, монотонный спуск.

+2
Мне по работе нужно к своим данным подобрать подходящий метод оптимизации, поэтому я меркантильно заинтересован, чтоб дискуссия не затухала. Тема интересует многих — новые статьи появляются
Сравнивая свою реализацию с кодами на других языках, подумал, может кому интересно будет посмотреть на R и с этой точки зрения.
Скрытый текст
(правда, качеством пониже чем эта, не в обиду другим авторам).
(правда, качеством пониже чем эта, не в обиду другим авторам).
Сравнивая свою реализацию с кодами на других языках, подумал, может кому интересно будет посмотреть на R и с этой точки зрения.
Выложил свой код R-код для задачи коммивояжера.
Пока без отжига, поскольку еще в процессе экспериментов с поведением температуры.
Заодно вожусь с ГА, чтобы сравнить с «отжигом». Может позже подискутируем и об этом, если найдутся желающие.
Нижеследующий код производит расчет и строит картинки (см. мой комментарии выше).
Один прогон из 100к итераций совершается в R 3.01 около 1.5 мин на маке c i5.
Заодно вожусь с ГА, чтобы сравнить с «отжигом». Может позже подискутируем и об этом, если найдутся желающие.
Нижеследующий код производит расчет и строит картинки (см. мой комментарии выше).
Один прогон из 100к итераций совершается в R 3.01 около 1.5 мин на маке c i5.
n.cities=100
####### Init
## Матрица координат
coors=data.frame(cbind(x=runif(n.cities), y=runif(n.cities)))
## Случайно выбранный маршрут -- вектор индексов городов в случайной последовательности
s0=sample(1:n.cities)
######## Functions ##############
# Нарисовать один вариант
plot.s<-function(s=s0) {
crs=rbind(coors[s,], coors[s[1],])
plot(crs$x,crs$y,type="b",axes=F)
}
#Подсчитать длину кольцевого пути
E<-function(s=s0){
crs=rbind(coors[s,], coors[s[1],])
sum(sqrt(diff(crs$x)^2+diff(crs$y)^2))
}
#Сгенерировать следующий вариант рутем изменения направления обхода между двумя выбранными городами на противоположный
next.s<-function(s=s0){
ii=sample(1:length(s),2)
s[ii[1]:ii[2]]<-s[ii[2]:ii[1]]
return(s)
}
# Зарустить одн раз
runOnce<-function(s=s0, n.iter=100000, plo=T) {
Es=E(s)
for (i in 1:n.iter){
ns=next.s(s)
Ens=E(ns)
cat(i, Es,Ens,"\n")
if (Ens<Es){
s=ns
Es=Ens
if (plo){
plot.s(s)
title(paste("i=",i,"E=",signif(Es,3)))
}
}
}
return(s)
}
######## End of Functions #######
#########################
## Main
## Здесь лучше работать в интерактивном режиме
plot.s(s0)
title(paste("Randomly generated route,",n.cities," cities, E=",signif(E(s0),3)))
### Один "сеанс"
st=system.time(runOnce())
mtext(paste(" time(s): ",st["elapsed"]))
## Результаты 16 попыток
op<-par(mfcol=c(4,4),mar=c(0,0,2,0))
for (j in 1:16){
s=runOnce(plo=F,n.iter=100000)
plot.s(s)
title(paste("E=",signif(E(s),3)))
}
+1
Вообще почти ничего не смыслю в данной области, поэтому возможно скажу какую-то очевидную вещь. Но мне кажется алгоритм наверное можно было бы ускорить, если ввести некую оценочную фукцию, которая бы отражала разницу энергий между итерациями. Как только оценочная фукция перестает уменьшаться (или перестает достаточно быстро или стабильно уменьшаться) можно прекращать итерации.
0
Спасибо за статью, в свое время, когда учился, использовал для решения задачи коммивояжёра генетические алгоритмы.
Из замечаний, в статье отсутствует реализация функции CalculateEnergy().
Не могли бы вы ее дополнить?
Из замечаний, в статье отсутствует реализация функции CalculateEnergy().
Не могли бы вы ее дополнить?
0
Проясните пожалуйста момент с генерацией нового расстояния. Почему "менять местами два произвольных города в маршруте" меньше влияет на E, чем "инвертировать путь".
В первом случае мы видим изменение расстояний в четырёх местах
1*7*3,4,5,6*2*
А во втором, только в двух (ведь если мы идём в обратную сторону, расстояние не меняется)
1*7,6,5,4,3,2*
В первом случае мы видим изменение расстояний в четырёх местах
1*7*3,4,5,6*2*
А во втором, только в двух (ведь если мы идём в обратную сторону, расстояние не меняется)
1*7,6,5,4,3,2*
+1
По личному опыту, на практике этот алгоритм работает лучше генетического. Почему так с точки зрения теории — сказать не возьмусь. Люди говорят, что в целом на практике отжиг применяется гораздо чаще.
Думаю, надо отметить более акцентировано, что трудность использования метода имитации отжига заключается именно в настройке функции температуры.
P.S. Я тоже писал об этом алгоритме.
Думаю, надо отметить более акцентировано, что трудность использования метода имитации отжига заключается именно в настройке функции температуры.
P.S. Я тоже писал об этом алгоритме.
+3
Да, кстати, спасибо и за ту статью.
Меня немного отпугнула Java, поскольку я уже больше 20 лет, как сам отошел к скриптовым языкам.
Сейчас посмотрел ее — кое что для себя «выцепил» новое.
Очень полезными нашел комментарии к той статье.
В своих задачах я как-то применял ГА и меня устраивало.
Сейчас у меня назревает следующий раунд в связи с поступлением новых данных. И я, похоже, запАл на метод отжига.
Так что ждите реализации в R.
Меня немного отпугнула Java, поскольку я уже больше 20 лет, как сам отошел к скриптовым языкам.
Сейчас посмотрел ее — кое что для себя «выцепил» новое.
Очень полезными нашел комментарии к той статье.
В своих задачах я как-то применял ГА и меня устраивало.
Сейчас у меня назревает следующий раунд в связи с поступлением новых данных. И я, похоже, запАл на метод отжига.
Так что ждите реализации в R.
0
>Первое что приходит в голову – менять местами два произвольных города в маршруте. Идея правильная, но такое изменение слишком слабо влияет на E, метод будет работать долго и не факт, что успешно.
По-моему, наоборот. Такое изменение, напротив, сильно влияет на E и, вероятнее всего, его увеличивает.
Вот что говорит на этот счет английская википедия:
>In the traveling salesman problem above, for example, swapping two consecutive cities in a low-energy tour is expected to have a modest effect on its energy (length); whereas swapping two arbitrary cities is far more likely to increase its length than to decrease it. Thus, the consecutive-swap neighbour generator is expected to perform better than the arbitrary-swap one
По-моему, наоборот. Такое изменение, напротив, сильно влияет на E и, вероятнее всего, его увеличивает.
Вот что говорит на этот счет английская википедия:
>In the traveling salesman problem above, for example, swapping two consecutive cities in a low-energy tour is expected to have a modest effect on its energy (length); whereas swapping two arbitrary cities is far more likely to increase its length than to decrease it. Thus, the consecutive-swap neighbour generator is expected to perform better than the arbitrary-swap one
+2
Да, для меня такой способ генерации нового состояния тоже не показался совсем очевидным.
От свойств данных будет очень сильно все зависеть.
Но всему критерий практика.
Иногда быстрее реализовать разные варианты алгоритма и попробовать на своих (или тестовых) наборах данных.
Я так обычно делаю.
От свойств данных будет очень сильно все зависеть.
Но всему критерий практика.
Иногда быстрее реализовать разные варианты алгоритма и попробовать на своих (или тестовых) наборах данных.
Я так обычно делаю.
0
Я не про «неочевидность» говорю, с этим как раз вопросов нет, вполне логично, что новые изменения не должны вызывать совершенно случайное изменение энергии, особенно с понижением температуры, потому что тогда будет под вопросом сходимость алгоритма.
Я говорю про формулировку в статье, написано, что «такое изменение слишком слабо влияет на энергию», в то время как на практике — совсем наоборот, поэтому его и не используют.
Я говорю про формулировку в статье, написано, что «такое изменение слишком слабо влияет на энергию», в то время как на практике — совсем наоборот, поэтому его и не используют.
+2
Да, Вы правы, тут ошибка.
Попробую объяснить почему.
Если представить города в виде графа, то видно, что для того, чтобы поменять местами два произвольных города нужно изменить четыре ребра. В случае, когда мы «переворачиваем» подпоследовательность — изменяется только два. Следовательно, влияние на E меньше (что хорошо).
Тогда встаёт вопрос почему вторая эвристика лучше?
Тут Википедия совершенно права, при перестановке двух произвольных элементов вероятность получить плохое состояние выше. Попытаюсь проиллюстрировать на примере:
Меняем A и B. Даже получив выигрыш за счёт ребер XB и AY, мы много потеряли на последовательности между A и B (рёбра BZ и WA).
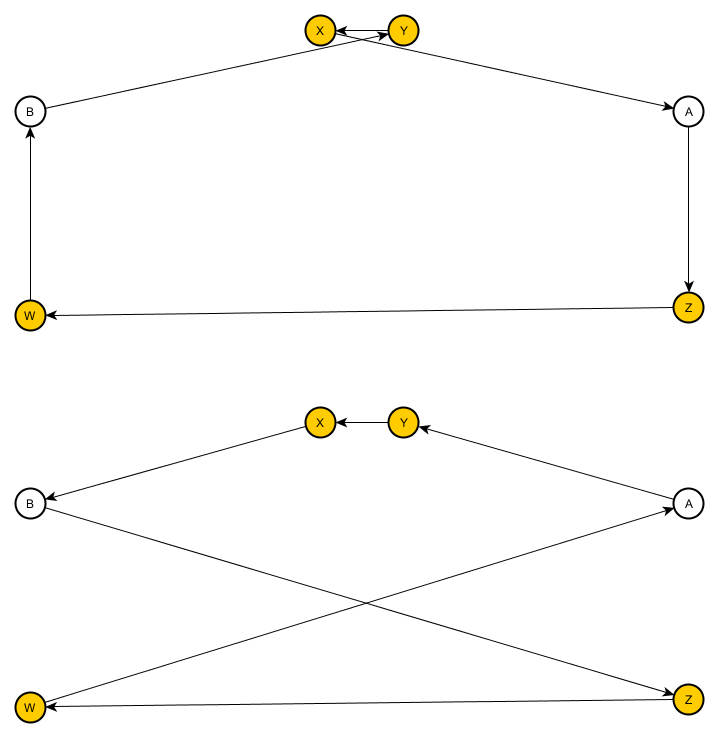
В случае с другим способом генерации, мы меняем только два ребра, не трогая саму подпоследовательность и гарантировано не делая её хуже.

Такое объяснение, конечно, не подходит на роль полноценного доказательства. Постараюсь, когда будет больше свободного времени найти правильные слова и дополнить статью.
Спасибо за замечание.
Попробую объяснить почему.
Если представить города в виде графа, то видно, что для того, чтобы поменять местами два произвольных города нужно изменить четыре ребра. В случае, когда мы «переворачиваем» подпоследовательность — изменяется только два. Следовательно, влияние на E меньше (что хорошо).
Тогда встаёт вопрос почему вторая эвристика лучше?
Тут Википедия совершенно права, при перестановке двух произвольных элементов вероятность получить плохое состояние выше. Попытаюсь проиллюстрировать на примере:
Меняем A и B. Даже получив выигрыш за счёт ребер XB и AY, мы много потеряли на последовательности между A и B (рёбра BZ и WA).

В случае с другим способом генерации, мы меняем только два ребра, не трогая саму подпоследовательность и гарантировано не делая её хуже.

Такое объяснение, конечно, не подходит на роль полноценного доказательства. Постараюсь, когда будет больше свободного времени найти правильные слова и дополнить статью.
Спасибо за замечание.
+1
В/К статье есть еще несколько вопросов, которые не грех было бы обсудить.
Трудновато это делать в формате комментария, а на статью-отклик не хватает, к сожалению, прочих ресурсов.
Трудновато это делать в формате комментария, а на статью-отклик не хватает, к сожалению, прочих ресурсов.
0
1.Мы случайно экспериментируем с функцией T (временем или количеством итераций, что у вас там). А вдруг при 10T найдется лучшее решение? И при 100T еще лучшее? Как оценить точность приближения? (тест в студию, где заранее полностью просчитаны глобальный минимум и локальные минимумы и при различных T как успешно ваша программа находит глобальный минимум)
2.Область обсчета и точки заведомо конечны. Что будете делать, когда они огромны (почти бесконечны)? Как оценивать будете, что в таком-то направлении считать невыгодно, а в другом выгодно и в какой момент программа остановится?
3.Предлагаю вам написать ваш программу на Lua и посмотреть, насколько выгодно она находит глобальный минимум в самых жестких условиях, где ваш алгоритм будет конкурировать с другими известными алгоритмами при поиске максимально выгодного свертывания белков — на foldit.
2.Область обсчета и точки заведомо конечны. Что будете делать, когда они огромны (почти бесконечны)? Как оценивать будете, что в таком-то направлении считать невыгодно, а в другом выгодно и в какой момент программа остановится?
3.Предлагаю вам написать ваш программу на Lua и посмотреть, насколько выгодно она находит глобальный минимум в самых жестких условиях, где ваш алгоритм будет конкурировать с другими известными алгоритмами при поиске максимально выгодного свертывания белков — на foldit.
0
Очень хорошая и интересная статья!
Местами, на мой вкус, слишком формализовано, но это я говорю как человек который более-менее «в теме». Для людей, впервые знакомящихся с данным материалом, зато будет легко вникнуть и разобраться.
Данный пост сподвиг меня на написание своей статьи на эту же тему. Вернее, конкретно эта фраза: «Первое что приходит в голову – менять местами два произвольных города в маршруте. Идея правильная, но такое изменение непредсказуемо влияет на, метод будет работать долго и не факт, что успешно.». Я как раз недавно сам решал задачу коммивояжера и придумал очень похожий на метод отжига алгоритм и использовал как раз идею случайного обмена местами двух городов. Кому интересно — почитайте.
Местами, на мой вкус, слишком формализовано, но это я говорю как человек который более-менее «в теме». Для людей, впервые знакомящихся с данным материалом, зато будет легко вникнуть и разобраться.
Данный пост сподвиг меня на написание своей статьи на эту же тему. Вернее, конкретно эта фраза: «Первое что приходит в голову – менять местами два произвольных города в маршруте. Идея правильная, но такое изменение непредсказуемо влияет на, метод будет работать долго и не факт, что успешно.». Я как раз недавно сам решал задачу коммивояжера и придумал очень похожий на метод отжига алгоритм и использовал как раз идею случайного обмена местами двух городов. Кому интересно — почитайте.
+1
Почему функция распределения вероятностей имеет именно такой вид, а не какой-нибудь другой?
0
Sign up to leave a comment.
Введение в оптимизацию. Имитация отжига