Comments 70
Благодарю за очередную интересную статью.
p.s. такую статью в один заход не осилить)
p.s. такую статью в один заход не осилить)
Ничего себе. Спасибо вам за такой большущий труд, очень познавательно!
Пожалуйста! Если читателям понравится подобный стиль изложения, то планируются еще статьи.
Я вот особо не углублялся раньше в эту тему, но ваши статьи написаны интересно и понятно. Теперь буду следить за новыми статьями.
нам нравится!
Нам действительно нравится, а вы немного обрисуйте темы будущих статей, пожалуйста, если, конечно, есть уже задумки.
Wavelet-сжатие и JPEG2000. С отсылкой к этой статье. Тут можно будет найти много общего :)
Думаю даже этого бы хватило, чтобы защитить диссертацию… :)
Спасибо Вам за проделанную работу!
Спасибо Вам за проделанную работу!
Монументально! За такие статьи хабр приплачивать должен…
Так приплачивает же: habrahabr.ru/ppa/faq/
Если они различаются по цветам, или видна только одна картинка, то, скорее всего, у вас IE (любой версии).
Или Safari.
Отличная статья!
Спасибо большое! Иллюстрации просто супер
Алгоритм Хаффмана создает оптимальные коды по весу символов. Но арифметическое кодирование учитывает еще и их расположение.
Нет. Арифметическое кодирование — тоже исключительно энтропийное. Просто Хаффман ограничил нас только целочисленной длиной символа, а вот арифметическое позволяет делать как бы дробное число бит на символ, как раз ровно, сколько нужно, чтобы получить оптимальный код. Поэтому оно эффективнее.
А данные с распределением вида 4 «a», 2 «b», 1 «c» и 1 «d» (т.е. хорошие для Хаффмана) они закодируют одинаково, арифметическое даст на один бит больше. В принципе реальна такая реализация, что даже выход этих двух алгоритмов совпадёт побитово (за исключением этого лишнего бита).
спасибо огромное! знал как это програмить, но никогда не знал, какие страшные формулы за этим скрываются :)
пишите еще, очень интересно!
пишите еще, очень интересно!
UFO just landed and posted this here
Черт, как бы я хотел понимать такие статьи…
Положу пока на полку.
Положу пока на полку.
Fil молодец!
ОМГ, у вас книгу издательство не приняло, наверно, поэтому тут пишете ;)
Можно поподробней про самый первый график? Что значит «два соседних пикселя» (по всем направлениям?) и по какому принципу ставятся синие точки на графике? Не хочется читать дальше не поняв основу.
UFO just landed and posted this here
Четвертый черный канал загружается, но, в итоге, не используется. Вот если бы мы добавили его ко второй картинке, то цвета стали бы правильными (темнее).
UFO just landed and posted this here
Спасибо за поправку! То есть, если я правильно понимаю, преобразование CMYK -> RGB может производиться по разным формулам?
UFO just landed and posted this here
Получается, что у кодера второй картинки и у большинства декодеров совпадают цветовые профили? И, скорее всего, они (кодер и декодеры) предполагают, что картинка будет отображаться на rgb-экране? И разработчики IE использовали какой-то свой профиль?
UFO just landed and posted this here
Ага профиль нашел
(9 таких же секций, по одной на каждый скан в прогрессивном кодировании)
Содержимое секций APP не описывается стандартом.
Секция APP2
(9 таких же секций, по одной на каждый скан в прогрессивном кодировании)
Содержимое секций APP не описывается стандартом.
Пишут, что в винде надо запускать хром с ключом --enable-monitor-profile, но у меня все равно картинки одинаковые, что с профилем, что без. Ладно, переживу :)
UFO just landed and posted this here
В Safari, кстати, картинки с домиком получились разные
UFO just landed and posted this here
Прочитал статью и понял, насколько я туп… Вот на этой картинке, что по осям?
Что значит «значение точки по оси X — значение первого пикселя, по оси Y — второго»? Какого — первого? Какого — второго? Что такое «значение пикселя»? На картинке с енотом есть пиксели, они могут быть представлены как (x,y,a), где a — яркость. Как из этих троек получилась картинка в спойлере?
Скрытый текст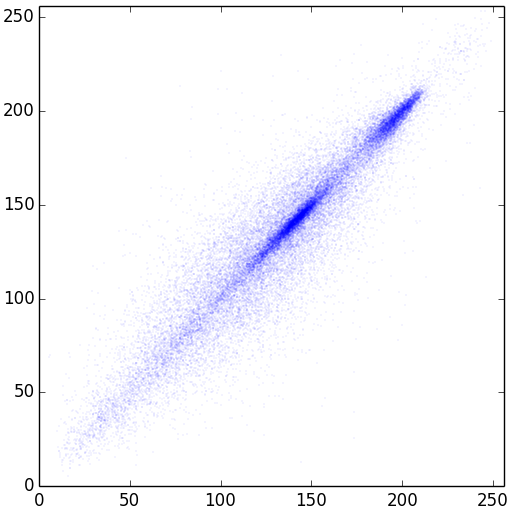
Что значит «значение точки по оси X — значение первого пикселя, по оси Y — второго»? Какого — первого? Какого — второго? Что такое «значение пикселя»? На картинке с енотом есть пиксели, они могут быть представлены как (x,y,a), где a — яркость. Как из этих троек получилась картинка в спойлере?
Для начала проверим насколько зависимы два соседних пикселя. <...> Отметим их на координатной плоскости точками так, что значение точки по оси X — значение первого пикселя, по оси Y — второго.Картинка с енотом у нас чёрно-белая, значит, используется значение единственного параметра K (или как его там в grayscale обозначают).
Каждый пиксель в grayscale можно однозначно определить тремя цифрами — (x,y,k) — где k — это яркость. если мы отводим 1 байт на яркость, то да, это 0..255
На картинке из спойлера каждый пиксель тоже можно определить тройкой чисел — (x', y', k'). Вот мне и интересно, как преобразовыаются пиксели из первой картинки во вторую. У автора написано «для всех пар изображения» — это значит, всего будет (256*256)*(256*256-1)/2 пар. Или я как-то иначе понимаю слова «для всех пар»?
На картинке из спойлера каждый пиксель тоже можно определить тройкой чисел — (x', y', k'). Вот мне и интересно, как преобразовыаются пиксели из первой картинки во вторую. У автора написано «для всех пар изображения» — это значит, всего будет (256*256)*(256*256-1)/2 пар. Или я как-то иначе понимаю слова «для всех пар»?
Как уже ответили ниже, значение пикселя серого изображения — одно число от 0 до 255. Мы же рассматриваем по 2 соседних пикселя. На графике одной точке соответствуют именно эти 2 пикселя. По X на графике — значение первого пикселя, по Y — второго.
Все равно туплю. Каких соседних? По горизонтали? Вертикали? Диагонали? Или вообще каждый с каждым?
В данном случае по горизонтали. То есть: x0y0 и x1y0, x2y0 и x3y0..., итого 256*256/2 = 32768 точек. Но вообще, не так уж важно — по вертикали или горизонтали, потому что нас интересует выявление зависимостей между соседними. Попробуйте сделать подобный график но для вертикали и вы увидите, что графики почти не отличаются.
Не знаю, обсуждалось ли выше, но
Как же выглядит эта дискретная функция? На ум лишь приходит чередование чёрных и белых пикселей, но тогда 1-й коэффициент будет 0.5? Или я что-то не понимаю?
Для примера подумайте, как будет выглядеть дискретная функция, коэффициенты разложения которой равны нулю, кроме последнего.
Как же выглядит эта дискретная функция? На ум лишь приходит чередование чёрных и белых пикселей, но тогда 1-й коэффициент будет 0.5? Или я что-то не понимаю?
А теперь, точно так же поделим на четверки и визуально определим базис в четырехмерном пространстве…
Очень подняло настроение. Огромное спасибо за статью.
Очень подняло настроение. Огромное спасибо за статью.
2-мерное преобразование енота [x]
Всё чётко! Красава! =)
Божественно крутой пост.
Заметил маленькую ошибку:
Для нашего изображения размером 256 на 256 получим 256*256/2 точек:
Но получим мы 256*255/2 точек.
Количество пар из 256 элементов есть С2n = n!/(2 × (n-2)!)
Под точкой понимается точка на плоскости XY с координатами:
x = get_pixel(2*n, m);
y = get_pixel(2*n+1, m);
где n ∈ [0, 127], m ∈ [0, 255]
То есть просто рассматриваются соседние пары пикселей
x = get_pixel(2*n, m);
y = get_pixel(2*n+1, m);
где n ∈ [0, 127], m ∈ [0, 255]
То есть просто рассматриваются соседние пары пикселей
Спасибо за разъяснение! От понимания этого построения зависят все нижеследующие рассуждения, а у меня на этом месте случился «затык».
Осталось уточнить деталь: а как быть, если строках и столбцах исходного изображения нечетное количество пикселей?
Моё собственное предположение: считывать пары не строкам слева направо, а в попеременном направлении, методом «бустрофедон».
Да, можно так. Но задумываться над такими тонкостями нужно только для реализации (не очень хорошей) альтернативы JPEG, в которой разбитие изображение производится не по 8x8, а по 2x1. В контексте этой статьи это не важно. Целью являлось показать то, что на фотографиях существует корреляция соседних пикселей. И, грубо говоря, если есть корреляция, значит есть избыточность, которую мы можем убрать для уменьшения размера.
Кстати, если JPEG-ом закодировать изображение со сторонами не кратными 8, то оно будет расширено кодером до кратного и заполнено каким-либо цветом, или просто мусором, чтобы не тратить время на очистку буфера. Этот излишек просто не показывается просмотрщиками.
Кстати, если JPEG-ом закодировать изображение со сторонами не кратными 8, то оно будет расширено кодером до кратного и заполнено каким-либо цветом, или просто мусором, чтобы не тратить время на очистку буфера. Этот излишек просто не показывается просмотрщиками.
Sign up to leave a comment.
Изобретаем JPEG