Comments 39
Спасибо. Будет замечательно, если расскажете про потоки (с приведением хорошей реализации), например, применительно к канонической задаче о назначении.
0
Не увидел описания самой сути алгоритма поиска в ширину (только код).
+1
Поиск в ширину — тема следующей статьи, а тут и кода нет
0
UFO just landed and posted this here
Прошел по Вашей ссылке, нашел следующий алгоритм:
Он отличается от того, что написано у меня, порядком обхода соседей — в этом коде он прямой, а у меня — обратный.
А вот BFS получится из моего (как и из этого) кода заменой стека на очередь.
Насчет невозможности обхода дерева — Вы имеете в виду, что некоторые вершины окажутся непосещенными? Насколько я понимаю, это невозможно, но буду рад увидеть пример.
Код
procedure ОБХОД-В-ГЛУБИНУ-1($p$: вершина);
begin
Посетить вершину $p$ и поместить ее в пустой стек S;
while Стек S непуст do
Пусть $p$ — вершина, находящаяся на верхушке стека S;
if у $p$ есть непосещенные смежные вершины then
Пусть $q$ — непосещенная вершина, смежная вершине $p$;
Пройти по ребру ($p,q$), посетить вершину $q$ и поместить ее в стек S
else Удалить вершину $p$ из стека S
end
end
end;
begin
Посетить вершину $p$ и поместить ее в пустой стек S;
while Стек S непуст do
Пусть $p$ — вершина, находящаяся на верхушке стека S;
if у $p$ есть непосещенные смежные вершины then
Пусть $q$ — непосещенная вершина, смежная вершине $p$;
Пройти по ребру ($p,q$), посетить вершину $q$ и поместить ее в стек S
else Удалить вершину $p$ из стека S
end
end
end;
Он отличается от того, что написано у меня, порядком обхода соседей — в этом коде он прямой, а у меня — обратный.
А вот BFS получится из моего (как и из этого) кода заменой стека на очередь.
Насчет невозможности обхода дерева — Вы имеете в виду, что некоторые вершины окажутся непосещенными? Насколько я понимаю, это невозможно, но буду рад увидеть пример.
0
Недавно программировал алгоритм поиска слов в игре Балда.
Представил поле как список смежных вершин и проходил по нему алгоритмом поиска в глубину, что обеспечило полный перебор.
Правда, получился всё равно не полный перебор, поскольку я отсекал все несуществующие начала слов (например, если первым оказался твёрдый знак), сверяя текущее состояние прохода (некая последовательность букв) с очень широким и очень неглубоким деревом, построенным по словарю.
Представил поле как список смежных вершин и проходил по нему алгоритмом поиска в глубину, что обеспечило полный перебор.
Правда, получился всё равно не полный перебор, поскольку я отсекал все несуществующие начала слов (например, если первым оказался твёрдый знак), сверяя текущее состояние прохода (некая последовательность букв) с очень широким и очень неглубоким деревом, построенным по словарю.
0
Продолжайте цикл статей, это полезно.
Сам занимаюсь этой тематикой: читаю английские статьи (русских нет) и интересуюсь алгоритмами динамики в соц. сетях.
А именно: по сети течет информация, необходим алгоритм, который в ключевых узлах сети будет снимать максимум информации, при этом число узлов, куда нужно поставить устройство съема должно быть минимально. На эту тему я мало чего нашел, а численных расчетов не видел вообще.
По теме двудольных графов (2-mode, bipartite): есть ли у вас модификации DFS него?
Сам занимаюсь этой тематикой: читаю английские статьи (русских нет) и интересуюсь алгоритмами динамики в соц. сетях.
А именно: по сети течет информация, необходим алгоритм, который в ключевых узлах сети будет снимать максимум информации, при этом число узлов, куда нужно поставить устройство съема должно быть минимально. На эту тему я мало чего нашел, а численных расчетов не видел вообще.
По теме двудольных графов (2-mode, bipartite): есть ли у вас модификации DFS него?
0
Спасибо.
Не очень понял суть проблемы. Возможно, поможет поиск точек сочленения — это делается тем же DFS'ом, собираюсь про это рассказать в ближайшем будущем. А по теме двудольных графов я что-то не могу ничего вспомнить, кроме проверки на двудольность, паросочетаний (в двух вариантах: напрямую и потоком) и венгерки. Про это расскажу.
Не очень понял суть проблемы. Возможно, поможет поиск точек сочленения — это делается тем же DFS'ом, собираюсь про это рассказать в ближайшем будущем. А по теме двудольных графов я что-то не могу ничего вспомнить, кроме проверки на двудольность, паросочетаний (в двух вариантах: напрямую и потоком) и венгерки. Про это расскажу.
0
Любой рекурсивный алгоритм можно переписать в нерекурсивном виде.
Это чаще всего делается для того чтобы избежать переполнения стека. Не хочу показаться занудой, но при приведенной Вами реализации Вы можете на него наткнуться из-за того, что в каждой итерации цикла выделяете память для двух целочисленных, хотя могли определить их вне цикла и при каждой итерации просто менять их значения
-1
Это же локальные переменные, они находятся по одному и тому же адресу, ничего не выделяется каждый раз. Если мы вынесем их вне цикла, единственное различие будет — изменение области видимости.
Провел эксперимент, написав вот такой код:
Диспетчер задач как сразу после запуска, так и через несколько десятков минут показывает потребление только 400 кб памяти
Провел эксперимент, написав вот такой код:
int main(void)
{
int x = 1;
while (true)
{
int a = x, b = x;
a += x;
b += a;
x = a;
}
return 0;
}
Диспетчер задач как сразу после запуска, так и через несколько десятков минут показывает потребление только 400 кб памяти
+1
Может кто подскажет, как модернизировать этот алгоритм так, чтобы он искал путь к выходу, который будет проходить через определенную точку в лабиринте и при этом не будет проходить через одну и туже ячейку дважды. Буду весьма признателен!
0
Можно найти путь до этой точки, удалить ребра (или вершины, я что-то плохо понял), ему соответствующие, и найти новый путь. Но не факт, что это будет работать
0
Плохо поняли условие? Имеется ввиду, что есть определенное место (вершина графа), через которое нужно обязятельно пройти по пути к выходу (еще какая-то определенная вершина графа), но вершини пути не должны повторяться дважды!
0
Значит, нужно удалять вершины. Но я почти уверен, что это неверное решение.
0
Есть более медленное гарантированно верное решение — напишу его сюда, как будет время. Но, мне кажется, можно как-то модифицировать DFS
0
Удалять вершины — не совсем подходит, потому как можем, даже при существовании верного пути, его себе отрезать, если придем в промежуточную точку заведомо неверным маршрутом…
0
Да, первая идея частенько бывает неверной.
Самое простое решение, которое я смог придумать пока что — это найти точки сочленения, после чего построить новый граф. Граф будет двудольным: компоненты вершинной двусвязности будут вершинами одной доли, а точки сочленения — вершинами другой. Ребро проводим в случае, если точка сочленения лежит в компоненте двусвязности.
Полученный граф (очевидно) будет деревом. Найдем в этом дереве единственный путь из начала в выделенную вершину и единственный путь из выделенной вершины в конец — если они пересекаются, значит, ответ «путь не существует». Если же они не пересекаются — то до компоненты двусвязности, в которой лежит искомая точка, можно добираться как угодно, а внутри компоненты (очевидно) работает первый алгоритм — ищем путь, удаляем, ищем второй путь.
Точки сочленения (и, соответственно, компоненты вершинной двусвязности) ищутся модифицированным DFSом, я об этом собираюсь рассказать в следующих статьях.
e-maxx.ru/algo/cutpoints
Самое простое решение, которое я смог придумать пока что — это найти точки сочленения, после чего построить новый граф. Граф будет двудольным: компоненты вершинной двусвязности будут вершинами одной доли, а точки сочленения — вершинами другой. Ребро проводим в случае, если точка сочленения лежит в компоненте двусвязности.
Полученный граф (очевидно) будет деревом. Найдем в этом дереве единственный путь из начала в выделенную вершину и единственный путь из выделенной вершины в конец — если они пересекаются, значит, ответ «путь не существует». Если же они не пересекаются — то до компоненты двусвязности, в которой лежит искомая точка, можно добираться как угодно, а внутри компоненты (очевидно) работает первый алгоритм — ищем путь, удаляем, ищем второй путь.
Точки сочленения (и, соответственно, компоненты вершинной двусвязности) ищутся модифицированным DFSом, я об этом собираюсь рассказать в следующих статьях.
e-maxx.ru/algo/cutpoints
0
ищем путь, удаляем, ищем второй путь.
Не очевидно, почему после удаления всего первого пути компонента не распадётся на части так, что проход до «выхода» уже окажется невозможным. Ясно, что ситуацию, когда она распадётся, придумать легко (прежде, чем идти ко входу, обойдём все вершины, соседние с нашей точкой). Но почему существует путь, который не разрушает связности?
0
А за какую сложность нужно решить задачу? Вроде как придумал 100%-верный (:D) алгоритм за O(VE).
0
Это интересно. Я думал, там без полного перебора путей (в худшем случае) не обойтись.
0
Я, кажется, придумал рассмотреть дерево DFS и на нем сделать динамику за квадрат. Завтра потестим
0
Сразу могу предложить такой тест:
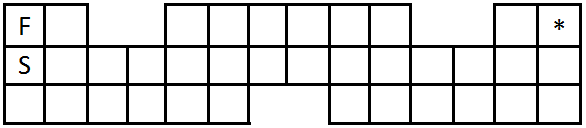
Надо дойти от S до * и вернуться к F, не пройдя ни одной клетки дважды. Если алгоритм его выдержит — шансы на правильность есть.
Конечно, лучше подошёл бы пример, где ответа нет, несмотря на отсутствие точек сочленения. Я такого пока не нашёл, но и доказать, что его не существует, тоже пока не смог.

Надо дойти от S до * и вернуться к F, не пройдя ни одной клетки дважды. Если алгоритм его выдержит — шансы на правильность есть.
Конечно, лучше подошёл бы пример, где ответа нет, несмотря на отсутствие точек сочленения. Я такого пока не нашёл, но и доказать, что его не существует, тоже пока не смог.
0
Я тоже не смог ни доказать, ни опровергнуть. А еще я точно знаю алгоритм, который пройдет этот тест. Днем потестирую, если заработает — напишу
0
А ещё лучше — вот так:

Чтобы у алгоритма не возникло желания сразу искать единственно возможное решение.

Чтобы у алгоритма не возникло желания сразу искать единственно возможное решение.
0
Да неважно. Добавляем еще одну вершину — сток, соединяем ее с вершинами S и F. * — исток, пропускные способности всех вершин — 1. Ищем поток, потом декомпозируем его
0
Поток с пропускными способностями вершин? Пока не слышал :) Но, наверное, получится.
Я вижу другой подход.
Удаляем F. Если точки сочленения не появилось — идём из F в любую соседнюю вершину, это новая F.
Если появились точки сочленения X пробуем их удалить. Дальше смотрим, оказались ли S и * оказались в разных компонентах. Если да, то возвращаем точки сочленения, строим путь из S в *, и идём по нему до последней точки из X (а точку F возвращаем обратно). Если нет — тоже возвращаем точки сочленения, строим путь из F в * (не проходящий через S), и если на нём есть точки из X — идём до последней из них. Если нет — делаем один шаг.
Как-то так, детали надо продумать (например, что если после удаления F единственной точкой сочленения оказалась S?)
Я вижу другой подход.
Удаляем F. Если точки сочленения не появилось — идём из F в любую соседнюю вершину, это новая F.
Если появились точки сочленения X пробуем их удалить. Дальше смотрим, оказались ли S и * оказались в разных компонентах. Если да, то возвращаем точки сочленения, строим путь из S в *, и идём по нему до последней точки из X (а точку F возвращаем обратно). Если нет — тоже возвращаем точки сочленения, строим путь из F в * (не проходящий через S), и если на нём есть точки из X — идём до последней из них. Если нет — делаем один шаг.
Как-то так, детали надо продумать (например, что если после удаления F единственной точкой сочленения оказалась S?)
0
Исходный код
#define _CRT_SECURE_NO_WARNINGS
#include <cstring>
#include <algorithm>
#include <vector>
#include <stack>
#include <queue>
#include <cstdio>
#include <map>
#include <string>
#include <iostream>
using namespace std;
struct edge
{
int v, c, f, r;
edge(int _v, int _c, int _r) : v(_v), c(_c), f(0), r(_r)
{};
};
const int INF = 3;
vector<vector<edge> > edges;
vector<int> mark;
vector<pair<int, int> > p;
int TIME;
stack<int> dfs_stack;
bool DFS(int v, int t)
{
dfs_stack.push(v);
while (!dfs_stack.empty() && v != t)
{
v = dfs_stack.top();
dfs_stack.pop();
for (int i = 0; i < (int)edges[v].size(); ++i)
{
if (mark[edges[v][i].v] == TIME || edges[v][i].f == edges[v][i].c)
{
continue;
}
mark[edges[v][i].v] = TIME;
p[edges[v][i].v] = make_pair(v, i);
dfs_stack.push(edges[v][i].v);
}
}
while (!dfs_stack.empty())
{
dfs_stack.pop();
}
return v == t;
}
bool DFS2(int v, int t)
{
dfs_stack.push(v);
while (!dfs_stack.empty() && v != t)
{
v = dfs_stack.top();
dfs_stack.pop();
for (int i = 0; i < (int)edges[v].size(); ++i)
{
if (mark[edges[v][i].v] == TIME || edges[v][i].f <= 0)
{
continue;
}
mark[edges[v][i].v] = TIME;
p[edges[v][i].v] = make_pair(v, i);
dfs_stack.push(edges[v][i].v);
}
}
while (!dfs_stack.empty())
{
dfs_stack.pop();
}
return v == t;
}
int flow(int s, int d)
{
TIME = 1;
mark.assign(edges.size(), 0);
p.assign(edges.size(), make_pair(0, 0));
int ans = 0;
for (; DFS(s, d); ++TIME)
{
++ans;
for (int v = d; v != s; v = p[v].first)
{
++edges[p[v].first][p[v].second].f;
--edges[v][edges[p[v].first][p[v].second].r].f;
}
}
return ans;
}
vector<vector<int> > decompose(int s, int d)
{
vector<vector<int> > ans;
for (++TIME; DFS2(s, d); ++TIME)
{
vector<int> path;
for (int v = d; v != s; v = p[v].first)
{
path.push_back(v);
--edges[p[v].first][p[v].second].f;
++edges[v][edges[p[v].first][p[v].second].r].f;
}
path.push_back(s);
reverse(path.begin(), path.end());
ans.push_back(path);
}
return ans;
}
void add_edge(vector<vector<edge> > &edges, int s, int d, int c)
{
edges[s].push_back(edge(d, c, (int)edges[d].size()));
edges[d].push_back(edge(s, 0, (int)edges[s].size() - 1));
}
void add_vertex_restrictions(int r)
{
int n = (int)edges.size();
vector<vector<edge> > new_edges(n * 2);
for (int i = 0; i < n; ++i)
{
add_edge(new_edges, i * 2, i * 2 + 1, r);
}
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < (int)edges[i].size(); ++j)
{
add_edge(new_edges, 2 * i + 1, 2 * edges[i][j].v, edges[i][j].c);
}
}
edges = new_edges;
}
void solve(vector<string> world)
{
pair<int, int> start = make_pair(-1, -1);
pair<int, int> finish = make_pair(-1, -1);
pair<int, int> middle = make_pair(-1, -1);
int n = (int)world.size();
int m = (int)world[0].size();
for (int i = 0; i < n; ++i)
{
if ((int)world[i].size() != m)
{
cout << "Different lengths of lines!\n";
return;
}
for (int j = 0; j < m; ++j)
{
if (world[i][j] == 'S')
{
if (start.first == -1)
{
start = make_pair(i, j);
}
else
{
cout << "Two cells marked as start!\n";
return;
}
}
if (world[i][j] == 'F')
{
if (finish.first == -1)
{
finish = make_pair(i, j);
}
else
{
cout << "Two cells marked as finish!\n";
return;
}
}
if (world[i][j] == '*')
{
if (middle.first == -1)
{
middle = make_pair(i, j);
}
else
{
cout << "Two cells marked as middle!\n";
return;
}
}
}
}
if (start.first < 0)
{
cout << "No cells marked as start!\n";
return;
}
if (finish.first < 0)
{
cout << "No cells marked as finish!\n";
return;
}
if (middle.first < 0)
{
cout << "No cells marked as middle!\n";
return;
}
edges.assign(n * m + 1, vector<edge>());
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < m; ++j)
{
if (world[i][j] == '#')
{
continue;
}
if (world[i][j] == 'F' || world[i][j] == 'S')
{
add_edge(edges, i * m + j, n * m, INF);
}
if (i > 0 && world[i - 1][j] != '#')
{
add_edge(edges, i * m + j, (i - 1) * m + j, INF);
}
if (i < n - 1 && world[i + 1][j] != '#')
{
add_edge(edges, i * m + j, (i + 1) * m + j, INF);
}
if (j > 0 && world[i][j - 1] != '#')
{
add_edge(edges, i * m + j, i * m + j - 1, INF);
}
if (j < m - 1 && world[i][j + 1] != '#')
{
add_edge(edges, i * m + j, i * m + j + 1, INF);
}
}
}
add_vertex_restrictions(1);
int f = flow((middle.first * m + middle.second) * 2 + 1, n * m * 2);
if (f < 2)
{
cout << "No paths found :\'(\n";
return;
}
vector<vector<int> > paths = decompose((middle.first * m + middle.second) * 2 + 1, n * m * 2);
vector<vector<int> > compressed_paths(paths.size());
for (int i = 0; i < (int)paths.size(); ++i)
{
for (int j = 0; j < (int)paths[i].size(); ++j)
{
if (paths[i][j] % 2 == 1)
{
compressed_paths[i].push_back(paths[i][j] / 2);
}
}
}
if (compressed_paths[0].back() != start.first * m + start.second)
{
swap(compressed_paths[0], compressed_paths[1]);
}
reverse(compressed_paths[0].begin(), compressed_paths[0].end());
for (int i = 0; i < compressed_paths[0].size() - 1; ++i)
{
cout << "(" << compressed_paths[0][i] / m << ", " << compressed_paths[0][i] % m << ")\n";
}
for (int i = 0; i < compressed_paths[1].size(); ++i)
{
cout << "(" << compressed_paths[1][i] / m << ", " << compressed_paths[1][i] % m << ")\n";
}
}
int main(void)
{
vector<string> world;
string s;
while (true)
{
getline(cin, s);
if (s == "")
{
break;
}
world.push_back(s);
}
solve(world);
getline(cin, s);
return 0;
}
0
Это в точности тот алгоритм, который я описывал выше. На этих двух тестах (и еще на нескольких небольших ручных тестах) работает корректно.
В окно консоли нужно ввести лабиринт. S, F, * — заимствованная у Вас нотация, # — непроходимая клетка, все остальное — проходимая клетка
В окно консоли нужно ввести лабиринт. S, F, * — заимствованная у Вас нотация, # — непроходимая клетка, все остальное — проходимая клетка
0
Да, по идее решение должно работать для лабиринтов размером приблизительно до 1000x1000.
Работать — подразумевается «находить корректный ответ менее, чем за пару секунд используя менее, чем пару сотен метров памяти»
Работать — подразумевается «находить корректный ответ менее, чем за пару секунд используя менее, чем пару сотен метров памяти»
0
Сложность роли не играет. Главное получить хоть какое-то вменяемое решение!
0
Решение за O(V*E).
Пусть S — точка старта, F — точка финиша, M — промежуточная точка.
Запускаем BFS от точки M, для каждой вершины запоминаем её расстояние до M и шаг пути к М (индекс предыдущей вершины).
Идём от S и F в сторону M, пока не столкнёмся (для этого смотрим на расстояния, и если они разные, то делаем шаг из более далёкой точки, а если одинаковые — из обеих точек). Точки, по которым прошли, помечаем как «точки пути из F или из S».
Начало цикла
Если мы столкнулись в точке M — решение найдено.
Пусть мы столкнулись в другой точке X.
Временно выбрасываем X из графа (объявляем её недоступной). Но направление пути из неё к M не забываем.
Перезапускаем BFS, но на этот раз останавливаем его, как только найдём точку Y, помеченную как «точку пути из F или из S». Если не нашли (граф получился несвязным), решения нет.
Двигаясь из Y в сторону M (по старым ссылкам) стираем старый конец пути.
Прописываем в Y новое направление в сторону M (в обход точки X) и новое расстояние.
Если Y была «на пути из F», то точку X объявляем лежащей «на пути из S» и наоборот.
Идём от точек Y и X в сторону M, пока не столкнёмся.
Конец цикла.
Решение не очень элегантное — 120 строк на C#. Но задачка хорошая.
Пусть S — точка старта, F — точка финиша, M — промежуточная точка.
Запускаем BFS от точки M, для каждой вершины запоминаем её расстояние до M и шаг пути к М (индекс предыдущей вершины).
Идём от S и F в сторону M, пока не столкнёмся (для этого смотрим на расстояния, и если они разные, то делаем шаг из более далёкой точки, а если одинаковые — из обеих точек). Точки, по которым прошли, помечаем как «точки пути из F или из S».
Начало цикла
Если мы столкнулись в точке M — решение найдено.
Пусть мы столкнулись в другой точке X.
Временно выбрасываем X из графа (объявляем её недоступной). Но направление пути из неё к M не забываем.
Перезапускаем BFS, но на этот раз останавливаем его, как только найдём точку Y, помеченную как «точку пути из F или из S». Если не нашли (граф получился несвязным), решения нет.
Двигаясь из Y в сторону M (по старым ссылкам) стираем старый конец пути.
Прописываем в Y новое направление в сторону M (в обход точки X) и новое расстояние.
Если Y была «на пути из F», то точку X объявляем лежащей «на пути из S» и наоборот.
Идём от точек Y и X в сторону M, пока не столкнёмся.
Конец цикла.
Решение не очень элегантное — 120 строк на C#. Но задачка хорошая.
0
Довольно интересное решение, хотя, конечно, хотелось бы доказательства =)
У вас довольно сложное сведение задачи к BFS, а у меня используются просто три (реально больших и сложных) кирпичика-алгоритма: алгоритм Форда-Фалкерсона, декомпозиция потока, раздваивание вершин.
Интересно, можно ли Ваше решение сделать тоже за O(V + E)
У вас довольно сложное сведение задачи к BFS, а у меня используются просто три (реально больших и сложных) кирпичика-алгоритма: алгоритм Форда-Фалкерсона, декомпозиция потока, раздваивание вершин.
Интересно, можно ли Ваше решение сделать тоже за O(V + E)
0
Кстати, если подумать, мы с Вами делаем одно и то же.
Только Вы поддерживаете в каждый момент времени больше данных, за что платите быстродействием.
А мне приходится восстанавливать эти данные в конце, за что я плачу размером кода.
Как говорится, у умных людей мысли сходятся =)
Только Вы поддерживаете в каждый момент времени больше данных, за что платите быстродействием.
А мне приходится восстанавливать эти данные в конце, за что я плачу размером кода.
Как говорится, у умных людей мысли сходятся =)
0
Кажется, есть совсем простое решение.
Добавляем вершину K, соединённую только с F и S.
Ищем кратчайший путь R={r0,r1,...,rk} от M до K (на самом деле, нам годится любой путь, лишь бы несоседние вершины на нём не были соединены ребром графа).
Удаляем все вершины пути R из графа, разбиваем то, что осталось, на связные области.
Для каждой области G_i находим самую раннюю и самую позднюю вершины из R, которые соединены с вершинами из G_i. Пусть это r_{a_i} и r_{b_i}. Запоминаем путь между этими вершинами, проходящий по G_i.
Утверждается, что для каждого 0<m<k найдётся такое i, что a_i<m<b_i, То есть, отрезок [0,r] можно покрыть отрезками [a_i,b_i] так, что соседние отрезки будут перекрываться по меньшей мере по двум вершинам.
Теперь мы можем построить два пути из M в K, в каждом из них будут чередоваться сегмент, проходящий по R и сегмент [r_{a_i},r_{b_i}], проходящий по какому-нибудь G_i, идущий в обход следующего сегмента, проходящего по R (и принадлежащего другому пути).
Как-то так. К сожалению, алгоритма Форда-Фалкерсона я не знаю (мне дочка как-то пыталась объяснить, но я всё благополучно забыл), так что не могу сказать, не получилось ли случайно то же, что у Вас.
Добавляем вершину K, соединённую только с F и S.
Ищем кратчайший путь R={r0,r1,...,rk} от M до K (на самом деле, нам годится любой путь, лишь бы несоседние вершины на нём не были соединены ребром графа).
Удаляем все вершины пути R из графа, разбиваем то, что осталось, на связные области.
Для каждой области G_i находим самую раннюю и самую позднюю вершины из R, которые соединены с вершинами из G_i. Пусть это r_{a_i} и r_{b_i}. Запоминаем путь между этими вершинами, проходящий по G_i.
Утверждается, что для каждого 0<m<k найдётся такое i, что a_i<m<b_i, То есть, отрезок [0,r] можно покрыть отрезками [a_i,b_i] так, что соседние отрезки будут перекрываться по меньшей мере по двум вершинам.
Теперь мы можем построить два пути из M в K, в каждом из них будут чередоваться сегмент, проходящий по R и сегмент [r_{a_i},r_{b_i}], проходящий по какому-нибудь G_i, идущий в обход следующего сегмента, проходящего по R (и принадлежащего другому пути).
Как-то так. К сожалению, алгоритма Форда-Фалкерсона я не знаю (мне дочка как-то пыталась объяснить, но я всё благополучно забыл), так что не могу сказать, не получилось ли случайно то же, что у Вас.
0
Окрашивать вершины и выбрать кратчайший путь, содержащий искомую вершину?
0
Sign up to leave a comment.
Графы для самых маленьких: DFS