В качестве введения
В настоящее время Байесовские методы получили достаточно широкое распространение и активно используются в самых различных областях знаний. Однако, к сожалению, не так много людей имеют представление о том, что же это такое и зачем это нужно. Одной из причин является отсутствие большого количества литературы на русском языке. Поэтому здесь попытаюсь изложить их принципы настолько просто, насколько смогу, начав с самых азов (прошу прощения, если кому-то это покажется слишком простым).
В дальнейшем я бы хотел перейти к непосредственно Байесовскому анализу и рассказать об обработке реальных данных и о, на мой взгляд, отличной альтернативе языку R (о нем немного писалось тут) — Python с модулем pymc. Лично мне Python кажется гораздо более понятным и логичным, чем R с пакетами JAGS и BUGS, к тому же Python дает гораздо большую свободу и гибкость (хотя в Python есть и свои трудности, но они преодолимы, да и в простом анализе встречаются нечасто).
Немного истории
В качестве краткой исторической справки скажу, что формула Байеса была опубликована аж в 1763 году спустя 2 года после смерти ее автора, Томаса Байеса. Однако, методы, использующие ее, получили действительно широкое распространение только к концу ХХ века. Это объясняется тем, что расчеты требуют определенных вычислительных затрат, и они стали возможны только с развитием информационных технологий.
О вероятности и теореме Байеса
Формула Байеса и все последующее изложение требует понимания вероятности. Подробнее о вероятности можно почитать на Википедии.
На практике вероятность наступления события есть частота наступления этого события, то есть отношение количества наблюдений события к общему количеству наблюдений при большом (теоретически бесконечном) общем количестве наблюдений.
Рассмотрим следующий эксперимент: мы называем любое число из отрезка [0, 1] и смотрим за тем, что это число будет между, например, 0.1 и 0.4. Как нетрудно догадаться, вероятность этого события будет равна отношению длины отрезка [0.1, 0.4] к общей длине отрезка [0, 1] (другими словами, отношение «количества» возможных равновероятных значений к общему «количеству» значений), то есть (0.4 — 0.1) / (1 — 0) = 0.3, то есть вероятность попадания в отрезок [0.1, 0.4] равна 30%.
Теперь посмотрим на квадрат [0, 1] x [0, 1].
Допустим, мы должны называть пары чисел (x, y), каждое из которых больше нуля и меньше единицы. Вероятность того, что x (первое число) будет в пределах отрезка [0.1, 0.4] (показан на первом рисунке как синяя область, на данный момент для нас второе число y не важно), равна отношению площади синей области к площади всего квадрата, то есть (0.4 — 0.1) * (1 — 0) / (1 * 1) = 0.3, то есть 30%. Таким образом можно записать, что вероятность того, что x принадлежит отрезку [0.1, 0.4] равна p(0.1 <= x <= 0.4) = 0.3 или для краткости p(X) = 0.3.
Если мы теперь посмотрим на y, то, аналогично, вероятность того, что y находится внутри отрезка [0.5, 0.7] равна отношению площади зеленой области к площади всего квадрата p(0.5 <= y <= 0.7) = 0.2, или для краткости p(Y) = 0.2.
Теперь посмотрим, что можно узнать о значениях одновременно x и y.
Если мы хотим знать, какова вероятность того, что одновременно x и y находятся в соответствующих заданных отрезках, то нам нужно посчитать отношение темной площади (пересечения зеленой и синей областей) к площади всего квадрата: p(X, Y) = (0.4 — 0.1) * (0.7 — 0.5) / (1 * 1) = 0.06.
А теперь допустим мы хотим знать какова вероятность того, что y находится в интервале [0.5, 0.7], если x уже находится в интервале [0.1, 0.4]. То есть фактически у нас есть фильтр и когда мы называем пары (x, y), то мы сразу отбрасывает те пары, которые не удовлетворяют условию нахождения x в заданном интервале, а потом из отфильтрованных пар мы считаем те, для которых y удовлетворяет нашему условию и считаем вероятность как отношение количества пар, для которых y лежит в вышеупомянутом отрезке к общему количеству отфильтрованных пар (то есть для которых x лежит в отрезке [0.1, 0.4]). Мы можем записать эту вероятность как p(Y|X). Очевидно, что эта вероятность равна отношению площади темной области (пересечение зеленой и синей областей) к площади синей области. Площадь темной области равна (0.4 — 0.1) * (0.7 — 0.5) = 0.06, а площадь синей (0.4 — 0.1) * (1 — 0) = 0.3, тогда их отношение равно 0.06 / 0.3 = 0.2. Другими словами, вероятность нахождения y на отрезке [0.5, 0.7] при том, что x уже принадлежит отрезку [0.1, 0.4] равна p(Y|X) = 0.2.
Можно заметить, что с учетом всего вышесказанного и всех приведенных выше обозначений, мы можем написать следующее выражение
p(Y|X) = p(X, Y) / p(X)
Кратко воспроизведем всю предыдущую логику теперь по отношению к p(X|Y): мы называем пары (x, y) и фильтруем те, для которых y лежит между 0.5 и 0.7, тогда вероятность того, что x находится в отрезке [0.1, 0.4] при условии, что y принадлежит отрезку [0.5, 0.7] равна отношению площади темной области к площади зеленой:
p(X|Y) = p(X, Y) / p(Y)
В двух приведенных выше формулах мы видим, что член p(X, Y) одинаков, и мы можем его исключить:
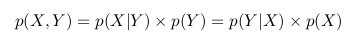
Мы можем переписать последнее равенство как
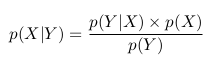
Это и есть теорема Байеса.
Интересно еще заметить, что p(Y) это фактически p(X,Y) при всех значениях X. То есть, если мы возьмем темную область и растянем ее так, что она будет покрывать все значения X, она будет в точности повторять зеленую область, а значит, она будет равна p(Y). На языке математики это будет означать следующее:
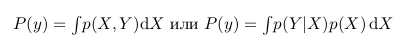
Тогда мы можем переписать формулу Байеса в следующем виде:
Применение теоремы Байеса
Давайте рассмотрим следующий пример. Возьмем монетку и подкинем ее 3 раза. С одинаковой вероятностью мы можем получить следующие результаты (О — орел, Р — решка): ООО, ООР, ОРО, ОРР, РОО, РОР, РРО, РРР.
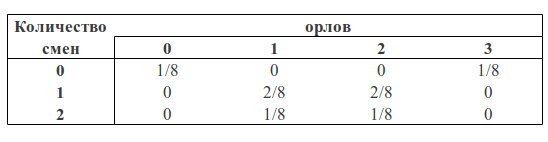
Мы можем посчитать какое количество орлов выпало в каждом случае и сколько при этом было смен орел-решка, решка-орел:
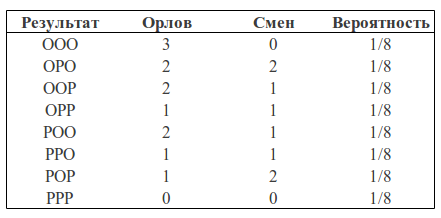
Мы можем рассматривать количество орлов и количество изменений как две случайные величины. Тогда таблица вероятностей будет иметь следуюший вид:
Теперь мы можем увидеть формулу Байеса в действии.
Но прежде проведем аналогию с квадратом, который мы рассматривали ранее.
Можно заметить, что p(1O) есть сумма третьего столбца («синяя область» квадрата) и равна сумме всех значений ячеек в этом столбце: p(1O) = 2/8 + 1/8 = 3/8
p(1С) есть сумма третьей строки («зеленая область» квадрата) и, аналогично, равна сумме всех значений ячеек в этой строке p(1С) = 2/8 + 2/8 = 4/8
Вероятность того, что мы получили одного орла и одну смену равна пересечению этих областей (то есть значение в клетке пересечения третьего столбца и третьей строки) p(1С, 1О) = 2/8
Тогда, следуя формулам описанным выше, мы можем посчитать вероятность получить одну смену, если мы получили одного орла в трех бросках:
p(1С|1О) = p(1С, 1О) / p(1О) = (2/8) / (3/8) = 2/3
или вероятность получить одного орла, если мы получили одну смену:
p(1О|1С) = p(1С, 1О) / p(1С) = (2/8) / (4/8) = 1/2
Если мы посчитаем вероятность получить одну смену при наличии одного орла p(1О|1С) через формулу Байеса, то получим:
p(1О|1С) = p(1С|1О) * p(1О) / p(1С) = (2/3) * (3/8) / (4/8) = 1/2
Что мы и получили выше.
Но какое практическое значение имеет приведенный выше пример?
Дело в том, что, когда мы анализируем реальные данные, обычно нас интересует какой-то параметр этих данных (например, среднее, дисперсия и пр.). Тогда мы можем провести следующую аналогию с вышеприведенной таблицей вероятностей: пусть строки будут нашими экспериментальными данными (обозначим их Data), а столбцы — возможными значениями интересующего нас параметра этих данных (обозначим его
). Тогда нас интересует вероятность получить определенное значение параметра на основе имеющихся данных 
.Мы можем применить формулу Баейса и записать следующее:
А вспомнив формулу с интегралом, можно записать следующее:
То есть фактически как результат нашего анализа мы имеет вероятность как функцию параметра. Теперь мы можем, например, максимизировать эту функцию и найти наиболее вероятное значение параметра, посчитать дисперсию и среднее значение параметра, посчитать границы отрезка, внутри которого интересующий нас параметр лежит с вероятностью 95% и пр.
Вероятность
называют апостериорной вероятностью. И для того, чтобы посчитать ее нам надо иметь
— функцию правдоподобия и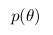 
— априорную вероятность.Функция правдоподобия определяется нашей моделью. То есть мы создаем модель сбора данных, которая зависит от интересующего нас параметра. К примеру, мы хотим интерполировать данные с помощью прямой y = a * x + b (таким образом мы предполагаем, что все данные имеют линейную зависимость с наложенным на нее гауссовым шумом с известной дисперсией). Тогда a и b — это наши параметры, и мы хотим узнать их наиболее вероятные значения, а функция правдоподобия — гаусс со средним, заданным уравнением прямой, и данной дисперсией.
Априорная вероятность включает в себя информацию, которую мы знаем до проведения анализа. Например, мы точно знаем, что прямая должна иметь положительный наклон, или, что значение в точке пересечения с осью x должно быть положительным, — все это и не только мы можем инкорпорировать в наш анализ.
Как можно заметить, знаменатель дроби является интегралом (или в случае, когда параметры могут принимать только определенные дискретные значения, суммой) числителя по всем возможным значениям параметра. Практически это означает, что знаменатель является константой и служит для того, что нормализировать апостериорную вероятность (то есть, чтобы интеграл апостериорной вероятности был равен единице).
На этом я бы хотел закончить свой пост (продолжение тут). Буду рад вашим комментариям.
