Comments 124
А правда, что математики все же сомневаются в безгрешности Пеановской арифметики?
+10
Зависит от того, как это понимать. Непротиворечивость её вроде как доказана. С другой стороны, не любое арифметическое утверждение можно доказать, исходя из аксиом Пеано. Это следует из теоремы Гёделя о неполноте.
+20
Минус, наверное, за то, что я забыл уточнить: из второй теоремы Гёделя о неполноте.
Ещё и в карму кто-то напыщил… забавные люди.
Ещё и в карму кто-то напыщил… забавные люди.
+26
Забавности хабралюдям не занимать.
+21
Да, конечно, из-за этого :) Сразу вспомнился анекдот:
На лекции по линейной алгебре. Препод что-то пишет на доске. На последней парте студенты играют в карты. Один из них что-то не так покрыл и второй на всю аудиторию:
— Ты что, совсем охренел?!
Препод:
— Спокойно! Сейчас все объясню.
На лекции по линейной алгебре. Препод что-то пишет на доске. На последней парте студенты играют в карты. Один из них что-то не так покрыл и второй на всю аудиторию:
— Ты что, совсем охренел?!
Препод:
— Спокойно! Сейчас все объясню.
+36
UFO just landed and posted this here
Мало того, что ошибочные, так ещё и недоказуемые :)
+1
Странным это мне кажется, на самом деле. Столько юзеров минусовало статью, но ни один не удосужился написать «статья — гуано», или «статья не нужна», или «буква ℕ слишком маленькая, и я ненавижу тебя за это». Я понимаю, конечно, что минус — он, в некотором роде… как по-русски сказать «self-descriptive»? Но всё же.
0
Вы драматизируете :-) Неплохой рейтинг у вашей статьи (конечно, если не сравнивать с предыдущей, где 200+). Так что не вешайте нос и продолжайте в том же духе: интересно читать!
0
Насколько я знаю современное положение вещей — нет, непротиворечивость аксиоматики Пеано не доказана. Более того, относительно недавно была очень серьезная попытка доказать ее противоречивость, которая, к счастью, провалилась.
+1
Гедель учит, что ее непротиворечивость вроде как нельзя доказать ее собственными средствами.
0
Меня на первом курсе вызвали к доске и попросили доказать это тождество методами теории Маркова. Мда. Матиндукция.
0
На втором курсе, декан факультета, ведя очередную лекцию, попросил нас возвести число 10 в степень j, т.е.в 10^(sqrt(-1)). Вот тогда, у нас случился разрыв шаблона
0
j — это, кажется, уже кватернион. Корень из минус единицы — это i.
+1
в разных областях по-разному :) Лично я просто привык, что i — это функция тока от времени i(t) поэтому мне легче использовать j в качестве мнимой единицы.
+3
j как кватернион — это тоже корень из -1. Как и k, и вообще любой единичный вектор в базисе {i,j,k}. И любой из них является мнимой единицей своего экземпляра поля C. Так что, неважно, какой из них брать. Лишь бы поняли.
+4
Например, в электродинамике часто используют обозначение j для мнимой единицы. Из соображений удобства.
upd: выше упомянули об этом.
upd: выше упомянули об этом.
0
У Вас хотя бы степень… Нас синус просили посчитать =)
0
Забавнее было бы посчитать ii (Мнимая единица в степени мнимой единицы). Забавно тем, что результат — число вещественное.
+2
UFO just landed and posted this here
Вот только комплексное число в комплексной степени — это не число, потому что возведение в комплексную степень — многозначная функция (поскольку логарифм — многозначная функция).
Например, i^i = e^(Ln(i) * i) = e^-((pi/2)+2*k*pi), k — любое целое.
Например, i^i = e^(Ln(i) * i) = e^-((pi/2)+2*k*pi), k — любое целое.
+4
Забавно тем, что результат — число вещественное.
Может вы ошиблись?
ii — не вещественное. Ни одно из них.
Вещественным будет поворот на π/2, то есть iiπ/2 + kπ, k∈ℤ
+1
Недавно видел такое доказательство, что 2х2=5.
Возьмем равенство
16 + 45 = 25 + 36
Разобьем часть слагаемых на произведения:
16 + 9*5 = 25 + 9*4
Перенесем некоторые слагаемые в другие части равенства — естественно, изменяя знаки на противоположные:
16-9*4=25-9*5
теперь к обеим частям добавим по 81/4.
16-9*4+81/4=25-9*5+81/4
Заметим, что в обеих частях стоят полные квадраты:
16-2*4*9/2+81/4=(4-9/2)2
25-2*5*9/2+81/4=(5-9/2)2
Извлекая квадратный корень из обеих частей равенства, получаем что
4-9/2=5-9/2
Откуда немедленно следует, что 4=5, иначе говоря, 2х2=5.
/конечно, тут есть ошибка в рассуждениях, и она элементарна, кто скажет, в чем она заключается?/
Возьмем равенство
16 + 45 = 25 + 36
Разобьем часть слагаемых на произведения:
16 + 9*5 = 25 + 9*4
Перенесем некоторые слагаемые в другие части равенства — естественно, изменяя знаки на противоположные:
16-9*4=25-9*5
теперь к обеим частям добавим по 81/4.
16-9*4+81/4=25-9*5+81/4
Заметим, что в обеих частях стоят полные квадраты:
16-2*4*9/2+81/4=(4-9/2)2
25-2*5*9/2+81/4=(5-9/2)2
Извлекая квадратный корень из обеих частей равенства, получаем что
4-9/2=5-9/2
Откуда немедленно следует, что 4=5, иначе говоря, 2х2=5.
/конечно, тут есть ошибка в рассуждениях, и она элементарна, кто скажет, в чем она заключается?/
+2
Извлечение квадратного корня из отрицательного числа
0
4-9/2 < 0 => sqrt( (4-9/2)^2 ) = 9/2-4
Задачка интересная, спасибо. Взял на вооружение.
Задачка интересная, спасибо. Взял на вооружение.
+1
Есть более простой способ доказать 2x2=5:
Возьмём два простых равенства:
20-20=0
25-25=0
Так, как они равны 0, то равны друг другу и левые части этих равенств:
20-20=25-25
В каждой части равенства, вынесем общий множитель за скобки:
4(5-5)=5(5-5)
В левой части, разложим 4 на множители:
2*2(5-5)=5(5-5)
Сократим обе части равенства на одинаковый множитель (5-5) и получим:
2*2=5
Здесь, конечно тоже закралась небольшая ошибка...
Возьмём два простых равенства:
20-20=0
25-25=0
Так, как они равны 0, то равны друг другу и левые части этих равенств:
20-20=25-25
В каждой части равенства, вынесем общий множитель за скобки:
4(5-5)=5(5-5)
В левой части, разложим 4 на множители:
2*2(5-5)=5(5-5)
Сократим обе части равенства на одинаковый множитель (5-5) и получим:
2*2=5
Здесь, конечно тоже закралась небольшая ошибка...
0
Здесь на мой взгляд ошибка более очевидная, деление на ноль сразу бросается в глаза :)
+7
Здесь она более явная, поди про то, что на ноль делить нельзя все знают. Мой пример для гуманитариев похитрее будет, имхо.
0
В общем то оно так.
Бывает летом выедем куда-нибудь на природу, в лагерь, и показываю это «доказательство», как головоломку молодым «пионерам», и сидят затылок чешут: Вроде всё просто, а «втыкнуть» не могут.
Бывает летом выедем куда-нибудь на природу, в лагерь, и показываю это «доказательство», как головоломку молодым «пионерам», и сидят затылок чешут: Вроде всё просто, а «втыкнуть» не могут.
0
Да и для уставших инженеров тоже :)
В твоем примере очевидно из постановки, что проблема будет в неправильном раскрытии корня из квадрата, но из-за большого количества цифр и дробей я первоначально потратил больше времени на то, чтобы вычислить, в какой строчке была сделана такая ошибка.
В примере с целыми числами то место, где получается ноль сразу бросается в глаза.
В твоем примере очевидно из постановки, что проблема будет в неправильном раскрытии корня из квадрата, но из-за большого количества цифр и дробей я первоначально потратил больше времени на то, чтобы вычислить, в какой строчке была сделана такая ошибка.
В примере с целыми числами то место, где получается ноль сразу бросается в глаза.
0
Ошибка в
Извлекая квадратный корень из обеих частей равенства, получаем что
4-9/2=5-9/2
нужно использовать по модулю
| 4-9/2 | = |5-9/2|
Извлекая квадратный корень из обеих частей равенства, получаем что
4-9/2=5-9/2
нужно использовать по модулю
| 4-9/2 | = |5-9/2|
+3
Нет, 2x2 не содержится в школьной аксиоматике, так как умножение вводится как «много сложений». Таблица умножения появляется позже.
+4
Интересный вопрос. Умножение определяется как много сложений, однако в дальнейшем это практически не используется. Что ж, если таблица умножения выводится из сложения, то доказательство будет очень коротким: 2 x 2 = 2 + 2 = 4.
+3
Точнее, я хотел сказать следующее: определение умножения через сложение избыточно. Таблица умножения всё равно учится наизусть, а из неё и из правил умножения можно вывести связь со сложением.
-2
Проще доказать эксперементально ;)
+4
По идее, в линейной алгебре утверждается что ряд натуральных чисел начинается с нуля, то есть {0}=0;
тогда натуральные числа примут вид бесконречного множества {{0},1,2,3,...,n,...}
тогда натуральные числа примут вид бесконречного множества {{0},1,2,3,...,n,...}
-1
{0}=0
Что-что, простите?
0
Ну, то есть это нулевое множество, множество не соостоящее ни из какого элемента.
+1
Вы немного путаете. Это определение Фреге-Рассела, оно альтернативно аксиоматике Пеано.
0
Ну, да, Фреге-Рассел.
Я не думаю, что этот ноль что-то меняет в доказательстве. Можно считать, что там появился еще один элемент)
Я не думаю, что этот ноль что-то меняет в доказательстве. Можно считать, что там появился еще один элемент)
0
" {0}=0 " — ординалы же?
0
Позволю себе немного позанудствовать, хотя, раз уж мы доказываем, что 2*2=4, то это вполне уместно (ну или я сам ошибаюсь, что вполне вероятно):
Первая аксиома в оригинале звучит по-другому. В википедии, например, целые две аксиомы:
«следующее за натуральным числом есть натуральное число» и «всякое натуральное число следует только за одним натуральным числом».
Например, если я рассмотрю множество «1», «2» и «3» и задам следующий порядок: «1»->«2», «2»->«3», «3»->«2», то такая конструкция будет удовлетворять всем трём вашим аксиомам (но не оригинальным).
Первая аксиома в оригинале звучит по-другому. В википедии, например, целые две аксиомы:
«следующее за натуральным числом есть натуральное число» и «всякое натуральное число следует только за одним натуральным числом».
Например, если я рассмотрю множество «1», «2» и «3» и задам следующий порядок: «1»->«2», «2»->«3», «3»->«2», то такая конструкция будет удовлетворять всем трём вашим аксиомам (но не оригинальным).
+1
Ох ты ж шайтан… Да, разумеется. Во второй аксиоме забыл добавить «все остальные числа имеют одно и только одно предыдущее».
Странно, что вы первый это заметили.
Странно, что вы первый это заметили.
0
Ага, или даже конструкция 1->2, 2->2
upd. Sirian обновил аксиоматику комментарием выше, теперь всё хорошо :)
upd. Sirian обновил аксиоматику комментарием выше, теперь всё хорошо :)
+1
Математики компактны, потому что они ограничены и замкнуты.
судя по минусу не все помнят эту шутку, ну и ладно
судя по минусу не все помнят эту шутку, ну и ладно
+11
UFO just landed and posted this here
Для тех, кто хочет больше: Э. Ландау. Основы анализа
0
Всегда считал, что в его аксиоматике используется 0, а не 1. (Точнее нам так преподавали на мат. логике)
0
все намного проще: 2 х 2 = 4, оптом 3, в розницу 5
+1
Хоть и учился на прикладной математике, теорию чисел нам давали в очень ограниченном объеме. Но, IMHO, под аксиомы, приведенные в статье, попадают гораздо больше последовательностей, чем только натуральные числа в том виде, в котором их привыкли видеть (1, 2, 3, ...). Например, последовательность (2,4,6....) отвечает всем трем аксиомам.
0
А по поводу «странных доказательств» — я придумал перед экзаменом по ТФКП «доказательство», что любое комплексное число равно своему модулю. И даже группой не смогли сразу найти ошибку. Правда, препод в секунду нашел косяк, но многие, кому я потом показывал, ошибку в выкладках найти не могли.
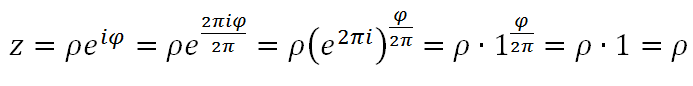

+1
UFO just landed and posted this here
Именно. Неверно потому, что подобная формула для комплексных не применяется, т.к. когда меняем порядок возведения в степень, мы вместо возведения в вещественную степень комплексного числа (что является многозначной функцией) переходим к возведению в степень целого, что многозначной уже не является.
0
Третье равенство верное.
a^(b*c)=(a^b)^c
a^(b*c)=(a^b)^c
0
Не для комплексных чисел.
+1
Докажете? На сколько я помню комплексное число является результатом возведения в степень. В том числе, и в комплексную. А операции, IMHO, здесь корректны. За исключением одного перехода. Но не третьего :-)
0
ну e^2pi*i != 1
0
Я наизусть этого не помню, честно сказать — помню только, что эти формулы неверны. Но гугление быстро дает результат, так, например, это описано и в Вики и в других документах.
Из них следует что неправильный как раз-таки переход по указанной вами формуле, а все остальное — только следствие из этого.
Как я понимаю, доказательством этого как раз и служит данный парадокс.
Из них следует что неправильный как раз-таки переход по указанной вами формуле, а все остальное — только следствие из этого.
Как я понимаю, доказательством этого как раз и служит данный парадокс.
0
1. Бегло просмотрел документы. Фигня для начинающих. Они приводят какие-то парадоксы, забывая про многозначность функций.
2. Парадокса нет. Есть математически неверный переход (равенство). А вот какое — это и был вопрос к общественности. Если внимательно почитать пункт 1 и посмотреть на формулу — то ответ найдется сразу.
2. Парадокса нет. Есть математически неверный переход (равенство). А вот какое — это и был вопрос к общественности. Если внимательно почитать пункт 1 и посмотреть на формулу — то ответ найдется сразу.
0
Чем вас не устраивает доказательство от противного?
Насколько я понимаю, оно вполне строгое — предположим, что ваша формула верна для любых a, b и c.
Тогда, воспользовавшись выкладками с вики или из пдф, получаем неверное равенство, опровергая предположение о том, что формула верна.
Насколько я понимаю, оно вполне строгое — предположим, что ваша формула верна для любых a, b и c.
Тогда, воспользовавшись выкладками с вики или из пдф, получаем неверное равенство, опровергая предположение о том, что формула верна.
0
1. Моя формула НЕ ВЕРНА. Именно об этом я и писал. Вопрос — где именно она не верна.
2. Выкладки в WiKi — не во всем верны. Если честно — читать ПОЛНОСТЬЮ (все буквы) некогда, да и не хочется. При кратком просмотре — в статье на ВиКи есть базовые формулы. И есть попытка построить парадоксы (типа 1=-1, i=-i). Но эти парадоксы — суть неполного применения базовой теории.
2. Выкладки в WiKi — не во всем верны. Если честно — читать ПОЛНОСТЬЮ (все буквы) некогда, да и не хочется. При кратком просмотре — в статье на ВиКи есть базовые формулы. И есть попытка построить парадоксы (типа 1=-1, i=-i). Но эти парадоксы — суть неполного применения базовой теории.
0
Ну на первый взгляд я бы сказал, что в третьем.
Хотя, вероятно, вы правы. Вы сейчас про четвертое?
Ведь причина ошибки — «равенство многозначных функций не означает равенства их аргументов», наверное правильнее сказать, что четвертое равенство неверное, а третье — просто… Эм… Опрометчиво, в том плане, что начиная такие преобразования, как в третьем, можно забыть о такой ошибке, как в четвертом.
Хотя, вероятно, вы правы. Вы сейчас про четвертое?
Ведь причина ошибки — «равенство многозначных функций не означает равенства их аргументов», наверное правильнее сказать, что четвертое равенство неверное, а третье — просто… Эм… Опрометчиво, в том плане, что начиная такие преобразования, как в третьем, можно забыть о такой ошибке, как в четвертом.
0
Четвертое тоже верно.
0
exp(2Pi*i*f) не равно 1^f, значит четвертое уже неверно, разве нет?
0
exp (2*Pi*i*f) = exp(2*Pi*i)^f=1^f.
Ошибки не вижу.
Ошибки не вижу.
0
exp(2Pi*i*f)=cos(2Pi*f)+i*sin(2Pi*f), не равно 1^f для вещественных f.
0
Опять ошибся местом. Спать надо больше.
0
Почему не равно?
Если честно, лень делать преобразования. Я верю в тригонометрическую форму комплексного числа и операции с ним. Но в своем рассуждении Вы практически ответили на изначальный вопрос. Думаю, Вы уже догадались, что неправильный переход именно пятый. 1^f != 1. А многие про это забывают.
Если честно, лень делать преобразования. Я верю в тригонометрическую форму комплексного числа и операции с ним. Но в своем рассуждении Вы практически ответили на изначальный вопрос. Думаю, Вы уже догадались, что неправильный переход именно пятый. 1^f != 1. А многие про это забывают.
0
Не могу согласиться. Может, я упускаю что-то фундаментальное, но 1^f при вещественном f равно единице, поэтому это равенство верное.
А вот exp(2Pi*i*f) не равно 1^f, подставьте, хотя бы, f=0.5 в это простое равенство. Получим
exp(2Pi*i*0.5) = 1^0.5
exp(Pi*i) = 1
-1 = 1
Значит как минимум этот переход неверен.
Призываю общественность хабра нас рассудить. Допускаю, что мог ошибиться, слишком давно проходил подобные вещи, но пока ошибки в своих рассуждениях не вижу.
А вот exp(2Pi*i*f) не равно 1^f, подставьте, хотя бы, f=0.5 в это простое равенство. Получим
exp(2Pi*i*0.5) = 1^0.5
exp(Pi*i) = 1
-1 = 1
Значит как минимум этот переход неверен.
Призываю общественность хабра нас рассудить. Допускаю, что мог ошибиться, слишком давно проходил подобные вещи, но пока ошибки в своих рассуждениях не вижу.
+1
но 1^f при вещественном f равно единице, поэтому это равенство верноеВот оно, Ваше заблуждение. Возведите единицу в степень 1/2. Получите ДВА результата — единица и «минус единица». Если возвести в степень 1/3, то будет ТРИ числа — единица, и два комплексно-сопряженных числа. Если единицу возводить в иррациональную степень, то количество значений будет бесконечно, ЕМНИП. Возведение в степень — функция, в общем случае. многозначная.
0
Все, согласен. Почему-то думал, что это относится только к комплексным основаниям с ненулевой мнимой частью, был неправ. В самом деле 1^f в общем случае многозначная.
0
Кстати, 1^f=(1^0)^f=1^(0*f)=1^0=1. Где ошибка на этот раз?
+2
Ноль это очень уж странная сущность. Не стоит его использовать в преобразованиях с умножением и делением. Именно ноль был виной всех безобразий выше (4=5 и т.п.)
0
В «4=5» проблемой был неэквивалентный и неправильный переход «4*0=5*0 => 4=5», который все нашли. В каком месте ошибка в моей цепочке переходов?
0
IMHO, использование нуля в преобразованиях не есть хорошая практика. При корректных выводах можно получить один из правильных ответов, но умножение на ноль «съедает» прочие возможные варианты результата.
0
Без нуля цепочка выглядела бы так:
2 = 4^(1/2) = ((-2)^2)^(1/2) = (-2)^(2*(1/2)) = (-2)^1 = -2.
2 = 4^(1/2) = ((-2)^2)^(1/2) = (-2)^(2*(1/2)) = (-2)^1 = -2.
0
Без нуля цепочка начиналась бы так:
±2 = 4^(1/2) =…
±2 = 4^(1/2) =…
0
Так ведь «4^(1/2)» — это не степенная, а показательная функция — a^x, «a» и «x» вещественные, a>0. Непрерывная функция, имеющая в каждой точке одно значение. Всё, как в школе, всё корректно. Значение функции a^x в точке x=1/2 при основании a=4 это никакое не -2, посмотрите на график :) Остальные возведения в степень тоже однозначны — либо a^x (a>0), либо x^n (n — целое, x!=0).
0
4^(1/2) не функция, а операция надо константами. Вы написали цепочку операций над константами. Я Вам указал на причину парадокса. Если рассматривать только школьную программу — то да, парадокс есть. К тому же, далеко не во всех школах рассказывают про комплексные числа. А вот то, что корень квадратный из четырех равен плюс/минус двум — рассказывают практически во всех.
0
Это не причина парадокса, а способ его обойти. Любая операция, пусть даже над константами — это значение функции от двух переменных при подстановке конкретных значений. Операция возведения в степень a^b корректно определена в двух случаях — как степенная или как показательная функция (либо a>0, b любое вещественное, либо b целое, a!=0, либо a=0, b натуральное). Там, где области определений пересекаются, тоже всё корректно — значения совпадают.
А парадокса нет. Есть один маленький факт, про который все (и я в том числе) забыли. И он относится именно к операциям, которые здесь описаны — безо всяких многозначностей квадратного корня. Какой?
А комплексные числа тут вообще ни при чем, в этой цепочке их нет. Квадратный корень тоже в явном виде не упоминается, 1/2 можно заменить на что-нибудь другое, хоть на 5/6 (только константы придётся поменять).
А парадокса нет. Есть один маленький факт, про который все (и я в том числе) забыли. И он относится именно к операциям, которые здесь описаны — безо всяких многозначностей квадратного корня. Какой?
А комплексные числа тут вообще ни при чем, в этой цепочке их нет. Квадратный корень тоже в явном виде не упоминается, 1/2 можно заменить на что-нибудь другое, хоть на 5/6 (только константы придётся поменять).
0
Насчёт того, что «что корень квадратный из четырех равен плюс/минус двум» — уже не помню. У меня такое ощущение, что нас учили, что запись sqrt(4) означает только +2, и никогда не -2, а уравнение x^2=4 имеет два корня — sqrt(4) и -sqrt(4). И говорить, что sqrt(x^2)=x, ссылаясь на то, что «корень имеет два значения», категорически нельзя — надо пользоваться формулой sqrt(x^2)=|x|.
Мне-то это не понадобилось, вступительных экзаменов я не сдавал. Но думаю, что у тех, кто усвоил эти правила, на первой и последней задачах было огромное преимущество перед теми, кто «знал, что у корня два значения»: шансов запутаться, работая с однозначной функцией, намного меньше.
Мне-то это не понадобилось, вступительных экзаменов я не сдавал. Но думаю, что у тех, кто усвоил эти правила, на первой и последней задачах было огромное преимущество перед теми, кто «знал, что у корня два значения»: шансов запутаться, работая с однозначной функцией, намного меньше.
0
Хотя нет, «плюс-минус 2» — это, конечно, причина, если смотреть в корень (и применять аппарат ТФКП). Но и в исходном виде все равенства, на первый взгляд, верные… ошибка-то где (если применять школьную математику, а не ТФКП)?
0
UFO just landed and posted this here
Похоже, у хабра есть предел глубины дерева комментариев.
0
нельзя отделить i от фи, так как показательная форма представления комплексного числа — это вещь в себе
0
Можно. Это просто возведение в степень.
0
Нет. exp(x+i*y) это вполне определённая однозначная функция, обладающая свойствами показательной, и в случае рационального x+i*y, т.е. x=p/q, y=0, совпадающая с одним из значений e^(p/q) (а именно, с вещественным положительным). Поэтому мы можем сказать, что exp(a+b)=exp(a)*exp(b), но вот написать exp(a*b)=(exp(a))^b уже нельзя (если b не является целым) — слева у нас число, а справа множество. Которое, кстати, для иррациональных b можно определить только через функцию exp: exp(a)^b = exp(a*b) * exp(2*pi*k*b*i), где k пробегает все целые числа.
0
Что-то, похоже, Вы запутались и сами себе противоречите.
exp(a*b)=(exp(a))^b — это правило со школы. Оно для обычной топологии и общепринятых операциях умножения/сложения/возведения в степень вполне себе работает. А почему Вы решили, что слева число при том, что справа множество — это, увы, Вы не объяснили.
exp(a*b)=(exp(a))^b уже нельзя (если b не является целым) — слева у нас число, а справа множество
exp(a*b)=(exp(a))^b — это правило со школы. Оно для обычной топологии и общепринятых операциях умножения/сложения/возведения в степень вполне себе работает. А почему Вы решили, что слева число при том, что справа множество — это, увы, Вы не объяснили.
0
Я всего лишь хочу сказать, что exp(x) (функция экспоненты, сумма сходящегося ряда x^n/n!) и выражение e^x как частный случай общего возведения в степень это разные вещи. exp(x) — функция. При любом x принимает одно значение. e^x при нецелых x является многозначной: e^(1/2) принимает 2 значения sqrt(e) и -sqrt(e), e^(1/3) — три значения, e^(2*pi*i) — бесконечно много значений exp(4*pi^2*k).
Почему не объяснил? По Вашим комментариям я сделал вывод, что Вам это очевидно. Увы, я ошибался.
Вообще, во всём этом топике, когда мы пишем a=b, то во многих случаях имеем в виду «a принадлежит b» или «a является подмножеством b». И пока множество расширяется, проблем нет — мы пишем 1=1^(1/2), имея в виду, что то, что слева является одним из возможных значений того, что справа. Точно так же мы можем написать 1^(1/3)=(1^(2/3))^(1/2) — множество справа шире, чем множество слева, включение a^(x*y)=(a^x)^y работает (при несимметричной интерпретации равенства, описанной выше). Обратное включение (a^x)^y=a^(x*y) гарантированно выполняется для только для целых y, в остальных случаях оно может быть неверным: если мы напишем, что (1^(2/3))^(1/2)=1^(1/3), то одним из значений «слева» будет -1, а «справа» его уже не будет.
«правило со школы» — хорошо сказано. Учитывая, что в школе многозначных функций не проходят. Хотя там уже говорят, что (a^2)^(1/2) это вовсе не a^1, а |a^1| — так что отдельные намёки на то, что формула может не работать, уже есть.
Почему не объяснил? По Вашим комментариям я сделал вывод, что Вам это очевидно. Увы, я ошибался.
Вообще, во всём этом топике, когда мы пишем a=b, то во многих случаях имеем в виду «a принадлежит b» или «a является подмножеством b». И пока множество расширяется, проблем нет — мы пишем 1=1^(1/2), имея в виду, что то, что слева является одним из возможных значений того, что справа. Точно так же мы можем написать 1^(1/3)=(1^(2/3))^(1/2) — множество справа шире, чем множество слева, включение a^(x*y)=(a^x)^y работает (при несимметричной интерпретации равенства, описанной выше). Обратное включение (a^x)^y=a^(x*y) гарантированно выполняется для только для целых y, в остальных случаях оно может быть неверным: если мы напишем, что (1^(2/3))^(1/2)=1^(1/3), то одним из значений «слева» будет -1, а «справа» его уже не будет.
«правило со школы» — хорошо сказано. Учитывая, что в школе многозначных функций не проходят. Хотя там уже говорят, что (a^2)^(1/2) это вовсе не a^1, а |a^1| — так что отдельные намёки на то, что формула может не работать, уже есть.
-1
Что ж, Ваша точка зрения понятна и имеет Но, увы, лично мне принять ее тяжело. Если Вы считаете, что exp(x) и e^x вещи разные — то и такая точка зрения имеет право на существование. Хотя я всегда был уверен, что это просто разные записи одного и того же. И, собственно, выражения вида
Предлагаю на сим закончить «каменты» к данному топику, чтобы осталось время на чтение новых постов.
когда мы пишем a=b, то во многих случаях имеем в виду...и приводят к вышеприведенным парадоксам. В общем, я свое мнение донес до общественности, коллеги-оппоненты тоже. В моих выкладках тоже не все «в шоколаде», посему особо придираться не буду.
Предлагаю на сим закончить «каменты» к данному топику, чтобы осталось время на чтение новых постов.
0
Конкретно в случае «е» это одно и то же только потому, что математики договорились считать запись e^x записью экспоненты. Так же, как a^x при вещественных a и x, a>0 — вполне конкретной ветвью функции. И когда начинают смешиваться разные понимания этих операций, то и возникает сначала путаница, а потом парадоксы…
+1
exp (2*Pi*i) == 1 (by definition)
0
Здесь был не тот комментарий. Но «каменты» удалять нельзя.
0
+10
Будет обидно, если псто не успеет набрать сотню. Я уже пообещал инвайт хорошему человеку :)
0
Sign up to leave a comment.

Просто, как дважды два четыре