Comments 62
Ну почему не в пятницу-то, а? Вечер на кафедре прошёл зря :)
+16
Насколько мне известно, в задорной форме задачки с «очевидным ответом» этот факт изложил и пустил гулять по интернетам vinograd19. Но такого ясного и подробного объяснения он не давал. Спасибо большое!
+1
Спасибо! Было интересно повспоминать.
+1
И тут я понял как же давно был универ.
+31
UFO just landed and posted this here
Хабр весьма к месту отображает в «похожих» статью математика может приносить физические страдания.
Как-то стыдно, что вроде считаю себя технарём, а выкладки с большим количеством интегралов и дробей до сих вызывают чувство тревоги (примерно такое же как если бы попросили длинные числа перемножить и не ошибиться нигде).
Как-то стыдно, что вроде считаю себя технарём, а выкладки с большим количеством интегралов и дробей до сих вызывают чувство тревоги (примерно такое же как если бы попросили длинные числа перемножить и не ошибиться нигде).
+12
Спасибо за статью, наталкивался на эту шутку ранее, но почему так получается стало ясно только теперь.
Отдельный плюс за стиль написания.
Отдельный плюс за стиль написания.
+3
Ой…
-2
Это все, конечно, невероятно круто и интересно, но ведь для данной конкретной цепочки, если стоит цель придумать формулу, чтобы восьмой член отличался от всех семи предыдущих, можно просто взять банальную формулу:
a(n)=Pi/2+[n/8]*M, где [x] — целая часть числа x, а M — любое отличное от 0 число (например, 1).
То есть троллинг можно было бы устроить и более доступными средствами.
А так — да, решение для ценителей.
a(n)=Pi/2+[n/8]*M, где [x] — целая часть числа x, а M — любое отличное от 0 число (например, 1).
То есть троллинг можно было бы устроить и более доступными средствами.
А так — да, решение для ценителей.
0
Но тут фишка что по исходной формуле явно не видно отсечения целой части. Поэтому кажется что «найдена закономерность».
+1
Наверное (говорю так, потому что не проследил всю цепочку рассуждений).
Кстати, если бы программа работала бы не с символьными вычислениями, а и приближенными численными расчетами, то разницу между первыми 7-ю интегралами и восьмым можно было бы вообще списать на ошибку округления. Она (разница) составляет менее 10^(-10) в относительном выражении.
Кстати, если бы программа работала бы не с символьными вычислениями, а и приближенными численными расчетами, то разницу между первыми 7-ю интегралами и восьмым можно было бы вообще списать на ошибку округления. Она (разница) составляет менее 10^(-10) в относительном выражении.
+1
Есть ещё одна вещь, которая похожим образом противоречит интуиции.
Первообразная от функции x^k равна как известно x^(k+1)/(k+1). Для любого k кроме -1. Даже для k=-1-eps или -1+eps.
Для k=-1 же первообразная равна логарифму.
Если посмотреть на функцию высшего порядка F(k) = \int ( x^k ), то сложно интуитивно представить, почему в точке 0 у неё такая особенность и она принимает совершенно непохожее на окрестность значение.
Первообразная от функции x^k равна как известно x^(k+1)/(k+1). Для любого k кроме -1. Даже для k=-1-eps или -1+eps.
Для k=-1 же первообразная равна логарифму.
Если посмотреть на функцию высшего порядка F(k) = \int ( x^k ), то сложно интуитивно представить, почему в точке 0 у неё такая особенность и она принимает совершенно непохожее на окрестность значение.
+9
Я единственный, кому захотелось узнать, чему будет равен девятый член последовательности?
+7
Протечёт ещё сильнее и будет ещё больше отличаться от пи-пополам.
0
Девятый посчитать несложно — в «хвостике» свёртки, выползшем за 1, только один полиномиальный сегмент, и интеграл равен
17708695183056190642497315530628422295569865119/35417390788301195294898352987527510935040000000*pi
(примерно 0.49999999403980919242*pi). Вот с десятым будет хуже — cумма 1/3+1/5+...+1/15+1/17-1/19 будет больше 1, и придётся разбираться ещё с одним сегментом, который просчитать гораздо сложнее.
17708695183056190642497315530628422295569865119/35417390788301195294898352987527510935040000000*pi
(примерно 0.49999999403980919242*pi). Вот с десятым будет хуже — cумма 1/3+1/5+...+1/15+1/17-1/19 будет больше 1, и придётся разбираться ещё с одним сегментом, который просчитать гораздо сложнее.
+7
Д.Т. Письменный. Конспект лекций по высшей математике.
Там полно похожих красивых задачек, входящих в курс обучения, между прочим.
Там полно похожих красивых задачек, входящих в курс обучения, между прочим.
0
Хм… А у нас как раз на полке этот Письменный завалялся. Что-то я там не припомню красивых задачек, голимая теория. Может, конкретно скажете, в каком томе, в какой главе, на какой странице искать?
0
Есть книжка В.Босса «Интуиция и математика», (а также его же серия книг по разным разделам математики, изучаемой в универе, где он рассказывает об узких или плохопонимаемых местах).
Кажется, автор немного сомнителен ( http://dxdy.ru/topic74332.html ), но пишет весьма интересно, а эта книжка и вообще полностью состоит из не очень интуитивных задачек, и очень крута.
Кажется, автор немного сомнителен ( http://dxdy.ru/topic74332.html ), но пишет весьма интересно, а эта книжка и вообще полностью состоит из не очень интуитивных задачек, и очень крута.
0
У нас все эти аналитические разделы умудрились впихнуть в курс обычной высшей математики и отдельно мат.анализа и функ. анализа не было. И весь курс высшей математики ужали в 3 семестра. Может поэтому я мало что помню, хотя за 1й курс была 5 по математике.
Правда и прошло с тех пор уже 10 лет, а не понадобилось ни разу.
Правда и прошло с тех пор уже 10 лет, а не понадобилось ни разу.
+3
Какой вопрос, такой ответ. Я считаю, что таких вопросов можно придумать кучу. Например, вот один.
Какое число продолжает следующий ряд: 1, 2, 4, 8, 16, 32, 64, 128…
P.S. Правильный ответ 29.
Какое число продолжает следующий ряд: 1, 2, 4, 8, 16, 32, 64, 128…
P.S. Правильный ответ 29.
-4
ну и формулу прикладываем. можно было сразу — в collapse
+1
Ну, например, такая формула (для x=1..9) подходит:
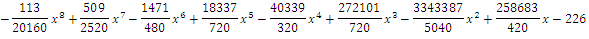
Не знаю, её ли имел в виду автор :-)

Не знаю, её ли имел в виду автор :-)
0
под ответ подогнать формулу любой вольфрам умеет, а вот что аффтар имелло ввиду?
мы ж об интегралах говорим, так что я жду интегральный ряд
мы ж об интегралах говорим, так что я жду интегральный ряд
0
В том-то и проблема, что ответов на вопрос, поставленный в начале статьи, очень много. А приведённый – лишь один из них.
В моём случае, это следующий элемент поля, которое использовалось для построения подстановки шифра AES. lany привёл другой возможный вариант, хотя его формула будет генерировать другой ряд с 9-ю первыми одинаковыми значениями.
В моём случае, это следующий элемент поля, которое использовалось для построения подстановки шифра AES. lany привёл другой возможный вариант, хотя его формула будет генерировать другой ряд с 9-ю первыми одинаковыми значениями.
0
Научите подгонять формулу по данным. Я ввел в ВольфрамАльфу нижеследующее и не получил формулы.
(1,1), (2, 2), (3, 4), (4, 8), (5, 16), (6, 32), (7, 64), (8, 128), (9, 29)
(1,1), (2, 2), (3, 4), (4, 8), (5, 16), (6, 32), (7, 64), (8, 128), (9, 29)
+1
Я просто решил систему линейных уравнений в Maple:
1^8*a+1^7*b+1^6*c+1^5*d+1^4*e+1^3*f+1^2*g+1*h+i=1
2^8*a+2^7*b+2^6*c+2^5*d+2^4*e+2^3*f+2^2*g+2*h+i=2
3^8*a+3^7*b+3^6*c+3^5*d+3^4*e+3^3*f+3^2*g+3*h+i=4
4^8*a+4^7*b+4^6*c+4^5*d+4^4*e+4^3*f+4^2*g+4*h+i=8
5^8*a+5^7*b+5^6*c+5^5*d+5^4*e+5^3*f+5^2*g+5*h+i=16
6^8*a+6^7*b+6^6*c+6^5*d+6^4*e+6^3*f+6^2*g+6*h+i=32
7^8*a+7^7*b+7^6*c+7^5*d+7^4*e+7^3*f+7^2*g+7*h+i=64
8^8*a+8^7*b+8^6*c+8^5*d+8^4*e+8^3*f+8^2*g+8*h+i=128
9^8*a+9^7*b+9^6*c+9^5*d+9^4*e+9^3*f+9^2*g+9*h+i=29
В Альфу, наверно, столько не введёшь, там поле ввода ограничено. Может, как-то по-другому можно, не знаю.
1^8*a+1^7*b+1^6*c+1^5*d+1^4*e+1^3*f+1^2*g+1*h+i=1
2^8*a+2^7*b+2^6*c+2^5*d+2^4*e+2^3*f+2^2*g+2*h+i=2
3^8*a+3^7*b+3^6*c+3^5*d+3^4*e+3^3*f+3^2*g+3*h+i=4
4^8*a+4^7*b+4^6*c+4^5*d+4^4*e+4^3*f+4^2*g+4*h+i=8
5^8*a+5^7*b+5^6*c+5^5*d+5^4*e+5^3*f+5^2*g+5*h+i=16
6^8*a+6^7*b+6^6*c+6^5*d+6^4*e+6^3*f+6^2*g+6*h+i=32
7^8*a+7^7*b+7^6*c+7^5*d+7^4*e+7^3*f+7^2*g+7*h+i=64
8^8*a+8^7*b+8^6*c+8^5*d+8^4*e+8^3*f+8^2*g+8*h+i=128
9^8*a+9^7*b+9^6*c+9^5*d+9^4*e+9^3*f+9^2*g+9*h+i=29
В Альфу, наверно, столько не введёшь, там поле ввода ограничено. Может, как-то по-другому можно, не знаю.
+1
вариант а-ля мапл выше работает и в вольфраме, только заранее записывать в редакторе и вставлять разом цопипастой
-1
А интерполяционного интеграла нету случаем?
0
Боюсь, что не понял, о чём вы. Попробуйте поискать на mathworld.wolfram.com/, там у вещей, реализованных в Mathematica, указан их Mathematica-синтаксис, который понимает WolframAlpha.
0
Проще 2^N mod 227. Магических констант меньше.
+3
+5
Тем кто любит всякие мат.загадки рекомендую вот этот пост: hexlet.org/open_lectures/13zeros/
+1
Формул не видно, но после того, как разрешили двойные факториалы, решение за 12 нулей находится легко: ((3^2)!!-1)*2+(3!-1)! Если факториалы только обычные — то лучше 14 нулей не видно: ((3!)+1)!/(2+1/2)-2^3.
0
Не очень понял, «формул не видно»?
0
Формулы появились… 2^3*(6^2*(6+1)-1) — это не 14, а 15 нулей… А в последней формуле (48-6-1)*(48-1)-1 — опечатка, должно быть (48-6-1)*(48+1)-1 — но она действительно работает.
0
А касательно нулей, за 12 слишком легко, попробуйте за 11 :)
0
A, очевидно. Берём моё решение за 12: ((3^2)!!-1)*2+(3!-1)! и вместо 3^2 пишем !4.
0
0
Формулы картинкой куда-то съехали, поэтому текстом:
\left\lceil \frac{!(!4)\cdot2}{\lceil !(3!) / 2\rceil} \right\rceil
(!(3!-1)+1)^2\oplus((3!)!!+1)
\left\lceil \frac{!(!4)\cdot2}{\lceil !(3!) / 2\rceil} \right\rceil
(!(3!-1)+1)^2\oplus((3!)!!+1)
0
Оба ваших решения верны. Добавлю их в пост?
0
C целой частью, скорее всего, любое число можно получить из одной тройки, используя достаточное количество факториалов и квадратных корней… Но против XOR возразить нечего (кроме того, что двоичная система — уже дополнительная условность, которой в предыдущих операциях не было)… правда, тогда можно использовать и побитовые AND и OR, и открываются новые возможности.
[sqrt((3!)!)] = 26
[sqrt(26)]=5
[sqrt(5!)]=10
[sqrt(10!)]=1904 (это уже даёт решение за 10 нулей — 1904+26*4)
[sqrt(1904)]=43 ((43-2)*(48+1)-1 — снова 10 нулей)
[sqrt(sqrt(sqrt(26!)))]=2116
sqrt(2116)=46
[sqrt(sqrt(sqrt(sqrt(46!))))]=4062 ( (4062-46)/2 — уже 8 нулей!)
Дальше из исходной тройки можно получить 1989, 44, 2520, 50, 7, 70, 8, 200, 14, 543, 23, 633, 25, 1408, 37… В конечном итоге, наверное, и до 2008 можно будет добраться.
[sqrt((3!)!)] = 26
[sqrt(26)]=5
[sqrt(5!)]=10
[sqrt(10!)]=1904 (это уже даёт решение за 10 нулей — 1904+26*4)
[sqrt(1904)]=43 ((43-2)*(48+1)-1 — снова 10 нулей)
[sqrt(sqrt(sqrt(26!)))]=2116
sqrt(2116)=46
[sqrt(sqrt(sqrt(sqrt(46!))))]=4062 ( (4062-46)/2 — уже 8 нулей!)
Дальше из исходной тройки можно получить 1989, 44, 2520, 50, 7, 70, 8, 200, 14, 543, 23, 633, 25, 1408, 37… В конечном итоге, наверное, и до 2008 можно будет добраться.
0
Кстати, да:
6 = 3!
5 = [6!2-2]
10 = [5!2-1]
43 = [10!2-2]
44 = [43!2-5]
7 = [44!2-6]
8 = [7!2-2]
14 = [8!2-2]
4 = [14!2-4]
24 = 4!
30 = [24!2-4]
106 = [30!2-4]
21 = [106!2-7]
290 = [21!2-3]
201 = [290!2-8]
884 = [201!2-7]
148 = [884!2-10]
10904 = [148!2-6]
250 = [10904!2-14]
7042 = [250!2-7]
860 = [7042!2-13]
126 = [860!2-10]
2007 = [126!2-6], 2008 = -[-126!2-6]
Полагаю, что можно добраться и до 2008 = [x!2-y] без верхней целой части (замаскированной под целую часть от -x), только числа в цепочке будут больше.
6 = 3!
5 = [6!2-2]
10 = [5!2-1]
43 = [10!2-2]
44 = [43!2-5]
7 = [44!2-6]
8 = [7!2-2]
14 = [8!2-2]
4 = [14!2-4]
24 = 4!
30 = [24!2-4]
106 = [30!2-4]
21 = [106!2-7]
290 = [21!2-3]
201 = [290!2-8]
884 = [201!2-7]
148 = [884!2-10]
10904 = [148!2-6]
250 = [10904!2-14]
7042 = [250!2-7]
860 = [7042!2-13]
126 = [860!2-10]
2007 = [126!2-6], 2008 = -[-126!2-6]
Полагаю, что можно добраться и до 2008 = [x!2-y] без верхней целой части (замаскированной под целую часть от -x), только числа в цепочке будут больше.
0
Конечно.
0
Sign up to leave a comment.


Нескучные интегралы