Всем привет!
Сегодня я расскажу тебе, %USERNAME%, обашмаках и сургуче, капусте, королях координатах, проекциях, геодезических системах и совсем чуть-чуть о веб-картографии. Устраивайся поудобнее.
Как говорил ещё Артур Кларк, любая достаточно развитая технология неотличима от магии. Так и в веб-картографии — я думаю, все давно привыкли пользоваться географическими картами, но далеко не каждый представляет себе, как это всё работает.
Вот, казалось бы, простая вещь — географические координаты. Широта и долгота, что может быть проще. А вот представьте, что вы очутились на необитаемом острове. Смартфон утонул, а других средств связи у вас нет. Остаётся только написать письмо с просьбой о помощи и по старинке выбросить его в море в запечатанной бутылке.
Вот только незадача — вы совершенно не знаете, где находится ваш необитаемый остров, а без указания координат никто вас не найдёт, даже если выловит ваше письмо. Что делать? Как определить координаты без GPS?
Итак, немного теории для начала. Чтобы сопоставить точкам на поверхности сферы координаты, необходимо задать начало отсчета — фундаментальную плоскость для отсчёта широт и нулевой меридиан для отсчёта долгот. Для Земли обычно используются плоскость экватора и гринвичский меридиан соответственно.
Широтой (обычно обозначается φ) называют угол между направлением на точку из центра сферы и фундаментальной плоскостью. Долготой (обычно обозначается θ или λ) называют угол между плоскостью проходящего через точку меридиана и плоскостью нулевого меридиана.
Как же определить свою широту, т.е. угол между плоскостью земного экватора и точкой, в которой ты находишься?
Посмотрим на тот же чертёж под другим углом, спроецировав его на плоскость нашего меридиана. Добавим также к чертежу плоскость горизонта (касательную плоскость к нашей точке):
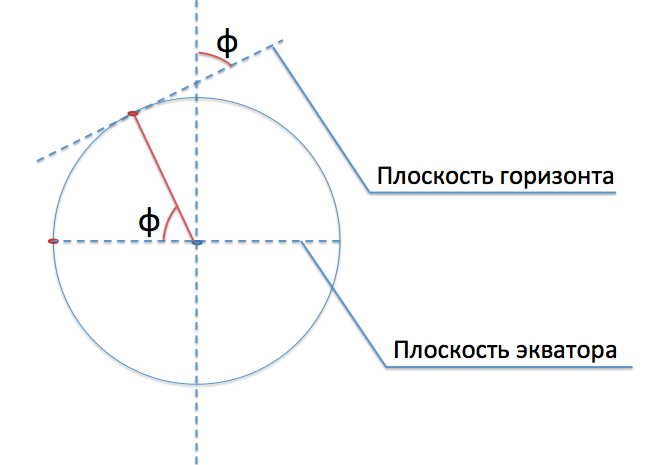
Видим, что искомый угол между направлением на точку и плоскостью экватора равен углу между плоскостью горизонта и осью вращения Земли.
Итак, как же нам найти этот угол? Вспомним красивые картинки звёздного неба с большой выдержкой:
Вот эта точка в центре всех описываемых звездами окружностей — полюс мира. Измерив её высоту над горизонтом, мы получим широту точки наблюдения.
Остаётся вопрос, как найти полюс мира на звёздном небе. Если вы в Северном полушарии, то всё довольно просто:
— найдите ковш Большой Медведицы;
— проведите мысленно прямую через две крайние звезды ковша — Дубхе и Мерак;
— эта прямая укажет вам на ручку ковша Малой Медведицы. Крайняя звезда этой ручки — Полярная — почти в точности совпадает с Северным Полюсом мира.
Полярная звезда всегда находится на севере, а её высота над горизонтом равна широте точки наблюдения. Если вас угораздит попасть на Северный полюс, Полярная звезда будет у вас точно над головой.
В Южном полушарии всё не так просто. Рядом с южным полюсом мира нет крупных звёзд, и вам придётся найти созвездие Южный Крест, мысленно продлить вниз его бОльшую перекладину и отсчитать 4.5 её длины — где-то в этой области будет находиться южный полюс мира.
Само созвездие найти легко — вы много раз видели его на флагах разных стран — Австралии, Новой Зеландии и Бразилии, например.
С широтой определились. Перейдём к долготе. Как определить долготу на необитаемом острове?
На самом деле, это очень непростая проблема, потому что, в отличие от широты, точка отсчета долготы (нулевой меридиан) выбирается произвольным образом и ни к каким наблюдаемым ориентирам не привязана. Испанский король Филипп II в 1567 году назначил солидное вознаграждение тому, кто предложит метод определения долготы; в 1598 году при Филиппе III оно доросло до 6 тысяч дукатов единовременно и 2 тысячи дукатов ренты пожизненно — очень приличная сумма по тем временам. Задача определения долготы в течение нескольких десятилетий была идеей фикс математиков, как теорема Ферма в 20-м веке.
В итоге, долготу стали определять с помощью вот этого прибора:
По сути, этот прибор остаётся самым надёжным способом определения долготы (не считая GPS/Глонасс) и в наши дни. Этот прибор… (барабанная дробь)… морской хронометр.
В самом деле, при изменении долготы меняется часовой пояс. По разнице локального времени и гринвичского легко определить собственную долготу, причём очень точно. Каждая минута разницы времён соответствует 15 угловым минутам долготы.
Соответственно, если у вас есть часы, настроенные по гринвичскому времени (на самом деле, неважно по какому — достаточно знать часовой пояс того места, по времени которого идут ваши часы) — не спешите их переводить. Дождитесь местного полдня, и разница времён подскажет вам долготу вашего острова. (Определить момент полдня очень легко — следите за тенями. В первой половине дня тени укорачиваются, во второй — удлиняются. Момент, когда начали удлиняться тени — астрономический полдень в данной местности.)
Оба метода определения координат, кстати, хорошо описаны в романе Жюля Верна «Таинственный остров».
Итак, мы сумели определить свою широту и долготу с погрешностью в несколько градусов, т.е. пару сотен километров. Для записки в бутылке такой точности, быть может, ещё хватит, а вот для географических карт уже нет.
Частично эта погрешность обусловлена несовершенством используемых инструментов, но есть и другие источники ошибок. Землю можно считать шаром только в первом приближении — вообще же Земля совсем не шар, а геоид — тело, больше всего похожее на сильно неровный эллипсоид вращения. Для того, чтобы точно приписать каждой точке земной поверхности координаты нужны правила — каким образом конкретную точку на геоиде спроецировать на сферу.
Такой набор правил должен быть универсальным для всех географических карт в мире — иначе одни и те же координаты будут в разных системах обозначать разные точки земной поверхности. В настоящий момент практически все географические сервисы используют единую систему присвоения точке координат — WGS 84 (WGS = World Geodetic System, 84 — год принятия стандарта).
WGS 84 определяет т.н. референсный эллипсоид — повехность, к которой приводятся координаты для удобства вычислений. Параметры этого эллипсоида следующие:
— большая полуось (экваториальный радиус): a = 6378137 метров;
— сжатие: f = 1 / 298.257223563.
Из экваториального радиуса и сжатия можно получить полярный радиус, он же малая полуось (b = a * (1 — f) ≈ 6356752 метра).
Любой точке земной поверхности, таким образом, ставится в соответствие три координаты: долгота и широта (на референсном эллипсоиде) и высота над его поверхностью. В 2004 году WGS 84 был дополнен стандартом Earth Gravitational Model (EGM96), который уточняет уровень моря, от которого отсчитываются высоты.
Интересно, что нулевой меридиан в WGS 84 вовсе не гринвичский (проходящий через ось пассажного инструмента Гринвичской обсерватории), а т.н. IERS Reference Meridian, который проходит на 5.31 угловой секунды восточнее гринвичского.
Допустим, мы научились определять свои координаты. Теперь нужно научиться отображать накопленные географические знания экране монитора. Да вот незадача — сферических мониторов в мире как-то не очень много (не говоря уже о мониторах в форме геоида). Нам нужно каким-то образом отобразить карту на плоскость — спроецировать.
Один из самых простых способов — спроецировать сферу на цилиндр, а потом развернуть этот цилиндр на плоскость. Такие проекции называются цилиндрическими, их характерное свойство — все меридианы отображаются на карте вертикальными прямыми.
Проекций сферы на цилиндр можно придумать много. Наиболее известная из цилиндрических проекций — проекция Меркатора (по имени широко использовавшего её в своих картах фламандского картографа и географа Герарда Кремера, более известного под латинизированной фамилией Меркатор).
Математически она выражается следующим образом (для сферы):
x = R · λ;
y = R · ln(tg(π/4 + φ/2), где R — радиус сферы, λ — долгота в радианах, φ — широта в радианах.
На выходе получаем обычные декартовы координаты в метрах.
Карта в проекции Меркатора выглядит вот так:
Легко заметить, что проекция Меркатора очень существенно искажает формы и площади объектов. Например, Гренландия на карте занимает в два раза большую площадь, чем Австралия — хотя в реальности Австралия в 3.5 раза больше Гренландии.
Чем же так хороша эта проекция, что стала так популярна несмотря на существенные искажения? Дело в том, что у проекции Меркатора есть важное характеристическое свойство: она сохраняет углы при проецировании.
Допустим, мы хотим проплыть от Канарских островов к Багамским. Проведём прямую линию на карте, соединяющую точки отправления и прибытия.
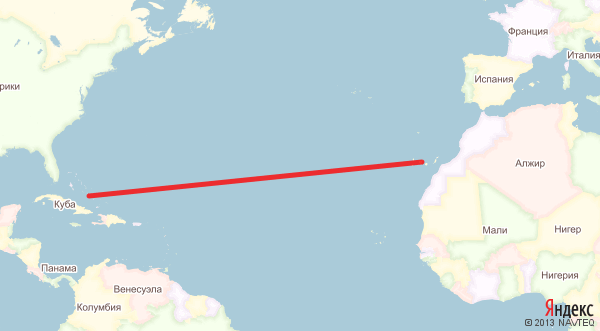
Так как все меридианы в цилиндрических проекциях параллельны, а проекция Меркатора ещё и сохраняет углы, то наша линия пересечёт все меридианы под одинаковым углом. А это означает, что проплыть вдоль этой линии нам будет очень просто: достаточно сохранять на всём протяжении путешествия один и тот же угол между курсом судна и направлением на полярную звезду (или направлением на магнитный север, что менее точно), причём нужный угол можно легко измерить банальным транспортиром.
Подобные линии, пересекающие все меридианы и параллели под одинаковым углом, называются локсодромами. Все локсодромы в проекции Меркатора изображаются прямыми на карте, и именно это замечательное свойство, крайне удобное для морской навигации, и принесло меркаторовской проекции широкую популярность среди моряков.
Следует заметить, что сказанное не совсем верно: если мы проецируем сферу, а движемся по геоиду, то путевой угол определится не совсем верно и приплывём мы не совсем туда. (Расхождение может быть довольно заметным — всё-таки, экваториальный и полярный радиусы Земли различаются более чем на 20 километров.) Эллипсоид тоже можно спроецировать с сохранением углов, хотя формулы для эллиптической проекции Меркатора значительно сложнее, чем для сферической (обратное преобразование вообще не выражается в элементарных функциях). Полное и подробное описание математики проекции Меркатора на эллипсоиде можно найти здесь.
Когда мы в Яндексе начинали делать свои карты, нам показалось логичным использовать эллиптическую меркаторовскую проекцию. К сожалению, многим другим картографическим веб-сервисам так не показалось, и они используют сферическую проекцию. Поэтому долгое время нельзя было показывать поверх карты Яндекса тайлы, скажем, OSM — они расходились по оси y, чем ближе к полюсу — тем заметнее. В версии API 2.0 мы решили не плыть против течения, и предоставили возможность как работать с картой в произвольной проекции, так и показывать на карте одновременно несколько слоёв в разных проекциях — как удобнее.
Путешествовать по локсодроме очень просто, но за эту простоту приходится платить: локсодрома отправит вас в путешествие по неоптимальному маршруту. В частности, путь вдоль параллели (если это не экватор) не является кратчайшим!
Для того, чтобы найти кратчайший путь на сфере, нужно провести окружность с центром в центре сферы, проходящую через эти две точки (или, что то же самое, пересечь сферу с плоскостью, проходящей через две точки и центр сферы).
Невозможно спроецировать сферу на плоскость так, чтобы кратчайшие пути при этом переходили в прямые отрезки; проекция Меркатора, разумеется, не исключение, и ортодромы в ней выглядят сильно искаженными дугами. Некоторые пути (через полюс) в проекции Меркатора корректно изобразить невозможно:
Примерно так проецируется кратчайший путь из Анадыря в Кардифф: сначала улетаем в бесконечность строго на север, а потом возвращаемся из бесконечности строго на юг.
В случае движения по сфере кратчайшие пути строятся довольно просто с помощью аппарата сферической тригонометрии, а вот в случае эллипсоида задача существенно усложняется — кратчайшие пути не выражаются в элементарных функциях.
(Замечу, что эта проблема, конечно же, не решается выбором сферической проекции Меркатора — построение кратчайших путей осуществляется на референсном эллипсоиде WGS 84 и никак не зависит от параметров проекции.)
В ходе разработки API Яндекс.Карт версии 2.0 перед нами встала непростая задача — параметризовать построение кратчайших путей так, чтобы:
— можно было легко пользоваться встроенными функциями для расчета кратчайших путей на эллипсоиде WGS 84;
— можно было легко задать собственную систему координат с собственными методами расчета кратчайших путей.
API Карт ведь можно использовать не только для показа карт земной поверхности, но и, скажем, поверхности Луны или какого-нибудь игрового мира.
Для построения кратчайших путей (геодезических линий) в общем случае используется следующее простенькое и незатейливое уравнение:
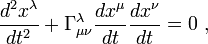
Здесь
— т.н. символы Кристоффеля, выражающиеся через частные производные фундаментального метрического тензора.
Заставлять пользователя ТАКИМ образом параметризовать свою область картографирования нам показалось несколько негуманным :).
Поэтому мы решили пойти другим путём, более приближенным к Земле и потребностям наших пользователей. В геодезии проблемы построениях кратчайших путей составляют т.н. первую (прямую) и вторую (обратную) геодезические задачи.
Прямая геодезическая задача: дана исходная точка, направление движения (обычно — путевой угол, т.е. угол между направлением на север и направлением движения) и пройденное расстояние. Требуется найти конечную точку и конечное направление движения.
Обратная геодезическая задача: даны две точки. Требуется найти расстояние между ними и направление движения.
Обратите внимание, что направление движения (путевой угол) — непрерывная функция, которая изменяется на протяжении всего пути.
Имея в своём распоряжении функции решения этих задач, мы с их помощью можем решить необходимые нам кейсы в API Карт: вычисление расстояний, отображение кратчайших путей и построение окружностей на земной поверхности.
Мы заявили следующий интерфейс для пользовательских координатных систем:
solveDirectProblem(startPoint, direction, distance) — Решает так называемую первую (прямую) геодезическую задачу: где мы окажемся, если выйдем из указанной точки в указанном направлении и пройдём, не сворачивая, указанное расстояние.
solveInverseProblem(startPoint, endPoint, reverseDirection) — Решает так называемую вторую (обратную) геодезическую задачу: построить кратчайший маршрут между двумя точками на картографируемой поверхности и определелить расстояние и направление движения.
getDistance(point1, point2) — возвращает кратчайшее (вдоль геодезической линии) расстояние между двумя заданными точками (в метрах).
(Функция getDistance выделена отдельно для тех случаев, когда расчет расстояний можно выполнить намного быстрее, чем решение обратной задачи.)
Этот интерфейс показался нам достаточно простым для реализации в случаях, если пользователь картографирует какую-то нестандартную поверхность или пользуется нестандартными координатами. Со своей стороны мы написали две стандартных реализации — для обычной декартовой плоскости и для референсного эллипсоида WGS 84. Для второй реализации мы использовали формулы Винсенти. Кстати, непосредственно реализовывал эту логику runawayed, передаём ему привет :).
Все эти геодезические возможности доступны в API Яндекс.Карт, начиная с версии 2.0.13. Welcome!
Сегодня я расскажу тебе, %USERNAME%, о
Как говорил ещё Артур Кларк, любая достаточно развитая технология неотличима от магии. Так и в веб-картографии — я думаю, все давно привыкли пользоваться географическими картами, но далеко не каждый представляет себе, как это всё работает.
Вот, казалось бы, простая вещь — географические координаты. Широта и долгота, что может быть проще. А вот представьте, что вы очутились на необитаемом острове. Смартфон утонул, а других средств связи у вас нет. Остаётся только написать письмо с просьбой о помощи и по старинке выбросить его в море в запечатанной бутылке.
Вот только незадача — вы совершенно не знаете, где находится ваш необитаемый остров, а без указания координат никто вас не найдёт, даже если выловит ваше письмо. Что делать? Как определить координаты без GPS?
Итак, немного теории для начала. Чтобы сопоставить точкам на поверхности сферы координаты, необходимо задать начало отсчета — фундаментальную плоскость для отсчёта широт и нулевой меридиан для отсчёта долгот. Для Земли обычно используются плоскость экватора и гринвичский меридиан соответственно.
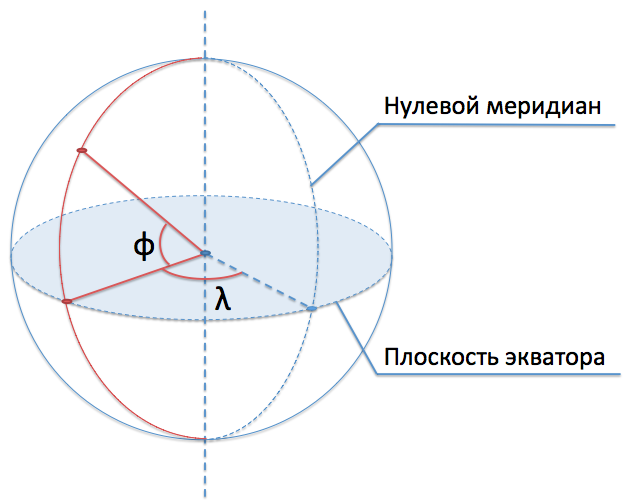
Широтой (обычно обозначается φ) называют угол между направлением на точку из центра сферы и фундаментальной плоскостью. Долготой (обычно обозначается θ или λ) называют угол между плоскостью проходящего через точку меридиана и плоскостью нулевого меридиана.
Как же определить свою широту, т.е. угол между плоскостью земного экватора и точкой, в которой ты находишься?
Посмотрим на тот же чертёж под другим углом, спроецировав его на плоскость нашего меридиана. Добавим также к чертежу плоскость горизонта (касательную плоскость к нашей точке):
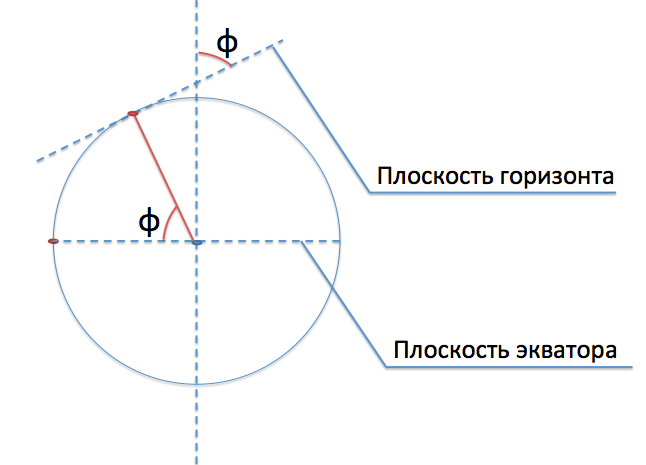
Видим, что искомый угол между направлением на точку и плоскостью экватора равен углу между плоскостью горизонта и осью вращения Земли.
Итак, как же нам найти этот угол? Вспомним красивые картинки звёздного неба с большой выдержкой:
Вот эта точка в центре всех описываемых звездами окружностей — полюс мира. Измерив её высоту над горизонтом, мы получим широту точки наблюдения.
Остаётся вопрос, как найти полюс мира на звёздном небе. Если вы в Северном полушарии, то всё довольно просто:
— найдите ковш Большой Медведицы;
— проведите мысленно прямую через две крайние звезды ковша — Дубхе и Мерак;
— эта прямая укажет вам на ручку ковша Малой Медведицы. Крайняя звезда этой ручки — Полярная — почти в точности совпадает с Северным Полюсом мира.
Полярная звезда всегда находится на севере, а её высота над горизонтом равна широте точки наблюдения. Если вас угораздит попасть на Северный полюс, Полярная звезда будет у вас точно над головой.
В Южном полушарии всё не так просто. Рядом с южным полюсом мира нет крупных звёзд, и вам придётся найти созвездие Южный Крест, мысленно продлить вниз его бОльшую перекладину и отсчитать 4.5 её длины — где-то в этой области будет находиться южный полюс мира.
Само созвездие найти легко — вы много раз видели его на флагах разных стран — Австралии, Новой Зеландии и Бразилии, например.
С широтой определились. Перейдём к долготе. Как определить долготу на необитаемом острове?
На самом деле, это очень непростая проблема, потому что, в отличие от широты, точка отсчета долготы (нулевой меридиан) выбирается произвольным образом и ни к каким наблюдаемым ориентирам не привязана. Испанский король Филипп II в 1567 году назначил солидное вознаграждение тому, кто предложит метод определения долготы; в 1598 году при Филиппе III оно доросло до 6 тысяч дукатов единовременно и 2 тысячи дукатов ренты пожизненно — очень приличная сумма по тем временам. Задача определения долготы в течение нескольких десятилетий была идеей фикс математиков, как теорема Ферма в 20-м веке.
В итоге, долготу стали определять с помощью вот этого прибора:
По сути, этот прибор остаётся самым надёжным способом определения долготы (не считая GPS/Глонасс) и в наши дни. Этот прибор… (барабанная дробь)… морской хронометр.
В самом деле, при изменении долготы меняется часовой пояс. По разнице локального времени и гринвичского легко определить собственную долготу, причём очень точно. Каждая минута разницы времён соответствует 15 угловым минутам долготы.
Соответственно, если у вас есть часы, настроенные по гринвичскому времени (на самом деле, неважно по какому — достаточно знать часовой пояс того места, по времени которого идут ваши часы) — не спешите их переводить. Дождитесь местного полдня, и разница времён подскажет вам долготу вашего острова. (Определить момент полдня очень легко — следите за тенями. В первой половине дня тени укорачиваются, во второй — удлиняются. Момент, когда начали удлиняться тени — астрономический полдень в данной местности.)
Оба метода определения координат, кстати, хорошо описаны в романе Жюля Верна «Таинственный остров».
Координаты на геоиде
Итак, мы сумели определить свою широту и долготу с погрешностью в несколько градусов, т.е. пару сотен километров. Для записки в бутылке такой точности, быть может, ещё хватит, а вот для географических карт уже нет.
Частично эта погрешность обусловлена несовершенством используемых инструментов, но есть и другие источники ошибок. Землю можно считать шаром только в первом приближении — вообще же Земля совсем не шар, а геоид — тело, больше всего похожее на сильно неровный эллипсоид вращения. Для того, чтобы точно приписать каждой точке земной поверхности координаты нужны правила — каким образом конкретную точку на геоиде спроецировать на сферу.
Такой набор правил должен быть универсальным для всех географических карт в мире — иначе одни и те же координаты будут в разных системах обозначать разные точки земной поверхности. В настоящий момент практически все географические сервисы используют единую систему присвоения точке координат — WGS 84 (WGS = World Geodetic System, 84 — год принятия стандарта).
WGS 84 определяет т.н. референсный эллипсоид — повехность, к которой приводятся координаты для удобства вычислений. Параметры этого эллипсоида следующие:
— большая полуось (экваториальный радиус): a = 6378137 метров;
— сжатие: f = 1 / 298.257223563.
Из экваториального радиуса и сжатия можно получить полярный радиус, он же малая полуось (b = a * (1 — f) ≈ 6356752 метра).
Любой точке земной поверхности, таким образом, ставится в соответствие три координаты: долгота и широта (на референсном эллипсоиде) и высота над его поверхностью. В 2004 году WGS 84 был дополнен стандартом Earth Gravitational Model (EGM96), который уточняет уровень моря, от которого отсчитываются высоты.
Интересно, что нулевой меридиан в WGS 84 вовсе не гринвичский (проходящий через ось пассажного инструмента Гринвичской обсерватории), а т.н. IERS Reference Meridian, который проходит на 5.31 угловой секунды восточнее гринвичского.
Плоские карты
Допустим, мы научились определять свои координаты. Теперь нужно научиться отображать накопленные географические знания экране монитора. Да вот незадача — сферических мониторов в мире как-то не очень много (не говоря уже о мониторах в форме геоида). Нам нужно каким-то образом отобразить карту на плоскость — спроецировать.
Один из самых простых способов — спроецировать сферу на цилиндр, а потом развернуть этот цилиндр на плоскость. Такие проекции называются цилиндрическими, их характерное свойство — все меридианы отображаются на карте вертикальными прямыми.
Проекций сферы на цилиндр можно придумать много. Наиболее известная из цилиндрических проекций — проекция Меркатора (по имени широко использовавшего её в своих картах фламандского картографа и географа Герарда Кремера, более известного под латинизированной фамилией Меркатор).
Математически она выражается следующим образом (для сферы):
x = R · λ;
y = R · ln(tg(π/4 + φ/2), где R — радиус сферы, λ — долгота в радианах, φ — широта в радианах.
На выходе получаем обычные декартовы координаты в метрах.
Карта в проекции Меркатора выглядит вот так:
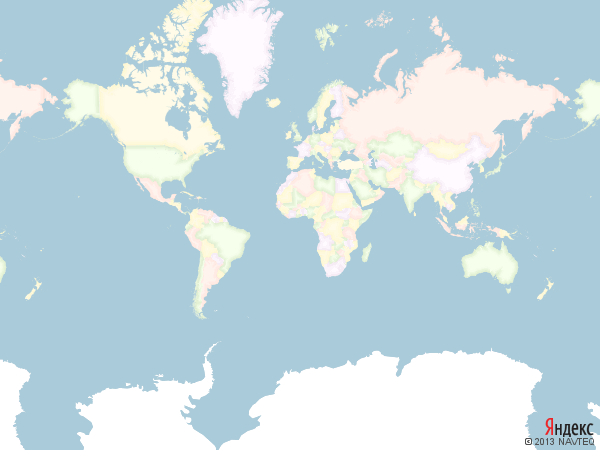
Легко заметить, что проекция Меркатора очень существенно искажает формы и площади объектов. Например, Гренландия на карте занимает в два раза большую площадь, чем Австралия — хотя в реальности Австралия в 3.5 раза больше Гренландии.
Чем же так хороша эта проекция, что стала так популярна несмотря на существенные искажения? Дело в том, что у проекции Меркатора есть важное характеристическое свойство: она сохраняет углы при проецировании.
Допустим, мы хотим проплыть от Канарских островов к Багамским. Проведём прямую линию на карте, соединяющую точки отправления и прибытия.
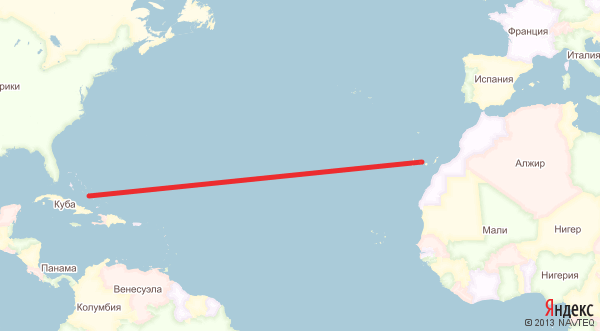
Так как все меридианы в цилиндрических проекциях параллельны, а проекция Меркатора ещё и сохраняет углы, то наша линия пересечёт все меридианы под одинаковым углом. А это означает, что проплыть вдоль этой линии нам будет очень просто: достаточно сохранять на всём протяжении путешествия один и тот же угол между курсом судна и направлением на полярную звезду (или направлением на магнитный север, что менее точно), причём нужный угол можно легко измерить банальным транспортиром.
Подобные линии, пересекающие все меридианы и параллели под одинаковым углом, называются локсодромами. Все локсодромы в проекции Меркатора изображаются прямыми на карте, и именно это замечательное свойство, крайне удобное для морской навигации, и принесло меркаторовской проекции широкую популярность среди моряков.
Следует заметить, что сказанное не совсем верно: если мы проецируем сферу, а движемся по геоиду, то путевой угол определится не совсем верно и приплывём мы не совсем туда. (Расхождение может быть довольно заметным — всё-таки, экваториальный и полярный радиусы Земли различаются более чем на 20 километров.) Эллипсоид тоже можно спроецировать с сохранением углов, хотя формулы для эллиптической проекции Меркатора значительно сложнее, чем для сферической (обратное преобразование вообще не выражается в элементарных функциях). Полное и подробное описание математики проекции Меркатора на эллипсоиде можно найти здесь.
Когда мы в Яндексе начинали делать свои карты, нам показалось логичным использовать эллиптическую меркаторовскую проекцию. К сожалению, многим другим картографическим веб-сервисам так не показалось, и они используют сферическую проекцию. Поэтому долгое время нельзя было показывать поверх карты Яндекса тайлы, скажем, OSM — они расходились по оси y, чем ближе к полюсу — тем заметнее. В версии API 2.0 мы решили не плыть против течения, и предоставили возможность как работать с картой в произвольной проекции, так и показывать на карте одновременно несколько слоёв в разных проекциях — как удобнее.
Геодезические задачи
Путешествовать по локсодроме очень просто, но за эту простоту приходится платить: локсодрома отправит вас в путешествие по неоптимальному маршруту. В частности, путь вдоль параллели (если это не экватор) не является кратчайшим!
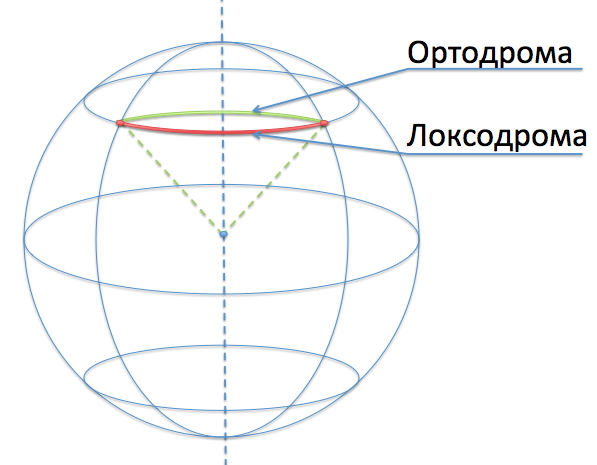
Для того, чтобы найти кратчайший путь на сфере, нужно провести окружность с центром в центре сферы, проходящую через эти две точки (или, что то же самое, пересечь сферу с плоскостью, проходящей через две точки и центр сферы).
Невозможно спроецировать сферу на плоскость так, чтобы кратчайшие пути при этом переходили в прямые отрезки; проекция Меркатора, разумеется, не исключение, и ортодромы в ней выглядят сильно искаженными дугами. Некоторые пути (через полюс) в проекции Меркатора корректно изобразить невозможно:
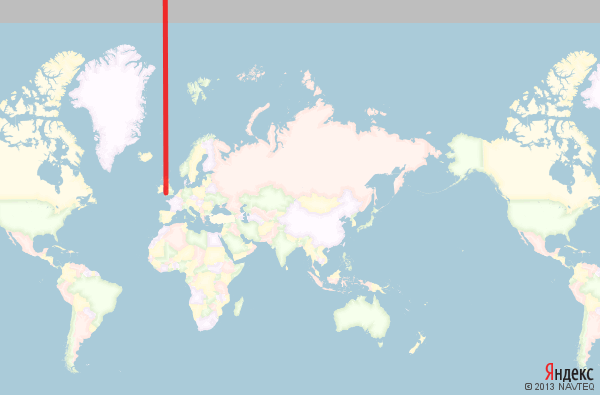
Примерно так проецируется кратчайший путь из Анадыря в Кардифф: сначала улетаем в бесконечность строго на север, а потом возвращаемся из бесконечности строго на юг.
В случае движения по сфере кратчайшие пути строятся довольно просто с помощью аппарата сферической тригонометрии, а вот в случае эллипсоида задача существенно усложняется — кратчайшие пути не выражаются в элементарных функциях.
(Замечу, что эта проблема, конечно же, не решается выбором сферической проекции Меркатора — построение кратчайших путей осуществляется на референсном эллипсоиде WGS 84 и никак не зависит от параметров проекции.)
В ходе разработки API Яндекс.Карт версии 2.0 перед нами встала непростая задача — параметризовать построение кратчайших путей так, чтобы:
— можно было легко пользоваться встроенными функциями для расчета кратчайших путей на эллипсоиде WGS 84;
— можно было легко задать собственную систему координат с собственными методами расчета кратчайших путей.
API Карт ведь можно использовать не только для показа карт земной поверхности, но и, скажем, поверхности Луны или какого-нибудь игрового мира.
Для построения кратчайших путей (геодезических линий) в общем случае используется следующее простенькое и незатейливое уравнение:
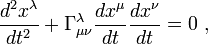
Здесь
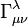— т.н. символы Кристоффеля, выражающиеся через частные производные фундаментального метрического тензора.Заставлять пользователя ТАКИМ образом параметризовать свою область картографирования нам показалось несколько негуманным :).
Поэтому мы решили пойти другим путём, более приближенным к Земле и потребностям наших пользователей. В геодезии проблемы построениях кратчайших путей составляют т.н. первую (прямую) и вторую (обратную) геодезические задачи.
Прямая геодезическая задача: дана исходная точка, направление движения (обычно — путевой угол, т.е. угол между направлением на север и направлением движения) и пройденное расстояние. Требуется найти конечную точку и конечное направление движения.
Обратная геодезическая задача: даны две точки. Требуется найти расстояние между ними и направление движения.
Обратите внимание, что направление движения (путевой угол) — непрерывная функция, которая изменяется на протяжении всего пути.
Имея в своём распоряжении функции решения этих задач, мы с их помощью можем решить необходимые нам кейсы в API Карт: вычисление расстояний, отображение кратчайших путей и построение окружностей на земной поверхности.
Мы заявили следующий интерфейс для пользовательских координатных систем:
solveDirectProblem(startPoint, direction, distance) — Решает так называемую первую (прямую) геодезическую задачу: где мы окажемся, если выйдем из указанной точки в указанном направлении и пройдём, не сворачивая, указанное расстояние.
solveInverseProblem(startPoint, endPoint, reverseDirection) — Решает так называемую вторую (обратную) геодезическую задачу: построить кратчайший маршрут между двумя точками на картографируемой поверхности и определелить расстояние и направление движения.
getDistance(point1, point2) — возвращает кратчайшее (вдоль геодезической линии) расстояние между двумя заданными точками (в метрах).
(Функция getDistance выделена отдельно для тех случаев, когда расчет расстояний можно выполнить намного быстрее, чем решение обратной задачи.)
Этот интерфейс показался нам достаточно простым для реализации в случаях, если пользователь картографирует какую-то нестандартную поверхность или пользуется нестандартными координатами. Со своей стороны мы написали две стандартных реализации — для обычной декартовой плоскости и для референсного эллипсоида WGS 84. Для второй реализации мы использовали формулы Винсенти. Кстати, непосредственно реализовывал эту логику runawayed, передаём ему привет :).
Все эти геодезические возможности доступны в API Яндекс.Карт, начиная с версии 2.0.13. Welcome!