Решил создать серию постов об анализе данных. Несколько лет работаю в этой (и как оказалось, весьма интересной) области информатики. Предлагаю Вашему вниманию анализ данных с точки зрения Теории приближенных множеств.
Теория приближенных множеств (rough sets) была разработана [Zdzisław Pawlak, 1982] как новый математический подход для описания неопределенности, неточности и неуверенности. Она основана на утверждении, что с каждым объектом универсума мы связываем некоторую информацию (данные, знания). Объекты, характеризуемые одинаковой информацией, являются неразличимыми (сходными) с точки зрения имеющейся о них информации. Отношение неразличимости, порождаемое таким способом, является математической основой теории приближенных (грубых) множеств.
Основой концепции теории приближенных множеств являются операции аппроксимации множеств.
Дадим теперь понятие аппроксимации приближенных множеств:
Приближенные множества находят применение при работе с таблицами данных, которые называются также таблицами атрибут-значение, или информационными системами, или таблицами принятия решений (decision tables). Таблица принятия решений (decision table) – это тройка Τ = (U, C, D), где
U – это множество объектов,
С – это множество атрибутов условий (condition attributes),
D – это множество атрибутов решений (decision attributes).
Множества:
U = {U1, U2, U3, U4, U5, U6, U7, U8}
C = {Головная боль, Температура}
D = {Грипп}
Возможные значения атрибутов:
VГоловная боль = {да, нет}
VТемпература = {нормальная, высокая, очень высокая}
VГрипп = {да, нет}
Разбиение множества U в соответствии со значениями атрибута Головная боль имеет вид:
Разбиение множества U в соответствии со значениями атрибута Температура имеет вид:
Разбиение множества U в соответствии со значениями атрибута решения Грипп имеет вид:
Представленые в этой таблице данные, например U5 и U7 — противоречивые, а U6 и U8 — повторяются.
Собственно используя приближенные множества мы можем «извлечь» из неточных, противоречивых данных те, которые «полезны нам».
В следующих постах будет продемонстрирована практическая реализация (в Python) анализа данных с использаванием данной теории, в том числе:
О чем пойдет речь?
Теория приближенных множеств (rough sets) была разработана [Zdzisław Pawlak, 1982] как новый математический подход для описания неопределенности, неточности и неуверенности. Она основана на утверждении, что с каждым объектом универсума мы связываем некоторую информацию (данные, знания). Объекты, характеризуемые одинаковой информацией, являются неразличимыми (сходными) с точки зрения имеющейся о них информации. Отношение неразличимости, порождаемое таким способом, является математической основой теории приближенных (грубых) множеств.
Основой концепции теории приближенных множеств являются операции аппроксимации множеств.
Дадим теперь понятие аппроксимации приближенных множеств:
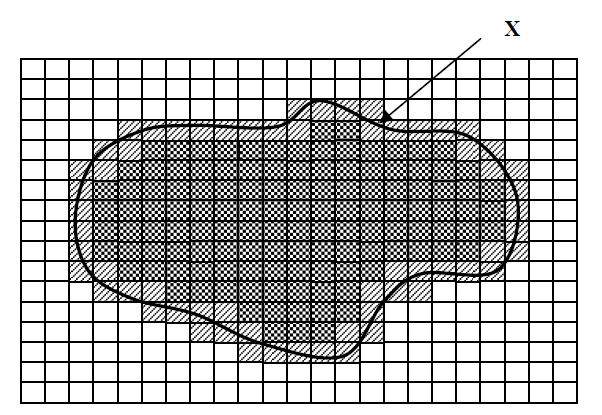
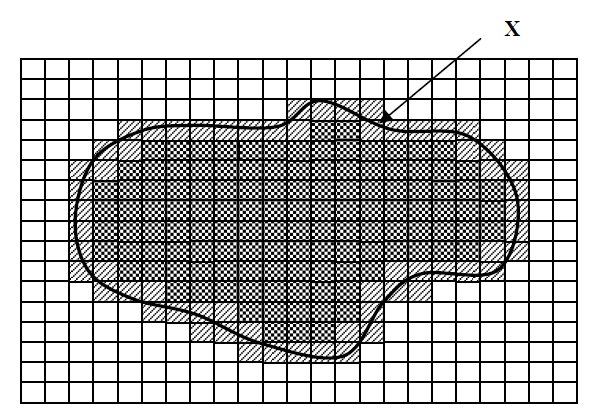
- Нижняя аппроксимация множества Х
 включает в себя элементы, которые действительно принадлежат множеству Х.
включает в себя элементы, которые действительно принадлежат множеству Х. - Верхняя аппроксимация множества Х
 +
+  включает в себя элементы, которые возможно принадлежат множеству Х.
включает в себя элементы, которые возможно принадлежат множеству Х. - Граница (разница между верхней и нижней аппроксимацией)
 представляет собой область неразличимости.
представляет собой область неразличимости.
Собственно применение
Приближенные множества находят применение при работе с таблицами данных, которые называются также таблицами атрибут-значение, или информационными системами, или таблицами принятия решений (decision tables). Таблица принятия решений (decision table) – это тройка Τ = (U, C, D), где
U – это множество объектов,
С – это множество атрибутов условий (condition attributes),
D – это множество атрибутов решений (decision attributes).
Пример таблицы
| U | C | D | |
| Головная боль | Температура | Грипп | |
| U1 | да | нормальная | нет |
| U2 | да | высокая | да |
| U3 | да | нормальная | нет |
| U4 | да | очень высокая | нет |
| U5 | нет | высокая | нет |
| U6 | нет | очень высокая | да |
| U7 | нет | высокая | да |
| U8 | нет | очень высокая | да |
Анализ таблицы
Множества:
U = {U1, U2, U3, U4, U5, U6, U7, U8}
C = {Головная боль, Температура}
D = {Грипп}
Возможные значения атрибутов:
VГоловная боль = {да, нет}
VТемпература = {нормальная, высокая, очень высокая}
VГрипп = {да, нет}
Разбиение множества U в соответствии со значениями атрибута Головная боль имеет вид:
- Sда = {1, 2, 3, 4}
- Sнет = {5, 6, 7, 8}
- S = {{1, 2, 3, 4}, {5, 6, 7, 8}}
Разбиение множества U в соответствии со значениями атрибута Температура имеет вид:
- Sнормальная = {1, 3}
- Sвысокая = {2, 5, 7}
- Sочень высокая = {4, 6}
- S = {{1, 3}, {2, 5, 7}, {4, 6}}
Разбиение множества U в соответствии со значениями атрибута решения Грипп имеет вид:
- Sда = {2, 6, 7, 8}
- Sнет = {1, 3, 4, 5}
- S = {{2, 6, 7, 8}, {1, 3, 4, 5}}
Представленые в этой таблице данные, например U5 и U7 — противоречивые, а U6 и U8 — повторяются.
| U5 | нет | высокая | нет |
| U6 | нет | очень высокая | да |
| U7 | нет | высокая | да |
| U8 | нет | очень высокая | да |
Собственно используя приближенные множества мы можем «извлечь» из неточных, противоречивых данных те, которые «полезны нам».
Над чем будем работать?
В следующих постах будет продемонстрирована практическая реализация (в Python) анализа данных с использаванием данной теории, в том числе:
- Алгоритм принятия решения, состоящий из решающих правил типа «ЕСЛИ … ТО…»
- Алгоритм LEM, LEM2 [Grzymała-Busse, 1992] генерирования решающих правил типа «ЕСЛИ … ТО…»
 включает в себя элементы, которые действительно принадлежат множеству Х.
включает в себя элементы, которые действительно принадлежат множеству Х. включает в себя элементы, которые возможно принадлежат множеству Х.
включает в себя элементы, которые возможно принадлежат множеству Х.