Число 6174 по-настоящему таинственное. На первый взгляд может показаться, что в нём нет ничего уникального. Но как мы увидим дальше, каждый кто умеет считать, может обнаружить секрет, который делает число 6174 таким особенным.
Это простое действие, но Капрекар обнаружил, что оно ведёт к удивительному результату. Давайте посмотрим, как это работает, например, на числе 2005. Из этих цифр мы можем получить максимальное число 5200, а минимальное — 0025, то есть 25. Вычитания будут выглядеть так:
5200 — 0025 = 5175
7551 — 1557 = 5994
9954 — 4599 = 5355
5553 — 3555 = 1998
9981 — 1899 = 8082
8820 — 0288 = 8532
8532 — 2358 = 6174
7641 — 1467 = 6174
Когда мы достигаем 6174, функция повторяет сама себя, возвращая 6174 каждый раз. Мы называем число 6174 неподвижной точкой для данной функции. Это число заставляет ряд вычитаний остановиться, но неужели только в этом его особенность? Здесь нас ждёт ещё один сюрприз. Давайте попробуем повторить операцию на каком-нибудь другом числе, например, 1789.
9871 — 1789 = 8082
8820 — 0288 = 8532
8532 — 2358 = 6174
Мы опять получили 6174!

Когда мы начинали с 2005, до достигли 6174 за семь шагов, а для 1789 процесс занял три шага. На самом деле, вы получите 6174 для любого четырёхзначного числа, в котором все разряды не являются одинаковыми. Это изумительно, не правда ли? Функция Капрекара настолько проста, но даёт такой интересный результат. И это становится ещё интереснее, когда мы подумаем о причинах, почему все четырёхзначные числа достигают таинственного числа 6174.
9 ≥ a ≥ b ≥ c ≥ d ≥ 0
где a, b, c, d не являются одинаковыми цифрами, максимальным числом является abcd, а минимальным — dcba.
Мы можем вычислить результат функции Капрекара, составив систему уравнений.
abcd
-dcba
____
ABCD
что даёт следующий результат
D = 10 + d — a (если a > d)
C = 10 + c — 1 — b = 9 + c — b (если b > c — 1)
B = b — 1 — c (если b > c)
A = a — d
для чисел, где a>b>c>d.
Результат начнёт повторяться, если итоговое число ABCD может быть записано первоначальными четырьмя цифрами a, b, c и d. Так что мы можем найти неподвижную точку функции Капрекара, перебрав все возможные комбинации {a, b, c, d} и проверяя, выполняются ли вышеупомянутые условия. Каждая из 4! = 24 комбинаций даёт систему из четырёх уравнений с четырьмя неизвестными, так что у нас не должно возникнуть проблемы с решением этой системы для a, b, c и d.
Выходит, что только одно из этих комбинаций имеет целочисленное решение, которое удовлетворяет требованию 9 ≥ a ≥ b ≥ c ≥ d ≥ 0. Это комбинация ABCD = bdac, и единственное решение системы уравнений — это a=7, b=6, c=4 и d=1. То есть ABCD = 6174. Для одинаковых разрядов {a,b,c,d} у системы нет валидного решения. Поэтому число 6174 является единственной неподвижной точкой функции Капрекара — наше таинственное число уникально.
Для трёхзначных чисел наблюдается тот же феномен. Например, применение функции Капрекара к числу 753 даёт следующее:
753 — 357 = 396
963 — 369 = 594
954 — 459 = 495
954 — 459 = 495
Число 495 является уникальной неподвижной точкой для трёхзначных чисел, и все трёхзначные числа в итоге сводятся к нему. Можете проверить сами.
Таблица внизу демонстрирует результат: каждое число достигает 6174 максимум за семь итераций. Если вы не достигли 6174 за семь итераций, значит у вас просто ошибка в вычислениях и нужно попробовать снова!
Моя компьютерная программа проверила все 8991 чисел, но Малкольм Лайнс в своей статье [Lines, Malcolm E., A number for your thoughts: facts and speculations about numbers..., Bristol: Hilger (1986)] доказывает, что достаточно проверить всего 30 возможных четырёхзначных чисел, чтобы проверить функцию Капрекара.
Как и раньше, давайте представим четыре цифры как abcd, где
9 ≥ a ≥ b ≥ c ≥ d ≥ 0.
Давайте вычислим первое действие в цепочке. Максимальным числом является 1000a+100b+10c+d, а минимальным — 1000d+100c+10b+a. Так что операция вычитания сведётся к следующей:
1000a + 100b + 10c + d — (1000d + 100c + 10b + a)
= 1000(a-d) + 100(b-c) + 10(c-b) + (d-a)
= 999(a-d) + 90(b-c)
Положительное значение (a-d) находится в пределах от 1 до 9, а (b-c) — от 0 до 9. Перебирая все возможные варианты, мы можем увидеть все возможные результаты первого действия вычитания. Они показаны в таблице.

Нам интересны только числа, в которых разряды не одинаковы и
a ≥ b ≥ c ≥ d,
поэтому мы берём только те, в которых (a-d) ≥ (b-c). Так что мы можем игнорировать всю серую зону в таблице, содержащую числа, в которых
(a-d) < (b-c).
Теперь мы перегруппируем числа в таблице в нисходящем порядке, чтобы получить готовое минимальное число для второго вычитания.
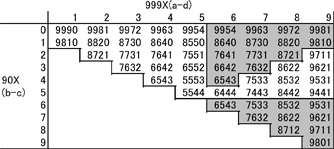
Мы можем игнорировать дубликаты (серая зона) и остаётся ровно 30 чисел для продолжений операции. На следующей схеме показаны маршруты, каким образом все эти числа приходят к неизменному результату 6174.
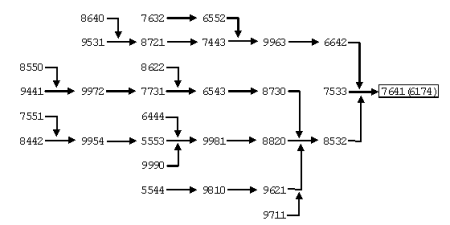
Из этой схемы вы можете увидеть, как все четырёхзначные числа достигают 6174 и это происходит максимум за семь итераций. Но даже после этого мне кажется, что число 6174 остаётся довольно таинственным. Полагаю, что Капрекар, который открыл это число, был чрезвычайно умным и у него было много времени на обдумывание этой проблемы!
82 — 28 = 54
54 — 45 = 9
90 — 09 = 81
81 — 18 = 63
63 — 36 = 27
72 — 27 = 45
54 — 45 = 9
Через короткое время мы убедимся, что все двузначные числа образуют цикл 9→81→63→27→45→9. В отличие от трёх- и четырёхзначных чисел, тут нет уникальной неподвижной точки.
А что с пятизначными числами? Есть ли для них уникальная неподвижная точка, такая как 6174 и 495? Чтобы ответить на этот вопрос, нам придётся проделать аналогичную операцию: проверить все 120 комбинаций {a,b,c,d,e} для ABCDE, чтобы соблюдались условия:
9 ≥ a ≥ b ≥ c ≥ d ≥ e ≥ 0
и
abcde — edcba = ABCDE.
К счастью, все необходимые вычисления уже сделаны на компьютере и известно, что для функции Капрекара на пятизначных числах нет уникальной постоянной точки. Но все пятизначные числа сводятся к одному из трёх циклов:
71973→83952→74943→62964→71973
75933→63954→61974→82962→75933
59994→53955→59994
Как отмечает Малкольм Лайнс в своей статье, требуется много времени для проверки чисел с шестью и большим количеством разрядов, и эта работа становится чрезвычайно нудной. Чтобы спасти вас от такой судьбы, следующая таблица содержит постоянные точки всех чисел от двух до десяти разрядов (для остальных — см. Mathews Archive of Recreational Mathematics).
Давайте остановимся и обдумаем прекрасную головоломку, составленную японским автором Юкио Ямамото.
Если вы перемножите два пятизначных числа, то можете получить результат 123456789. Угадайте эти два числа.
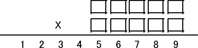
Это очень красивая головоломка, и вы можете предположить, что за ней скрывается какая-то большая математическая теория. Но на самом деле её красота исключительно случайна, есть и другие похожие, но не такие красивые примеры:
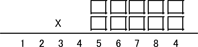
(Мы можем дать вам подсказку для решения этих задач, а вот ответы.)
Если я покажу вам головоломку Ямамото, то вам будет интересно её решать, потому что она красивая, но если я покажу вам вторую головоломку, то она может вообще вас не заинтересовать. Я думаю, что проблема Капрекара похожа на задачку Ямамото по поиску чисел. Нам нравятся такие задачки, потому что они красивые. И по той же причине нам кажется, что в них должно быть нечто большее, чем простая случайность. Такие недоразумения не раз приводили к научным открытиям в математики и науке прошлого.
Достаточно ли знать, что все четырёхзначные числа сводятся к числу 6174 в результате функции Капрекара, но не знать почему? До сих пор никто не мог с уверенностью сказать, что уникальная неподвижная точка для трёх- и четырёхзначных чисел — это просто случайный феномен. Она кажется настолько удивительным свойством, что мы можем ожидать, что за ней стоит какая-то большая теорема из теории чисел. Если бы мы смогли ответить на этот вопрос, возможно, в итоге оказалось бы, что перед нами просто красивое недоразумение, но мы надеемся, что это не так.
Функция Капрекара
В 1949 году математик Д. Р. Капрекар из города Долали (Индия) придумал математическое действие, которое теперь известно как функция Капрекара. Для начала выберите любое число, в котором разряды не повторяются (то есть не 1111, 2222 и т.д.). Затем переставьте цифры так, чтобы получить самое большое число из максимально возможных и самое малое из возможных. Потом нужно вычесть из большего меньшее — и повторить операцию с получившимся числом.Это простое действие, но Капрекар обнаружил, что оно ведёт к удивительному результату. Давайте посмотрим, как это работает, например, на числе 2005. Из этих цифр мы можем получить максимальное число 5200, а минимальное — 0025, то есть 25. Вычитания будут выглядеть так:
5200 — 0025 = 5175
7551 — 1557 = 5994
9954 — 4599 = 5355
5553 — 3555 = 1998
9981 — 1899 = 8082
8820 — 0288 = 8532
8532 — 2358 = 6174
7641 — 1467 = 6174
Когда мы достигаем 6174, функция повторяет сама себя, возвращая 6174 каждый раз. Мы называем число 6174 неподвижной точкой для данной функции. Это число заставляет ряд вычитаний остановиться, но неужели только в этом его особенность? Здесь нас ждёт ещё один сюрприз. Давайте попробуем повторить операцию на каком-нибудь другом числе, например, 1789.
9871 — 1789 = 8082
8820 — 0288 = 8532
8532 — 2358 = 6174
Мы опять получили 6174!

Когда мы начинали с 2005, до достигли 6174 за семь шагов, а для 1789 процесс занял три шага. На самом деле, вы получите 6174 для любого четырёхзначного числа, в котором все разряды не являются одинаковыми. Это изумительно, не правда ли? Функция Капрекара настолько проста, но даёт такой интересный результат. И это становится ещё интереснее, когда мы подумаем о причинах, почему все четырёхзначные числа достигают таинственного числа 6174.
Только 6174?
Из разрядов каждого четырёхзначного числа можно получить максимальное число, если переставить цифры в нисходящем порядке, а минимальное число получается перестановкой их в восходящем порядке. Для четырёх разрядов a, b, c, d:9 ≥ a ≥ b ≥ c ≥ d ≥ 0
где a, b, c, d не являются одинаковыми цифрами, максимальным числом является abcd, а минимальным — dcba.
Мы можем вычислить результат функции Капрекара, составив систему уравнений.
abcd
-dcba
____
ABCD
что даёт следующий результат
D = 10 + d — a (если a > d)
C = 10 + c — 1 — b = 9 + c — b (если b > c — 1)
B = b — 1 — c (если b > c)
A = a — d
для чисел, где a>b>c>d.
Результат начнёт повторяться, если итоговое число ABCD может быть записано первоначальными четырьмя цифрами a, b, c и d. Так что мы можем найти неподвижную точку функции Капрекара, перебрав все возможные комбинации {a, b, c, d} и проверяя, выполняются ли вышеупомянутые условия. Каждая из 4! = 24 комбинаций даёт систему из четырёх уравнений с четырьмя неизвестными, так что у нас не должно возникнуть проблемы с решением этой системы для a, b, c и d.
Выходит, что только одно из этих комбинаций имеет целочисленное решение, которое удовлетворяет требованию 9 ≥ a ≥ b ≥ c ≥ d ≥ 0. Это комбинация ABCD = bdac, и единственное решение системы уравнений — это a=7, b=6, c=4 и d=1. То есть ABCD = 6174. Для одинаковых разрядов {a,b,c,d} у системы нет валидного решения. Поэтому число 6174 является единственной неподвижной точкой функции Капрекара — наше таинственное число уникально.
Для трёхзначных чисел наблюдается тот же феномен. Например, применение функции Капрекара к числу 753 даёт следующее:
753 — 357 = 396
963 — 369 = 594
954 — 459 = 495
954 — 459 = 495
Число 495 является уникальной неподвижной точкой для трёхзначных чисел, и все трёхзначные числа в итоге сводятся к нему. Можете проверить сами.
Насколько быстро появляется 6174?
Был примерно 1975 год, когда я впервые услышал о числе 6174 от друга, и тогда я был весьма впечатлён. Я думал, что будет довольно просто объяснить причины этого феномена, но я никак не мог найти объяснение. Я проверил на компьютере все четырёхзначные числа. Программа занимала около 50 строчек на Visual Basic и она проверила все 8991 четырёхзначных комбинаций от 1000 до 9999, где знаки не повторяются.Таблица внизу демонстрирует результат: каждое число достигает 6174 максимум за семь итераций. Если вы не достигли 6174 за семь итераций, значит у вас просто ошибка в вычислениях и нужно попробовать снова!
| Итерации | Количество чисел |
| 0 | 1 |
| 1 | 356 |
| 2 | 519 |
| 3 | 2124 |
| 4 | 1124 |
| 5 | 1379 |
| 6 | 1508 |
| 7 | 1980 |
Как и раньше, давайте представим четыре цифры как abcd, где
9 ≥ a ≥ b ≥ c ≥ d ≥ 0.
Давайте вычислим первое действие в цепочке. Максимальным числом является 1000a+100b+10c+d, а минимальным — 1000d+100c+10b+a. Так что операция вычитания сведётся к следующей:
1000a + 100b + 10c + d — (1000d + 100c + 10b + a)
= 1000(a-d) + 100(b-c) + 10(c-b) + (d-a)
= 999(a-d) + 90(b-c)
Положительное значение (a-d) находится в пределах от 1 до 9, а (b-c) — от 0 до 9. Перебирая все возможные варианты, мы можем увидеть все возможные результаты первого действия вычитания. Они показаны в таблице.

Нам интересны только числа, в которых разряды не одинаковы и
a ≥ b ≥ c ≥ d,
поэтому мы берём только те, в которых (a-d) ≥ (b-c). Так что мы можем игнорировать всю серую зону в таблице, содержащую числа, в которых
(a-d) < (b-c).
Теперь мы перегруппируем числа в таблице в нисходящем порядке, чтобы получить готовое минимальное число для второго вычитания.

Мы можем игнорировать дубликаты (серая зона) и остаётся ровно 30 чисел для продолжений операции. На следующей схеме показаны маршруты, каким образом все эти числа приходят к неизменному результату 6174.

Из этой схемы вы можете увидеть, как все четырёхзначные числа достигают 6174 и это происходит максимум за семь итераций. Но даже после этого мне кажется, что число 6174 остаётся довольно таинственным. Полагаю, что Капрекар, который открыл это число, был чрезвычайно умным и у него было много времени на обдумывание этой проблемы!
Два разряда, пять разрядов, шесть и больше...
Мы уже убедились, что четырёх- и трёхзначные числа достигают уникальной неподвижной точки, но что насчёт чисел с другим количеством знаков? Оказывается, для них результат не такой впечатляющий. Давайте попробуем двузначное число, например, 28:82 — 28 = 54
54 — 45 = 9
90 — 09 = 81
81 — 18 = 63
63 — 36 = 27
72 — 27 = 45
54 — 45 = 9
Через короткое время мы убедимся, что все двузначные числа образуют цикл 9→81→63→27→45→9. В отличие от трёх- и четырёхзначных чисел, тут нет уникальной неподвижной точки.
А что с пятизначными числами? Есть ли для них уникальная неподвижная точка, такая как 6174 и 495? Чтобы ответить на этот вопрос, нам придётся проделать аналогичную операцию: проверить все 120 комбинаций {a,b,c,d,e} для ABCDE, чтобы соблюдались условия:
9 ≥ a ≥ b ≥ c ≥ d ≥ e ≥ 0
и
abcde — edcba = ABCDE.
К счастью, все необходимые вычисления уже сделаны на компьютере и известно, что для функции Капрекара на пятизначных числах нет уникальной постоянной точки. Но все пятизначные числа сводятся к одному из трёх циклов:
71973→83952→74943→62964→71973
75933→63954→61974→82962→75933
59994→53955→59994
Как отмечает Малкольм Лайнс в своей статье, требуется много времени для проверки чисел с шестью и большим количеством разрядов, и эта работа становится чрезвычайно нудной. Чтобы спасти вас от такой судьбы, следующая таблица содержит постоянные точки всех чисел от двух до десяти разрядов (для остальных — см. Mathews Archive of Recreational Mathematics).
| Разряды | Постоянная точка |
| 2 | Нет |
| 3 | 495 |
| 4 | 6174 |
| 5 | Нет |
| 6 | 549945, 631764 |
| 7 | Нет |
| 8 | 63317664, 97508421 |
| 9 | 554999445, 864197532 |
| 10 | 6333176664, 9753086421, 9975084201 |
Прекрасно, но в чём причина?
Мы убедились, что все трёхзначные числа сводятся к 495, а все четырёхзначные — к 6174 в результате вычисления функции Капрекара. Но я не объяснил, почему все эти числа имеют уникальную неподвижную точку. Этот феномен случаен или у него есть более глубокое математическое объяснение? Прекрасно и таинственно то, что это может быть простой случайностью.Давайте остановимся и обдумаем прекрасную головоломку, составленную японским автором Юкио Ямамото.
Если вы перемножите два пятизначных числа, то можете получить результат 123456789. Угадайте эти два числа.

Это очень красивая головоломка, и вы можете предположить, что за ней скрывается какая-то большая математическая теория. Но на самом деле её красота исключительно случайна, есть и другие похожие, но не такие красивые примеры:

(Мы можем дать вам подсказку для решения этих задач, а вот ответы.)
Если я покажу вам головоломку Ямамото, то вам будет интересно её решать, потому что она красивая, но если я покажу вам вторую головоломку, то она может вообще вас не заинтересовать. Я думаю, что проблема Капрекара похожа на задачку Ямамото по поиску чисел. Нам нравятся такие задачки, потому что они красивые. И по той же причине нам кажется, что в них должно быть нечто большее, чем простая случайность. Такие недоразумения не раз приводили к научным открытиям в математики и науке прошлого.
Достаточно ли знать, что все четырёхзначные числа сводятся к числу 6174 в результате функции Капрекара, но не знать почему? До сих пор никто не мог с уверенностью сказать, что уникальная неподвижная точка для трёх- и четырёхзначных чисел — это просто случайный феномен. Она кажется настолько удивительным свойством, что мы можем ожидать, что за ней стоит какая-то большая теорема из теории чисел. Если бы мы смогли ответить на этот вопрос, возможно, в итоге оказалось бы, что перед нами просто красивое недоразумение, но мы надеемся, что это не так.