Comments 58
А я всегда думал что это называется дерево поиска, по крайней мере в университете нам так давали эту структуру данных и описана она в замечательной книге «Алгоритмы и структуры данных» Н. Вирта именно под этим названием.
-5
Если бы я был тобой, я бы сначала сравнил двоичную кучу и дерево поиска хотя-бы с помощью википедии.
+7
они очень похоже. разница только в том, что (вики) «все слои, кроме, может быть, последнего, заполнены полностью, последний слой заполняется слева направо.» в остальном они одинаковы. для простого дерева поиска это не обязательно. для сбалансированного другие заморочки.
0
Автор, ну расскажи в двух словах где применяется например.
+5
heap sort на ней построен, если память не подводит…
0
Мда. Было про сортировку уже. Сорри.
0
Про heapSort, собственно, я в статье написал.
0
Имхо, следовало отметить, что хотя в heapSort гарантируется N log N (в отличие от qsort, где может быть и N^2), константный множитель больше, поэтому среднее время сортировки заметно превышает таковое для qsort.
+1
Был бы еще он естественный — цены бы ему не было.
А то так перетряхивает массив в процессе выполнения…
А то так перетряхивает массив в процессе выполнения…
0
Например, там, где нужно быстро извлекать максимальный/минимальный элемент. Уже упомянутый алгоритм Дейкстры с хипом и, думаю, другие алгоритмы на графах. Еще, например, выбор m максимальных/минимальных элементов из массива.
+1
Многопутевое слияние. Например, во внешних сортировках.
+1
Хорошая статья, однако неплохо бы добавить примеров применения binary heap, дабы у читателя не возникло ощущения что он слушает лекцию про абстрактные материи. Сортировка это круто, но ведь двоичную кучу придумали не только для этого :)
0
Применяется, например, для ускорения алгоритма Дейкстры («узкое место» — нахождение самой близкой вершины). Правда, последний раз я её там писал, когда кодил на Delphi, а теперь использую красно-черные деревья — std::set, потому что они уже реализованы.
0
Спасибо, я знаю :)
Мой комментарий был как раз про то, что неплохо бы увидеть эти примеры в статье.
Мой комментарий был как раз про то, что неплохо бы увидеть эти примеры в статье.
0
priority_queue в С++ реализована с помощью бинарной кучи. И на практике алгоритм Дейкстры, использующий priority_queue оказывается немного быстрее варианта с set.
А еще в STL также реализованы функции push_heap, pop_heap, make_heap и sort_heap.
А еще в STL также реализованы функции push_heap, pop_heap, make_heap и sort_heap.
0
UFO just landed and posted this here
UFO just landed and posted this here
Пост не полон без доказательства того, что построение действительно O(n). Ну, или хотя бы упоминания о тонкостях.
+3
Хотя, впрочем, чего я докапываюсь. Отличный повод вспомнить первый курс, спасибо за статью.
-1
O(n) требуется, чтобы построить дерево, не обращая внимание на соблюдение основного свойства кучи. Чтобы упорядочить binaryHeap, log2N раз вызываем метод heapify, сложность которого O(log2N), то есть процесс упорядочения более быстр. Поэтому итоговая оценка O(n).
+1
Точнее, метод heapify вызывается (log2N)/2 раз, что, впрочем, ничего не меняет.
0
Он же вызывается O(n) раз, нет?
public void buildHeap(int[] sourceArray)
{
list = sourceArray.ToList();
for (int i = /* !!! */ heapSize / 2; i >= 0; i--)
{
heapify(i);
}
}
0
OH SHI~
Вы правы, я ошибся.
Вы правы, я ошибся.
0
То есть всё-таки построение отъедает N log N? Тогда поправьте статью :-)
0
Нет, нет отъедает:) Итак:
Метод heapify вызывается только для поддеревьев, состоящих более чем из одного элемента. То есть для деревьев высоты 2, 3,…, H (пусть H=log2N — высота дерева), причем поддеревьев высоты k всего есть 2H-k.
heapify «жрет» не более O(log2N), а на самом деле O(h), где h — высота поддерева, для которого heapify вызывается. Тогда итоговая сложность упорядочения будет равна (k пробегает по всем значениям высот поддеревьев, которые нас интересуют)
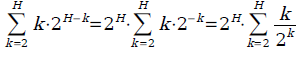
причем 2H — это количество вершин в дереве, то есть N. А сумма
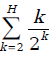
не превосходит некоторой константы (хотите доказательство?). Значит, общее время работы алгоритмы все-таки O(N) :)
Метод heapify вызывается только для поддеревьев, состоящих более чем из одного элемента. То есть для деревьев высоты 2, 3,…, H (пусть H=log2N — высота дерева), причем поддеревьев высоты k всего есть 2H-k.
heapify «жрет» не более O(log2N), а на самом деле O(h), где h — высота поддерева, для которого heapify вызывается. Тогда итоговая сложность упорядочения будет равна (k пробегает по всем значениям высот поддеревьев, которые нас интересуют)

причем 2H — это количество вершин в дереве, то есть N. А сумма

не превосходит некоторой константы (хотите доказательство?). Значит, общее время работы алгоритмы все-таки O(N) :)
+2
UFO just landed and posted this here
Мда. Не думал, что на хабре будут выкладывать стандартные алгоритмы/стрруктуры, которые можно найти в большенстве учебников/справочников. Могу сразу посоветовать «Корман. Алгоритмы и структуры данных. 2е издание», «Кнут. Все 3 тома» и сайт e-maxx.ru с описаниями и кодами большенства (а то чуть ли не всех) частоиспользуемых алгоритмов.
-2
Не думал, что на хабре будут выкладывать стандартные алгоритмы/стрруктуры, которые можно найти в большенстве учебников/справочников.
Например вот эти статьи вам тоже не нравятся? А структуры данных описанные в них спокойно можно найти в Кормене/Кнуте или на емаксе.
«Фуууу, хабр уже не торт, расходимся пацаны !»
0
Только недавно кто-то оставлял комментарий, не смог найти автора:
Действительно. Что делает техническая статья на развлекательном и новостном ресурсе?
+4
Извиняюсь, проглядел я их) Да, тоже не нравятся. Хотя согласен с тем, что декартово дерево не сильно тривиально для понимания и в нём много особенностей, так что с его описанием я не спорю.
0
UFO just landed and posted this here
Потомки гарантированно есть у первых heapSize/2 вершин.
for (int i = heapSize / 2; i >= 0; i--)
Мне кажется, или нужно сдвинуть верхнюю границу цикла?
for (int i = heapSize / 2 — 1; i >= 0; i--)
Дерево на первом рисунке имеет 10 вершин, т.о. потомки есть у первых пяти вершин, но индексы-то с нуля идут.
0
Для интересующихся визуализатор:
rain.ifmo.ru/cat/view.php/vis/heaps/bls-2006
rain.ifmo.ru/cat/view.php/vis/heaps/bls-2006
+1
+5
Вероятно, я слегка запоздал с комментарием, но всё же )
====
Наиболее очевидный способ построить binary heap из неупорядоченного массива – это по очереди добавить все его элементы. Временная оценка такого алгоритма O(N log2 N).
====
Далее говорится о том, что при построении кучи методом обхода с конца массива (точнее, примерно с середины, по сути) сложность будет линейной. Вопрос. Чем эти 2 случая принципиально отличаются? При обходе с начала мы имеем те же N уровней высоты/глубины, но «просеивание» выполняем вверх, а не вниз, как при обходе с конца. Оба варианта «просеивания» имеют логарифмическую сложность. Кто-то может объяснить, в чем тут подвох? )
====
Наиболее очевидный способ построить binary heap из неупорядоченного массива – это по очереди добавить все его элементы. Временная оценка такого алгоритма O(N log2 N).
====
Далее говорится о том, что при построении кучи методом обхода с конца массива (точнее, примерно с середины, по сути) сложность будет линейной. Вопрос. Чем эти 2 случая принципиально отличаются? При обходе с начала мы имеем те же N уровней высоты/глубины, но «просеивание» выполняем вверх, а не вниз, как при обходе с конца. Оба варианта «просеивания» имеют логарифмическую сложность. Кто-то может объяснить, в чем тут подвох? )
0
Я очень внимательно прочитал Ваш комментарий вверху и согласен с тем, что для «обратного» прохода по неупорядоченному массиве можно построить кучу за O(n).
Но почему этого нельзя сделать для варианта «прямого» прохода по массиву? Ведь тут работает та же формула. Для каждого уровня глубины h от 0 до log2(n) мы выполняем для
того же количества узлов на каждом уровне глубины операцию «просеивания» вверх, которая в худшем случае выполняется за h обменов.
Но почему этого нельзя сделать для варианта «прямого» прохода по массиву? Ведь тут работает та же формула. Для каждого уровня глубины h от 0 до log2(n) мы выполняем для
того же количества узлов на каждом уровне глубины операцию «просеивания» вверх, которая в худшем случае выполняется за h обменов.
0
Если добавлять каждую вершину в конец дерева, ее придется проталкивать вверх, а не вниз. Это невыгодно, так как сложность проталкивания вверх пропорциональна высоте уже построенного дерева, а вниз — высоте поддерева.
Пример на пальцах: если в дереве 15 вершин и используется оптимальный метод, то есть только одна вершина, которую (возможно) придется протолкнуть вниз на 3 уровня. На рисунке красная.
Если же добавлять вершины по одной, то есть 8 вершин, которые (возможно) придется проталкивать вверх на 3 уровня. Это зеленые вершины.
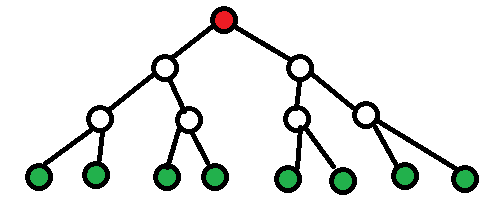
Пример на пальцах: если в дереве 15 вершин и используется оптимальный метод, то есть только одна вершина, которую (возможно) придется протолкнуть вниз на 3 уровня. На рисунке красная.
Если же добавлять вершины по одной, то есть 8 вершин, которые (возможно) придется проталкивать вверх на 3 уровня. Это зеленые вершины.

0
Кажется, я сообразил. При построении кучи методом «обратного» обхода массива у нас будет в худшем случае (для изображенного Вами варианта дерева): 4 * 1 замены для узлов глубины 2, 2 * 2 замены для узлов глубины 1 и 3 замены для корня. Итого 11. При этом мы полностью пропускаем узлы, не имеющие детей.
При использовании метода «прямого» обхода массива в худшем случае у нас будет 2 замены для узлов уровня глубины 1, 4 * 2 замены для узлов уровня глубины 2 и 8 * 3 замен для узлом самого нижнего уровня глубины — третьего. Итого 34.
Таким образом, вариант добавления узлов в начало дерево (с обходом с конца массива) более экономичен. Я правильно понял?
При использовании метода «прямого» обхода массива в худшем случае у нас будет 2 замены для узлов уровня глубины 1, 4 * 2 замены для узлов уровня глубины 2 и 8 * 3 замен для узлом самого нижнего уровня глубины — третьего. Итого 34.
Таким образом, вариант добавления узлов в начало дерево (с обходом с конца массива) более экономичен. Я правильно понял?
0
Sign up to leave a comment.
Articles
Change theme settings

Структуры данных: двоичная куча (binary heap)