Comments 49
Единственное, что про SIFT должно бы сразу быть сказано, это то, что алгоритм запатентован и использовать его в коммерческих целях нельзя (без согласования с David G. Lowe).
+3
Да, действительно забыл, алгоритм запатентован и использовать его в комерческих целях без согласия правообладателя нельзя. Текст подправил.
+2
Отлично, только там еще «использосвание» поправьте.
Добро пожаловать, кстати :)
Да и замочек с топика лучше снять («доступен только подписчикам блога») — тогда больше людей прочитает.
Добро пожаловать, кстати :)
Да и замочек с топика лучше снять («доступен только подписчикам блога») — тогда больше людей прочитает.
0
А для некоммерческого использования? И, имхо, только на территории США и близких соседей.
0
Алгоритм запатентован в США. В РФ патентов на алгоритмы нет.
+2
Получается, что у нас можно создавать коммерческий продукт, который может продаваться в том же США и не покупать лицензию у автора??? Если уж у нас поддерживается копираит, то исключительные права автора должны соблюдаться вне зависимости от того, где получен патент. ИМХО
+1
Насколько я понимаю, вы, продавая продукт в России не будете нарушать законодательство РФ.
Продавая продукт в США, вы будете нарушать законодательство США.
Право автора на алгоритм в США есть, а в РФ — нет.
Продавая продукт в США, вы будете нарушать законодательство США.
Право автора на алгоритм в США есть, а в РФ — нет.
+4
Не силен я конечно в этом, но продавая такой продукт, нарушаются не законы, а права установленные какими-то там международными конференциями или собраниями. Получается, что эти права международные, а то как их защищают законы — это уже дело какой-то конкретной страны. У нас в стране эти права защищщаются. Ведь для того, чтобы пользоваться виндой нужно купить лицензию, вне зависимости от того в какой стране вы ею пользуетесь, хотя написана она была черт знает где. Если что не так — правьте))
0
Конкретно эти права (право автора на алгоритм) — не являются международными.
Права на книги, музыку, видео, программы защищаются международным образом; права на алгоритм (который суть идея того, как что-то делать) защищаются только в США.
Скажем так — если вы реализуете этот алгоритм сами, вас могут преследовать в США, но не в России.
Если вы используете библиотеку автора (суть программный код) без лицензии и разрешения, вас могут преследовать и в США, и в России.
Права на книги, музыку, видео, программы защищаются международным образом; права на алгоритм (который суть идея того, как что-то делать) защищаются только в США.
Скажем так — если вы реализуете этот алгоритм сами, вас могут преследовать в США, но не в России.
Если вы используете библиотеку автора (суть программный код) без лицензии и разрешения, вас могут преследовать и в США, и в России.
+1
Вы путаете патент и авторские права. Авторские права распространяются на код. Если вы код сделаете сами, то он ваш.
А с продажами в США — ну будут вас преследовать по американским законам. И? Если вы не будете иметь счетов на территории страны и не будете туда приезжать, в чём проблема-то?
А с продажами в США — ну будут вас преследовать по американским законам. И? Если вы не будете иметь счетов на территории страны и не будете туда приезжать, в чём проблема-то?
0
В России ведь алгоритмы непатентуемы, а законодательство США на нас не распространяется.
0
>следует обратится
tsya.ru
tsya.ru
-3
Ей-богу, хуже первонахов уже.
+9
пусть учатся! может хоть в ворд научаться вставлять перед тем как статью запостить
-3
А почему именно разность гауссианов берется в качестве фильтра? Что особого в экстремумах этой разности?
+1
Вопрос хороший. Отвечу немного издалека.
Доказано, что точки экстремума масштабно-нормированного лапласиана гауссиана(LoG) дают наиболее устоичивые относительно масштаба точечные особенности (по сравнению с тем же детектором Харриса, который достаточно прост и широко распространен). Производная масштабно-нормирована, если она умножена на свой масштаб (sigma). В лапласиане присутствуют вторые производные, поэтому его масштабно-нормированная версия умножается на sigma^2.
Так же, существует уравнение диффузии, которое описывает масштабируемое пространство
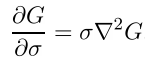
Если производную аппроксимировать разностной, то получится следующее
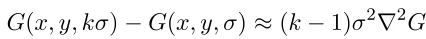
Слева получается разность гауссианов, а справа LoG. Причем эта аппроксимация тем точнее, чем ближе k к единице. Кстати, исходя из величины k выбирается шаг с которым строятся изображения в пирамидах.
Доказано, что точки экстремума масштабно-нормированного лапласиана гауссиана(LoG) дают наиболее устоичивые относительно масштаба точечные особенности (по сравнению с тем же детектором Харриса, который достаточно прост и широко распространен). Производная масштабно-нормирована, если она умножена на свой масштаб (sigma). В лапласиане присутствуют вторые производные, поэтому его масштабно-нормированная версия умножается на sigma^2.
Так же, существует уравнение диффузии, которое описывает масштабируемое пространство
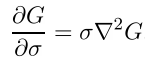
Если производную аппроксимировать разностной, то получится следующее
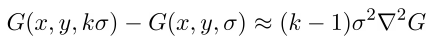
Слева получается разность гауссианов, а справа LoG. Причем эта аппроксимация тем точнее, чем ближе k к единице. Кстати, исходя из величины k выбирается шаг с которым строятся изображения в пирамидах.
+3
Получается что-то типа условия Куранта?
0
Я так понял, вы про условие Куранта — Фридрихса — Леви?
Если да, то можно сказать что здесь что-то подобное. Настолько я помню, это условие накладывает ограничение на шаг, здесь же ограничения на шаг накладываются из эмпирических соображений. Эта формула скорее подходит больше как иллюстрация, нежели как принцип выбора величины шага.
Если да, то можно сказать что здесь что-то подобное. Настолько я помню, это условие накладывает ограничение на шаг, здесь же ограничения на шаг накладываются из эмпирических соображений. Эта формула скорее подходит больше как иллюстрация, нежели как принцип выбора величины шага.
+1
потому что абсолютно не учитывается временной захват, если распознаваемый субъект движется.
0
А где-нибудь можно посмотреть код/реализацию?
+1
Сделайте доброе дело — напишите статью в русскую википедию об этом замечательном алгоритме.
+1
Спасибо за статью!
Опередили меня — всё собирался выложить описание этого алгоритма :)
Опередили меня — всё собирался выложить описание этого алгоритма :)
0
Спасибо за статью. Не встречалось ли вам описание алгоритма с иллюстрациями на конкретных примерах, что дает каждый шаг? Математическое описание довольно тяжело дается, курс матанализа уже подзабылся :)
0
Не встречалось, а что дает каждый шаг я вроде и так описал:
Если честно, то я даже не знаю как можно норм иллюсстрировать эти шаги. Вообще, по этои тематике есть только несколько статей на английском. У самого автора есть еще статьи, но они представляют собой либо промежуточные результаты, либо посвещены какому-либо одному этапу. На русском ни одной статьи (толковой) по этому алгоритму не встречал:)
- сначала через пирамиды находятся нужные точки
- для отсеивания плохих точек делаются проверки
- находиться направление особой точки, что в дальнейшем обеспечивает инвариантность относительно поворота исходного изображения
- строится дескриптор
Если честно, то я даже не знаю как можно норм иллюсстрировать эти шаги. Вообще, по этои тематике есть только несколько статей на английском. У самого автора есть еще статьи, но они представляют собой либо промежуточные результаты, либо посвещены какому-либо одному этапу. На русском ни одной статьи (толковой) по этому алгоритму не встречал:)
0
Вы все здорово описали, для имплементации алгоритма этого вполне достаточно. Мне же интересно, почему и зачем делается каждый шаг. Например, у меня есть догадки, зачем строить пирамиду гауссианов и считать их разность, но если была бы иллюстрация как эта разность выглядит на реальной картинке и для какой точки достигается локальный экстремум, задумка автора раскрылась бы полнее. Опять же, подбор нужных коэффициентов k, N — требует практических экспериментов. Мне немного помогли разобраться иллюстрации в статье Yu Meng-а.
Видимо, остается один путь — поэкспериментировать с одной из реализаций.
Ещё заметил, что этот алгоритм неплохо ложится на нейросети (пространство масштабов, свертки, поиск экстремумов — все это можно поручить нейросети). Не попадались исследования в таком ключе?
Видимо, остается один путь — поэкспериментировать с одной из реализаций.
Ещё заметил, что этот алгоритм неплохо ложится на нейросети (пространство масштабов, свертки, поиск экстремумов — все это можно поручить нейросети). Не попадались исследования в таком ключе?
0
Пирамида гауссианов строится, чтобы по ней в дальнейшем считать направления ключевой точки и дескрипторы, а разности гауссианов для нахождения самих этих точек. Про DoG можно почитать и посмотреть результаты работы этого фильтра в Wiki. Чисто визуально DoG выделяет края, контуры обьектов, а его точки экстремума находятся в особо различимых местах(например, в углах, возле границ объектов и т.д.) Почему именно DoG, с чисто теоретической стороны я уже описал выше. А подбором коэффициентов занимался сам автор (похоже долго и упорно). В его статье много графиков зависимостей некоторых параметров, от входных данных, и рекомендаций по выбору значений этих параметров. Согласен, что у Yu Meng'а некоторые моменты описаны четче.
Насчет нейросетей, то я ничего по этому поводу не встречал. Правда, сама идея построения дескриптора взята автором (по его словам) из какой-то работы по изучению зрения приматов и построения мат модели неиронной сети, отвечающей за это дело (в статье есть упоминание, не помню только где, если сильно надо то поищу). Еще видел одну статью, в которой приводилась аппаратная реализация построения пирамид, для внедрения этого дела в робототехнику.
Насчет нейросетей, то я ничего по этому поводу не встречал. Правда, сама идея построения дескриптора взята автором (по его словам) из какой-то работы по изучению зрения приматов и построения мат модели неиронной сети, отвечающей за это дело (в статье есть упоминание, не помню только где, если сильно надо то поищу). Еще видел одну статью, в которой приводилась аппаратная реализация построения пирамид, для внедрения этого дела в робототехнику.
+1
такая свёртка плохо работает для геометрически искажённыхх объектов — к примеру, для спутниковых снимков или для снимков на фишай
0
Не совсем понял: сам механизм свертки или свертка с каким-то конкретным ядром?
Вообще никто и не говорил, что это идеально работает во всех случаях. Все равно спасибо за заметку:)
Вообще никто и не говорил, что это идеально работает во всех случаях. Все равно спасибо за заметку:)
0
Сам механизм свёртки: гауссиан не инвариантен к линейным искажениям. Соответственно, свёртка, базирующаяся на вычленении AP(attraction point) только на основании анализа гауссианов при сильных геометрических искажениях будет лагать. Ну и беда с текстурированными изображениями — тоже, как это у вас в статье отмечено.
+1
Не совсем понятно, где будет находиться сам пиксель ключевой точки внутри её окрестности?
0
Похоже речь идет о последней картинке. Вопрос в том, как может ключевая точка находится в центре окна, т.е. «между» пикселями? Если да, то тут есть некоторая тонкость.
Во-первых, центр окна действительно находится «между» пикселями, но он не совпадает с ключевой точкой, а находится ближе всего к ней.
Во-вторых, он лежит ближе всего не к простым координатам ключевой точки, а к уточненным. Простые координаты — это те, которые найдены на пирамиде DoG, а уточненные координаты — это те, которые вычисляются с субпиксельной точностью по многочлену Тейлора. Поскольку простые координаты — целые числа, то непонятно какой из четырех «углов» их пикселя брать за центр окна. С уточненными координатами таких проблем не возникает, т.к. они вещественные.
Во-первых, центр окна действительно находится «между» пикселями, но он не совпадает с ключевой точкой, а находится ближе всего к ней.
Во-вторых, он лежит ближе всего не к простым координатам ключевой точки, а к уточненным. Простые координаты — это те, которые найдены на пирамиде DoG, а уточненные координаты — это те, которые вычисляются с субпиксельной точностью по многочлену Тейлора. Поскольку простые координаты — целые числа, то непонятно какой из четырех «углов» их пикселя брать за центр окна. С уточненными координатами таких проблем не возникает, т.к. они вещественные.
0
Подскажите хорошую реализацию на GPU, работающую под Linux, желательно OpenSource.
0
Я уже давно этой темой не занимался, поэтому не подскажу. А вообще, если у вас не курсовая/диплом/..., то может будет лучше посмотреть на другие алгоритмы (хотя бы тот же SURF, для него и реализация на GPU в opencv есть). Все таки, Lowe со своей работой был в некотором смысле первопроходцем. С тех пор уже не мало времени прошло.
0
Sign up to leave a comment.
Построение SIFT дескрипторов и задача сопоставления изображений