Наверное, любой сервис, на котором вообще есть поиск, рано или поздно приходит к потребности научиться исправлять ошибки в пользовательских запросах. Errare humanum est; пользователи постоянно опечатываются и ошибаются, и качество поиска от этого неизбежно страдает — а с ним и пользовательский опыт.
При этом каждый сервис обладает своей спецификой, своим лексиконом, которым должен уметь оперировать исправитель опечаток, что в значительной мере затрудняет применение уже существующих решений. Например, такие запросы пришлось научиться править нашему опечаточнику:
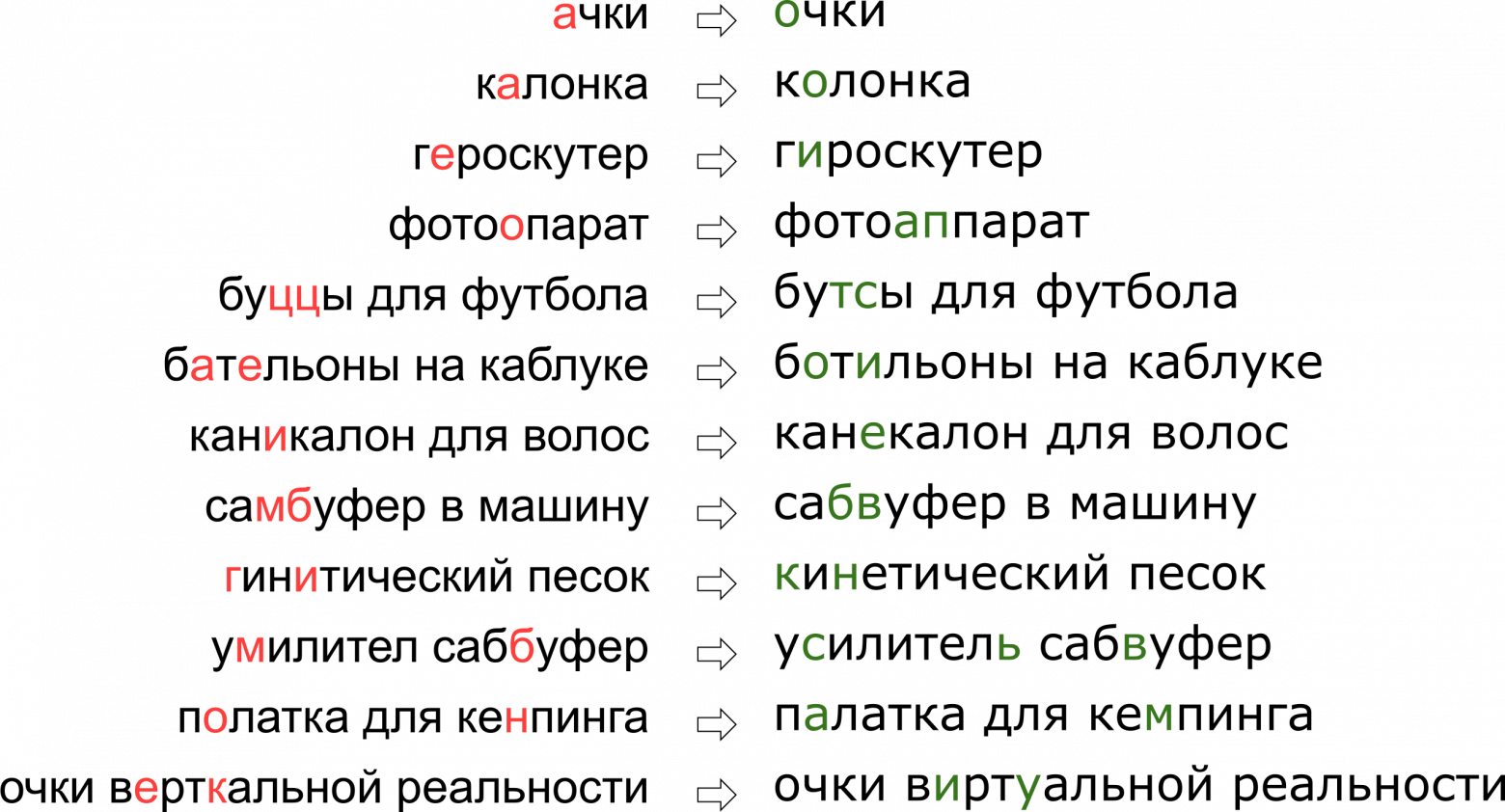
Может показаться, что мы отказали пользователю в его мечте о вертикальной реальности, но на самом деле буква К просто стоит на клавиатуре рядом с буквой У.
В этой статье мы разберём один из классических подходов к исправлению опечаток, от построения модели до написания кода на Python и Go. И в качестве бонуса — видео с моего доклада «”Очки верткальной реальности”: исправляем опечатки в поисковых запросах» на Highload++.
Итак, нам пришёл опечатанный запрос и его надо исправить. Обычно математически задача ставится таким образом:
Эта постановка — самая элементарная — предполагает, что если нам пришёл запрос из нескольких слов, то мы исправляем каждое слово по отдельности. В реальности, конечно, мы захотим исправлять всю фразу целиком, учитывая сочетаемость соседних слов; об этом я расскажу ниже, в разделе “Как исправлять фразы”.
Неясных моментов здесь два — где взять словарь и как посчитать . Первый вопрос считается простым. В 1990 году [1] словарь собирали из базы утилиты spell и доступных в электронном виде словарей; в 2009 году в Google [4] поступили проще и просто взяли топ самых популярных слов в Интернете (вместе с популярными ошибочными написаниями). Этот подход взял и я для построения своего опечаточника.
. Первый вопрос считается простым. В 1990 году [1] словарь собирали из базы утилиты spell и доступных в электронном виде словарей; в 2009 году в Google [4] поступили проще и просто взяли топ самых популярных слов в Интернете (вместе с популярными ошибочными написаниями). Этот подход взял и я для построения своего опечаточника.
Второй вопрос сложнее. Хотя бы потому, что его решение обычно начинается с применения формулы Байеса!
Теперь вместо исходной непонятной вероятности нам нужно оценить две новые, чуть более понятные: — вероятность того, что при наборе слова
— вероятность того, что при наборе слова  можно опечататься и получить
можно опечататься и получить  , и
, и  — в принципе вероятность использования пользователем слова
— в принципе вероятность использования пользователем слова  .
.
Как оценить ? Очевидно, что пользователь с большей вероятностью путает А с О, чем Ъ с Ы. А если мы исправляем текст, распознанный с отсканированного документа, то велика вероятность путаницы между rn и m. Так или иначе, нам нужна какая-то модель, описывающая ошибки и их вероятности.
? Очевидно, что пользователь с большей вероятностью путает А с О, чем Ъ с Ы. А если мы исправляем текст, распознанный с отсканированного документа, то велика вероятность путаницы между rn и m. Так или иначе, нам нужна какая-то модель, описывающая ошибки и их вероятности.
Такая модель называется noisy channel model (модель зашумлённого канала; в нашем случае зашумлённый канал начинается где-то в центре Брока пользователя и заканчивается по другую сторону его клавиатуры) или более коротко error model — модель ошибок. Эта модель, которой ниже посвящен отдельный раздел, будет ответственна за учёт как орфографических ошибок, так и, собственно, опечаток.
Оценить вероятность использования слова — — можно по-разному. Самый простой вариант — взять за неё частоту, с которой слово встречается в некотором большом корпусе текстов. Для нашего опечаточника, учитывающего контекст фразы, потребуется, конечно, что-то более сложное — ещё одна модель. Эта модель называется language model, модель языка.
— можно по-разному. Самый простой вариант — взять за неё частоту, с которой слово встречается в некотором большом корпусе текстов. Для нашего опечаточника, учитывающего контекст фразы, потребуется, конечно, что-то более сложное — ещё одна модель. Эта модель называется language model, модель языка.
Первые модели ошибок считали , подсчитывая вероятности элементарных замен в обучающей выборке: сколько раз вместо Е писали И, сколько раз вместо ТЬ писали Т, вместо Т — ТЬ и так далее [1]. Получалась модель с небольшим числом параметров, способная выучить какие-то локальные эффекты (например, что люди часто путают Е и И).
, подсчитывая вероятности элементарных замен в обучающей выборке: сколько раз вместо Е писали И, сколько раз вместо ТЬ писали Т, вместо Т — ТЬ и так далее [1]. Получалась модель с небольшим числом параметров, способная выучить какие-то локальные эффекты (например, что люди часто путают Е и И).
В наших изысканиях мы остановились на более развитой модели ошибок, предложенной в 2000 году Бриллом и Муром [2] и многократно использованной впоследствии (например, специалистами Google [4]). Представим, что пользователи мыслят не отдельными символами (спутать Е и И, нажать К вместо У, пропустить мягкий знак), а могут изменять произвольные куски слова на любые другие — например, заменять ТСЯ на ТЬСЯ, У на К, ЩА на ЩЯ, СС на С и так далее. Вероятность того, что пользователь опечатался и вместо ТСЯ написал ТЬСЯ, обозначим — это параметр нашей модели. Если для всех возможных фрагментов
— это параметр нашей модели. Если для всех возможных фрагментов  мы можем посчитать
мы можем посчитать  , то искомую вероятность
, то искомую вероятность  набора слова s при попытке набрать слово w в модели Брилла и Мура можно получить следующим образом: разобьем всеми возможными способами слова w и s на более короткие фрагменты так, чтобы фрагментов в двух словах было одинаковое количество. Для каждого разбиения посчитаем произведение вероятностей всех фрагментов w превратиться в соответствующие фрагменты s. Максимум по всем таким разбиениям и примем за значение величины
набора слова s при попытке набрать слово w в модели Брилла и Мура можно получить следующим образом: разобьем всеми возможными способами слова w и s на более короткие фрагменты так, чтобы фрагментов в двух словах было одинаковое количество. Для каждого разбиения посчитаем произведение вероятностей всех фрагментов w превратиться в соответствующие фрагменты s. Максимум по всем таким разбиениям и примем за значение величины  :
:
Давайте посмотрим на пример разбиения, возникающего при вычислении вероятности напечатать «аксесуар» вместо «аксессуар»:
 и
и  ещё не так плохи, то
ещё не так плохи, то  и
и  , скорее всего, сделают итоговый «счёт» этого разбиения совсем печальным. Более удачное разбиение выглядит как-то так:
, скорее всего, сделают итоговый «счёт» этого разбиения совсем печальным. Более удачное разбиение выглядит как-то так:
Здесь всё сразу стало на свои места, и видно, что итоговая вероятность будет определяться преимущественно величиной .
.
Как вычислить
Несмотря на то, что возможных разбиений для двух слов имеется порядка , с помощью динамического программирования алгоритм вычисления
, с помощью динамического программирования алгоритм вычисления  можно сделать довольно быстрым — за
можно сделать довольно быстрым — за  . Сам алгоритм при этом будет очень сильно напоминать алгоритм Вагнера-Фишера для вычисления расстояния Левенштейна.
. Сам алгоритм при этом будет очень сильно напоминать алгоритм Вагнера-Фишера для вычисления расстояния Левенштейна.
Мы заведём прямоугольную таблицу, строки которой будут соответствовать буквам правильного слова, а столбцы — опечатанного. В ячейке на пересечении строки i и столбца j к концу алгоритма будет лежать в точности вероятность получить . Например, если у нас заполнена таблица
. Например, если у нас заполнена таблица
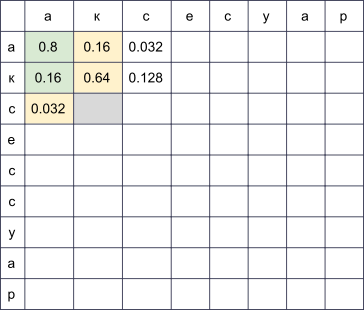
, то для заполнения ячейки в четвёртой строке и третьем столбце (серая) нужно взять максимум из величин и
и  . При этом мы пробежались по всем ячейкам, подсвеченным на картинке зелёным. Если также рассматривать модификации вида
. При этом мы пробежались по всем ячейкам, подсвеченным на картинке зелёным. Если также рассматривать модификации вида  и
и  , то придётся пробежаться и по ячейкам, подсвеченным жёлтым.
, то придётся пробежаться и по ячейкам, подсвеченным жёлтым.
Сложность этого алгоритма, как я уже упомянул выше, составляет : мы заполняем таблицу
: мы заполняем таблицу  , и для заполнения ячейки (i, j) нужно
, и для заполнения ячейки (i, j) нужно  операций. Впрочем, если мы ограничим рассмотрение фрагментами не больше какой-то ограниченной длины
операций. Впрочем, если мы ограничим рассмотрение фрагментами не больше какой-то ограниченной длины  (например, не больше двух букв, как в [4]), сложность уменьшится до
(например, не больше двух букв, как в [4]), сложность уменьшится до  . Для русского языка в своих экспериментах я брал
. Для русского языка в своих экспериментах я брал  .
.
Как максимизировать
Мы научились находить за полиномиальное время — это хорошо. Но нам нужно научиться быстро находить наилучшие слова во всём словаре. Причём наилучшие не по
за полиномиальное время — это хорошо. Но нам нужно научиться быстро находить наилучшие слова во всём словаре. Причём наилучшие не по  , а по
, а по  ! На деле нам достаточно получить какой-то разумный топ (например, лучшие 20) слов по
! На деле нам достаточно получить какой-то разумный топ (например, лучшие 20) слов по  , который мы потом отправим в модель языка для выбора наиболее подходящих исправлений (об этом ниже).
, который мы потом отправим в модель языка для выбора наиболее подходящих исправлений (об этом ниже).
Чтобы научиться быстро проходить по всему словарю, заметим, что таблица, представленная выше, будет иметь много общего для двух слов с общими префиксами. Действительно, если мы, исправляя слово «аксесуар», попробуем заполнить её для двух словарных слов «аксессуар» и «аксессуары», мы заметим, что первые девять строк в них вообще не отличаются! Если мы сможем организовать проход по словарю так, что у двух последующих слов будут достаточно длинные общие префиксы, мы сможем круто сэкономить вычисления.
И мы сможем. Давайте возьмём словарные слова и составим из них trie. Идя по нему поиском в глубину, мы получим желаемое свойство: большинство шагов — это шаги от узла к его потомку, когда у таблицы достаточно дозаполнить несколько последних строк.
Этот алгоритм, при некоторых дополнительных оптимизациях, позволяет нам перебирать словарь типичного европейского языка в 50-100 тысяч слов в пределах сотни миллисекунд [2]. А кэширование результатов сделает процесс ещё быстрее.
Как получить
Вычисление для всех рассматриваемых фрагментов — самая интересная и нетривиальная часть построения модели ошибок. Именно от этих величин будет зависеть её качество.
для всех рассматриваемых фрагментов — самая интересная и нетривиальная часть построения модели ошибок. Именно от этих величин будет зависеть её качество.
Подход, использованный в [2, 4], сравнительно прост. Давайте найдём много пар , где
, где  — правильное слово из словаря, а
— правильное слово из словаря, а  — его опечатанный вариант. (Как именно их находить — чуть ниже.) Теперь нужно извлечь из этих пар вероятности конкретных опечаток (замен одних фрагментов на другие).
— его опечатанный вариант. (Как именно их находить — чуть ниже.) Теперь нужно извлечь из этих пар вероятности конкретных опечаток (замен одних фрагментов на другие).
Для каждой пары возьмём составляющие её и
и  и построим соответствие между их буквами, минимизирующее расстояние Левенштейна:
и построим соответствие между их буквами, минимизирующее расстояние Левенштейна:
После прохода по всем парам за вероятность
за вероятность  принимается количество замен α → β, встретившихся в наших парах (с учётом встречаемости соответствующих слов), делённое на количество повторений фрагмента α.
принимается количество замен α → β, встретившихся в наших парах (с учётом встречаемости соответствующих слов), делённое на количество повторений фрагмента α.
Как найти пары ? В [4] предлагается такой подход. Возьмём большой корпус сгенерированного пользователями контента (UGC). В случае Google это были просто тексты сотен миллионов веб-страниц; в нашем — миллионы пользовательских поисковых запросов и отзывов. Предполагается, что обычно правильное слово встречается в корпусе чаще, чем любой из ошибочных вариантов. Так вот, давайте для каждого слова находить близкие к нему по Левенштейну слова из корпуса, которые значительно менее популярны (например, в десять раз). Популярное возьмём за
? В [4] предлагается такой подход. Возьмём большой корпус сгенерированного пользователями контента (UGC). В случае Google это были просто тексты сотен миллионов веб-страниц; в нашем — миллионы пользовательских поисковых запросов и отзывов. Предполагается, что обычно правильное слово встречается в корпусе чаще, чем любой из ошибочных вариантов. Так вот, давайте для каждого слова находить близкие к нему по Левенштейну слова из корпуса, которые значительно менее популярны (например, в десять раз). Популярное возьмём за  , менее популярное — за
, менее популярное — за  . Так мы получим пусть и шумный, но зато достаточно большой набор пар, на котором можно будет провести обучение.
. Так мы получим пусть и шумный, но зато достаточно большой набор пар, на котором можно будет провести обучение.
Этот алгоритм подбора пар оставляет большое пространство для улучшений. В [4] предлагается только фильтр по встречаемости ( в десять раз популярнее, чем
в десять раз популярнее, чем  ), но авторы этой статьи пытаются делать опечаточник, не используя какие-либо априорные знания о языке. Если мы рассматриваем только русский язык, мы можем, например, взять набор словарей русских словоформ и оставлять только пары со словом
), но авторы этой статьи пытаются делать опечаточник, не используя какие-либо априорные знания о языке. Если мы рассматриваем только русский язык, мы можем, например, взять набор словарей русских словоформ и оставлять только пары со словом  , найденном в словаре (не лучшая идея, потому что в словаре, скорее всего, не будет специфичной для сервиса лексики) или, наоборот, отбрасывать пары со словом s, найденном в словаре (то есть почти гарантированно не являющимся опечатанным).
, найденном в словаре (не лучшая идея, потому что в словаре, скорее всего, не будет специфичной для сервиса лексики) или, наоборот, отбрасывать пары со словом s, найденном в словаре (то есть почти гарантированно не являющимся опечатанным).
Чтобы повысить качество получаемых пар, я написал несложную функцию, определяющую, используют ли пользователи два слова как синонимы. Логика простая: если слова w и s часто встречаются в окружении одних и тех же слов, то они, вероятно, синонимы — что в свете их близости по Левенштейну значит, что менее популярное слово с большой вероятностью является ошибочной версией более популярного. Для этих расчётов я использовал построенную для модели языка ниже статистику встречаемости триграмм (фраз из трёх слов).
Итак, теперь для заданного словарного слова w нам нужно вычислить — вероятность его использования пользователем. Простейшее решение — взять встречаемость слова в каком-то большом корпусе. Вообще, наверное, любая модель языка начинается с собирания большого корпуса текстов и подсчёта встречаемости слов в нём. Но ограничиваться этим не стоит: на самом деле при вычислении P(w) мы можем учесть также и фразу, слово в которой мы пытаемся исправить, и любой другой внешний контекст. Задача превращается в задачу вычисления
— вероятность его использования пользователем. Простейшее решение — взять встречаемость слова в каком-то большом корпусе. Вообще, наверное, любая модель языка начинается с собирания большого корпуса текстов и подсчёта встречаемости слов в нём. Но ограничиваться этим не стоит: на самом деле при вычислении P(w) мы можем учесть также и фразу, слово в которой мы пытаемся исправить, и любой другой внешний контекст. Задача превращается в задачу вычисления  , где одно из
, где одно из  — слово, в котором мы исправили опечатку и для которого мы теперь рассчитываем
— слово, в котором мы исправили опечатку и для которого мы теперь рассчитываем  , а остальные
, а остальные  — слова, окружающие исправляемое слово в пользовательском запросе.
— слова, окружающие исправляемое слово в пользовательском запросе.
Чтобы научиться учитывать их, стоит пройтись по корпусу ещё раз и составить статистику n-грамм, последовательностей слов. Обычно берут последовательности ограниченной длины; я ограничился триграммами, чтобы не раздувать индекс, но тут всё зависит от вашей силы духа (и размера корпуса — на маленьком корпусе даже статистика по триграммам будет слишком шумной).
Традиционная модель языка на основе n-грамм выглядит так. Для фразы её вероятность вычисляется по формуле
её вероятность вычисляется по формуле
где — непосредственно частота слова, а
— непосредственно частота слова, а  — вероятность слова
— вероятность слова  при условии, что перед ним идут
при условии, что перед ним идут  — не что иное, как отношение частоты триграммы
— не что иное, как отношение частоты триграммы  к частоте биграммы
к частоте биграммы  . (Заметьте, что эта формула — просто результат многократного применения формулы Байеса.)
. (Заметьте, что эта формула — просто результат многократного применения формулы Байеса.)
Иными словами, если мы захотим вычислить , обозначив частоту произвольной n-граммы за
, обозначив частоту произвольной n-граммы за  , мы получим формулу
, мы получим формулу
Логично? Логично. Однако трудности начинаются, когда фразы становятся длиннее. Что, если пользователь ввёл впечатляющий своей подробностью поисковый запрос в десять слов? Мы не хотим держать статистику по всем 10-граммам — это дорого, а данные, скорее всего, будут шумными и не показательными. Мы хотим обойтись n-граммами какой-то ограниченной длины — например, уже предложенной выше длины 3.
Здесь-то и пригождается формула выше. Давайте предположим, что на вероятность слова появиться в конце фразы значительно влияют только несколько слов непосредственно перед ним, то есть что
Положив , для более длинной фразы получим формулу
, для более длинной фразы получим формулу

Обратите внимание: фраза состоит из пяти слов, но в формуле фигурируют n-граммы не длиннее трёх. Это как раз то, чего мы добивались.
Остался один тонкий момент. Что, если пользователь ввёл совсем странную фразу и соответствующих n-грамм у нас в статистике и нет вовсе? Было бы легко для незнакомых n-грамм положить , если бы на эту величину не надо было делить. Здесь на помощь приходит сглаживание (smoothing), которое можно делать разными способами; однако подробное обсуждение серьёзных подходов к сглаживанию вроде Kneser-Ney smoothing выходит далеко за рамки этой статьи.
, если бы на эту величину не надо было делить. Здесь на помощь приходит сглаживание (smoothing), которое можно делать разными способами; однако подробное обсуждение серьёзных подходов к сглаживанию вроде Kneser-Ney smoothing выходит далеко за рамки этой статьи.
Обговорим последний тонкий момент перед тем, как перейти к реализации. Постановка задачи, которую я описал выше, подразумевала, что есть одно слово и его надо исправить. Потом мы уточнили, что это одно слово может быть в середине фразы среди каких-то других слов и их тоже нужно учесть, выбирая наилучшее исправление. Но в реальности пользователи просто присылают нам фразы, не уточняя, какое слово написано с ошибкой; нередко в исправлении нуждается несколько слов или даже все.
Подходов здесь может быть много. Можно, например, учитывать только левый контекст слова в фразе. Тогда, идя по словам слева направо и по мере необходимости исправляя их, мы получим новую фразу какого-то качества. Качество будет низким, если, например, первое слово оказалось похоже на несколько популярных слов и мы выберем неправильный вариант. Вся оставшаяся фраза (возможно, изначально вообще безошибочная) будет подстраиваться нами под неправильное первое слово и мы можем получить на выходе полностью нерелевантный оригиналу текст.
Можно рассматривать слова по отдельности и применять некий классификатор, чтобы понимать, опечатано данное слово или нет, как это предложено в [4]. Классификатор обучается на вероятностях, которые мы уже умеем считать, и ряде других фичей. Если классификатор говорит, что нужно исправлять — исправляем, учитывая имеющийся контекст. Опять-таки, если несколько слов написаны с ошибкой, принимать решение насчёт первого из них придётся, опираясь на контекст с ошибками, что может приводить к проблемам с качеством.
В реализации нашего опечаточника мы использовали такой подход. Давайте для каждого слова в нашей фразе найдём с помощью модели ошибок топ-N словарных слов, которые могли иметься в виду, сконкатенируем их во фразы всевозможными способами и для каждой из
в нашей фразе найдём с помощью модели ошибок топ-N словарных слов, которые могли иметься в виду, сконкатенируем их во фразы всевозможными способами и для каждой из  получившихся фраз, где
получившихся фраз, где  — количество слов в исходной фразе, посчитаем честно величину
— количество слов в исходной фразе, посчитаем честно величину
Здесь — слова, введённые пользователем,
— слова, введённые пользователем,  — подобранные для них исправления (которые мы сейчас перебираем), а
— подобранные для них исправления (которые мы сейчас перебираем), а  — коэффициент, определяемый сравнительным качеством модели ошибок и модели языка (большой коэффициент — больше доверяем модели языка, маленький коэффициент — больше доверяем модели ошибок), предложенный в [4]. Итого для каждой фразы мы перемножаем вероятности отдельных слов исправиться в соответствующие словарные варианты и ещё домножаем это на вероятность всей фразы в нашем языке. Результат работы алгоритма — фраза из словарных слов, максимизирующая эту величину.
— коэффициент, определяемый сравнительным качеством модели ошибок и модели языка (большой коэффициент — больше доверяем модели языка, маленький коэффициент — больше доверяем модели ошибок), предложенный в [4]. Итого для каждой фразы мы перемножаем вероятности отдельных слов исправиться в соответствующие словарные варианты и ещё домножаем это на вероятность всей фразы в нашем языке. Результат работы алгоритма — фраза из словарных слов, максимизирующая эту величину.
Так, стоп, что? Перебор фраз?
фраз?
К счастью, за счёт того, что мы ограничили длину n-грамм, найти максимум по всем фразам можно гораздо быстрее. Вспомните: выше мы упростили формулу для так, что она стала зависеть только от частот n-грамм длины не выше трёх:
так, что она стала зависеть только от частот n-грамм длины не выше трёх:
Если мы домножим эту величину на и попытаемся максимизировать по
и попытаемся максимизировать по  , мы увидим, что достаточно перебрать всевозможные
, мы увидим, что достаточно перебрать всевозможные  и
и  и решить задачу для них — то есть для фраз
и решить задачу для них — то есть для фраз  . Итого задача решается динамическим программированием за
. Итого задача решается динамическим программированием за  .
.
Сразу оговорюсь: данных в моём распоряжении было не так много, чтобы заводить какой-то сложный MapReduce. Так что я просто собрал все тексты отзывов, комментариев и поисковых запросов на русском языке (описания товаров, увы, приходят на английском, а использование результатов автоперевода скорее ухудшило, чем улучшило результаты) с нашего сервиса в один текстовый файл и поставил сервер на ночь считать триграммы простым скриптом на Python.
В качестве словарных я брал топ слов по частотности так, чтобы получалось порядка ста тысяч слов. Исключались слишком длинные слова (больше 20 символов) и слишком короткие (меньше трёх символов, кроме захардкоженных известных русских слов). Отдельно пощадил слова по регулярке
При подсчёте биграмм и триграмм во фразе может встретиться несловарное слово. В этом случае это слово я выбрасывал и бил всю фразу на две части (до и после этого слова), с которыми работал отдельно. Так, для фразы «А вы знаете, что такое «абырвалг»? Это… ГЛАВРЫБА, коллега» учтутся триграммы “а вы знаете”, “вы знаете что”, “знаете что такое” и “это главрыба коллега” (если, конечно, слово “главрыба” попадёт в словарь...).
Дальше всю обработку данных я проводил в Jupyter. Статистика по n-граммам грузится из JSON, производится постобработка, чтобы быстро находить близкие друг к другу по Левенштейну слова, и для пар в цикле вызывается (довольно громоздкая) функция, выстраивающая слова и извлекающая короткие правки вида сс → с (под спойлером).
Сам подсчёт правок выглядит элементарно, хотя длиться может долго.
Эта часть реализована в виде микросервиса на Go, связанного с основным бэкендом через gRPC. Реализован алгоритм, описанный самими Бриллом и Муром [2], с небольшими оптимизациями. Работает он у меня в итоге примерно вдвое медленнее, чем заявляли авторы; не берусь судить, дело в Go или во мне. Но по ходу профилировки я узнал о Go немного нового.
Здесь без особых сюрпризов был реализован алгоритм динамического программирования, описанный в разделе выше. На этот компонент пришлось меньше всего работы — самой медленной частью остаётся применение модели ошибок. Поэтому между этими двумя слоями было дополнительно прикручено кэширование результатов модели ошибок в Redis.
По итогам этой работы (занявшей примерно человекомесяц) мы провели A/B тест опечаточника на наших пользователях. Вместо 10% пустых выдач среди всех поисковых запросов, которые мы имели до внедрения опечаточника, их стало 5%; в основном оставшиеся запросы приходятся на товары, которых просто нет у нас на платформе. Также увеличилось количество сессий без второго поискового запроса (и ещё несколько метрик такого рода, связанных с UX). Метрики, связанные с деньгами, впрочем, значимо не изменились — это было неожиданно и сподвигло нас к тщательному анализу и перепроверке других метрик.
Стивену Хокингу как-то сказали, что каждая включенная им в книгу формула вдвое уменьшит число читателей. Что ж, в этой статье их порядка полусотни — поздравляю тебя, один из примерно читателей, добравшихся до этого места!
читателей, добравшихся до этого места!
[1] M. D. Kernighan, K. W. Church, W. A. Gale. A Spelling Correction Program Based on a Noisy Channel Model. Proceedings of the 13th conference on Computational linguistics — Volume 2, 1990.
[2] E.Brill, R. C. Moore. An Improved Error Model for Noisy Channel Spelling Correction. Proceedings of the 38th Annual Meeting on Association for Computational Linguistics, 2000.
[3] T. Brants, A. C. Popat, P. Xu, F. J. Och, J. Dean. Large Language Models in Machine Translation. Proceedings of the 2007 Conference on Empirical Methods in Natural Language Processing.
[4] C. Whitelaw, B. Hutchinson, G. Y. Chung, G. Ellis. Using the Web for Language Independent Spellchecking and Autocorrection. Proceedings of the 2009 Conference on Empirical Methods in Natural Language Processing: Volume 2.
При этом каждый сервис обладает своей спецификой, своим лексиконом, которым должен уметь оперировать исправитель опечаток, что в значительной мере затрудняет применение уже существующих решений. Например, такие запросы пришлось научиться править нашему опечаточнику:
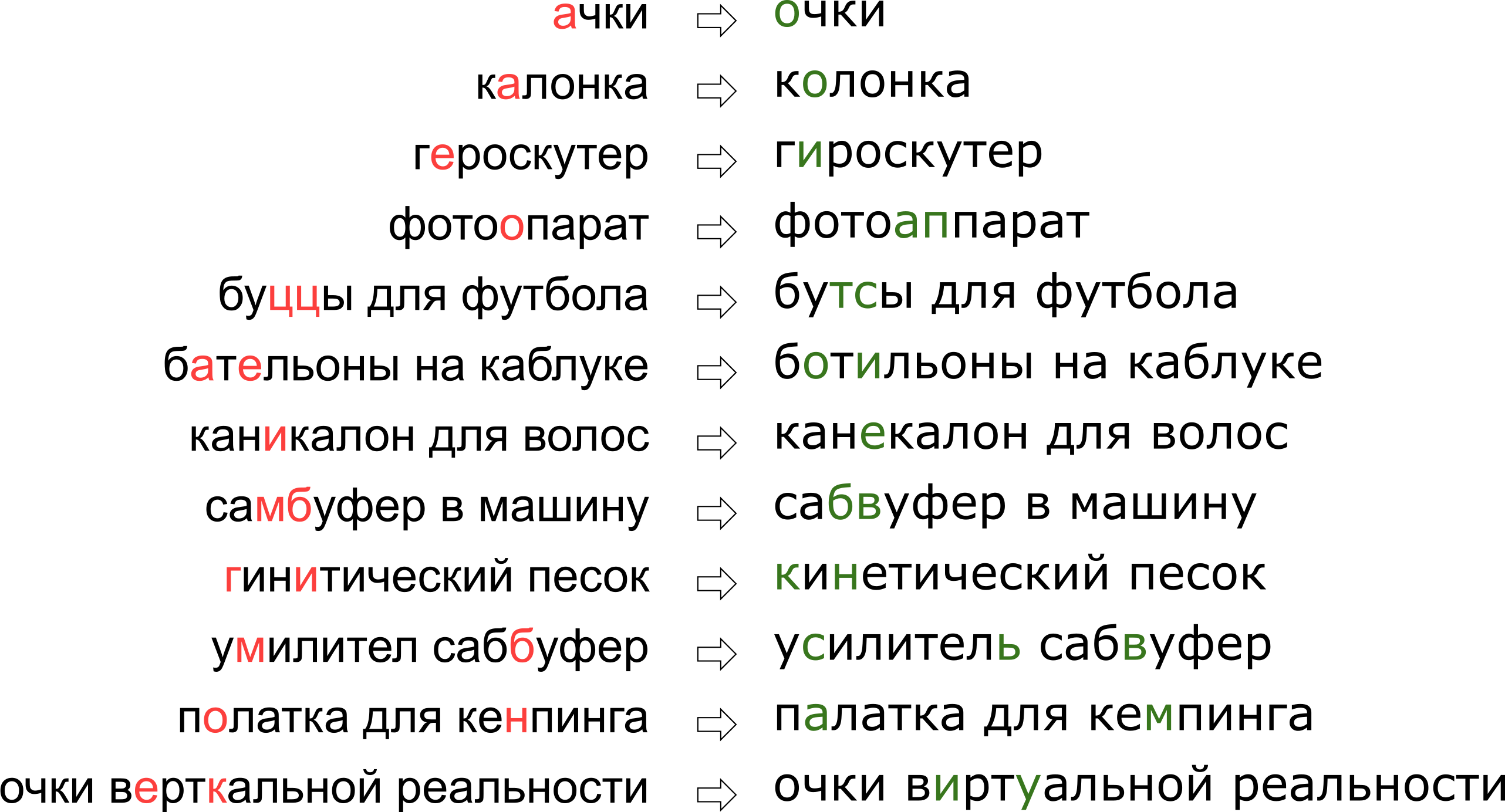
Может показаться, что мы отказали пользователю в его мечте о вертикальной реальности, но на самом деле буква К просто стоит на клавиатуре рядом с буквой У.
В этой статье мы разберём один из классических подходов к исправлению опечаток, от построения модели до написания кода на Python и Go. И в качестве бонуса — видео с моего доклада «”Очки верткальной реальности”: исправляем опечатки в поисковых запросах» на Highload++.
Постановка задачи
Итак, нам пришёл опечатанный запрос и его надо исправить. Обычно математически задача ставится таким образом:
- дано слово
, переданное нам с ошибками;
- есть словарь
правильных слов;
- для всех слов w в словаре есть условные вероятности
того, что имелось в виду слово
, при условии, что получили мы слово
;
- нужно найти слово w из словаря с максимальной вероятностью
.
Эта постановка — самая элементарная — предполагает, что если нам пришёл запрос из нескольких слов, то мы исправляем каждое слово по отдельности. В реальности, конечно, мы захотим исправлять всю фразу целиком, учитывая сочетаемость соседних слов; об этом я расскажу ниже, в разделе “Как исправлять фразы”.
Неясных моментов здесь два — где взять словарь и как посчитать
Второй вопрос сложнее. Хотя бы потому, что его решение обычно начинается с применения формулы Байеса!
Теперь вместо исходной непонятной вероятности нам нужно оценить две новые, чуть более понятные:
Как оценить
Такая модель называется noisy channel model (модель зашумлённого канала; в нашем случае зашумлённый канал начинается где-то в центре Брока пользователя и заканчивается по другую сторону его клавиатуры) или более коротко error model — модель ошибок. Эта модель, которой ниже посвящен отдельный раздел, будет ответственна за учёт как орфографических ошибок, так и, собственно, опечаток.
Оценить вероятность использования слова —
Модель ошибок
Первые модели ошибок считали
В наших изысканиях мы остановились на более развитой модели ошибок, предложенной в 2000 году Бриллом и Муром [2] и многократно использованной впоследствии (например, специалистами Google [4]). Представим, что пользователи мыслят не отдельными символами (спутать Е и И, нажать К вместо У, пропустить мягкий знак), а могут изменять произвольные куски слова на любые другие — например, заменять ТСЯ на ТЬСЯ, У на К, ЩА на ЩЯ, СС на С и так далее. Вероятность того, что пользователь опечатался и вместо ТСЯ написал ТЬСЯ, обозначим
Давайте посмотрим на пример разбиения, возникающего при вычислении вероятности напечатать «аксесуар» вместо «аксессуар»:
Здесь всё сразу стало на свои места, и видно, что итоговая вероятность будет определяться преимущественно величиной
Как вычислить 
Несмотря на то, что возможных разбиений для двух слов имеется порядка
Мы заведём прямоугольную таблицу, строки которой будут соответствовать буквам правильного слова, а столбцы — опечатанного. В ячейке на пересечении строки i и столбца j к концу алгоритма будет лежать в точности вероятность получить
s[:j] при попытке напечатать w[:i]. Для того, чтобы её вычислить, достаточно вычислить значения всех ячеек в предыдущих строках и столбцах и пробежаться по ним, домножая на соответствующие 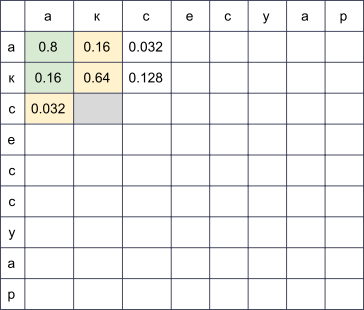
, то для заполнения ячейки в четвёртой строке и третьем столбце (серая) нужно взять максимум из величин
Сложность этого алгоритма, как я уже упомянул выше, составляет
Как максимизировать 
Мы научились находить
Чтобы научиться быстро проходить по всему словарю, заметим, что таблица, представленная выше, будет иметь много общего для двух слов с общими префиксами. Действительно, если мы, исправляя слово «аксесуар», попробуем заполнить её для двух словарных слов «аксессуар» и «аксессуары», мы заметим, что первые девять строк в них вообще не отличаются! Если мы сможем организовать проход по словарю так, что у двух последующих слов будут достаточно длинные общие префиксы, мы сможем круто сэкономить вычисления.
И мы сможем. Давайте возьмём словарные слова и составим из них trie. Идя по нему поиском в глубину, мы получим желаемое свойство: большинство шагов — это шаги от узла к его потомку, когда у таблицы достаточно дозаполнить несколько последних строк.
Этот алгоритм, при некоторых дополнительных оптимизациях, позволяет нам перебирать словарь типичного европейского языка в 50-100 тысяч слов в пределах сотни миллисекунд [2]. А кэширование результатов сделает процесс ещё быстрее.
Как получить 
Вычисление
Подход, использованный в [2, 4], сравнительно прост. Давайте найдём много пар
Для каждой пары возьмём составляющие её
После прохода по всем парам
Как найти пары
Этот алгоритм подбора пар оставляет большое пространство для улучшений. В [4] предлагается только фильтр по встречаемости (
Чтобы повысить качество получаемых пар, я написал несложную функцию, определяющую, используют ли пользователи два слова как синонимы. Логика простая: если слова w и s часто встречаются в окружении одних и тех же слов, то они, вероятно, синонимы — что в свете их близости по Левенштейну значит, что менее популярное слово с большой вероятностью является ошибочной версией более популярного. Для этих расчётов я использовал построенную для модели языка ниже статистику встречаемости триграмм (фраз из трёх слов).
Модель языка
Итак, теперь для заданного словарного слова w нам нужно вычислить
Чтобы научиться учитывать их, стоит пройтись по корпусу ещё раз и составить статистику n-грамм, последовательностей слов. Обычно берут последовательности ограниченной длины; я ограничился триграммами, чтобы не раздувать индекс, но тут всё зависит от вашей силы духа (и размера корпуса — на маленьком корпусе даже статистика по триграммам будет слишком шумной).
Традиционная модель языка на основе n-грамм выглядит так. Для фразы
где
Иными словами, если мы захотим вычислить
Логично? Логично. Однако трудности начинаются, когда фразы становятся длиннее. Что, если пользователь ввёл впечатляющий своей подробностью поисковый запрос в десять слов? Мы не хотим держать статистику по всем 10-граммам — это дорого, а данные, скорее всего, будут шумными и не показательными. Мы хотим обойтись n-граммами какой-то ограниченной длины — например, уже предложенной выше длины 3.
Здесь-то и пригождается формула выше. Давайте предположим, что на вероятность слова появиться в конце фразы значительно влияют только несколько слов непосредственно перед ним, то есть что
Положив
Обратите внимание: фраза состоит из пяти слов, но в формуле фигурируют n-граммы не длиннее трёх. Это как раз то, чего мы добивались.
Остался один тонкий момент. Что, если пользователь ввёл совсем странную фразу и соответствующих n-грамм у нас в статистике и нет вовсе? Было бы легко для незнакомых n-грамм положить
Как исправлять фразы
Обговорим последний тонкий момент перед тем, как перейти к реализации. Постановка задачи, которую я описал выше, подразумевала, что есть одно слово и его надо исправить. Потом мы уточнили, что это одно слово может быть в середине фразы среди каких-то других слов и их тоже нужно учесть, выбирая наилучшее исправление. Но в реальности пользователи просто присылают нам фразы, не уточняя, какое слово написано с ошибкой; нередко в исправлении нуждается несколько слов или даже все.
Подходов здесь может быть много. Можно, например, учитывать только левый контекст слова в фразе. Тогда, идя по словам слева направо и по мере необходимости исправляя их, мы получим новую фразу какого-то качества. Качество будет низким, если, например, первое слово оказалось похоже на несколько популярных слов и мы выберем неправильный вариант. Вся оставшаяся фраза (возможно, изначально вообще безошибочная) будет подстраиваться нами под неправильное первое слово и мы можем получить на выходе полностью нерелевантный оригиналу текст.
Можно рассматривать слова по отдельности и применять некий классификатор, чтобы понимать, опечатано данное слово или нет, как это предложено в [4]. Классификатор обучается на вероятностях, которые мы уже умеем считать, и ряде других фичей. Если классификатор говорит, что нужно исправлять — исправляем, учитывая имеющийся контекст. Опять-таки, если несколько слов написаны с ошибкой, принимать решение насчёт первого из них придётся, опираясь на контекст с ошибками, что может приводить к проблемам с качеством.
В реализации нашего опечаточника мы использовали такой подход. Давайте для каждого слова
Здесь
Так, стоп, что? Перебор
К счастью, за счёт того, что мы ограничили длину n-грамм, найти максимум по всем фразам можно гораздо быстрее. Вспомните: выше мы упростили формулу для
Если мы домножим эту величину на
Реализация
Собираем корпус и считаем n-граммы
Сразу оговорюсь: данных в моём распоряжении было не так много, чтобы заводить какой-то сложный MapReduce. Так что я просто собрал все тексты отзывов, комментариев и поисковых запросов на русском языке (описания товаров, увы, приходят на английском, а использование результатов автоперевода скорее ухудшило, чем улучшило результаты) с нашего сервиса в один текстовый файл и поставил сервер на ночь считать триграммы простым скриптом на Python.
В качестве словарных я брал топ слов по частотности так, чтобы получалось порядка ста тысяч слов. Исключались слишком длинные слова (больше 20 символов) и слишком короткие (меньше трёх символов, кроме захардкоженных известных русских слов). Отдельно пощадил слова по регулярке
r"^[a-z0-9]{2}$" — чтобы уцелели версии айфонов и другие интересные идентификаторы длины 2.При подсчёте биграмм и триграмм во фразе может встретиться несловарное слово. В этом случае это слово я выбрасывал и бил всю фразу на две части (до и после этого слова), с которыми работал отдельно. Так, для фразы «А вы знаете, что такое «абырвалг»? Это… ГЛАВРЫБА, коллега» учтутся триграммы “а вы знаете”, “вы знаете что”, “знаете что такое” и “это главрыба коллега” (если, конечно, слово “главрыба” попадёт в словарь...).
Обучаем модель ошибок
Дальше всю обработку данных я проводил в Jupyter. Статистика по n-граммам грузится из JSON, производится постобработка, чтобы быстро находить близкие друг к другу по Левенштейну слова, и для пар в цикле вызывается (довольно громоздкая) функция, выстраивающая слова и извлекающая короткие правки вида сс → с (под спойлером).
Код на Python
def generate_modifications(intended_word, misspelled_word, max_l=2):
# Выстраиваем буквы слов оптимальным по Левенштейну образом и
# извлекаем модификации ограниченной длины. Чтобы после подсчёта
# расстояния восстановить оптимальное расположение букв, будем
# хранить в таблице помимо расстояний указатели на предыдущие
# ячейки: memo будет хранить соответствие
# i -> j -> (distance, prev i, prev j).
# Дальше немного непривычно страшного Python кода - вот что
# бывает, когда язык используется не по назначению!
m, n = len(intended_word), len(misspelled_word)
memo = [[None] * (n+1) for _ in range(m+1)]
memo[0] = [(j, (0 if j > 0 else -1), j-1) for j in range(n+1)]
for i in range(m + 1):
memo[i][0] = i, i-1, (0 if i > 0 else -1)
for j in range(1, n + 1):
for i in range(1, m + 1):
if intended_word[i-1] == misspelled_word[j-1]:
memo[i][j] = memo[i-1][j-1][0], i-1, j-1
else:
best = min(
(memo[i-1][j][0], i-1, j),
(memo[i][j-1][0], i, j-1),
(memo[i-1][j-1][0], i-1, j-1),
)
# Отдельная обработка для перепутанных местами
# соседних букв (распространённая ошибка при
# печати).
if (i > 1
and j > 1
and intended_word[i-1] == misspelled_word[j-2]
and intended_word[i-2] == misspelled_word[j-1]
):
best = min(best, (memo[i-2][j-2][0], i-2, j-2))
memo[i][j] = 1 + best[0], best[1], best[2]
# К концу цикла расстояние по Левенштейну между исходными словами # хранится в memo[m][n][0].
# Теперь восстанавливаем оптимальное расположение букв.
s, t = [], []
i, j = m, n
while i >= 1 or j >= 1:
_, pi, pj = memo[i][j]
di, dj = i - pi, j - pj
if di == dj == 1:
s.append(intended_word[i-1])
t.append(misspelled_word[j-1])
if di == dj == 2:
s.append(intended_word[i-1])
s.append(intended_word[i-2])
t.append(misspelled_word[j-1])
t.append(misspelled_word[j-2])
if 1 == di > dj == 0:
s.append(intended_word[i-1])
t.append("")
if 1 == dj > di == 0:
s.append("")
t.append(misspelled_word[j-1])
i, j = pi, pj
s.reverse()
t.reverse()
# Генерируем модификации длины не выше заданной.
for i, _ in enumerate(s):
ss = ts = ""
while len(ss) < max_l and i < len(s):
ss += s[i]
ts += t[i]
yield ss, ts
i += 1Сам подсчёт правок выглядит элементарно, хотя длиться может долго.
Применяем модель ошибок
Эта часть реализована в виде микросервиса на Go, связанного с основным бэкендом через gRPC. Реализован алгоритм, описанный самими Бриллом и Муром [2], с небольшими оптимизациями. Работает он у меня в итоге примерно вдвое медленнее, чем заявляли авторы; не берусь судить, дело в Go или во мне. Но по ходу профилировки я узнал о Go немного нового.
- Не используйте
math.Max, чтобы считать максимум. Это примерно в три раза медленнее, чемif a > b { b = a }! Только взгляните на реализацию этой функции:
// Max returns the larger of x or y. // // Special cases are: // Max(x, +Inf) = Max(+Inf, x) = +Inf // Max(x, NaN) = Max(NaN, x) = NaN // Max(+0, ±0) = Max(±0, +0) = +0 // Max(-0, -0) = -0 func Max(x, y float64) float64 func max(x, y float64) float64 { // special cases switch { case IsInf(x, 1) || IsInf(y, 1): return Inf(1) case IsNaN(x) || IsNaN(y): return NaN() case x == 0 && x == y: if Signbit(x) { return y } return x } if x > y { return x } return y }
Если только вам ВДРУГ не нужно, чтобы +0 обязательно был больше -0, не используйтеmath.Max.
- Не используйте хэш-таблицу, если можете использовать массив. Это, конечно, довольно очевидный совет. Мне пришлось перенумеровывать символы юникода в числа в начале программы так, чтобы использовать их как индексы в массиве потомков узла trie (такой lookup был очень частой операцией).
- Коллбеки в Go недёшевы. В ходе рефакторинга во время код ревью некоторые мои потуги сделать decoupling ощутимо замедлили программу при том, что формально алгоритм не изменился. С тех пор я остаюсь при мнении, что оптимизирующему компилятору Go есть, куда расти.
Применяем модель языка
Здесь без особых сюрпризов был реализован алгоритм динамического программирования, описанный в разделе выше. На этот компонент пришлось меньше всего работы — самой медленной частью остаётся применение модели ошибок. Поэтому между этими двумя слоями было дополнительно прикручено кэширование результатов модели ошибок в Redis.
Результаты
По итогам этой работы (занявшей примерно человекомесяц) мы провели A/B тест опечаточника на наших пользователях. Вместо 10% пустых выдач среди всех поисковых запросов, которые мы имели до внедрения опечаточника, их стало 5%; в основном оставшиеся запросы приходятся на товары, которых просто нет у нас на платформе. Также увеличилось количество сессий без второго поискового запроса (и ещё несколько метрик такого рода, связанных с UX). Метрики, связанные с деньгами, впрочем, значимо не изменились — это было неожиданно и сподвигло нас к тщательному анализу и перепроверке других метрик.
Заключение
Стивену Хокингу как-то сказали, что каждая включенная им в книгу формула вдвое уменьшит число читателей. Что ж, в этой статье их порядка полусотни — поздравляю тебя, один из примерно
Бонус
Ссылки
[1] M. D. Kernighan, K. W. Church, W. A. Gale. A Spelling Correction Program Based on a Noisy Channel Model. Proceedings of the 13th conference on Computational linguistics — Volume 2, 1990.
[2] E.Brill, R. C. Moore. An Improved Error Model for Noisy Channel Spelling Correction. Proceedings of the 38th Annual Meeting on Association for Computational Linguistics, 2000.
[3] T. Brants, A. C. Popat, P. Xu, F. J. Och, J. Dean. Large Language Models in Machine Translation. Proceedings of the 2007 Conference on Empirical Methods in Natural Language Processing.
[4] C. Whitelaw, B. Hutchinson, G. Y. Chung, G. Ellis. Using the Web for Language Independent Spellchecking and Autocorrection. Proceedings of the 2009 Conference on Empirical Methods in Natural Language Processing: Volume 2.