itmai Dec 18 2020 at 16:53

3D ML. Часть 5: Свертки на графах

13 min

6.9K

IT-центр МАИ corporate blogPython*Working with 3D-graphics*Artificial Intelligence

Tutorial

В предыдущих заметках данной серии мы уже успели поговорить о датасетах и инструментах, функциях потерь и примерах прикладных задач, а сейчас пора перейти к “ядру” любой подобласти глубокого обучения — к их архитектурам. Но, прежде чем разбираться с тем как устроены целые архитектуры, стоит разобраться в их составных частях, делающих их пригодными для применения к неевклидовым данным.

Наверное вы уже догадались, что речь сегодня пойдет о сверточных операторах на графах.

Серия 3D ML на Хабре:

Репозиторий на GitHub для данной серии заметок.

Заметка от партнера IT-центра МАИ и организатора магистерской программы “VR/AR & AI” — компании PHYGITALISM.

Откуда брать информацию и на чем практиковаться?

Про графы, свертки и машинное обучение по отдельности сказано и написано многое. Если рассматривать эти три темы в одной, то список источников сокращается, однако, у неподготовленного исследователя, который решил разобраться в данном вопросе, скорее всего, не возникнет четкого понимания куда смотреть и с чего начать.

Здесь стоит отметить, что свертки на графах можно рассматривать как в общем виде, не привязываясь к конкретной предметной области, так и учитывать особенности данных с которыми вы работаете.

С наиболее общего ракурса, тема сверток на графах хорошо освещена в обзорной статье “Representation Learning on Graphs: Methods and Applications” [1]. Методам машинного обучения на графах посвящены целые университетские спецкурсы, наиболее известным из которых является Stanford CS224W: Machine Learning with Graphs. По мотивам этого курса есть разбор от русскоязычного сообщества исследователей Sberloga, в котором есть записи обсуждения лекций, примеры кода, разбор разных аспектов теории и практики и многое другое. Также стоит отметить вот эту статью с хабра от ODS, в которой упоминается о схожем сообществе для разбора стенфордского курса и заодно изложены несколько основных подходов к получению скрытых представлений графов (т.н. эмбеддинги).

В более сжатом виде есть несколько серий заметок на эту тему на Medium:

How to do Deep Learning on Graphs with Graph Convolutional Networks от Tobias Skovgaard Jepsen;
Вводная теоретико-практическая заметка A Gentle Introduction to Graph Neural Networks (Basics, DeepWalk, and GraphSage) и практико-ориентированная заметка Hands-on Graph Neural Networks with PyTorch & PyTorch Geometric от Kung-Hsiang, Huang (Steeve);
Курс по основам машинного обучения от Jan H. Jensen с точки зрения приложения к химии (здесь графы моделируют молекулярные структуры);
Серия заметок на Medium от Бориса Князева — взгляд на обработку графов методами машинного обучения с точки зрения компьютерного зрения.

Для области 3D ML методы и алгоритмы, основанные на извлечении информации из графовых структур, являются важным подспорьем. Объекты интереса — это зачастую полигональный меш, который сам по себе является пространственным графом (см. например работу [15]), или облако точек, которое также можно мыслить как графовую структуру, если соединять между собою точки в облаке по определенным правилам (см. например работу [14]). Про различные виды сверток на графах, применительно к задачам 3D ML, можно прочитать в нашем обзоре про алгоритмы семантической сегментации облака точек.

С точки зрения инструментов, в основном исследователи в данной области пользуются либо собственноручно написанными библиотеками, либо библиотеками, которые первоначально предназначались для работы с графами в предметной области (например библиотека python rdkit или python NetworkX). На наш взгляд, наиболее удобной библиотекой для построения собственных глубоких архитектур на основе графовых сверток является PyTorch Geometric (на странице с документацией можно найти различные примеры графовых датасетов, методов их обработки и загрузки, и различных сверточных слоев). В репозитории библиотеки TensorFlow Graphics также можно найти пример “Semantic mesh segmentation”, в котором, с помощью встроенных в библиотеку сверточных операторов, конструируют небольшую глубокую архитектуру для решения задачи семантической сегментации меша. Рекомендуем всем начинающим 3D ML исследователям самостоятельно разобрать описанные выше примеры.

Ниже, в основном повторяя данный туториал Бориса Князева из пункта 4, мы постараемся разобраться в том как устроены свертки на графах на базовом уровне, чем они отличаются от сверток на изображениях.

Граф как неевклидова структура

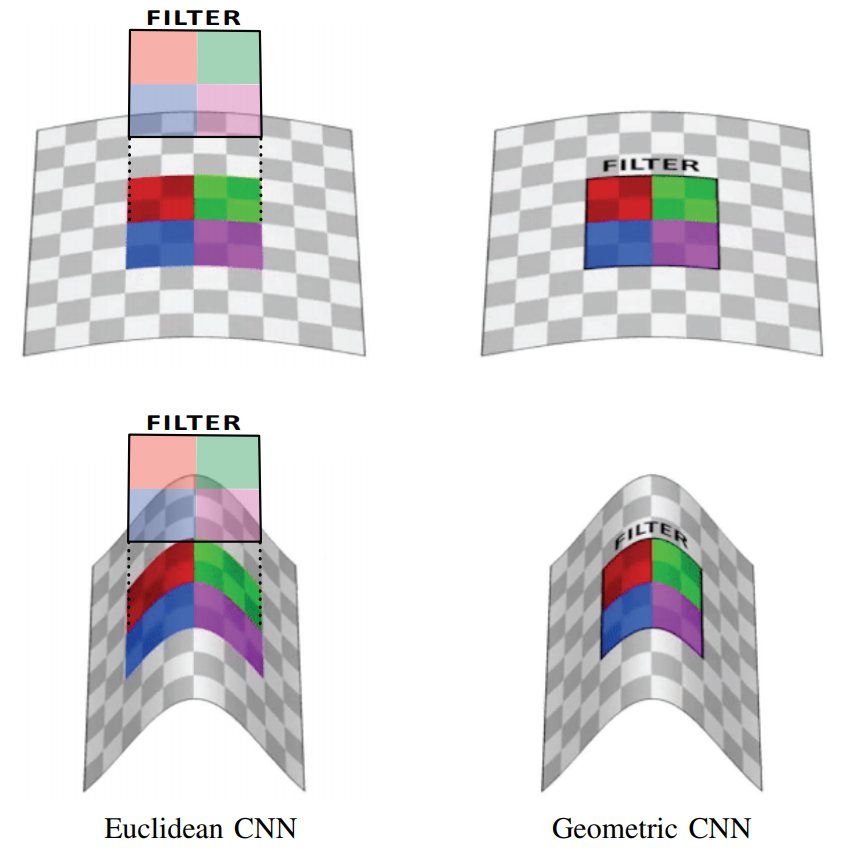
Рис.1 Пример из статьи [2]: левые изображения демонстрируют, что стандартная свертка (Euclidean CNN) будет по разному обрабатывать данные в зависимости от типа поверхности к которой ее применяют, что, в свою очередь, мотивирует к созданию геометрических сверток (Geometric CNN, правые изображения).

Свертка — замечательный инструмент, позволяющий “аккумулировать” информацию о близлежащих (локальных) частях в данных. В случае с изображениями, мы естественным образом предполагаем, что соседние пиксели скорее всего связаны семантически (являются частью одного объекта). Поскольку одна и та же свертка применяется ко всем пикселям изображения, оператор, основанный на ней, становится независим к размеру изображения и занимает меньше памяти. Исходя из этого соображения, становится несложно понять, почему сверточные сети стали так популярны для обработки изображений.

Более формально, общие свойства евклидовых и неевклидовых данных были описаны в обзорной статье “Geometric deep learning: going beyond Euclidean data” [2] (всем познающим 3D ML, на наш взгляд, обязательно к ознакомлению).

Кратко перечислим свойства евклидовых данных:

Инвариантность к сдвигу (shift-invariance): если на изображении объект интереса (например, автомобиль) будет не в верхней левой части, а в правой нижней, то сверточный фильтр все равно сможет определить местоположение автомобиля. Чуть более формально: это свойство данных позволяет применять один и тот же оператор на всех частях данных.
Локализованность данных (locality): группа близлежащих частей данных скорее всего отвечает за определенный объект (в случае автомобиля это может быть группа пикселей, отвечающих за колесо или номер автомобиля). Формально, это позволяет нам применять относительно небольшого размера свертки, для того чтобы локализовать на изображениях объект интереса.
Иерархичность данных (compositionality or hierarchy): крупномасштабные и мелкомасштабные структуры внутри одного объекта данных, скорее всего, семантически связаны отношением “является составной частью” (для автомобиля группа пикселей определяющая автомобиль, состоит из более мелких групп определяющих составные части автомобиля: фары, капот, колеса и т.д.).

Для графов эти свойства обычно не выполняются. Наша задача — научиться конструировать такой же удобный как классические свертки инструмент для неевклидовых структур данных (в нашем случае для графов).

Для того, чтобы лучше понять идею стоящую за такой конструкцией, попытаемся взглянуть на изображения (евклидова структура) как на графы (неевклидова структура).

Рис.2 Слева: изображение из датасета MNIST; справа: граф построенный по пикселям данного изображения. (см. работу [3]).

Структуру изображения, являющуюся многомерным массивом, у которого для каждого пикселя определены два соседа вдоль каждого измерения, можно представить в виде регулярной узловой решетки, как на изображении ниже. Для подобных визуализаций используется библиотека python NetworkX. На хабре есть хорошая вводная статья в этот фреймворк.

Как создать граф на изображении ниже:

import networkx as nx

G = nx.grid_graph([4, 4])
nx.draw(G)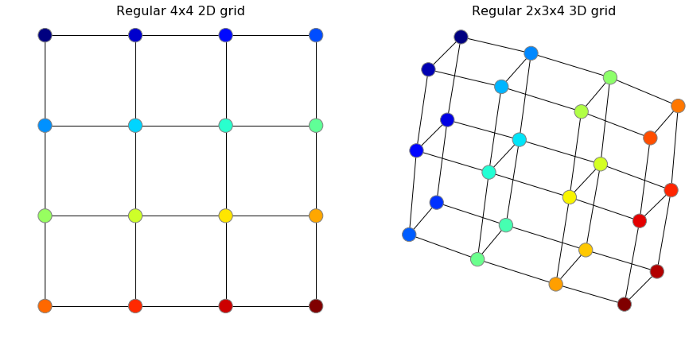

Теперь попробуем применить стандартные свертки для таких регулярных сетей и попытаемся понять, почему такой подход сложно обобщить на графы произвольной структуры.

В качестве примера можно рассмотреть свертку, определяемую матрицей $W_{3 \times 3}$ . Пусть в узлах нашей решетки хранятся некоторые числовые значения, например, интенсивность цвета пикселя записанные в матрицу — $X_{ij}$ . Применение свертки обычно выражено в виде скалярного произведения (dot product) матрицы фильтра на матрицу значений в узлах сетки (это может быть подграф всей сети), совпадающую по размерам с фильтром (см. рисунок ниже). Хороший и подробный туториал по применению сверток к изображениям содержится в статье “A guide to convolution arithmetic for deep learning” [4].

Обратим внимание, что каждому узлу фильтра всегда найдется узел в данных, к какой бы точке данных мы не прикладывали этот фильтр. Для графов общего вида это утверждение не верно, что, соответственно, создает нам проблемы, если мы попытаемся применить данный фильтр к ним.

Операторы, вроде скалярного произведения, рассмотренного выше, относят к классу агрегирующих функций — методов сохранения информации о многих объектах в одном (в данном случае, результатом свертки является одно число, полученное из 9 исходных). Другим способом агрегировать информацию является использование т.н. pooling операций в сверточных сетях. Здесь важно заметить, что такие операции инвариантны к перестановке пикселей, в отличие от скалярного произведения рассмотренного выше, поскольку в общем случае

$X_1 W_1 + X_2 W_2 \ne X_2 W_1 + X_1 W_2$

Кстати, рассмотрение изображений как регулярных графовых сетей приводит к интересному результату. Мы можем рассматривать иное разбиение изображения на составные части нежели исходные пиксели, например каким-либо способом объединять группы пикселей в т.н. “суперпиксели” и строить свертки нерегулярной структуры над ними. Про такой подход к обработке изображений можно прочитать в данной заметке.

Рис.3 Пример построение суперпикселей разного разрешения на изображении из работы [5].

Теперь попробуем обобщить свертки на нерегулярные графы. Здесь мы столкнемся со следующей проблемой: граф в общем виде — совокупность двух множеств (вершины — $inline$ , и связи между этими вершинами — $inline$ ), а множества — инвариантный к перестановке элементов тип данных. Это значит, что мы можем случайным образом перемешать вершины графа (с учетом соответствующего перемешивания связей) и при этом сам граф останется прежним, но как было отмечено выше — свертка зависит от порядка элементов.

Поскольку не существует какой-то канонической расстановки вершин произвольного графа, требуется определить операцию свертки так, чтобы она не зависела от этой расстановки. Наиболее популярные способы определить свертку на графе — использование операторов на основе усреднения (averaging) [6] или суммирования (summation) [7] по всем соседям рассматриваемой вершины, с последующим умножением на матрицу весов $inline$ . Таким образом, мы агрегируем всех соседей вместе с самой вершиной и проецируем граф через свертку в пространство другой размерности. Про различные виды агрегирующих операторов на графах можно прочитать в статье [8].

Рассмотрим для лучшего понимания граф состоящий из 5 вершин на изображении ниже (рис.4). Применяя агрегирующий оператор на основе суммирования для вершины $inline$ получим новое значение признака этой вершины:

$display$

Таким образом, после применения оператора агрегирования, исходный граф сохраняет свою структуру, но в вершинах хранятся признаки с агрегированной информацией о соседях и теперь можно использовать матрицу признаков в вершинах графа для дальнейшей работы вне зависимости от того, как вершины исходно были пронумерованы.

Рис.4 Пример нерегулярных графов и схематичное изображение соседей рассматриваемых вершин $inline$ .

Поскольку рассмотренные выше агрегирующие операторы применяются ко всем вершинам графа и позволяют собрать информацию о соседях в одном месте их называют “свертками” на графе. Однако, сконструированные таким образом свертки никак не учитывают топологию графа. Попробуем разобраться, как можно улучшить эти операторы с учетом топологического фактора.

Конструируем сверточный слой для графов

Сначала вспомним, как конструируется полносвязный слой в классической полносвязной архитектуре (В качестве примера будем держать в голове классификацию рукописных цифр из MNIST). Пусть $X^{(l)}$ — вектор значений на $inline$ -ом слое, $W^{(l)}$ — матрица весов $inline$ -го слоя. Тогда линейный полносвязный линейный слой может быть записан в виде:

$X^{(l+1)} = X^{(l)} W^{(l)}.$

После матричного умножения, в глубоком обучении принято налагать нелинейность (активационная функция нейрона), однако, если мы говорим о MNIST данных, оказывается можно обойтись только линейной частью и добиться доли правильных ответов на тестовой выборке в 91% (здесь есть пример реализации такой сети).

Теперь давайте попробуем ввести в эту формулу множитель, который описывал бы топологию данных (в нашем случаи — графа). Для этого мы будем использовать матрицу смежности — $inline$ . Ниже приведен пример неориентированного графа и его матрицы смежности. Обратите внимание, что различные варианты нумерации вершин графа приводят к различным матрицам смежности.

Рис.5 Неориентированный граф из 5 вершин и его матрица смежности (голубой цвет — 0, желтый — 1) для двух вариантов нумерации вершин графа.

Давайте определим матрицу смежности для регулярной сети, соответствующей растровому изображению размера $28 \times 28$ в примере с MNIST. Для этого этого воспользуемся стандартными приемами из numpy:

import numpy as np
from scipy.spatial.distance import cdist
img_size = 28  # MNIST image width and height
col, row = np.meshgrid(np.arange(img_size), np.arange(img_size))
coord = np.stack((col, row), axis=2).reshape(-1, 2) / img_size
dist = cdist(coord, coord)  # рис. 6 (левое изображение)
sigma = 0.2 * np.pi  # width of a Gaussian
A = np.exp(-dist ** 2 / sigma ** 2) # рис.6 (изображение в центре)

В данном случае, матрица dist — матрица смежности для полносвязного графа с $inline$ вершинами, матрица $inline$ — матрица смежности с учетом пространственной близости (здесь используется эвристическое соображение о том, что близлежащие пиксели должны сильнее коррелировать друг с другом чем те, что лежат на расстоянии). Этот способ определять матрицы смежности для задач, связанных с обработкой изображений, — популярный, но далеко не единственный (см. альтернативы в работах [2, 9]).

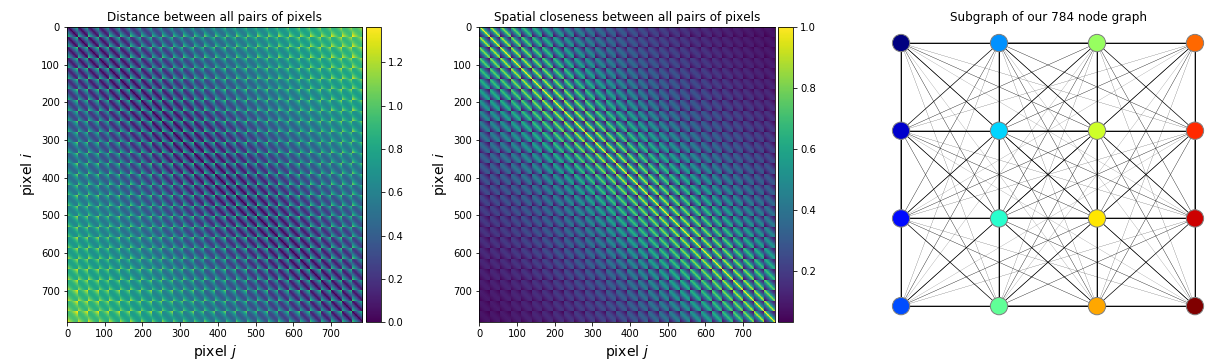
Рис.6 Слева-направо: матрица смежности в форме расстояний между пикселями, матрица смежности в форме пространственной близости, подграф полносвязного графа рассматриваемого изображения $28 \times 28$ .

Теперь, на основе матрицы смежности $inline$ , мы сможем сконструировать т.н. нормированную матрицу смежности $\mathcal{A}$ . Ее можно сконструировать разными способами, но два наиболее популярных подхода следующие:

$\mathcal{A} = A$ и тогда матричное умножение $\mathcal{A} X^{(l)}$ эквивалентно суммированию признаков по соседним вершинам [7];
$\mathcal{A} = \frac{A}{\|A\|}$ и тогда матричное умножение $\mathcal{A} X^{(l)}$ эквивалентно усреднению признаков по соседним вершинам [6].

В итоге, после выбора способа нормализации матрицы смежности, мы сможем сконструировать линейный полносвязный слой вида:

$X^{(l+1)} = \mathcal{A} X^{(l)} W^{(l)}.$

Если к результату матричного умножения в правой части применить нелинейную функции активации, то мы сконструируем нелинейный полносвязный слой.

Можно написать достаточно простой код на основе операторов PyTorch, чтобы увидеть разницу в реализации обычного полносвязного слоя и полносвязного слоя с графовой сверткой:

import torch
import torch.nn as nn

C = 2  # Input feature dimensionality
F = 8  # Output feature dimensionality
W = nn.Linear(in_features=C, out_features=F)  # Trainable weights

# Fully connected layer
X = torch.randn(1, C)  # Input features
Z = W(X)  # Output features : torch.Size([1, 8])

#Graph Neural Network layer
N = 6  # Number of nodes in a graph
X = torch.randn(N, C)  # Input feature
A = torch.rand(N, N)  # Adjacency matrix (edges of a graph)
Z = W(torch.mm(A, X))  # Output features: torch.Size([6, 8])

Полный код для данного примера можно найти в оригинальном репозитории здесь. Кстати, если вы попытаетесь сравнить качество обучения на MNIST для обычной и для графовой модели, вы обнаружите, что качество отличается несущественно. Это происходит по той причине, что для данного конкретного датасета, связи между пикселями в рукописных цифрах и так очень сильны, но что более важно, оператор $\mathcal{A} X^{(l)}$ здесь есть не что иное, как Гауссовский фильтр, поэтому такая архитектура графовой сети приводит фактически к тому, что у нас есть обычная сверточная нейронная сеть с фиксированным Гауссовским фильтром. Чтобы сверточная архитектура на регулярных графах работала лучше, можно применить ряд трюков, которые описаны в работах [10, 11, 12].

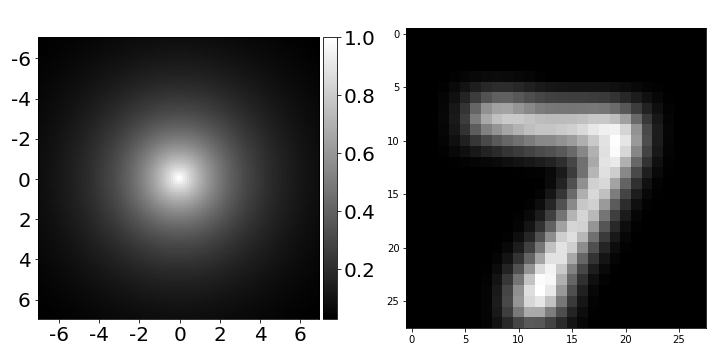
Рис.7 Гауссовский фильтр, использовавшийся в нейронной сети, описанной выше (слева) и результат его применения к изображению (справа).

В качестве примера подобного трюка, можно рассмотреть слой, который позволяет детектировать границу разделения между любой парой пикселей:

import torch.nn as nn           # using PyTorch
nn.Sequential(nn.Linear(4, 64), # map coordinates to a hidden layer
             nn.ReLU(),         # nonlinearity
             nn.Linear(64, 1),  # map hidden representation to edge
             nn.Tanh())         # squash edge values to [-1, 1]

Рис.8 2D-фильтр нейронной сети, описанной выше, с центром в красной точке. Усреднение (слева, точность 92,24%), обучение на основе координат (посередине, точность 91,05%), обучение на основе координат с некоторыми трюками (справа, точность 92,39%).

Код для создание подобной gif:

import imageio  # to save GIFs
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.distance import cdist
import cv2  # optional (for resizing the filter to look better)

img_size = 28
# Create/load some adjacency matrix A (for example, based on coordinates)
col, row = np.meshgrid(np.arange(img_size), np.arange(img_size))
coord = np.stack((col, row), axis=2).reshape(-1, 2) / img_size
dist = cdist(coord, coord)  # distances between all pairs of pixels
sigma = 0.2 * np.pi  # width of a Gaussian (can be a hyperparameter when training a model)

A = np.exp(- dist / sigma ** 2)  # adjacency matrix of spatial similarity
# above, dist should have been squared to make it a Gaussian (forgot to do that)

scale = 4
img_list = []
cmap = mpl.cm.get_cmap('viridis')
for i in np.arange(0, img_size, 4):  # for every row with step 4
    for j in np.arange(0, img_size, 4):  # for every col with step 4
        k = i*img_size + j
        img = A[k, :].reshape(img_size, img_size)
        img = (img - img.min()) / (img.max() - img.min())
        img = cmap(img)
        img[i, j] = np.array([1., 0, 0, 0])  # add the red dot
        img = cv2.resize(img, (img_size*scale, img_size*scale))
        img_list.append((img * 255).astype(np.uint8))
imageio.mimsave('filter.gif', img_list, format='GIF', duration=0.2)

Можно заметить, что фильтр, который мы только что обучили (в середине), выглядит странно. Это связано с тем, что задача довольно сложная, поскольку мы оптимизируем две модели одновременно: модель, которая предсказывает разделяющую поверхность для групп пикселей, и модель, предсказывающая класс цифры. Чтобы узнать лучшие фильтры (например, тот, что справа), нам нужно применить некоторые другие приемы, которые можно найти в работе [13].

Выводы

Графовые нейронные сети (GNN) — это очень гибкое и интересное семейство нейронных сетей, которые могут быть применены к действительно сложным данным. Как всегда, такая гибкость должна иметь определенную цену. В случае GNN — это трудность регуляризации модели путем определения таких операторов как свертка. Исследования в этом направлении продвигаются довольно быстро, так что GNN найдут применение во все более широких областях машинного обучения и компьютерного зрения.

Рис.9 Граф работ по конструированию GNN архитектур из туториала Бориса Князева “Anisotropic, Dynamic, Spectral and Multiscale Filters Defined on Graphs”.

Более детальный обзор подходов к конструированию сверток на графах, вы сможете найти в оригинальном туториале от Бориса Князева и его продолжениях.

Тем из вас, кому стало интересно как же расшифровывается формула с обложки, рекомендуем к ознакомлению статью [6].

Для всех кому интересно углубиться в тему сверток на графах, рекомендуем прочитать оставшиеся два туториала в серии заметок Бориса Князева на Medium.

Источники:

Hamilton, W.L., Ying, R. and Leskovec, J., 2017. Representation learning on graphs: Methods and applications. arXiv preprint arXiv:1709.05584. [paper]
Bronstein, M.M., Bruna, J., LeCun, Y., Szlam, A. and Vandergheynst, P., 2017. Geometric deep learning: going beyond euclidean data. IEEE Signal Processing Magazine, 34(4), pp.18-42. [paper]
Fey, M., Eric Lenssen, J., Weichert, F. and Müller, H., 2018. Splinecnn: Fast geometric deep learning with continuous b-spline kernels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 869-877). [paper]
Dumoulin, V. and Visin, F., 2016. A guide to convolution arithmetic for deep learning. arXiv preprint arXiv:1603.07285. [paper]
Achanta, R., Shaji, A., Smith, K., Lucchi, A., Fua, P. and Süsstrunk, S., 2012. SLIC superpixels compared to state-of-the-art superpixel methods. IEEE transactions on pattern analysis and machine intelligence, 34(11), pp.2274-2282. [paper]
Kipf, T.N. and Welling, M., 2016. Semi-supervised classification with graph convolutional networks. arXiv preprint arXiv:1609.02907. [paper]
Xu, K., Hu, W., Leskovec, J. and Jegelka, S., 2018. How powerful are graph neural networks?.. arXiv preprint arXiv:1810.00826. [paper]
Hamilton, W., Ying, Z. and Leskovec, J., 2017. Inductive representation learning on large graphs. In Advances in neural information processing systems (pp. 1024-1034). [paper]
Defferrard, M., Bresson, X. and Vandergheynst, P., 2016. Convolutional neural networks on graphs with fast localized spectral filtering. Advances in neural information processing systems, 29, pp.3844-3852. [paper]
Jia, X., De Brabandere, B., Tuytelaars, T. and Gool, L.V., 2016. Dynamic filter networks. In Advances in neural information processing systems (pp. 667-675). [paper]
Simonovsky, M. and Komodakis, N., 2017. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 3693-3702). [paper]
Knyazev, B., Lin, X., Amer, M.R. and Taylor, G.W., 2018. Spectral multigraph networks for discovering and fusing relationships in molecules. arXiv preprint arXiv:1811.09595. [paper]
Knyazev, B., Lin, X., Amer, M.R. and Taylor, G.W., 2019. Image classification with hierarchical multigraph networks. arXiv preprint arXiv:1907.09000. [paper]
Wang, Y., Sun, Y., Liu, Z., Sarma, S.E., Bronstein, M.M. and Solomon, J.M., 2019. Dynamic graph cnn for learning on point clouds. Acm Transactions On Graphics (tog), 38(5), pp.1-12. [paper]
Verma, N., Boyer, E. and Verbeek, J., 2018. Feastnet: Feature-steered graph convolutions for 3d shape analysis. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 2598-2606). [paper]

Tags:

Hubs:

3D ML. Часть 5: Свертки на графах

Откуда брать информацию и на чем практиковаться?

Граф как неевклидова структура

Конструируем сверточный слой для графов

Выводы

Articles

Information