Ручная сегментация легких занимает около 10 минут и требуется определенная сноровка, чтобы получить такой же качественный результат, как при автоматической сегментации. Автоматическая сегментация занимает около 15 секунд.
Я предполагал, что без нейронной сети удастся получить точность не выше 70%. Также я предполагал, что морфологические операции – это только подготовка изображения к более сложным алгоритмам. Но в результате обработки тех, хоть и немногочисленных 40 образцов томографических данных, что есть на руках, алгоритм выделил легкие без ошибок, причём после теста на первых пяти случаях алгоритм уже не претерпевал значительных изменений и с первого применения правильно отработал на остальных 35 исследованиях без изменения настроек.
Также нейронные сети имеют минус – для их обучения нужны сотни обучающих образцов лёгких, которые придётся размечать вручную.
Содержание
- Строение дыхательной системы
- Шкала Хаунсфилда
- Математическая морфология
- Алгоритм Ли и RLE-компрессия
- Пороговое преобразование базового объема
- Отсечение внешнего воздуха
- Выделение максимального по объему объекта
- Закрытие сосудов внутри лёгких
- Алгоритм сегментации дыхательных органов
- Реализация алгоритма в среде MATLAB
- Заключение
Строение дыхательной системы
Дыхательная система включает в себя дыхательные пути и лёгкие. Выделяют верхний и нижний отделы дыхательных путей. Точкой разделения между нижними и верхними дыхательными путями является точка пересечения пищевых и дыхательных каналов. Всё, что выше гортани – верхний отдел, а остальное – нижний.
Перечислим дыхательные органы:
Носовая полость: — нос, гайморовы пазухи и т.д.
Глотка — канал, по которому перемещается пища и воздух.
Гортань – отвечает за образование голоса. Находится на уровне шейных позвонков C4-C6.
Трахея – трубка, соединяющая гортань и бронхи.
Бронхи – дыхательные каналы, основная часть которых находится внутри лёгких.
Лёгкие – основной дыхательный орган.

Шкала Хаунсфилда
Годфри Хаунсфилд — британский инженер-электрик, который вместе с американским теоретиком Алланом Кормаком разработал компьютерную томографию, за что получил Нобелевскую премию в 1979 году.

Шкала Хаунсфилда — количественная шкала рентгеновской плотности, которая измеряется в единицах Хаунсфилда, обозначаемых HU.
Рентгеновская плотность вычисляется на основе коэффициента ослабления вещества, то есть степени уменьшения мощности излучения при прохождении через это вещество.
Рентгеновская плотность вычисляется по формуле:
где — линейные коэффициенты ослабления для измеряемого вещества, воды и воздуха.
Рентгеновская плотность бывает отрицательной, потому что нулевая рентгеновская плотность соответствует воде. А значит все вещества, через которые рентгеновские волны проходят с меньшим уменьшением мощности излучения, чем через воду (например, легочные ткани, воздух), будут иметь отрицательную рентгеновскую плотность.
Ниже перечислены приблизительные рентгеновские плотности для различных тканей:
- Воздух: -1000 HU.
- Дыхательные органы: от -950 до -300 HU.
- Кровь (без контрастирования сосудов): от 0 до 100 HU.
- Кости: от 100 до 1000 HU.

Ссылки на Википедию: шкала Хаунсфилда, Годфри Хаунсфилд, коэффициент ослабления.
Математическая морфология
Основное место среди выбранных в данной статье алгоритмов занимают морфологические операции.
В области компьютерного зрения морфологическими операциями называют группу алгоритмов по преобразованию формы объектов. Чаще всего морфологические операции применяют к бинаризованным изображениям, где вокселям объектов соответствуют единицы, а пустоте нули.
К основным морфологическим операциям относят:
Морфологическая дилатация (dilation, расширение) — добавление новых вокселей ко всем краевым вокселям объектов. То есть по всем граничным вокселям совершается проход с ядром с заданной формой (шар, куб, крест и т.д.). Данную операцию часто применяют для соединения множества рядом стоящих объектов в единый объект.
Морфологическая эрозия (erosion, размывание) — уничтожение всех вокселей, лежащих на границе объектов. Эта операция обратна дилатации. Данная операция бывает полезна для удаления шума в виде множества мелких объектов, соединенных между собой. Однако, данный метод удаления шума стоит использовать только в случае, если сегментируемый объект имеет толщину значительно большую, чем радиус эрозии.
Морфологическое закрытие (closing) — это дилатация с последующей эрозией. Применяется для закрытия отверстий внутри объектов и для объединения рядом стоящих объектов.
Морфологическое открытие (opening) — это эрозия с последующей дилатацией. Применяется для удаления мелких шумовых объектов и для разделения объектов на несколько объектов.


Алгоритм Ли и RLE-компрессия
Для выделения объектов в бинаризованном воксельном объёме используется алгоритм Ли. Данный алгоритм изначально был придуман для поиска кратчайшего пути. Но мы используем его для выделения и перемещения объектов из одного трехмерного массива вокселей в другой. Его суть состоит в параллельном перемещении во всех возможных направлениях из начальной точки. Для трехмерного случая возможны 26 либо 6 направлений движения из заданного вокселя (если воксель не находится с краю изображения).
Для оптимизации по быстродействию был применен алгоритм кодирования длин серий (run-length encoding). Его суть заключается в том, что последовательности единиц и нулей заменяются цифрой, равной количеству элементов в последовательности. Например, строка “00110111” может быть заменена как: “2;2;1;3”. Это позволяет уменьшить количество обращений к памяти.
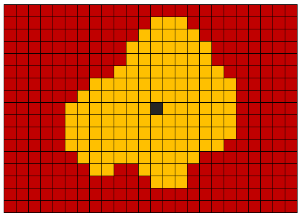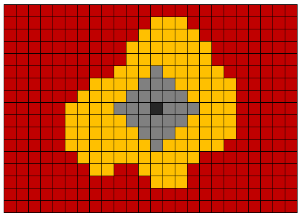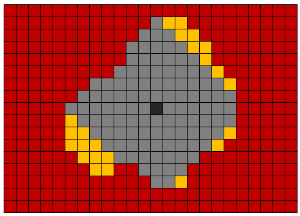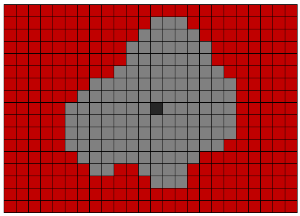

Ссылки на Википедию: алгоритм Ли, алгоритм RLE.
Пороговое преобразование базового объема
С помощью томографа получены данные о рентгеновской плотности в каждой точке пространства. Воксели воздуха имеют рентгеновскую плотность в промежутке от -1100 до -900 HU, а воксели дыхательных органов от -900 до -300 HU. Поэтому можем убрать все лишние воксели, имеющие рентгеновскую плотность больше -300 HU. В итоге получим бинаризованный воксельный объём, содержащий только дыхательные органы и воздух.
Отсечение внешнего воздуха
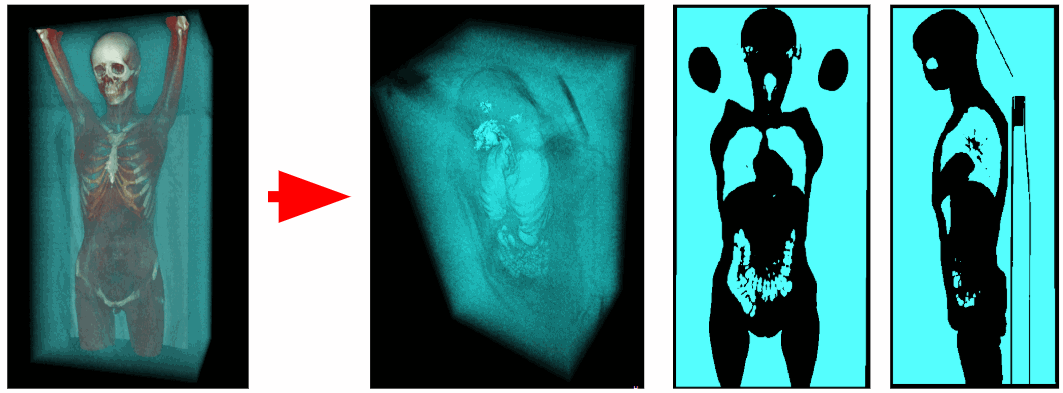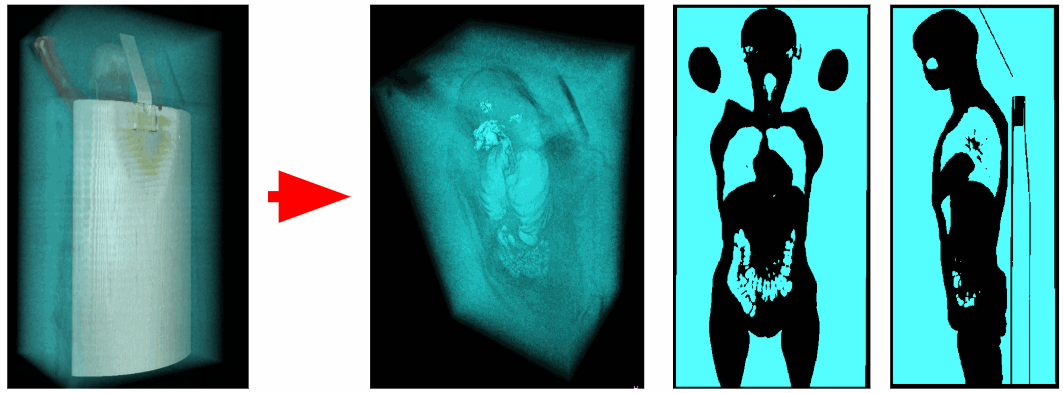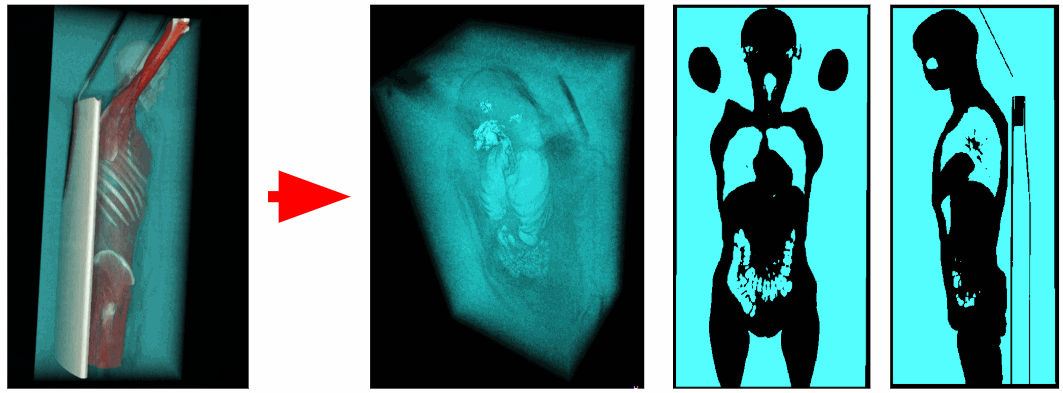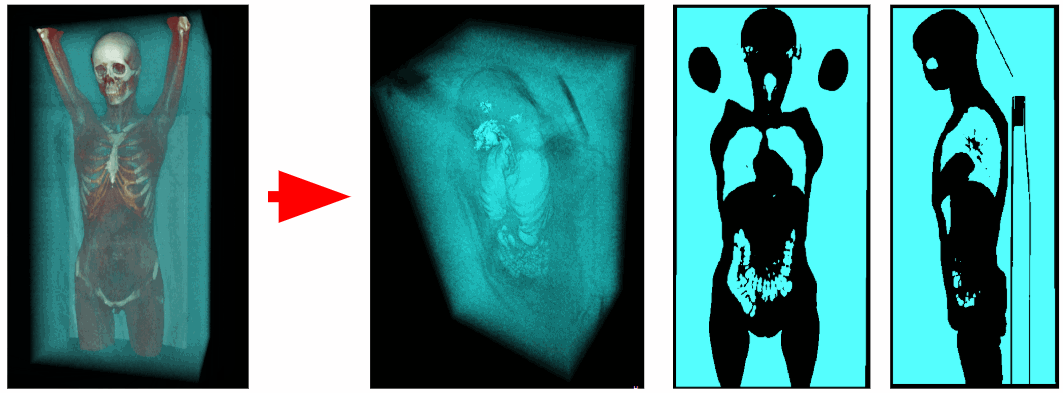
Для выделения внутреннего воздуха тела удалим все объекты, которые прилегают к углам воксельной сцены. Таким образом избавимся от внешнего воздуха.

Однако, не во всех случаях будет удалён воздух внутри стола томографа, так как он может не иметь связи с углами сцены.

Поэтому просканируем не только углы, но и все воксели, лежащие на любой из краевых плоскостей сцены. Но в результате почему-то удалились и сами лёгкие. Оказывается, трахея тоже имела связь с верхней плоскостью сцены.
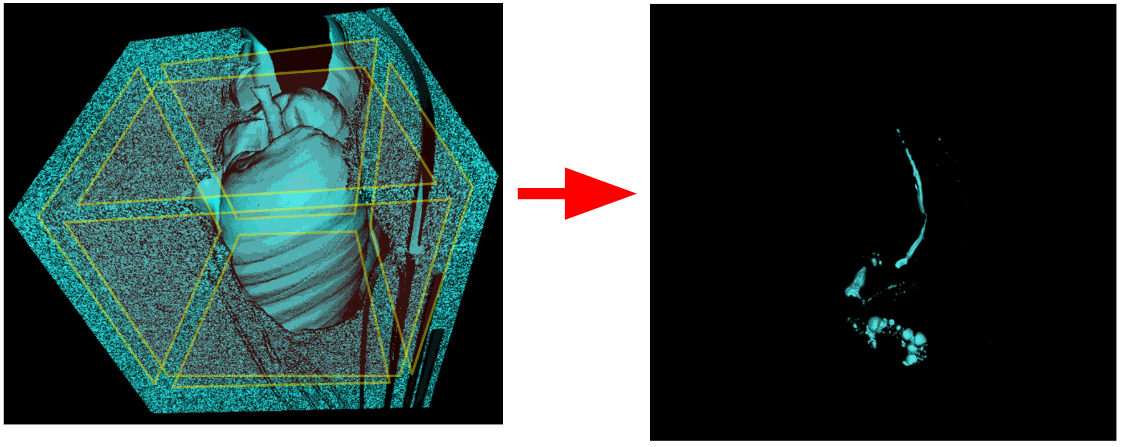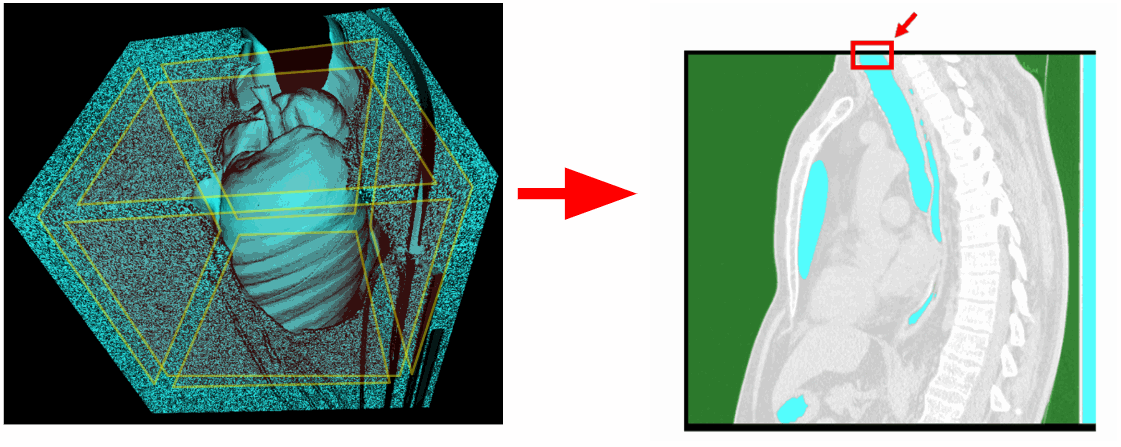
Придётся исключить верхнюю плоскость из зоны сканирования. Также бывают исследования, в которых лёгкие были захвачены не полностью и нижняя плоскость имеет связь с легкими. Так что при желании можно исключить и нижнюю плоскость.

Но такой метод действует только на грудных исследований. В случае же захвата полного объёма тела на снимке появится связь внутреннего и внешнего воздуха через носовую полость. Поэтому необходимо применить морфологическую эрозию для разделения внутреннего и внешнего воздуха.
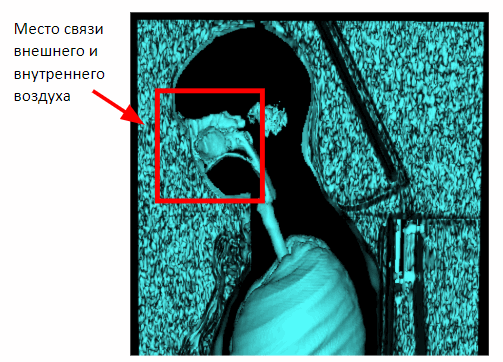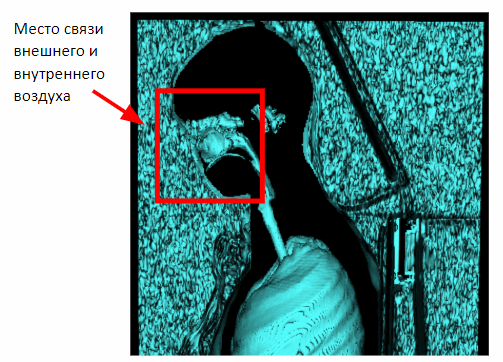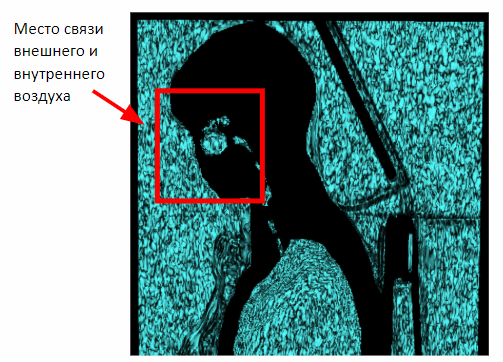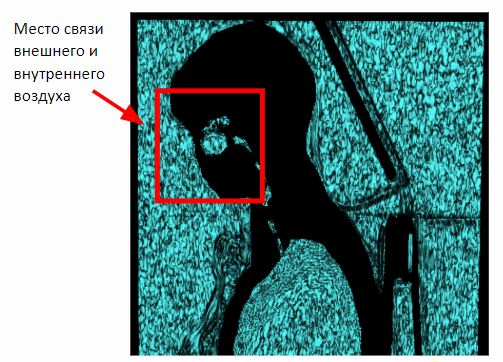
После применения эрозии можем вернуться к полученному ранее методу сегментации внешнего воздуха по признаку соседства с боковыми плоскостями сцены.

Выделив внешний воздух, можно было бы сразу отнять его из общего объёма воздуха и лёгких и получить внутренний воздух тела и легкие. Но есть одна проблема. После эрозии была потеряна часть информации о внешнем воздухе. Чтобы восстановить её, применим дилатацию внешнего воздуха.

Далее вычитаем внешний воздух из всего воздуха и дыхательных органов и получаем внутренний воздух и дыхательные органы.


Выделение максимального по объему объекта
Далее выделим дыхательные органы как максимальный по объему объект. Дыхательные органы — это отдельный объект. Связи между легкими и воздухом внутри желудочно-кишечного тракта нет.


Стоит заметить, что важен правильный выбор порога рентгеновской плотности на начальном шаге порогового преобразования. Иначе в некоторых случаях может не оказаться связи между двумя лёгкими в результате низкого разрешения. Например, если считать, что воксели дыхательных органов имеют рентгеновскую плотность от -500 HU и менее, то в случае, приведённом ниже, выделение дыхательных органов как крупнейшего по объёму объекта приведёт к ошибке, так как отсутствует связь между двумя лёгкими. Поэтому следует повысить порог до -300 HU.

Закрытие сосудов внутри лёгких
Для захвата сосудов внутри лёгких применим морфологическое закрытие, то есть дилатацию с последующей эрозией с тем же радиусом. Рентгеновская плотность сосудов составляет около -100..100 HU.

Крупные кровеносные пути не закрылись. Но в этом и нет необходимости. Цель данной операции была в уничтожении множества мелких отверстий внутри легких для упрощения дальнейшей сегментации легких.
Алгоритм сегментации дыхательных органов
В итоге получаем следующий алгоритм сегментации дыхательных органов:
- Пороговое преобразование базового объёма по порогу < -300 HU.
- Морфологическая эрозия радиусом 3 мм для разделения внешнего и внутреннего воздуха.
- Выделение внешнего воздуха по признаку соседства с граничными боковыми плоскостями воксельной сцены.
- Морфологическая дилатация внешнего воздуха для восстановления потерянной в результате эрозии информации.
- Вычитание внешнего воздуха из всего воздуха и дыхательных органов для получения внутреннего воздуха и дыхательных органов.
- Выделение максимального по объёму объекта.
- Морфологическое закрытие сосудов внутри лёгких.

Реализация алгоритма в среде MATLAB
Метод getRespiratoryOrgans
% Возвращает весь объем органов дыхания (объем легких и дыхательных путей)
% без разделения левого и правого легкого.
% V = базовый объем с данными по радиоплотности в единицах Хаунсфилда.
% cr = радиус морфологического закрытия сосудов.
% ci = количество итераций морфологического закрытия сосудов (например, 3 раза
% делают дилатацию и после этого 3 раза делают эрозию.
function RO = getRespiratoryOrgans(V,cr,ci)
% Пороговое преобразование базового объёма
% по порогу < -300 HU.
AL=~imbinarize(V,-300);
% Морфологическая эрозия радиусом 3 мм для
% разделения внешнего и внутреннего воздуха.
SE=strel('sphere',3);
EAL=imerode(AL,SE);
% Выделение внешнего воздуха по признаку соседства
% с граничными боковыми плоскостями воксельной сцены.
EA=getExternalAir(EAL);
% Морфологическая дилатация внешнего воздуха для
% восстановления потерянной в результате эрозии информации.
DEA=EA;
for i=1:4
DEA=imdilate(DEA,SE);
DEA=DEA&AL;
end
% Вычитание внешнего воздуха из всего воздуха и дыхательных
% органов для получения внутреннего воздуха и дыхательных органов.
IAL=AL-DEA;
% Выделение максимального по объёму объекта.
RO=getMaxObject(IAL);
% Морфологическое закрытие сосудов внутри лёгких.
RO=closeVoxelVolume(RO,3,2);Метод getExternalAir
% Возвращает объем, связанный с краевыми поверхностями трехмерного объема
% (кроме верхней поверхности, поскольку легкие могут иметь
% соединение с верхней поверхностью).
% EAL = эродированный бинаризованный объем легких и воздуха.
function EA = getExternalAir(EAL)
% Функция bwlabeln сегментирует объекты: воксели одного
% объекта приравнивает к единице, другого – к двойке и т.д.
V=bwlabeln(EAL);
% Запрашиваем такие характеристики объектов, как ограничительный бокс
% и список всех вокселей объекта.
R=regionprops3(V,'BoundingBox','VoxelList');
n=height(R);
% Создаём 3-D матрицу для хранения вокселей внешнего воздуха.
s=size(EAL);
EA=zeros(s,'logical');
% Произведём перебор всех найденных объектов в цикле
% с целью нахождения объектов, принадлежащих внешнему воздуху.
for i=1:n
% Определим координаты x и y, принадлежащие самым крайним
% вокселям объекта.
x0=R(i,1).BoundingBox(1);
y0=R(i,1).BoundingBox(2);
x1=x0+R(i,1).BoundingBox(4);
y1=y0+R(i,1).BoundingBox(5);
% Если крайние воксели объекта соприкасаются с боковыми
% плоскостями сцены, то копируем все воксели данного объекта
% в матрицу EA.
if (x0 < 1 || x1 > s(1)-1 || y0 < 1 || y1 > s(2)-1)
% Преобразуем данные о координатах вокселей объекта к
% матричному типу: [[x1 y1 z1][x2 y2 z3] … [xn yn zn]].
mat=cell2mat(R(i,2).VoxelList);
ms=size(mat);
% Заполняем матрицу, содержащую воксели внешнего воздуха.
for j=1:ms(1)
x=mat(j,2);
y=mat(j,1);
z=mat(j,3);
EA(x,y,z)=1;
end
end
endМетод getMaxObject
% Возвращает самый большой объект в трехмерном объеме "V".
% O = воксели самого большого объекта.
% m = объем самого большого объекта.
function [O,m] = getMaxObject(V)
% Сегментируем объекты.
V=bwlabeln(V);
% Запрашиваем информацию об объёме объектов и координатах
% вокселей объектов.
R=regionprops3(V,'Volume','VoxelList');
% Определяем индекс максимального по объёму объекта.
v=R(:,1).Volume;
[m,i]=max(v);
% Создаём 3-D матрицу для хранения вокселей крупнейшего
% объекта.
s=size(V);
O=zeros(s,'logical');
% Переносим воксели крупнейшего объекта в новую матрицу.
mat=cell2mat(R(i,2).VoxelList);
ms=size(mat);
for j=1:ms(1)
x=mat(j,2);
y=mat(j,1);
z=mat(j,3);
O(x,y,z)=1;
endИсходный код можно скачать по ссылке.
Заключение
Следующими статьями планируются:
- сегментация трахеи и бронхов;
- сегментация легких;
- сегментация долей легких.
Будут рассматриваться такие алгоритмы, как:
- дистанционное преобразование (distance transform);
- преобразование ближайших соседей (nearest neighbor transform, также известный как feature transform);
- вычисление собственных значений матрицы Гессе для сегментации плоских 3D объектов;
- сегментация методом водораздела (watershed segmentation).