В предыдущем посте мы подробно рассказывали, чему учим студентов на направлении «Промышленное программирование». Для тех, чья сфера интересов лежит в более теоретической области, например, привлекают новые парадигмы программирования или абстрактная математика, используемая в теоретических исследованиях по программированию, существует другая специализация — «Языки программирования».
Сегодня я расскажу о своем исследовании в области реляционного программирования, которым занимаюсь в университете и в качестве студента-исследователя в лаборатории языковых инструментов JetBrains Research.
Что такое реляционное программирование? Обычно мы запускаем функцию с аргументами и получаем результат. А в реляционном случае можно делать наоборот: зафиксировать результат и один аргумент, а второй аргумент получить. Главное — правильно написать код и запастись терпением или хорошим кластером.

Меня зовут Дмитрий Розплохас, я студент первого курса магистратуры питерской Вышки, а в прошлом году окончил бакалавриат Академического университета по направлению «Языки программирования». С третьего курса бакалавриата также являюсь студентом-исследователем в лаборатории языковых инструментов JetBrains Research.
Реляционное программирование — это когда вместо функций вы описываете отношения между аргументами и результатом. Если язык под это заточен, можно получить определенные бонусы, например, возможность запускать функцию в обратную сторону (по результату восстанавливать возможные значения аргументов).
Вообще, так можно делать в любом логическом языке, но интерес к реляционному программированию возник одновременно с появлением около десяти лет назад минималистичного чистого логического языка miniKanren, который позволил удобно описывать и использовать подобные отношения.
Вот несколько самых передовых примеров использования: можно написать чекер доказательств и использовать его для поиска доказательства (Near et al., 2008) или создать интерпретатор какого-то языка и использовать его для генерации программ по набору тестов (Byrd et al., 2017).
miniKanren — язык небольшой, для описания отношений в нем используются только базовые математические конструкции. Это встраиваемый язык, его примитивы — библиотека для какого-то внешнего языка, и маленькие программки на miniKanren можно использовать внутри программы на другом языке.
Внешних языков, подходящих для miniKanren, целая куча. Изначально был Scheme, мы работаем с версией для Ocaml (OCanren), а полный список можно посмотреть на minikanren.org. Примеры в этой статье тоже будут на OCanren. Многие реализации добавляют вспомогательные функции, но мы сосредоточимся только на ядре языка.
Начнём с типов данных. Условно их можно разделить на два вида:
Например, если мы хотим работать с массивами в самом miniKanren, то его надо описать через термы по аналогии с функциональными языками — как односвязный список. Список — это либо пустой список (обозначается каким-нибудь простым термом), либо пара из первого элемента списка («голова») и остальных элементов («хвост»).
Программа на языке miniKanren — это соотношение между некоторыми переменными. При запуске программа выдаёт все возможные значения переменных в общем виде. Часто реализации позволяют ограничить количество ответов в выводе, например, найти только первый — поиск не всегда останавливается после нахождения всех решений.
Можно записать несколько соотношений, которые определяются друг через друга и даже вызываются рекурсивно, как функции. Например, ниже мы вместо функции определим отношение
определим отношение  : список
: список  является конкатенацией списков
является конкатенацией списков  и
и  . Функции, возвращающие отношения, традиционно заканчивают на «o», чтобы отличать их от обычных функций.
. Функции, возвращающие отношения, традиционно заканчивают на «o», чтобы отличать их от обычных функций.
Отношение записывается как некоторое утверждение относительно своих аргументов. У нас есть четыре базовые операции:
Отношение может вызывать само себя рекурсивно. Например, надо определить отношение «элемент лежит в списке». Решать эту задачу будем через разбор тривиальных случаев, как в функциональных языках:
лежит в списке». Решать эту задачу будем через разбор тривиальных случаев, как в функциональных языках:
Базовая версия языка строится на этих четырех операциях. Также существуют расширения, позволяющие использовать и другие операции. Наиболее полезное из них — disequality constraint для задания неравенства двух термов (=/=).
Несмотря на минималистичность, miniKanren достаточно выразительный язык. Вот, например, как выглядит реляционная конкатенация двух списков. Функция двух аргументов превращается в трехместное отношение « является конкатенацией списков
является конкатенацией списков  и
и  ».
».
Решение структурно не отличается от того, как бы мы это писали на функциональном языке. Мы разбираем два случая, объединённые дизъюнкцией:
Можем сделать запрос к этому отношению, зафиксировав первый и второй аргумент — получим конкатенацию списков:
⇒
Можем зафиксировать последний аргумент — получим все разбиения данного списка на два.
⇒
Можно что угодно другое. Чуть более нестандартный пример, в котором мы зафиксируем лишь часть аргументов:
⇒
С точки зрения теории ничего впечатляющего здесь нет: всегда можно просто запустить перебор всех возможных вариантов для всех аргументов, проверяя для каждого набора не ведут ли они себя относительно заданной функции/отношения так, как нам бы хотелось (см. «Алгоритм британского музея»). Интерес представляет то, что здесь перебор (иначе говоря, поиск решения) пользуется исключительно структурой описанного отношения, благодаря чему может быть относительно эффективен на практике.
Поиск идет по отношению накапливая информацию о различных переменных в текущем состоянии. Про каждую переменную мы либо ничего не знаем, либо знаем, как она выражается через термы, значения и другие переменные. Например:
Проходя через унификацию, мы смотрим на два терма с учетом этой информации и либо обновляем состояние, либо обрываем поиск, если два терма не могут быть унифицированы. Например, выполнив унификацию b = c, мы получим новую информацию: x = 10, y = z. А вот унификация b = Nil вызовет противоречие.
Поиск в конъюнктах мы выполняем последовательно (чтобы информация накапливалась), а в дизъюнкции мы разделяем поиск на две параллельные ветки и идем дальше, чередуя шаги в них — это так называемый interleaving search. Благодаря этому чередованию поиск является полным — каждое подходящее решение будет найдено через конечное время. Например, в языке Prolog это не так. Там выполняется что-то вроде обхода в глубину (который может зависнуть на бесконечной ветке), а interleaving search по сути является хитрой модификацией обхода в ширину.
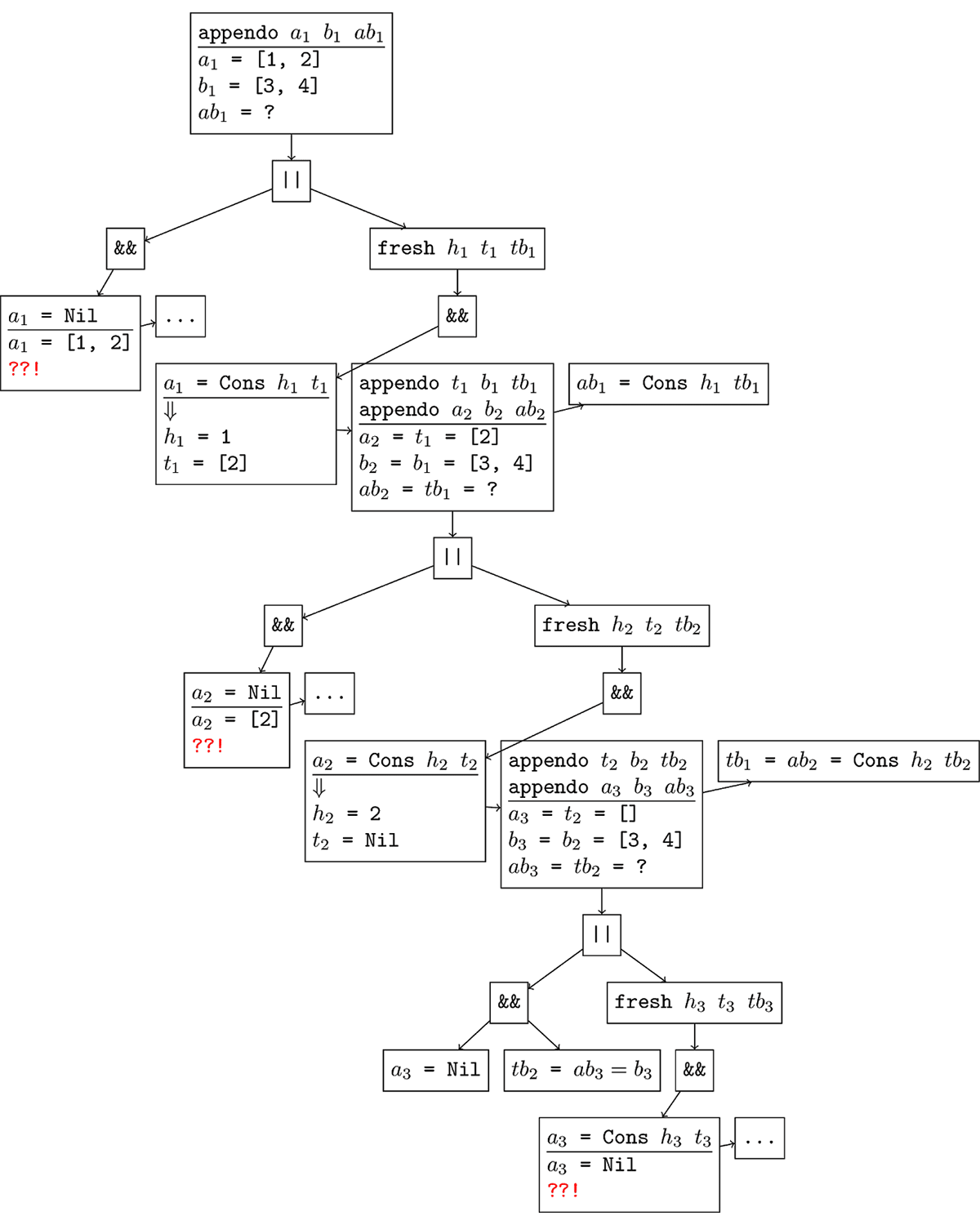
Давайте теперь посмотрим как работает первый запрос из предыдущего раздела. Так как в appendo есть рекурсивные вызовы, мы допишем к переменным индексы, чтобы их отличать. На рисунке ниже представлено дерево перебора. Стрелочками отмечены направления распространения информации (за исключением возврата из рекурсии). Между дизъюнкциями информация не распространяется, а между конъюнкциями распространяется слева направо.
Как всегда: вам обещают, что всё будет супер декларативно, а на деле нужно подстраиваться под язык и писать всё специальным образом (держа в голове как всё будет исполняться), чтобы работало хоть что-то, кроме простейших примеров. Это разочаровывает.
Одна из первых проблем, с которыми сталкивается начинающий программист на miniKanren — всё очень сильно зависит от того, в каком порядке вы опишите условия (конъюнкты) в программе. При одном порядке всё ок, а поменяли два конъюнкта местами и всё стало работать очень медленно или вообще не завершилось. Это неожиданно.
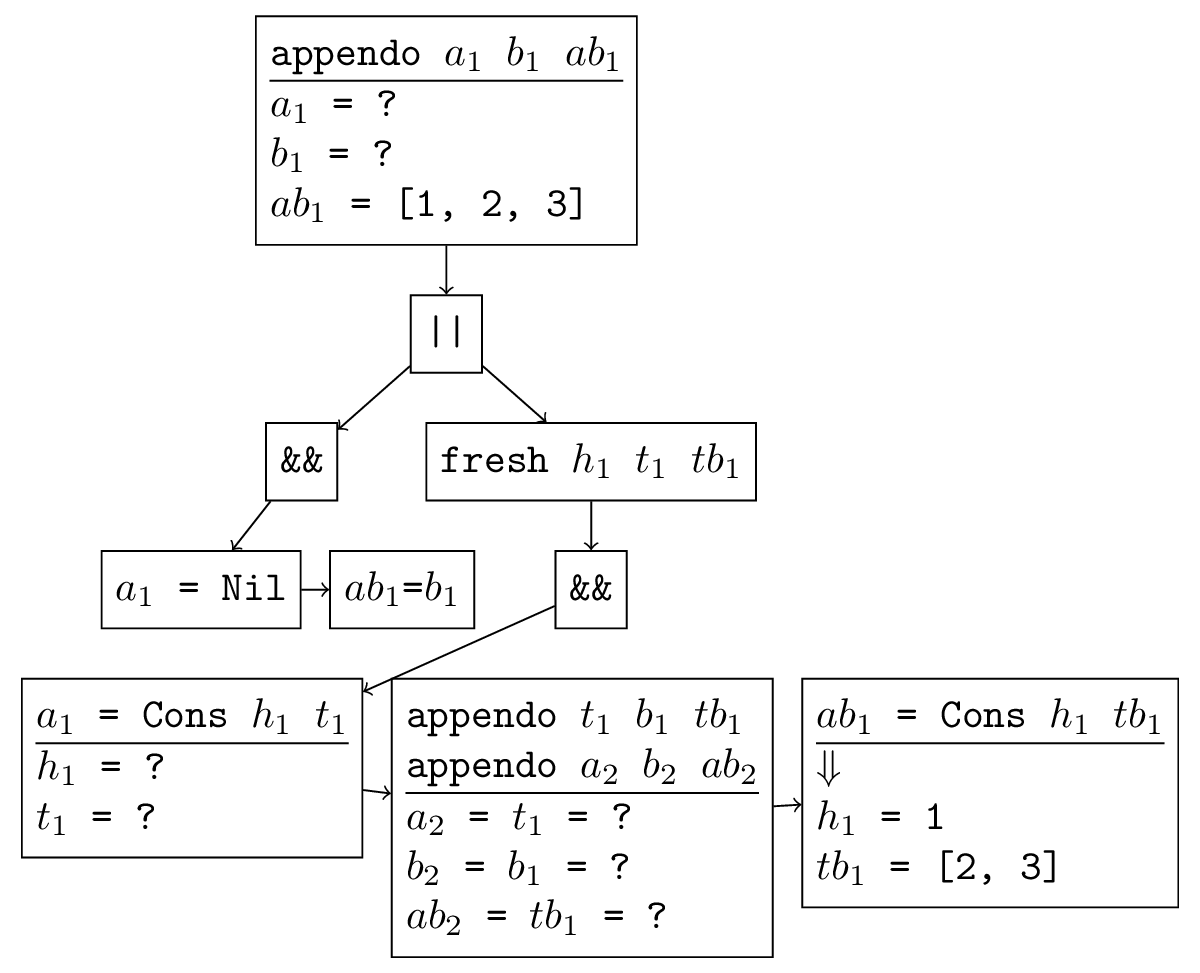
Даже в примере с appendo запуск в обратную сторону (генерация разбиений списка на два) не завершается, если явно не указать, сколько ответов вы хотите (тогда поиск оборвется, после того как будет найдено нужное количество).
Допустим, мы зафиксируем исходные переменные так: a = ?, b = ?, ab = [1, 2, 3] (см. рис. ниже) Во второй ветке при рекурсивном вызове эта информация никак не будет использоваться (переменная ab и ограничения на и
и  появляются только после этого вызова). Поэтому при первом рекурсивном вызове все его аргументы будут свободными переменными. Этот вызов будет генерировать всевозможные тройки из двух списков и их конкатенации (и эта генерация никогда не завершится), а дальше среди них будут выбираться те, для которых третий элемент получился ровно такой, какой нам нужно.
появляются только после этого вызова). Поэтому при первом рекурсивном вызове все его аргументы будут свободными переменными. Этот вызов будет генерировать всевозможные тройки из двух списков и их конкатенации (и эта генерация никогда не завершится), а дальше среди них будут выбираться те, для которых третий элемент получился ровно такой, какой нам нужно.
Всё не настолько плохо, как может показаться на первый взгляд, потому что перебирать эти тройки мы будем большими группами. Списки с одинаковой длиной, но разными элементами, никак не отличаются с точки зрения функции, поэтому попадут в одно решение — на месте элементов будут свободные переменные. Тем не менее, мы всё равно будем перебирать все возможные длины списков, хотя нужна нам только одна, и мы знаем, какая. Это очень нерациональное использование (неиспользование) информации при поиске.
Этот конкретный пример легко исправить: нужно просто перенести рекурсивный вызов в конец и всё заработает как надо. До рекурсивного вызова будет происходить унификация с переменной ab и рекурсивный вызов будет производиться от хвоста данного списка (как нормальная рекурсивная функция). Это определение с рекурсивным вызовом в конце будет хорошо работать во всех направлениях: к рекурсивному вызову мы успеваем накопить всю возможную информацию об аргументах.
Однако в любом чуть более сложном примере, когда есть несколько содержательных вызовов, одного конкретного порядка, для которого всё будет хорошо, не существует. Самый простой пример: разворачивание списка при помощи конкатенации. Фиксируем первый аргумент — нужен именно этот порядок, фиксируем второй — нужно поменять вызовы местами. Иначе долго ищется и поиск не завершается.
Так происходит потому, что interleaving search обрабатывает конъюнкты последовательно, а как сделать по-другому, не лишившись при этом приемлемой эффективности, никто не смог придумать, хотя и пытались. Конечно, все решения когда-нибудь найдутся, но при неправильном порядке они будут искаться так нереально долго, что никакого практического смысла в этом нет.
Существуют техники написания программ, позволяющие избежать этой проблемы. Но многие из них требуют особого мастерства и воображения для применения, а в результате получаются очень большие программы. Пример — техника term size bounding и определение бинарного деления с остатком через умножение с её помощью. Вместо того, чтобы тупо записать математическое определение
приходится писать рекурсивное определение на 20 строчек + большую вспомогательную функцию, которые нереально прочитать (я до сих пор не понимаю, что там делается). Его можно найти в диссертации Уилла Берда в разделе Pure Binary Arithmetic.
С учетом всего вышесказанного, хочется придумать какую-то модификацию поиска, чтобы просто и естественно написанные программы тоже работали.
Мы заметили, что когда всё плохо, поиск не будет завершаться, если явно не указать количество ответов и не оборвать его. Поэтому решили бороться именно с незавершаемостью поиска — это гораздо легче конкретизировать, чем «работает долго». Вообще, конечно, хочется просто ускорить поиск, но это гораздо сложнее формализовать, так что мы начали с менее амбициозной задачи.
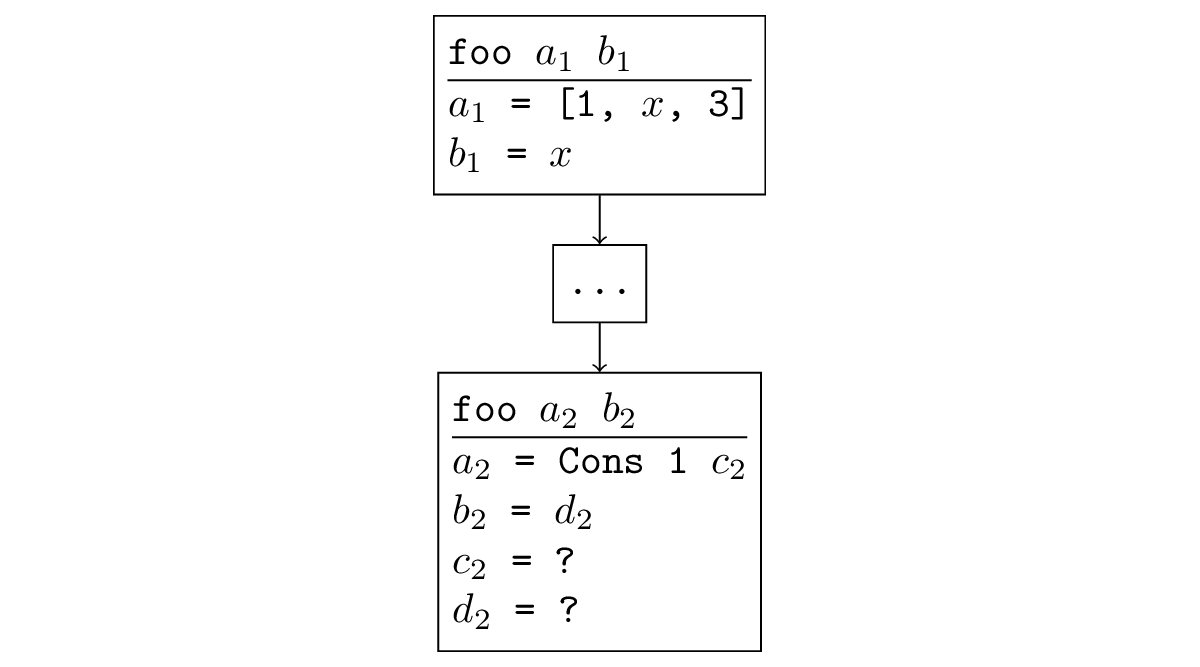
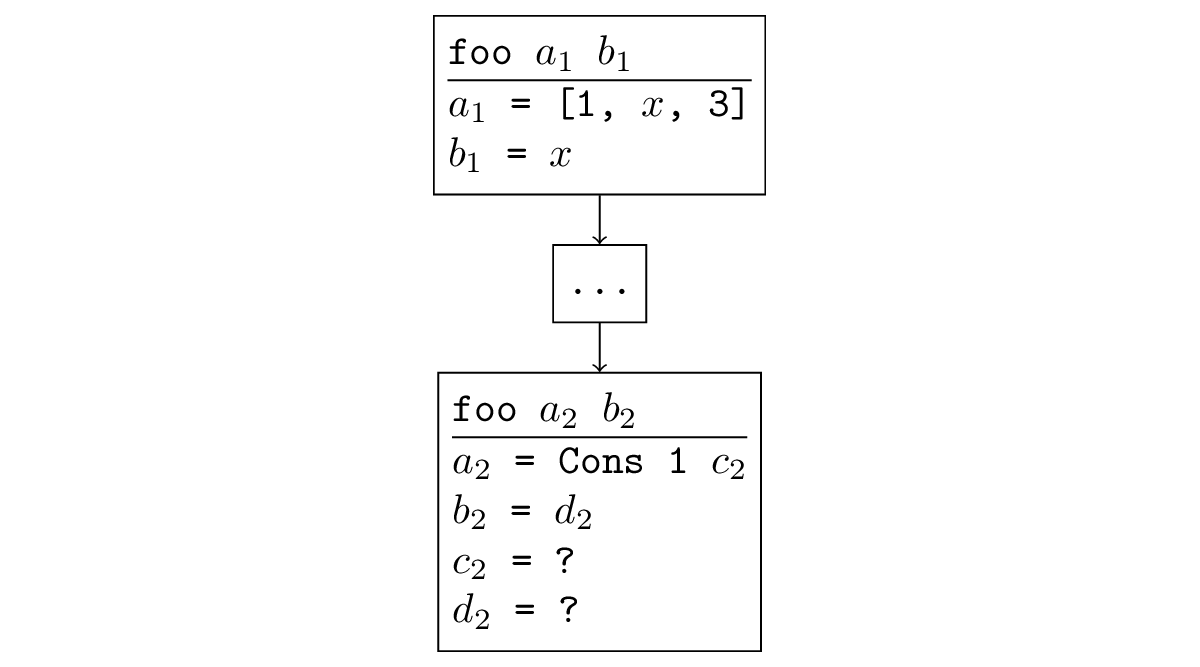
В большинстве случаев, когда поиск расходится, происходит ситуация, которую легко отследить. Если некоторая функция вызывается рекурсивно, и при рекурсивном вызове аргументы у нас такие же или менее конкретные, то и в рекурсивном вызове снова генерируется ещё одна такая подзадача и возникает бесконечная рекурсия. Формально это звучит так: существует подстановка, применив которую к новым аргументам, мы получим старые. Например, на рисунке ниже рекурсивный вызов является обобщением исходного: можно подставить = [x, 3],
= [x, 3],  = x и получить исходный вызов.
= x и получить исходный вызов.
Можно проследить, что такая ситуация случается и в уже встреченных нами примерах расходимости. Как я писал раньше, при запуске appendo в обратную сторону будет произведен рекурсивный вызов со свободными переменными вместо всех переменных, что, конечно, менее конкретно, чем исходный вызов, в котором третий аргумент был зафиксирован.
Если мы запустим reverso с аргументами x =? и xr = [1, 2, 3], то можно проследить, что первый рекурсивный вызов опять произойдет с двумя свободными переменными, поэтому новые аргументы снова очевидным образом можно перевести в предыдущие.
С помощью этого критерия мы можем детектировать расходимость в процессе исполнения программы, понимать, что при данном порядке всё плохо, и динамически менять его на другой. Благодаря этому, в идеале, для каждого вызова подберется как раз нужный порядок.
Можно это делать наивно: если в конъюнкте обнаружилась расходимость, то забиваем на все ответы которые он уже нашел и откладываем его исполнение на потом, «пропуская вперед» следующий конъюнкт. Тогда, возможно, когда мы будем его исполнять дальше, будет известно уже больше информации и расходимости не возникнет. В наших примерах это приведет как раз к желаемому swap-у конъюнктов.
Есть и менее наивные способы, которые позволяют, например, не терять уже проделанной работы, откладывая исполнение. Уже с наиболее тупым вариантом изменения порядка исчезла расходимость во всех простых примерах, страдающих от некоммутативности конъюнкции, которые мы знаем, в том числе:
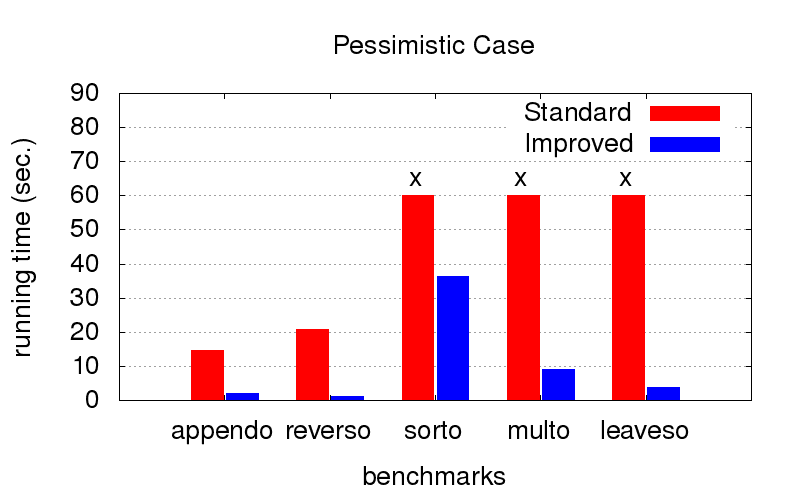
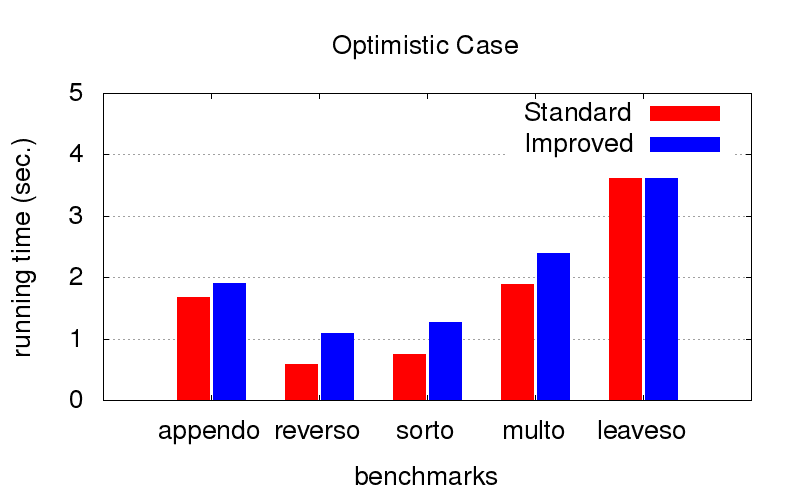
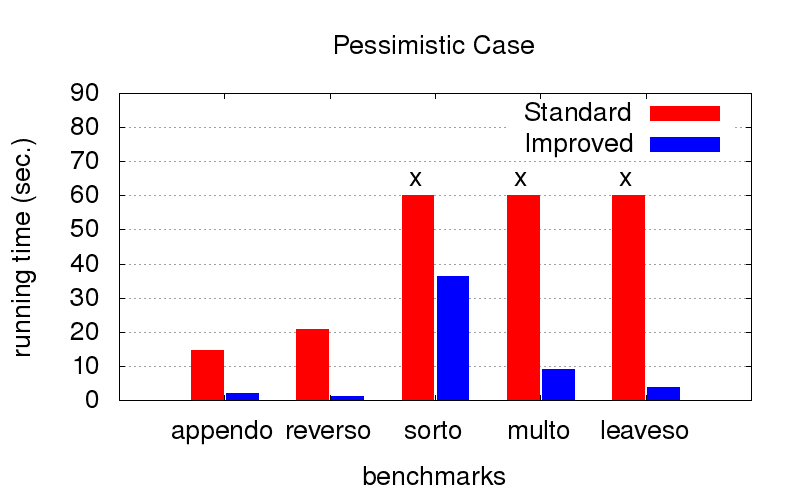
Это оказалось для нас неожиданным сюрпризом. Кроме расходимости оптимизация также борется с тормознутостью программ. На диаграммах ниже показано время исполнения программ с двумя разными порядками в конъюнкциях (условно говоря, одного самого хорошего и одного из многих плохих). Запускалось на компе с конфигурацией Intel Core i7 CPU M 620, 2.67GHz x 4, 8GB RAM с операционной системой Ubuntu 16.04.
Когда порядок и так оптимальный (мы подбираем его руками), оптимизация немного замедляет исполнение, но не критично
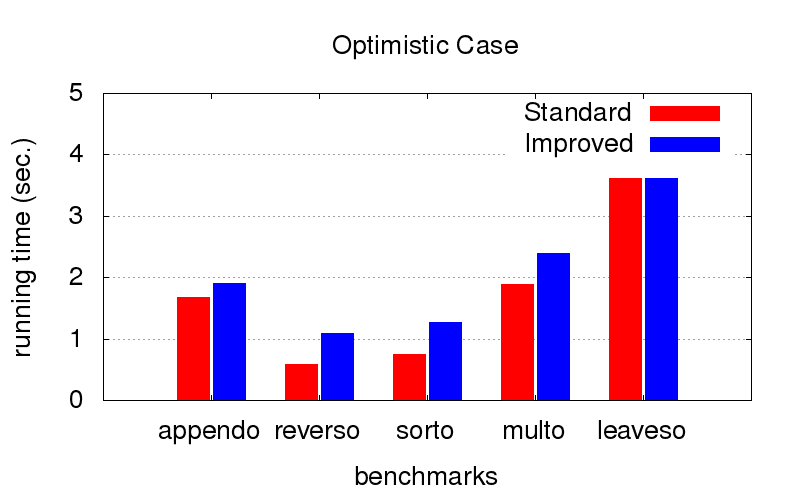
Зато когда порядок не оптимальный (например, подходящий только для запуска в другую сторону), с оптимизацией получается значительно быстрее. Крестики означают, что мы просто не смогли дождаться окончания, работает значительно дольше
Всё это базировалось чисто на интуиции и мы захотели это строго доказать. Теория всё-таки.
Для того, чтобы что-то доказать, нужна формальная семантика языка. Мы описали операционную семантику для miniKanren’а. Это упрощенная и математизированная версия реальной реализации языка. Здесь используется сильно ограниченная (поэтому простая в использовании) версия, в которой можно задать только завершающееся исполнение программ (поиск должен быть конечным). Но для наших целей ровно это и нужно.
Для доказательства критерия сначала формулируется лемма: исполнение программы из более общего состояния будет работать дольше. Формально: дерево вывода в семантике имеет большую высоту. Это доказывается индукцией, но нужно очень аккуратно обобщить утверждение, иначе индуктивное предположение окажется недостаточно сильным. Из этой леммы следует, что если при исполнении программы сработал критерий, то у дерева вывода есть собственное поддерево большей или равной высоты. Это дает противоречие, так как для индуктивно заданной семантики все деревья конечны. Значит, в нашей семантике исполнение данной программы невыразимо, из чего следует, что поиск в ней не завершается.
Предложенный способ является консервативным: мы что-то меняем, только когда убедились, что всё уже совсем плохо и хуже сделать невозможно, поэтому мы ничего не ломаем в плане завершимости программ.
Главное доказательство содержит довольно много деталей, поэтому у нас было желание формально верифицировать его, записав в Coq-е. Однако это оказалось довольно непросто технически, поэтому мы остудили свой пыл и всерьез занялись автоматической верификацией только в магистратуре.
В середине работы мы представили это исследование на постерной сессии ICFP-2017 на Student Research Competition. Там мы встретились с создателями языка — Уиллом Бердом и Дэниелом Фридманом — и они сказали, что это содержательно и надо посмотреть на это подробнее. Кстати говоря, Уилл вообще дружит с нашей лабораторией в JetBrains Research. Все исследования касающиеся miniKanren у нас начались, когда в 2015 году Уилл провел в Петербурге летнюю школу по реляционному программированию.
Через год мы привели нашу работу к более-менее законченному виду и презентовали статью на конференции Principles and Practice of Declarative Programming 2018.
Мы захотели продолжить заниматься формальной семантикой для miniKanren и строгим доказательством всяких его свойств. В литературе обычно свойства (часто далеко не очевидные) просто постулируются и демонстрируются на примерах, но никто ничего не доказывает. Например, главная книжка по реляционному программированию представляет из себя список вопросов и ответов, каждый из которых посвящен какому-то конкретному кусочку кода. Даже для утверждения о полноте interleaving search (а это одно из важнейших преимуществ miniKanren перед стандартным Prolog’ом) не получается найти строгую формулировку. Так жить нельзя, решили мы, и, получив благословение от Уилла, взялись за работу.
Напомню, что семантика, разработанная нами на предыдущем этапе, имела значительное ограничение: описывались только программы с конечным поиском. В miniKanren’е незавершающиеся программы тоже представляют интерес, потому что они могут перечислять бесконечное множество ответов. Поэтому нам нужна была более крутая семантика.
Существует множество различных стандартных способов задания семантики языка программирования, нам нужно было только выбрать один из них и адаптировать под конкретный случай. Мы описали семантику как labeled transition system — множество возможных состояний в процессе поиска и переходы между этими состояниями, некоторые из которых снабжены пометкой, что значит, что на данном этапе поиска нашелся очередной ответ. Исполнение конкретной программы, таким образом, задается последовательностью таких переходов. Эти последовательности могут быть конечными (приходящими в терминальное состояние) или бесконечными, описывая одновременно завершающиеся и незавершающиеся программы. Чтобы совсем математически строго задать такой объект, нужно использовать коиндуктивное определение.
Описанная выше семантика является операционной — она отражает настоящую реализацию поиска. Кроме неё мы используем также денотационную семантику, которая сопоставляет программам и конструкциям языка некоторые математические объекты естественным образом (например, отношения в программе рассматриваются как отношения на множестве термов, конъюнкция — это пересечение отношений и т.д.). Стандартный способ задавать такую семантику известен как наименьшая Эрбранова модель, и для miniKanren’а это уже было сделано ранее (тоже в нашей лаборатории).
После этого полноту поиск в языке, а заодно и корректность, можно сформулировать как эквивалентость этих двух семантик — совпадение множеств ответов для конкретной программы в них. Нам удалось это доказать. Интересно (и немножко грустно), что мы при этом обошлись без коиндукции, использовав несколько вложенных индукций с разными параметрами.
В качестве следствия мы получаем также корректность некоторых полезных языковых преобразований (в плане множества получаемых решений): если преобразование очевидно не меняет соответствующий математический объект, например, переупорядочивание конъюнктов или использование дистрибутивности конъюнкции или дизъюнкции, то и результаты поиска не меняются.
Теперь мы хотим использовать семантику для доказательств других полезных свойств языка, например, критериев завершимости/расходимости или корректности дополнительных языковых конструкций.
Также мы более обстоятельно взялись за строгое описание нашей формализации с помощью Coq’a. Преодолев множество различных сложностей и вложив много сил, мы смогли на данный момент задать операционную семантику языка и провести несколько доказательств, которые на бумажке имели вид «Очевидно. Qed». Мы не теряем веры в себя.
Сегодня я расскажу о своем исследовании в области реляционного программирования, которым занимаюсь в университете и в качестве студента-исследователя в лаборатории языковых инструментов JetBrains Research.
Что такое реляционное программирование? Обычно мы запускаем функцию с аргументами и получаем результат. А в реляционном случае можно делать наоборот: зафиксировать результат и один аргумент, а второй аргумент получить. Главное — правильно написать код и запастись терпением или хорошим кластером.

О себе
Меня зовут Дмитрий Розплохас, я студент первого курса магистратуры питерской Вышки, а в прошлом году окончил бакалавриат Академического университета по направлению «Языки программирования». С третьего курса бакалавриата также являюсь студентом-исследователем в лаборатории языковых инструментов JetBrains Research.
Реляционное программирование
Общие факты
Реляционное программирование — это когда вместо функций вы описываете отношения между аргументами и результатом. Если язык под это заточен, можно получить определенные бонусы, например, возможность запускать функцию в обратную сторону (по результату восстанавливать возможные значения аргументов).
Вообще, так можно делать в любом логическом языке, но интерес к реляционному программированию возник одновременно с появлением около десяти лет назад минималистичного чистого логического языка miniKanren, который позволил удобно описывать и использовать подобные отношения.
Вот несколько самых передовых примеров использования: можно написать чекер доказательств и использовать его для поиска доказательства (Near et al., 2008) или создать интерпретатор какого-то языка и использовать его для генерации программ по набору тестов (Byrd et al., 2017).
Синтаксис и игрушечный пример
miniKanren — язык небольшой, для описания отношений в нем используются только базовые математические конструкции. Это встраиваемый язык, его примитивы — библиотека для какого-то внешнего языка, и маленькие программки на miniKanren можно использовать внутри программы на другом языке.
Внешних языков, подходящих для miniKanren, целая куча. Изначально был Scheme, мы работаем с версией для Ocaml (OCanren), а полный список можно посмотреть на minikanren.org. Примеры в этой статье тоже будут на OCanren. Многие реализации добавляют вспомогательные функции, но мы сосредоточимся только на ядре языка.
Начнём с типов данных. Условно их можно разделить на два вида:
- Константы — это какие-то данные из языка, в который мы встроились. Строчки, числа, даже массивы. Но для базового miniKanren это всё чёрный ящик, константы можно только проверять на равенство.
- «Терм» — это кортеж из нескольких элементов. Обычно используются так же, как конструкторы данных в Haskell: конструтор данных (строка) плюс ноль или больше параметров. В OCanren используются обычные конструкторы данных из OCaml.
Например, если мы хотим работать с массивами в самом miniKanren, то его надо описать через термы по аналогии с функциональными языками — как односвязный список. Список — это либо пустой список (обозначается каким-нибудь простым термом), либо пара из первого элемента списка («голова») и остальных элементов («хвост»).
let emptyList = Nil
let list_123 = Cons (1, Cons (2, Cons (3, Nil)))
Программа на языке miniKanren — это соотношение между некоторыми переменными. При запуске программа выдаёт все возможные значения переменных в общем виде. Часто реализации позволяют ограничить количество ответов в выводе, например, найти только первый — поиск не всегда останавливается после нахождения всех решений.
Можно записать несколько соотношений, которые определяются друг через друга и даже вызываются рекурсивно, как функции. Например, ниже мы вместо функции
Отношение записывается как некоторое утверждение относительно своих аргументов. У нас есть четыре базовые операции:
- Унификация или равенство (===) двух термов, термы могут включать переменные. Например, можно записать отношение «список
состоит из одного элемента
»:
let isSingletono x l = l === Cons (x, Nil) - Конъюнкция (логическое «и») и дизъюнкция (логическое «или») — как в обычной логике. В OCanren обозначаются как &&& и |||. А вот логического отрицания в MiniKanren принципиально нет.
- Добавление новых переменных. В логике это квантор существования. Например, чтобы проверить список на непустоту, надо проверить, что список состоит из головы и хвоста. Они не являются аргументами отношения, поэтому требуется создать новые переменные:
let nonEmptyo l = fresh (h t) (l === Cons (h, t))
Отношение может вызывать само себя рекурсивно. Например, надо определить отношение «элемент
- Либо голова списка равна
- Либо
лежит в хвосте
let membero l x =
fresh (h t) (
(l === Cons (h, t)) &&&
(x === h ||| membero t x)
)
Базовая версия языка строится на этих четырех операциях. Также существуют расширения, позволяющие использовать и другие операции. Наиболее полезное из них — disequality constraint для задания неравенства двух термов (=/=).
Несмотря на минималистичность, miniKanren достаточно выразительный язык. Вот, например, как выглядит реляционная конкатенация двух списков. Функция двух аргументов превращается в трехместное отношение «
let appendo a b ab =
(a === Nil &&& ab === b) |||
(fresh (h t tb) (* Синтаксический сахар: после fresh неявно добавляются &&& *)
(a = Cons (h, t))
(appendo t b tb)
(ab === Cons (h, tb)))
Решение структурно не отличается от того, как бы мы это писали на функциональном языке. Мы разбираем два случая, объединённые дизъюнкцией:
- Если первый список пуст, то второй список и результат конкатенации равны.
- Если первый список непуст, то разбираем его на голову и хвост и конструируем результат с помощью рекурсивного вызова отношения.
Можем сделать запрос к этому отношению, зафиксировав первый и второй аргумент — получим конкатенацию списков:
run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q)⇒
q = Cons (1, Cons (2, Cons (3, Cons (4, Nil))))Можем зафиксировать последний аргумент — получим все разбиения данного списка на два.
run 4 (λ q r -> appendo q r (Cons (1, Cons (2, Cons (3, Nil)))))⇒
q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) |
q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) |
q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) |
q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil
Можно что угодно другое. Чуть более нестандартный пример, в котором мы зафиксируем лишь часть аргументов:
run 1 (λ q r -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil))))))⇒
q = 2, r = Cons (3, Cons (4, Nil))Как это работает
С точки зрения теории ничего впечатляющего здесь нет: всегда можно просто запустить перебор всех возможных вариантов для всех аргументов, проверяя для каждого набора не ведут ли они себя относительно заданной функции/отношения так, как нам бы хотелось (см. «Алгоритм британского музея»). Интерес представляет то, что здесь перебор (иначе говоря, поиск решения) пользуется исключительно структурой описанного отношения, благодаря чему может быть относительно эффективен на практике.
Поиск идет по отношению накапливая информацию о различных переменных в текущем состоянии. Про каждую переменную мы либо ничего не знаем, либо знаем, как она выражается через термы, значения и другие переменные. Например:
b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?
Проходя через унификацию, мы смотрим на два терма с учетом этой информации и либо обновляем состояние, либо обрываем поиск, если два терма не могут быть унифицированы. Например, выполнив унификацию b = c, мы получим новую информацию: x = 10, y = z. А вот унификация b = Nil вызовет противоречие.
Поиск в конъюнктах мы выполняем последовательно (чтобы информация накапливалась), а в дизъюнкции мы разделяем поиск на две параллельные ветки и идем дальше, чередуя шаги в них — это так называемый interleaving search. Благодаря этому чередованию поиск является полным — каждое подходящее решение будет найдено через конечное время. Например, в языке Prolog это не так. Там выполняется что-то вроде обхода в глубину (который может зависнуть на бесконечной ветке), а interleaving search по сути является хитрой модификацией обхода в ширину.
Давайте теперь посмотрим как работает первый запрос из предыдущего раздела. Так как в appendo есть рекурсивные вызовы, мы допишем к переменным индексы, чтобы их отличать. На рисунке ниже представлено дерево перебора. Стрелочками отмечены направления распространения информации (за исключением возврата из рекурсии). Между дизъюнкциями информация не распространяется, а между конъюнкциями распространяется слева направо.

- Мы начинаем с внешнего вызова appendo. Левая ветка дизъюнкции отмирает из-за противоречия: список
не пуст.
- В правой ветке вводятся вспомогательные переменные, которые затем используются для «разбирания» списка
на голову и хвост.
- После этого происходит рекурсивный вызов appendo для a=[2], b=[3, 4], ab=?, в котором происходят аналогичные операции.
- А вот в третьем вызове appendo уже имеем a=[], b=[3,4], ab=?, и тогда левая дизъюнкция как раз срабатывает, после чего мы получаем информацию ab=b. А вот в правой ветке получается противоречие.
- Теперь мы можем выписать всю доступную информацию и восстановить ответ, подставив значения переменных:
a_1 = [1, 2]
b_1 = [3, 4]
ab_1 = Cons h_1 tb_1
h_1 = 1
a_2 = t_1 = [2]
b_2 = b_1 = [3, 4]
ab_2 = tb_1 = Cons h_2 tb_2
h_2 = 2
a_3 = t_2 = Nil
b_3 = b_2 = b_1 = [3, 4]
ab_3 = tb_2 = b_3 = [3, 4]
- Отсюда следует, что
= Cons (1, Cons (2, [3, 4])) = [1, 2, 3, 4], что и требовалось.
Чем я занимался в бакалавриате
Всё тормозит
Как всегда: вам обещают, что всё будет супер декларативно, а на деле нужно подстраиваться под язык и писать всё специальным образом (держа в голове как всё будет исполняться), чтобы работало хоть что-то, кроме простейших примеров. Это разочаровывает.
Одна из первых проблем, с которыми сталкивается начинающий программист на miniKanren — всё очень сильно зависит от того, в каком порядке вы опишите условия (конъюнкты) в программе. При одном порядке всё ок, а поменяли два конъюнкта местами и всё стало работать очень медленно или вообще не завершилось. Это неожиданно.
Даже в примере с appendo запуск в обратную сторону (генерация разбиений списка на два) не завершается, если явно не указать, сколько ответов вы хотите (тогда поиск оборвется, после того как будет найдено нужное количество).
Допустим, мы зафиксируем исходные переменные так: a = ?, b = ?, ab = [1, 2, 3] (см. рис. ниже) Во второй ветке при рекурсивном вызове эта информация никак не будет использоваться (переменная ab и ограничения на

Всё не настолько плохо, как может показаться на первый взгляд, потому что перебирать эти тройки мы будем большими группами. Списки с одинаковой длиной, но разными элементами, никак не отличаются с точки зрения функции, поэтому попадут в одно решение — на месте элементов будут свободные переменные. Тем не менее, мы всё равно будем перебирать все возможные длины списков, хотя нужна нам только одна, и мы знаем, какая. Это очень нерациональное использование (неиспользование) информации при поиске.
Этот конкретный пример легко исправить: нужно просто перенести рекурсивный вызов в конец и всё заработает как надо. До рекурсивного вызова будет происходить унификация с переменной ab и рекурсивный вызов будет производиться от хвоста данного списка (как нормальная рекурсивная функция). Это определение с рекурсивным вызовом в конце будет хорошо работать во всех направлениях: к рекурсивному вызову мы успеваем накопить всю возможную информацию об аргументах.
Однако в любом чуть более сложном примере, когда есть несколько содержательных вызовов, одного конкретного порядка, для которого всё будет хорошо, не существует. Самый простой пример: разворачивание списка при помощи конкатенации. Фиксируем первый аргумент — нужен именно этот порядок, фиксируем второй — нужно поменять вызовы местами. Иначе долго ищется и поиск не завершается.
reverso x xr =
(x === Nil &&& xr == Nil) |||
(fresh (h t tr)
(x === Cons (h, t))
(reverso t tr)
(appendo tr (Cons (h, Nil)) xr))
Так происходит потому, что interleaving search обрабатывает конъюнкты последовательно, а как сделать по-другому, не лишившись при этом приемлемой эффективности, никто не смог придумать, хотя и пытались. Конечно, все решения когда-нибудь найдутся, но при неправильном порядке они будут искаться так нереально долго, что никакого практического смысла в этом нет.
Существуют техники написания программ, позволяющие избежать этой проблемы. Но многие из них требуют особого мастерства и воображения для применения, а в результате получаются очень большие программы. Пример — техника term size bounding и определение бинарного деления с остатком через умножение с её помощью. Вместо того, чтобы тупо записать математическое определение
divo n m q r =
(fresh (mq)
(multo m q mq)
(pluso mq r n)
(lto r m))
приходится писать рекурсивное определение на 20 строчек + большую вспомогательную функцию, которые нереально прочитать (я до сих пор не понимаю, что там делается). Его можно найти в диссертации Уилла Берда в разделе Pure Binary Arithmetic.
С учетом всего вышесказанного, хочется придумать какую-то модификацию поиска, чтобы просто и естественно написанные программы тоже работали.
Оптимизируем
Мы заметили, что когда всё плохо, поиск не будет завершаться, если явно не указать количество ответов и не оборвать его. Поэтому решили бороться именно с незавершаемостью поиска — это гораздо легче конкретизировать, чем «работает долго». Вообще, конечно, хочется просто ускорить поиск, но это гораздо сложнее формализовать, так что мы начали с менее амбициозной задачи.
В большинстве случаев, когда поиск расходится, происходит ситуация, которую легко отследить. Если некоторая функция вызывается рекурсивно, и при рекурсивном вызове аргументы у нас такие же или менее конкретные, то и в рекурсивном вызове снова генерируется ещё одна такая подзадача и возникает бесконечная рекурсия. Формально это звучит так: существует подстановка, применив которую к новым аргументам, мы получим старые. Например, на рисунке ниже рекурсивный вызов является обобщением исходного: можно подставить
Можно проследить, что такая ситуация случается и в уже встреченных нами примерах расходимости. Как я писал раньше, при запуске appendo в обратную сторону будет произведен рекурсивный вызов со свободными переменными вместо всех переменных, что, конечно, менее конкретно, чем исходный вызов, в котором третий аргумент был зафиксирован.
Если мы запустим reverso с аргументами x =? и xr = [1, 2, 3], то можно проследить, что первый рекурсивный вызов опять произойдет с двумя свободными переменными, поэтому новые аргументы снова очевидным образом можно перевести в предыдущие.
reverso x x_r (* x = ?, x_r = [1, 2, 3] *)
fresh (h t t_r)
(x === Cons (h, t))
(* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil)))
x = Cons (h, t) *)
(reverso t t_r)
(* критерий: можно подставить t=x, t_r=[1,2,3], получили исходный вызов *)
С помощью этого критерия мы можем детектировать расходимость в процессе исполнения программы, понимать, что при данном порядке всё плохо, и динамически менять его на другой. Благодаря этому, в идеале, для каждого вызова подберется как раз нужный порядок.
Можно это делать наивно: если в конъюнкте обнаружилась расходимость, то забиваем на все ответы которые он уже нашел и откладываем его исполнение на потом, «пропуская вперед» следующий конъюнкт. Тогда, возможно, когда мы будем его исполнять дальше, будет известно уже больше информации и расходимости не возникнет. В наших примерах это приведет как раз к желаемому swap-у конъюнктов.
Есть и менее наивные способы, которые позволяют, например, не терять уже проделанной работы, откладывая исполнение. Уже с наиболее тупым вариантом изменения порядка исчезла расходимость во всех простых примерах, страдающих от некоммутативности конъюнкции, которые мы знаем, в том числе:
- сортировка списка чисел (она же генерация всех перестановок списка),
- арифметика Пеано и двоичная арифметика,
- генерация двоичных деревьев заданного размера.
Это оказалось для нас неожиданным сюрпризом. Кроме расходимости оптимизация также борется с тормознутостью программ. На диаграммах ниже показано время исполнения программ с двумя разными порядками в конъюнкциях (условно говоря, одного самого хорошего и одного из многих плохих). Запускалось на компе с конфигурацией Intel Core i7 CPU M 620, 2.67GHz x 4, 8GB RAM с операционной системой Ubuntu 16.04.
Когда порядок и так оптимальный (мы подбираем его руками), оптимизация немного замедляет исполнение, но не критично
Зато когда порядок не оптимальный (например, подходящий только для запуска в другую сторону), с оптимизацией получается значительно быстрее. Крестики означают, что мы просто не смогли дождаться окончания, работает значительно дольше
Как ничего не сломать
Всё это базировалось чисто на интуиции и мы захотели это строго доказать. Теория всё-таки.
Для того, чтобы что-то доказать, нужна формальная семантика языка. Мы описали операционную семантику для miniKanren’а. Это упрощенная и математизированная версия реальной реализации языка. Здесь используется сильно ограниченная (поэтому простая в использовании) версия, в которой можно задать только завершающееся исполнение программ (поиск должен быть конечным). Но для наших целей ровно это и нужно.
Для доказательства критерия сначала формулируется лемма: исполнение программы из более общего состояния будет работать дольше. Формально: дерево вывода в семантике имеет большую высоту. Это доказывается индукцией, но нужно очень аккуратно обобщить утверждение, иначе индуктивное предположение окажется недостаточно сильным. Из этой леммы следует, что если при исполнении программы сработал критерий, то у дерева вывода есть собственное поддерево большей или равной высоты. Это дает противоречие, так как для индуктивно заданной семантики все деревья конечны. Значит, в нашей семантике исполнение данной программы невыразимо, из чего следует, что поиск в ней не завершается.
Предложенный способ является консервативным: мы что-то меняем, только когда убедились, что всё уже совсем плохо и хуже сделать невозможно, поэтому мы ничего не ломаем в плане завершимости программ.
Главное доказательство содержит довольно много деталей, поэтому у нас было желание формально верифицировать его, записав в Coq-е. Однако это оказалось довольно непросто технически, поэтому мы остудили свой пыл и всерьез занялись автоматической верификацией только в магистратуре.
Публикация
В середине работы мы представили это исследование на постерной сессии ICFP-2017 на Student Research Competition. Там мы встретились с создателями языка — Уиллом Бердом и Дэниелом Фридманом — и они сказали, что это содержательно и надо посмотреть на это подробнее. Кстати говоря, Уилл вообще дружит с нашей лабораторией в JetBrains Research. Все исследования касающиеся miniKanren у нас начались, когда в 2015 году Уилл провел в Петербурге летнюю школу по реляционному программированию.
Через год мы привели нашу работу к более-менее законченному виду и презентовали статью на конференции Principles and Practice of Declarative Programming 2018.
Чем я занимаюсь в магистратуре
Мы захотели продолжить заниматься формальной семантикой для miniKanren и строгим доказательством всяких его свойств. В литературе обычно свойства (часто далеко не очевидные) просто постулируются и демонстрируются на примерах, но никто ничего не доказывает. Например, главная книжка по реляционному программированию представляет из себя список вопросов и ответов, каждый из которых посвящен какому-то конкретному кусочку кода. Даже для утверждения о полноте interleaving search (а это одно из важнейших преимуществ miniKanren перед стандартным Prolog’ом) не получается найти строгую формулировку. Так жить нельзя, решили мы, и, получив благословение от Уилла, взялись за работу.
Напомню, что семантика, разработанная нами на предыдущем этапе, имела значительное ограничение: описывались только программы с конечным поиском. В miniKanren’е незавершающиеся программы тоже представляют интерес, потому что они могут перечислять бесконечное множество ответов. Поэтому нам нужна была более крутая семантика.
Существует множество различных стандартных способов задания семантики языка программирования, нам нужно было только выбрать один из них и адаптировать под конкретный случай. Мы описали семантику как labeled transition system — множество возможных состояний в процессе поиска и переходы между этими состояниями, некоторые из которых снабжены пометкой, что значит, что на данном этапе поиска нашелся очередной ответ. Исполнение конкретной программы, таким образом, задается последовательностью таких переходов. Эти последовательности могут быть конечными (приходящими в терминальное состояние) или бесконечными, описывая одновременно завершающиеся и незавершающиеся программы. Чтобы совсем математически строго задать такой объект, нужно использовать коиндуктивное определение.
Описанная выше семантика является операционной — она отражает настоящую реализацию поиска. Кроме неё мы используем также денотационную семантику, которая сопоставляет программам и конструкциям языка некоторые математические объекты естественным образом (например, отношения в программе рассматриваются как отношения на множестве термов, конъюнкция — это пересечение отношений и т.д.). Стандартный способ задавать такую семантику известен как наименьшая Эрбранова модель, и для miniKanren’а это уже было сделано ранее (тоже в нашей лаборатории).
После этого полноту поиск в языке, а заодно и корректность, можно сформулировать как эквивалентость этих двух семантик — совпадение множеств ответов для конкретной программы в них. Нам удалось это доказать. Интересно (и немножко грустно), что мы при этом обошлись без коиндукции, использовав несколько вложенных индукций с разными параметрами.
В качестве следствия мы получаем также корректность некоторых полезных языковых преобразований (в плане множества получаемых решений): если преобразование очевидно не меняет соответствующий математический объект, например, переупорядочивание конъюнктов или использование дистрибутивности конъюнкции или дизъюнкции, то и результаты поиска не меняются.
Теперь мы хотим использовать семантику для доказательств других полезных свойств языка, например, критериев завершимости/расходимости или корректности дополнительных языковых конструкций.
Также мы более обстоятельно взялись за строгое описание нашей формализации с помощью Coq’a. Преодолев множество различных сложностей и вложив много сил, мы смогли на данный момент задать операционную семантику языка и провести несколько доказательств, которые на бумажке имели вид «Очевидно. Qed». Мы не теряем веры в себя.