Две недели назад мы были на Java-конференции в Питере — Joker 2017. Уже традиционно пришли туда не с пустыми руками, а с веселыми и сложными задачами, над которыми можно посмеяться и/или поломать голову. Спасибо всем, кто в эти два дня решал задачи, задавал вопросы и предлагал свои оригинальные решения. Поздравляем победителей!
Все задачи верно решили целых три человека:
— Рюрик Крылов (который к тому же сдал корешок из буклета с верными ответами самым первым)
— Евгений Крутень
— Василий Бригинец
Публикуем, как обещали, развернутые решения. Вынесли под спойлер, чтобы свои силы могли попробовать и те, кто пропустил конференцию.




Пока ждем появления на канале конференции видео с докладом Вовы Озерова про сериализацию, можно скачать слайды или посмотреть интервью Якова Жданова про то, зачем GridGain поддерживать открытый код, и кто придумывает нам задачи.
Все задачи верно решили целых три человека:
— Рюрик Крылов (который к тому же сдал корешок из буклета с верными ответами самым первым)
— Евгений Крутень
— Василий Бригинец
Публикуем, как обещали, развернутые решения. Вынесли под спойлер, чтобы свои силы могли попробовать и те, кто пропустил конференцию.

Задача №1

Решение
t — длительность происходящего действия в минутах,
r — количество написанных строк кода за время t,
k — количество кивков за время t.






Произведем замену




Решаем обычное квадратное уравнение: дискриминант, корень, два возможных решения:





Производим обратную замену:


и выбираем один корень, удовлетворяющий условию t1 < 60, который подставляем в уравнение:

Ответ: 10,185
r — количество написанных строк кода за время t,
k — количество кивков за время t.
Произведем замену
Решаем обычное квадратное уравнение: дискриминант, корень, два возможных решения:
Производим обратную замену:
и выбираем один корень, удовлетворяющий условию t1 < 60, который подставляем в уравнение:
Ответ: 10,185
Задача №2

Решение
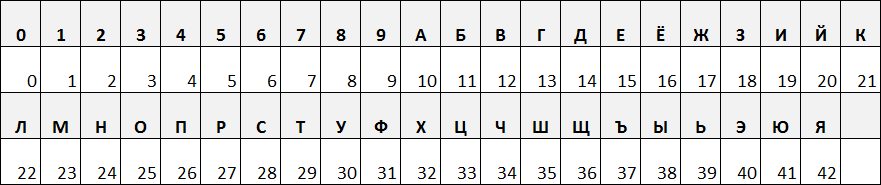
Имеем систему счисления с основанием 10 + 33 = 43

Приводим кириллические числа к десятичному представлению:
ПОСТ = {26, 25, 28, 29} = (((26 * 43) + 25) * 43 + 28) * 43 + 29 = 2114640
Аналогично:
ПОКАЙСЯ = {26, 25, 21, 10, 20, 28, 42} = 168103278466
МОЛИТВА = {23, 25, 22, 19, 29, 12, 10} = 149143339604
ПОКАЙСЯ + МОЛИТВА * ПОСТ = 315384639763481026
Приводим десятичный результат к кириллическому представлению, для этого ищем первый старший разряд, который будет нулевым:


Последовательно делим остаток на 43 в степени от 10 до 0:











{14, 25, 22, 7, 4, 24, 37, 32, 0, 18, 31} = ДОЛ74НЪХ0ЗФ
Ответ: ДОЛ74НЪХ0ЗФ
Приводим кириллические числа к десятичному представлению:
ПОСТ = {26, 25, 28, 29} = (((26 * 43) + 25) * 43 + 28) * 43 + 29 = 2114640
Аналогично:
ПОКАЙСЯ = {26, 25, 21, 10, 20, 28, 42} = 168103278466
МОЛИТВА = {23, 25, 22, 19, 29, 12, 10} = 149143339604
ПОКАЙСЯ + МОЛИТВА * ПОСТ = 315384639763481026
Приводим десятичный результат к кириллическому представлению, для этого ищем первый старший разряд, который будет нулевым:
Последовательно делим остаток на 43 в степени от 10 до 0:
{14, 25, 22, 7, 4, 24, 37, 32, 0, 18, 31} = ДОЛ74НЪХ0ЗФ
Ответ: ДОЛ74НЪХ0ЗФ
Задача №3

Решение
С учетом начальных условий подсчитаем количество возможных сочетаний:
Герман: 2 туза из 4 = = 6.
= 6.
Старуха: 2 пики из 9 числовых = = 36.
= 36.
Флоп: 3 карты из оставшихся 48 в колоде = = 17296.
= 17296.
Всего подходят 6 * 36 * 17296 = 3735936 комбинаций.
Теперь рассмотрим подходящие варианты.
У Германа во всех вариантах также: 2 туза из 4 = = 6.
= 6.
Варианты с рукой старухи:
1) нет 3 и 7 в руке, остается 2 из 7 = = 21.
= 21.
2) одна 3 или 7 в руке, это 2 * 7 сочетаний = 14.
3) и 3 и 7 в руке = 1.
Проверяем, что мы рассмотрели все комбинации 21 + 14 + 1 = 36.
Теперь находим количество подходящих сочетаний для флопа:
1) в колоде осталось 2 туза, 4 тройки и 4 семерки = 2 * 4 * 4 = 32 сочетания.
2) в колоде осталось 2 туза, 3 карты одного числа и 4 другой = 2 * 3 * 4 = 24 сочетания.
3) в колоде осталось 2 туза, 3 тройки и 3 семерки = 2 * 3 * 3 = 18 сочетаний.
Общее количество подходящих сочетаний:
6 * 21 * 32 + 6 * 14 * 24 + 6 * 1 * 18 = 6156
Искомая вероятность 6156 / 3735936 = 0,00164777983348751156336725254394
Ответ: 0,00165 или 0,165 %
Герман: 2 туза из 4 =
Старуха: 2 пики из 9 числовых =
Флоп: 3 карты из оставшихся 48 в колоде =
Всего подходят 6 * 36 * 17296 = 3735936 комбинаций.
Теперь рассмотрим подходящие варианты.
У Германа во всех вариантах также: 2 туза из 4 =
Варианты с рукой старухи:
1) нет 3 и 7 в руке, остается 2 из 7 =
2) одна 3 или 7 в руке, это 2 * 7 сочетаний = 14.
3) и 3 и 7 в руке = 1.
Проверяем, что мы рассмотрели все комбинации 21 + 14 + 1 = 36.
Теперь находим количество подходящих сочетаний для флопа:
1) в колоде осталось 2 туза, 4 тройки и 4 семерки = 2 * 4 * 4 = 32 сочетания.
2) в колоде осталось 2 туза, 3 карты одного числа и 4 другой = 2 * 3 * 4 = 24 сочетания.
3) в колоде осталось 2 туза, 3 тройки и 3 семерки = 2 * 3 * 3 = 18 сочетаний.
Общее количество подходящих сочетаний:
6 * 21 * 32 + 6 * 14 * 24 + 6 * 1 * 18 = 6156
Искомая вероятность 6156 / 3735936 = 0,00164777983348751156336725254394
Ответ: 0,00165 или 0,165 %
Пока ждем появления на канале конференции видео с докладом Вовы Озерова про сериализацию, можно скачать слайды или посмотреть интервью Якова Жданова про то, зачем GridGain поддерживать открытый код, и кто придумывает нам задачи.