Comments 8
Масштабируемость. Любой объект необходимо беспрепятственно увеличивать и уменьшать. Дефекты геометрии неуместны.
Мне кажется, здесь нужно уточнить, что значит "масштабируемость", и что значит "дефекты". Потому что полигональный меш (faces) можно масштабировать без дефектов, т. к. это векторное представление. И, на самом деле, как это указано далее, на экране мы все равно видим полигональный меш, даже если геометрическое ядро использует NURBS. Мне кажется, это очень важный аспект, который должен быть подробнее раскрыт в этой статье.
Гладкость. Сетка из треугольников для работы с чертежами не подходит — на чертеже нужны гладкие и чёткие контуры, а сетка создаст визуальную грязь.
Опять же, здесь нет ясности, почему она не подходит, ведь на экране мы все равно ее же и видим, хотелось бы понять, чем чертеж отличается от изображения на экране (насколько мне удалось понять, тот же SolidWorks выводит в dxf кусочно-линейное представление при экспорте чертежа). Стоит ли ожидать, что при экспорте из КОМПАС в какой-либо векторный формат мы увидим чистые кривые NURBS?
Точность. Движение управляющих органов станка с числовым программным управлением, который работает с 3D-моделью, намного проще задавать с помощью математических формул.
Насколько это реализуемо в действительности? Есть какие-либо форматы CAM (G-Code, например), которые принимают хотя бы NURBS в качестве исходных данных? Насколько мне известно, G-CODE может делать окружности и полярную систему координат.
И насколько верно то, что граничное представление на основе NURBS является точным? Я все время в популярных статьях читаю, что NURBS — это математически точное гладкое представление, но мой опыт мне говорит, что невозможно найти аналитическое пересечение двух кубических NURBS поверхностей как и невозможно с помощью NURBS точно представить винтовую поверхность (спираль). Я все время читаю разные статьи про NURBS, и у меня складывается впечатление, что эту проблему того, что NURBS — это приближенное представление объектов, производители инженерного софта предпочитают умалчивать. Есть ли у вашей компании какие-то идеи насчет того, как можно эту ситуацию исправить? Неужели человечество и дальше будет пользоваться инженерными программами, которые неспособны точно представлять детали? Я понимаю, что математически это пока невозможно, но все же?
Нужно уточнить, что значит «масштабируемость», и что значит «дефекты».«Масштабируемость» означает, что при любом масштабе изображение будет настолько гладким, насколько гладкая сама модель. Круглое всегда остаётся круглым, угол — углом. Под «дефектом» же подразумевается нарушение изложенного принципа.
Полигональный меш (faces) можно масштабировать без дефектов, т. к. это векторное представление. И, на самом деле, как это указано далее, на экране мы все равно видим полигональный меш, даже если геометрическое ядро использует NURBS.Информация о форме геометрической модели в граничном представлении задаётся аналитически. Точность её отображения на экране определяется на уровне приложения и расчёт мешей производится таким образом, чтобы модель визуально казалась гладкой. Если мы возьмём исходную полигональную модель, то, вне зависимости от выбранной САПР, при увеличении масштаба мы сперва увидим увеличивающиеся треугольники, а затем модель станет угловатой. Ограничение в этом случае задаётся на уровне 3D-модели — с какой точностью изначально был рассчитан меш, например при записи STL, с такой точностью нам и придется работать дальше.
Сетка из треугольников для работы с чертежами не подходит — на чертеже нужны гладкие и чёткие контуры, а сетка создаст визуальную грязь.Рассмотрим куб. При проецировании его граничного представления на плоскость получаем квадрат. В случае с полигональным представлением мы увидим при проецировании квадрат с диагональю. Теперь представьте проецирование цилиндра в чертёж. Диагоналей будет гораздо больше. Они и образуют ту визуальную грязь, о которой упоминалось выше:
Опять же, здесь нет ясности, почему она не подходит, ведь на экране мы все равно ее же и видим, хотелось бы понять, чем чертеж отличается от изображения на экране.
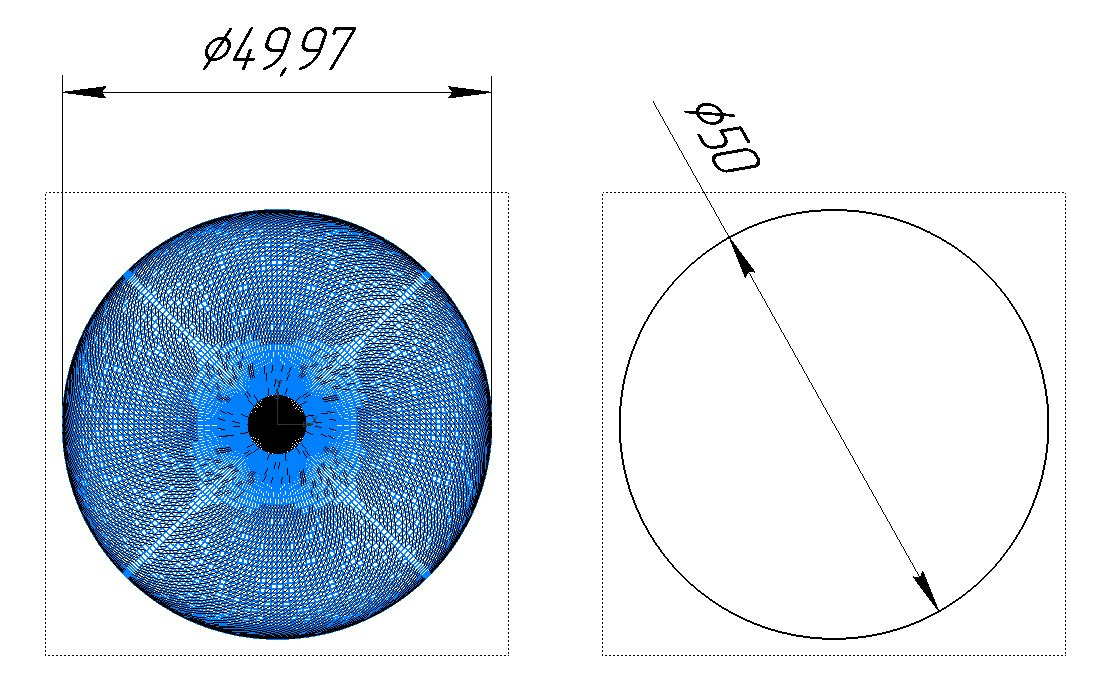
Кстати, обратите внимание на автоматически проставляемый размер в КОМПАС-3D, который для шара в полигональном формате STL (проекция слева) отобразился с погрешностью.
Хотелось бы понять, чем чертеж отличается от изображения на экране (насколько мне удалось понять, тот же SolidWorks выводит в dxf кусочно-линейное представление при экспорте чертежа). Стоит ли ожидать, что при экспорте из КОМПАС в какой-либо векторный формат мы увидим чистые кривые NURBS?КОМПАС-3D при экспорте кривых в векторные форматы (в том числе при экспорте чертежей) в общем случае передает именно NURBS, а не кусочно-линейное представление.
Движение управляющих органов станка с числовым программным управлением, который работает с 3D-моделью, намного проще задавать с помощью математических формул.Речь идёт о том, что при наличии граничного представления модели, при желании, можно построить более точную траекторию режущего инструмента. При полигональном представлении модели этого сделать нельзя, так как исходная информация о форме изготавливаемого объекта отсутствует и заменена приближенной.
Насколько это реализуемо в действительности? Есть какие-либо форматы CAM (G-Code, например), которые принимают хотя бы NURBS в качестве исходных данных? Насколько мне известно, G-CODE может делать окружности и полярную систему координат.
Если говорить о технической стороне разработки программ, то наши друзья из компании DP Technology (разработчики CAM-системы ESPRIT) подсказывают, что им встречались публикации, в которых отдельные энтузиасты предлагали собственные версии G-кода, способного выполнять «NURBS interpolation». Это может быть полезно для 5-осевых операций, так как значительно сокращается траектория движения инструмента и, соответственно, уменьшается размер управляющей программы для станка с ЧПУ. Но пока это всё остаётся в области науки.
И насколько верно то, что граничное представление на основе NURBS является точным?В граничном представлении NURBS кривые и поверхности точно проходят по заданным дискретным местам пространства (точкам или кривым), в остальных точках пространства к ним предъявляется требование гладкости и только. Так как исходные данные для построения NURBS объектов являются дискретными, то NURBS кривые и поверхности в граничном представлении считаются точными, потому что они точно соответствуют исходным требованиям. Более того, NURBS объектами можно точно представить форму почти всех аналитических кривых и поверхностей (очень громоздко, но можно). Всё, для чего известны аналитические законы, в граничном представлении описывается другими объектами, например, кривыми и поверхностями второго порядка. Для объектов, которые не поддаются аналитическому описанию, граничное представление использует специальные приёмы. Так, для точного описания кривой пересечения двух кубических NURBS поверхностей применяются итерационные методы: кривая пересечения представляется набором точек, которые служат начальными приближениями для определения положения точки кривой пересечения с требуемой точностью. Таким образом, положение точек кривой пересечения при каждом обращении к кривой насчитывается заново итерационными методами по лежащей в кривой информации.
Спасибо за ваши уточнения! Мне кажется, их нужно включить в статью.
В граничном представлении NURBS кривые и поверхности точно проходят по заданным дискретным местам пространства (точкам или кривым), в остальных точках пространства к ним предъявляется требование гладкости и только. Так как исходные данные для построения NURBS объектов являются дискретными, то NURBS кривые и поверхности в граничном представлении считаются точными, потому что они точно соответствуют исходным требованиям.
То есть (далее я могу ошибаться), мы берем, например, пересечение двух поверхностей, скажем, кубических, используя любой доступный науке численный алгоритм(неточный). То есть, мы получаем неточное кусочно-линейное представление кривых пересечения. Далее, мы берем кубические кривые и делаем аппроксимацию (подгоняем их параметры) таким образом, чтобы эти кривые в точности проходили через неточные точки кусочно-линейного приближения (полученные, скажем, решением уравнения принадлежности точки одновременно двум кубическим поверхностям по методу Ньютона). Между этими неточными точками, по которым точно проходит кривая, ни о каком точном представлении пересечения тоже не может быть речи, а требования предъявляются только к гладкости (непрерывности). Получается, что аналитическое NURBS представление с любой степенью точности (гладко) может выразить неточное пересечение поверхностей?
То есть в кривой пересечения лежит некоторая информация (это не обязательно множество точек; могут лежать пересекаемые поверхности и некоторые данные о параметре кривой), которая позволяет рассчитать точку на пересечении поверхностей с максимальной машинной точностью, выше которой не имеет смысла уточнять.
Никаких кусочно-линейных представлений, кубических кривых, аппроксимационных кривых в кривой пересечения нет. Кривая пересечения поверхностей — это объект, который для указанного параметра выдает точку в пространстве (как и все другие кривые).
Надеемся, это пояснение ответит вопрос о точности кривой пересечения.
[удалено]
Как математическая библиотека КОМПАС-3D превратилась в C3D Toolkit для разработчиков САПР → часть 1