samsergey Jul 8 2023 at 08:05

Бардак в идеальном мире. Часть 1

Medium

14 min

27K

Математика — наука точная и имеет дело с идеальными моделями. Иной раз это даже рассматривается как недостаток: мол, модели ваши, конечно, элегантны, изящны и красивы, но реальный мир быстро наведёт в этих идеальных построениях такой бардак, что на самом деле всё будет совсем не так, как вы, математики, описываете. И линий‑то идеально прямых не бывает, и число $\pi$ мы никогда «точно» не узнаем, и большинство уравнений на свете решается только приближённо, в общем, это всё нереально правильно и упорядочено.

Всё верно, но математика, как Чак Норрис, настолько крута, что способна порождать и внутри идеальных моделей хаос, непредсказуемость и чёрт знает что! И, как полагается неимоверно крутому персонажу, она способна, как породить этот хаос, так и дать ему математически точное объяснение. Да, я из тех философов, что полагают: всемогущий создатель может создать камень, который он не сможет поднять. Знакомство с теорией разрешимости, собственно, и делает эту задачу признаком всемогущества. Есть серьёзные основания полагать, что хаос, неопределённость и неразрешимость, не просто не мешают науке и мышлению, а являются её неотъемлемыми частями и залогом непрекращающегося развития.

Постановка задачи

Нашим рабочим примером станут идеальные прыжки идеального шарика на идеальном столике с идеальной пружинкой в поле силы тяжести, конечно же, идеальном. Падение шарика линейно, колебания столика на пружинке линейны, все уравнения решаются аналитически. Что же может пойти не так?

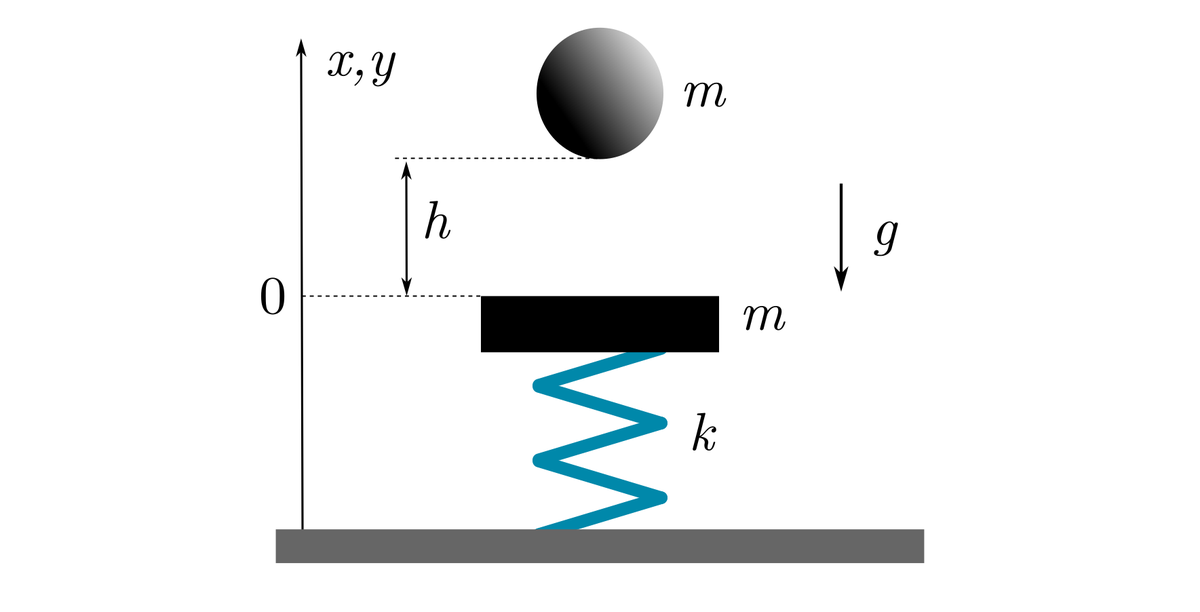
Давайте засучим рукава и пройдёмся по этой задачке, как физики, начав с уравнений движения. Для падающего с высоты шарика с массой m получим такую задачу Коши (дифференциальное уравнение, плюс начальные условия):

$m x''(t) = -mg,\quad x(0) = h,\ x'(0) = 0.$

Для подпружиненного столика, на который падает шарик, такую задачу:

$m y''(t) = -k y(t),\quad y(0) = 0,\ y'(0) = 0.$

Оба уравнения не выражают ничего сложнее второго закона Ньютона. Координаты и отсчитываются в одной системе, с нулём в точке равновесия столика (так мы исключаем из уравнений действие силы тяжести на столик). Для простоты, положим что и столик и шарик имеют одинаковую массу.

При любом анализе мы заинтересованы в минимизации числа параметров. В нашем случае, их четыре: масса шарика и столика, ускорение свободного падения, жёсткость пружины и начальное положение шарика. Подбирая подходящие масштабы длины и времени, мы способны свести их к количество к единице. Для этого станем измерять величины и в неизвестных пока единицах а время — в единицах попутно введя обобщённые координаты и импульсы системы:

$x = Lq_1,\ x' = \frac{L}{T}p_1,\ y = Lq_2,\ y' = \frac{L}{T}p_2.$

Используя такие масштабы, наши уравнения и начальные условия можно переписать:

$\begin{align*}&\frac{L}{T^2} \dot{p}_1 = -g,\quad Lq_1(0) = h,\ p_1 = 0\\ &m\frac{L}{T^2} \dot{p}_2 = -k L q_2,\quad q_2(0) = 0,\ p_2(0) = 0.\end{align*}$

Здесь величины $q_{1,2}, p_{1,2}$ безразмерны, а точки обозначают производную по безразмерному времени. Теперь мы можем выбрать такие масштабы, какие нам надо, например, подобрать их так, чтобы все коэффициенты в уравнениях стали единичными: $T = \sqrt{k/m},\ L = mg/k.$ В этих масштабах наши уравнения примут чудесный безразмерный вид:

$\begin{align*}&\dot{p}_1 = -1,\quad q_1(0) = E,\ p_1(0) = 0\\ &\dot{p}_2 = -q_2,\quad q_2(0) = 0,\ p_2(0) = 0.\end{align*}$

Остался лишь один параметр тоже безразмерный, который отражает начальное положением шарика и вместе с тем, его потенциальную энергию: $E = \frac{kh}{mg},$ а значит, и энергию всей системы.

Оба наших уравнения элементарно решаются в аналитическом виде: шарик — падает, столик — колеблется:

$\begin{align*}&q_1 = A+Bt-\frac12 t^2, && p_1 = B-t,\\ &q_2 = C\sin(t + \Phi), && p_2 = C\cos(t + \Phi).\end{align*}$

Здесь все параметры $A,B,C,\Phi$ берутся из начальных условий. Остался один нюанс: когда шарик, падая, сталкивается со столиком, они идеально упруго обмениваются импульсами, а так как массы у них одинаковые, в момент их соударения происходит обмен скоростями: $p_1 \leftrightarrow p_2,$ когда

Получается, что вместо численного решения дифференциальных уравнений, можно просто рассчитать параболу и синусоиду, найти точку их пересечения, и в ней поменять начальные условия, передав шарику скорость столика, а столику — скорость шарика, после чего продолжить расчёт. Точку пересечения параболы и синусоиды легко отыскать численно, например, надёжным методом Ньютона. Вот как может выглядеть решение, для :

Обмен импульсами приводит к тому, что траектории шарика и столика гладко переходят друг в друга, образуя две гладкие траектории, в которых верхние кусочки это параболы, а нижние — синусоиды.

Математика — наука точная и имеет дело с идеальными моделями.-10

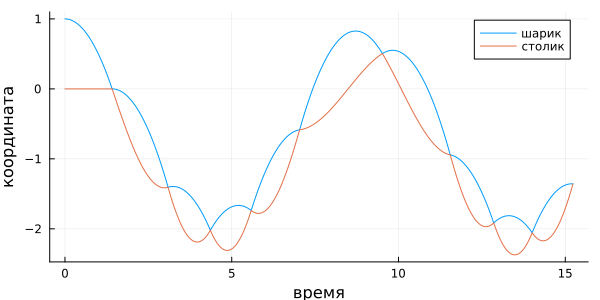
Ну, что же, шарик прыгает, столик дрыгается. Энергия в системе сохраняется (всё же идеально!), так что прыгать и дрыгаться всё может неограниченно долго. Чего же тут может быть интересного?

Смотреть на траектории шарика и столика прикольно только на протяжении пары десятков подскоков, дальше, становится неинтересно, потому что информация не накапливается и анализировать её приходится в динамике, что непросто. Здесь может пригодиться полезный прибор — стробоскоп. Пока происходит независимое движение шарика и стола, смотреть особенно не на что, мы можем включать «вспышку» стробоскопа в момент их соударения и фиксировать состояние системы в эти моменты. Так мы сможем накопить информацию о сотнях и тысячах соударений. Вот пример такого расчёта:

Высоты десяти тысяч соударений для начального положения шарика x₀ = 1. — Высоты десяти тысяч соударений для E = 1.

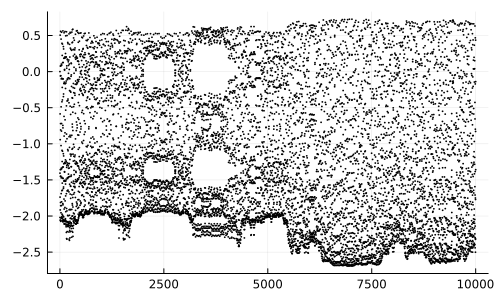
Своеобразная картина: не просто невнятный туман, а туман с каким‑то намёком на структуру. Впрочем, никакой особой закономерности в этом «сигнале» не усматривается. Давайте воспользуемся нашей единственной «ручкой» настройки и станем менять энергию системы.

Меняем начальную высоту шарика и начинаются чудеса. — Меняем энергию системы и начинаются чудеса.

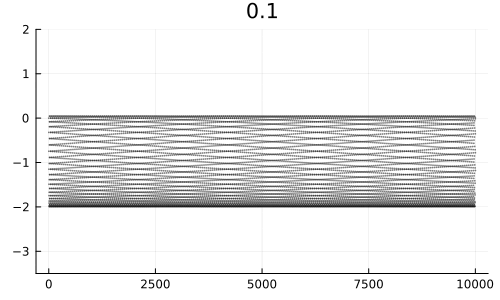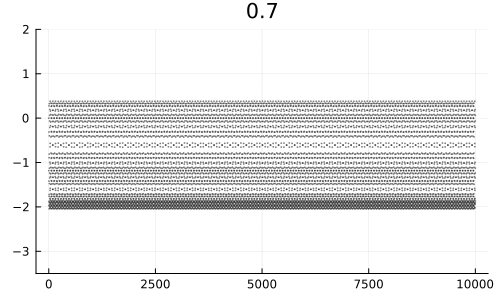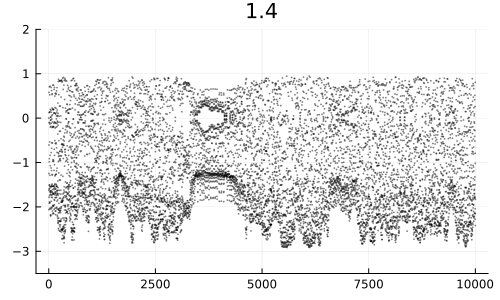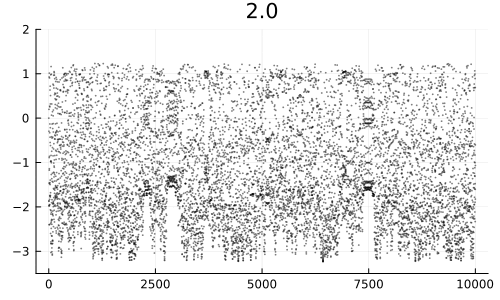
Система «ожила». Для небольших начальных высот движение регулярное, но по мере достижения определённого порога оно становится сложным и напоминает какие‑то инопланетные сигналы из научной фантастики.

Простое регулярное (периодическое) движение можно различить глазами, но лучше с этим справляется спектр сигнала. Вот как он меняется при изменении энергии:

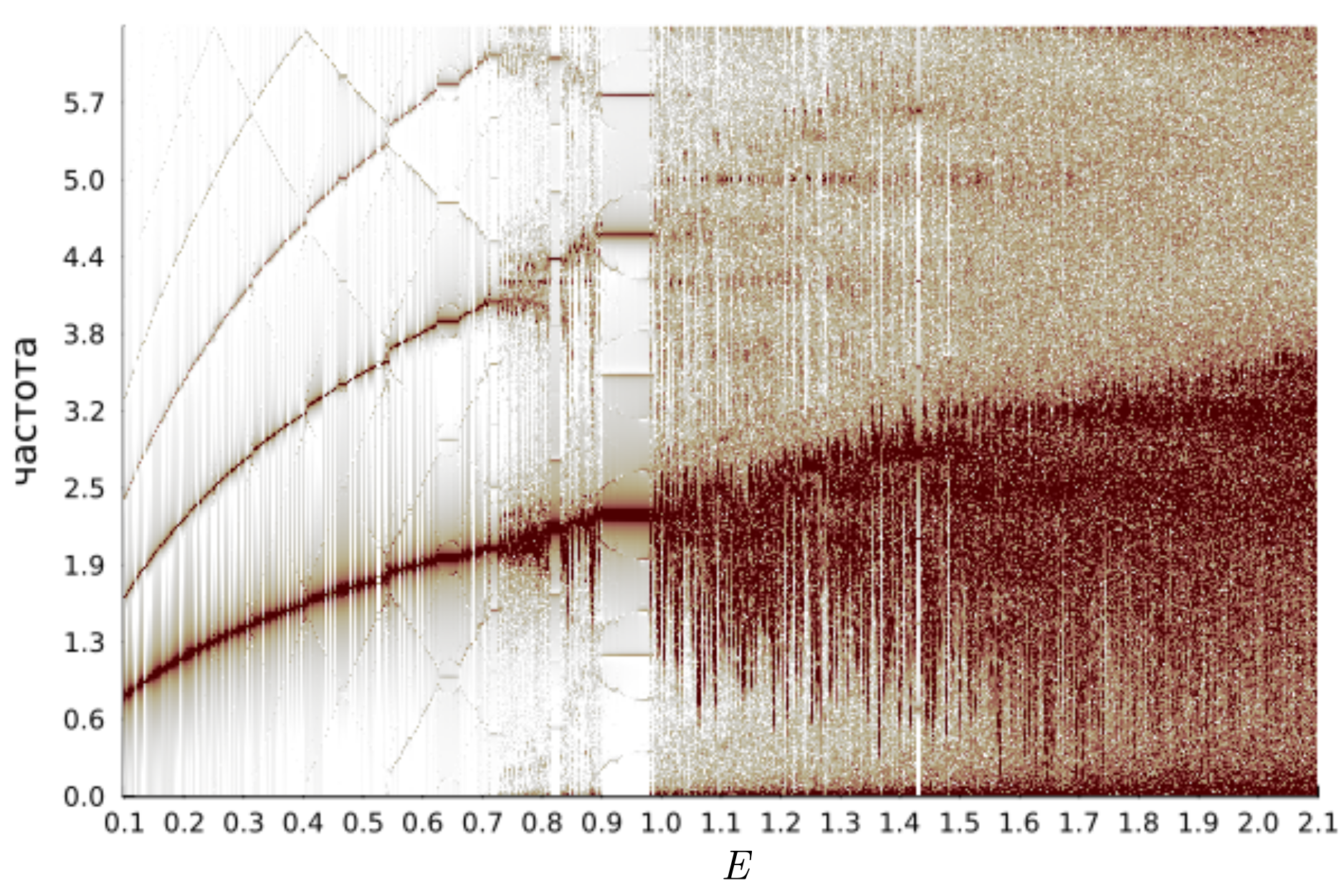
Численные значения частоты здесь не играют особой роли и носят условный характер.

Теперь отчётливо видно, что при значениях параметра нарушается периодичность ударов и начинается сложный сигнал. Кроме того, отклонения от периодичности появляются на интервале . Спектральный анализ часто используется при работе с динамическими системами и позволяет получить качественную характеристику процесса, наряду с другими инструментами, такими как экспонента Ляпунова или размерность Хаусдорфа.

Однако спектр не сильно помогают нам выявить структуру сложного сигнала: видно только, что он становится сложным и содержит все частоты, приближаясь по своим спектральным характеристикам к шуму.

В таком случае вместо физического пространства, имеет смысл обратиться к фазовому пространству, которое не содержит информации о времени, зато полностью отражает состояние системы: значения обобщенных координат и импульсов. Таким образом, каждая точка этого пространства представляет все необходимые начальные условия, и, как правило, задаёт единственную фазовую траекторию, которая проходит через эту точку. Фазовой траекторией называется непрерывное многообразие состояний, через которое проходит система в течение времени, выступающего в качестве неявного параметра. Траектория представляет собой некую одномерную линию в многомерном пространстве состояний.

Для автономных детерминированных систем, то есть, полностью определяемых начальными условиями задачи (таких, как наша), любая точка траектории однозначно задаёт её полностью. Это означает, что различные траектории не должны пересекаться. Позже мы увидим, что бывают так называемые особые точки, в которых пересекаются особые траектории. Эти исключения важны, но нетипичны, почти все точки фазового пространства принадлежат непересекающимся фазовым траекториям.

Сечения Пуанкаре

Рассматривая одновременное движение шарика и столика, мы попадаем в четырёхмерное фазовое пространство , в котором фазовые траектории определяются суммарной энергией системы.

Наши два тела почти всегда двигаются независимо, но встречаясь, они упруго сталкиваются. В результате фазовые траектории шарика и столика образуют сложнейший клубок в четырёхмерном пространстве. Анализировать или рассматривать его мало смысла. Вместо этого мы опять сосредоточим своё внимание только на моментах столкновений шарика и столика, то есть, на тех, в которых совпадают их координаты. Геометрически это соответствует сечению одномерной фазовой траектории, вложенной в четырёхмерное пространство, гиперплоскостью . Это сечение породит дискретное множество точек, вложенных в секущее подпространство , которое уже будет трёхмерным и обозримым.

Точки соударений на фазовой траектории системы.

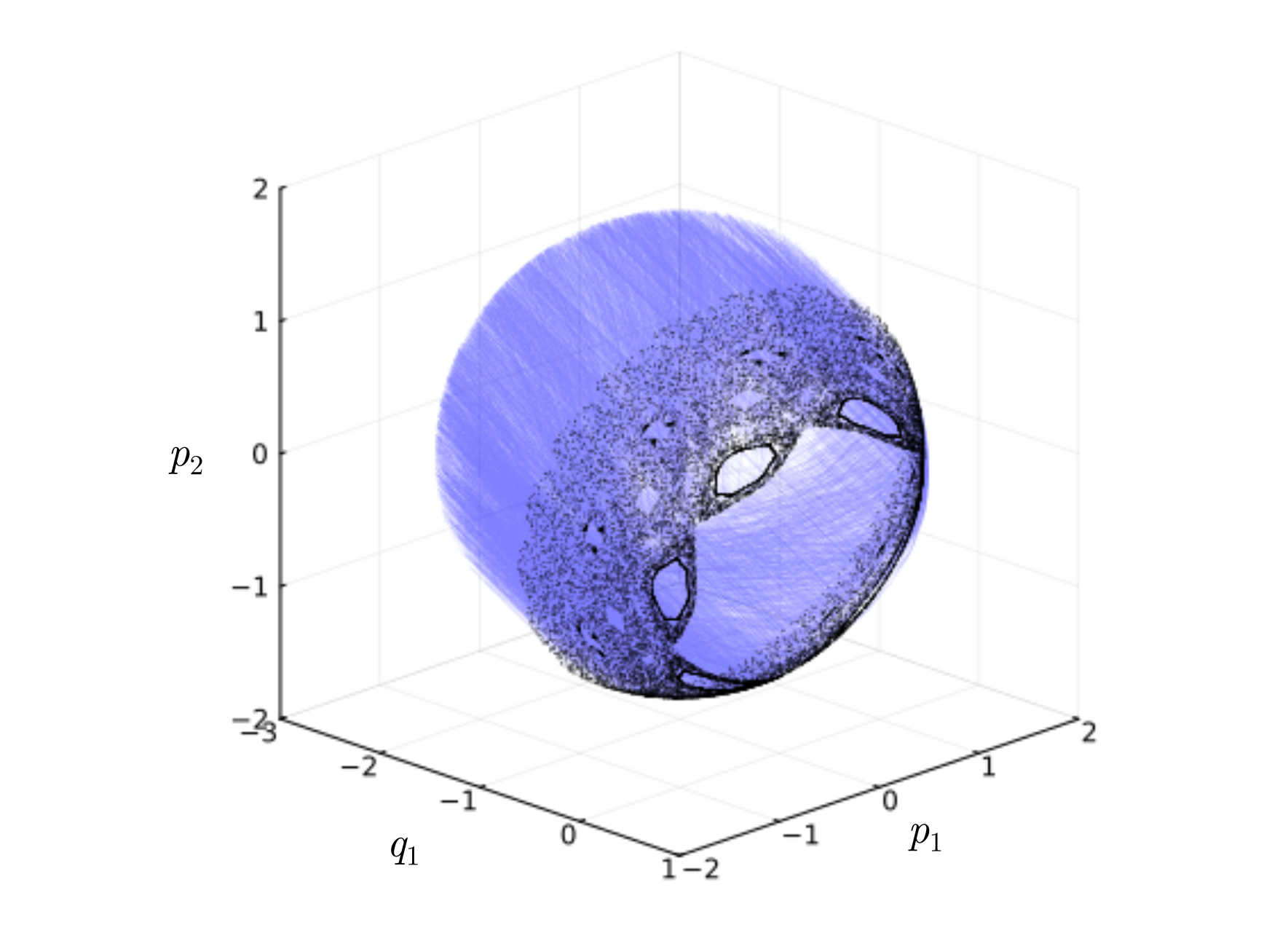
Выше мы назвали этот метод «стробоскопическим», однако в теории динамических систем такое построение принято называть сечением Пуанкаре. Для более вразумительного трёхмерного фазового пространства, схематично его можно показать так им образом:

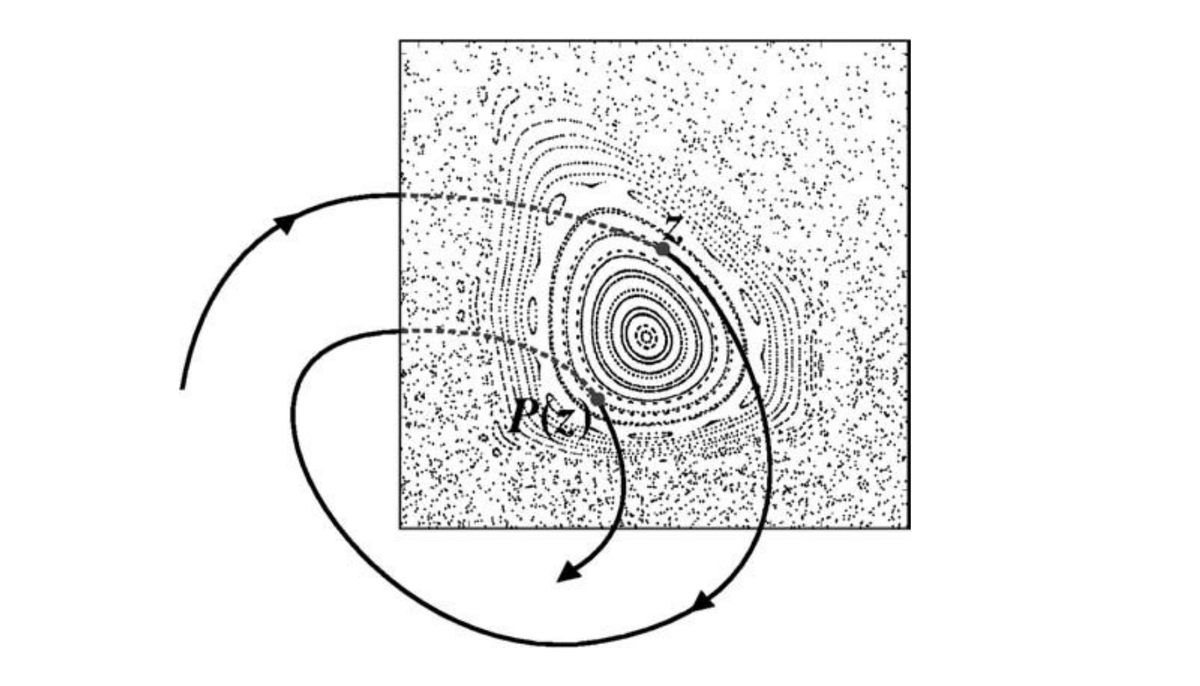
Сечение линии траектории некоторой плоскостью. Дискретное множество точек сечения Пуанкаре принадлежит плоскости и показывает структуру траектории.

Таким образом, постепенно абстрагируясь от исходной системы дифференциальных уравнений движения, мы пришли к дискретному отображению $P: (q_1,p_1,p_2)_i \to (q_1,p_1,p_2)_{i+1},$ которое для заданной точки соударения шарика и столика, возвращает следующую точку соударения. Технически это преобразование вычисляется через поиск точки пересечения параболы и синусоиды — физических траекторий шарика и столика, как показано на рисунке.

Преобразование , которое отображает сечение Пуанкаре в себя, называется отображением Пуанкаре. Последовательность точек, образуемая отображением, называется его орбитой. Вот пример одной такой орбиты:

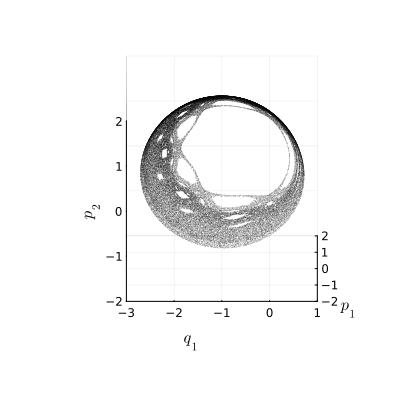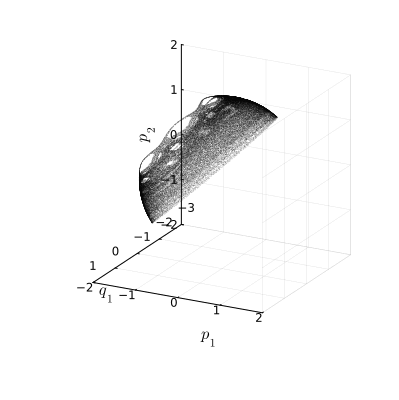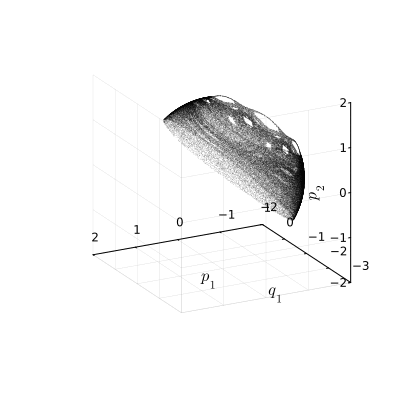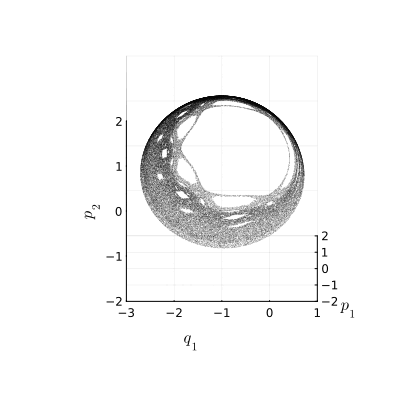
Математика — наука точная и имеет дело с идеальными моделями.-16

Стало куда интереснее! Во‑первых, мы видим уже не беспорядочное облако точек, в хаосе просматривается кое‑какая структура с более или менее симметрично расположенными пустотами в море беспорядка. Но самое примечательное свойство этого множества состоит в том, что оно, похоже, лежит на сфере, то есть, двумерно. Это означает, что существует какая‑то жёсткая связь между координатами, какое‑то уравнение, описывающее поверхность, которой принадлежат точки состояний.

С точки зрения физики, такое уравнение очевидно — это закон сохранения энергии в изолированной системе. Запишем сумму всех видов энергии в какой-то момент времени:

$q_1+\frac12p_1^2+\frac12q_2^2+\frac12p_2^2 = E.$

А так как в момент соударения , то для множества стробоскопических точек мы получаем уравнение: которое легко привести к каноническому виду уравнения сферы:

Теперь очевидно, что точки соударений действительно, лежат на сферической поверхности c радиусом $\sqrt{2E+1}$ и с центром в точке . Это уравнение, кстати, даёт нижнюю границу для возможной энергии:

Пример, показанный выше, был рассчитан для начального соударения с фазовыми координатами $(0, -\sqrt{2}, 0)$ . Этой точке соответствует энергия , однако тому же значению энергии соответствуют и другие начальные положения и скорости тел при их соударении. Перебирая точки на сфере, мы можем получить сечение Пуанкаре для семейства разных орбит, имеющих одинаковую энергию. Вот пример построения такого семейства:

Изобразив орбит побольше, и поиграв с цветами можно получить очень симпатичную картину. Неправда ли, сечение Пуанкаре похоже на гигантскую газовую планету!

Математика — наука точная и имеет дело с идеальными моделями.-20

Как видно, орбиты бывают разными. Одни из них представляют собой односвязные замкнутые линии, другие распадаются на множество несвязных замкнутых линий, наконец, есть хаотичные орбиты, заполняющие поверхность сферы облаком точек. Проще всего наблюдать орбиты именно этих типов, но кроме них есть периодические орбиты состоящие из конечного набора точек. Анализ отображения , структуры его орбит, переход орбит из одного типа в другой, по мере увеличения энергии системы, и представляет предмет исследования системы методами теории хаоса гамильтоновых систем.

Гамильтоновыми называют замкнутые изолированные автономные системы, в которых нет потерь энергии. Кажется, что в реальном мире такие системы найти или построить трудно, поскольку абсолютно изолированных систем практически не бывает. Тем не менее они встречаются и анализировать их имеет смысл. Вести себя по‑гамильтоновски и демонстрировать при этом хаотическое поведение, будет неидеальная механическая система, в которой подавляющая часть энергии сосредоточена в движении и потенциальных полях. Диссипация или приток энергии извне в такие системы если и происходит, то он пренебрежимо мал на масштабах времени, в течение которого происходит отображение Пуанкаре. Даже если после тысяч и миллионов таких отображений будет заметен вклад внешних возмущений и потерь, мы всё равно будем наблюдать эффекты гамильтоновой динамики в определённом диапазоне временных масштабов.

В основном, примеры таким систем встречаются в квантовой механике или в теории квантовых полей. Но их можно найти и в механике. Например, в атмосфере газовых гигантов вихри имеют колоссальные размеры, массы и импульсы, так что вязкость пренебрежимо мала по сравнению с их инерцией. В движении планет, а также спутников и колец вокруг них, силы тяжести и инерции также несоизмеримо больше приливных потерь или влияния внешних тел. Именно методы анализа гамильтонова хаоса разработанные Колмогоровым, Арнольдом и Мозером, позволили разобраться с формированием структуры планетарных систем и колец. Как гамильтоновые системы можно рассматривать осцилляторы со многими степенями свободы, нелинейные бильярды и даже информационные сети.

Давайте полюбуемся на семейства орбит отображения Пуанкаре для различных энергий. Посмотрите, как появляются первые признаки хаоса, и как постепенно хаотическое море затапливает фазовое пространство.

Понижаем размерность ещё на единицу

Мы с вами прошли по цепочке абстракций: Уравнения движения ⟶ траектории движения ⟶ фазовые траектории ⟶ сечение и отображение Пуанкаре ⟶ орбиты отображения Пуанкаре.

То, что орбиты лежат на двумерной поверхности в фазовом пространстве, позволяет нам совершить ещё один шаг на пути к упрощению нашей системы, и перейти от трёхмерного сечения Пуанкаре к плоскости. Введя стандартные сферические координаты: широту и долготу , мы можем построить преобразованию точек на сфере: $\Pi : (\varphi_i,\theta_i) \to (\varphi_{i+1},\theta_{i+1}).$ Оно уже не имеет очевидного механического смысла, но работать с ним будет гораздо проще, поскольку оно преобразует двумерное пространство.

Для того чтобы построить сферические координаты, следует определиться с экватором и нулевым меридианом. Для этого воспользуемся физическими симметриями нашей системы. Физики и математики помешаны на симметриях, и неспроста: это самые живучие свойства систем, которые проходят сквозь все абстракции.

Во‑первых, наша механическая система описывается уравнениями, инвариантными относительно направления времени $t \to -t$ . Во‑вторых, если мы обратим время вспять, и одновременно с этим произведём замену $(p_1,p_2)\to(-p_1,-p_2)$ то получим точно такую же орбиту.

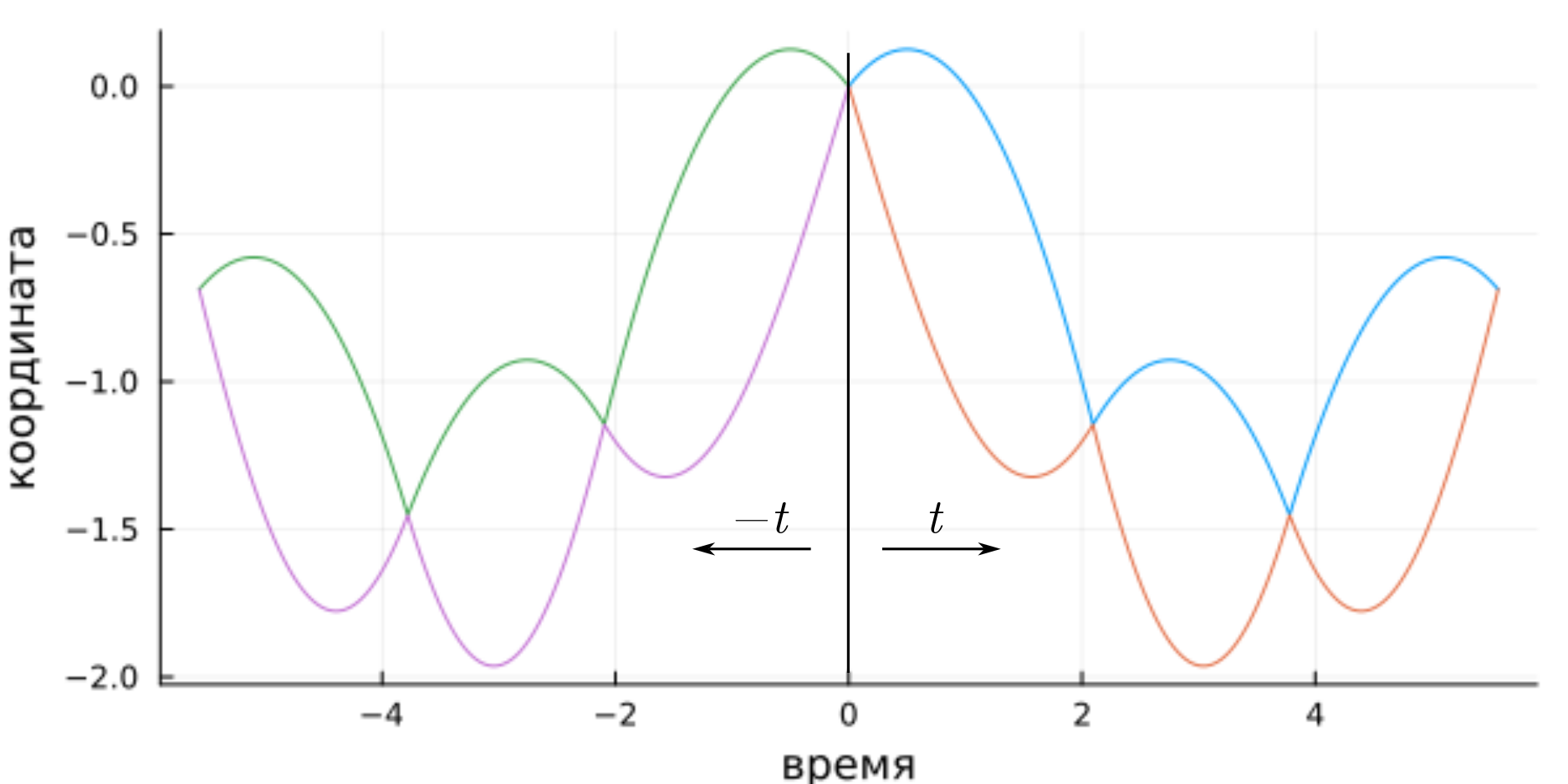
Симметрия относительно направления времени и смены знаков скоростей. При смене направления времени, траектории полностью совпадут.

В‑третьих, при обмене импульсами во время удара, происходит замена $(p_1,p_2)\to(p_2,p_1).$ Если одновременно с ней мы сменим направление времени, то останемся на одной орбите, просто продолженной «в прошлое».

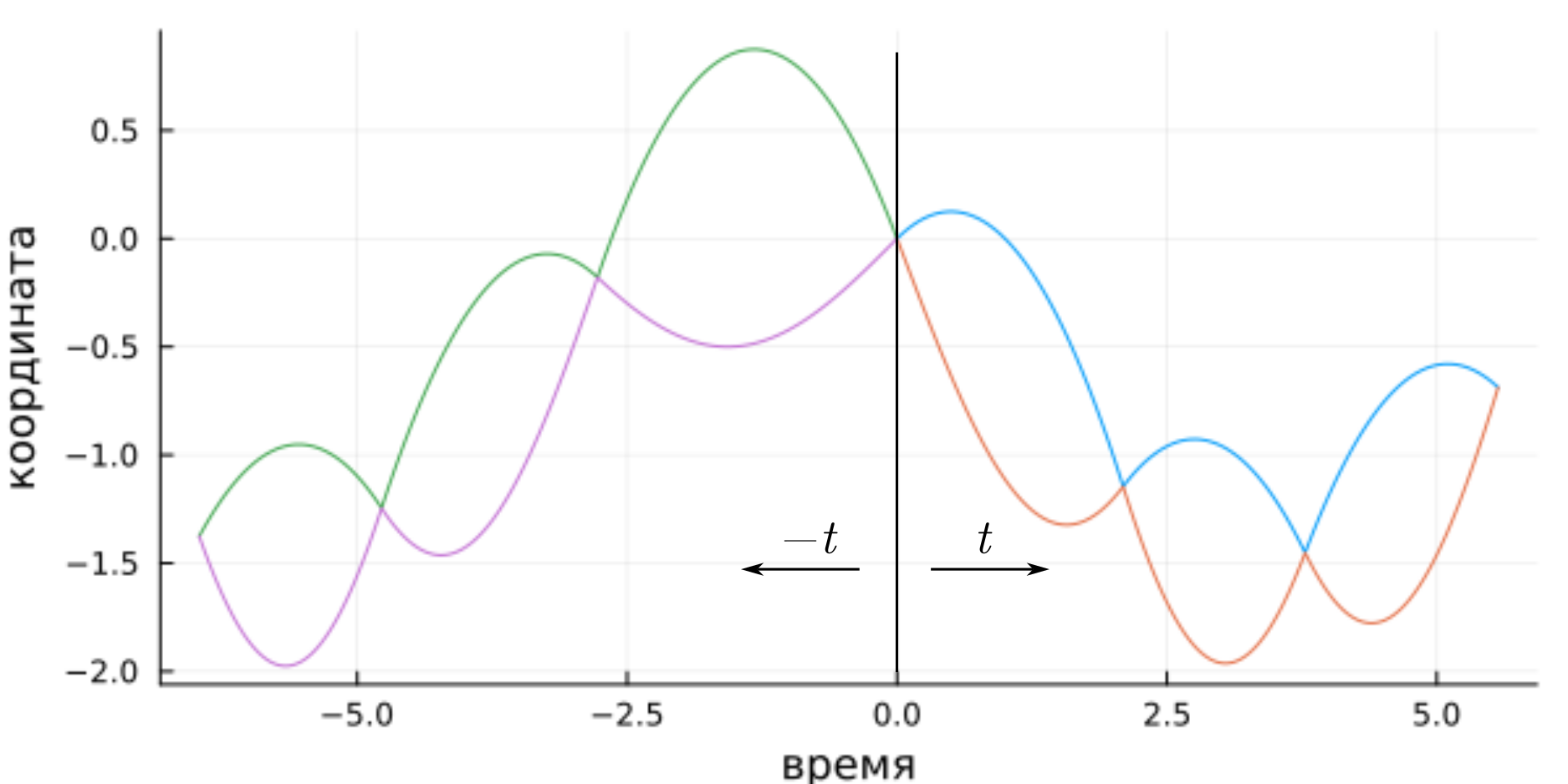
Симметрия относительно направления времени и обмена импульсами.

Фазовое пространство никак не связано направлением времени, зато в нём физические симметрии превращаются в геометрические. Наши две симметрии тоже имеют чудесное геометрическое представление: замене $(p_1,p_2)\to(-p_1,-p_2)$ соответствует зеркальная симметрия относительно плоскости а замене $(p_1,p_2)\to(p_2,p_1)$ — зеркальная симметрия относительно плоскости Вот как выглядит семейство орбит с этими двумя плоскостями симметрии.

Семейство орбит и плоскости симметрии фазового пространства. В плоскости (ẋ, ẏ) они превращаются в оси симметрии. — Семейство орбит и плоскости симметрии фазового пространства.

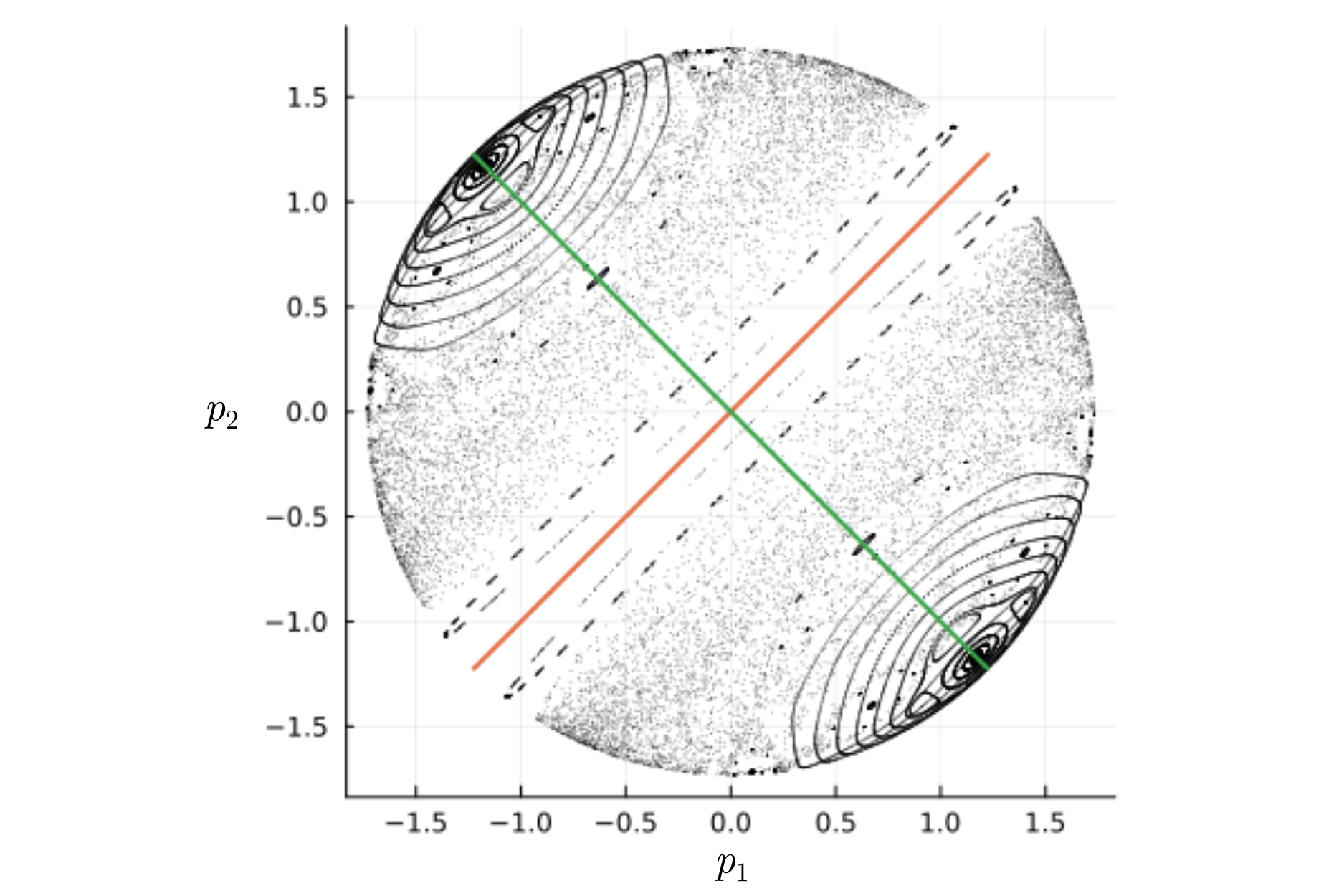
Теперь очевидно, что за экватор имеет смысл принять линию (красную на рисунке), а за нулевой меридиан — линию (зелёную). Точке пересечения нулевого меридиана с экватором соответствует состояние системы в равновесии — шарик лежит на столике и оба покоятся. При таком выборе переход из фазовых координат в координаты на сфере, соответствующей энергии производится несложно:

$\theta = \mathrm{arccos}\left(\frac{p_1-p_2}{\sqrt{4E+2}}\right),\quad \varphi = \mathrm{arctg}\left(\frac{1}{\sqrt{2}}\frac{p_1+p_2}{q_1+1}\right).$

Симметрия относительно экватора позволяет ограничиться анализом орбит только одного «полушария» сферы. В таком случае можно построить карту орбит либо в цилиндрической, либо в азимутальной проекции.

Стоит заметить, что на этих картах показаны только некоторые орбиты. На тех участках, что остались белыми какие‑то орбиты тоже есть. Каждая точка на сфере принадлежит какой‑то орбите, однако если попытаться показать их все, то выйдет невразумительная каша.

Динамика отображения

В нашем распоряжении оказался занятный объект: отображение сферы саму на себя (автоморфизм), про которое мы знаем только как оно вычисляется. Наш автоморфизм не похож на функцию, его график нарисовать непросто. Главное преимущество отображения $\Pi$ над всеми предыдущими степенями абстракции состоит в том, что оно действует на полусфере, топологически эквивалентной диску — компактному объекту, который можно изобразить и увидеть целиком, не прибегая ни к каким ухищрениям. При этом, такое до предела упрощённое преобразование всё ещё содержит симметрии исходной физической системы и демонстрирует самую интригующую его особенность — способность порождать хаос.

Предлагаю пока без глубокого анализа поэкспериментировать с преобразованием $\Pi$ , чтобы почувствовать его свойства. Напомню, что для каждого значения полной энергии системы однозначно определяется некоторая сфера в сечении Пуанкаре и отображение $\Pi$ на ней. Так что мы имеем дело с семейством отображений, параметризованных величиной

Эксперимент 1

А что если от отдельных точек соударений, которые мы рассматривали до этого, попробовать перейти ко всему диску целиком? Давайте посмотрим на то, как отображение $\Pi$ для разных энергий обходится с координатной сеткой в азимутальной проекции.

Преобразование меридианов и параллелей отображением Пуанкаре для различных энергий.

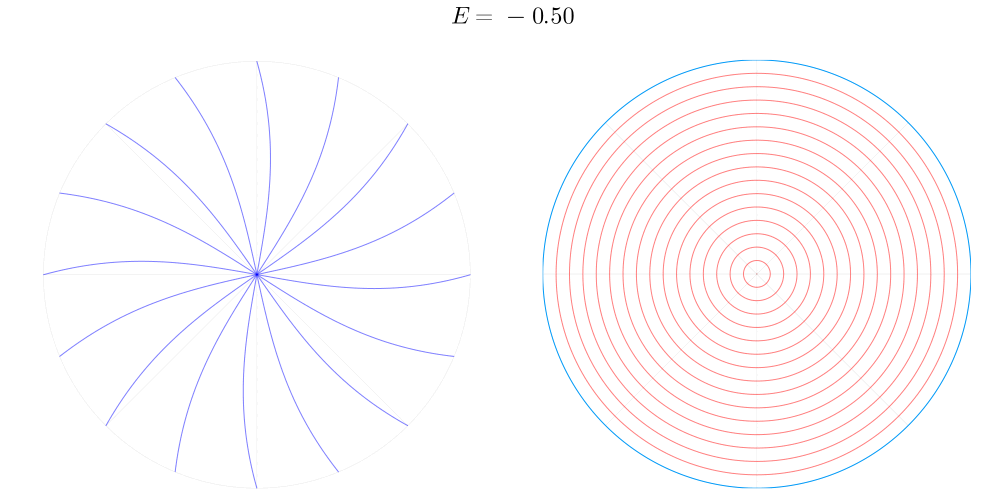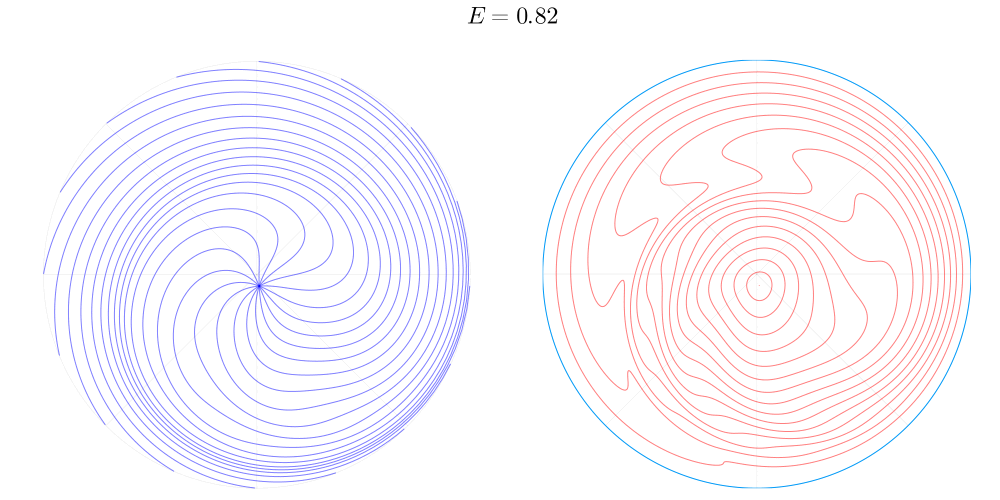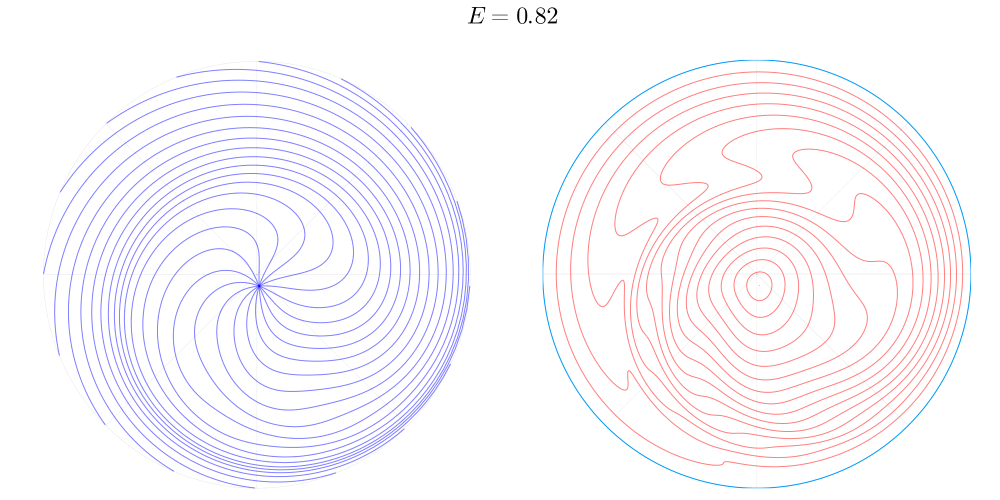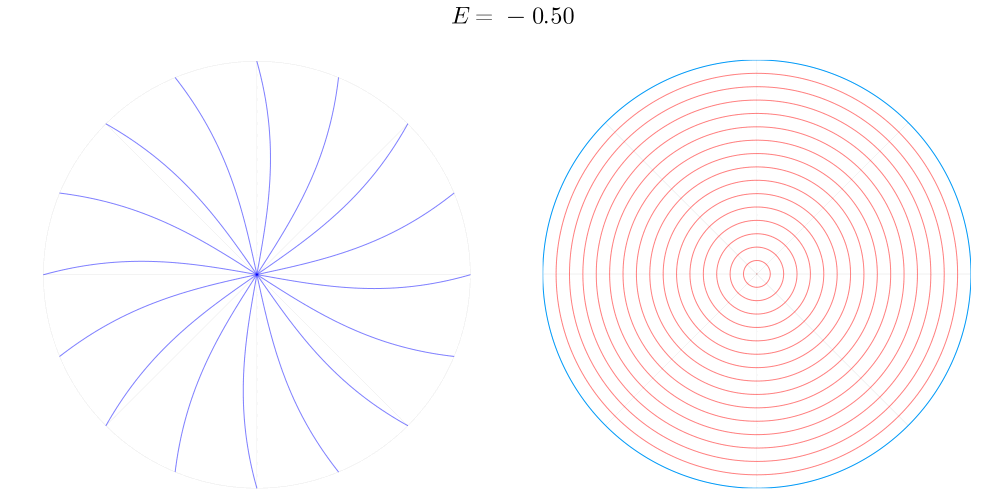
Несмотря на достаточно сложное нелинейное действие отображения, в этом эксперименте проявляется очень важное его свойство: оно непрерывно и сохраняет топологию диска. Здесь нет противоречия с тем, что $\Pi$ дискретно во времени, смысл топологической непрерывности состоит в том, что малую окрестность любой точки $\Pi$ отображает в окрестность образа этой точки. В нашем эксперименте сохранение топологии проявляется в том, что координатные линии, причудливо искривляясь, во-первых, нигде не разрываются, а во-вторых не образуют новых пересечений.

Всё это делает отображение П гомеоморфизмом, то есть, непрерывным отображением сферы саму на себя. Это важное свойство. На результаты этого преобразования, представленных в виде облака точек, мы уже насмотрелись. Точки образуют дискретное множество, которое непросто анализировать, в этом дискретном тумане теряется суть. Непрерывность позволит нам увидеть тонкие детали и выявить механизм возникновения хаоса из порядка.

Наш эксперимент продемонстрировал ещё одно важное свойство отображения $\Pi$ — его гладкость. Оно не только не производит разрывов в координатных линиях сетки, но и оставляет их гладкими кривыми, имеющими, по крайней мере, хорошие первые производные. А это значит, что к такому отображению применимы методы математического анализа: его можно дифференцировать, отыскивать особые точки и вычислять всевозможные локальные характеристики, такие как матрица Якоби и её спектр.

Эксперимент 2

Давайте посмотрим теперь на то, как непрерывное и гладкое отображение Пуанкаре порождает хаос. Зафиксируем значение энергии и будем применять к двум линиям координатной сетки отображение $\Pi^n$ , повышая степень

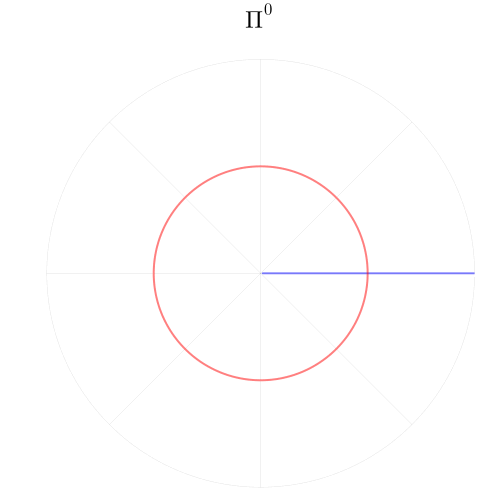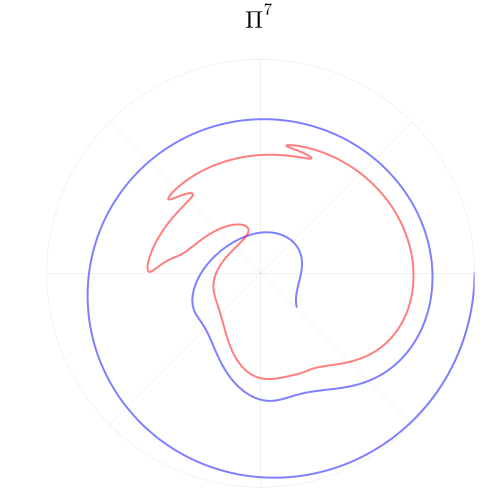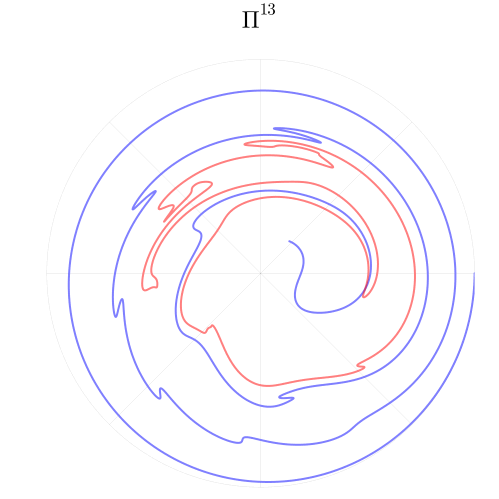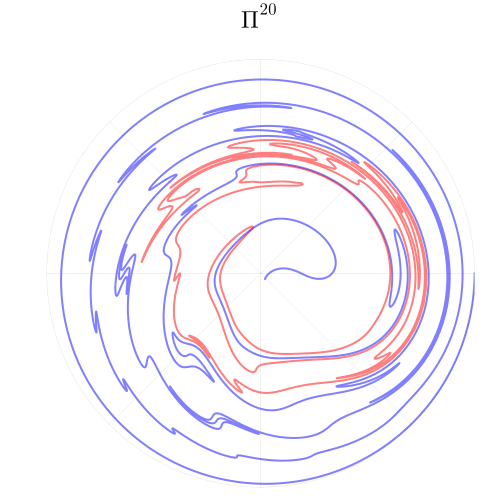
Сегодня будет много мультиков, так что берегите трафик!-12

Мы становимся свидетелями ключевого механизма в теории динамического хаоса — перемешивания фазового пространства. Два множества точек, красные и синие, оказываются перемешаны, при этом изначально близкие точки становятся далёкими, а удалённые — сближаются. Но при всём притом, преобразование умудряется оставаться непрерывным и гладким. Таким же свойством обладает развитая турбулентность на крупных масштабах.

Мы можем более детально взглянуть на то что делается с отдельными точками «внутри» перемешивания, плавно меняя фазу (угол $\varphi$ ) начальных множеств.

Сегодня будет много мультиков, так что берегите трафик!-13

Красота! А ведь это ещё не хаос, а просто сложное движение. В приведённом выше примере отображение $\Pi$ было применено всего 25 раз. Для изображения хаотических орбит в предыдущих иллюстрациях, использовались десятки тысяч итераций!

Именно перемешивание фазового пространства ответственно за чувствительность к начальным условиям, которая приводит к тому, что при попытке рассчитать движение системы из двух очень близких начальных состояний, мы быстро обнаружим, что наши решения, неотличимые вначале, станут отличаться всё сильнее и сильнее, пока не разойдутся окончательно. Впрочем, далеко они всё равно уйти не смогут, поскольку сфера компактна и любые две точки обречены оставаться в её пределах.

Для сравнения полезно взглянуть на то, как обстоят дела при малых энергиях на которых хаоса мы не наблюдали.

Сегодня будет много мультиков, так что берегите трафик!-14 — В этом примере

После 25 итераций по линиям бежит характерная рябь, но перемешивания не происходит. Конечно, после сотни применений отображения $\Pi$ линия сильно вытянется и кое где закрутится вихрями, но наш предыдущий опыт построения орбит из десятков тысяч итераций показывает, что тем не менее, для малых энергий все орбиты остаются стабильными. Нам предстоит понять каким образом происходит качественный скачок (бифуркация), превращающий рябь и вихри в настоящий хаос.

Эксперимент 3

Размышляя о высокой чувствительности к начальным условиям, мы можем прийти к выводу, что в таких системах численный расчёт имеет мало смысла. Может быть источником хаоса в этой системе является метод Ньютона, дающий лишь хорошее, но конечное приближение к новой точке, а также ограниченность числа разрядов, используемых при вычислениях? Это и так и не так. Давайте сравним семейства орбит, вычисленные с использованием чисел с плавающей точкой различной разрядности.

Каждая орбита содержит по 10 000 точек. Видно что при совсем уж низкой разрядности картина теряется, но уже с использованием Float16 структура орбит принимает знакомые очертания. При дальнейшем повышении разрядности меняется только хаотический туман, но и в нём сохраняется некая «тонкая структура» в виде островов порядка. Получается, что хаотические орбиты ожидаемо чувствительны к точности вычислений, однако остаются строго в своих границах. Самое же главное: переход от порядка к хаосу, сложная структура орбит и природа перемешивания, происходят не из‑за ошибок округления и полностью определяются непрерывным и гладким преобразованием $\Pi$ и его свойствами.

Эксперимент 4

Напоследок, давайте выясним, как под действием преобразования формируются отдельные орбиты в хаотическом режиме . Для этого, как и прежде, выстроим ряд точек вдоль нулевого меридиана, а потом будем накапливать их отображения.

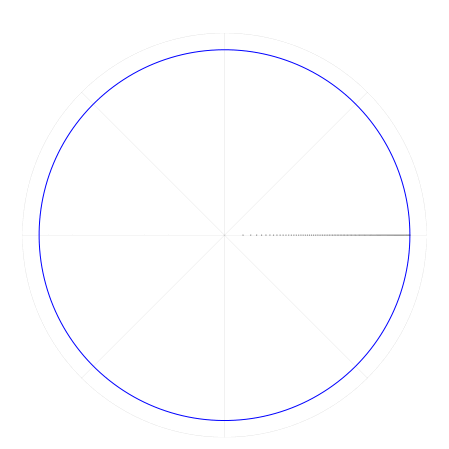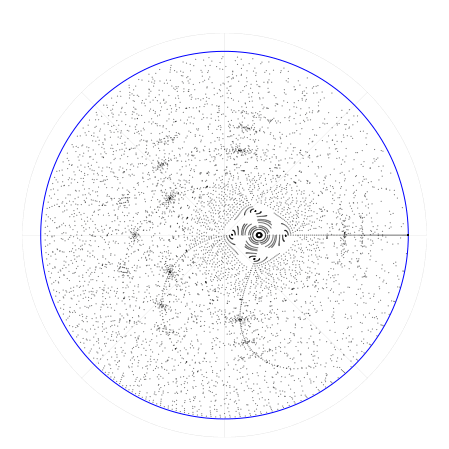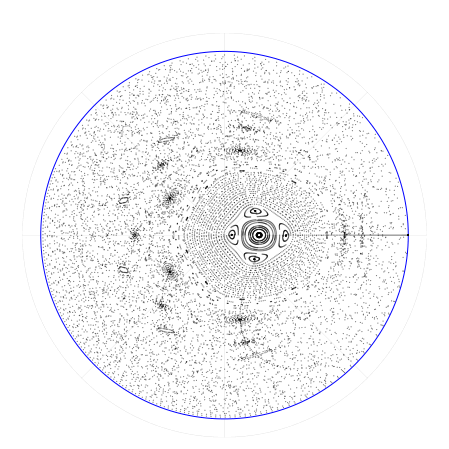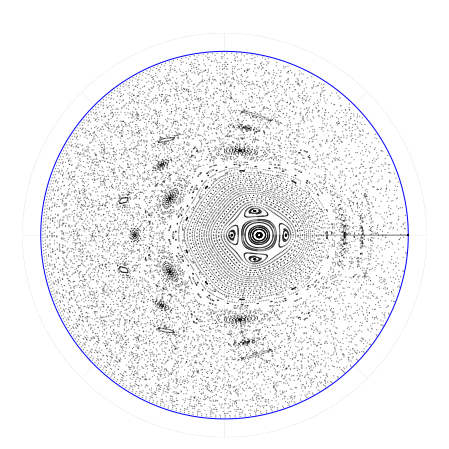
Сегодня будет много мультиков, так что берегите трафик!-15

Это один из самых полезных наших экспериментов. Он показывает структуру особых точек, полюсов, и динамику их окрестностей. О смысле и свойствах этих структур мы поговорим в следующий раз.

Tags:

Hubs:

Mathematics