Путешествие в тысячу ли начинается с одного шага. (Лао-Цзы)
Что делает код хорошим? Большинство программистов ответят: хороший код должен быть структурирован, легко читаем и понятен. Но так ли важно качество кода, если он медленный? В большинстве задач производительность кода не критична, хотя и желательна. Но есть задачи, время выполнения которых столь огромно, что выигрыш в производительности доминирует над всем остальным.
Я говорю про NP-трудные задачи (NP-трудность - недетерминированная полиномиальная трудность по времени) и на одной из данного класса хочу акцентировать ваше внимание. Задаче коммивояжера.
Мы не будем рассматривать эвристические алгоритмы, нам нужно точное решение.
На данный момент не существует известного алгоритма способного найти точное решение задачи коммивояжёра в общем виде за число шагов выраженного, как полином фиксированной степени от размера входных данных.
В прошлой работе мы ознакомились с решением задачи коммивояжера на минимум методом динамического программирования. Метод конечно замечательный, но он ограничен объёмом памяти системы. Уже при n = 28 вершин, 16 Гб оперативной памяти недостаточно, а использовать память жёсткого диска очень неэффективно. Возможно, используя хитроумные подходы структурирования и сжатия памяти можно несколько улучшить алгоритм, но ненамного. Нужен иной подход, если мы хотим рассчитывать матрицы большего размера.
Метод ветвей и границ, пожалуй, самый известный и эффективный метод нахождения точного решения задачи коммивояжёра. Не будем тут останавливаться на его описании, в интернете существует множество подробных мануалов с примерами. Для новичков рекомендую статью где, на мой взгляд, всё описано понятным языком.
Так же в своё время разобраться с тонкостями алгоритма мне помогла работа. Как и её автор, я прошёл тот же путь, и совершил ровно те же ошибки, главная из которых заключалась в том, что при невозможности получить приемлемые результаты, начал использовать эвристики. Ещё один любопытный подход.
Хочу обозначить одну тонкость метода ветвей и границ, которую мало кто освещает:
На этапе выбора элемента ветвления и разделения решения на два подмножества M1 (содержащие ребро с максимальным штрафом) и M2 (не содержит ребро с максимальным штрафом), при рассмотрении множества M1 вычеркиваем относящиеся к выбранной клетке строку и столбец, а также заменяем значение ячейки соответствующей обратному пути на бесконечность.
Но вот что скрывается под понятием обратного элемента? Во многих реализациях, что я видел, смысл определения выражен не верно, проиллюстрируем.

Есть некий граф, для которого на предыдущих этапах мы уже нашли рёбра [0, 3], [3, 5], [6, 7], [7, 1] и на текущем шаге рассматриваем ребро [5, 6] множества M1.
Так вот обратным элементом для ребра [5, 6], будет не ребро [6, 5] (как можно было подумать), а ребро [1, 0]. И вычёркиваем данное ребро затем, чтобы избежать в графе подцикл. Естественно, мы так же вычёркиваем все дуги, исходящие из [5] (вычеркивание строки) и входящие в [6] (вычеркивание столбца).
Так вот, для получения обратного элемента нужно найти голову и хвост пути, вместе с которым добавленное ребро образует единую ветвь и уже для такого пути взять обратный элемент.
Игнорирование сего факта очень часто заводит полный перебор в тупик, про точное решение промолчу.
Далее по ходу текста я буду выдвигать утверждения, которые кому-то могут показаться спорными, просто примите за факт.
Метод ветвления и границ при полном переборе очень эффективный метод, но у него есть одна отвратительная черта: рекурсия. Мы постоянно делим дерево решений на два подмножества, каждое из которых занимает место в памяти, плюс добавим сюда расходы на рекурсию и служебные переменные, при больших размерах дерева ветвлений это огромная проблема. Мало того, что оперативной памяти может просто не хватать, так ещё и обращение к разным участкам памяти не самое дешёвое удовольствие.
Авторский подход заключается в том, чтобы рассматривать задачу коммивояжёра не как академическую, а как инженерную.
Вся суть сводится к тому, что мы несколько отклоняемся от алгоритма, предложенного Литлом, в сторону увеличения количества шагов при обходе дерева ветвлений, но зато значительно выигрывая из-за организации таких шагов.
Алгоритм состоит в применении трёх мета шагов:
Производим приведение матрицы (редукция строк, столбцов), выбираем нулевой элемент с максимальной оценкой для разбиения.
На каждом ветвлении между выбором множества M1 или M2, всегда двигаться в M1, пока мы не достигнем дна. В матрице останется только один элемент, не предусматривающий ветвления, так мы получаем опорное решение. Сравниваем лучшее с текущим решением и запоминаем его, если оно короче.
Далее мы возвращаемся на уровень выше, проверяем для него множество M2 и вычёркиваем клетку. Переходим к шагу 1.
Отдельно остановлюсь на условиях, при которых мы можем досрочно прекратить дальнейшее обследование ветви дерева ветвлений, тем самым сократив объём вычислений.
На первом шаге, если мы понимаем, что в какую-либо вершину или из неё больше невозможно проложить ни одного маршрута;
На втором шаге, если видим, что лучший из найденных пока маршрутов меньше нижней текущей границы;
На третьем шаге, если лучший из найденных пока маршрутов меньше суммы нижней текущей границы и максимальной оценки на шаге;
Для себя назвал подход алгоритмом ныряльщика. Уж больно напоминает мне, как охотник за жемчугом ныряет на дно, хватает раковину, отплывает в сторону, снова ныряет. Дно водоёма не ровное, это и есть дерево ветвления. У пловца есть верёвка, которую выбирают до натяжения, каждый раз как ныряльщик достигает дна. И так до тех пор, пока он не сможет больше достигать дна, кроме одного места, что и окажется минимальным возможным решением.
Вы можете спросить, к чему эти сложности? Именно так мы избавляемся от хвостовой рекурсии при расчёте множества М2 и гарантируем, что глубина рекурсии для множества M1 никогда не превысит n.
А если применить ещё небольшой фокус с выделением памяти только на стеке, не используя динамическое выделение памяти в куче (просить память у ОС относительно дорого), то алгоритм не будет покидать сверхбыструю память L1 процессора. То есть при таком подходе мы не будем использовать ужасную медленную оперативную память, ну разве что только при переключении потоков в ОС.
Например, при n = 33 программе требуется не более 63КБ стека, при любых входных данных.
Из прочих неочевидных оптимизаций:
Предлагаю хранить индексы матрицы одним куском с данными, это здорово сокращает количество операций при копировании в матрицу меньшего размера, а также повышает локальность данных;
Использовать только 32 битные переменные для всего, нужно для выравнивания обращений в памяти (выровненные обращения происходят быстрее);
Использовать максимальное число для расчётов inf = 2147483647 (0x7fffffff), для того чтобы при сложении двух бесконечностей не получать переполнение регистра (не нужно проверять);
Умышленный отказ от операций деления (очень дорогая инструкция);
Переменные по возможности высвобождаются сразу, как перестают быть нужными;
Объединить этап редукции с выбором нулевого элемента для разбиения, для уменьшения количества обращений к матрице;
Последняя оптимизация интересна в том, что за один проход можно получить сразу два параметра: минимальное значение для редукции по строке и минимум по той же строке для анализа нулей. Для этого для каждого элемента матрицы применяем функцию two_lows, которая находит два минимума за один проход, что сокращает почти вдвое число обращений к матрице на данном этапе. Аналогично и для столбцов.
Алгоритм изначально разрабатывался на Pascal, затем я конвертировал его на Си и внёс множество изменений не доступных Паскалю, добившись ещё более чем двукратного увеличения производительности на шаг. Для удобства работы в Python обернул в динамическую библиотеку и тестировал производительность уже на ней.
Для самых любознательных
Код внешней библиотеки на Си
//=======================================================================
// Задача коммивояжера (TSP) точное решение — метод ветвей и границ (by ReBuilder)
// https://habr.com/ru/post/708072/
//=======================================================================
const unsigned int inf = 0x7fffffff; // 2147483647
typedef struct TVector {
unsigned int src;
unsigned int dest;
} TVector;
typedef struct TMatrixObj {
unsigned int global_min; // Глобальный текущий минимум расчёта
unsigned int n; // Реальный размер матрицы
unsigned int step; // Шаг алгоритма
TVector *v; // Указатель на массив векторов сохранённых рёбер на текущем шаге [откуда, куда]
TVector *v_best; // Указатель на массив векторов, лучший на текущий момент [откуда, куда]
} TMatrixObj;
void matrix_evaluation(struct TMatrixObj *m, unsigned int *pm, unsigned int index, unsigned int n);
//=======================================================================
// Сохраняет два минимальных элемента при добавлении нового
void two_lows(unsigned int *a, unsigned int *b, unsigned int c)
{
if (c <= *a)
{
*b = *a;
*a = c;
}
else
if (c < *b)
*b = c;
}
//=======================================================================
void matrix_reduction(unsigned int *pm, unsigned int n, unsigned int *max_sum, unsigned int *max_i, unsigned int *max_j)
{
unsigned int sum = 0;
// Организуем кеш для подсчёта веса строки
unsigned int line_cache[n + 1];
// Для каждой строки находим минимум
for (unsigned int i = 1; i < n; i++)
{
unsigned int min1 = pm[i * n + 1];
unsigned int min2 = inf;
two_lows(&min1, &min2, pm[i * n + 2]);
for (unsigned int j = 3; j < n; j++)
two_lows(&min1, &min2, pm[i * n + j]);
// Если хоть одна точка источник не имеет выходов то обрываем расчёт
if (min1 == inf)
{
pm[0] = inf;
return;
}
// Вычитаем минимум из каждой строки (Редукция строк)
if (min1 > 0)
{
if (min2 < inf)
min2 -= min1;
for (unsigned int j = 1; j < n; j++)
if (pm[i * n + j] < inf)
pm[i * n + j] -= min1;
// Прибавляем минимальный элемент к нижней границе
sum += min1;
}
line_cache[i] = min2;
}
*max_sum = 0;
*max_i = inf;
// Для каждого столбца находим минимум
for (unsigned int i = 1; i < n; i++)
{
unsigned int min1 = pm[1 * n + i];
unsigned int min2 = inf;
two_lows(&min1, &min2, pm[2 * n + i]);
for (unsigned int j = 3; j < n; j++)
two_lows(&min1, &min2, pm[j * n + i]);
// Если хоть одна точка назначения не имеет входов то обрываем расчёт
if (min1 == inf)
{
pm[0] = inf;
return;
}
if (min1 > 0)
{
if (min2 < inf)
min2 -= min1;
// Вычитаем минимум из каждого столбца (Редукция столбцов)
// Находим элемент для разбиения, и верхнюю оценку
unsigned int temp_val;
for (unsigned int j = 1; j < n; j++)
{
temp_val = pm[j * n + i];
if (temp_val < inf)
{
temp_val -= min1;
pm[j * n + i] = temp_val;
if (temp_val == 0)
{
temp_val = line_cache[j] + min2;
if (temp_val >= *max_sum)
{
*max_sum = temp_val;
*max_i = j;
*max_j = i;
}
}
}
}
// Прибавляем минимальный элемент к нижней границе
sum += min1;
}
else
{
// Находим элемент для разбиения, и верхнюю оценку
unsigned int temp_val;
for (unsigned int j = 1; j < n; j++)
if (pm[j * n + i] == 0)
{
temp_val = line_cache[j] + min2;
// выбираем значение с максимальной суммой минимумов по строке и столбцу
if (temp_val >= *max_sum)
{
*max_sum = temp_val;
*max_i = j;
*max_j = i;
}
}
}
}
// Нижняя граница - стоимость меньше которой невозможно построить маршрут
// Если нет элемента для разбиения, то блочим ветку
if (*max_i == inf)
pm[0] = inf;
else
pm[0] += sum;
}
//=======================================================================
int head_search(unsigned int *pm, struct TVector *v, unsigned int n, unsigned int index, unsigned int dj)
{
unsigned int l = 0;
do
{
if (v[l].src == dj)
{
dj = v[l].dest;
l = 0;
continue;
}
l++;
} while (l < index);
for (l = 1; l < n; l++)
if (pm[l * n + 0] == dj)
break;
return l;
}
//=======================================================================
int tail_search(unsigned int *pm, struct TVector *v, unsigned int n, unsigned int index, unsigned int di)
{
unsigned int l = 0;
do
{
if (v[l].dest == di)
{
di = v[l].src;
l = 0;
continue;
}
l++;
} while (l < index);
for (l = 1; l < n; l++)
if (pm[0 * n + l] == di)
break;
return l;
}
//=======================================================================
void martix_in_depth(struct TMatrixObj *m, unsigned int *pm, unsigned int n, unsigned int index, unsigned int di, unsigned int dj)
{
unsigned int new_matrix[n * n];
// Копируем матрицу в массив меньшего размера
{
unsigned int *src = pm;
unsigned int *dest = new_matrix;
for (unsigned int i = 0; i <= n; i++)
{
if (i == di)
{
src += n + 1;
continue;
}
for (unsigned int j = 0; j <= n; j++)
{
if (j == dj)
{
src++;
continue;
}
*dest++ = *src++;
}
}
}
if (n > 3)
{
// Запрещаем переходы в уже пройденные узлы графа.
// Чтобы избежать подциклы в векторе найденых рёбер ищем голову и хвост цепочек,
// вместе с которыми добавленное ребро образует единую ветвь.
// Для найденый индексов в матрице меньшего размера ищем обратные индексы
unsigned int i = head_search(new_matrix, m->v, n, index, m->v[index].dest);
unsigned int j = tail_search(new_matrix, m->v, n, index, m->v[index].src);
// Зануляем обратный элемент в матрице меньшего размера.
// Должен находиться всегда!!!
new_matrix[i * n + j] = inf;
}
else if (n == 2)
{
// Если в матрице остался только один элемент
new_matrix[0] += new_matrix[3];
// Если текущее решение лучшее из найденных, запоминаем его
if (new_matrix[0] < m->global_min)
{
m->global_min = new_matrix[0];
for (unsigned int i = 0; i <= index; i++)
{
m->v_best[i].src = m->v[i].src;
m->v_best[i].dest = m->v[i].dest;
}
//memcpy(m->v_best, m->v, (m->n-1) * sizeof(TVector));
m->v_best[index + 1].src = new_matrix[1 * n + 0];
m->v_best[index + 1].dest = new_matrix[0 * n + 1];
}
return;
}
// Производим раcчёт для слоя ниже
matrix_evaluation(m, new_matrix, index + 1, n);
}
//=======================================================================
void matrix_evaluation(struct TMatrixObj *m, unsigned int *pm, unsigned int index, unsigned int n)
{
unsigned int max_sum, max_i, max_j;
do
{
m->step++;
// Производим приведение матрицы, находим элемент для разбиения, и верхнюю оценку
matrix_reduction(pm, n, &max_sum, &max_i, &max_j);
// Если нет возможного пути, то блочим ветку
if (pm[0] >= inf)
return;
// Расчитываем множество М1
// Если лучший из найденых пока маршрутов больше нижней границы,
// то вычёркиваем текущую строку и столбец и переходим к уменьшиной матрице
if (m->global_min > pm[0])
{
// Сохраняем индексы элемента разбиения в вектор локального результата
m->v[index].src = pm[max_i * n + 0];
m->v[index].dest = pm[0 * n + max_j];
// Погружаемся на слой ниже
martix_in_depth(m, pm, n - 1, index, max_i, max_j);
}
// Расчитываем множество М2
// Исключаем пункт из множества
pm[max_i * n + max_j] = inf;
// Производим повторную оценку после вычерка вершины (множество М2)
// Так как хвостовая рекурсия дороже итерации, оформляем цикл
}
while (m->global_min >= pm[0] + max_sum);
}
//=======================================================================
#ifdef __cplusplus
extern "C" {
#endif
int tsp_branch(unsigned int n, int *p)
{
if ((n < 2) || (n > 64))
return 0;
struct TMatrixObj m;
m.n = n;
struct TVector v_best[n];
struct TVector v[n - 1];
m.v = v;
m.v_best = v_best;
unsigned int work_matrix[(n + 1) * (n + 1)];
//-----------------------------------------------------------------------
// Производим первичную инициализацию рабочей матрицы
m.global_min = inf;
m.step = 0;
work_matrix[0] = 0;
for (unsigned int i = 1; i < m.n + 1; i++)
{
work_matrix[i * (m.n + 1) + 0] = i;
work_matrix[0 * (m.n + 1) + i] = i;
}
{
int *src = p;
for (unsigned int i = 1; i < m.n + 1; i++)
for (unsigned int j = 1; j < m.n + 1; j++, src++)
if ((i != j)&&(*src >= 0))
work_matrix[i * (m.n + 1) + j] = *src;
else
work_matrix[i * (m.n + 1) + j] = inf;
}
//-----------------------------------------------------------------------
// Начинаем расчёт
matrix_evaluation(&m, work_matrix, 0, m.n + 1);
//-----------------------------------------------------------------------
// Вывод результата
if (m.global_min < inf)
{
p[0] = m.global_min;
p[1] = m.step;
unsigned int v_result[n];
for (unsigned int i = 0; i < n; i++)
{
v_result[v_best[i].src - 1] = v_best[i].dest;
}
unsigned int j = 0;
for (unsigned int i = 2; i < m.n + 1; i++)
{
p[i] = v_result[j] - 1;
j = v_result[j] - 1;
}
p[n + 1] = 0;
return n + 2;
}
else
{
return 0;
}
//-----------------------------------------------------------------------
}
#ifdef __cplusplus
}
#endifПример вызова на Python
from ctypes import *
import numpy as np
import random
import matplotlib.pyplot as plt
import networkx as nx
from datetime import datetime
#------------------------------------------------------------------------------------
def distance(x1, y1, x2, y2):
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
#------------------------------------------------------------------------------------
def tsp_branch(n, py_arr, lib):
if n < 2:
return {}
flatten_arr = list(np.concatenate(py_arr).flat)
l = [-1] * (n * n - len(flatten_arr))
flatten_arr = (flatten_arr + l)[:n * n:]
int_arr = (c_int * (n * n))(*flatten_arr)
res = lib.tsp_branch(n, byref(int_arr))
if res > 0:
l = list(int_arr)[:res:]
return {'len' : l.pop(0), 'steps' : l.pop(0), 'path' : l}
else:
return {}
#------------------------------------------------------------------------------------
lib_c = cdll.LoadLibrary(r"tsp_branch.dll")
lib_c.tsp_branch.argtypes = [c_int, c_void_p]
lib_c.tsp_branch.restype = c_int
#------------------------------------------------------------------------------------
INF = -1
#random.seed(1)
n = 26
v1 = []
points = {}
for i in range(n):
points[i] = (random.randint(1, 10000), random.randint(1, 10000))
input_matrix = []
for i, vi in points.items():
m1 = []
for j, vj in points.items():
if i == j:
m1.append(INF)
else:
m1.append(int(distance(vi[0], vi[1], vj[0], vj[1])))
v1.append([i, j, int(distance(vi[0], vi[1], vj[0], vj[1]))])
input_matrix.append(m1.copy())
plt.figure(figsize=(6, 6))
graph = nx.Graph()
graph.add_nodes_from(points)
# Добавляем дуги в граф
for i in v1:
graph.add_edge(i[0], i[1], weight=i[2])
#-----------------------------------------------------------------
start_time = datetime.now()
res1 = tsp_branch(n, input_matrix, lib_c)
print(datetime.now() - start_time)
print('min_len =', res1['len'], ', steps =', res1['steps'], res1['path'])
if 'path' in res1:
d1 = []
for i, v in enumerate(res1['path']):
d1.append([res1['path'][i-1], res1['path'][i]])
#-----------------------------------------------------------------
# Рисуем всё древо
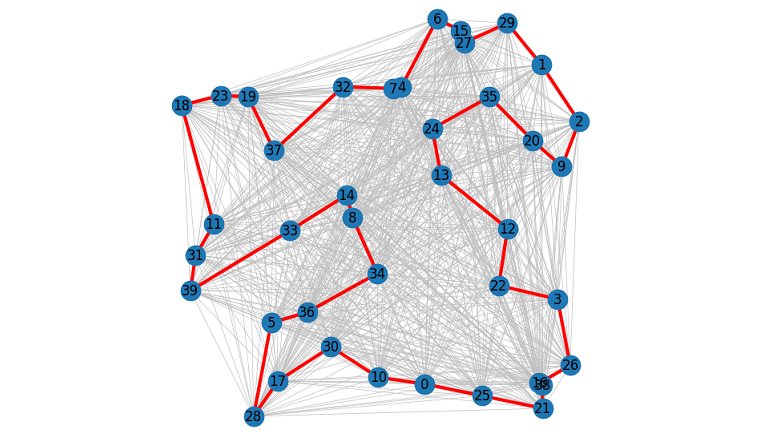
nx.draw(graph, points, width=0.5, edge_color="#C0C0C0", with_labels=True)
nx.draw(graph, points, width=3, edge_color="red", edgelist=d1, style="-")В отличие от детерминированного алгоритма динамического программирования, метод ветвей и границ является стохастическим, и время работы очень сильно варьируется от набора входных данных.
Была проведена серия испытаний на случайном наборе точек на плоскости для оценки производительности алгоритма от количества вершин графа. Каждая серия состояла из тысячи случайно сгенерированных наборов.
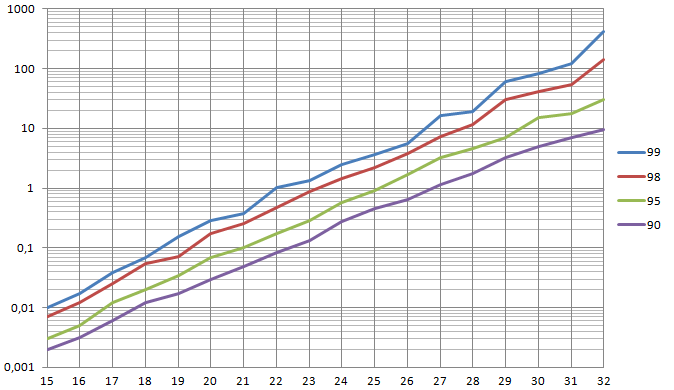
Графики были построены по 99, 98, 95 и 90 перцентилям от размера графа и времени в секундах. 99 перцентиль говорит о том, что мы найдём решение задачи в среднем в 99 случаях из ста, за указанное время для похожего набора входных данных.
Как вы можете заметить подход не панацея, но при определённых условиях даёт весьма неплохие результаты.
Как бонус алгоритм неплохо себя чувствует на не полно связанных матрицах (отсутствующие связи задаются как отрицательные числа или inf), а также на не симметричных матрицах. Последнее особо важно для задач транспортной логистики, где расстояние в точку доставки не равно обратному пути, из-за того, что дороги могут быть односторонними.

Теперь о минусах, хоть алгоритм переваривает абсолютно любые матрицы для поиска минимального решения, но на некоторых экземплярах делает это крайне неэффективно. Одним из таких примеров это задача коммивояжёра на максимум.

Задача коммивояжёра на максимум
import random
import matplotlib.pyplot as plt
import networkx as nx
import numpy as np
import copy
from ctypes import *
from datetime import datetime
#-----------------------------------------------------------------
def distance(x1, y1, x2, y2):
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
#-----------------------------------------------------------------
def tsp_branch(n, py_arr, lib):
if n < 2:
return {}
flatten_arr = list(np.concatenate(py_arr).flat)
l = [-1] * (n * n - len(flatten_arr))
flatten_arr = (flatten_arr + l)[:n * n:]
int_arr = (c_int * (n * n))(*flatten_arr)
res = lib.tsp_branch(n, byref(int_arr))
if res > 0:
l = list(int_arr)[:res:]
return {'len' : l.pop(0), 'steps' : l.pop(0), 'path' : l}
else:
return {}
#-----------------------------------------------------------------
#random.seed(1)
n = 7
INF = -1
#-----------------------------------------------------------------
v1 = []
points = {}
for i in range(n):
points[i] = (random.randint(1,1000), random.randint(1,1000))
input_matrix = []
for i, vi in points.items():
m1 = []
for j, vj in points.items():
if i==j:
m1.append(INF)
else:
m1.append(round(distance(vi[0], vi[1], vj[0], vj[1])))
v1.append([i,j,round(distance(vi[0], vi[1], vj[0], vj[1]))])
input_matrix.append(m1.copy())
#-----------------------------------------------------------------
lib = cdll.LoadLibrary(r"tsp_branch.dll")
lib.tsp_branch.argtypes = [c_int, c_void_p]
lib.tsp_branch.restype = c_int
plt.figure(figsize=(5, 5))
graph = nx.Graph()
graph.add_nodes_from(points)
# Добавляем дуги в граф
for i in v1:
graph.add_edge(i[0], i[1], weight=i[2])
#-----------------------------------------------------------------
# Задача коммивояжора на минимум
start_time = datetime.now()
res1 = tsp_branch(n, input_matrix, lib)
date_diff = (datetime.now() - start_time).total_seconds()
print(date_diff)
print(res1['len'], res1['steps'], res1['path'])
if 'path' in res1:
d1 = []
for i, v in enumerate(res1['path']):
d1.append([res1['path'][i-1], res1['path'][i]])
#-----------------------------------------------------------------
# Задача коммивояжора на максимум
input_matrix_max = copy.deepcopy(input_matrix)
for i in range(len(input_matrix_max)):
for j in range(len(input_matrix_max)):
if i != j:
input_matrix_max[i][j] = 1000 - input_matrix_max[i][j]
start_time = datetime.now()
res2 = tsp_branch(n, input_matrix_max, lib)
date_diff = (datetime.now() - start_time).total_seconds()
print(date_diff)
res2['len'] = 0
for i, val in enumerate(res2['path']):
res2['len'] += input_matrix[res2['path'][i-1]][res2['path'][i]]
print(res2['len'], res2['steps'], res2['path'])
if 'path' in res2:
d2 = []
for i, v in enumerate(res2['path']):
d2.append([res2['path'][i-1], res2['path'][i]])
# -----------------------------------------------------------------
nx.draw(graph, points, width=1, edge_color="#C0C0C0", with_labels=True)
nx.draw(graph, points, width=2, edge_color="blue", edgelist=d1, style="-")
nx.draw(graph, points, width=2, edge_color="red", edgelist=d2, style="-")Хоть я и обожаю Python, но для ресурсоёмких задач он не подходит совершенно, даже с numpy. Привожу пример ранней наивной реализации с использование pandas чисто в целях ознакомления для новичков, но возможно кого-то подвигнет на изучение.
Python
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
import networkx as nx
import sys
if not sys.warnoptions:
import warnings
warnings.simplefilter("ignore")
pd.set_option('display.max_rows', 500)
pd.set_option('display.max_columns', 500)
pd.set_option('display.width', 1000)
#------------------------------------------------------------------------------------
def distance(x1, y1, x2, y2):
return ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5
#------------------------------------------------------------------------------------
def in_deep_matrix(p, y, x):
# Возвращает новую матрицу меньшего размера, за вычитом строки и столбца
return p.drop([y], axis = 0).drop([x], axis = 1)
#------------------------------------------------------------------------------------
def reduction_matrix(p):
# Производим редуцирование матрицы, возвращаем нижнюю границу
bottom_line = 0
# Находим минимум по каждой строке и вычитаем его
for index, row in p.iterrows():
min = row.min()
if np.isinf(min):
return np.inf
bottom_line += min
for key, value in row.iteritems():
p[key][index] -= min
# Находим минимум по каждому столбцу и вычитаем его
for key, value in p.iteritems():
min = value.min()
if np.isinf(min):
return np.inf
bottom_line += min
for index, row in value.iteritems():
p[key][index] -= min
return bottom_line
#------------------------------------------------------------------------------------
def partition_matrix(p):
# Ищем элемент для разбиения матрицы на m1 и m2
# Для этого производим оценку нулевых элементов матрицы
max_sum = 0
index_i = None
index_j = None
for index, row in p.iterrows():
for key, value in p.iteritems():
if p[key][index] == 0:
min_i = np.inf
min_j = np.inf
for k, v in p[key].items(): # по столбецу
if k != index and v < min_i:
min_i = v
for k, v in p.loc[index].items():
if k != key and v < min_j:
min_j = v
l = min_i + min_j
if l > max_sum:
max_sum = l
index_i = index
index_j = key
return [index_i, index_j, max_sum]
#------------------------------------------------------------------------------------
def reverse_index(l, i, j):
# Находим обрытный индекс для матрицы
def in_dict(d, v):
while v in d:
v = d[v]
return v
ln = len(l)
d1 = {l[k][0]: l[k][1] for k in range(0, ln, 1)}
d2 = {l[k][1]: l[k][0] for k in range(0, ln, 1)}
return [in_dict(d1, i), in_dict(d2, j)]
#------------------------------------------------------------------------------------
def evaluation_matrix(p, res, bottom_line):
# Оценка матрицы, поиск решения
if len(p) == 1:
res['steps'] += 1
bottom_line += p.iat[0, 0]
# Если текущее решение лучше, запоминаем его
if bottom_line < res['global_min']:
res['global_min'] = bottom_line
res['local_result'].append([p.index[0], p.columns[0]])
res['best_result'] = res['local_result'].copy()
print('Решение лучше:', bottom_line, res['best_result'], 'шаг: ', res['steps'])
return
# Производим редуцирование матрицы, возвращаем минимальную нижнюю границу
bottom_line += reduction_matrix(p)
if np.isinf(bottom_line):
return
max_sum = 0
while True:
res['steps'] += 1
# Находим элемент для разбиения на подмножества m1 и m2
i, j, max_sum = partition_matrix(p)
# Больше нет элементов для разбиения
if i is None:
return
v_len = len(res['local_result'])
# Рассматриваем m1 (соглашаемся на разбиение по элементу)
if bottom_line < res['global_min']:
res['local_result'].append([i, j])
p1 = in_deep_matrix(p, i, j)
# Вычёркиваем обратный элемент только для матрицы большей чем 2х2, чтоб не получить inf
if len(p1) > 2:
i_reverse, j_reverse = reverse_index(res['local_result'], i, j)
p1[j_reverse][i_reverse] = np.inf
evaluation_matrix(p1, res, bottom_line)
# Рассматриваем m2
if res['global_min'] < bottom_line + max_sum:
return
p[j][i] = np.inf # Исключаем не выбранный элемент
res['local_result'] = res['local_result'][:v_len] # Обрезаем список пути
#------------------------------------------------------------------------------------
def return_res(res):
l = res['best_result']
if l:
d = {l[k][0]: l[k][1] for k in range(len(l))}
li =[]
a = l[0][0]
for v in range(len(l)):
li.append(a)
a = d[a]
return li
else:
return []
#------------------------------------------------------------------------------------
#random.seed(1)
n = 13
v1 = []
points = {}
for i in range(n):
points[i] = (random.randint(1,1000), random.randint(1,1000))
input_matrix = []
for i, vi in points.items():
m1 = []
for j, vj in points.items():
if i==j:
m1.append(np.inf)
else:
m1.append(int(distance(vi[0], vi[1], vj[0], vj[1])))
v1.append([i,j,int(distance(vi[0], vi[1], vj[0], vj[1]))])
input_matrix.append(m1.copy())
plt.figure(figsize=(6, 6))
graph = nx.Graph()
graph.add_nodes_from(points)
# Добавляем дуги в граф
for i in v1:
graph.add_edge(i[0], i[1], weight=i[2])
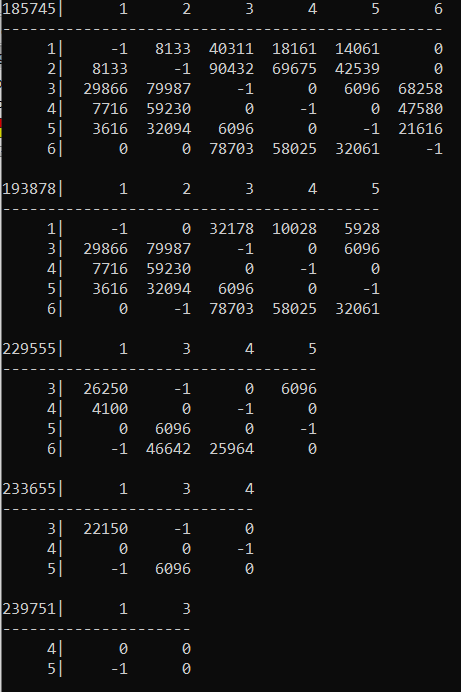
f1 = pd.DataFrame(input_matrix)
print(f1)
# Инициализация массива решений
res = {'global_min':np.inf, 'best_result': [], 'local_result':[], 'steps':0}
# Запуск нахождения решения
evaluation_matrix(f1, res, 0)
print('Результат:', res['global_min'], return_res(res), 'всего шагов:', res['steps'])
# Рисуем всё древо
nx.draw(graph, points, width=1, edge_color="#C0C0C0")
# Рисуем оптимальный путь
nx.draw_networkx(graph, points, with_labels=True, edgelist=res['best_result'], arrows=True, edge_color="blue", width=5)Я работал над данным алгоритмом более трёх лет наездами. Проект, для которого предназначался этот алгоритм, остался в далёком прошлом, но мне думается, что общественности будут любопытны мои наработки на данном поприще.
Буду рад откликам, замечаниям, предложениям, возражениям.
Код, приведённый к статье, разработан вашим покорным слугой и может быть использован вами под лицензией GNU GPL.
P.S. C Наступающим Новым годом!