Sergey_Kovalenko May 18 2022 at 22:43

Алгоритмы на кристалле. Глава 1 (продолжение): Быстродействие элементарных схем

31 min

5.3K

Algorithms*Mathematics*Manufacture and development of electronics*

Успел не все, что запланировал. Текст бы еще надо хорошенько причесать, но раз обещал в среду, пока публикую что есть. В этой части в общих чертах описаны процессы, которые происходят в цифровых электрических схемах, а так же ограничения, которые накладывают законы реального мира на процесс вычислений. Главными результатами являются понятия латентности и глубины формальной логической схемы, а так же связь этих величин с предельной тактовой частотой материализованного вычислительного устройства.

Следующая статья.
Предыдущая статья
Примерное оглавление будущей книги.

Текст, конечно, получился объемным — не самая веселая часть предмета. Я спешил разобрать парочку интересных и использующихся на практике схем, но был вынужден отложить их до следующей статьи. В качестве залога на обложке вы видите одну из них. Если сравнивать содержание будущей книги с настольной игрой, то собственно игра начнется со следующей статьи, а эту и предыдущую стоит воспринимать как брошюру правил. Правила — быть может не самая интересная часть процесса, но не освоив их в достаточной мере, вам трудно будет эффективно и с пониманием играть.

Возможно, в вашем браузере с первого раза не будут правильно отображаться формулы. Если так, попробуйте перезагрузит страницу — на моем компьютере этот фокус работает.

Приятного чтения.

Некоторые исправления и замечания к предыдущей статье

Уже после того, как предыдущая часть была мной опубликована, я осознал, что некоторые выбранные мной термины и понятия не вполне удобны. Прийти к этому пониманию мне помогли в том числе и здоровая критика моих читателей, в частности пользователей СВЕТ_ТЬМЫ и karambaso. Я считаю, будет правильным внести небольшие правки прямо сейчас, тем более, что эти статьи являются черновиком и их предназначение как раз и состоит в том, чтобы в процессе своего написания улучшаться и становиться удобнее для восприятия читателем.

Логическая схема и диаграмма значений

Первая правка будет касаться самого понятия логической схемы. Изначально в понятие схемы была включена и ее конструкция и то, какие именно значения ее компоненты (шины, порты и блоки) принимают на каждом такте. Ожидаемо, в какой-то момент повествования пришлось говорить о конструкции отдельно от значений. Как назвать конструкцию? Скелетом или остовом схемы? Хорошо, а если есть похожая конструкция из логических блоков портов и шин, но элементам которой нельзя приписать на каждый такт значения таким образом, чтобы они удовлетворяли аксиомам схемы, тогда вся эта конструкция уже не скелет?

В общем поломав немного голову, я решил поступить так.

Впредь под термином логическая схема мы будем понимать любое множество правильно соединенных между собой портов, логических блоков и шин. Под правильностью соединения подразумевается соответствие всей конструкции аксиомам P1 — P3, B1 – B3 и до тех пор, пока мы говорим об элементарных схемах – аксиомам C*. Отдельно мы будем выделять логические схемы, удовлетворяющие конструкционной аксиоме A* и называть последние схемами без циклов функциональной зависимости, или коротко: функционально ациклическими схемами.

В свою очередь логическую схему (в ее новом понимании), вместе с приписанными на каждый такт значениями ее портам, шинам, и состояниям регистров, мы будем называть допустимой диаграммой значений, если и только если совокупность этих значений удовлетворяет всем оставшимся аксиомам, а именно: T, P4-P7, S1, S2, B4, B5, E1-E11. Таким образом выходит, что старое понятие логической схемы мы, по сути, приравняли новому понятию допустимой диаграммы значений.

С изменением названий терминов поменяется звучание теоремы о функциональной ацикличности. Новая ее формулировка ставится проще и звучит теперь так:

если некоторая (элементарная) логическая схема не содержит циклов функционального влияния, то для любых заданных на каждый такт значений ее внешних выходных портов и любых заданных на момент нулевого такта значениях состояний ее регистров метод прямого распространения данных позволяет построить ту единственную допустимую диаграмму этой схемы, для которой состояния регистров на нулевом и значения внешних выходных портов на каждом такте совпадают с заданными.

Пояснения, касающиеся понятия внешних входных и внешних выходных портов на схеме

Да, наверное, это сбивает столку. Если слышишь две фразы: «внешний выходной порт схемы» и «выходной порт логического блока», то интуитивно проводишь между ними параллель. Кажется очевидными, что назначение, которому служит внешний выходной порт на схеме, должно быть аналогично роли, которую играет выходной порт у логического блока.

Однако, это не так. Наши формальные определения с такой аналогией идут в разрез.

Мысленный ряд здесь должен быть другим. Он строится на предположении, что не все устройства, влияющие на поведение схемы, изображены на ней целиком. Если устройство изображено на схеме целиком, то все порты этого устройства имеют атрибут внутренних. Внешними же названы те порты, которые сами присутствуют на схеме, а вот устройства, которым они принадлежат, в эту схему непосредственно не включены.

Согласно этой точке зрения, дистанционно вынесенные на материнскую плату компьютера входные порты принтера, монитора, и аудиосистемы – являются для платы внешними входными, то есть физически присутствующими на ней входными портами тех устройств, которые сами размещены за ее пределами. С другой стороны, так же дистанционно размещенные на плате выходные порты мыши, клавиатуры и сканера – являются по отношению к плате внешними выходными портами.

Указанная интерпретация на первый взгляд противоречит тому обстоятельству, что разъемы на плате, куда подключаются кабели от принтера, монитора и аудиосистемы, по своему смыслу являются выходными портами самой материнской платы, рассматриваемой как единое устройство, а разъемы, куда подключаются клавиатура и мышь – ее входными портами.

В действительности между обеими трактовками никаких противоречий нет. Все зависит от выбранной точки зрения.

Если вы рассматриваете материнскую плату как обособленное цельное устройство, то расположенные на ней разъемы для клавиатуры и мыши имеют смысл входных портов, то есть тех, на которые должны быть поданы электрические импульсы в процессе работы, а разъемы для монитора и принтера – как выходные порты, поскольку последние сами являются источниками цифрового сигнала.

В то же время, если плату рассматривать «изнутри»: как собранную из отдельных устройств логическую схему, то «обратная» стороны разъема для клавиатуры будет выглядеть, как дистанционно вынесенный порт выхода (клавиатура порождает импульсы), а обратная сторона разъема для монитора – как типичный порт входа (на него нужно отправлять импульсы).

Из незначительного — изменилось графическое изображение портов: теперь полукруги, обозначающие внутренние порты, крепятся к своим блокам снаружи. Так больше места и кое-что еще, но об этом плюсе вы узнаете в следующей статье.

Замена термина «фронт распространения сигнала» на «фронт распространения данных»

Словосочетания «фронт сигнала» имеет устоявшееся значение в физике электрических цепей и электротехнике, особенно в контексте «передний фронт сигнала» и «задний фронт сигнала». Чтобы не сбивать с толку ненужными ассоциациями представителей этих профессий, впредь вместо использовавшегося в прошлой статье термина «фронт распространения сигнала» (параграф, посвященный методу прямого распространения данных), для названия того же понятия мы будем использовать термин «фронт распространения данных».

Далее. Немного изменен смысл и алгоритм построения фронтов распространения данных. Теперь каждый порт входа, если тот единственный порт выхода, с которым он соединен общей шиной, принадлежит фронту $F_{i-1}$ , то сам этот порт входа будет включен во фронт $inline$ . Из-за нового этого упростились определения и доказанные результаты (доказательство теоремы о функциональной ацикличности теперь можно понять не запутавшись в нем). Все изменения уже внесены в текст.

Статическая дисциплина

Изменения там, где их нет.

Со стороны читателя может прозвучать обоснованный вопрос, почему «метод прямого распространения данных» получил именно такое название, ведь определяющая его процедура построения фронтов относится к одному единственного такту, а в продолжение любого такта значения всех элементов абстрактной схемы по определению остаются неизменными. Почему для описания статической картины значений были выбраны «динамические» термины “фронт” и “распространение”, повседневное значение которых неразрывно связанны с чем-то меняющимся и непостоянным. Ответы на эти вопросы на самом деле важны как для лучшего понимания самой теории, так и для осознания пределов ее применимости.

Вернемся к истокам. В самом начале было сказано, что прообразом абстрактных логических схем являются реально существующие электрические (или другого рода) логические схемы, в которых реальные физические устройства обмениваются и преобразуют настоящие электрические (или другого рода) импульсы. По сути вычислительные возможности именно этих реальных логических схем и являются настоящим объектом нашего изучения, а выстроенная в последствии теория – это всего лишь стандартный метод исследования.

Переход от непосредственно явления к его теории позволяет исследователю игнорировать все несущественные второстепенные черты явления и тем самым сконцентрировать свое внимание на главном. В рамках этой книги главной чертой цифровых электрических схем считается их способность производить символьные вычисления. Собственно вопросу эффективной организации таких вычислений и посвящена книга.

Конечно, деление черт на существенные и несущественные происходит всегда весьма условно и зачастую в погоне за простотой теории приходится жертвовать кое-чем действительно важным. Например, наша теория не отражает такие важные особенности работы микросхем, как конечность скорости распространения сигналов, временные задержки в обработке сигналов элементами схемы, размер схемы, ее предельную рабочую частоту, потребляемую мощность и характеристики тепловыделения. О каждой из этих особенностей мы еще будем говорить в этой книге, сейчас же нас особенно интересуют первые две.

Гидродинамическая аналогия

В рамках этого параграфа мы ненадолго выйдем за рамки теории и будем говорить не о формальных понятиях а об их значениях в реальном мире.

То, какое значение передается по проводу в цифровой электрической схеме: логический “ноль” или логическая ”единица” – (обычно) определяется по уровню напряжения в проводе. Изменения напряжения, как и все в этом мире, не происходят и не распространяются мгновенно. Чтобы описать, как происходят эти изменения, нам, вообще говоря, пришлось бы прибегнуть к науке об электричестве.

С моей стороны, однако, было бы неправильно предполагать у читателя этих знаний (да и сам я почти все забыл), поэтому с вашего позволения я прибегну пусть и не к совсем точной, но зато к наглядной и простой аналогии.

То, чем он является и то, как он со временем себя ведет, уровень напряжения в проводе во многом напоминает уровень воды в длинном оросительном канале.

Представьте, что канал изначально пуст, а на одном из его концов только что открылся шлюз, соединяющий канал с полноводным водохранилищем. Уровень воды в канале не станет высоким мгновенно: с открытием шлюза вдоль всей длины канала прокатится приливная волна. По мере того, как волна будет продвигаться все дальше, ее сила постепенно начнет ослабевать, поэтому, когда фронт волны в итоге ударится о стену в конце канала, уровень воды отнюдь не по все его длине достигнет отметки наполнения. Потребуется еще некоторое время, чтобы канал полностью наполнился водой.

Распространение приливной волны вдоль реки

Теперь представьте, что после того, как канал наполнен, шлюз, соединявший его с водохранилищем, перекрыли, но зато отрыли соседний шлюз, ведущий в бескрайние иссушенные солнцем поля. Процесс, сопровождавший наполнение канала, повторится с точностью до наоборот. По каналу прокатится теперь уже волна отлива. До тех пор, пока фронт отлива не достигнет дальнего конца канала, уровень воды там ничуть не изменится, а после – еще продолжительное время будет плавно падать, пока канал полностью не опорожнится.

Можно сделать вывод, что величина задержки времени между тем, как сработает шлюз и тем, как на противоположном конце канала уровень воды достигнет стабильного значения, зависит от главным образом длины канала, а также от отношения объема канала (емкости) к величине потока чрез шлюз. Почти то же самое утверждение будет верно и для однобитных шин (проводов) цифровой электрической схемы.

Выстраивая аналогию дальше, можно сказать, что функционирование каждого выходного порта вычислительного схемы подобно работе двух только что описанных шлюзов. Послать в шину “единицу” – это как открыть шлюз, соединяющий канал с водохранилищем, сохраняя при этом закрытым шлюз, ведущий в поля. Послать “ноль” – это как открыть шлюз в сторону поля, при закрытом шлюзе из водохранилища. Таким образом значения портов выхода – это либо роль шлюза “наполнения”, либо роль шлюза “опорожнения” для соединенной с портом шины.

Работу входных портов можно сравнить с работой механического поплавкового уровнемера с двумя главными значениями: “канал полон” и ” канал пуст”. Если напряжения в той точке провода, где расположен входной порт, выше некоторой отметки a, то этот порт приобретает логическое значение “1”, если же уровень напряжения в этой точке падает ниже, чем некоторая отметка b < a, то логическим значением будет “0”. Уровни напряжения, которые выше a, либо ниже b, условимся называть регулярными. Логическое значения порта входа в моменты, кода уровень напряжения находится где-то между b и a, считается не определенным.

Физический такт в отличие от формального – это некоторый довольно продолжительный отрезок времени, на протяжении которого напряжения в портах и шинах могут непрерывно меняться. Длина физического такта подбирается так, чтобы при любом сценарии вычислений к концу такта уровни напряжений на всех шинах и портах схемы успели бы прийти к какому-то окончательному регулярному значению, которые за тем уже бы не менялись, сколько этот такт не продлевай. То (регулярное) значение порта или шины, которое на текущем такте уже не будет больше меняться, мы назовем стабильным.

Вспомним, что функциональными в нашей теории мы назвали те (элементарные) логические блоки, у которых значения портов выхода на каждом такте однозначно определяется значениями их портов входа. Для физических устройств, которые реализуют блоки функционального типа, характерно то, что их работа вообще не привязана к физическим тактам: каждый раз, как только уровни напряжения на всех входных портах функционального блока достигают регулярных значений (а это может происходить неоднократно за один физический такт), почти сразу после этого каждый его выходной порт приобретает правильное с точки зрения логики этого блока значение. Поскольку значение порта выхода – это либо роль шлюза “наполнения”, либо роль шлюза “опорожнения” для соединенной с ним шины, то из сказанного мы можем сделать два вывода:

если начиная в некоторый момент уровни напряжения на входных портах функционального блока достигли стабильных регулярных значений, то спустя некоторое время в проводах (однобитных шинах), с которыми соединены порты выхода этого блока, урони напряжения также достигнут стабильных регулярных значений (все каналы будут в конце концов либо наполнены либо опорожнены);
если в продолжение некоторого обозримого будущего уровни напряжения на входных портах
функционального блока могут изменится, то вообще говоря нельзя гарантировать, что в этот период значения его выходных портов, а следовательно и уровни напряжения в присоединенных к ним проводах (однобитных шинах), не изменятся тоже.

(рисунок, объясняющий, почему в предыдущих предложениях так много “вообще говоря”).

Оговорка: “вообще говоря”, имевшая место в пункте 2) связана конечно с тем, что не во всех ситуациях изменение одного конкретного входного порта функционального блока должно сказаться на значениях его выходных портов. Все зависит от логической функции, которую реализует блок, его физического устройства и того, как меняются уровни напряжения на остальных его входных порта. Тем не менее от фразы “вообще говоря” можно избавится, если считать, что логика работы блока нам не известна. В таком случае мы действительно не сможем гарантировать стабильности значений на выходных портах функционального блока прежде, чем у нас появится гарантия стабилизировались напряжения на его портах входа.

Переходные процессы, происходящие в продолжение одного физического такта

Внутри аксиоматической теории значения шин и портов на протяжении каждого такта по определению остается неизменным. В некотором смысле формальный такт даже не “длится” – вместо этого он всего лишь “существует” подобно фотографии, запечатлевшей показания приборов в кабине самолета.

Как уже упоминалось, физический такт в отличие от формального – это продолжительный отрезок времени, длина которого подбирается так, чтобы уровни напряжений на всех шинах и портах схемы успели стабилизироваться на каком-нибудь из регулярных значений.

Собственно, с позиции символьных вычислений, нам интересны именно эти предельные стабильные значения, и совершенно не важно, как именно уровни напряжений в портах и шинах к ним пришли. По этой причине теория логических схем была создана нами так, чтобы в каждом из формальных тактов значения шин и портов оставались статичными, а от такта к такту менялись скачком. Для целей нашего исследования переходные процессы – это второстепенная черта, которой можно пренебречь. Тем не менее, чтобы создавать по-настоящему эффективные логические схемы, кое-какое представление о переходных процессах иметь все-таки необходимо.

К концу каждого физического такта уровни напряжения на всех портах и во всех шинах схемы приходят к стабильным регулярным значениям. Рассмотри мгновение, когда очередной такт завершился и только что начался следующий. Вполне возможно, что стабильные значения напряжений в портах и шинах в конце этого нового такта должны быть другими, нежели они были в конце предыдущего такта. Проследим в таком случае, где зарождаются и как распространяются изменения уровней электрического напряжения в компонентах схемы.

В рамках принятой нами упрощенной картины мира единственной причиной изменения уровня напряжения в проводе (однобитной шине) может быть только изменение режима работы соединенного с ней выходного порта (с «наполнить» на «опорожнить», или наоборот).

В самые первые мгновения нового такта такими портами не могут быть выходные порты функциональных блоков. Действительно, изменения по шинам распространяются не мгновенно, поэтому некоторое время уровень напряжения в тех точках шин, где к ним прикреплены входные порты любых, в том числе и функциональных блоков, будет оставаться неизменными. Раз некоторое время не будет меняться стабильное в прошлом значение входных портов, то в этот же период останутся неизменными режимы работы выходных портов любого из функциональных блоков.

И так, претендентами на роль затравок изменений напряжений в схеме остаются только внешние выходные порты и выходные порты регистров, другими словами, те порты, из них которых по определению состоит нулевой фронт распространения данных $inline$ . Следовательно, первыми претерпят изменения уровни напряжения в тех шинах, началом которых служат порты из $inline$ .

Здесь может возникнуть догадка, что в этих же шинах, возмущенные первыми, уровни напряжения первыми и придут к стабильным значениям. Но это не совсем так. Не всегда будет верным и предположение, что следующие порты, которых коснутся изменения, обязательно должны принадлежать фронту $inline$ . На деле все сильно зависит от длинны шин и характеристик блоков, из которых собрана схема.

Однако некоторая чуть более аккуратно сформулированная мысль все же естественно связывает нумерацию фронтов и порядок, в котором происходит стабилизации напряжений в шинах. Чтобы избавится от частых оговорок, будем считать, что о каждом блоке схемы нам известно, является ли он функциональным или нет, но ничего более конкретного о внутренней логике его работы мы не знаем.

Пусть $p_{in}$ – какой-нибудь выходной порт, относящийся к фронту $inline$ . В таком случае тот выходной порт $p'_{out}$ , с которым общей шиной соединен $p_{in}$ , обязательно входит во фронт $F_{i-1}$ (смотрите алгоритм построения фронтов). Следовательно, значение $p_{in}$ , стабилизируется никак не раньше, чем перестанет меняться значение, то есть, режим, в котором работает порт $p'_{out}$ .

Пусть теперь $p_{out}$ – это какой-нибудь выходной порт, относящийся к фронту $inline$ . Из правила построения фронта $inline$ следует, что блок, которому принадлежит $inline$ , обязательно является функциональным, более того: среди входных портов этого блока есть по крайней мере один такой, который соединен общей шиной с некоторым выходным портом $p'_{out}$ , принадлежащим фронту $F_{i-1}$ . Поскольку логика работы блоков остается для нас тайной, то мы не сможем гарантировать, что значение порта $inline$ на этом такте больше не изменится, раньше, чем мы сможем гарантировать то же самое для порта $p'_{out}$ .

Объединяя две последних цепочки рассуждений в одну, получаем следующее утверждение:
Если логика работы блоков остается для нас тайной, то мы не сможем гарантировать, что значения всех портов фронта $inline$ пришли к стабильным значениям, раньше, чем мы сможем гарантировать, что стабилизировались значения во всех шинах, находящихся в соединении с выходными портами фронта $F_{i-1}$ .

Латентность логической схемы

Главный вопрос и декомпозиция проблемы

Длительность одного такта трудно сделать меньше, чем время, за которое напряжения во всех шинах и портах схемы гарантированно смогут прийти к стабильным значениям. Последнюю величину назовем временем релаксации схемы. Получается, что чем меньше время релаксации, тем выше может быть сделана тактовая частота, то есть, выше достижимая вычислительная производительность схемы. Пусть перед нами стоит задача, пользуясь заранее определенными физическими блоками и известной технологией их соединения, спроектировать логическую схему, которая бы реализовывала некоторый алгоритм. Поскольку для одного и того же алгоритма существует, вообще говоря, много возможных схем его реализации (микроархитектурных решений), то естественным образом возникает вопрос:

Как выбор того или иного микроархитектурного решения влияет на максимально возможную тактовую частоту схемы, изготовленной в соответствии с этим решением?

Точно рассчитать время релаксации вычислительной схемы – задача не из просты. Ее решение требует симуляции или даже натурного эксперимента, а результат существенно зависит от технологии, выбранной для изготовления будущей схемы. Безусловно, рассуждая только на уровне абстрактных схем и логических блоков, точно определить время релаксации не получиться, однако кое-какие оценки асимптотического поведения его величины, так называемые O-большое оценки, – дать все-таки можно.

На время релаксации физической схемы влияют главным образом два обстоятельства. Первое из них – это то, что электрические сигналы в шинах распространяются с конечной скоростью, поэтому на преодоление пути от одного блока к другому им требуется некоторое время. Второе заключается в том, что и каждому блоку требуется некоторое время (время реакции, задержка блока), чтобы значения его выходных портов успели отреагировать на изменившиеся значения портов входа.

Разумно предположить, что если схема состоит из небольшого числа блоков и ее размер на кристалле поэтому мал, или в ней заведомо не велика протяженность самого длинного пути, по которому может пройти сигнал за один такт, то величина времени релаксации будет главным образом обусловлена задержками внутри отдельных блоков. Именно эти случаем мы сейчас и займемся, а о том, какой подход следует применять к большим схемам, поговорим позже.

Упрощенная модель релаксации

Пусть каждый такт – это длящийся отрезок времени, настолько продолжительный, что дальнейшее увеличение его длины не приведет ни к каким дополнительным изменениям значений портов и шин в этот период. Значения каждого порта или шины в каждый момент такта может быть либо определено и тогда являться неким двоичным словом, либо не определено. То определённое значение порта или шины, которое больше до конца такта не изменится, как раньше, будем называть стабильным.

Будем считать, что сигналы от порта к торту передаются мгновенно. Таким образом значение каждого выходного порта и всех входных портов, с которыми тот соединен общей шиной, одинаковы любой момент времени. В частности, все эти значения либо определены, либо – нет, и каждое из них стабильно тогда и только тогда, когда стабильны все остальные.

Далее, пусть для каждого функционального блока $inline$ известно то максимальное время $inline$ , которое может пройти между моментом, когда последний раз менялись и с тех пор являются определёнными значений всех его входных портов, и моментом, когда после этого перестанет меняться и станет определенным значения каждого его выходного порта. Величину этого времени назовем задержкой функционального блока. Будем считать, что блоки, относящиеся к одному и тому же элементарному типу, имеют одинаковое время задержки.

Регистры отличаются от функциональных блоков тем, что значения, принимаемые на текущем такте их портами входа, никак не влияют на значения, которые примет в этот такт их порт выхода, однако первые должны определить то, каково будет внутреннее состояние регистра в следующий такт времени. В свою очередь стабильное значение порта выхода регистра на каждом такте должно совпадать со значением внутреннего состояния, в котором в тот момент находится регистр. Достижение равенства в обоих случаях может требовать времени, поэтому для каждого типа регистров определим задержку стабилизации состояния и задержку стабилизации данных.

Задержка стабилизации состояния регистра $inline$ , $inline$ – это время которое должно пройти с момента, когда последний раз изменились и с тех пор остаются определенными значения всех входных портов регистра, до начала следующего такта, чтобы можно было гарантировать, что смена внутреннего состояния регистра между этими тактами произойдет правильно. Величина задержки стабилизации состояния $inline$ одинакова для всех регистров одного типа.

Задержка стабилизации данных $inline$ равна времени, которое должно пройти с момента начала следующего такта, чтобы можно было гарантировать, что значение выходного порта регистра R правильно соответствует его внутреннему состоянию. Величина задержки стабилизации данных $inline$ одинакова для всех регистров одного типа.

Пусть имеется некоторая элементарная логическая схема без циклов функционального влияния. Будем отсчитывать время с того момента $inline$ очередного такта ее работы, когда значения всех внешних выходных портов схемы только что стали определенными и до конца такта уже не изменятся. Оценим сверху время, необходимое на то, чтобы каждый порт схемы успел принять окончательные для этого такта значения. Оценку $inline$ этого времени для конкретного порта $inline$ назовем оценкой запаздывания (стабилизации) $inline$ .

Каждому внешнему выходному порту схемы по условию для этого понадобится дополнительно 0 единиц времени.

У блоков констант нет портов входа, поэтому даже на нулевом такте значение выходных портов блока-константы $inline$ станет определенным и стабильным спустя не более, чем время задержки $inline$ .

Выходному порту любого из регистров, чтобы принять окончательное значение, понадобится время не большее, чем его задержка стабилизации данных $inline$ .

Стоит заметить, что внешние выходные порты, выходные порты блоков-констант и выходные порты регистров как раз составляют формально определенный нами фронт распространения данных $inline$ . Следовательно, все порты фронта $inline$ приобретут определенные стабильные значения за вполне определенное конечное время. Все оставшиеся порты – это либо внешние порты входа схемы, либо входные и выходные порты функциональных блоков.

Рассмотрим на схеме любой функциональный блок $inline$ . Пусть $inline$ – все его входные порты. Предположим, что для каждого входного порта $inline$ нам уже известна оценка его запаздывания ${t(p)}_i$ ), то есть время, когда значение этого порта гарантированно станет определенным и стабильным. В таком случае, мы можем утверждать, что в момент времени $inline$ значения всех выходных портов этого блока также гарантированно будут иметь определенные и стабильные значения.

Примем число $inline$ за оценку запаздывания каждого из выходных портов блока B, а также за оценку запаздывания всех тех входных портов схемы, с которыми любой их выходных портов блока B связан общей шиной. Сможем ли мы, систематически повторяя только что использованный прием, приписать оценку запаздывания каждому порту схемы?

Будем рассуждать по индукции. Моменты, когда каждый порт фронта $inline$ гарантированно будет иметь стабильное определенное значение, мы уже оценили.

Каждый входной порт, принадлежащий фронту $inline$ примет определенное и окончательное для этого такта значение в тот же самый момент, что и единственный выходной порт фронта $F_{i-1}$ , с которым он соединен общей шиной.

Предположим, что для всех портов, принадлежащих фронтам $F_0…F_{i-1}$ , моменты времени, когда их значения гарантированно окажутся определенными и стабильными, уже оценены. Согласно алгоритму построения фронта $inline$ каждый включенный в него входной порт соединен общей шиной с каким-либо выходным портом фронта $F_{i-1}$ . В таком случае мы автоматически получаем оценку запаздывания и для каждый входного порта из фронта $inline$ .

Пусть теперь $inline$ – какой-нибудь выходной порт фронта $inline$ . В таком случае $inline$ принадлежит некоторому функциональному блоку B, каждый входной порт $inline$ которого содержится в одном из фронтов $inline$ . Отсюда следует, что оценка запаздывания $inline$ каждого порта $inline$ нам уже известна, а значит мы можем сделать эту оценку и для порта $inline$ , и тем самым завершить индуктивный шаг.

Поскольку логическая схема по условию не содержит циклов функциональной зависимости, то каждый ее порт содержится в одном из фронтов $inline$ . Следовательно, каждый порт получит оценку своего запаздывания, то есть величины времени между тем, когда определенными и стабилизации сделались значения всех внешних выходных портов схемы, и моментом, когда можно гарантировать, что и значение этого конкретного порта также являются определенным и стабильным.

Зачем нам вообще понадобилось вычислять оценку запаздывания портов?

Если мы использовать схему, как вычислительное устройство и для этого каждый такт специальным образом формируем значения внешних выходных портов схемы, то хотим, чтобы результаты расчетов, то есть значения внешних входных портов схемы, были на каждом такте корректны.

Чтобы на конкретном такте значения внешних входных портов схемы гарантированно приняли корректные значения, нам придется выждать время равное максимуму из оценок запаздывания, приписанных этим портам. Обозначим это время, как $inline$ .

Чтобы получать корректные данные на каждом из тактов, мы должны быть уверены, что все регистры схемы правильно меняют свои внутренние состояния. Пусть $inline$ – это максимум из оценок запаздывания, приписанных входным портам регистров, $inline$ – регистры, на входных портах которых этот максимум достигнут, $inline$ – максимум задержки стабилизации состояния среди $inline$ . Для того, чтобы на каждом такте гарантировать корректность работы регистров, после стабилизации значений внешних выходных портов прежде, чем очередной такт завершиться, должно проходить не менее $inline$ единиц времени.

Наибольшее из чисел $inline$ и $inline$ условимся называть задержкой или латентностью логической схемы. Продолжительность физического такта работы вычислительной схемы вообще говоря не может быть меньше величины ее латентности.

Поскольку процесс вычисления латентности схемы требует оперирования только со стационарными, не меняющимися на протяжении физического такта значениями, то мы можем поместить его внутрь той формальной аксиоматической теории логических схем, что была разработана нами ранее. Действительно, все, что для этого требуется – это назначить каждому функциональному типу элементарных блоков B формальную величину задержки (∆t)_B, а каждому типу регистров $inline$ – формальную величину задержки состояния (∆ts)_R и формальную величину задержки данных (∆td)_R.

Абстрактную логическую схему $inline$ , всем функциональным блокам и регистрам которой приписаны формальные задержки будем называть логической схемой с задержками.

Формальную задержку блоков прямого соответствия, реализация которых, как уже говорилось, не требует никаких физических устройств, чаще всего можно считать равной нулю. То же самое касается и блоков-констант (провод высокого и низкого напряжения). Фактические задержки в устройствах, реализующих остальные типы блоков, сильно зависят от технологии, но почти в любой из них будут иметь один порядок величины. Для O-большое оценок латентности схемы (а значит и предельной частоты ее работы) задержки всех блоков, кроме блоков прямого соответствия и блоков констант, удобно считать равной 1. Выбор каких-то других (ненулевых) значений на O-большое оценки все рано никак не повлияет.

Следующие два подраздела этого параграфа содержат несколько полезных результатов о вычислении запаздывания портов и величины латентности схемы. Их содержания также может рассматриваться с чисто формальной стороны.

Критический путь

Алгоритм, который мы использовали для приписывания портам логической схемы оценок запаздывания и отыскания латентности всей схемы целиком во многом похож на графовый алгоритм планирования порядка выполнения взаимозависимых работ на производстве (так называемые диаграммы Ганта). Нам будет полезно развить эту аналогию дальше.

Направленным графом $inline$ называют пару множеств $inline$ (vertices) – вершин и $inline$ (edges) – ребер вместе с двумя отношениями: “вершине $inline$ быть началом ребра $inline$ ” и “ вершине $inline$ быть концом ребра $inline$ ”. При этом должны еще выполнятся два простых требования:

Для каждого ребра должна существовать в точности одна вершина, которая служила бы ему началом.
Для каждого ребра должна существовать в точности одна вершина, которая служила бы ему концом.

Самый маленький направленный граф с непустым множеством ребер состоит из всего одного ребра и всего одной вершины, которая служит ему и началом, и концом.

Направленная петля

Конечная последовательность ребер $inline$ называется направленным путем в графе $inline$ , если началом каждому следующему ребру в этой последовательности служит вершина, являющаяся концом для предыдущего ребра. Если началом ребра $inline$ служит вершина $inline$ , а концом $inline$ – вершина $inline$ , то мы будем говорить, что путь $inline$ соединяет вершину $inline$ с вершиной $inline$ , $inline$ при этом называть началом пути $inline$ , а $inline$ – его концом. Последнее определение не симметрично: если некоторый путь соединяет $inline$ с $inline$ , то, вообще говоря, не верно, что тот же путь соединяет $inline$ с $inline$ .

Направленный путь, начало и конец которого совпадают, называется направленным циклом. Если в направленным графе нельзя построить ни одного направленного цикла, то такой граф называют (направленно) ациклическим. В ациклических графах ни один путь не может включать одно и то же ребро дважды.

Любое множество ребер $e_i, e_{i+1}, … e_{i+k}$ , взятых в пути $inline$ в порядке их следования, так же будет путем. Путь $e_i, e_{i+1},…e_{i+k}$ мы будем называть фрагментом пути $inline$ . Всякий фрагмент пути вида $inline$ называют начальным отрезком пути $inline$ , а фрагмент вида $e_k, e_{k+1}, … e_n$ – его конечным отрезком.

Пусть $inline$ – направленный граф, $inline$ и $inline$ – некоторое подмножество его вершин. Обо всяком пути, который соединяет некоторую вершину $inline$ из $inline$ с некоторой вершиной $inline$ из $inline$ , будем говорить, что этот путь соединяет множество $inline$ с множеством $inline$ . В частности, если $inline$ состоит из единственной вершины $inline$ , то мы будем говорить о пути, соединяющем множество $inline$ с вершиной $inline$ , или если множество $inline$ состоит из единственной вершины $inline$ – то о пути, соединяющем вершину $inline$ с множеством $inline$ .

В том случае, когда каждому ребру e направленного графа приписан некоторый действительнозначный вес $inline$ , граф называют взвешенным. Во взвешенном графе можно говорить о длине $inline$ направленных путей (и циклов). Длина пути полагается равной сумме весов тех ребер, из которых составлен путь: $inline$ .

Пусть $inline$ – направленный взвешенный граф с неотрицательными весами, и конечным множеством ребер, $inline$ и $inline$ – некоторое подмножества его вершин. Если существует хотя бы один путь, соединяющий $inline$ и $inline$ , то среди всех путей, соединяющих $inline$ и $inline$ , очевидно найдется путь (возможно, не один) с минимальной длиной. Если граф $inline$ к тому же еще и ациклический, то среди всех путей, соединяющих $inline$ и $inline$ , найдется путь (возможно, не один) с максимальной длиной. Это тривиальные утверждения, которые читатель, я верю, сможет доказать сам.

Позже нам понадобится одна простенькая

Лемма 1 (об экстремальных свойствах путей с минимальной и максимальной длиной):
Пусть $inline$ – направленный взвешенный граф с неотрицательными весами, и конечным множеством ребер, $inline$ и $inline$ – некоторое подмножества его вершин, $inline$ – любой путь, соединяющий $inline$ с $inline$ , минимальной (максимальной) длины, тогда:

!) любой начальный отрезок пути $inline$ будет путем минимальной (максимальной) длины, соединяющим множество $inline$ с вершиной, расположенной на конце этого отрезка;

!!) любой конечный отрезок пути $inline$ будет путем минимальной (максимальной) длины, соединяющим вершину, расположенную в начале этого отрезка, с множеством $inline$ ;

!!!) всякий фрагмент пути $inline$ будет путем минимальной (максимальной) длины, соединяющим вершину, находящуюся в начале этого фрагмента, с вершиной, находящейся на его конце.

Докажем !), доказательства остальных пунктов проводятся аналогично.

Пусть $inline$ – начальный отрезок пути $inline$ , и a – вершина, которая служит концом ребру $inline$ .
Докажем от противного, что $inline$ – один из путей с минимальной (максимальной) длинной, соединяющих множество $inline$ с вершиной $inline$ .

Если это не так, то существует путь $inline$ соединяющий множество $inline$ с вершиной a, длина которого строго меньше (строго больше), чем у пути $inline$ . Однако в таком случае путь $e_1'',…e_{m+n-k}''$ , где $e_1''=e_1', … e_m''=e_m', \ \ e_{m+1}''=e_{k+1}, … e_{m+n-k}''=e_n$ ,
получающийся объединением пути $inline$ с путем $e_{k+1},…e_n$ , будет соединять $inline$ и $inline$ и по длине строго уступать (строго превышать) путь $inline$ . Полученное противоречие доказывает !)

На этом необходимое знакомство с теорий графов завершено и теперь мы снова возвращаемся к алгоритму оценки запаздываний портов логической схемы.

Согласно определению, данному в прошлой статье, порт p имеет непосредственное функциональное влияние на порт $inline$ , если и только если выполняется одно из двух условий: либо $inline$ должен являться портом выхода, соединенным одной шиной с портом входа p', либо p является портом входа, а $inline$ — портом выхода у одного и того же функционального блока.

Пусть $inline$ – правильно построенная логическая схема. На множество портов схемы $inline$ вместе с определенным на этом множестве отношением “ порту $inline$ иметь непосредственное функциональное влияние на порт $inline$ ” можно смотреть как на направленный граф. По определению в этом графе ребро с началом в порте $inline$ и концом в порте $inline$ существует тогда и только тогда, когда $inline$ непосредственно функционально влияет на $inline$ .

На самом деле для наших целей будет удобно немного расширить множество вершин такого графа и доопределить в нем некоторое количество дополнительных ребер.

Для каждой правильно построенная логической схемы $inline$ определим ассоциированный с $inline$ направленный граф $inline$ , исходя из следующих правил:

Множество вершин $inline$ включает в себя все порты схемы $inline$ , а также еще две дополнительные вершины для каждого входящего в ее состав регистра $inline$ : $inline$ , $inline$ , одну дополнительную вершину $inline$ для каждого входящего в ее состав блока-константы $inline$ и одну дополнительную вершину $inline$ для каждого внешнего выходного порта $inline$ . Вершины $inline$ и $inline$ мы будем называть мнимым портом входа и мнимым портом выхода регистра $inline$ , $inline$ – мнимым входом блока-константы $inline$ , $inline$ — мнимым спутником внешнего выходного порта $inline$ (Называть дополнительные вершины мнимыми портами – это всего лишь удобная абстракция, на самой схеме $inline$ мнимых портов конечно нет).
Если вершинами $inline$ и $inline$ графа $inline$ являются “настоящие” порты $inline$ и $inline$ схемы $inline$ , то по определению направленное ребро от $inline$ к $inline$ существует тогда и только тогда, когда $inline$ непосредственно функционально влияет на $inline$ .
Пусть $inline$ – какой-то регистр в $inline$ , порты $inline$ – это все (настоящие) порты входа $inline$ , $inline$ — его единственный (настоящий) порт выхода. Единственным ребром с началом в вершине $inline$ является ребро с концом в $inline$ . Для всякого входного порта $inline$ регистра $inline$ в $inline$ существует единственное ребро, соединяющее $inline$ с $inline$
Пусть $inline$ – блок-константа, $inline$ – его единственный (настоящий) порт выхода, в $inline$ существует единственное ребро с началом в $inline$ и концом в $inline$ .
Пусть p — внешний выходной порт, а in(p) — его мнимый спутник, в $inline$ существует единственное ребро с началом в $inline$ и концом в $inline$
Никаких других ребер в $inline$ нет.

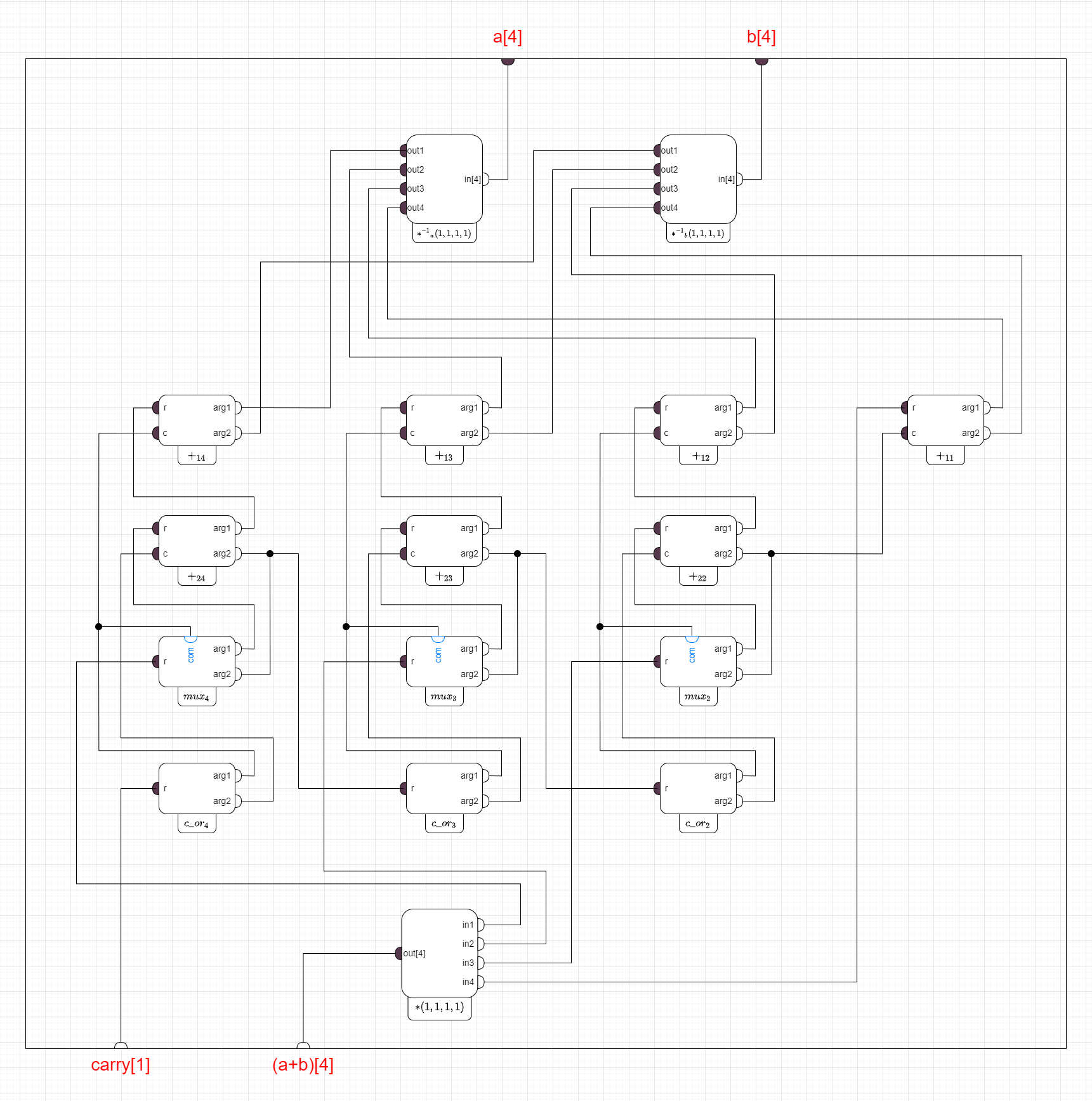
В качестве примера я еще раз привожу схему пульсара из прошлой статьи, а ниже — ассоциированный с ним граф.

(Схема «пульсар»)

(Граф, ассоциированный с «пульсаром»)

Попытайтесь самостоятельно доказать следующую простую

Лемма 2 (о свойствах путей в ассоциированном со схемой графе):
Пусть $inline$ – правильно построенная схема.

!) Ассоциированный с ней граф $inline$ в точности тогда является ациклическим, когда $inline$ не имеет циклов функционального влияния.

!!) Пусть $inline$ –произвольный путь в $inline$ , тогда все его ребра, за исключением быть может первого $inline$ и последнего $inline$ , можно поделить на две группы. Каждое ребро первой группы проведено от “настоящего” порта входа к “настоящему” порту выхода, одного и того же функционального блока. Каждое ребро второй группы проведено от “настоящего” порта выхода к одному из тех “настоящих” портов входа, с которым этот порт выхода соединен общей шиной. В последовательности $inline$ ребра обоих групп строго чередуются.

Пусть теперь $inline$ – правильно составленная схема с задержками. В ассоциированном с $inline$ графе $inline$ наличие задержек можно выразить, сделав $inline$ взвешенным. Припишем всем ребрам G(S) неотрицательные веса исходя из инструкций:

Всякому ребру, проведенному от “настоящего” порта выхода к “настоящему” порту входа припишем вес 0 (задержки в шинах нет).
Всякому ребру, проведенному от “настоящего” порта входа к “настоящему” порту выхода и поэтому соединяющему два порта одного и того же функционального логического блока $inline$ , припишем вес $inline$ .
Всякому ребру, проведенному от мнимого порта $inline$ блока-константы $inline$ к его порту выхода, припишем вес $inline$ .
Всякому ребру, проведенному от мнимого входного порта $inline$ регистра $inline$ к его “настоящему” порту выхода присвоим вес $inline$ .
Всякому ребру, проведенному от некоторого “настоящего” входного порта регистра $inline$ к его мнимому порту выхода out® присвоим вес $inline$ .
Всякому ребру, проведенному от мнимого спутника $inline$ к самому порту $inline$ , присвоим вес 0.

Читателю предоставляется возможность самостоятельно проверить, что приведенный список инструкций позволяет присвоить веса всем ребрам графа $inline$ .

Среди всех вершин $inline$ нам будет удобно особо выделить два подмножества. К множеству $inline$ начальных портов отнесем все мнимые спутники внешних портов выхода, мнимые входы регистров и мнимые входы блоков-констант. К множеству $inline$ терминальных портов – все внешние порты входа и мнимые порты выхода регистров.

Связь определенного выше взвешенного графа $inline$ с алгоритмом оценки запаздываний портов содержится в следующей

Теорема о критическом пути:

Пусть $inline$ –правильно построенная логическая схема с задержками без циклов функциональной зависимости, $inline$ – ассоциированный с $inline$ взвешенный направленный граф, тогда:

!) Величина (формального) запаздывания любого порта $inline$ в $inline$ равна наибольшей длине среди тех путей в $inline$ , которые соединяют множество начальных портов $inline$ с портом $inline$ .

!!) Латентность схемы $inline$ равна наибольшей длине среди тех путей в $inline$ , которые соединяют множество начальных портов $inline$ с множеством терминальных портов $inline$

Доказательство этой теоремы почти дословно повторяет рассуждения предыдущего подраздела.

Доказательство !).

Сначала нужно убедится, что !) справедливо для всех портов фронта $inline$ .

В каждый внешний порт выхода p ведет только одно ребро длины 0, началом которому служит мнимый спутник $inline$ , в сам мнимый спутник $inline$ не служит концом никакому ребру графа $inline$ . Отсюда следует, что всякий путь $inline$ , который закончится в $inline$ , состоит из единственного ребра длины 0 и поэтому сам имеет нулевую длину.

В вершину, являющуюся портом выхода некоторого регистра $inline$ , ведет только один путь: он состоит из единственного ребра с началом в $inline$ и весом $inline$ .

В вершину, являющуюся портом выхода некоторого блока-константы $inline$ , ведет только один путь: он состоит из единственного ребра с началом в $inline$ и весом $inline$ . И так, для $inline$ утверждение !) выполняется. Пусть мы уже доказали, что !) для портов входящих в любой из фронтов $F_0…F_{i-1}$ , покажем, что оно справедливо и для портов фронта $inline$ .

По определению формальное запаздывание всякого входного порта $inline$ в схеме $inline$ совпадает с запаздыванием того единственного выходного порта $inline$ , с которым $inline$ соединен общей шиной. Если входной порт $inline$ , принадлежащий фронту $inline$ , то соединенный с ним общей шиной выходной порт $inline$ обязан принадлежать фронту $F_{i-1}$ . Для входного порта p в графе $inline$ есть только одно ребро, концом которому служит вершина $inline$ – это ребро $inline$ , проведенное из $inline$ в $inline$ весом 0.

Если $inline$ – какой-либо путь, соединяющий множество начальных портов $inline$ с портом $inline$ , то его начальный отрезок $e_1,…e_{n-1}$ – это путь, соединяющий $inline$ с $inline$ , а элемент $inline$ – есть $e_{p'p}$ . Отсюда следует, что путь максимальной длины из $inline$ в p существует тогда и только тогда, когда существует путь максимальной длины из $inline$ в $inline$ и длины, этих путей равны. По предположению индукции путь максимальной длины из $inline$ в $inline$ существует, а длина всякого такого пути равна запаздыванию $inline$ , следовательно, то же самое можно сказать и о порте $inline$ .

И так, на все входные порты фронта $inline$ индуктивное предположение обобщено. Осталось рассмотреть случай, когда порт $inline$ принадлежит фронту $inline$ и является выходным.

Такое может быть, только если $inline$ служит выходным портом некоторому функциональному блоку $inline$ , причем $inline$ не является блоком-константой. Из правила построения фронтов вытекает, что все порты входа $inline$ блока $inline$ должны принадлежать объединению фронтов $inline$ .

Пусть $inline$ – максимальное запаздывание, которое имеют порты $inline$ . Формальное запаздывание порта $inline$ по определению равно максимуму запаздываний, приписанных портам $inline$ , увеличенному на $inline$ , то есть $inline$ .

Каждое ребро, которое ведет в выходной порт $inline$ блока $inline$ , есть ребро e_{p_i p}, проведенное из какого-либо входного порта $inline$ блока $inline$ в $inline$ . Длина всех таких ребер одинакова и равна $inline$ . По предположению индукции запаздывание каждого $inline$ равно длине наиболее протяженного пути в $inline$ , соединяющего $inline$ с $inline$ .

Пусть $inline$ — один из тех входных портов $inline$ блока $inline$ , запаздывание которого среди них максимально, то есть равно $inline$ . Далее, пусть $inline$ – любой из наиболее протяженных путей, соединяющий множество начальных портов $inline$ с портом $inline$ . Согласно индуктивным выкладкам, длина пусти $e_1,…e_{n-1}$ равна $inline$ .

Дополним путь $e_1,…e_{n-1}$ ребром $e_{p'p}$ , проведенным из $inline$ в p. Получившийся путь $inline$ ( $e_n= e_{p'p}$ ) соединяет множество начальных портов $inline$ с портом $inline$ , а его длина равна $inline$ , то есть совпадает с запаздыванием порта $inline$ .

Доказательство !) будет полностью завершено, если мы покажем, что ни один путь, соединяющий множество начальных портов $inline$ с портом $inline$ , не может быть длиннее, чем $inline$ .

Предположим обратное: пусть $inline$ — какой либо путь, который соединяет множество начальных портов $inline$ с портом $inline$ и имеет длину строго большую, чем $inline$ . Поскольку единственными ребрами в $inline$ , концом которым служит выходной порт $inline$ , являются ребра, проведенные из портов $inline$ , то начальный отрезок $e_1',… e_{m-1}'$ упомянутого пути – есть путь, соединяющий $inline$ с некоторым портом входа $inline$ блока $inline$ . В таком случае $inline$ есть ребро e_{p_i p}, и его длина равна $inline$ . Из соотношения $L(e_1',… e_m' )=L(e_1',… e_{m-1}' )+L(e_m' )=L(e_1',… e_{m-1}' )+∆t_B$ следует, что длина пути $e_1',… e_{m-1}'$ должна быть строго больше $inline$ , но этого не может быть, поскольку $inline$ – это максимум для длин путей, соединяет множество начальных портов $inline$ с множеством ${p_1,…p_n}$ входных портов блока $inline$ .

Полученное противоречие и тот факт, что в правильно составленной логической схеме без циклов функционального влияния каждый порт принадлежит какому-либо фронту распространения данных, полностью доказывают !).

Доказательство !!)

По определению латентность логической схемы с задержками равна максимуму среди запаздываний ее внешних портов входа и запаздываний входных портов каждого регистра R, увеличенных на $inline$ . Множество терминальных портов $inline$ состоит из внешних входных потов и мнимых выходных портов регистров. Для каждого из внешних портов и каждого входного порта всякого регистра мы уже доказали, что его запаздывание равно максимуму длины среди тех путей, которые соединяют в $inline$ множество начальных портов $inline$ с этим портом. Чтобы доказать утверждение !!), достаточно удостовериться, что для каждого регистра R максимум задержек его входных портов увеличенный на $inline$ равен длине одного из наиболее протяженных путей, соединяющих множество $inline$ с мнимым выходным портом $inline$ этого регистра.

Не самая сложная задача. Пусть $inline$ какой-либо регистр на схеме $inline$ , $inline$ – его “настоящие” входные порты. Каждое ребро в $inline$ , концом которому приходится мнимый порт out®, проведено из некоторого входного порта $inline$ этого самого регистра. Длина всех таких ребер одинакова и равна $inline$ . Дальнейшие подробности доказательства предоставляются читателю.

Глубина схемы

Алгоритм, приведенный в предыдущем разделе, позволяет вычислить латентность схемы имея под рукою хотя бы карандаш и лист бумаги. Но в действительности, сравнить латентность двух схем “по порядку величины” можно чуть ли ни на глаз.

Ранее мы определили отношение непосредственного функционального влияния для портов логической схемы, теперь мы сделаем то же самое для целых ее блоков:

Функциональный блок $inline$ непосредственно функционально влияет на функциональный логический блок B’ в том и только в том случае, когда некоторый входной порт блока $inline$ и некоторый выходной порт блока $inline$ соединены одной шиной. Ни в каком другом случае никакой блок не оказывает непосредственного функционального влияния на другой блок схемы.

На некоторый блоки схемы непосредственно функционально могут влиять, вообще говоря, сразу несколько других ее блоков, при этом некоторые функциональные блоки могут влиять, вообще говоря, на несколько блоков сразу. Если в схеме нет циклов функционального влияния, то ни один блок не может непосредственно функционально влиять сам на себя.

Пусть $inline$ – правильно составленная логическая схема без циклов функционального влияния. Всякую последовательности функциональных логических блоков схемы $inline$ , такую что каждый предыдущий блок в этой последовательности непосредственно функционально влияет на следующий, назовем цепочкой функционально-зависимых блоков. Никакой логический блок в такой цепочке не встретиться дважды (докажите). Отсюда, в частности, следует, что число блоков в таких цепочках и число самих цепочек функционально-зависимых блоков конечно, если логическая схема конечна и лишена циклов функционального влияния.

Выделим все цепочки функционально-зависимых блоков, у которых первый по порядку блок имеет по крайней мере один входной порт, соединенный общей шиной либо с внешним выходным портом, либо с выходным портом какого-нибудь регистра, либо с выходным портом какого-либо блока константы, а последний по порядку блок имеет по крайней мере один выходной порт, соединенный общей шиной либо с внешним входным портом, либо с одним из входных портов какого-нибудь регистра.

Среди выделенных цепочек найдем ту, в которых число $inline$ функциональных блоков, не являющихся блоками-константами или блоками прямого соответствия, максимально (возможно, таких цепочек будет несколько). Это самое число $inline$ традиционно и называют глубиной логической схемы. Важность и польза этого понятия раскрывается в следующей

Теорема о сравнении латентности двух схем:

Пусть каждому блоку константе и каждому блоку прямого соответствия приписана нулевая задержка. Величинам задержки $inline$ блоков других функциональных типов, а также величинам задержки стабилизации данных $inline$ и задержки стабилизации состояния $inline$ каждого типа регистров приписаны строго положительные значения. Обозначим ка $∆_{min}$ – минимальное, а $∆_{mах}$ – максимальное из этих значений.

Далее, пусть $inline$ и $inline$ две правильно составленные схемы с задержками без циклов функционального влияния, $inline$ и $inline$ – глубина и латентность первой схемы, $inline$ и $inline$ – глубина и латентность второй схемы, тогда:

$\frac{L\left(S_1\right)}{L\left(S_2\right)}\le \frac{∆mах}{∆min} * \frac{K(S_1)+2}{K(S_2)}≈ \frac{K(S_1)+2}{K(S_2)}$

Доказательство теоремы.

Латентность $inline$ равна длине наиболее продолжительного пути, соединяющего во взвешенном графе $inline$ множество $inline$ его начальных портов с множеством $inline$ терминальных портов этого графа. Длина каждого пути в $inline$ только увеличится, если всем ребрам графа, имевших до этого положительный вес приписать новый вес $∆_{mах}$ , а веса остальных ребер –оставить по-прежнему равными нулю.

Пусть $inline$ – какой-либо в графе $inline$ , соединяющий множество $inline$ с множеством $inline$ .
Путь $inline$ начинается либо в мнимом спутнике внешнего выходного порта, либо в мнимом входном порте блока-константы, либо в мнимом входном порте одного из регистров. В любом случае ребро $inline$ будет соединять настоящий “выходной” порт с настоящим “входным” портом и поэтому иметь длину 0 (проверьте). Таким образом вклад первых двух ребер $inline$ в его длину составляет не более $∆_{mах}$ .

Заканчивается путь $inline$ либо во внешнем входном порте, либо в мнимом выходном порте одного из регистров. Вклад последнего ребра в длину $inline$ само собой разумеется тоже больше, чем $∆_{mах}$ .

Мысленно пройдемся по пути $inline$ начиная с третьего ребра и заканчивая предпоследним.

Ребро $inline$ , если оно не последнее в $inline$ , согласно лемме 2 должно соединять какой-то из входных портов некоторого функционального блока с каким-то из выходных портов этого же блока. Обозначим упомянутый функциональный блок как $inline$ . Блок $inline$ не может быть блоком-константой (почему?). Если $inline$ – это блок прямого соответствия, то вес $inline$ равен 0, иначе вес $inline$ равен $∆_{mах}$ .

Ребро $inline$ , если оно не последнее и вообще в $inline$ имеется, соединяет служивший концом ребру $inline$ выходной порт блока $inline$ с некоторым “настоящим” портом входа. В любом случае вес этого ребра равен 0.

Ребро $inline$ , если оно не последнее и вообще в π имеется, согласно лемме 2 должно соединять какой-то из входных портов некоторого функционального блока с каким-то из выходных портов этого же блока. Обозначим упомянутый функциональный блок как $inline$ . Блок $inline$ не может быть блоком-константой (у констант нет настоящих портов входа, а в их мнимых портах входа не заканчивается ни одно ребро). Если $inline$ – это блок прямого соответствия, то вес $inline$ равен 0, иначе вес $inline$ равен $∆_{mах}$ .

Блок $inline$ непосредственно функционально влияет на блок $inline$ .
…
Продолжая следовать вдоль π до тех пор, пока не достигнем последнего ребра, мы обнаружим, что набираемая последовательность $inline$ — является цепочкой функционально-зависимых блоков и что его длина фрагмента π с третьего по предпоследнее ребро – есть количество не являющихся блоками прямого соответствия элементов этой цепочки, умноженному на $∆_{mах}$ . Вклад в длину π остальных ребер, как мы показали раньше, не превышает $2∆_{mах}$ . Из последнего немедленно следует неравенство $L(S_1 )≤∆_{mах}*(K(S_1 )+2)$ .

Почти дословно повторяя приведенные рассуждения можно показать (сделайте это), что
$L(S_2 )≥∆_{min}*K(S_2 )$ откуда утверждение теоремы уже следует тривиальным образом.

Tags:

Hubs: